Арифметика. Применение теории делимости к решению неопределенных уравнений
Курсовая работа
Арифметика. Применение
теории делимости к решению неопределенных уравнений
Введение
делимость уравнение арифметика
Решение различного вида уравнений является одной из
содержательных линий школьного курса математики, но при этом, методы решения
уравнений с несколькими неизвестными практически не рассматриваются. Вместе с
тем, решение уравнений от нескольких неизвестных в целых числах является одной
из древнейших математических задач. Большинство методов решения таких уравнений
основаны на теории делимости целых чисел, интерес к которой в настоящее время
определяется бурным развитием информационных технологий. В связи с этим,
учащимся будет небезынтересно познакомиться с методами решения некоторых
уравнений в целых числах, тем более что на олимпиадах разного уровня очень
часто предлагаются задания, предполагающие решение какого-либо уравнения в
целых числах.
Предлагаемый курс рассчитан в первую очередь на школьников
8-11 классов, обучающихся по естественно-математическому, экономическому и
общеобразовательному профилю. На первых занятиях предполагается рассмотреть
вопросы теории делимости целых чисел, которые используются при решении
уравнений в целых числах.
Цель курса развитие устойчивого познавательного интереса к
математике через знакомство учащихся с методами решения некоторых уравнений в
целых числах.
В результате освоения курса учащиеся должны знать и уметь:
· получить опыт самостоятельного решения
уравнений в целых числах, используя имеющиеся алгоритмы;
· на основе усвоенных теоретических знаний
творчески перерабатывать известные алгоритмы для решения задач с изменившимися
условиями.
Предлагаемая вниманию учащихся и учителей разработка,
является попыткой напомнить о существовании такого типа уравнений и некоторых
методах их решения.
Особенно стоит обратить внимание на использование алгоритма
Евклида для нахождения НОД, который почти не применяется в общеобразовательной
школе, особенно второй алгоритм, где используется остаток от деления, частное и
делимое.
На применение остатка от деления существует вообще немного
задач. Хотя его, так сказать, неофициальное использование не менее, чем
арифметических операций.
В работе рассматриваются неопределенные уравнения первой
степени с двумя неизвестными, т.е. уравнения вида aх + bу = c, где a, b - целые числа, отличные
от нуля, а с - произвольное целое число. Такие уравнения часто встречаются на
олимпиадах. Меня заинтересовало, когда впервые появились такие уравнения, кто и
каким способом решал эти уравнения, чем способы отличаются.
Цель: обобщение теоретического и исторического материала по
теме «Неопределенные уравнения первой степени».
Объект исследования: неопределенные уравнения первой степени.
Предмет исследования: методы решения неопределенного уравнения первой степени с
двумя неизвестными.
Гипотеза: неопределенные уравнения первой степени решаются
различными методами.
Проблема
решения уравнений в целых числах: от Диофанта до доказательства теоремы Ферма
Алгебраические уравнения или системы алгебраических уравнений
с целыми коэффициентами, имеющие число неизвестных, превосходящее число
уравнений, когда стоит задача найти целые или рациональные решения называются
диофантовыми (неопределенными).
Решение уравнений в целых числах является одной из древнейших
математических задач. Наибольшего расцвета эта область математики достигла в
Древней Греции. Основным источником, дошедшим до нашего времени, является
произведение Диофанта - «Арифметика». Диофант суммировал и расширил накопленный
до него опыт решения неопределенных уравнений в целых числах.
История сохранила нам мало черт биографии замечательного
александрийского ученого-алгебраиста Диофанта. По некоторым данным Диофант жил
до 364 года н.э. Достоверно известно лишь своеобразное жизнеописание Диофанта,
которое по преданию было высечено на его надгробии и представляло
задачу-головоломку:
«Бог ниспослал ему быть мальчиком шестую часть жизни; добавив
к сему двенадцатую часть, Он покрыл его щеки пушком; после седьмой части Он
зажег ему свет супружества и через пять лет после вступления в брак даровал ему
сына. Увы! Несчастный поздний ребенок, достигнув меры половины полной жизни
отца, он был унесен безжалостным роком. Через четыре года, утешая постигшее его
горе наукой о числах, он [Диофант] завершил свою жизнь» (попробуйте решить
задачу самостоятельно).
Эта головоломка служит примером тех задач, которые решал
Диофант. Он специализировался на решении задач в целых числах. Такие задачи в
настоящее время известны под названием диофантовых.
Наиболее известной, решенной Диофантом, является задача «о
разложении на два квадрата». Ее эквивалентом является известная всем теорема
Пифагора. Эта теорема была известна в Вавилонии, возможно ее знали и в Древнем
Египте, но впервые она была доказана, в пифагорейской школе. Так называлась
группа интересующихся математикой философов по имени основателя школы Пифагора
(ок. 580-500 г. до н.э.).
Жизнь и деятельность Диофанта протекала в Александрии, он
собирал и решал известные и придумывал новые задачи. Позднее он объединил их в
большом труде под названием «Арифметика». Из тринадцати книг, входивших в
состав «Арифметики», только шесть сохранились до Средних веков и стали
источником вдохновения для математиков эпохи Возрождения, в том числе и для
Пьера де Ферма.
Пьер де Ферма родился 20 августа 1601 года на юго-западе
Франции. Он не занимался профессионально математикой, но был одним из
величайших в истории математики «любителем».
Изучая задачи и решения Диофанта, Ферма черпал в них
вдохновение и занимался решением аналогичных и более интересных задач. Ферма
записывал для себя лишь самое необходимое для того, чтобы убедиться в
правильности полученного решения.
При чтении второй книги «Арифметики», Ферма наткнулся на
целую серию наблюдений, задач и решений, связанных с теоремой Пифагора и
пифагоровыми тройками. Например, Диофант рассматривал существование особых
троек, образующих так называемые «хромые треугольники», у которых две более
короткие стороны x и y отличаются по длине только на единицу (например, x = 20,
y = 21, z = 29 и 202 + 212 = 292).
Вместо уравнения Пифагора x2 + y2 = z2
Ферма занялся рассмотрением уравнения x3 + y3 = z3.
Он всего лишь изменил степень на единицу, но его новое уравнение не допускало
никаких решений в целых числах. Таким образом, незначительное изменение
превратило уравнение, допускающее бесконечно много решений в целых числах, в
уравнение, не имеющее ни одного решения в целых числах.
Ферма подверг уравнение Пифагора еще большему изменению,
попробовав заменить степень 2 на целые числа бульшие 3, и обнаружил, что найти
решение в целых числах каждого из этих уравнений очень трудно. И Ферма доказал,
что вообще не существует трех целых чисел x, y, z, которые удовлетворяли бы
уравнению
n + yn = zn, где n = 3, 4,
5,…
На полях «Арифметики» Диофанта, рядом с задачей 8, Ферма
оставил такое замечание: «Невозможно для куба быть записанным в виде суммы двух
кубов, или для четвертой степени быть записанной в виде суммы двух четвертых
степеней, или, в общем, для любого числа, которое есть степень больше двух,
быть записанной в виде суммы двух таких же степеней. Я нашел поистине
удивительное доказательство этого предложения, но поля здесь слишком узки для
того, чтобы вместить его». Это замечание Ферма сделал в1637 году.
За прошедшие столетия были доказаны все утверждения Ферма,
содержавшиеся в примечаниях на полях «Арифметики» Диофанта, и только Великая
теорема Ферма, до недавнего времени, упорно не поддавалась усилиям математиков.
Великая теорема Ферма обрела известность как самая трудная «головоломка»
математики. 358 лет многие великие математики (К.Г. Баше, Л. Эйлер, Дж. Валлис
Ж. Лагранж и др.) пытались доказать эту теорему, но только в конце 20 века в
1995 году она была доказана американскими математиками Э. Уайлсом и Р.
Тейлором.
В настоящее время проблема решения неопределенных уравнений в
целых числах хорошо разработана. Мы рассмотрим здесь некоторые методы решения
уравнений в целых числах и способы доказательства того, что уравнение не имеет
решений в целых числах. Многие из этих методов предполагают применение
некоторых понятий и алгоритмов теории делимости. В связи с этим, прежде чем
переходить непосредственно к методам решения неопределенных уравнений в целых
числах обратимся к основным понятиям и алгоритмам теории делимости целых чисел.
1. Признаки делимости
Признаки делимости на 10, 5 и 2
Признак делимости на 10: «На 10 делятся все те
натуральные числа, запись которых оканчивается цифрой 0; если запись числа
оканчивается любой другой цифрой, то число не делится на 10».
Другими словами, на 10 делятся те, и только те числа,
которые оканчиваются цифрой 0.
Признак делимости на 5: «На 5 делятся все те
натуральные числа, запись которых оканчивается цифрой 0 или цифрой 5; если
запись числа оканчивается любой другой цифрой, то число не делится на 5».
Другими словами, на 5 делятся те, и только те числа, которые
оканчиваются цифрой 0 или цифрой 5.
Признак делимости на 2: «На 2 делятся
те, и только те числа, которые оканчиваются четной цифрой, т.е. на 0, 2, 4, 6,
8».
Другими словами, на 2 делятся те, и только те числа,
которые оканчиваются четной цифрой.
Признак
делимости на 4 и на 25
На 4 (или на 25) делятся те, и только те числа, которые
оканчиваются двумя нулями или у которых две последние цифры образуют число,
делящееся на 4 (или на 25).
Признак
делимости на 8 и на 125
На 8 (или на 125) делятся те, и только те числа, которые
оканчиваются тремя нулями или у которых три последние цифры образуют число,
делящееся на 8 (или на 125).
Признак
делимости на 3 и на 9
На 3 (или на 9) делятся те, и только те числа, сумма цифр
которых делится на 3 (или на 9).
Признак
делимости на 7, 11 и 13
Если разность, полученная от вычитания числа, образованного
тремя последними цифрами данного числа, из числа, образованного всеми
остальными цифрами (или наоборот), равна 0 или делится на 7, или на 11, или на
13, то все данное число делится на 7, или на 11, или на 13.
2.
Теорема о делимости данного числа на произведение двух взаимно простых чисел
Если данное число делится на каждое из двух
взаимно простых чисел, то оно делится и на их произведение
На основании этой теоремы можно установить признак делимости
на число, которое может быть представлено в виде произведения двух взаимно
простых чисел.
1. Чтобы данное число делилось на 6, необходимо и
достаточно, чтобы оно делилось на 2 и на 3.
. Чтобы данное число делилось на 15, необходимо и
достаточно, чтобы оно делилось на 3 и на 5.
Аналогично можно установить признаки делимости на 18, на 22,
на 24 и т.д.
Пример 1.
Найдите все пятизначные числа вида 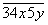 , каждое из которых делится на 36.
, каждое из которых делится на 36.
Решение
36 можно представить в виде произведения двух множителей, признаки
делимости, на каждый из которых известны. Так, 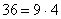 . Значит, на 36 будут делиться те, и только те числа, которые
одновременно делятся и на 9, и на 4.
. Значит, на 36 будут делиться те, и только те числа, которые
одновременно делятся и на 9, и на 4.
Признак делимости на 9: «На 9 делятся те и только те числа, сумма цифр которых делится
на 9. Если сумма цифр числа не делится на 9, тогда оно не делится на 9».
Признак делимости на 4: «На 4 делятся те, и только те числа, которые оканчиваются двумя
нулями или у которых две последние цифры образуют число, делящееся на 4».
Надо заметить, что значения цифр x и y могут быть следующие: 0, 1, 2, 3, 4, 5,
6, 7, 8, 9.
Сумма цифр данного числа равна: 3 + 4 + x + 5 + y = 12 + x + y.
Данное число не может оканчиваться двумя нулями, поскольку
предпоследняя цифра числа равна 5, значит, применим вторую часть признака
делимости на 4:»… две последние цифры должны выражать число, делящееся на 4.
Две последние цифры данного числа образуют двузначное число: 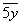 .
.
Оно делится на 4 только при двух значениях y: 2, 6.
При y = 2, сумма цифр числа станет равна: 12 + x + y = 12 + x + 2 = 14 + x.
Полученная сумма будет делится на 9 при одном значении x, равном 4 (тогда получим сумму 18). При всех других
значениях x эта сумма не делится на 9.
Находим первое число, удовлетворяющее условию задачи: 34452.
В самом деле, сумма цифр этого числа равна 18 - делится на 9,
последние две цифры образуют двузначное число 52, которое делится на 4,
наконец, проверим делением. При делении числа 34452 на 36 получим 957.
При y = 6, сумма цифр числа станет равна: 12 + x + y = 12 + x + 6 = 18 + x.
Эта сумма делится на 9 при следующих значениях x: 0 и 9.
Находим еще два числа, удовлетворяющие условию задачи: 34056 и 34956.
Проверка. При делении 34056 на 36 получим 946, а при делении 34956
получим 971.
Ответ:
34452, 34056, 34956.
Пример 2.
Найдите все пятизначные числа вида 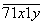 , каждое из которых делится на 45.
, каждое из которых делится на 45.
Чтобы число делилось на 45, необходимо и достаточно, чтобы
оно делилось на 9 и на 5.
Признак делимости на 9: «На 9 делятся те и
только те числа, сумма цифр которых делится на 9. Если сумма цифр числа не
делится на 9, тогда оно не делится на 9».
Признак делимости на 5: «На 5 делятся те и
только те числа, которые оканчиваются либо цифрой 0, либо цифрой 5».
Рассмотрим два случая
-й случай, когда число оканчивается цифрой 0, тогда y = 0.
Чтобы число делилось на 9, его сумма цифр, которая равна 7 +
1 + x
+ 1 + 0 = x
+ 9.
x может равняться либо 0, либо 9, чтобы полученная сумма
делилась на 9.
В результате получаем два искомых числа: 71010 и
71910.
2-й случай, когда число оканчивается цифрой 5, тогда y = 5.
Сумма цифр числа, в этом случае, равна: 7 + 1 + x + 1 + 5 = x + 14.
Чтобы сумма делилась на 9, x = 4.
Получим еще одно искомое число: 71415.
Ответ: 71010, 71910, 71415.
Пример 3.
Найдите все пятизначные числа вида 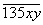 , каждое из которых делится на 45.
, каждое из которых делится на 45.
Решение
Чтобы число делилось на 45, необходимо и достаточно, чтобы
оно делилось на 9 и на 5.
Признак делимости на 9: «На 9 делятся те и
только те числа, сумма цифр которых делится на 9. Если сумма цифр числа не
делится на 9, тогда оно не делится на 9».
Признак делимости на 5: «На 5 делятся те и
только те числа, которые оканчиваются либо цифрой 0, либо цифрой 5».
Рассмотрим два случая
-й случай, когда число оканчивается цифрой 0, тогда y = 0.
Чтобы число делилось на 9, его сумма цифр, которая равна 1 +
3 + 5 + x
= x + 9.
x может равняться либо 0, либо 9, чтобы полученная сумма делилась
на 9.
В результате получаем два искомых числа: 13500 и
13590.
2-й случай, когда число оканчивается цифрой 5, тогда y = 5.
Сумма цифр числа, в этом случае, равна: 1 + 3 + 5 + x + 5 = x + 14.
Чтобы сумма делилась на 9, x = 4.
Получим еще одно искомое число: 13545.
Ответ: 13500, 13590, 13545.
Пример 4.
Найдите все пятизначные числа вида 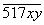 , каждое из которых делится на 6 и на 9.
, каждое из которых делится на 6 и на 9.
Решение
На 6 будут делится все те числа, которые делятся на 3 и на 2.
Признак делимости на 3: «На 3 делятся те и
только те числа, сумма цифр которых делится на 3».
Признак делимости на 2: «На 2 делятся те и
только те числа, которые оканчиваются четной цифрой или нулем, т.е. на 0, 2, 4,
6, 8».
Признак делимости на 9: «На 9 делятся те и
только те числа, сумма цифр которых делится на 9».
Таким образом, если число делится на 9, тогда оно и подавно
будет делится на 3.
Чтобы число делилось на 6 и на 9, необходимо и достаточно,
чтобы его сумма цифр делилась на 9 и оно оканчивалось четной цифрой.
Сумма цифр числа 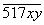 равна 5 + 1 + 7 + x + y = x + y + 13.
равна 5 + 1 + 7 + x + y = x + y + 13.
Рассмотрим несколько случаев:
1) если y = 0, тогда
сумма цифр равна x + 13 и она будет делиться на 9, если x будет равен 5, искомое число: 51750;
) если y = 2, тогда сумма цифр равна x + 15 и она будет делиться на 9, если x будет равен 3, искомое число: 51732;
) если y = 4, тогда сумма цифр равна x + 17 и она будет делиться на 9, если x будет равен 1, искомое число: 51714;
) если y = 6, тогда сумма цифр равна x + 19 и она будет делиться на 9, если x будет равен 8, искомое число: 51786;
) если y = 8, тогда сумма цифр равна x + 21 и она будет делиться на 9, если x будет равен 6, искомое число: 51768.
Ответ:
51750, 51732, 51714, 51786, 51768.
3. Деление. Деление с остатком
Определение деления
Разделить число a на число b - значит найти такое
новое число, на которое надо умножить b, чтобы получить a.
Отсюда вытекает следующее определение действия: делением
называется такое арифметическое действие, посредством которого по данному произведению
двух чисел и одному из них (известному множителю) находят другое число
(неизвестный множитель).
При делении данное произведение называется делимым,
данный сомножитель - делителем, а искомый сомножитель - частным.
Отсюда ясно, что деление есть действие, обратное умножению.
Деление числа a на число b можно записать двумя способами:
1) 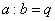 или 2)
или 2) 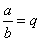 , причем каждое из этих равенств означает, что при делении числа a на число b в частном получается натуральное число q.
, причем каждое из этих равенств означает, что при делении числа a на число b в частном получается натуральное число q.
Деление с остатком
При требовании, чтобы частное было целым числом, деление
числа a на число b возможно не всегда.
Например, при нельзя разделить 23 на 4, потому что нет такого
целого числа, на которое можно было бы умножить 4 и получить произведение,
равное 23.
Но можно указать наибольшее целое число, при умножении
которого на 4, получается целое число наиболее близкое к 23. Таким числом
является 5. При умножении 5 на 4 получим 20.
Разность между делимым 23 и 20 равна 3 - называется остатком
от деления.
Само же деление в таких случаях называется делением с
остатком.
Случай, когда в частном получается целое число и никакого
остатка не будет, называется делением без остатка или делением нацело,
частное же называется полным частным или просто частным.
Если при делении числа a на число b получается неполное
частное q
и остаток r,
то записывается это так.
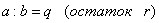 , или
, или 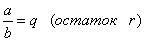 .
.
При делении с остатком неполным частным называется наибольшее
число, которое при умножении на делитель дает произведение, не превосходящее
делимое. Разность между делимым и этим произведением называется остатком.
Отсюда следует, что остаток при делении должен быть всегда
меньше делителя, так как если бы остаток был равен делителю или был бы
больше его, то частное тогда не было бы наибольшим из возможных чисел. Если
остаток вычесть из делимого, то полученная разность (a - r) разделится на данный делитель b без остатка, причем в частном по-прежнему получится число q.
По смыслу деления разность 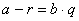 .
.
Отсюда: 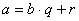 (по смыслу деления).
(по смыслу деления).
Последнее равенство показывает, что в случае деления с остатком
делимое равно делителю, умноженному на частное, плюс остаток.
Примечание.
В дальнейшем, выражение: одно число делится на другое без остатка (нацело)
- заменим выражением: одно число делится на другое.
Число a в этом
случае называется кратным числу b.
Общее определение деления натуральных чисел
В множестве натуральных чисел делению без остатка и делению с
остатком можно дать следующее определение:
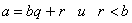 .
.
Из равенства 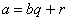 следует, что
следует, что
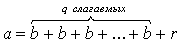 .
.
Так как r < b, то частное q показывает, какое наибольшее число раз делитель содержится в
делимом. Если делитель b не
равен нулю, то действие деление всегда возможно и всегда дает единственный
результат.
. Теорема о делении на данное число делимого,
делителя и остатка
. Если при делении с остатком делимое и делитель
делятся на какое-нибудь число, то и остаток делится на это же число.
. Если остаток при делении и делитель делятся на
какое-нибудь число, то и делимое делится на то же число.
Наибольший общий делитель нескольких чисел
Общим делителем данных чисел называется число, на
которое делятся все данные числа.
Наибольшим общим делителем данных чисел
называется наибольший из их общих делителей.
Наибольший общий делитель (N) чисел a, b, …, e обозначается символом
(a; b; …; e) = N.
Для сокращения вместо выражения «наибольший общий делитель»
часто пишут только начальные буквы этих слов НОД.
Пример: НОД (35; 25) = 5.
Взаимно
простые числа
Взаимно простыми числами называются те числа,
наибольший общий делитель которых есть единица.
Если НОД (a; b; c; …) = 1, то числа a, b, c, … - взаимно простые.
Если каждое из чисел a, b, c, … оказывается взаимно
простым с каждым другим из них, то числа a, b, c, … называются попарно
простыми. Очевидно, что в случае двух чисел понятия «взаимно простые» и
«попарно простые» совпадают.
Пример 1. Числа 29, 53, 100, 104 - взаимно простые, так
как, кроме 1, они не имеют никакого общего делителя НОД (29; 53; 100; 104) = 1.
Пример 2. Числа 24, 17, 11 не только взаимно простые, но
и попарно простые; действительно, НОД (24; 17) = НОД (24; 11) = НОД (17; 11) =
1.
5.
Теоремы, на которых основано нахождение наибольшего общего делителя
Случай,
когда два числа делятся одно на другое
Теорема. Если одно из двух данных чисел делится на
другое, то меньшее из них есть их наибольший общий делитель.
Случай,
когда два числа не делятся одно на другое
Теорема. Если большее из двух данных чисел не делится
на меньшее, то их наибольшим общим делителем будет наибольший общий делитель
меньшего числа и остатка от деления большего числа на меньшее.
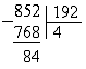
Даны числа: 8084 и 1504;
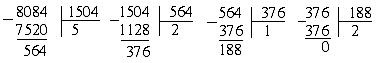
Если оба слагаемых делятся на 188, тол и сумма 8084 делится на это
же число. И это число есть наибольший общий делитель чисел 8084 и 1504. Если бы
эти числа имели общий делитель больший 188, то он был бы делителем и 564, а для
564 и 1504 делитель 188 является наибольшим: 8084: 188 = 43; 1504: 188 = 8.
Алгоритм
Евклида
Под алгоритмом будем понимать последовательность
правил, строго следуя которым можно решить ту или иную задачу.
Задача будет считаться решенной, если для ее решения
установлен определенный алгоритм.
Алгоритм Евклида служит для отыскания наибольшего общего
делителя двух чисел способом последовательного деления.
Пусть a и b - натуральные числа, причем a > b и a не делится на b.
Допустим, что:
1) 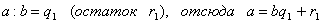 ,
,
) 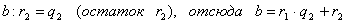 ,
,
) 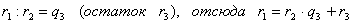 ,
,
) 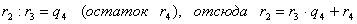 ,
,
…………………………………………………………………….
n) 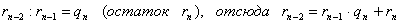 ,
,
n + 1) 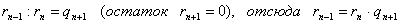 .
.
Ряд равенств:
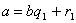 ,
, 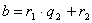 ,
,  ,
, 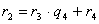 , …,
, …, 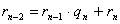 ,
, 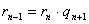 ,
,
выражающих зависимость между делимым, делителем, частным и
остатком при последовательном делении большего числа на меньшее, меньшего на
первый остаток, первого остатка на второй остаток и т.д., известен под
названием алгоритма Евклида.
Рассматриваемый ряд равенств конечен. В самом деле, по смыслу
деления ряд остатков (следовательно, и ряд делителей) 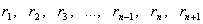 есть ряд убывающих целых чисел, который
обязательно должен закончиться некоторым остатком
есть ряд убывающих целых чисел, который
обязательно должен закончиться некоторым остатком 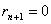 , вследствие того, что число возможных
остатков конечно, так как оно не может быть больше числа b. Итак, каковы бы ни были числа a и b, в результате
последовательного деления большего числа на меньшее, меньшего на первый
остаток, первого остатка на второй остаток и т.д., мы обязательно получим
некоторый остаток
, вследствие того, что число возможных
остатков конечно, так как оно не может быть больше числа b. Итак, каковы бы ни были числа a и b, в результате
последовательного деления большего числа на меньшее, меньшего на первый
остаток, первого остатка на второй остаток и т.д., мы обязательно получим
некоторый остаток 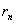 , на который предыдущий остаток
, на который предыдущий остаток 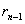 разделится без остатка, и, следовательно,
число
разделится без остатка, и, следовательно,
число 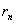 будет последним, не равным нулю остатком,
а значит, т последним делителем. Таким образом, возможность дальнейшего деления
отпадает.
будет последним, не равным нулю остатком,
а значит, т последним делителем. Таким образом, возможность дальнейшего деления
отпадает.
Правило для нахождения НОД двух чисел способом последовательного
деления.
Теорема. Чтобы найти НОД двух чисел способом последовательного
деления, надо большее из данных чисел разделить на меньшее, затем, меньшее - на
первый остаток, первый остаток - на второй, второй - на третий и т.д. до тех
пор, пока не получится в остатке 0. Тогда последний делитель (иначе, последний
не равный нулю остаток) будет наибольшим общим делителем данных чисел.
Евклид применял свой алгоритм не только в арифметике, но и в
геометрии для отыскания общей меры двух отрезков путем последовательного
наложения.
Основные
свойства НОД
Теорема 1. На всякое число, на которое делятся без
остатка два данных числа, делится и их наибольший общий делитель.
Пример. НОД (3540; 450) = 30. Кроме того, данные числа
3540 и 450 имеют общие делители 1. 2, 3, 5, 6, 10, 15.
Очевидно, что на каждый из этих общих делителей делится без
остатка НОД чисел 3540 и 450, т.е. число 30.
Теорема 2. Всякое число, на которое делится без остатка
наибольший общий делитель двух данных чисел, есть общий делитель этих чисел.
Пример. НОД (3540; 450) = 30. Делителями 30 являются
числа: 1. 2, 3, 5, 6, 10, 15. Очевидно, что на каждое из этих чисел делятся
3540 и 450.
Теорема 3. Если каждое из двух данных чисел a и b умножить на какое-либо
натуральное число m, то и наибольший общий делитель данных чисел
умножится на то же число m.
Пример. НОД
(558; 540) = 18. Умножив каждое из данных чисел на 2, будем иметь: НОД (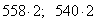 ) = 36.
) = 36.
Теорема 4. Если каждое из двух данных чисел a и b разделить на один из общих делителей этих чисел, то и их
наибольший общий делитель разделится на это число.
Пример. НОД
(864; 192) = 96. Разделив каждое из данных чисел 864 и 192 на один из их общих
делителей, например на 32, получим:
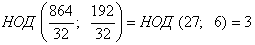 .
.
Следовательно, НОД данных чисел уменьшится в 32 раза.
Следствие.
На основании последней теоремы при нахождении НОД можно сделать упрощения в тех
случаях, когда сразу видны общие делители данных чисел. В этом случае данные
числа следует разделить на общий делитель и найти НОД полученных частных, затем
найденный НОД частных следует умножить на то число, на которое вначале
разделили данные числа. Полученное произведение и будет НОД данных чисел.
Пример.
Пусть требуется найти НОД чисел 7200 и 8400. Сначала разделим данные числа на
100, от этого НОД чисел 7200 и 8400 уменьшится в 100 раз. Потом найдем НОД
частных 72 и 84, который будет равен 12. Наконец, 12 умножим на 100, получим
1200. Значит НОД (7200; 8400) = 1200.
Теорема
о частных, полученных от деления данных чисел на их НОД
Если данные числа разделить на их НОД, то
полученные частные будут числа взаимно простые.
Если НОД (a; b; c; …; l) = m, тогда 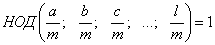 .
.
Пример. НОД
(108; 60) = 12. 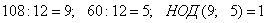 . Следовательно, 9 и 5 числа взаимно
простые числа.
. Следовательно, 9 и 5 числа взаимно
простые числа.
Теорема
о делимости произведения двух чисел на число, взаимно простое с одним из
сомножителей
Если произведение двух сомножителей делится без
остатка на какое-либо число, взаимно простое с одним из сомножителей, то другой
сомножитель делится на это число.
Если ab = p; p делится на c, НОД (a; c) = 1, тогда b делится на c.
Пример. 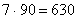 . Произведение двух сомножителей делится
на 15; один из сомножителей - 7 - взаимно простое с 15, НОД (7; 15) = 1.
Следовательно, по теореме, второй сомножитель должен делиться на 15.
Действительно, 90: 15 = 6.
. Произведение двух сомножителей делится
на 15; один из сомножителей - 7 - взаимно простое с 15, НОД (7; 15) = 1.
Следовательно, по теореме, второй сомножитель должен делиться на 15.
Действительно, 90: 15 = 6.
6.
Применение теории делимости к решению неопределенных уравнений в целых числах
Определение. Неопределенные уравнения - уравнения,
содержащие более одного неизвестного
Под одним решением неопределенного уравнения
понимается совокупность значений неизвестных, которая обращает данное уравнение
в верное равенство.
Пример 1.
Решить в целых числах уравнение 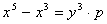 , где y и p - простые числа.
, где y и p - простые числа.
Решение
Преобразуем уравнение 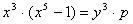 . Если имеются целые решения этого уравнения, тогда
. Если имеются целые решения этого уравнения, тогда 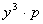 делится на
делится на 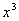 , так как НОД (x3, x2 - 1) =
1, но y3 и p являются взаимно простыми числами, т.е.
, так как НОД (x3, x2 - 1) =
1, но y3 и p являются взаимно простыми числами, т.е. 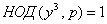 , значит, p не делится на x3, следовательно, y3 делится
на x3, что возможно, если x = y, т.е. x - простое
число. Тогда
, значит, p не делится на x3, следовательно, y3 делится
на x3, что возможно, если x = y, т.е. x - простое
число. Тогда 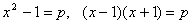 , что возможно, если
, что возможно, если 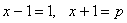 , т.е. x = 2, y = 2, p = 3.
, т.е. x = 2, y = 2, p = 3.
Ответ: x = 2, y = 2, p = 3.
Пример 2.
Найти целые решения уравнения 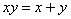 .
.
Преобразуем уравнение 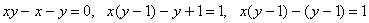 ,
,
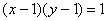 . Произведение целых чисел будет равно 1 в двух случаях, когда
каждый из сомножителей равен 1, и когда каждый из сомножителей равен -1.
. Произведение целых чисел будет равно 1 в двух случаях, когда
каждый из сомножителей равен 1, и когда каждый из сомножителей равен -1.
Получим совокупность двух систем уравнений:
(1) 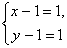 и (2)
и (2) 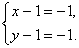
Решим каждую систему уравнений:
(1)  (2)
(2) 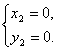
Ответ: 
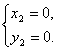
Пример 3.
Найти все целые решения уравнения: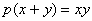 , где p - простое число.
, где p - простое число.
Решение
Преобразуем уравнение:
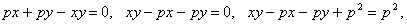
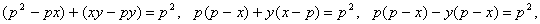
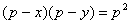 .
.
Произведение двух множителей равно целому числу 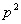 . Очевидно, что каждый из множителей
должен быть числом целым, следовательно, получим системы уравнений, которые
представляют всевозможные случаи, когда множители целые и их произведение равно
. Очевидно, что каждый из множителей
должен быть числом целым, следовательно, получим системы уравнений, которые
представляют всевозможные случаи, когда множители целые и их произведение равно
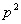 ,
,
(1) 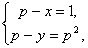 (2)
(2) 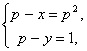 (3)
(3) 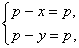 (4)
(4) 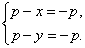
В результате решения систем, получаем:
(1) 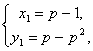 (2)
(2) 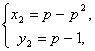 (3)
(3) 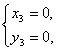 (4)
(4) 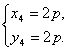
Ответ: 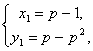
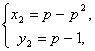
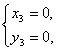
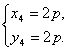
Пример 4.
Найти все целые решения уравнения: 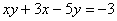 .
.
Решение
Преобразуем уравнение: 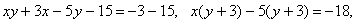
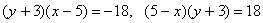 .
.
Произведение двух целых сомножителей равно 18. Чтобы выяснить,
каким числам могут быть равны эти сомножители, найдем все делители числа 18:
имеет делители: 1, 2, 3, 6, 9, 18. Если первый множитель равен
первому из делителей 18, тогда второй множитель будет равен последнему -
получим шесть пар решений:
(1) 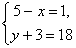 (2)
(2) 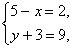 (3)
(3) 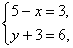
(4) 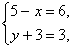 (5)
(5) 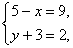 (6)
(6) 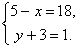
(1) 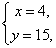 (2)
(2) 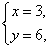 (3)
(3) 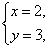 (4)
(4) 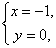 (5)
(5) 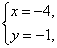 (6)
(6) 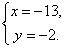
Ответ: 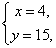
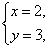
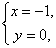
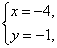
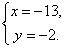
Пример 5.
Найти натуральные значения корней уравнения
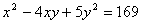 .
.
Решение
Преобразуем уравнение: 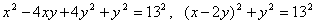 .
.
Отсюда получаем четыре системы уравнений:
(1) 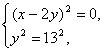 (2)
(2) 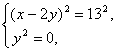 (3)
(3) 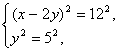 (4)
(4) 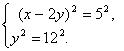
Поскольку x и y - натуральные числа, находим:
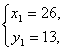
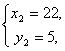
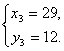
Ответ: 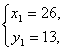
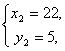
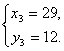
7. Уравнения вида ax + by = c, где a, b, c - целые числа, отличные от нуля
Теорема 1. Если
НОД (a; b) = d, то
существуют такие целые числа x
и y, что имеет место равенство 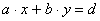 .
.
(Это равенство называется линейной комбинацией или линейным
представлением наибольшего общего делителя двух чисел через сами эти
числа.)
Пример.
Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.
Решение
1) Применим алгоритм Евклида и найдем НОД (1232, 1672):
НОД (1232, 1672) = 88.
) Выразим 88 последовательно через неполные частные и
остатки, используя полученные равенства, начиная с конца:
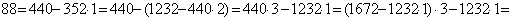
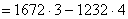 , т.е.
, т.е. 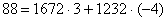 .
.
Теорема 2.
Если в уравнении ax + by = l (a, b) = 1, то уравнение имеет по крайней мере
одно целое решение.
Справедливость этой теоремы следует из теоремы 1. Таким образом,
чтобы найти одно целое решение уравнения ах + by = 1, если (а, b) = 1,
достаточно представить число 1 в виде линейной комбинации чисел а и b.
Пример.
Найти целое решение уравнения 15x + 37y = 1.
Решение
1) Применим алгоритм Евклида и найдем НОД (15, 37):
НОД (15, 37) = 1
) Выразим 1 последовательно через неполные частные и остатки,
используя полученные равенства, начиная с конца:
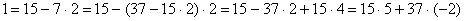 , т.е.
, т.е.
x0 = 5, y0 = -2.
Теорема 3.
Если в уравнении ах + by = с (а, b) = d > 1 и с не делится на d, то
уравнение целых решений не имеет.
Для доказательства теоремы достаточно предположить противное.
Пример.
Найти целое решение уравнения 16x - 34y = 7.
Решение
(16, 34) = 2, 7 не делится на 2, уравнение целых решений не
имеет.
Теорема 4. Если в уравнении ах + by = с (a, b) = d > 1
и c делится на d, то оно равносильно
уравнению а1х + b1у = c1, в котором (a1,
b1) = 1.
При доказательстве теоремы следует показать, что произвольное
целое решение первого уравнения является также решением второго уравнения и
обратно.
Теорема 5. Если в уравнении ах + by = с (а, b) = 1, то все
целые решения этого уравнения заключены в формулах:
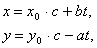
где x0, y0 - целое решение уравнения ах + by
= 1, t - любое целое число.
При доказательстве теоремы следует показать, во-первых, что
приведенные формулы действительно дают решения данного уравнения и, во-вторых,
что произвольное целое решение этого уравнения заключено в приведенных
формулах.
Приведенные теоремы позволяют установить следующее правило решения
в целых числах уравнения ах + by = с, где (а, b) = 1:
) находится целое решение уравнения ах + by = 1 путем
представления 1 как линейной комбинации чисел а и b (существуют и другие
способы отыскания целых решений этого уравнения, например при использовании
цепных дробей);
2)
составляется общая формула целых решений данного уравнения:
где x0, y0 - целое решение уравнения ах + by
= 1, t-любое целое число.
Придавая t определенные целые значения, можно получить частные
решения данного уравнения: наименьшие по абсолютной величине, наименьшие
положительные (если можно) и т.д.
Пример 1.
Найти целые решения уравнения 407х - 2816у = 33.
Решение
) Упрощаем данное уравнение, приводя его к виду 37х - 256у =
3.
2) Решаем уравнение 37x - 256y = 1.
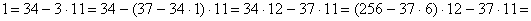
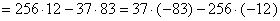 .
.
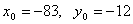 .
.
) Найдем решения данного уравнения по формулам: 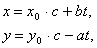
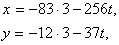
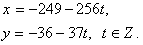
Ответ: 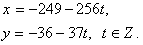
Пример 2.
Найти наибольшее трехзначное число, которое при делении на 17 дает остаток 9, а
при делении на 22 дает остаток 4.
Решение
Пусть частное от деления трехзначного числа на 17 равно x, тогда искомое число равно: 17x + 9, причем 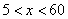 . Так как при
. Так как при 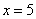 получаем двузначное число, а при x = 6 - уже трехзначное; при x = 60 получим четырехзначное число, а при x = 59 будет число трехзначное.
получаем двузначное число, а при x = 6 - уже трехзначное; при x = 60 получим четырехзначное число, а при x = 59 будет число трехзначное.
Пусть частное от деления трехзначного числа на 22 равно y, тогда искомое число равно: 22y + 4, причем 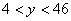 . Этот промежуток устанавливаем аналогично
промежутку для значений x.
. Этот промежуток устанавливаем аналогично
промежутку для значений x.
По условию: 17x + 9 = 22y + 4, 22y - 17x = 5 - это неопределенное уравнение.
) Решим уравнение: -17x + 22y = 1.
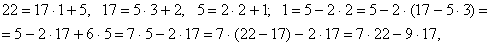
значит,
) Общий вид всех целых решений данного уравнения:
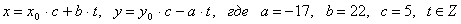 .
.
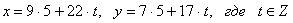 .
.
Положим 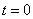 , тогда
, тогда 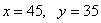 , если t = 1, тогда x = 67, y = 52 - эти значения уже выходят за
пределы промежутков
, если t = 1, тогда x = 67, y = 52 - эти значения уже выходят за
пределы промежутков 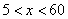 и
и 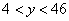 .
.
Поскольку требуется найти наибольшее трехзначное число, то
удовлетворять условию задачи будут значения 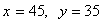 .
.
Искомое трехзначное число будет равно:
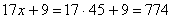 или
или 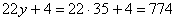 .
.
Ответ: 774.
Заключение
Методы решения неопределенных уравнений первой степени
складывались веками. Именно Диофант положил начало всему этому большому
математическому разделу, в чем его огромнейшая заслуга. Окончательный итог был
подведен уже в Средние века.
В ходе работы мы получили ответ на вопрос о разрешимости
неопределенных уравнений первой степени в целых числах; научились решать такие
уравнения с помощью алгоритма Евклида; решили задачу, математической моделью
которой является данное уравнение; решили в целых числах разными методами
неопределенное уравнение первой степени; создали буклет «Методы решения
неопределенных уравнений первой степени». Проведенное нами исследование методов
решения неопределенных уравнений первой степени позволяет нам сделать следующие
выводы:
во всех методах, которые мы рассмотрели используются свойства
делимости чисел;
зная одно частное решение уравнения, можно найти общее
решение уравнения;
теория неопределенного уравнения первой степени с двумя
переменными была завершена в XVII.
Библиография
1. А.А. Бухштаб. Теория чисел. - М.:
Государственное учебно-педагогическое издательство министерства просвещения
РСФСР, 1960.
. Ю.В. Матисеевич. Десятая проблема Гильберта. -
М.: «Физматлит», 1973 г.
. Ю. Соловьев. Неопределенные уравнения первой
степени: Квант, 1992 г.
. А.О. Гельфонд. Решение уравнений в целых
числах. Популярные лекции по математике, - М.: «Гостехиздат», 1957 г.
. Е.Л. Литвер. Теория чисел. - М.:МГУ, 1966 г.
. К.Ф. Гаусс. Труды по теории чисел. - М, 1959 г.