Функции и принципы работы математического сопроцессора

Функции и принципы работы математического сопроцессора

Введение

Математический сопроцессор - сопроцессор для расширения командного множества центрального процессора и обеспечивающий его функциональностью модуля операций с плавающей запятой, для процессоров, не имеющих интегрированного модуля.

Целью дипломной работы являются изучение темы:

- изучение функций и принципа работы математического сопроцессора.

Для достижения этой цели необходимо решить ряд задач, а именно:

изучить основные понятия математического сопроцессора;

изучить принцип работы математического сопроцессора;

изучить функции математического сопроцессора;

- рассчитать себестоимость рабочего места и экономическую эффективность;

- углубить знания, полученные в ходе теоретических и практических занятий.

Математический сопроцессор выполняют операции с плавающей запятой, которые потребовали бы больших затрат машинного времени от основного процессора. Выигрыш можно получить только при выполнении программ, написанных с расчетом на использование сопроцессора. Сопроцессоры выполняют такие сложные операции как точное деление, вычисление тригонометрических функций, извлечение квадратного корня и нахождение логарифма в 10-100 раз быстрее основного процессора. Точность результатов при этом значительно выше той, которая обеспечивается вычислителями, входящими в состав самих процессоров. Операции сложения, вычитания и умножения выполняются основным процессором и не передаются сопроцессору.

математический сопроцессор деление тригонометрический

1. Общая часть

.1 История математических сопроцессоров

С учетом того, что большинство современных приложений и игр требуют огромного количества вычислений именно над вещественными числами (числа с плавающей точкой), то общая производительность процессора зависит от того, насколько быстро он их обрабатывает. Для этих целей в процессоре существует специальный модуль, получивший название Floating-Point Unit (FPU) - модуль вычислений с плавающей точкой. В то же время производительность этого модуля зависит не только от рабочей частоты процессора, но и от его конструктивных особенностей.

В начале эволюции IBM-совместимых компьютеров вычисления над вещественными числами брал на себя математический сопроцессор, конструктивно выполненный отдельно от центрального процессора. Однако уже в 486-м процессоре Intel применила встроенный модуль вычислений с плавающей точкой, значительно увеличив при этом скорость работы процессора с вещественными числами. Впоследствии на встроенный FPU перешли и другие производители процессоров для персональных компьютеров.

При работе с вещественными числами существует тот же нюанс, что и в целочисленных операциях - команда не может быть выполнена за один такт ядра процессора. И если в 486-х процессорах для обработки целочисленных команд уже начал использоваться пятиступенчатый конвейер, то FPU был по-прежнему не конвейерного типа, т.е. следующая команда с плавающей точкой всегда должна была дожидаться выполнения предыдущей. Это существенно тормозило работу процессора с мультимедийными приложениями. А последние в то время уже начали стремительно набирать обороты в своих "запросах". Поэтому вполне естественно, что Intel, начиная с процессоров Pentium, стала применять конвейер не только в целочисленных, но и в вещественных операциях. Корпорация AMD, в свою очередь, пошла по несколько иному пути - вместо конвейеризации FPU она начала внедрять в свою продукцию технологию 3DNow, которая также была направлена на повышение производительности в операциях с вещественными числами. Эта технология столкнулась с множеством проблем в своей реализации. Думаю, многие помнят, как AMD K6-2, призванный конкурировать с Pentium II в целочисленных операциях, на процентов тридцать отставал от него в обработке вещественных чисел.

В Athlon'ах и последующих процессорах корпорация AMD перешла на конвейерный тип FPU. Более того, в новых процессорах AMD применила в модуле вычислений с плавающей точкой не только супер конвейеризацию, но и суперскалярность - в одном процессоре стало располагаться, грубо говоря, три модуля FPU, каждый из которых принимает участие в вычислениях с плавающей точкой. Другими словами, с выходом процессоров Athlon/Duron продукция AMD перестала уступать в скорости вычислений над вещественными числами своему конкуренту - корпорации Intel. А это сыграло очень существенную роль в расстановке сил этих извечных соперников на современном процессорном рынке.(Floating Point Unit) используется для ускорения и упрощения вычислений с плавающей точкой.

Сопроцессор (другое название FPU) ориентирован на математические вычисления - в нем отсутствуют операции с битами, зато расширен набор математических функций: тригонометрические, логарифм и т.д.

До некоторых моделей 80486 FPU исполнялся в виде отдельной микросхемы, устанавливаемой опционально. В некоторых 486 и во всех Pentium (и выше), FPU интегрирован в процессор, поэтому можно считать, что он присутствует в каждом более-менее современном компьютере. Начиная с Pentium Pro FPU имеет дополнительные команды, упрощающие сравнение чисел. В любом случае, если FPU недоступен, или не поддерживает какие-либо ф-ции, то возможна их программная эмуляция.

Несмотря на объемность данной главы, использовать FPU очень просто, что видно из примера. Но нужно понимать особенности работы сопроцессора, чтобы избежать теоретических ошибок.

Первым математическим сопроцессором для персонального компьютера IBM стал i8087 производства Intell, который появился в 1980 году. Со временем, помимо чисто Intell-x сопроцессоров, появились сопроцессор и ряда других фирм. CYRIX предлагал один из самых быстрых сопроцессоров, основанных на классической архитектуре. Причем гарантировалась полная совместимость с сопроцессорами Intell. Производительность этой микросхемы несколько выше потому, что все критичные по времени выполнения операции реализованы в данной микросхеме с использованием жесткой логики (аппаратный умножитель, отдельное арифметико-логическое устройство для вычисления мантиссы и т.д.). Повышение производительности особенно заметно при вычислении квадратного корня или тригонометрических функций. Он еще и точнее Intell-го.была основана в 1981 году несколькими инженерами, покинувшими Intell. Выполнение простых операций с одинарной точностью на сопроцессоре Weitek происходит менее чем за 200 нс., тогда как сопроцессор, использующий классическую архитектуру, выполняет подобные операции за 1.5 с. Обращение к сопроцессору происходит как бы через ОЗУ. Таким образом, загрузив операнды в область памяти, соответствующей сопроцессору, следующей командой можно уже считывать результат. Применение сопроцессора Weitek имеет смысл только тогда, когда он поддерживается программным обеспечением. В связи с этим сопроцессор Weitek находит достаточно ограниченное применение.

Линейка математических сопроцессоров, выпускаемых компанией Intel для повышения скорости и точности выполнения операций с плавающей запятой. Сопроцессоры имели схожую архитектуру с сопроцессорами Intel 8087, но не были совместимы по разъемам и работали асинхронно с центральным процессором.

Использование математического сопроцессора значительно повышало скорость выполнения программ, особенно, содержащих большое количество операций с плавающей точкой.

Они предназначались для линейки процессоров 80286, также некоторые сопроцессоры использовались с процессорами Intel 80386. Более того, до 1987 года, пока не были выпущены математические сопроцессоры Intel 80387, это были единственные сопроцессоры, способные работать с процессорами Intel 80386. Они могли использоваться даже с процессорами Cyrix Cx486SLC, но после выхода сопроцессоров Intel 80387 его использование стало предпочтительнее, так как он выигрывал у Intel 80287 по всем показателям.

В зависимости от модификации, сопроцессоры работали на тактовой частоте - от 5 до 20 МГц. На рис.1 показан математический сопроцессор Intel 80387.

Рис.1 Математический сопроцессор Intel 80387

Линейка математических сопроцессоров, производимых компанией Intel с 1987 года. Сопроцессоры значительно расширяли возможности процессоров 80386 по обработке чисел с плавающей запятой, предоставляя более 50 новых инструкций, и соответствовали требованиям стандарта IEEE 754-1985.

Для процессоров 80386SX разрабатывалась своя серия модификаций сопроцессоров 80387 с индексом SX, так как процессоры 80386SX имели 16-разрядную внешнюю шину данных.

Сопроцессоры 80387 работали на той же частоте, что и процессоры 80386, и поддерживали тактовые частоты - 16, 20, 25 и 33 МГц. Эта линейка сопроцессоров была быстрее сопроцессоров 80287, и программы, разработанные для сопроцессоров 80287, были совместимы с новыми версиями сопроцессоров, так что они быстро вытеснили своих предшественников.

Компания Intel несколько запоздала с выпуском математического сопроцессора, поэтому часто с процессорами 80386 использовались математические сопроцессоры 80287.

Производительность такой связки была значительно меньше возможностей, достигнутых впоследствии связкой 386-ой процессор-387-ой сопроцессор, но на тот момент особого выбора не было. На рис.2 показан математический сопроцессор Intel80387.

Рис.2 Математический сопроцессор Intel80387

Линейка математических сопроцессоров, выпускаемых компанией Intel с сентября 1991 года. На рис.3 показан математический сопроцессор Intel 80487.

Рис.3 математический сопроцессор Intel80487

Использовались совместно с процессорами Intel 486 SX для ускорения обработки операций с вещественными числами.

На самом деле, сопроцессор 80487 был больше, чем сопроцессор. Он представлял собой полноценный процессор Intel 486 DX с несколько измененной распиновкой.

.2 Математический сопроцессор

Математический сопроцессор - сопроцессор для расширения командного множества центрального процессора и обеспечивающий его функциональностью модуля операций с плавающей запятой, для процессоров, не имеющих интегрированного модуля. На рис. 4 показан математической сопроцессор на материнской плате.

Рис.1.Математический сопроцессор

Несмотря на то, что практически все процессоры, начиная с 486-го, оснащены встроенным сопроцессором, их быстродействие может изменяться. Исторически сложилось так, что сопроцессоры производства Intel работают быстрее, чем сопроцессоры AMD и Cyrix, однако в последнее время ситуация начинает изменяться.

Модуль операций с плавающей запятой (или с плавающей точкой) - часть процессора для выполнения широкого спектра математических операций над вещественными числами.

Простым целочисленным процессорам для работы с вещественными числами и математическими операциями требуются соответствующие процедуры поддержки и время для их выполнения. Модуль операций с плавающей запятой поддерживает работу с ними на уровне примитивов - загрузка, выгрузка вещественного числа (из специализированных регистров) или математическая операция над ними выполняется одной командой, за счёт этого достигается значительное ускорение таких операций.

Математические сопроцессоры называют ещё процессорами с плавающей запятой, потому что они особенно ярко проявляют свои возможности в этой области математики. Числа с плавающей запятой часто используются в научных расчетах и представляются, как правило, мантиссой и ординатой. Преимущество, получаемое от установки математического сопроцессора, зависит от того какие задачи решаются на компьютере. Согласно утверждению Intel сопроцессор может уменьшить время выполнения математических операций, таких как умножение, деление, возведение в степень на 80% и более. Скорость выполнения простых операций, таких как сложение и вычитание практически не уменьшается.

Конструктивно заложенные в микропроцессор сигналы, позволяют передавать работу сопроцессору и затем получать результаты обработки.

Чтобы использовать арифметический сопроцессор, находящийся в составе компьютера, необходимы программы, которые могут выдавать специальные коды, необходимые для запуска сопроцессора.

Микропроцессоры 8088, 80286, 80386 сконструированы так, что они позволяют использовать арифметические сопроцессоры 8087, 80287, 80387 фирмы "Intel"-соответственно. Более поздние модели микропроцессоров имеют встроенные сопроцессоры.

С практической точки зрения, производительность системы, касающейся подготовки текстов и ведения базы данных - функций, не требующих сложных математических расчётов, не может быть улучшена математическим сопроцессором. Сопроцессор и главный микропроцессор могут работать на разных тактовых частотах (от собственных тактовых генераторов).

Выполняемая программа должна сама определять наличие сопроцессора и после этого использовать написанные для него инструкции; в противном случае сопроцессор только потребляет ток и ничего не делает. Большинство современных программ, рассчитанных на применение сопроцессоров, обнаруживают его присутствие и используют предоставляемые возможности. Наиболее эффективно сопроцессоры используются в программах со сложными математическими расчетами: в электронных таблицах, базах данных, статистических программах и системах автоматизированного проектирования. В то же время при работе с текстовыми редакторами сопроцессор совершенно не используется.

Простым "целочисленным" процессорам для работы с вещественными числами и математическими операциями требуются соответствующие процедуры поддержки и время для их выполнения. Модуль операций с плавающей запятой поддерживает работу с ними на уровне примитивов - загрузка, выгрузка вещественного числа (из специализированных регистров) или математическая операция над ними выполняется одной командой, за счёт этого достигается значительное ускорение таких операций. Внутри FPU числа хранятся в 80-битном формате с плавающей запятой, для записи же или чтения из памяти могут использоваться:

вещественные числа в трёх форматах: коротком (32 бита), длинном (64 бита) и расширенном (80 бит).

двоичные целые числа в трёх форматах: 16, 32 и 64 бита.

упакованные целые десятичные числа (BCD) числа - длина максимального числа составляет 18 упакованных десятичных цифр (72 бита).также поддерживает специальные численные значения:

деморализованные вещественные числа - числа, которые меньше минимального нормализованного числа. При формировании такого значения в некотором регистре стека в соответствующем этому регистру теге регистра TWR формируется специальное значение (10);

бесконечность (положительная и отрицательная), возникает при делении на нуль ненулевого значения, а также при переполнениях. При формированиитакого значения в некотором регистре стека в соответствующем этому регистру теге регистра TWR формируется специальное значение (10).

-нечисло <#"725387.files/image005.gif">

Рис. 5

Как правило, в качестве FPU использовался сопроцессор 68881 16 МГц или 68882 25 МГц. Практически любой современный процессор имеет встроенный сопроцессор.

Компания Weitek также выпускала математические сопроцессоры для платформ 68000 и MIPS.

1.7 Устройство FPU

Все процессоры Intel <#"725387.files/image006.gif">

Рис. 7 Отверстия выводов

Рис. 8. Панель для сопроцессора 80387SX

Вставить арифметический сопроцессор в панель. Обратить внимание, что первый вывод микросхемы сопроцессора должен вставляться в первый вывод панельки. Первый вывод на микросхеме сопроцессора и на панели может выделяться маленькой точкой, стрелкой, треугольником. Иногда первый вывод обозначается закругленным (спиленным) углом на корпусе сопроцессора и панели.

У микросхемы 80387DX только два ряда выводов. Вставить ее в центр панельки, так чтобы внешний ряд отверстий на панельке остался свободным. На рис.8 показан внешний вид сопроцессора, установленного в панель.

Неиспользованные выводы предназначены для установки других моделей сопроцессоров, которые имеют большее количество выводов, чем 80387DX. В качестве такого сопроцессора может быть использован, например, Weitek 3167.

Перед тем как вставлять сопроцессор в панель, нужно проверить все его выводы. Если они искривились, аккуратно выпрямите их.

Для большинства компьютеров, после установки сопроцессора необходимо соответствующим образом установить переключатели на системной плате и поменять конфигурацию, записанную в CMOS-памяти. Более подробную информацию можно узнать из документации на системную плату.

Собрать компьютер, закрыть корпус системного блока и включить питание. Теперь проверить работу арифметического сопроцессора. Воспользуйтесь для этого программой CheckIt.

.2 Принцип работы математического сопроцессора

При выполнении сложных математических расчетов в формате с плавающей точкой, математический сопроцессор работает во многом, как и простой процессор. Используя цифровую логику, он обрабатывает информацию, представленную множеством битов (в формате с плавающей точкой), и делает это по программе, представленной другим множеством битов, составляющим инструкции. Эти операции выполняются внутри специальной внутренней памяти сопроцессора.

Для вычислений сопроцессор первоначально загружает одно число в один регистр, а второе число - во второй регистр. Затем он читает программную команду, говорящую, какую операцию нужно выполнить над этими двумя числами. Эта команда запускает другую миниатюрную программу, выполняемую внутри чипа сопроцессора. Данная программа и заставляет его найти искомый результат. Множество внутренних команд сопроцессора, предназначенных для выполнения различных операций, понятных сопроцессору, называется его микрокодом (как это имеет место и для простого процессора).

Когда результат получен, его выдача говорит о готовности сопроцессора выполнить следующую программу, которая может приказать ему сделать что-либо с полученным на предыдущем шаге результатом.

Обычный процессор работает аналогично: загружает значения, читает команды и выполняет микрокоманды. Сопроцессор имеет преимущества перед общецелевым процессором при работе в формате с плавающей точкой, потому что его командное множество включает математические операции высокого уровня и потому, что его внутренние цепи более настроены на выполнение таких операций. Например, простой процессор может найти иррациональный корень, но ему придется работать в цикле сотен простых команд, выполнить сотни интеграции в области Эвклидовой математики, чтобы найти ответ. Сопроцессор решает эту задачу одной инструкцией. Они проектируются с учетом области применения. Сопроцессор подключается к системной шине, параллельно с центральным процессором, и может работать только с ним.

Сопроцессор не имеет индивидуальной программы, и не может самостоятельно инициировать выборку команды из памяти. Команды сопроцессора записаны вместе с командами центрального процессора и хранятся в памяти. Выборку команды осуществляет только центральный процессор, а команда попадает в оба процессора, но каждый из них выполняет только свои команды. Если выбранная команда оказывается командой центрального процессора, то он выполняет ее обычным образом, если сопроцессор не привлекается. Он игнорирует их. Если выбранная команда - это команда сопроцессора, то действие центрального процессора зависит от специфики команды.

Если команда не связана с обращением к памяти, то центральный процессор игнорирует и переходит к выполнению следующей. Но если команда требует обращение к памяти за операндом, то центральный процессор вычисляет физический адрес операнда и обращается к памяти. При этом сопроцессор перехватывает с общей шины адрес операнда, а в операции со считыванием данных и данные. После этого сопроцессор выполняет команду.

Команды могут выполняться параллельно с центральным процессором. Обычно команда сопроцессора выполняется большее количество времени, чем центральный процессор. И для него операции загрузки и сохранения могут быть довольно сложны, так как он работает с преобразованием чисел из формата в формат. Таким образом, во время работы сопроцессора центральный процессор может простаивать, что не неэффективно.

Для вычислений сопроцессор первоначально загружает одно число в один регистр, а второе число - во второй регистр. Затем он читает программную команду, говорящую, какую операцию нужно выполнить над этими двумя числами. Эта команда запускает другую миниатюрную программу, выполняемую внутри чипа сопроцессора. Данная программа и заставляет его найти искомый результат. Множество внутренних команд сопроцессора, предназначенных для выполнения различных операций, понятных сопроцессору, называется его микрокодом (как это имеет место и для простого процессора).

Синхронизация по командам при работе арифметического сопроцессора.

Когда центральный процессор выбирает для выполнения команду сопроцессора, тот может быть занят операциями по выполнению предыдущих команд, и не может выполнять выбранную. Центральный процессор не может пропускать в сопроцессор команды быстрее, чем тот ее выполняет, следовательно, перед каждой командой сопроцессора находится спец. команда центрального процессора, которая проверяет текущие состояние сопроцессора, и если он занят переводит центральный процессор в состояние ожидания.

Синхронизация по данным при работе арифметического сопроцессора.

Если выполняемая сопроцессором команда записывает операнд в ячейку памяти перед последующей командой центрального процессора, которая использует ее, тогда тоже нужна аналогичная команда проверки состояния сопроцессора.

Если сопроцессор не успел записать данные в ячейку, которую будет использовать следующую команду, то центральный процессор должен ожидать завершения работы сопроцессора.

Математический сопроцессорпредназначен для быстрого выполнения арифметических операций с плавающей точкой, предоставления часто используемых вещественных констант (log₂10,log₂e,ln2), вычисления тригонометрических и прочих трансцендентных функций (tg,arctg,log).

Большинство современных математических сопроцессоров для представлениявещественныхчиселиспользуютстандарт IEEE 754-198.Старший разряд двоичного представления вещественного числа всегда кодирует знак числа.

Остальная часть разбивается на две части экспоненту и мантисса. Вещественное число вычисляется как:(-1)^S·2^E·M,где S - знаковый бит числа, Е - экспонента, М - мантисса.

<=M<2, то такое число называется нормализованным. При хранении нормализованных чисел сопроцессор отбрасывает целую часть мантиссы (она всегда 1), сохраняя лишь дробную часть. Экспонента кодируется со сдвигом на половину разрядной сетки, таким образом, удается избежать вопроса о кодировании знака экспоненты. Т.е. при 8-битной разрядности экспоненты код 0 соответствует числу -127, 1 - числу -126, ..., 255 числу +126 (экспонента вычисляется как код 127).

Стандарт IEEE-754 определяет три основных способа кодирования (типа) вещественных чисел:

вещественное ординарной точности;

вещественное двойной точности;

вещественное расширенной точности.

Стандарт IEEE 754 - широко распространённый стандарт формата представления чисел с плавающей точкой, используемый как в программных реализациях арифметических действий, так и во многих аппаратных (CPU и FPU) реализациях. Многие компиляторы языков программирования используют этот стандарт для хранения данных и выполнения математических операций.

Однако сопроцессор может производить обмен информацией с оперативной памятью, используя при этом адреса, сформированные в микропроцессоре. Стандартное соединение ВМ86 и ВМ87 приведено на рис. 6.

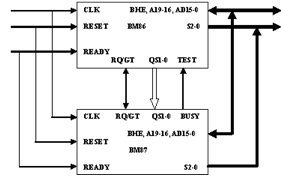
Рис. 6 Стандартное соединение ВМ86 и ВМ87

После прихода сигнала RESET (сброс) сопроцессор анализирует сигнал на линии BHE(выходной сигнал разрешения старшего байта шины данных), выясняя с каким микропроцессором он работает. Для ВМ86 на этой линии в первый момент будет ноль, а для ВМ88 - единица. После этого сопроцессор переходит в пассивное состояние.

Микропроцессор читает из оперативной памяти команды и заносит их в свою внутреннюю очередь. Сопроцессор эти команды перехватывает и также заносит их в свою внутреннюю очередь. В любой момент времени ситуация в обеих очередях должна быть одинаковой, поэтому сопроцессор следит за изменениями в очереди по линиям QS 1-0(входной сигнал кода состояния очереди команд).

Когда ВМ87 перехватывает команду, являющуюся командой сопроцессора, он начинает переходить в активный режим. Полностью активным он становится, когда микропроцессор начинает выполнять его команду.

Система команд сопроцессора включает в себя более 80 команд, однако микропроцессор воспринимает все их как одну команду esc (escape). С точки зрения микропроцессора имеется 3 разновидности этой команды.

команда работает с внутренними регистрами сопроцессора и не требует обращения к оперативной памяти. ВМ86 и ВМ87 одновременно начинают выполнение этой команды. При этом ВМ86 выполняет ее как команду nop (nooperation) и переходит к выполнению следующей команды программы, а ВМ87 продолжает правильное выполнение заданной команды. Далее оба процессора работают параллельно.

команда читает операнд, из оперативной памяти заносит его во внутренний регистр сопроцессора. Адрес перехватывает сопроцессор и заносит его в свой специальный внутренний регистр. Из оперативной памяти по выставленному адресу считывается слово, которое сопроцессор принимает, а микропроцессоригнорирует. Далее микропроцессор переходит к выполнению следующей команды программы. Операнды сопроцессора занимают в памяти до 10-ти байт, поэтому оставшийся "хвост" операнда сопроцессор должен считать самостоятельно. Для этих целей сопроцессор запрашивает у микропроцессора шину по линии RQ/GT и считывает остаток операнда из оперативной памяти, используя перехваченный адрес.

команда заносит в память содержимое внутреннего регистра сопроцессора. ВМ86 вырабатывает адрес, который перехватывает сопроцессор. По этому адресу из оперативной памяти считывается слово, которое игнорируют оба процессора. Затем ВМ87 запрашивает шину по линии RQ/GT и производит запись в оперативную память, используя перехваченный адрес.

Команды сопроцессора сложны, и для их выполнения требуется много времени. Поэтому высока вероятность того, что к началу выполнения следующей команды сопроцессора последний не успеет завершить выполнение предыдущей команды. Перед командами сопроцессора в программах рекомендуется ставить команду wait (ждать). Эта команда проверяет сигнал на входе TEST и, если там стоит единица, микропроцессор ждет, пока на входе TEST не появится ноль. Сигнал на вход TEST заводится с выхода BUSY (занят) сопроцессора. При этом если на BUSY стоит единица, значит ВМ87 занят выполнением команды.

2.3 Функции математического сопроцессора

Сопроцессоры выполняют такие сложные операции, как деление длинных операндов, вычисление тригонометрических функций, извлечение квадратного корня и нахождение логарифма, в 10-100 раз быстрее основного процессора и при этом значительно точнее Операции сложения, вычитания и умножения выполняются основным процессором и не передаются сопроцессору.

Сопроцессор работает параллельно с микропроцессором, это сокращает время вычислений, позволяя сопроцессору выполнять математические операции, в то время как микропроцессор занимается выполнением других функций.

Вся деятельность математического сопроцессора определяется центральным процессором, который может посылать математическому сопроцессору команды на выполнение программ и формирование результатов.

В обычном режиме центральный процессор выполняет все функции компьютера. И лишь, когда встречается задача, с которой лучше справится математический сопроцессор, ему выдаются данные и команды, а центральный процессор ожидает результаты. К таким задачам относятся, например, математические операции между вещественными числами (операции между числами с плавающей запятой), где числа представлены мантиссой и ординатой (десятичная степень числа, определяющая положение десятичной запятой).

Математический сопроцессор может уменьшить время выполнения математических операций, таких, как умножение, деление и возведение в степень, на 80 процентов и более. Скорость выполнения простых математических операций, таких, как сложение и вычитание, не изменяется. Как и любой другой микpопpоцессоp, сопроцессором работает по тем же принципам.

3. Экономическая часть

.1 Расчет себестоимости рабочего места техника

Себестоимость рабочего места техника представляет выраженные в денежной форме текущие на составление места по теме: функции и принцип работы математического сопроцессора.

Все затраты, образующие себестоимость продукции, группируются в связи с их экономическим содержанием по следующим элементам:

-       затраты на оплату труда;

-       отчисления на социальные нужды;

-       амортизация основных фондов и НМА;

-       материальные затраты;

-       затраты на электроэнергию;

-       прочие затраты.

Расчет фонда заработной платы

Затраты на оплату труда включают:

оплату труда основного производственного персонала, включая премии за производственные результаты;

стимулирующие и компенсирующие выплаты, в том числе в связи с повышением цен и индексацией доходов в пределах норм предусмотренными законодательством;

отчисления на социальные нужды в размере 30% от годового фонда оплаты труда.

Предусматривается повременная оплата труда. Для стимулирования труда, применяются коэффициент районного регулирования зарплаты и надбавку к должностному окладу за оперативность и ненормированный рабочий день 30%.

Расходы на оплату труда определяются по формуле:

Ф_от = (До + å Д) Рк ∙ Тк, (1)

где, До - должностной оклад, руб.;

å Д - сумма доплат, руб.;

Рк - коэффициент районного регулирования заработной платы - 1,4к - календарный фонд времени, мес.

Пример расчета зарплаты для техника:

Ф_от =(12200+3660)1,4Ч12 = 2204 руб.

Расчет отчислений на социальные нужды(З_сн)

З_СН выплачивается предприятием в пенсионные и социальные фонды РФ в соответствии с Федеральным законом от 20.07.04 №70-ФЗ. С изменениями и дополнениями 2014 год. Сумма затрат составляет в размере 30% от годового фонда заработной платы.

З_сн= 30 ∙ Ф_от /100 (2)

Основные производственные фонды

Основные производственные фонды - это стоимостное выражение средств труда, которое участвует во многих производственных циклах сохраняя свою натуральную форму.

Износ основных фондов учитывается по установленным нормам амортизации, сумма которой включается в себестоимость работ. После реализации работ начисленный износ накапливается в особом амортизационном фонде, который предназначается для новых накопительных вложений.

Амортизация основных фондов

К амортизации основных фондов относится все амортизационные отчисления по основным средствам за отчетный период.

Амортизация - это процесс постепенного перенесения стоимости основных фондов по мере износа на производимые работы, и накопление финансовых ресурсов в денежной форме в целях последующего воспроизводства основных фондов.

Размер амортизационных отчислений определяется на основе норм амортизационных отчислений и положения о порядке планирования, начислений и использования начислений.

Расчет амортизационных отчислений АО, руб. производится по формуле

АО = ОФбал ∙Na: 100 (3)

где, ОФбал - балансовая стоимость, руб.;- норма амортизации, %.

Пример расчета амортизационных отчислений для персонального компьютера

АО = 23839Ч2,5/100:12 =198 руб.

Остальные расчеты сведены в табл. 1

Таблица 1

Расчет амортизационных отчислений

Расчет амортизации нематериальных активов (НМА)

Амортизацию по НМА начисляют ежемесячно независимо от результатов деятельности компании. Возможности приостановить начисление амортизации законодательство не предусматривает. Ее начинают начислять с 1-го числа месяца, который следует за месяцем отражения того или иного объекта в составе НМА.

Пример амортизации нематериальных активов

АО_нма = 1Ч3650Ч10/100/12 = 30 руб.

Таблица 2. Расчет амортизации нематериальных активов (НМА)

Расчет стоимости материалов

К материальным затратам относятся основные материалы, в том числе покупные комплектующие изделия; вспомогательные материалы; износ малоценных и быстро изнашивающих предметов и др.

Стоимость единицы материалов устанавливается по прейскуранту оптовых цен с учетом транспортных и заготовительно-складских расходов.

Стоимость материалов З м руб. определяется по формуле

Зм=Рг∙Цед, (4)

где Рг - расход материалов;

Цед - цена за единицу, руб.

Пример расчета стоимости компьютерной мыши

Зм = 1Ч480 = 480 руб.

Остальные расчеты аналогичны, результаты расчетов сводятся в табл. 3.

Таблица 3

Расход и стоимости материалов

Расчет стоимости электроэнергии

Зэл.= N ∙ tсут ∙ Тэф∙Кз ∙Тэл, (5)

где Зэл. - затраты на электроэнергию, руб.- мощность потребителя, кВт.

Тэф-эффективное время работы время работы потребителя, дней.

Кз - коэффициент, учитывающий загрузку потребителя по мощности.

Тэл - тариф на электроэнергию, руб./квт.час

Расчет затрат на электроэнергию производится для компьютеров

З_эл=1Ч0,30Ч3Ч25.4Ч0,25Ч3,95=567 руб.

Остальные расчеты аналогичны и сводятся в табл.5

Таблица 5

Расчет стоимости электроэнергии для оборудования.

Прочие расходы

Прочие расходы - это износ нематериальных активов, представительские расходы, расходы на охрану труда и технику безопасности, на содержание помещения - охрана, уборка, ремонт, коммунальные услуги, услуги связи составляют 15% от фонда оплаты труда.

Определяются прочие затраты З_проч, руб. по формуле

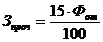 (6)

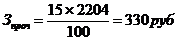
Расчет себестоимости

Себестоимость рабочего места Срм, руб. определяется по формуле

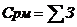
где 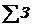- совокупность затрат, руб.;

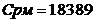
Данные предыдущих расчетов сводятся в табл. 6

Таблица 5

Себестоимость рабочего места

.2 Заключение по экономической эффективности

Для оценки уровня эффективности работы предприятия получаемый результат сопоставляется с затратами или используемыми ресурсами.

Расчеты показали, что затраты на себестоимость рабочего места техника составило 44468 рублей.

Проанализировав рынок технического обеспечения вычислительной техники и компьютерных сетей можно сделать вывод, что данная услуга пользуется спросом. За счет качества технического обслуживания, затраты на себестоимость рабочего места техника могут быть оправданы.В настоящие время нет необходимости доказывать целесообразность использования вычислительной техники в системах управления технологическими процессами, проектирования, научных исследований, административного управления, в учебном процессе, банковских расчетах, здравоохранении, сфере обслуживания.

Заключение

В данной дипломной работе, была изучена тема "Функции и принцип работы математических сопроцессоров", посредствам решения конкретных задач, а именно были закреплены знания:

общие понятия о математических сопроцессоров;

принцип работы математического сопроцессора;

функции математического сопроцессора;

история развития математических сопроцессоров.

Математический сопроцессор выполняет, такие сложные операции как точное деление, вычисление тригонометрических функций, извлечение квадратного корня и нахождение логарифма в 10-100 раз быстрее основного процессора. Точность результатов при этом значительно выше той, которая обеспечивается вычислителями, входящими в состав самих процессоров. Операции сложения, вычитания и умножения выполняются основным процессором и не передаются сопроцессору.

Список литературы

1. Автономов B.C. Процессоры / М.: Вита-Пресс, 2010. - 256 с.

2. Зыков Н.В. Единые требования к оформлению курсового и дипломного проекта (работы): методические указания для студентов технических специальностей: изд. 2, испр. и доп. / Н.В. Зыков. - Чита: ЗабГК, 2007. - 45 с.

. Леонтьев В.П. Новейшая энциклопедия персонального компьютера / В.П. Леонтьев. - М.: ОЛМА Медиа групп, 2011. - 928 с.

4. Мамедов О.Ю. Современные компьютеры / О.Ю. Мамедов. - М: Феникс, 2011.- 608 с.

5. Мураховский В.И. Основы процессоров / В.И. Мураховский. - М: Аст- пресс книга, 2009. - 392 с.

. Мюллер С. Все о компьютерах / С.Мюллер.- М.;Диалектис-Вильямс, 2010. - 992 с.

. Райзберг Б.А. Персональный компьютер / Б.А. Райзберг. - М.: ИНФА, 200-9. - 96 с.

8. Романов В.П. Техническое обслуживание средств вычислительной техники: учебное пособие: изд.3 / В.П.Романов. - СПб.: 2010. - 180 с.

9. Сергеев И.В. Основы ПК: учебное пособие: изд. 2 / И.В. Сергеев. - М.: Финансы и статистика, 2013. - 304 с.

10. Томпсон Р. Персональный компьютер / Р.Томпсон. - СПб.: БХВ-Петрбург, 2013. - 608 с.

. Хведюк М.А. РС для начинающих. Аппаратные средства / М.А. Хведюк. - СПб.: БХВ-Петербург, 2007. - 192 с.

. Чечевицына Л.И. ПК для новичков / Л.И. Чечевицына. - М.: Феникс, 2011. - 384 с.

. Белый В.А. Основы работы с персональный комьютером / Белый В.А. - М.: Феникс, 2011. - 334 с.