Однородная цепочка Ферми–Пасты-Улама
Оглавление
1.
Введение
2.
Однородная цепочка Ферми - Пасты - Улама
2.1
Нулевые граничные условия
2.2
Периодические граничные условия
3.
Неоднородная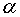 
-цепочка
Заключение
Спиок
литературы
1. Введение
Одной из наиболее важных работ, сильно
стимулировавшей изучение нелинейных динамических систем, стал компьютерный
эксперимент, поставленный физиком Энрико Ферми и математиками Станиславом
Уламом и Джоном Пастой летом 1952 г. в Лос-Аламосе (штат Нью-Мексико, США) [1].
Они недавно завершили работы в Манхэттенском проекте по созданию атомной бомбы,
для нужд которого математик Джон фон Нейман построил мощную (по тому времени)
вычислительную машину «МАНИАК-1». Машину нужно было загрузить задачей,
соответствующей её ресурсам, и Ферми предложил обратиться к старой проблеме П.
Дебая: объяснить конечную теплопроводность твердых тел.
В качестве модели твердого тела они рассмотрели цепочку
из массивных частиц (атомов), соединенных пружинками, которые играют роль сил
упругого взаимодействия (рис.1.1). Если пружины линейны, т.е. выполняется закон
Гука, то энергия переносится нормальными модами цепочки, которые не
взаимодействуют между собой. Следовательно, для передачи энергии с одного конца
цепочки на другой не требуется никакого перепада температуры, эффективная
теплопроводность оказывается бесконечной. Еще в 1914г. П. Дебай предположил,
что конечная теплопроводность обусловлена ангармоничностью пружин. Если пружины
нелинейны, т.е. возвращающая сила не пропорциональна деформации, то появляется
взаимодействие нормальных мод. Дебай полагал, что нелинейные взаимодействия
ограничат перенос энергии и приведут к конечности коэффициента теплопроводности.
Рис.1.1 Модель твердого тела.
В данной работе я рассматривал
квадратичную нелинейность, это так называемая 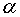-цепочка, хотя Ферми, Паста и Улам
также рассматривали и кубическую нелинейность
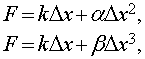
причем коэффициенты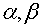 
выбираются
таким образом, чтобы нелинейные члены были малыми. Уравнение движения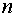 
-й частицы
имеет вид
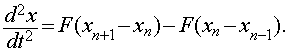
В среде программирования Delphi,
была написана программа позволяющая наблюдать динамику данной системы. В работе
рассматривались нулевые (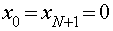
) и
периодические граничные (
,
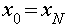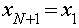) условия
[2]. Также в работе исследовалась неоднородная цепочка. Рассмотрим
последовательно эти случаи.
2. Однородная цепочка Ферми - Пасты
- Улама
.1 Нулевые граничные условия
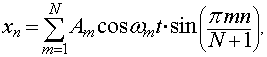
где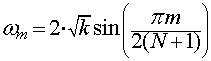 
, - собственные частоты мод, а
амплитуды 
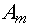- константы,
определяемые начальными условиями. В слабонелинейном случае эти моды
взаимодействуют между собой и амплитуды 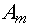начинают зависеть от времени. При
помощи дискретного преобразования Фурье можно найти выражение для энергии
собственных мод
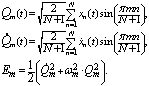
Ферми, Паста и Улам предполагали,
что если в начальный момент времени возбуждена низшая мода (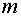
=1), то с
течением времени энергия начального возбуждения будет переходить в высшие моды,
пока не установится состояние при котором энергия всех мод примерно одинакова,
т.е. состояние теплового равновесия, которому соответствует равномерное
распределение энергии по степеням свободы. Однако энергия не термализовалась.
На рис.2.1 хорошо видно, что сначала возбуждаются несколько низших мод, а затем
через время порядка 150 периодов осцилляции первой моды, энергия почти
полностью возвращается в исходную моду. Данный расчет проведен для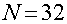 
, 
, 
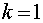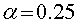. На рис.2.2
приведены графики для энергий высших мод. Видно, что моды с номерами выше
пятого не получают более 5% начальной энергии.
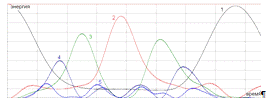
Рис. 2.1 Зависимость энергии низших
мод от времени в задаче Ферми-Пасты-Улама. , , ,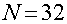 
.
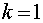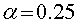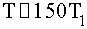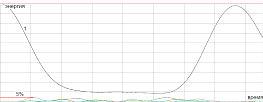
Рис.2.2 Зависимость энергии высших
мод от времени в задаче Ферми-Пасты-Улама. , , .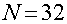
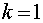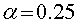Явление возвращаемости получило
название парадокса Ферми-Пасты-Улама, и было объяснено только в середине 60-х
годов американскими физиками Мартином Крускалом и Норманном Забуски. Они
показали, что отсутствие термализации системы связано с устойчивостью
образовавшейся в ней уединенной волны - солитона [3].
Если рассмотреть эволюцию данной
системы на более длительном интервале времени [4], то можно заметить, что
возврат энергии к первоначальному состоянию становится менее точным, т.е. можно
предположить что система все таки термализуется. Однако, через время порядка
3500 периодов осцилляции первой моду происходит практически полный возврат к
начальному состоянию. Так обнаруживается еще одно интересное свойство этой
нелинейной системы, сверхпериодичность (рис.2.3).
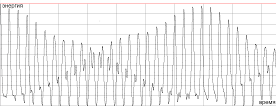
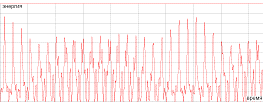
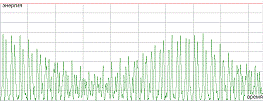
Рис.2.3 Явление сверхпериодичности
для первой (черный) , второй (красный) и третьей (зеленый) мод соответственно. , , ,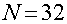
.
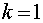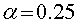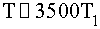Если рассмотреть влияние параметра
нелинейности на возврат энергии в ангармонической цепочке, то из рис.2.4 видно,
что с уменьшением нелинейности период возврата увеличивается, а сам возврат
становится более точным. Этого результата и стоило ожидать, т.к. при 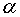=0
взаимодействие между модами отсутствует, и вся энергии сохраняется в
возбуждающей моде, т.е. период ее возврата можно считать равным бесконечности.
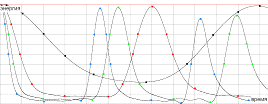
Рис.2.4 Зависимость периода возврата
от параметра нелинейности. Черному цвету соответствует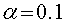 
, красному -
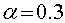, зеленому -
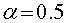, синему - 
.
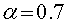Также стоит обратить внимания на
один факт из теории колебаний. Как известно, при наличии квадратичной
нелинейности, в спектре колебаний могут появиться частоты кратные исходным и их
комбинации. В этом можно убедиться, если начальное возбуждение задать в виде
второй или более высокой гармоники. Как видно из рис.2.5, энергия переходит
только в моды кратные возбуждающей. Если мы зададим суперпозицию второй и
третьей моды (рис.2.6), то на графике (рис.2.7) можно получить 1, 5, 7 моды.
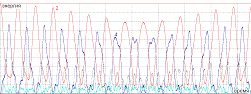
Рис.2.5 Начальное возбуждение в виде
второй моды. Энергия распределяется только между модами кратными возбуждающей.
Рис.2.6. Профиль начального
возмущения в виде суперпозиции 2-й и 3-й мод.
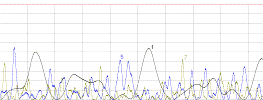
Рис.2.7 Начальное возбуждение в виде
суперпозиции 2-й и 3-й мод. На графике присутствуют 1,5 и 7 моды.
.2 Периодические граничные условия
Как уже говорилось, в работе также
была рассмотрена замкнутая в кольцо 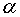-цепочка. В линейном случае решение
ищется в виде суперпозиции бегущих волн
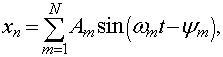
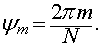
Результаты расчетов для данной
модели оказались аналогичными результатам для цепочки с закреплёнными концами.
На рис.2.8 показан распад синусоидального профиля волны на солитоны.[2],[3]
Видно, что вначале происходит укручение волны, затем на фронте волны возникают
осцилляции, которые растут и со временем превращаются в уединенные волны На
рис.2.9 и рис.2.10 показаны зависимости энергии низших мод от времени для
замкнутой в кольцо 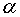-цепочки.
Расчет проводился для 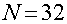, , 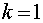.Период
возврата оказался порядка 37 периодов осцилляции первой моды, временной интервал
большого периода - порядка 650 периодов осцилляции.
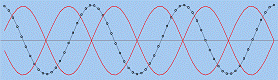
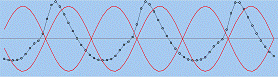
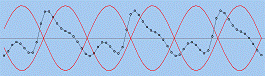
Рис.2.8 Распад синусоидального
профиля волны на солитоны.
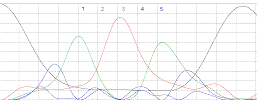
Рис 2.9 Зависимость энергии низших
мод от времени для замкнутой в кольцо 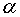-цепочки. , , , 
.
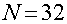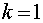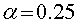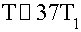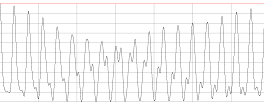
Рис.2.10 Явление сверхпериодичности
для первой моды для замкнутой в кольцо 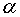-цепочки. , , ,
.
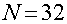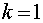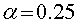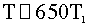3. Неоднородная 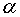-цепочка
однородная цепочка мода
возбуждение
Следующим этапом работы было
рассмотрение неоднородной цепочки. В своей работе я исследовал влияние
неоднородности на возвращаемость Ферми-Пасты-Улама. Под неоднородностью следует
понимать случайный разброс величины жесткости пружинок около некоторого
среднего значения. Было сделано предположение, что если отклонения не велики,
то можно пользоваться формулами для однородной цепочки. Расчеты показали, что
при достаточно большой амплитуде волны (А=4) происходит термализация энергии.
На рис.3.1 и рис.3.2 черным цветом показаны зависимости энергий мод от времени
для однородной цепочки (k=1), а красным для цепочки с жесткостью, заданной в
пределах k=1±0.05, горизонтальным линиям соответствует среднее значение энергии
содержащейся в рассматриваемой моде. Как видно средняя энергия содержащаяся в
первой моде уменьшилась, а средняя энергия содержащаяся в десятой моде наоборот
увеличилась,
т.е.
энергия из низших гармоник переходит в более высокие, и можно предположить, что
неоднородность в ангармонической цепочке приводит к термализации энергии
системы.
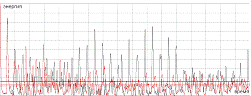
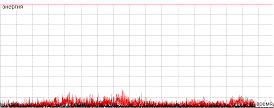
Рис.3.2 Зависимость энергии десятой
моды от времени. 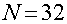, , 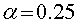черному
цвету соответствует 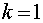, красному -
.
Заключение
В ходе выполнения курсовой работы
были получены классические результаты для однородной ангарманическо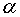й -цепочки при
различных граничных условиях. Наблюдались явления возврата Ферми - Пасты -
Улама, сверхпериодичности.
Также в работе была рассмотрена
неоднородная цепочка ФПУ, в результате чего был сделан вывод о том, что случайный
разброс величины жесткости пружинок около некоторого значения приводит к
термализации энергии в системе.
Спиок литературы
E.,
Pasta, J, Ulam S., Studies jf nonlinear problems // Los Alamos Sci. Lab. Report
LA - 1940, 1955.
Ферми
Э., Научные труды. Т.2. - М.: Наука, 1972.
Рыскин
Н.М., Трубецков Д.И. Нелинейные волны - М.: Наука. Физматлит,
2000.N.J., Kruskal M.D. Interaction of «solitons» in a collisionless plasma
and the reccurence of initial states // Phys. Rev. Lett.
1965. V. 15, № 6.
Флах
С.Г., Периодические орбиты, локалихация в пространстве нормальных мод и
проблема Ферми, Паста и Улама, Нелинейные волны ‘ 2006, - Нижний Новгород: ИПФ
РАН, 2007.
Рабинович
М.И., Трубецков Д.И. Введение в теорию колебаний и волн - М.: НИЦ «Регулярная и
хаотическая динамика», 2000.