Различные методы решения планиметрических задач

Различные методы решения планиметрических задач

Направление: математика

Содержание

Введение

I. Различные методы решения планиметрической задачи на примере конкретной задачи

. Методы, использующие дополнительные построения

1.1 «Прямая параллельная диагонали»

.2 «Средние линии треугольников»

.3 «Середины сторон трапеции»

.4 «Первый признак равенства треугольников»

.5 «Второй признак равенства треугольников»

.6 «Признаки равенства прямоугольных треугольников, свойства параллельных прямых»

. Методы, основанные на подобии треугольников

.1 «Подобие треугольников».

.2 «Коэффициент подобия треугольников»

.3 «Метод тригонометрической замены»

 3. Методы, использующие соотношение между углами и сторонами треугольника

.1 «Метод площадей и тригонометрия»

3.2 «Соотношение между углами и сторонами прямоугольного треугольника и подобие треугольников»

.3 «Метод высот»

4. Координатный метод

5. Методы, использующие векторный аппарат

.1 «Сложение векторов»

.2. «Коллинеарные векторы»Исследование

Заключение

Библиографический список

Приложение 1

Приложение 2

Введение

В математике известно много методов решения разных задач, которые актуальны и по сей день. К ним относятся:

·        методы с использованием дополнительных построений;

·        методы, основанные на подобии треугольников;

·        методы тригонометрической замены;

·        методы, использующие соотношение между углами и сторонами прямоугольного треугольника;

·        методы, использующие векторный аппарат.

Актуальность:

В заданиях группы В (планиметрия) единого государственного экзамена по математике содержаться такие задачи, при решении которых учащиеся испытывают определенные затруднения, что ведет к потере времени на экзамене.

Методы, предложенные в моей работе, позволяют решить эти задания быстро и легко.

Умение решать планиметрическую задачу несколькими способами - один из залогов успешного решения стереометрических задач.

Исходя из выше сказанного

Цель работы:

Изучить и систематизировать различные методы решения планиметрических задач на примере конкретной задачи.

Задачи:

1. Определить, действительно ли одну задачу можно решить несколькими методами.

2.      Познакомиться с многообразием решений планиметрических задач.

.        Найти самый рациональный способ решения.

.        Узнать какой из методов чаще всего используют ученики 8 - 10 классов.

Объект исследования:

Планиметрическая задача.

Предмет исследования:

Методы решения планиметрической задачи.

Гипотеза:

Владение различными методами решения задач позволит выпускнику выбирать наиболее рациональный метод.

Изучая в школе предмет «Геометрия», мы приобретаем набор методов решения планиметрических задач. Нами была выбрана планиметрическая задача, которую можно было решать различными методами. Прорешав ее известными нам методами, мы обратились к литературе за дополнительными методами решения. Провели классификацию этих методов. Выбрали более оптимальные. Предложили учащимся 8-11 классов решить данную задачу и выявили наиболее «популярные» методы решения.

подобие треугольник вектор тригонометрическая замена

I. Различные методы решения планиметрической задачи на примере конкретной задачи

Нами была выбрана планиметрическая задача, которую можно было решать различными методами.

Задача:

Найти среднюю линию MN трапеции ABCD с основаниями BC и AD, если BD = 6см, AC = 8см, ^AC.

1. Методы, использующие дополнительные построения (ДП)

1.1 «Прямая параллельная диагонали» [5, №33.8]

1. ДП: проведем CE||BD, CE∩AE=EÞBCED - параллелограмм, (BD||CE и BC||DE, BC=DE=a, CE=BD=6см.)

2. Рассмотрим ∆ACE: ÐACE=90° (BD||CE, AC^BD ÞAC^CE) AE=√AC²+CE²=√64+36=10. MN=1/2AE = 5.

Ответ: MN = 5см.

1.2 «Средние линии треугольников»

1. Д.П.: проведем средние линии ∆ABD (MK||BD) и ∆ACD (NK||AC)

2. Рассмотрим ∆ABD: MK=6/2=3см; ∆ACD: NK=8/ =4

3.∆MNK:Ð NKM=90° (MK||BD, NK||AC и BD^ACÞMK^NK) ÞMN=ÖMK²+KN²=√3²+4² =5

Ответ: MN=5

1.3 «Середины сторон трапеции»

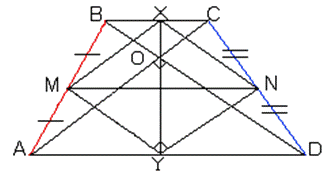
1. Соединим середины сторон трапеции. XMYN - параллелограмм (XN||BD, MY||BDÞXN||MY; XM||AC, NY||AC ÞXM||YN);

ÐMYN = 90° (AC||YN, BD||MY; BD^ACÞYN^MY) ÞXMYN - прямоугольник .YM=3(MY - средняя линия ∆ABDÞMY= 1/2BD); NY=4(NY - средняя линия ∆AС ÞNY=½ AC).

2. ∆MNY: MN=√3²+4²=5

Ответ: MN=5.

1.4 «Первый признак равенства треугольников»

1.Д.П.: Продлим AC на AM₁=OC и BD на DN₁=OB.

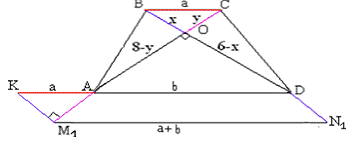
2. По теореме Пифагора в ∆M₁ON₁: M₁N₁=10.

3. Проведем M₁K||N₁D. MK∩AK=K.

4. ∆BOC=∆KAM₁ (поΙ признаку: =KM₁, OC=AM₁, по построению, ÐBOC=ÐKM₁A=90°, накрест лежащие при BN₁|| KM₁, M₁C - секущей) AK=BC.

5. M₁KDN₁ - параллелограмм, DK=M₁N₁ =10; MN =DK/2= (AD+BC)/2=5. Ответ: MN=5

1.5 «Второй признак равенства треугольников»

1.Д.П.: Продлим AC на AM₁=OC и BD на DN=OB.

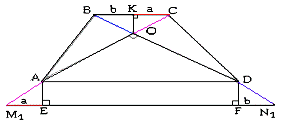
2. Рассмотрим ∆OMN, ÐNOM=90°, тогда по теореме Пифагора в ∆MON MN=10.

. Постоим: AE^MN, DF^MN, OK^BC.

4. ∆AME = ∆KOC и ∆DFN=∆BOK (по II признаку)Þ ME=KC, FN=BKÞMN=BC+AD=a+b=10ÞMN=10/2=5.

Ответ: MN=5.

1.6 «Признаки равенства прямоугольных треугольников, свойства параллельных прямых»

1. Д.П.: Через т. B проведем прямую EM₁||AC

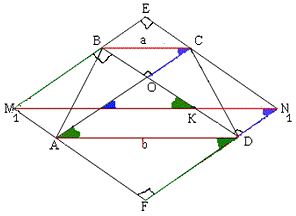
2.Через т.C проведем EN₁||BD.

3.Через т. D проведем прямую N₁F||AC.

4.Через т. A проведем прямую EM₁||BD.

.Получившийся четырехугольник M₁EN₁F - прямоугольник (E M₁||AC, M₁F||BD и AC^BDÞ M₁F^N₁F) EN₁=M₁F=6 и EM₁=N₁F=8,  по теореме Пифагора диагональ прямоугольника M₁N₁=10.

6.Пусть BC=a, AD=b из равенства прямоугольных треугольников М₁ВК и ADF M₁K=AD=b. Из равенства прямоугольных треугольников ВСО и КDN₁ KN₁=BC=a.

7. M₁K+KN₁=M₁N₁= a+bÞMN=M₁N₁/2=5

Ответ: MN=5.

2. Методы, основанные на подобии треугольников.

2.1 «Подобие треугольников». [1, п. 59]

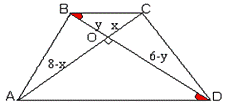
1.∆ BOC~∆AOD (по 2-м углам ÐBOC=ÐAOD=90° и ÐCBO=ÐADO как накрест лежащие при BC||AD, BD - секущая) y= 4/3x, x<3 (половины AC)

2.По теореме Пифагора:∆AOD: AD= Ö(8-х)²+ (6-у)², =4x/3ÞAD=√25/9x² - 100/3+100.

3. ∆ BOC: BC=5x/3 (по т.Пифагора).

4. MN= (AD+BC)/2, подставим: AD=√25/9x²-100/3+100 и BC=5x/3 получим: 3l²-5lx+25x-75=0. MN=25x2-12(25x-75) =25(x-6)², MN= (10x-30)/6=5x/3-5<0 - посторонний корень, MN= (5x-5x+30)/6=5

Ответ: MN=5.

2.2 «Коэффициент подобия треугольников». [1, п. 59]

1.∆ BOC~∆AOD 8-х=kx

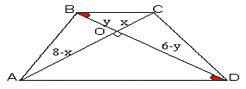
6-y=ky =8/k+1=6/k+1 (k - коэффициент подобия)

2. Рассмотрим∆ BOC и ∆AOD. По теореме Пифагора BC=√x²+y², AD=√(8-х)² + (6-у)²

3.MN=(AD+BC)/2 подставим x и y: MN = √(8²/(k+1)) + 6²/ (k+1))*(k+1))/2=√100/2=5

Ответ: MN = 5.

2.3 «Метод тригонометрической замены». [7].

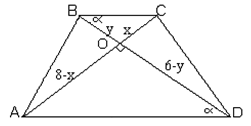
1. ∆BOC~∆AOD (ÐCBO=ÐADO - накрест лежащие при BC||AD (по определению трапеции) и BD-сек.) Þx/(8-x)=a/bÞa+b=8a/x. 2. MN= (a+b)/2=4a/x.

3.х/(8-х)=у/(6-у), то х/у=4/3.

4. ∆BOC: sina=х/а, tga=x/y=4/3, sina=4/5ÞMN=4/sina=5.

Ответ: MN = 5.

3. Методы, использующие соотношение между углами и сторонами треугольника

3.1 « Методы площадей и тригонометрия» [1,п. 66]

1. BB₁=CC₁=h

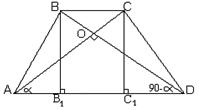
2. S_ABCD=½*d₁d₂*sinα=24.

3. S_ABCD=MN*h

4. Рассмотрим ∆BB₁D: sinα=(90-α)=h/6Þcosα=h/6.

5. Рассмотрим ∆CC₁A:sinα=h/8.

6. По основному тригонометрическому тождеству: sin²α+cos²α=1 Þh²/36+h²/64 =1Þh =24/5.

Ответ: MN = 5.

3.2 «Соотношение между углами и сторонами прямоугольного треугольника и подобие треугольников». [1,п. 66]

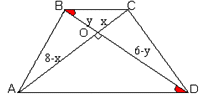
1. ∆BOC~∆AOD (ÐAOD=BOC=90°, ÐCBO=ÐADO - накрест лежащие при BC||AD)Þy=4x/3.

2. Рассмотрим ∆BOC tga=4/3Þcos =3/5(1+tg²a = 1/cos²a) 3. Рассмотрим ∆BOC OC/BC = cosa Þ BC = OC/cosa = 5x/3 4. Рассмотрим ∆AOD AO/AD = cosa Þ AD = AO/cosa = 5(6-x)/3 5. MN = (AD+BC)/2 = (5(x-6)/3+5x/3)/2 = 10/2 = 5

Ответ: MN = 5.

3.3 «Метод высот» [1,п. 66]

1. Д.П.: Построим BF^AD и CD^AD BE=CE=H

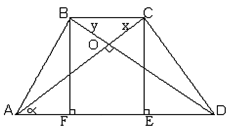
2. AE=Ö6²-H² (DACE, по теореме Пифагора), FD=Ö8²-H² (DDBF, по теореме Пифагора).

3. AE+FD=Ö36-H² +Ö64-H²=AF+FE+ED+EF=a+b.

4 MN=(a+b)/2=(Ö36-H² +Ö64-H²)/2.

5. ∆BOC~∆AODÞtga=4/3

6. DACE: tga=CE/DE=H/Ö36-H² =4/3

7. Решаем уравнение: 3H=4Ö36-H², H=4,8

8. Подставим H = 4,8 в уравнение: MN=(Ö36-H² +Ö64-H²)/2 Þ MN = (3,6+6,4)/2 = 5. Ответ: MN = 5.

4. Координатный метод. [5, §61-62; 2п. 39]

1. Зададим оси координат по прямым: BD и AC точка О(0; 0)

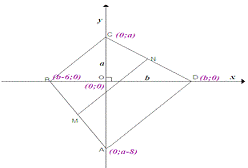
2. Координаты вершин: A(0; a-8); B(b-6; 0); C(0; a); D(b; 0).

3. Найдем координаты точек M, N:

M((b-6)/2; (a-8)/2), N(b/2; a/2)

4. Найдем длину =Ö((b-8)/2-b/2)²+((a-8)/2-2/2)²=Ö3²+4²=5

Ответ: MN =5.

5. Методы, использующие векторный аппарат

5.1 «Сложение векторов». [2, п.39]

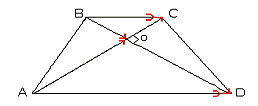
1. AD=AO+OD, BC=BO+OC (метод треугольника)

2. AD+BC = AO+OD+BO+OC = AC+BD Þ+BD = 2AD*BC*cos0+BC²+AD² = =AC²+2AC*BD*cos90°+BD² ÞAD+BC =10.

3. MN = (AD+BC)/2=5.

Ответ: MN = 5.

5.2 «Коллинеарные векторы» [2, п.39]

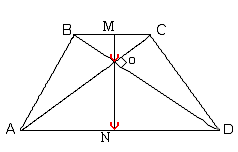
1. MO и ON - коллинеарные.

2. MO = ½(BO+OC), ON = ½ (OA+OD) Þ MO+ON = MN = =½(BO+CO+OA+OD) Þ MN = ½(CA+BD), ² = ¼ (CA²+2CF*BD*cos90°+BD²), MN² = ¼(6²+8²)=5

3. В методе 1.3 мы доказали, что M₁N₁ равна средней линии трапеции, следовательно MN =5.

Ответ: MN = 5.

ΙΙ. Исследование

Для того, что бы узнать какие из представленных в работе способов будут использовать ученики, для решения это задачи, мы предложили решить эту задачу группе учащихся 8-11 классов МОУ «Кормиловский лицей». Задачу решали 9 человек 8-9 классов и 8 человек 10-11 классов, наиболее интересующихся математикой. Оказалось, что ученики, чаще всего используют «метод, основанный на подобии треугольников» (2) с использованием теоремы Пифагора (Приложение 1). Но из-за того, что получались сложные подкоренные выражения, 3 ученика 8 класса недорешали эту задачу. Полученные данные представлены в диаграмме 1.

Методы решения, используемые учениками 8-11 классов (до консультации)

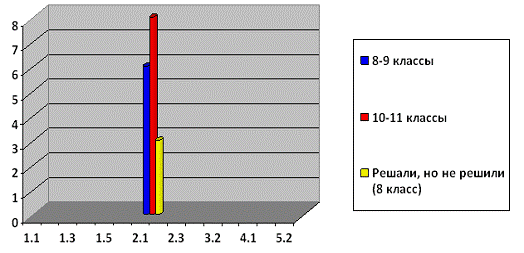
Диаграмма 1

Далее мы ознакомили учащихся 8-11 классов со списком методов решения данной задачи. И предложили решить ее как можно большим числом методов. Полученные результаты представлены в приложении 2. После консультации 1 ученик 8 класса решил еще одним методом и 1 ученик 9 класса решил эту задачу еще тремя методами. Учащиеся 10-11 классов решили эту задачу еще 3-7 методами (Диаграмма 2)

Учащиеся не использовали при решении задачи следующие методы:

·        метод, использующий векторный аппарат;

·        «сложение векторов»;

·        «коллинеарные векторы»;

·        первый, второй признаки равенства треугольников;

·        коэффициент подобия треугольников;

·        метод тригонометрической замены.

Методы решения, используемые учениками 8-11 классов (после консультации)

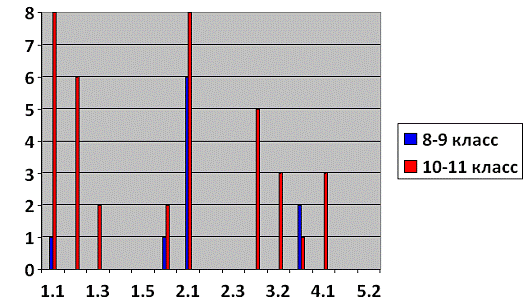
Диаграмма 2.

Заключение

В ходе нашей работы было выявлено 15 различных методов решения конкретной планиметрической задачи.

. Методы, использующие дополнительные построения (ДП);

.1. «Прямая, параллельная диагонали»

.2. «Средние линии треугольников»

.3. «Середины сторон трапеции»

.4. «Первый признак равенства треугольников»

.5. «Второй признак равенства треугольников»

.6. «Признаки равенства прямоугольных треугольников, свойства параллельных прямых»

. Методы, основанные на подобии треугольников

.2. «Коэффициент подобия треугольников»

.3. «Метод тригонометрической замены»

3. Методы, использующие соотношение между углами и сторонами треугольника

.1. «Метод площадей и тригонометрия»

.2. «Соотношение между углами и сторонами прямоугольного треугольника и подобие треугольников»

.3. «Метод высот»

. Координатный метод

. Методы, использующие векторный аппарат.

.1. «Сложение векторов»

.2. «Коллинеарные векторы»

Некоторые способы достаточно искусственны и не являются оптимальными.(2.3)

На наш взгляд, самым понятным и простым является метод, использующий дополнительные построения.

Кроме этого на примере решения этой задачи мы смогли увидеть многообразие геометрической теории, возможность ее успешного комбинирования с алгебраическим методом.

Проведенное исследование среди 8-11 классов показало, что большинство учащихся начинали решать эту задачу методом, основанным на подобии треугольника, и использованием теоремы Пифагора. Этот метод - достаточно трудоемкий, особенно для учащихся 8-9 классов. Учащиеся 10-11 классов также начинали решать эту задачу методом, основанным на подобии треугольника, и использованием теоремы Пифагора, но, столкнувшись с тем, что этот процесс достаточно трудоемкий, пришли к выводу, что данную задачу оптимальнее всего решать эту задачу методом дополнительных построений.

Учащиеся не использовали при решении задачи следующие методы:

·  метод, использующий векторный аппарат;

·        «сложение векторов»;

·        «коллинеарные векторы»;

·        первый, второй признаки равенства треугольников;

·        коэффициент подобия треугольников;

·        метод тригонометрической замены.

Библиографический список

1.Л.С. Атанасян, В.Ф. Бутузов и др. «Геометрия 7-9», Москва, «Просвещение», 2005г.

.И.Ф. Шарыгин «Факультативный курс по математике: решение задач », Москва, «Просвещение», 1989г.

.А.И. Громов, В.М. Савчин «Пособие - репетитор по математике», Ростов-на-Дону, «Феникс», 2001г.

.В.К. Егерев, и др. «Сборник задач по математике для поступающих в вузы, геометрия» под редакцией М.И. Сканави, Москва, «Оникс, Альянс-В», 2000г.

.Б.Г. Зив, В.М. Мейлер, А.Г. Баханский «Пособие для учащихся 7-11 классов общеобразовательных учреждений», Москва, «Просвещение», 2000г.

.Ж.Черняк, А. Черняк «Математика: решение наиболее трудных задач из Сканави», Москва, «Айрис, Пресс, Рольф» 1999г.

.К.С. Барыбин И.Н. Добрынин «Сборник задач по геометрии», Москва, «Учпедгиз», 1961г.

Приложение 1

Таблица «Методы решения, используемые учениками 8-11 классов» (до консультации)

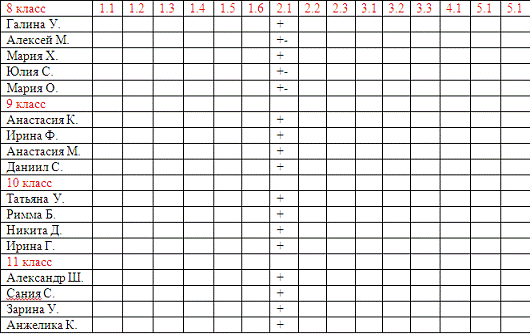
«+» - решили задачу

«+-» - решали, но не решили

Приложение 2.

Таблица «Методы решения, используемые учениками 8-11 классов» (после консультации)

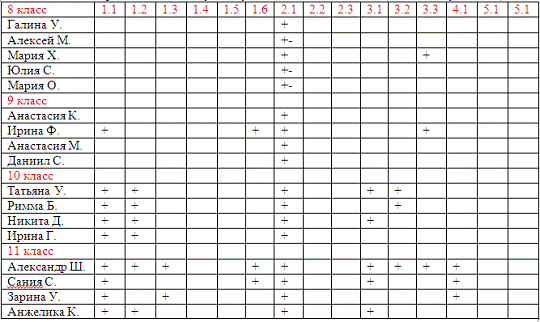
«+» - решили задачу

«+-» - решали, на не решили