Вариационные методы решения систем линейных уравнений
Вариационные методы
решения систем линейных уравнений
1.
Постановка задачи
Большое количество задач математики и физики сводится к
решению дифференциальных уравнений в частных производных, решение которых, в
свою очередь, приводит к решению систем линейных алгебраических уравнений
(СЛАУ). Методы решения СЛАУ, можно разделить на прямые методы, позволяющие
получить точное решение системы (к ним относится, например, метод Гаусса, метод
Крамера и т.д.) и итерационные методы, позволяющие получить решение системы с
заданным приближением. Среди итерационных методов особое место занимают методы
вариационного типа, особенностью которых является то, что при их использовании
нет необходимости знать границы спектра матрицы системы.
Итак, сформулируем задачу:
Дана система линейных уравнений
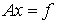
где A симметричная положительно определенная
матрица.
Требуется решить данную СЛАУ следующими итерационными методами
вариационного вида:
1. Метод минимальных невязок
2. Метод минимальных поправок
. Метод скорейшего спуска
. Метод сопряженных градиентов
Методы решения СЛАУ рассматриваются практически в каждой
книге по численным методам. Общее описание алгоритмов для каждого метода дано,
например, в книге Самарского А.А., Гулина А.В. «Численные методы» [3]. Также
популярными книгами являются: М.Ю. Баландин, Э.П. Шурина «Методы решения СЛАУ
большой размерности» [1], Y. Saad «Iterative Method for Sparse Linear System» [5]. В перечисленных
книгах, описаны такие методы как CG (Conjugate Gradient - метод сопряжённых
градиентов) и MinRES (Minimal Residual - метод минимальных невязок). В книге [5]
изложены не только базовые алгоритмы данных методов, но и указания к их
практической реализации.
2.
Описание методов решения задачи
.1
Метод минимальных невязок
Рассмотрим систему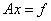 
с матрицей A=AT>0. Обозначим через
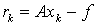(1)
невязку, которая получается при подстановке приближенного
значения xk, полученного на k-й итерации, в уравнение (1). Заметим, что
погрешность zk=xk-х и невязка rk связаны равенством Azk=rk.
Рассмотрим явный итерационный метод
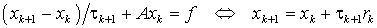, (2) <=> (3)
где параметр tk+l выбирается из условия
минимума погрешности ||rk+1|| при заданной норме ||rk||. Метод (2) называется
методом минимальных невязок.
Найдем явное выражение для параметра tk+l. Из (3) получаем
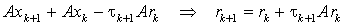, (4) => (5)
т.е. rk удовлетворяет тому же уравнению, что и
погрешность zk=xk-х. Возводя обе части уравнения (5) для невязки
скалярно в квадрат, получаем
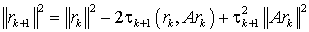(6)
Отсюда видно, что |||rk+1|| достигает минимума,
если
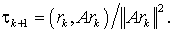(7)
Таким образом, в методе минимальных невязок переход от k-й итерации к (k+1) - й осуществляется
следующим образом. По найденному значению xk вычисляется вектор
невязки rk=Axk-f и по формуле (7)
находится параметр tk+l. Затем по формуле (3)
досчитывается вектор xk+1.
Метод минимальных невязок (3), (7) сходится с той же
скоростью, что и метод простой итерации с оптимальным параметром t.
2.2
Метод минимальных поправок
Рассмотрим неявный итерационный метод вида
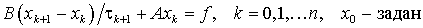, (8)
Запишем этот метод в виде
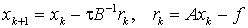. (9)
Вектор wk =B-1rk называется поправкой на (k+1) - й итерации. Она
удовлетворяет тому же уравнению, что и погрешность zk=xk-x неявного метода, т.е.
уравнению
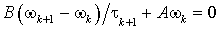. (10)
Будем предполагать, что B=BT>0. Методом минимальных поправок
называется неявный итерационный метод (8), в котором параметр tk+l выбирается из условия минимума нормы ||wk+1||B=(Bwk+1,wk+1)1/2 при заданном векторе wk. В случае B=Е метод минимальных поправок совпадает с методом минимальных
невязок.
Найдем выражение для итерационного параметра tk+l. Перепишем (10) в виде
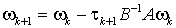
и вычислим
.
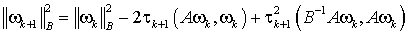Отсюда следует, что минимум этого выражения достигается при
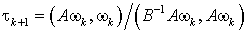. (11)
Для реализации метода минимальных поправок требуется на
каждой итерации решить две системы уравнений Bwk= rk и Bvk=Awk, откуда найдем вектор vk = B-1 Аwk (воспользуемся формулой
(9)).
Скорость сходимости метода минимальных поправок определяется
границами спектра обобщенной задачи на собственные значения
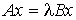. (12)
2.3
Метод скорейшего спуска
Рассмотрим явный метод (2) и выберем итерационный параметр tk+l из условия минимума ||zk+1||A при заданном векторе zk, где zk+1=xk+1-x. Поскольку погрешность zk удовлетворяет уравнению
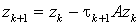, то
.
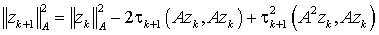Следовательно, это выражение достигает минимума, если
.
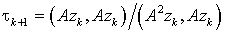Величина zk=xk-x здесь неизвестна (так
как неизвестно точное решение х), поэтому надо учесть, что Azk=rk=Axk-f, и вычислять tk+l по формуле
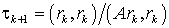. (13)
2.4.
Метод сопряженных градиентов
Пусть A - матрица системы 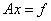. Рассмотрим следующий класс неявных
двухшаговых итерационных методов:
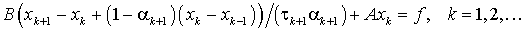. (14)
Здесь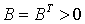 
, ak+l, tk+l - итерационные параметры, которые будут определены далее.
Начальное приближение x0 будем задавать произвольно, а вектор x1 вычислять по одношаговой формуле, которая получается из (14) при k=0 и al=1,
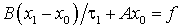. (15)
Если параметры ak+l, tk+l найдены, то новое
приближение xk+l выражается через два предыдущих значения хk и xk-1 по формуле
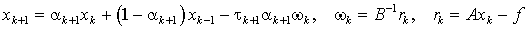. (16)
Для погрешности zk=xk-x из (16) получаем
уравнения
.
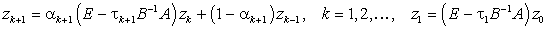Введем, как и ранее, вспомогательную функцию vk=A1/2zk, для которой ||vk||=||zk||A. Функция vk удовлетворяет уравнениям
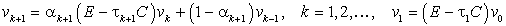.(17)
где C=A1/2B-1A1/2. Будем считать,
что A
и B - симметричные
положительно определенные матрицы, удовлетворяющие неравенствам
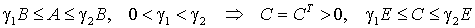. (18)
Исключая последовательно векторы vl, v2, ¼, vk-l из уравнений (17) находим, что
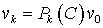, (19)
где Pk(C) - многочлен степени k от оператора С,
удовлетворяющий условию Pk(0)=E.
Поставим задачу выбрать итерационные параметры ak, tk так, чтобы при любом n=1, 2,… была бы
минимальной ||vn||=||zn||A.
Параметр t1 находится из условия минимума ||v1|| при заданном векторе v0. Так же, как и в методе
скорейшего спуска, получаем
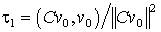. (20)
Отметим, что при таком выборе t1 выполняется равенство (Cv1, v0)=0, т.е. векторы v1 и v0 ортогональны в смысле
скалярного произведения
.
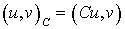Далее, рассмотрим погрешность (19) и запишем многочлен
Pk(C) в виде
где ai(k) - числовые коэффициенты,
определяемые параметрами ai, ti, i=l, 2,…, k. Тогда
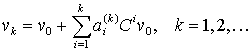. (22)
Найдем условия, которым должны удовлетворять коэффициенты ai(k), минимизирующие ||vn||2. Из (22)
получаем
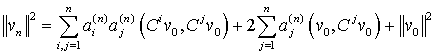, (23)
т.е. ||vn||2 является многочленом второй
степени по переменным a1(n),…, an(n). Приравнивая к нулю
частные производные ¶||vn||2/¶aj(n), j=1, 2,…, n, приходим к системе
уравнений
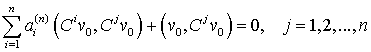, (24)
решение которой ai(n), i=1, 2,…, n и обращает в минимум ||vn||2.
3.
Алгоритмы и блок-схемы решения
.1
Метод минимальных невязок
1. Задаем вектор х0 (начальное приближение).
2. Положим xk = x0, k = 0 (номер итерации)
. Вычисляем вектор rk = Axk - b (невязка начального
приближения).
. Вычисляем скаляр τk+1 = (rk, Ark) / ||Ark||2.
. Вычисляем вектор xk+1 = xk + τk+1rk (очередное приближение).
. Вычисляем вектор rk+1 = rk - τk+1Ark. (невязка k+1 приближения).
. Проверяем выполнение неравенства ||r(k+1)||2 =<
0.001; если «да», то останавливаем работу алгоритма и выводим результаты.
. Положим k = k + 1 и вернемся к шагу 4.
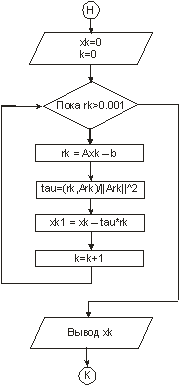
Рис. 1. Блок-схема метода минимальных невязок
3.2
Метод минимальных поправок
1. Задаем вектор х0 (начальное приближение),
матрицу B
= BT > 0.
2. Положим xk = x0, k = 0 (номер итерации)
. Вычисляем вектор rk = Axk - b (невязка начального
приближения).
. Вычисляем вектор ωk = rkBk-1.
. Вычисляем скаляр τk+1 = (Aωk, ωk) / (B-1Aωk, Aωk) (шаговый множитель).
. Вычисляем вектор xk+1 = xk - τk+1 B-1Aωk (очередное приближение).
. Вычисляем вектор rk+1 = Axk+1 - b. (невязка k+1 приближения).
. Положим k = k + 1.
. Проверяем выполнение неравенства ||rk||2 =<
0.001; если «да», то останавливаем работу алгоритма и выводим результаты, иначе
к шагу 3.
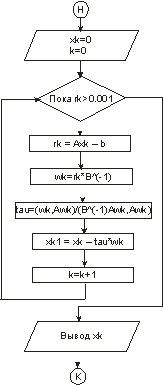
Рис. 2. Блок-схема метода минимальных поправок
3.3 Метод скорейшего спуска
1. Задаем вектор х(0) (начальное
приближение).
2. Положим xk = x0, k = 0 (номер итерации)
. Вычисляем вектор rk = Axk - b (невязка начального
приближения).
. Вычисляем скаляр τk+1 = (rk, rk) / (Ark, Ark) (шаговый множитель).
. Вычисляем вектор xk+1 = xk - τk+1rk (очередное приближение).
. Вычисляем вектор rk+1 = Axk+1 - b. (невязка k+1 приближения).
. Положим k = k + 1.
. Проверяем выполнение неравенства ||rk||2 =<
0.001; если «да», то останавливаем работу алгоритма и выводим результаты, иначе
возвращаемся к шагу 3.
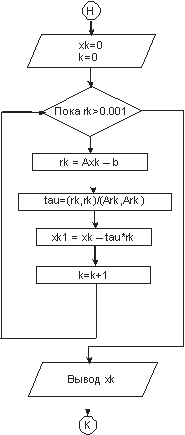
Рис. 3. Блок-схема метода скорейшего спуска
3.4
Метод сопряженных градиентов
1. Задаем вектор х(0) (начальное
приближение).
2. Положим xk = x0, k = 0 (номер
итерации)
. Вычисляем вектор rk = Axk - b
(невязка начального приближения).
. Положим вектор pk= rk
(сопряженный вектор)
. Вычисляем скаляр αk = (rk, rk)
/ (Apk, pk).
. Вычисляем вектор xk+1 = xk + αk pk (очередное приближение)
. Вычисляем вектор rk+1 = rk - αk Apk. (невязка k+1 приближения)
. Вычисляем скаляр βk = (rk+1, rk+1)
/ (rk, rk).
. Проверяем выполнение неравенства ||rk+1||2
=< 0.001; если «да», то останавливаем работу алгоритма и выводим результаты
. Вычисляем pk+1= rk+1+ βkpk
. Положим k = k + 1.
12. Возвращаемся к шагу 5.
4.
Руководство пользователя
В окне программы пользователю предлагается ввести размерность
матрицы системы и требуемую точность, также при желании можно задать величину
диагонального преобладания, либо убрать преобладание вообще (см. рис. 5).
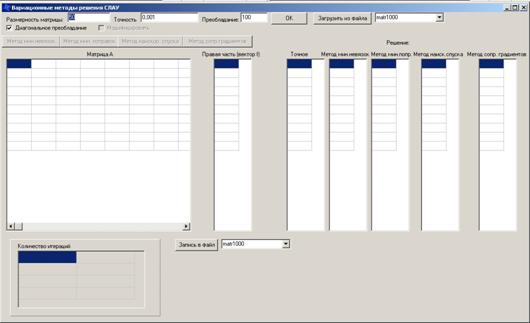
Рис. 5. Окно программы
При нажатии на кнопку ОК генерируется симметричная матрица
заданной размерности, а также правая часть. Далее, при нажатии на кнопку с
названием метода, в соответствующий столбец выводится решение и количество
итераций (см. рис. 6).
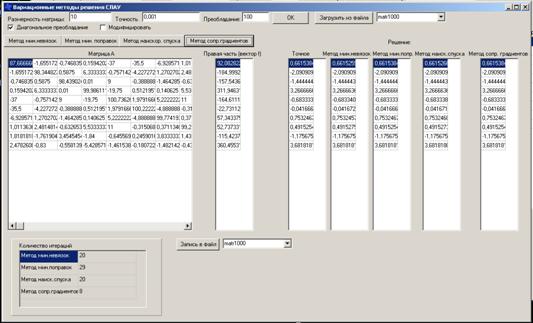
Рис. 6. Решение системы с матрицей размерностью 10х10
Матрицу можно модифицировать, прибавив к главной диагонали
заданную величину, для этого нужно ввести необходимую величину в поле
«Преобладание», поставить флаг «Модифицировать» и нажать ОК.
Также существует возможность записи сгенерированной матрицы в
файл и чтения существующей матрицы из файла. Пользователь может выбрать для
записи и чтения один из трёх файлов.
5.
Тестирование и оптимизация
Изначально программа тестировалась на симметричных матрицах с
диагональным преобладанием, то есть при построении матрицы на главную диагональ
прибавлялась 1000, что давало очень хорошую сходимость при заданной точности
0,001 у всех четырёх методов. При этом было видно, что наихудшую скорость
сходимости дает метод минимальных поправок, наилучшую - метод сопряжённых
градиентов. Разница в скорости сходимости становилась заметна, при размерности
матрицы больше чем 200х200 элементов, что видно на графике (см. рис. 7).
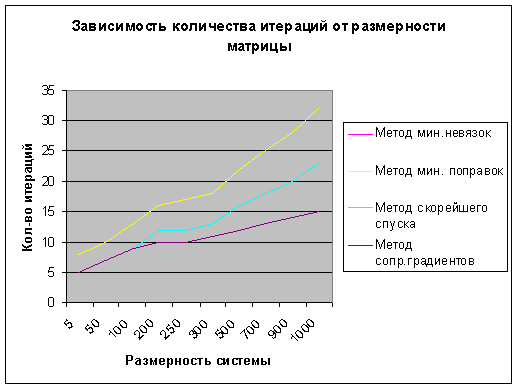
Рис. 7. Зависимость количества итераций от размерности матрицы
Для более наглядной демонстрации работы вариационных методов в
программу была добавлена возможность генерировать матрицы без диагонального
преобладания, а также с диагональным преобладанием, заданным пользователем. В
результате были сделаны следующие наблюдения: при отсутствии диагонального
преобладания метод минимальных невязок очень медленно сходится (за несколько
сотен тысяч итераций), при этом он сходится только для точности не меньше 0,01
и матриц размерностью не больше 50. Аналогичная ситуация наблюдается с методами
минимальных поправок и скорейшего спуска. Если задавать небольшое диагональное
преобладание, то скорость сходимости увеличивается. На рисунке 8 показано, как
изменяется количество итераций в зависимости от диагонального преобладания при
размерности матрицы 10х10 и точности, равной 0,01.
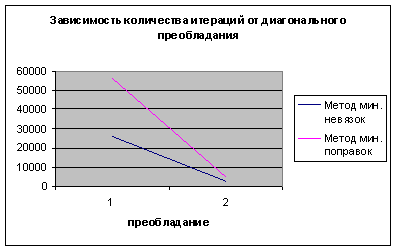
Рис. 8 Зависимость количества итераций от диагонального
преобладания
Что касается метода сопряжённых градиентов, то диагональное
преобладание незначительно влияет на скорость его сходимости, так, в случае
матрицы 10х10 элементов без диагонального преобладания и при точности, равной
0,01, метод минимальных невязок сошёлся за 25329 итераций, а метод сопряжённых
градиентов - за 11 итераций.
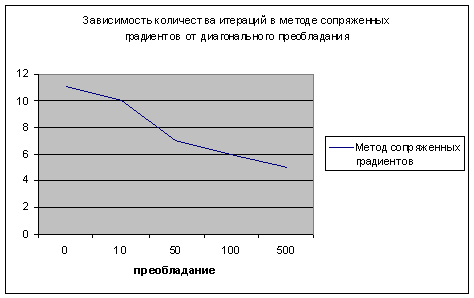
Рис. 9. Зависимость количества итераций в методе сопряженных
градиентов от диагонального преобладания
Таким образом, из всех исследованных методов метод сопряжённых
градиентов является наиболее эффективным.
Для хранения матриц и векторов были использованы динамические
массивы, что ускоряет работу программы и позволяет пользователю практически
неограниченно задавать размерность матрицы системы. Также в методе минимальных
поправок матрично-матричное умножение заменено матрично-векторным, что
позволяет значительно снизить время, затрачиваемое на вычисления.
Список
источников
1. Баландин
М.Ю., Шурина Э.П. «Методы решения СЛАУ большой размерности» - Новосибирск:
Изд-во НГТУ, 2000
. Бахвалов
Н.С., Жидков Н.М. «Численные методы» - М.: Наука, 1986
. Самарский
А.А., Гулин А.В. «Численные методы», Изд. Наука, 1989
. Фаддеев
В.К., Фаддеева В.Н. «Вычислительные методы линейной алгебры» - М.: Наука 1958.
5. Saad Y. Iterative methods for sparse linear systems.
Boston: PWS Publ. Co., 2000.
Приложение
// -
#include <vcl.h>
#include <time.h>
#include <math.h>
#include <stdio.h>
#pragma hdrstop
#include «Unit1.h»
// -
#pragma package (smart_init)
#pragma resource «*.dfm»*Form1;n, m;epsilon; // Точность**a; // Матрица
double *f; // Столбец правых частей*x; // Решение
double *ax;**b;ch=0;*tm;
// -
__fastcall TForm1:TForm1 (TComponent* Owner)
: TForm(Owner)
{[0]=StringGrid2;[1]=StringGrid3;[2]=StringGrid4;[3]=StringGrid5;[4]=StringGrid6;[5]=StringGrid7;[6]=StringGrid8;
}
// -
// Матрично-векторное умножениеmv_mult (double **a, double *x, double *ax)
{(int i=0; i<n; i++)
{[i]=0;(int j=0; j<n; j++)
{[i]+=a[i] [j]*x[j];
}
}
}
// -
// Векторное вычитаниеvv_substr (double *ax, double *f, double *r)
{(int i=0; i<n; i++)
{[i]=ax[i] - f[i];
}
}
// -
// Векторное сложение
void vv_addit (double *ax, double *f, double *r)
{(int i=0; i<n; i++)
{[i]=ax[i]+f[i];
}
}
// -
// Норма вектораnorma (double * vec)
{nr=0;(int i=0; i<n; i++)
{+=vec[i]*vec[i];
}(sqrt(nr));
}
// -
// Скалярное умножение векторов
double vv_mult (double *a, double *x)
{ax=0;(int i=0; i<n; i++)
{+=a[i]*x[i];
}(ax);
}
// -
// Проверка на заданную точность нормыcheck (double *a)
{mod;=norma(a);(mod<epsilon)
return(1);return(0);
}
// -
// Построение матрицы B для метода минимальных поправок
void mkB()
{=1;=new double* [n];(int i=0; i<n; i++)
{[i]=new double[n];(int j=0; j<n; j++)(i!=j)
b[i] [j]=0;b[i] [j]=a[i] [j] - 300;
}
}
// -
// Заполнение матрицы__fastcall TForm1: Button5Click (TObject *Sender)
{->Enabled=true;->Enabled=true;->Enabled=true;->Enabled=true;->Enabled=true;_t
t;(&t); srand((unsigned) t);=StrToInt (Edit1->Text);=StrToInt
(Edit3->Text);=StrToFloat
(Edit2->Text);->ColCount=n;->RowCount=n;(int i=0; i<6;
i++)[i]->RowCount=n;=new double [n];(CheckBox2->Checked==false) {=new
double* [n];=new double [n];=new double [n];(int i=0; i<n; i++)[i]=new
double [n];(int i=0; i<n; i++)
{b=rand()%200-100;c=rand()%100+1;[i] [j]=b/c;[j]
[i]=a[i] [j];((i==j)&&(CheckBox1->Checked==true)) a[i] [j]+=m;(i==j)
tm[i]=a[i] [j];->Cells[j] [i]=FloatToStr (a[i] [j]);->Cells[i]
[j]=FloatToStr (a[j] [i]);
}
}}(int i=0; i<n; i++)
{[i] [i]=tm[i]+(double) m;[i]+=m;->Cells[i]
[i]=FloatToStr (a[i] [i]);->Cells[i] [i]=FloatToStr (a[i] [i]);
}_mult (a, x, f);(int i=0; i<n;
i++)[0]->Cells[0] [i]=FloatToStr (f[i]);
}
матрица вариационный уравнение линейный