Блочные методы шифрования
Реферат
Курсовая работа:
Ключевые слова:
· Шифрование;
· Дешифрование;
· Блочный шифр;
· Сеть Фейстеля;
· Криптостойкость.
Цель работы:
Ознакомление с блочными методами
шифрования. Приобретение практических навыков шифрования и дешифрования
инфрормации с помощью сети Фейстеля.
Основные результаты:
В данной курсовой работе, шифруется
и дешифруется слово - Стрелец.
Для начала, каждая буква переводится
в двоичную систему, затем делится на 2 блока по 16 бит, а потом каждый блок
разбивается на 2 подблока по 8 бит.
После этого записывается
произвольный 32-битный ключ и разбивается на 4 подключа по 8 бит. Далее,
создаётся Sблок, состоящий из двух блоков - S1 и S2. Оба S блока представляют
собой перестановку чисел в диапазоне от 0 до 15. Таблица перестановки для каждого
S блока задается самостоятельно.
Шифрование и дешифрование
производится методом блочного шифра - сеть Фейстеля, описанного ниже.
Введение
Основным видом криптографического
преобразования информации является шифрование - процесс преобразования открытой
информации в зашифрованную информацию или процесс обратного преобразования
зашифрованной информации в открытую. Процесс преобразования открытой информации
в закрытую получил название шифрование, а процесс преобразования закрытой
информации в открытую - дешифрование.
За многовековую историю
использования шифрования информации человечеством изобретено множество методов
шифрования или шифров. Методом шифрования (шифром) называется совокупность
обратимых преобразований открытой информации в закрытую информацию в
соответствии с алгоритмом шифрования. Большинство методов шифрования не
выдержали проверку временем, а некоторые используются и до сих пор. Современные
методы шифрования должны отвечать следующим требованиям:
· стойкость шифра
противостоять криптоанализу (криптостойкость) должна быть такой, чтобы вскрытие
его могло быть осуществлено только путем решения задачи полного перебора
ключей;
· криптостойкость
обеспечивается не секретностью алгоритма шифрования, а секретностью ключа;
· шифртекст не должен
существенно превосходить по объему исходную информацию;
· ошибки, возникающие
при шифровании, не должны приводить к искажениям и потерям информации;
· время шифрования не
должно быть большим;
· стоимость
шифрования должна быть согласована со стоимостью закрываемой информации.
Криптостойкость шифра является его
основным показателем эффективности. Она измеряется временем или стоимостью
средств, необходимых криптоаналитику для получения исходной информации по
шифртексту, при условии, что ему неизвестен ключ.
Сохранить в секрете широко
используемый алгоритм шифрования практически невозможно. Поэтому алгоритм не
должен иметь скрытых слабых мест, которыми могли бы воспользоваться
криптоаналитики. Если это условие выполняется, то криптостойкость шифра определяется
длиной ключа, так как единственный путь вскрытия зашифрованной информации -
перебор комбинаций ключа и выполнение алгоритма расшифрования.
Таким образом, время и средства,
затрачиваемые на криптоанализ, зависят от длины ключа и сложности алгоритма
шифрования.
Теоретическая часть
В данной курсовой работе, был
использован блочный шифр - сеть Фейстеля.
Блочный шифр - разновидность
симметричного шифра. Особенностью блочного шифра является обработка блока
нескольких байт за одну итерацию (как правило 8 или 16). Блочные криптосистемы
разбивают текст сообщения на отдельные блоки и затем осуществляют
преобразование этих блоков с использованием ключа.
В блочных шифрах используются
следующие основные операции:
· сложение по модулю
2;
· сложение по модулю 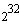 ;
;
· циклический сдвиг на
некоторое число битов;
· различные подстановки и
перемещение битов.
Сеть Фейстеля.
Широкое распространение в блочных
шифрах получила сеть Фейстеля, названная в честь американского инженера Хорста
Фейстела (1915-1990гг.). В ней входной блок делится на два подблока равной
длины, которые называют ветвями (правая R и левая L). Каждая ветвь
обрабатывается независимо от другой. Такое преобразование выполняется несколько
раундов. Считается, что приемлемое с точки зрения безопасности число раундоа -
от 8 до 32.
Структура i-ого раунда показана на
рис.1
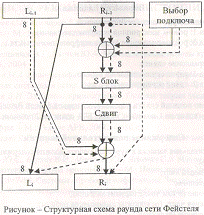
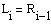
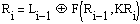
Здесь же штриховой линией обозначена
структура заключительного раунда
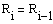
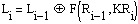
Функция F называется
образующей. В отношении её выбора четких стандартов не существует. Как правило,
эта функция представляет собой последовательность подстановок, перестановок и
циклических сдвигов, зависящих от подключа.
Сеть Фейстеля является
обратимой, т.е, процедуры шифрования и дешифрования совпадают с тем
исключением, что подключи при дешифровании используются в обратном порядке.
шифрование блочный
фейстель криптостойкость
Практическая часть
Таблица перевода чисел и
букв в двоичную систему
|
0
|
А
|
00000
|
|
1
|
Б
|
00001
|
|
2
|
В
|
00010
|
|
3
|
Г
|
00011
|
|
4
|
Д
|
00100
|
|
5
|
Е
|
00101
|
|
7
|
Ж
|
00110
|
|
8
|
З
|
00111
|
|
9
|
И
|
01000
|
|
10
|
Й
|
01001
|
|
11
|
К
|
01010
|
|
12
|
Л
|
01011
|
|
13
|
М
|
01100
|
|
14
|
Н
|
01101
|
|
15
|
О
|
01110
|
|
16
|
П
|
01111
|
|
17
|
Р
|
10000
|
|
18
|
С
|
10001
|
|
19
|
Т
|
10010
|
|
20
|
У
|
10011
|
|
21
|
Ф
|
10100
|
|
22
|
Х
|
10101
|
|
23
|
Ц
|
10110
|
|
24
|
Ч
|
10111
|
|
25
|
Ш
|
11000
|
|
26
|
Щ
|
11001
|
|
27
|
Ъ
|
11010
|
|
28
|
Ы
|
11011
|
|
29
|
Ь
|
11100
|
|
30
|
Э
|
11101
|
|
31
|
Ю
|
11110
|
|
32
|
Я
|
11111
|
Стрелец
|10100000|01010101|10010110|11001101|00000000
Ключ:
|00000000|00000000|00000000:00000000:00000000:00000000:00000000
|
S1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
15
|
14
|
13
|
12
|
11
|
10
|
9
|
8
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
|
S2
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
0
|
Шифрование.
1 часть
10001100
10100000
± К1
00000000
↓
10100000
↓Sблок
10 0
5 1
01010001
сдвиг на 2
01000101
±
11001001
↓
10100000
11001001
± К2
00000000
↓
11001001
↓Sблок
12 9
3 10
00111010 сдвиг на 2
11101000
±
01001000
↓
11001001
01001000
± К3
00000000
↓
01001000
↓Sблок
4 8
11 9
10111001 сдвиг на 2
11100110
±
00101111
↓
01001000
00101111
± К4
00000000
↓
00101111
↓Sблок
2 15
13 0
11010000 сдвиг на 2
01000011
±
00001011
↓
00001011
Дешифрование.
1 часть
00101111
± К4
00000000
↓
00101111
↓Sблок
2 15
13 0
11010000 сдвиг на 2
01000011
±
01001000
↓
00101111
01001000
± К3
00000000
↓
01001000
↓Sблок
4 8
11 9
10111001 сдвиг на 2
11100110
±
11001001
↓
01001000
11001001
±
К2
00000000
↓
11001001
↓Sблок
12 9
3 10
00111010 сдвиг на 2
11101000
±
10100000
↓
11001001
10100000
± К1
00000000
↓
10100000
↓Sблок
10 0
5 1
01010001 сдвиг на 2
01000101
±
10001100
↓
00101011
Шифрование.
2 часть
01010101
10010110
± К1
00000000
↓
10010110
↓Sблок
9 6
6 7
01100111 сдвиг на 2
10011101
±
11001000
↓
10010110
11001000
± К2
00000000
↓
11001000
↓Sблок
12 8
9
00111001 сдвиг на 2
11100100
±
01110010
↓
± К3
00000000
↓
01110010
↓Sблок
7 2
8 3
10000011
сдвиг на 2
00001110
±
11000110
↓
01110010
11000110
± К4
00000000
↓
11000110
↓Sблок
12 6
3 7
00110111 сдвиг на 2
11011100
±
10101110
↓
10101110
Дешифрование.
2 часть
11000110
± К4
00000000
↓
11000110
↓Sблок
12 6
3 7
00110111 сдвиг на 2
11011100
±
01110010
↓
11000110
01110010
± К3
00000000
↓
01110010
↓Sблок
7 2
8 3
10000011 сдвиг на 2
00001110
±
11001000
↓
01110010
11001000
± К2
00000000
↓
11001000
↓Sблок
12 8
3 9
00111001 сдвиг на 2
11100100
±
10010110
↓
11001000
10010110
± К1
00000000
↓
10010110
↓Sблок
9 6
6 7
01100111 сдвиг на 2
10011101
±
01010101
↓
10010110
01010101
Шифрование.
3 часть
11001101
00000000
± К1
00000000
↓
00000000
↓Sблок
0 0
15 1
11110001 сдвиг на 2
11000111
±
00001010
↓
00000000
00001010
± К2
00000000
↓
00001010
↓Sблок
0 10
15 11
11111011 сдвиг на 2
11101111
±
11101111
↓
00001010
11101111
± К3
00000000
↓
11101111
↓Sблок
14 15
1 0
00010000 сдвиг на 2
01000000
±
01001010
↓
11101111
01001010
± К4
00000000
↓
01001010
↓Sблок
4 10
11 11
10111011 сдвиг на 2
11101110
±
00000001
↓
00000001
Дешифрование.
3 часть
01001010
± К4
00000000
↓
01001010
↓Sблок
4 10
11 11
10111011 сдвиг на 2
11101110
±
11101111
↓
01001010
11101111
± К3
00000000
↓
11101111
↓Sблок
14 15
1 0
00010000 сдвиг на 2
01000000
±
00001010
↓
11101111
00001010
± К2
00000000
↓
00001010
↓Sблок
0 10
15 11
11111011 сдвиг на 2
11101111
±
00000000
↓
00001010
00000000
± К1
00000000
↓
00000000
↓Sблок
0 0
15 1
11110001 сдвиг на 2
11000111
±
11001101
↓
00000000
11001101
Заключение
Ознакомились с блочными методами
шифрования. Приобрели практические навыки шифрования и дешифрования информации
с помощью сети Фейстеля.
Список используемой литературы
1. Д.Н. Голышев, С.В. Моторин «Криптографическая защита
информации».
. Лекционный материал по дисциплине «Информационная
безопасность и защита информации».
. Д. . Голышев «Информационная безопасность и защита
информации».