Разработка оптико-электронного пеленгатора с фокальным матричным приёмником излучения
Исходные данные к работе
Оптико-электронный пеленгатор с
фокальным матричным приёмником излучения (МПИ) осуществляет обнаружение
малоразмерной цели на равномерном фоне в ИК спектральном диапазоне 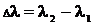
Объект и фон излучают как серые тела
с коэффициентом теплового излучения 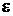 . В бортовой ЭВМ реализуется
алгоритм оптимальной фильтрации и принятие решения об обнаружении в
соответствии с критерием максимального правдоподобия.
. В бортовой ЭВМ реализуется
алгоритм оптимальной фильтрации и принятие решения об обнаружении в
соответствии с критерием максимального правдоподобия.
Пятно рассеяния оптической системы описывается
двумерной функцией Гаусса
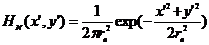 ,
,
с эффективным радиусом 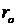 пятна
рассеяния; чувствительные элементы матричного ПИ имеют форму квадрата со
стороной
пятна
рассеяния; чувствительные элементы матричного ПИ имеют форму квадрата со
стороной 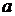 , причём
периоды расположения элементов
, причём
периоды расположения элементов 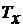 и
и 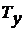 равны между собой. Соотношения
между указанными параметрами характеризуется коэффициентами
равны между собой. Соотношения
между указанными параметрами характеризуется коэффициентами 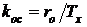 ,
, 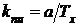 .
.

Рис. 1. Функциональная схема оптико-электронного
пеленгатора с фокальным матричным ПИ:
1 - оптическая система; 2 - фокальный матричный
ПИ; 3 - мультиплексор; 4 - система охлаждения; 5 - корректор неоднородности
характеристик чувствительных элементов; 6 - аналого-цифровой преобразователь; 7
- цифровой корректор неоднородности; 8 - корректор неработающих ячеек; 9 -
цифровая вычислительная система; 10 - цифровой выход.
Технические параметры:
температура фона 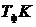 ;
;
температура объекта 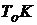 ;
;
коэффициент теплового излучения 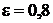 ;
;
площадь объекта 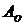 ,
, 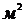 ;
;
·
рабочий
спектральный диапазон описывается функцией
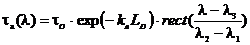 ,
,
Где
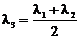 ;
;
показатель поглощения излучения
атмосферой 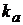 ,
, 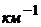 ;
;
коэффициент пропускания оптической
системы 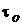 ;
;
фокусное расстояние объектива 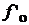 ,
, 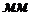 ;
;
диаметр входного зрачка 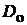 ,
, 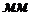 ;
;
пороговая чувствительность МПИ 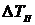 .
.
Перечень вопросов, подлежащих разработке в
домашнем задании:
исследовать зависимость вероятности
обнаружения малоразмерной цели оптико-электронным пеленгатором по критерию
максимального правдоподобия от размера пятна рассеяния объектива при
равновероятном положении пятна на пространственном периоде МПИ и значении
пикового отношения сигнала к шуму 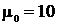 ;
;
оценить дальность действия  пеленгатора
при обнаружении объекта с вероятностью
пеленгатора
при обнаружении объекта с вероятностью 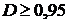 .
.
|
Вариант.
Параметр
|
1
|
|
температура
фона Тф, К
|
280
|
|
температура
объекта ТО, К
|
297
|
|
площадь
объекта
AO, м2
|
2
|
|
пороговая
чувствительность МПИ DTп , К
|
0,07
|
|
l1, мкм
|
8
|
|
l2, мкм
|
13
|
|
показатель
поглощения излучения атмосферой kа, км-1
|
0,09
|
|
диаметр
входного зрачка Do, мм
|
60
|
|
фокусное
расстояние объектива f’o, мм
|
100
|
|
эффективный
радиус пятна рассеяния rо, мкм
|
35
|
|
размеры
чувствительного элемента ПИ a, мкм
|
30
|
|
kпи, отн.ед.
|
0,75
|
|
коэффициент
пропускания оптической системы 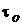 0,7 0,7
|
|
Решение:
1. Исследование зависимости
вероятности обнаружения малоразмерной цели оптико-электронным пеленгатором по
критерию максимального правдоподобия от размера пятна рассеяния объектива при
равновероятном положении пятна на пространственном периоде МПИ и значении
пикового отношения сигнала к шуму 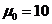 ;
;
Для каждого i-го
кадра отношение сигнал/шум после оптимальной фильтрации определяется
выражением:
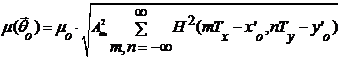 ,
,
где 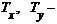 периоды расположения чувствительных
элементов в матричном ПИ;
периоды расположения чувствительных
элементов в матричном ПИ;
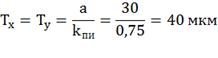
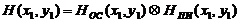 ,
,
где 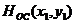 - функция рассеяния оптической
системы,
- функция рассеяния оптической
системы, 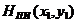 -
пространственный импульсный отклик чувствительных элементов ПИ.
-
пространственный импульсный отклик чувствительных элементов ПИ.
Свертку этих двух функций
осуществим, используя теорему моментов, согласно которой, функция 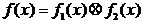 определяется
следующим выражением:
определяется
следующим выражением:
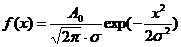 ,
,
Где
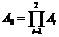 ,
, 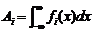 ,
,  .
.
В нашем случае функция рассеяния
оптической системы:
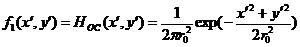 .
.
Пространственный импульсный отклик
чувствительных элементов ПИ:
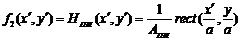
Очевидно, что А1= А2=1.
Таким образом А=1.
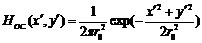
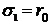
Для пространственного импульсного
отклика чувствительных элементов ПИ:
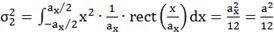 .
.
Тогда
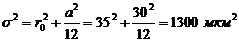
Таким образом, получим:
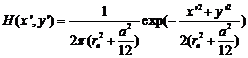
Тогда получим отношение сигнал/шум
после оптимальной фильтрации:
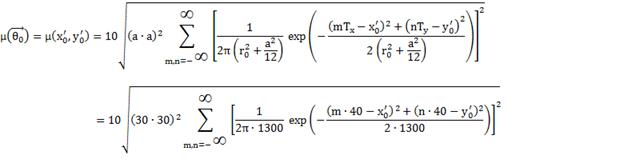
Условная вероятность правильного обнаружения
определяется по формуле:
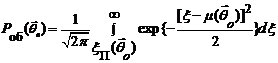
Где
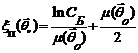
По критерию максимума правдоподобия
пороговое отношение правдоподобия 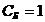 .
.
Тогда
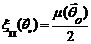
Таким образом, условная вероятность
правильного обнаружения:
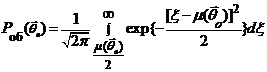 ,
,
Где


Рис. 2. График зависимости условной
вероятности правильного обнаружения цели от координат цели 
электронный пеленгатор
матричный излучение
Безусловную вероятность правильного
обнаружения в зависимости от пятна рассеяния объектива определяется как среднее
значение вероятности правильного обнаружения при равновероятном положении пятна
рассеяния на периоде расположения чувствительных элементов:
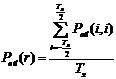
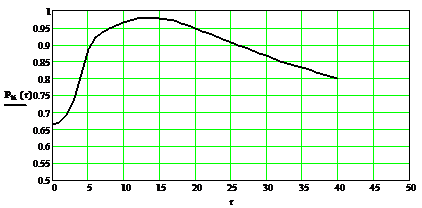
Рис. 3. График зависимости
безусловной вероятности правильного обнаружения цели от относительного размера
пятна рассеяния ОС
По графику определяем, что
максимальная вероятность обнаружения точечного объекта Робн=0,962 достигается
при радиусе кружка рассеяния r=23,2 мкм.
. Оценка дальности действия  пеленгатора
при обнаружении объекта с вероятностью
пеленгатора
при обнаружении объекта с вероятностью  .
.
Найдем длины волн максимальной
светимости цели и фона, используя закон смещения Вина:
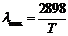
Длины волн максимальной светимости
цели и фона:
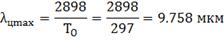
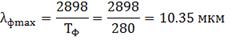
Спектральная плотность светимости
АЧТ:
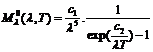 ,
, 
По закону Ламберта:
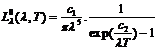 ,
,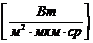
Нормированное спектральное
распределение приращения силы излучения от цели:
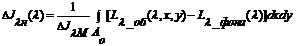 ,
,
где 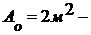 площадь проекции излучающей
поверхности объекта в направлении визирования,
площадь проекции излучающей
поверхности объекта в направлении визирования,
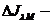 максимальное значение приращения
спектральной силы излучения цели.
максимальное значение приращения
спектральной силы излучения цели.
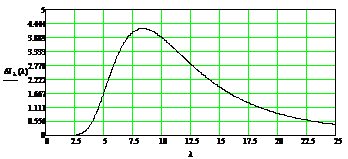
Рис. 4. Спектральное распределение приращения
силы излучения от цели в зависимости от длины волны
Найдем длину волны, при которой спектральное
распределение приращения силы излучения от цели будет максимальной: λmax=8,347
мкм.
А максимальное спектральное приращение силы
излучения от цели тогда будет равно:
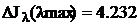
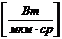
Рис. 5. Нормированное спектральное
распределение приращения силы излучения от цели в зависимости от длины волны
Идеальная спектральная чувствительность
приёмника КРТ представлена ниже:
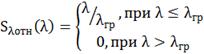 ,
,
где 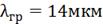 .
.
Рассчитаем отношение сигнал/шум:
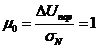
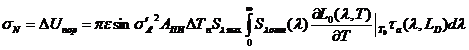 ,
,
где 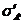 - задний апертурный угол.
- задний апертурный угол.
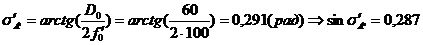
 ,
,
где 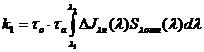 ,
, 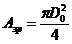
Таким образом, получаем зависимость
дальности до объекта от отношения сигнал/шум:
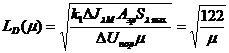 .
.
Найдём отношение сигнал/шум, при котором
обнаружение производится с вероятностью Робн>0,95.

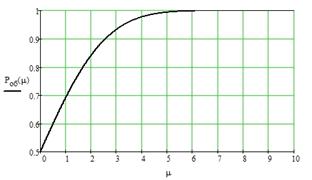
Рис. 6. График зависимости
вероятности правильного обнаружения цели от отношения сигнал/шум.
Отношение сигнал/шум, при котором
обнаружение производится с вероятностью Робн>0.95 соответствует
µ=3,4.
Тогда: 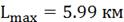 .
.