Проектирование РЭА

Введение

При конструкторском проектировании РЭА (радиоэлектронной аппаратуры) решаются задачи, связанные с поиском наилучшего варианта конструкции, удовлетворяющего требованиям технического задания и максимально учитывающего возможности технологической базы производства. Тесная взаимосвязанность задач и большая размерность каждой из них обычно не позволяет предложить метод поиска оптимального конструктивного решения в едином цикле в связи с трудностями создания общей математической модели, комплексно учитывающей особенности конструкторско-технологической базы производства. Поэтому разработка и реализация алгоритмов и методов решения отдельных задач этапа конструкторского проектирования: компоновки, размещения и трассировки, - до сих пор остаются актуальными проблемами, решение которых неотъемлемо связано с развитием систем автоматизации проектирования.

1. Алгоритмы конструкторского проектирования систем управления. Задача, критерии компоновки

компоновка радиоэлектронный алгоритм проектирование

Среди алгоритмов конструкторского проектирования (КП) выделяют два основных класса: конструктивные и итерационные.

Конструктивные алгоритмы формируют проектное решение за ряд последовательных шагов:

выбирается один элемент схемы рассматриваемого уровня;

к выбранному элементу по определенным правилам присоединяется второй;

к полученному комплексу элементов добавляется третий и т.д.

Алгоритмы, использующие подобную методологию, называются последовательными. Алгоритмы, в которых формируются несколько групп элементов в пределах одного шага, называются параллельными.

Итерационные алгоритмы требуют задания начального приближения решения задачи КП, которое затем улучшается. Начальное решение задается инженером-проектировщиком (пользователем САПР) или является результатом работы конструктивного алгоритма.

Анализ процесса конструирования электронных устройств (ЭУ) на основе существующих методов можно проводить, используя разные точки зрения. На входе процесса проектирования ЭУ имеется функциональная схема, которая содержит информацию о базовых элементах (в зависимости от уровня проектирования), о связях между элементами и внешних связях проектируемого ЭУ. Кроме того, задаются технологические параметры, например, при конструировании печатного узла - размер печатной платы, разрешенные для применения в данной разработке серии микросхем, шаг сетки трассировки и т.п. В результате проектирования должен получиться рисунок трассировки.

Общей целевой функцией Ф всего процесса проектирования печатной платы (ПП) следует считать число проведенных связей. Целевая функция Ф зависит от случайных входных параметров ж (например, числа базовых элементов, числа задействованных выводов элементов схем и т.д.), так и от переменных, статистически устойчивых для класса разработок в (размеры ПП, серии микросхем, разрешенных для применения и т.п.). Хотя оптимальный размер ПП может быть определен с достаточной точностью как функция входных параметров, этот вопрос практического применения не нашел, так как изготовление и применения плат различных размеров в одной разработке связано с изменением технологической оснастки производства.

Действия над входными величинами (ж, в) в процессе проектирования можно представить следующим образом. Обозначив совокупность используемых в САПР алгоритмов компоновки К, совокупность алгоритмов размещения Р и совокупность алгоритмов трассировки Т можно представить схему последовательной реализации основных алгоритмов (рис. 1)

Рисунок 1 - Процесс проектирования ЭУ

Возможно использование алгоритмов совместного решения задач компоновки и размещения, размещения и трассировки, компоновки и трассировки (при этом трассировка выполняется на условном коммутационном поле).

Общая задача проектирования формулируется следующим образом: имея заданные условия в и случайные воздействия ж, найти такую совокупность алгоритмов и критериев {К, Р, Т}, которая обеспечивала бы получение максимального конечного значения целевой функции Ф. Таким образом, имеется задача о выборе и принятии решения в условиях неопределенности. Оптимизация решения на каждом шаге отдельно не всегда дает в сумме оптимальное решение, особенно, если на промежуточных этапах слабо учитывается конечный критерий. Указанный недостаток является причиной поиска связей между основными этапами КП.

Задачи компоновки можно представить в виде сложных комбинаторных моделей, для которых в большинстве случаев отсутствуют эффективные точные методы решения даже при использовании ЭВМ. Тем не менее, анализ таких моделей представляет не только методический, но и практический интерес, так как в процессе формализации задачи часто вырабатываются эффективные приближенные алгоритмы ее решения.

Обычно задачи компоновки рассматриваются как процесс принятия решений в определенных или неопределенных условиях, в результате выполнения которого части логической схемы располагаются в конструктивных элементах i-го уровня, а эти элементы размещаются в конструктивных элементах (i+1) - го уровня и т.д., причем расположение выполняется с оптимизацией по выбранному критерию.

Можно выделить два основных класса задач компоновки: алгоритмы компоновки конструктивных узлов и алгоритмы компоновки типовых узлов (ячеек) (рис. 2). Алгоритмы первой группы можно классифицировать по критериям оптимизации, по ограничениям на формирование узлов или по структуре вычислительной процедуры.

Основными критериями оптимизации являются:

1)      минимум числа межузловых соединений.

А ограничениями:

)        количество элементов в узле;

)        число внешних выводов на узле.

С точки зрения вычислительной процедуры алгоритмы компоновки конструктивных узлов можно разделить на:

)        последовательные;

2)      параллельно последовательные;

3)      итерационные.

В алгоритмах первого типа вводится последовательный процесс компоновки узлов, на каждом шаге которого в очередной узел добавляется один из элементов схемы (например, алгоритм компоновки по приведений). В параллельно-последовательных алгоритмах сначала выделяется некоторое исходное количество групп элементов, которые потом распределяются по узлам с учётом ограничений и критериев на компоновку.

Последовательные и параллельно-последовательные алгоритмы применяются для создания базового (начального) варианта компоновки при заданных ограничениях на число элементов в узле число выводов на узле.

Итерационные алгоритмы компоновки служат для улучшения некоторого начального в соответствии с принятыми критериями и используются в сочетании с другими алгоритмами компоновки. Основной задачей алгоритмов компоновки типовых узлов является получение покрытия с минимальной суммарной стоимостью (минимум числа использованных типовых узлов). Структура алгоритмов зависит от особенностей используемого набора типовых узлов. 

. Алгоритмы компоновки, использующие методы целочисленного программирования

Для упрощения будем считать, что схема представлена взвешенным графом коммутационной схемы G = (E, U), где E - множество вершин, соответствующих элементам схемы, U - множество ребер соответствующих цепей, и матрицей соединений R=||r_ij||_nЧn, _n строки и столбцы которой соответствуют элементам схемы, а r_ij равен весу, приписанному соединению элементов е_i и e_j.

Пусть каждому элементу e_iE приписан некоторый вес p_i>0 (i=1, 2, …, п). Например, p_i может быть связан с размерами элемента, мощностью, рассеиваемой элементом, и т.п. Далее, пусть заданы ограничения на формирование узлов: максимальная вместимость узла k в максимальное число выводов на узле v.

Требуется осуществить при этих условиях компоновку элементов из E в узлы T_l (l=1, 2,…, г) таким образом, чтобы количество межузловых соединений было минимальным.

Введем матрицу переменных X=||x_il||_nЧг, в которой x_il=1, если e_iT_l, x_il=0 в противном случае. Поскольку элемент e_i может находиться лишь в одном узле,

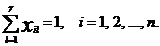      (2.1)

Ограничение на вместимость узла T_l приводит к следующим неравенствам:

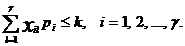 (2.2)

Число внешних соединений узла T_l может быть записано в виде

      (2.3)

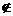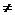Действительно, х_il=(1 - х_il) = 1 тогда и только тогда, когда e_iT_l, а e_jT_l (e_jT_s, sl₎.

Получим теперь выражение для критерия оптимизации. На основании (2.3) количество межузловых соединений:

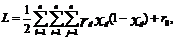  (2.4)

где r₀ - внешние соединения схемы.

Таким образом, задача состоит в минимизации функции (2.4) при ограничениях (2.1), (2.2) и дополнительных ограничениях:

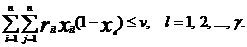         (2.5)

Отметим, что при p_i=l (i=l, 2,…, n) ограничение (2.2) равносильно ограничению на число элементов в узле.

Описанная задача оптимизации представляет собой задачу нелинейного целочисленного программирования, для которой отсутствуют эффективные методы решения.

Лоуером предложена оригинальная процедура, позволяющая при определенных ограничениях на формирование узлов свести задачу компоновки к известной задаче покрытия, возникающей при минимизации нормальных форм булевых функций. Для пояснения идеи метода введем некоторые определения.

Набор ограничений на формирование узлов выделяет допустимые узлы из всех возможных.

Разбиение Т₁ Т₂,…, T_г называется допустимым, если каждый узел T_s (s=1, 2, …, г) является допустимым. Набор ограничений называется регулярным, если из допустимости узла следует допустимость любого подмножества элементов этого узла. Очевидно, что ограничение на число элементов в узле является регулярным, а на число внешних соединений узла - нет.

Рассмотрим схему рисунке 3. Пусть ограничение по числу выводов v=3, тогда узел Т={е₁, е₂, е₃, е₄, е₅} является допустимым, однако Т'={е₁ е₂, е₄, е₅} является недопустимым узлом, поскольку имеет четыре внешних соединения.

Рисунок 3 - Нерегулярное ограничение

Пусть схема соединений задана графом G = (E, V, W). Рассмотрим некоторое разбиение К_г ={T₁, Т₂,…, T_г} схемы на допустимые узлы.

Эквивалентная задача минимизации функции:

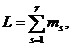    (2.5)

в которой m_s=|J_s| равно числу цепей, связанных с элементами узла T_s.

Рассмотрим теперь семейство P={T_s} непустых подмножеств множества удовлетворяющее следующему условию:

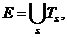     (2.6)

Т_s - допустимый узел. Отметим, что условие (2.6) разрешает повторные вхождения элементов в некоторые узлы: в общем случае T_s∩T_l ≠Ш при s≠l.

Имеет место следующая теорема: если набор ограничений регулярный, то минимум числа межузловых соединений при условии, что каждый элемент входит точно в один узел, равен минимальному числу межузловых соединений при условии, что каждый, элемент входит, по крайней мере, в один узел (2.6).

Справедливость теоремы устанавливается следующим образом.

Пусть L*_K и L*_P - соответственно минимальное значение функции (2.5) на множестве допустимых разбиений К и при более слабом условии (2.6). Область решений при условии (2.6) шире области решений задачи компоновки, поэтому L*_K ≤ L*_P.

Пусть Р* - некоторая совокупность узлов, для которой L (P*)=L*_p. Построим из Р* некоторое разбиение К путем устранения повторных вхождений элементов в узлы Т_sР*. Так как набор ограничений регулярный, то каждый из узлов К будет допустимым, при этом L*_K ≤ L(К)≤ L*_P, поскольку при устранение лишних вхождений число соединений не может увеличиться. Учитывая, что L*_P ≤ L*_K, окончательно получим L*_P = L(К)=L*_K, где К - разбиение, сконструированное указанным способом/

Таким образом, решение задачи компоновки может быть получено из задачи минимизации функции (2.5) при условий (2.6).

Пусть Р={Т_s} - множество всех допустимых узлов. Легко показать, что при решении этой задачи можно ограничиться рассмотрением лишь множества Р' ={T₁,…, Т_s,…, Т_р} максимально допустимых узлов.

Узел T_s называется максимально допустимым, если он имеет связную схему соединений и не является частью другого допустимого узла.

Будем искать минимум функции (2.5) на множестве Р'. Построим матрицу X = || х_si||_pЧn, строки которой соответствуют узлам из Р', а столбцы - элементам множества Е. Элемент матрицы х_si =1, если e_iT_s, и х_si=0 в противном случае. Присвоим строке i матрицы вес m_s, равный числу цепей, связанных с элементами узла T_s.

Тогда задача минимизации функции (2.5), становится эквивалентной отысканию такого подмножества строк матрицы X, которое покрывает все столбцы матрицы X и имеет минимальный суммарный вес. Заметим, что та же задача возникает при выборе по таблице простых импликант булевой функции подмножества импликант, имеющего минимальное суммарное число переменных. Отсюда следует, что теоретически возможно на данном этапе применять классические методы минимизации булевых функций. Приведем постановку полученной задачи в виде модели линейного целочисленного программирования:

Найти минимум функции

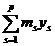        (2.7)

при следующих ограничениях:

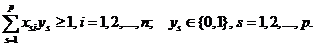   (2.8)

Решение задачи (2.7), (2.8) определяется набором переменных {y_s}. Если y_s = 1, то T_s Р' входит в решение задачи компоновки, и если y_s =0, то не входит. Отметим, что если положить m_s= 1, то получим задачу минимизации количества узлов компоновки: найти минимум функции

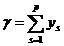      (2.9)

при ограничениях (2.8).

Рассмотренный выше способ сведения задачи компоновки к моделям линейного целочисленного программирования представляет скорее теоретический, чем практический интерес. Действительно, для схем реальной сложности число узлов р, включаемых в базовое множество, может быть много больше 1000. В связи с этим получение точного решения задачи одним из известных методов трудновыполнимо даже при использовании ЭВМ высокой производительности. Тем не менее рассмотренные модели могут быть основой для разработки эвристических алгоритмов компоновки.

3. Последовательные методы компоновки. Метод компоновки по связности

Рассматриваемый ниже метод занимает центральное место в группе последовательных алгоритмов компоновки. Его первоначальная версия была изложена в работе Гэмблина и получила название метода максимальной конъюнкции - минимальной дизъюнкции. Основу метода составляет последовательная процедура выделения из исходной схемы связанных групп элементов, осуществляемая с помощью операций конъюнкции и дизъюнкции над элементами схемы. Этот метод был использован для компоновки узлов (ячеек и панелей) в системе автоматизации фирмы IBM. Впоследствии появились различные модификации метода, учитывающие конкретные ограничения в задачах компоновки конструктивных узлов и модулей логических схем. Рассмотрим общую схему метода.

Пусть дана схема соединений элементов из множества E={e₁,…, е_п}. Определим последовательный процесс назначения элементов e_iE (i=1, …, n) в узлы T_r один из не распределенных элементов и приписывается очередному узлу.

Узел считается завершенным, если число элементов в узле равно заданному числу k либо назначение любого из нераспределенных элементов приводит к образованию такого числа внешних связей узла, которое превышает допустимое значение v.

После завершения очередного узла аналогичная процедура повторяется для следующего, причем кандидатами для назначения являются элементы, не включенные в предыдущие узлы. Процесс заканчивается, когда все элементы множества E распределены.

Тактика назначения состоит в следующем:

n⁰ 1. На очередном шаге процесса выделяются те из нераспределенных элементов, включение каждого из которых в данный узел не нарушает ограничений по числу элементов и выводов узла.

n⁰ 2. Элементом, включенным в узел на очередном шаге является тот из указанных в n⁰ 1 элементов, который имеет наибольшее число связей с элементами уже включенных в узел (максимальная конъюнкция). При нескольких таких элементах включается тот из них, который имеет минимальную дизъюнкцию с элементами узла.

Описанный выше последовательный процесс компоновки отражает общую схему метода максимальной конъюнкции - минимальной дизъюнкции. Конкретные алгоритмы, реализующие данный метод, отличаются способами представления схемы соединений и вычисления оценок, управляющих процессом компоновки.

Ниже рассматривается алгоритм компоновки, в котором схема представлена графом G=(E, V, W) (матрицей комплексов Q).

Формирование очередного узла T_r=(r=1,2, …, г) начинается с выбора базового элемента i^*_r из множества нераспределенных элементов I_r. В начале процесса все элементы считаются не распределенными, т.е. I₁=E.

Для элемента xI_r введем функционал

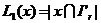,       (3.1)

определяющий число цепей, связывающих элемент х и элементы из множества I’_r=I_r\х. Для упрощения записи здесь и в дальнейшем будем отождествлять элемент (множество элементов) с множеством цепей, связанных с этим элементом (множеством элементов).

Базовый элемент i^*_r есть первый по порядку элемент из I_r, для которого функционал (3.1) принимает максимальное значение. Элемент i^*_r помещается в узел Т_r, а оставшиеся элементы I_r\i^*_r являются кандидатами для включения в узел Т_r на последующих шагах алгоритма. Таким образом, элемент i^*_r, помещаемый первым в узел, является как бы «центром группирования», к которому в последующем добавляются новые элементы.

Последовательность компоновки узла Т_r управляется функционалами L₂(x) и L₃(x).

Рассмотрим л-й шаг (л=1, 2,…, k-1) при назначении элементов в узел Т_r (r=1, 2,…, г). Пусть в узле уже размещено л элементов:

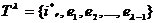       (3.2)

Функционал L₂(x) заданный на множестве нераспределенных к данному моменту элементов :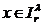

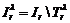     (3.3)

определяет число внешних соединений для узла

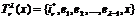,         (3.4)

полученного добавлением элемента 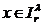в узел (3.2).

В том случае, когда L₂(x)>v, число внешних соединений превышает предельно допустимое. Так как процесс компоновки узлов является последовательным, то включение в узел Т_r, элементов, для которых L₂(x)>v, может привести к тому, что завершенный узел будет иметь недопустимое число внешних соединений. В силу этого такие элементы из рассмотрения исключаются.

Для формального задания L₂(x) обратимся к рисунку 4.

Рисунок 4 - Компоновка узла

Число выводов, требуемое для соединения элементов множества 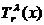 (3.4) с остальными элементами, равно

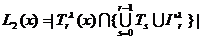,      (3.5)

где 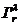-цепи, связанные с элементами множества  (3.3), за исключением элемента x.

С помощью функционала L₃(x) из элементов удовлетворяющих условию L₂(x)≤v, отбирается такой элемент, для которого число цепей, связанных с элементами из 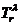 (3.2) максимально:

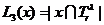.      (3.6)

Элемент x имеет максимальную конъюнкцию с множеством 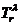. Если имеется несколько элементов с равными и максимальным значениям L₃(x), выбирается тот для которого L₂(x) минимальное значение.

В рассматриваемом алгоритме вместо вычисления дизъюнкции элемента x и множества  выбор (при равных значениях конъюнкции) осуществляется на основании значения L₂(x), что приводит к более экономной схеме вычислений.

4. Итерационные алгоритмы улучшения компоновки

Пусть имеется некоторый начальный вариант компоновки, полученный одним из последовательных алгоритмов либо вручную. Основой рассматриваемых алгоритмов компоновки является использование итерационного процесса обменов местами элементов или групп элементов, принадлежащих различным узлам, с целью минимизации некоторого критерия. Поскольку структура большинства алгоритмов этого типа имеет много общего, рассмотрим процесс улучшения компоновки применительно к произвольному критерию F.

Обозначим через К₀ некоторый исходный вариант компоновки элементов. Ему соответствует значение функции-критерия F₀. В некотором смысле структура итерационного процесса улучшения варианта К₀ аналогична градиентным методам оптимизации, в которых на каждой итерации осуществляется движение в области определения функции в направлении уменьшения ее значений. Изменениям переменных в данном случае соответствует перестановка элементов между различными узлами.

Пусть задано некоторое разбиение К₀ множества элементов Е на узлы T₁,…. T_i,…, T_j,…, Т_г.

Предположим, что произведен выбор пары элементов e_x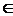T_i и e_y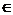T_j и они взаимно меняются местами. В этом случае получаем новый вариант разбиения К₁ с узлами

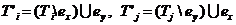,        (4.1).

которому соответствует значение критерия F₁.

Если ДF=F₀-F₁>0, то происходит уменьшение функции-критерия F и обмен, соответствующий данному случаю, считается успешным.

Рассматривая вариант компоновки K₁ снова как исходный, можно осуществить поиск другой пары элементов, обмен которых приведет к уменьшению значения F₁, и т.д. Таким образом, в ходе указанного итерационного процесса образуется последовательность вариантов компоновки K₀, K₁, К₂,…, К_s, которым отвечает монотонно убывающая последовательность значений критерия: F₀>F₁>F₂>… >F_s (рисунок 5). Поскольку значения функции F на множестве допустимых вариантов компоновки {К} ограничены снизу величиной абсолютного минимума функции F_*, естественно, что на некотором шаге процесс минимизации закончится, причем F_s≥F_*, т.е. мы получим вариант компоновки K_s, отвечающий локальному минимуму функции F.

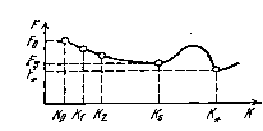
Рисунок 5 - Изменение критерия F

В этот момент обмен любой пары элементов уже не приводит
к уменьшению значения F_s. Для дальнейшего уменьшения F надо рассматривать, например, перестановки групп элементов из различных узлов.

Следует указать на возможность использования различных тактик при выборе пары элементов, обеспечивающих успешный обмен.

Одна из них состоит в следующем. Выбирается некоторый узел T_i и в нем произвольный элемент е_х. Осуществляются попытки обмена этого элемента последовательно со всеми элементами е_у, не принадлежащими рассматриваемому узлу, и рассчитывается приращение ДF(е_х, е_у). Для обмена выбирается первый элемент е_у, для которого ДF(e_x, e_y) >0.

Другой способ состоит в подборе такой пары элементов, для которой ДF(e_x, е_у) принимает максимальное значение. Очевидно, что в этом случае время поиска успешного обмена возрастает, однако в результате обмена число межузловых соединений будет меньше.

Из сказанного следует, что обобщенная характеристика эффективности любого итерационного алгоритма компоновки должна учитывать как время получения решения, так и степень его приближения к оптимальному. Вместе с тем, в настоящее время не представляется возможным дать теоретическую оценку эффективности различных алгоритмов компоновки. Наиболее реальным способом оценки является их экспериментальное сопоставление на задачах одного типа. Имеющиеся данные показывают, что итерационные алгоритмы наиболее целесообразно использовать для улучшения начального варианта компоновки, полученного одним из быстрых последовательных алгоритмов.

Для фиксации момента окончания итерационного процесса при реализации алгоритма на ЭВМ применяются различные правила. Например, может задаваться число итераций m либо параметр д, определяющий число итераций неявным образом:

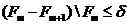.  (4.8)

Далее рассмотрим процесс расчета приращений.

Пусть задано некоторое разбиение множества Е= {e₁, e₂,…, е_п} на узлы T₁ Т₂,…, T_г.

Рассмотрим сначала случай, когда схема описана матрицей соединений R=||r_ij||_nЧn. Оценим изменение в количестве межузловых соединений при обмене местами элементов е_хT_i, и е_уТ_j. Поскольку при обмене перераспределяются лишь соединения элементов е_х и е_у, рассмотрим более детально структуру их соединений (рисунок 6).

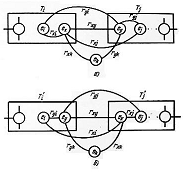
Рисунок 6 - Межузловые соединения: а) - до обмена, б) - после обмена.

Обозначим через U_ij, множество элементов {е_k: е_kТ_i и е_kТ_i}. Тогда в соответствии с рисунком 4, а количество межузловых соединений до обмена равно

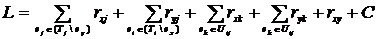,        (4.9)

где С - число межузловых соединений не участвующих в обмене элементов.

В соответствии с рисунком 4, б после обмена количество межузловых соединений станет равным

Вычитая (4.10) из (4.9), получим

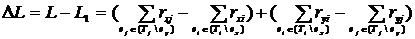  (4.11)

Пусть L_xj - число соединений e_x с элементами узла T_j, L_yi - число соединений e_y c элементами узла T_i:

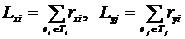,         (4.12)

а F_xi - число соединений e_x с элементами узла T_i и F_yj - число соединений e_y с элементами узла T_j

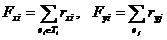    (4.13)

Тогда (4.11) принимает вид:

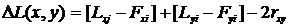        (4.14)

L_xi (L_yi) и F_xi (F_yj) соответственно внешние и внутренние соединения элементов e_x и e_y.

Для произвольного элемента e_xT_i удобно ввести характеристику D_x=L_xj-F_xi, представляющую собой разность числа внешних и внутренних соединений. Аналогично вводится характеристика D_у для e_yT_j.

С учётом принятых обозначений формула (4.14) приобретает вид

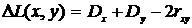         (4.15)

При обмене местами элементов e_xT_i и e_yT_j наряду с изменением количества межузловых соединений L происходит перераспределение внешних соединений для узлов T_i и T_j.

При задании схемы матрицей R суммарное число выводов на узлах V=2L, поэтому

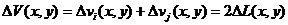,       (4.16)

где ДV (x, y) - изменение суммарного числа выводов на узлах, а Дv_i(x, y) и Дv_j(x, y) - изменение числа выводов на узлах T_i и T_j.

Получим теперь выражения для Дv_i(x, y) и Дv_j(x, y). Обратимся к рисунку 4. Число внешних выводов на узле равно числу соединений между элементами узла и элементами, не входящими в узел. В связи с этим для расчета Дv_i(x, y) можно использовать (4.15), если придать входящим в нее характеристикам D_x и D_y другой содержательный смысл.

Можно считать, что имеются два узла T_i и T_j*=U_ij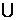T_j=E\T_i. Введем характеристики D^*_x и D_y:

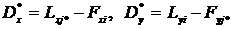(4.17)

тогда на основании (4.15)

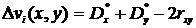.       (4.18)

Заметим, что

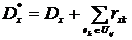, (4.19)

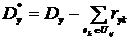  (4.20)

поэтому формулу (4.18) можно записать, учитывая (4.15), в такой форме:

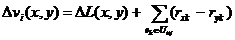         (4.21)

На основании (4.16) получим

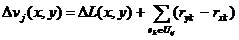              (4.22)

Пусть теперь схема задана одним из способов, при котором непосредственно учитываются соединения с размером p>2. Для формул приращений, аналогичных (4.15), (4.21) и (4.22) воспользуемся аппаратом алгебры соединений.

Число межузловых соединений L в этом случае будет равно

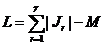,      (4.23)

где J_r - множество цепей, связанных с r-м узлом; M - общее количество цепей в схеме.

Найдем приращение количества межузловых соединений ДL (x, y) при обмене элемента e_xT_i с элементом e_yT_j.

Для упрощения будем обозначать множество цепей, связанных с некотором подмножеством элементов A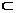E, тем же символом. Тогда в результате обмена новым узлам T’_i и T’_j будут отвечать множества цепей:

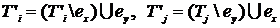(4.24)

В соответствии (4.23) после обмена количество межузловых соединений станет равно

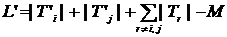  (4.25)

поскольку T’_r = T_r при r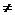i, j; r=1,2, …, г.

На основании (4.23) и (4.25) получим

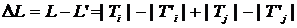.     (4.26)

Представим множества цепей узлов T_i и T_j в виде

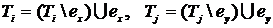. (4.27)

Подставляя в (4.26) выражения (4.24) и (4.27) и применяя тождество

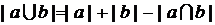,   (4.28)

получим после ряда упрощений формулу, аналогичную (4.11):

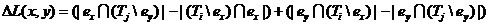      (4.29)

Пусть L_xy - число цепей, связывающих элемент е_х с элементами узла T_j, и F_xi - число цепей, связывающих е_х с элементами узла Т_i. Тогда

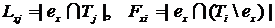. (4.30)

Аналогичные выражения имеют место для характеристик L_yi и F_yiэлемента е_у. Преобразуем теперь выражение для L_xj, используя тождество (4.28):

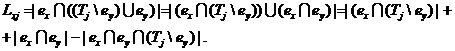   (4.31)

Осуществив подобное же преобразование выражения для L_yi и подставляя вместо первого и третьего членов в формуле (4.29) соответствующие выражения, получим

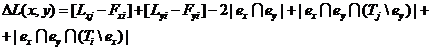        (4.32)

Обозначая, как и ранее в (4.14), члены в скобках (4.32) через D_x и D_y, окончательно придем к следующему результату:

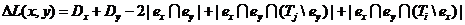(4.33)

Сравнение (4.33) с (4.15), полученной для задания схемы матрицей соединений R, показывает, что при представлении схемы цепями (комплексами) необходимо при расчете ДL учитывать поправочные члены, связанные с наличием многоконцевых цепей (р>2). Заметим, что член 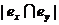равен числу цепей, соединяющих элементы е_х и е_у, и в (4.15) ему соответствует член r_ху.

Перейдем теперь к расчету изменений выводов на узлах. Согласно (4.19) число выводов на узле T_i равно

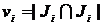,       (4.34)

где e_x и e_y - множества цепей, связанных соответственно с элементами узла T_i, и с элементами, не входящими в узел Т_i.

При обмене местами элементов е_х и е_у изменяется число выводов лишь на узлах T_i и T_j.

Вычислим приращение в числе выводов на узле T_i:

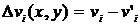          (4.35)

где v_i, - и v'_i - соответственно число выводов на узле до и после обмена. Заметим, что приращение числа выводов Дv_i(x, у) равно приращению числа соединений между элементами узла T_i и элементами, не входящими в узел T_i. Поэтому формула для расчета Дv_i(x, у) может быть непосредственно получена из (4.35) при замене узла T_j на множество элементов :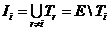

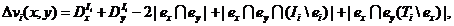   (4.36)

где

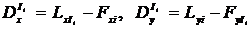      (4.37)

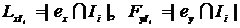.       (4.38)

Аналогичная формула имеет место для приращений числа выводов на узле T_j. Для ее получения необходимо лишь заменить везде в (4.36), (4.37), (4.38) символ I_i на I_j обозначающий множество элементов, не входящих в узел T_j: I;=E\T_j, символ х на у, а символ у на х.

Заметим, что для многоконцевых соединений равенство, аналогичное (4.16), уже не выполняется.

Пусть известен некоторый вариант разбиения схемы на г узлов. Можно считать, что в каждом узле содержится ровно k элементов, причем n=kг. В случае, когда в каком-либо узле число элементов k_r меньше k, всегда можно дополнительно ввести n_д=k-k_r фиктивных элементов, не связанных с другими элементами схемы: r_sj=0, s=n+1,…, n + n_д, j=1, 2,…, n + n_д.

Рассмотрим два узла T_i, и T_j, (i, j=1, 2    г). В соответствии с (4.15) приращение числа межузловых соединений при обмене местами элементов е_xT_i, и e_yT_j будет равно ДL (x, y)=D_x+D_y-2r_xv, где характеристики D_x и D_v рассчитываются по матрице соединений R.

Опишем процесс выбора пары элементов е_х и e_v для обмена. Сначала определяются характеристики D_z, для всех элементов е_z, принадлежащих T_i, или T_j. Число этих характеристик равно 2k.

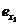
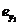
Далее находится пара элементов Т_i и T_j,
для которой (4.15) принимает максимальное значение. Если ДL (x, y)>0, то производится обмен. В результате образуются узлы Т’_i и Т’_j.

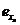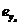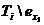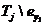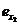Зафиксировав положение элементов  и  соответственно в узлах T'_j и T'_i, выполняем аналогичный расчет для элементов из множеств  и  и определяем новую пару элементов для обмена  и 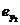. Процесс обменов продолжается до тех пор, пока на очередном шаге s+1 среди элементов  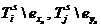не найдется ни одной пары, для которой ДL (x, у) > 0. Узлы T^s_i и T^s_j отвечают результату минимизации числа межузловых соединений между исходными узлами T_i и T_j.

Заметим, что при обмене элементов не все из рассчитанных на предыдущем шаге характеристик D изменяются. Имеют место следующие соотношения:

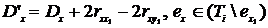
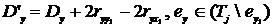  (4.39)

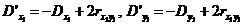        (4.40)

Справедливость (4.39) может быть легко проверена. Действительно, 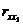 внутренних соединений элемента е_х в результате обмена становятся внешними по отношению к узлу T_i, а внешних соединений внутренними.

Отсюда непосредственно следует первое из соотношений (4.39). Остальные соотношения могут быть проверены аналогично.

Использование (4.39) и (4.40) существенно сокращает трудоемкость вычислений характеристик D при расчете приращений ДL (x, y) на каждой итерации. Для времени поиска пары элементов с ДL (x, y)>0 можно предварительно упорядочить характеристики D (сортировка).

Расположим характеристики D элементов из узлов T_i и T_j следующим образом:

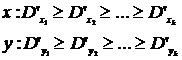.          (4.41)

Организуем процесс вычисления ДL (x, y) так, чтобы в первую очередь кандидатами для обмена были элементы, находящиеся в начале последовательностей x и y в (4.41), тогда если 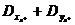меньше, чем максимальное из ранее найденных значений ДL (x, y), то по (4.15) среди оставшихся элементов {x_s: s>s_*} и {y_l: l>l_*} нет пары с большим значением ДL (x, y), поэтому поиск может быть прекращен.

Таким образом, предварительная сортировка D позволяет сократить количество просмотров для вычисления ДL (x, y)_max по сравнению с k² просмотрами при обычном переборе.

После окончания процесса минимизации числа соединений между узлами T_i и T_j (малая итерация) аналогичная процедура может быть применена к другой паре узлов. Так как имеется г узлов, то в принципе возможно осуществить р=г (г-1)/2 малых итераций. Совокупность малых итераций составляет одну большую. После окончания большой итерации минимизацию числа межузловых соединений можно продолжить, начиная снова с первой пары узлов. Процесс заканчивается, когда либо обмены элементов между двумя любыми узлами не приводят к уменьшению целевой функции, либо было проведено р_* больших итераций.

В рассмотренном выше алгоритме парных перестановок производится последовательная минимизация связей между парами узлов в начальном варианте компоновки. Однако возможны и другие способы организации итерационного процесса. Среди них отметим метод последовательного разделения и метод последовательного выделения.

Идея первого метода состоит в следующем. Для упрощения предположим, что число компонуемых узлов г=2^л. В качестве начального варианта используем какой-либо вариант разбиения п элементов на две группы А и В по n/2 элементов. Далее применяем основной алгоритм парных перестановок для узлов А и В. Полученные узлы снова разделяем на два и т.д. до получения узлов требуемого размера. Рисунок 7 иллюстрирует процесс разделения.

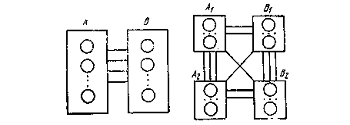
Рисунок 7 - Последовательное разделение

Вначале минимизируются связи между группами А и В, затем связи между группами A₁ и A₂ B₁, и В₃. Результат, полученный для одного уровня разделения, не ухудшается при последующих разделениях. Данный метод имеет наибольшую эффективность для схем, содержащих сильно связанные группы элементов, причем размеры этих групп приблизительно одинаковы.

Другой метод состоит в последовательном выделении (рисунок 6) из исходного множества n элементов групп по k элементов с использованием итерационного процесса обменов элементов, входящих в выделенную группу Т_i элементами из множества

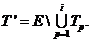(4.42)

Рисунок 8 - Последовательное выделение

Рассмотрим рисунок 8. Пусть получено разбиение исходного множества элементов на две группы Т₁ и T’₁=E\T₁. Указанное разбиение может быть, например, произведено с помощью алгоритма последовательной компоновки. Обычным образом производится минимизация числа соединений между узлом T_i и множеством элементов Т’₁. Далее из множества T’₁ выделяется следующая группа T₂ из k элементов и осуществляется аналогичная процедура минимизации для множеств T’₂ и T’₂=T’₁\T₂ и т.д. Процесс продолжается до тех пор, пока не будут выделены г узлов.

Метод минимизации соединений между всеми парами узлов разбиения имеет наибольшую точность, однако требует значительных затрат машинного времени. Эффективность метода последовательного разделения в большей степени зависит от структуры связей между группами элементов схемы.

В методе последовательного выделения существен «удачный» выбор первых элементов, поскольку в ходе процесса элементы, вошедшие в группы T_p(p<i) исключаются из рассмотрения.

Заключение

Рассмотренные выше алгоритмические методы компоновки, безусловно, не исчерпывают множества идей и методов, используемых в процессе автоматизации конструирования электронных устройств. Более того, каждый из этих методов в отдельности не дает оптимального по ряду параметров решения соответствующей задачи компоновки. При выборе метода решения конкретной задачи следует прежде всего учитывать недостатки и достоинства каждого из рассмотренных алгоритмов.

Главными достоинствами последовательных алгоритмов компоновки по связности является их скорость и простота реализации. Кроме того, они позволяют легко учитывать дополнительные ограничения на компоновку: несовместимость отдельных элементов в узле, априорно заданное функциональное распределение некоторых элементов схемы и др. Основным недостатком этих алгоритмов является локальный пошаговый характер оптимизации, приводящий к тому, что в начале процесса выделяются сильно связанные группы элементов, в то время как в последние узлы попадают малосвязанные или вообще несвязанные элементы. Это приводит при жестких ограничениях на число выводов к увеличению числа узлов. Отсюда ясно, что эффективность таких процедур должна быть выше при компоновке узлов с небольшим отношением числа элементов к числу выводов (печатных плат, панелей и т.д.). Кроме того, как показывают результаты алгоритм дает лучшие результаты для схем с относительно невысокой связностью.

В параллельно-последовательных алгоритмах компоновки в определенной мере устранен главный недостаток последовательных алгоритмов. Предварительное выделение набора групп элементов, обладающих существенными для конкретной задачи свойствами (число внешних соединений, внутренняя связность, функциональная завершенность), позволяет обеспечить более равномерное распределение элементов по узлам, а в ряде случаев приводит к значительно лучшим по качеству решениям. Хотя алгоритмы и более сложны в реализации, их быстродействие вполне приемлемо для схем реальной степени сложности.

Итерационные алгоритмы обладают тем несомненным преимуществом, что они всегда обеспечивают получение результата, не уступающего начальному варианту компоновки, и применимы при различных критериях оптимизации. При их реализации можно учесть и требование по равномер-ности распределения числа выводов на узлах. Основным недостатком итерационных алгоритмов является значительное время отыскания локально оптимального решения, особенно если начальный вариант компоновки имеет низкий показатель качества.

Список использованных источников

1 Автоматизированное проектирование средств и систем управления: курс лекций / Е.Е. Носкова, Д.В. Капулин, Ю.В. Краснобаев, С.В. Ченцов. - Красноярск: ИКИТ СФУ, 2010. - 272 с.

Деньдобренко, Б.Н., Малика, А.С. Автоматическое конструирование РЭА: Учебник для вузов / Б.Н. Деньдобренко, А.С. Малика. - М.: «Высш. школа», 1980. - 484 с.

Бондарик В.М. Системы автоматизированного проектирования. Курс лекций: Уч. пособие для студ. спец. «Медицинская электроника», «Электронно-оптические системы и технологии» дневной и заочной форм обуч. / В.М. Бондарик. - Мн.: БГУИР, 2006. - 272 с.

СТО 4.2-07-2012. Система менеджмента и качества. Общие требования к построению, изложению и оформлению документов учебной и научной деятельности. Введ. впервые; дата введения 27.02.2012. Красноярск, 2012. 57 с.