Уравнения свертки. Обобщенные функции
СОДЕРЖАНИЕ
Введение
.
Обобщенные функции
.1
Основные понятия
.2
Пространство обобщенных функций
.3
Дифференциальные уравнения в обобщенных функциях
.4
Свойства обобщенных производных
.5
Обобщенные функции, отвечающие квадратичным формам с комплексными коэффициентами
.
Операции над обобщенными функциями
.1
Свертка обобщенных функций
.2
Преобразование Лапласа обобщенных функций
.3
Преобразование Фурье обобщенных функций
Заключение
Список
использованных источников и литературы
Приложение
А Нахождение решения уравнения изгиба балки в математическом пакете Maple
Введение
Со времен Огюстена Коши понятие функции постоянно уточнялось и
претерпевало все более широкие обобщения и расширения. Обобщенные функции
являются крупнейшим достижение математики XX века. Обобщенные функции получают
сейчас все более широкое распространение в различных разделах математики и
физики.
Понятие обобщенной функции с одной стороны, дает возможность выразить в
математически корректной форме такие идеализированные понятия, как плотность
материальной точки (пространственная), плотность простого или двойного слоя,
интенсивность мгновенного источника и т.д. С другой стороны, в понятии
обобщенной функции находит отражение тот факт, что реально нельзя измерить
значение физические величины в точке, а можно измерять лишь ее средние значения
в достаточно малых окрестностях данной точки. Таким образом, понятие обобщенной
функции учитывает эту двойственную природу измерений и потому служит адекватным
аппаратом для описания распределений различных физических величин. В литературе
обобщенные функции часто называют распределением.
В
конце 20-х годов П. Дирак ввел так называемую 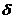 -функцию,
обладающую следующим свойством
-функцию,
обладающую следующим свойством 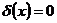 для
для 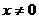 , если
, если 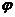 - любая
непрерывная функция, то
- любая
непрерывная функция, то 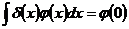 . Конечно и самому Дираку было ясно, что с
математической точки зрения это определение бессмысленно, что
. Конечно и самому Дираку было ясно, что с
математической точки зрения это определение бессмысленно, что 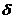 функция не есть функция, понимаемая в классическом
смысле. У О. Хевисайда в его операционном исчислении
функция не есть функция, понимаемая в классическом
смысле. У О. Хевисайда в его операционном исчислении 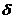 функция выступает как результат применения оператора
функция выступает как результат применения оператора 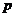 к единичной ступеньке. В середине 30-х годов С.Л.
Соболев заложил основы теории обобщенных функций как линейных непрерывных
функционалов над пространством достаточно «хороших» функций и успешно применял
их в исследовании задачи Коши для уравнения гиперболического типа. В
послевоенные годы Л. Шварц, опираясь на созданную школой Н. Бурбаки теорию
линейных локально выпуклых топологических пространств дал систематическое
изложение теории обобщенных функций в его знаменитой двухтомной монографии и
указал на ряд важных ее применений.
к единичной ступеньке. В середине 30-х годов С.Л.
Соболев заложил основы теории обобщенных функций как линейных непрерывных
функционалов над пространством достаточно «хороших» функций и успешно применял
их в исследовании задачи Коши для уравнения гиперболического типа. В
послевоенные годы Л. Шварц, опираясь на созданную школой Н. Бурбаки теорию
линейных локально выпуклых топологических пространств дал систематическое
изложение теории обобщенных функций в его знаменитой двухтомной монографии и
указал на ряд важных ее применений.
Отдельные
классы сингулярных обобщенных функций по существу рассматривались в пионерских
работах С. Бохнера, Ж. Адамара и М. Рисса в связи с задачами «регуляризации»
расходящихся рядов и интегралов.
И.М.
Гельфанд и Г.Е. Шилов расширяют понятие обобщенной функции включая в
рассмотрение целую шкалу пространств основных функций как бесконечно
дифференцируемых, так и аналитических. В 50-е годы Н.Н. Боголюбов впервые
показал фундаментальную роль обобщенной функции в описании процессов локального
взаимодействия элементарных частиц и применил их для построения аксиоматической
квантовой теории поля. В это же время методами теории обобщенных функции были
установлены фундаментальные результаты для произвольных дифференциальных
операторов с постоянными и аналитическими коэффициентами. Следует подчеркнуть,
что обобщенные функции обладают рядом замечательных свойств и преимуществ,
расширяющих возможности классического математического анализа. Например, любая
обобщенная функция оказывается бесконечно дифференцируемой, т.е. сходящиеся
ряды и последовательности их обобщенных функций можно почленно дифференцировать
бесконечно число раз. Поэтому использование техники обобщенных функций
существенной расширяет класс рассматриваемых задач и к тому же приводит к значительным
упрощениям, формализуя элементарные операции.
Целью
курсовой работы является исследование обобщенных функций и их применение на
практике, в частности, на примере нахождения решения изгиба балки в
математическом пакете Maple. Поставленная цель определила постановку следующих
задач:
– анализ существующих видов обобщенных функций;
– изучение пространства обобщенных функций;
– решение уравнений в обобщенных функциях.
Курсовая работа состоит из двух глав. В первой главе рассматривается
понятие обобщенных функций и их виды, пространство обобщенных функции,
дифференциальные уравнения в них. Вторая глава посвящена операциям с
обобщенными функциями, применение свертки к обобщенным функциям, исследование
преобразований Лапласа и Фурье, этапам вычислений в пакете Maple с краткими
сведениями о работе.
В заключении приводится пример нахождения решения уравнения изгиба балки
с применением обобщенных функций в математическом пакете Maple.
1. Обобщенные функции
.1 Основные понятия
Обобщенные функции -
математическое понятие, обобщающее классическое понятие функции. Обобщенные
функции были введены впервые в конце 20-х гг. XX в. П. Дираком в его
исследованиях по квантовой механике, где он систематически использует понятие
дельта-функции и ее производных. Основы математической теории обобщенных
функций были заложены С.Л. Соболевым в 1936 году при решении задачи Коши для
гиперболических уравнений, а в послевоенные годы французский математик Л. Шварц
дал систематическое изложение теории обобщенных функций. Важную роль в
формировании теории обобщенных функций сыграли работы Ж. Адамара, в которых в
связи с изучением фундаментальных решений волновых уравнений рассмотрены
сходящиеся интегралы, а также работы М. Рисса.
С другой стороны, к теории обобщенных функций вплотную подводит теория С.
Бохнера преобразований Фурье функций степенного роста. Эти преобразования Фурье
являются по существу обобщенными функциями и выступают у С. Бохнера как
формальные производные непрерывных функций. Обобщенные функции необыкновенно
быстро, буквально за два-три года, приобрели чрезвычайно широкую популярность.
Достаточно указать хотя бы на тот факт, что количество математических работ, в
которых встречается дельта-функция, возросло во много раз.
В дальнейшем теорию обобщенных функций интенсивно развивали многие
математики, главным образом из-за потребностей математической физики. Теория
обобщенных функций имеет многочисленные применения и все шире входит в обиход
физика, математика и инженера.
Формально
обобщенные функции определяются как линейные непрерывные функционалы над тем
или иным линейным пространством основных функций 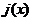 .
Основным пространством функций является, например, совокупность бесконечно
дифференцируемых финитных функций, снабженная надлежащей сходимостью (или
точнее топологией). При этом обычные локально суммируемые функции
.
Основным пространством функций является, например, совокупность бесконечно
дифференцируемых финитных функций, снабженная надлежащей сходимостью (или
точнее топологией). При этом обычные локально суммируемые функции 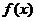 отождествляются с функционалами (регулярными
обобщенными функциями) вида:
отождествляются с функционалами (регулярными
обобщенными функциями) вида:
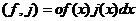 . (1)
. (1)
Произвольная
обобщенная функция 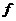 определяется как функционал
определяется как функционал 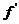 , задаваемый равенством:
, задаваемый равенством:
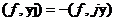 . (2)
. (2)
Следовательно,
каждая обобщенная функция бесконечно дифференцируема. Равенство (2) в силу (1)
есть не что иное, как обобщение формулы интегрирования по частям для
дифференцируемых в обычном смысле функций 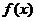 , так что
в этом случае оба понятия производной совпадают.
, так что
в этом случае оба понятия производной совпадают.
Сходимость
на (линейном) множестве обобщенных функций вводится как слабая сходимость
функционалов. Оказывается, что операция дифференцирования обобщенных функций
непрерывна, а сходящаяся последовательность обобщенных функций разрешает
почленное дифференцирование бесконечное число раз.
Вводятся
и другие операции над обобщенными функциями, например свертка, преобразование
Фурье и Лапласа. Теория этих операций приобретает наиболее простую и
законченную форму в рамках понятия обобщенных функций, расширяющих возможности
классического математического анализа. Поэтому использование обобщенные функции
существенно расширяет круг рассматриваемых задач и приводит к значительным
упрощениям, автоматизируя элементарные операции.
Примеры:
- 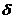 -функция
Дирака:
-функция
Дирака: 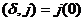 , описывает плотность массы (заряда), сосредоточенной
в точке
, описывает плотность массы (заряда), сосредоточенной
в точке 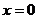 , единичный импульс;
, единичный импульс;
- 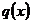 - функция Хевисайда:
- функция Хевисайда: 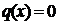 , при
, при 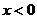 ,
, 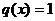 , при
, при 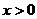 ,
, 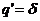 ;
производная от этой функции равна единичному импульсу;
;
производная от этой функции равна единичному импульсу;
- 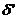 - плотность диполя момента в точке
- плотность диполя момента в точке 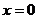 ,
ориентированного вдоль оси
,
ориентированного вдоль оси 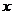 ;
;
- 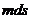 - плотность простого слоя на поверхности
- плотность простого слоя на поверхности 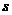 с
поверхностной плотностью
с
поверхностной плотностью 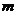 ;
;
- плотность
двойного слоя на поверхности 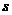 с
поверхностной плотностью момента
с
поверхностной плотностью момента 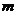 диполей,
ориентированных вдоль направления нормали
диполей,
ориентированных вдоль направления нормали 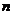 ;
;
- свертка
ньютонов, потенциал с плотностью 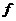 , где
, где 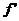 - любая обобщенная функция (например, из первых пяти
пунктов);
- любая обобщенная функция (например, из первых пяти
пунктов);
- общее решение
уравнения колебаний струны задается формулой 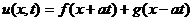 ,
где
,
где 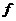 и
и 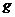 любые
обобщенные функции.
любые
обобщенные функции.
1.2 Пространство обобщенных функций 
обобщенный функция преобразование фурье
Совокупность
обобщенных функций, порождаемых основным пространством 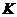 , образует пространство
, образует пространство 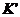 .
Рассмотрим подпространство обобщенных функций
.
Рассмотрим подпространство обобщенных функций 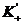 пространства
пространства
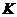 , состоящее их обобщенных функций, равных нулю вне
некоторого конечного интервала принадлежащего
, состоящее их обобщенных функций, равных нулю вне
некоторого конечного интервала принадлежащего 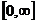 .
Применим в этом пространстве операцию умножения двух функций в виде свертки
этих функций. Если
.
Применим в этом пространстве операцию умножения двух функций в виде свертки
этих функций. Если 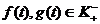 , то и
, то и 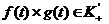 Кроме
того свертка обладает всеми свойствами обычной операции умножения. Роль единицы
в
Кроме
того свертка обладает всеми свойствами обычной операции умножения. Роль единицы
в 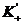 играет функция
играет функция 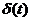 , так как
для
, так как
для 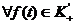
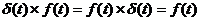 .
.
Пусть
существует 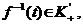 такая что
такая что 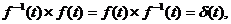 тогда
тогда 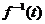 называется обратной обобщенной функцией
называется обратной обобщенной функцией 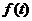 . Пространство
. Пространство 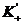 с
введенной операцией умножения образует алгебру (коммутативную) со сверткой.
с
введенной операцией умножения образует алгебру (коммутативную) со сверткой.
Пусть
существует алгебра со сверткой 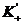 .
Обобщенная функция
.
Обобщенная функция  , так как она равна нулю всюду, кроме точки ноль.
Обобщенная функция
, так как она равна нулю всюду, кроме точки ноль.
Обобщенная функция 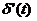 сосредоточена вначале координат, поэтому
сосредоточена вначале координат, поэтому 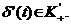 Далее,
Далее,
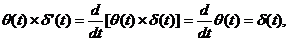 поэтому
поэтому 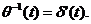
Теорема.
Пусть для 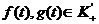 существуют обратные функции
существуют обратные функции 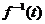 и
и 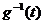 , тогда
свертка
, тогда
свертка 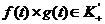 имеет обратную функцию вида
имеет обратную функцию вида 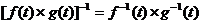 .
.
Действительно,
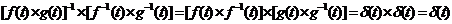 .
.
Есть
определенное в 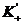 уравнение в свертках
уравнение в свертках 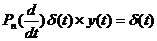 .
Свертка существует для любой обобщенной функции
.
Свертка существует для любой обобщенной функции 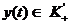 , так как
, так как
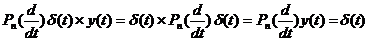 .
.
Следовательно,
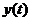 является фундаментальным решением уравнения
является фундаментальным решением уравнения 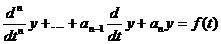 . В частности, фундаментальное решение уравнения
. В частности, фундаментальное решение уравнения 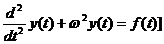 с оператором
с оператором 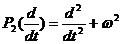 принадлежит
алгебре со сверткой
принадлежит
алгебре со сверткой 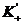 . Следовательно,
. Следовательно,
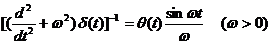 . (3)
. (3)
Существует операционный метод решения уравнения в свертках. Пусть имеется
уравнение:
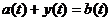 , (4)
, (4)
где
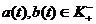 . Среди эффективных методов решения этого уравнения
возьмем метод преобразования Лапласа. Применяя преобразование Лапласа к левой и
правой части этого уравнения, получается:
. Среди эффективных методов решения этого уравнения
возьмем метод преобразования Лапласа. Применяя преобразование Лапласа к левой и
правой части этого уравнения, получается:
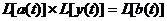 . (5)
. (5)
Отсюда
следует: 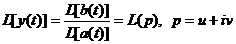 .
.
Если
для функции 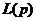 существует оригинал, принадлежащий
существует оригинал, принадлежащий 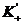 , то он и является искомым решением. В качестве
примера можно рассмотреть уравнение
, то он и является искомым решением. В качестве
примера можно рассмотреть уравнение 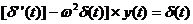 . С
помощью преобразования Лапласа, следует:
. С
помощью преобразования Лапласа, следует: 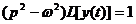 .
.
Следовательно,
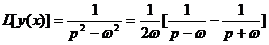 . (6)
. (6)
Поэтому
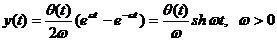 .(7)
.(7)
Существуют
регулярные и сингулярные обобщенные функции. Обобщенные функции, определяемые
локально интегрируемыми в 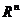 функциями по формуле
функциями по формуле 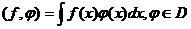 ,
называются регулярными обобщенными функциями. Остальные обобщенные функции
называются сингулярными обобщенными функциями.
,
называются регулярными обобщенными функциями. Остальные обобщенные функции
называются сингулярными обобщенными функциями.
Производные
обобщенной функции: пусть 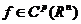 . Тогда при всех
. Тогда при всех 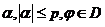 справедлива
формула интегрирования по частям:
справедлива
формула интегрирования по частям: 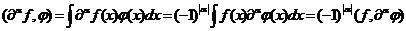 . Это
равенство будет (обобщенной) производной
. Это
равенство будет (обобщенной) производной 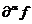 обобщенной
функции
обобщенной
функции 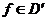 :
:  . В
частности, при
. В
частности, при 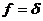 данное равенство принимает вид:
данное равенство принимает вид: 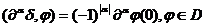 .
.
Первообразная
обобщенной функции: пусть n=1. Всякая непрерывная функция 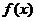 имеет (единственную с точностью до аддитивной
постоянной) первообразную:
имеет (единственную с точностью до аддитивной
постоянной) первообразную: 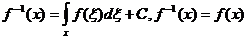 .
Обобщенная функция
.
Обобщенная функция 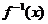 из
из 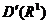 называется
первообразной обобщенной функции
называется
первообразной обобщенной функции 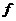 из
из 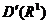 , если
, если 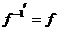 , т.е.
, т.е. 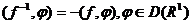 .
.
Обобщенные
функции не имеют значений в отдельных точках. Тем не менее, можно говорить об
обращении в нуль обобщенной функции в области.
Говорят,
что обобщенная функция 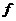 равна нулю в области
равна нулю в области 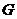 , если
, если 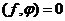 для всех
для всех 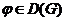 . Этот
факт будем записывать так:
. Этот
факт будем записывать так: 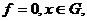 или
или 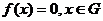 . В соответствии с этим определением обобщенные
функции
. В соответствии с этим определением обобщенные
функции 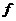 и
и 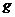 называются
равными в области
называются
равными в области 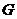 , если
, если 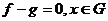 , при
этом:
, при
этом: 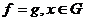 . В частности, обобщенные функции
. В частности, обобщенные функции 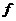 и
и 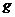 называются
равными
называются
равными 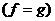 , если
, если 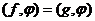 для всех
для всех
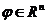 .
.
Пусть
обобщенная функция 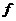 равна нулю в области
равна нулю в области 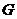 . Тогда
она, очевидно, равна нулю и в окрестности каждой точки этой области.
Справедливо и обратное.
. Тогда
она, очевидно, равна нулю и в окрестности каждой точки этой области.
Справедливо и обратное.
1.3 Дифференциальные уравнения в обобщенных функциях
Пусть
существует уравнение 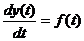 . Если
. Если 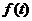 -
обычная функция, то ее решение есть первообразная, то есть
-
обычная функция, то ее решение есть первообразная, то есть 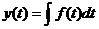 . Пусть теперь
. Пусть теперь 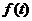 -
обобщенная функция.
-
обобщенная функция.
Определение.
Обобщенная функция 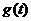 называется первообразной обобщенной функцией
называется первообразной обобщенной функцией 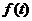 , если
, если 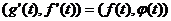 . Если
. Если 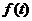 - сингулярная обобщенная функция, то возможны случаи,
когда ее первообразная - регулярная обобщенная функция. Например, первообразная
- сингулярная обобщенная функция, то возможны случаи,
когда ее первообразная - регулярная обобщенная функция. Например, первообразная
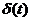 является
является 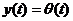 ; первообразная
; первообразная
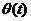 является функция
является функция  , а
решение уравнения
, а
решение уравнения 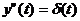 можно записать в виде:
можно записать в виде: 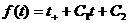 ,
где
,
где 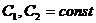 .
.
Есть
линейное уравнение 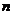 -го порядка с постоянными коэффициентами
-го порядка с постоянными коэффициентами
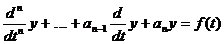 , (8)
, (8)
где
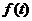 - обобщенная функция. Пусть
- обобщенная функция. Пусть 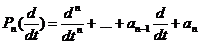 - дифференциальный полином
- дифференциальный полином 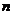 -го порядка.
-го порядка.
Определение.
Обобщенным решением дифференциального уравнения (8) называется обобщенная
функция 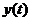 , для которой выполняется соотношение:
, для которой выполняется соотношение:
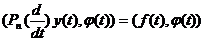 .
.
Если
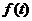 - непрерывная функция, тогда единственным решением
уравнения (8) является классическое решение.
- непрерывная функция, тогда единственным решением
уравнения (8) является классическое решение.
Определение.
Фундаментальным решением уравнения (8) называется любая обобщенная функция 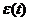 такая, что
такая, что 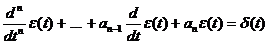 .
.
Функция
Грина - фундаментальное решение, удовлетворяющее граничному, начальному или
асимптотическому условию.
Теорема.
Решение уравнения (8) существует и имеет вид:
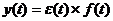 , (9)
, (9)
если только свертка определена.
Пример:
 .
.
Нетрудно
увидеть, что фундаментальным решением этого уравнения является 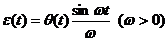 , так как
, так как
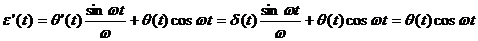 (10)
(10)
и
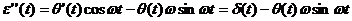 . (11)
. (11)
Поэтому
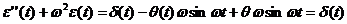 . (12)
. (12)
1.4 Свойства обобщенных производных
- Операция
дифференцирования 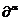 линейна и непрерывна из
линейна и непрерывна из 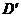 в
в 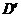 :
:
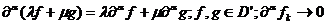 в
в 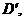
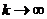 , если
, если 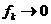 в
в 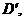
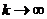 ;
;
- каждая
обобщенная функция бесконечно дифференцируема. Действительно, если 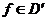 , то
, то 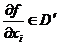 ; в свою
очередь
; в свою
очередь 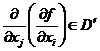 и т.д.;
и т.д.;
- результат
дифференцирования не зависит от порядка дифференцирования. Например,  ;
;
- если 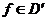 и
и 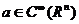 , то
справедлива формула Лейбница дифференцирования произведения
, то
справедлива формула Лейбница дифференцирования произведения 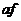 . Например,
. Например, 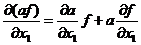 ;
;
- если
обобщенная функция 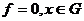 , то
, то 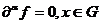 ;
;
- если ряд 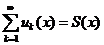 , составленный из локально интегрируемых функций
, составленный из локально интегрируемых функций 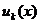 , сходится равномерно на каждом компакте, то его можно
почленно дифференцировать любое число раз (как обобщенную функцию), и
полученные ряды будут сходится в
, сходится равномерно на каждом компакте, то его можно
почленно дифференцировать любое число раз (как обобщенную функцию), и
полученные ряды будут сходится в 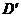 .
.
Пример.
Пусть 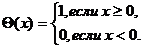
Функция
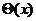 называется функцией Хевисайда или единичной функцией.
Она локально интегрируема и потому может рассматриваться как обобщенная
функция. Можно найти ее производную. Согласно определению,
называется функцией Хевисайда или единичной функцией.
Она локально интегрируема и потому может рассматриваться как обобщенная
функция. Можно найти ее производную. Согласно определению, 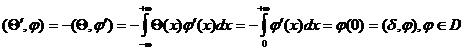 , т.е.
, т.е. 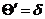 .
.
1.5 Обобщенные функция 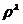 , отвечающие квадратичным формам с комплексными
коэффициентами
, отвечающие квадратичным формам с комплексными
коэффициентами
До
сих пор рассматривались исключительно квадратичные формы с вещественными
коэффициентами. В этом пункте исследуется пространство всех квадратичных форм 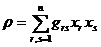 с комплексными коэффициентами.
с комплексными коэффициентами.
Задачей
является определение обобщенной функции 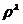 , где
, где 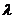 - комплексное число. Однако в общем случае
- комплексное число. Однако в общем случае 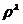 не будет однозначной аналитической функцией от
не будет однозначной аналитической функцией от 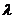 . Поэтому в пространстве всех квадратичных форм
. Поэтому в пространстве всех квадратичных форм 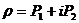 выделяют «верхнюю полуплоскость» квадратичных форм с
положительно определенной мнимой частью и определяют для них функцию
выделяют «верхнюю полуплоскость» квадратичных форм с
положительно определенной мнимой частью и определяют для них функцию 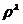 . А именно, если квадратичная форма
. А именно, если квадратичная форма 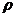 принадлежит этой «полуплоскости», то пологается
принадлежит этой «полуплоскости», то пологается 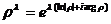 , где
, где  . Такая
функция
. Такая
функция 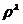 является однозначной аналитической функцией от
является однозначной аналитической функцией от 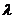 .
.
Можно
сопоставить теперь функции 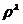 обобщенную
функцию
обобщенную
функцию 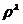 :
:
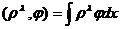 , (13)
, (13)
где
интегрирование ведется по всему пространству. Интеграл (13) сходится при 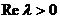 и является в этой полуплоскости аналитической
функцией от
и является в этой полуплоскости аналитической
функцией от 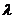 . Продолжая аналитически эту функцию, определяется
функционал
. Продолжая аналитически эту функцию, определяется
функционал 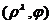 для других значений
для других значений 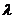 .
.
Для
квадратичных форм 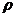 с положительно определенной мнимой частью находятся
особые точки функций
с положительно определенной мнимой частью находятся
особые точки функций 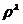 и вычисляются вычеты этих функций в особых точках.
и вычисляются вычеты этих функций в особых точках.
Обобщенная
функция 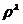 аналитически зависит не только от
аналитически зависит не только от 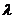 , но и от коэффициентов квадратичной формы
, но и от коэффициентов квадратичной формы 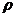 . Тем самым,
. Тем самым, 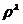 является
аналитической функцией в верхней «полуплоскости» всех квадратичных форм вида
является
аналитической функцией в верхней «полуплоскости» всех квадратичных форм вида 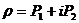 , где
, где 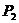 есть
положительно определенная форма. Следовательно,
есть
положительно определенная форма. Следовательно, 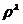 однозначно
определяется своими значениями на «мнимой полуоси», т. е. на множестве
квадратичных форм вида
однозначно
определяется своими значениями на «мнимой полуоси», т. е. на множестве
квадратичных форм вида 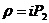 , где
, где 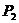 -
положительно определенная форма.
-
положительно определенная форма.
2. Операции над обобщенными функциями
.1 Свертка обобщенных функций
Пусть
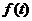 и
и 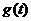 -
интегрируемые на любом конечном интервале функции. Свертка функций
-
интегрируемые на любом конечном интервале функции. Свертка функций 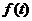 и
и 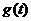 определяется
соотношением:
определяется
соотношением:
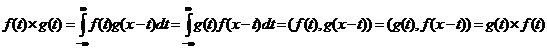 ,
,
если
только интеграл существует и интегрируем по любому конечному интервалу
переменной 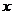 . Равенство двух интегралов легко проверить, сделав
замену
. Равенство двух интегралов легко проверить, сделав
замену 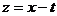 .
.
Если
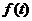 ,
, 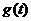 -
регулярные обобщенные функции и
-
регулярные обобщенные функции и 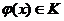 , то
можно записать:
, то
можно записать:
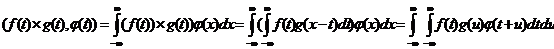
Произведение
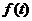 и
и 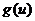 можно
рассматривать как прямое произведение
можно
рассматривать как прямое произведение 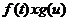 , так
что:
, так
что:
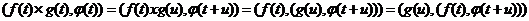 .
.
Это
соотношение определяет свертку обобщенных функций 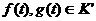 , в том числе и сингулярные обобщенные функции.
, в том числе и сингулярные обобщенные функции.
Свертка
обобщенных функций имеет следующие свойства:
- 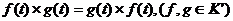 ;
;
- 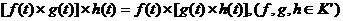 ;
;
- 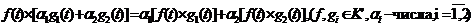 ;
;
- если 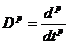 , то
, то
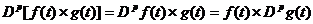 (14)
(14)
Доказательство
последнего соотношения. Действительно, для 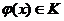
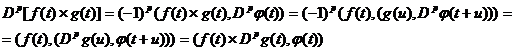
или
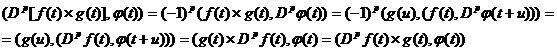
Примеры:
- 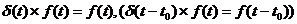 ;
;
- 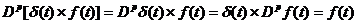 .
.
2.2 Преобразование Лапласа обобщенных функций
Пусть
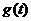 - обобщенная функция из
- обобщенная функция из 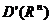 . Если
. Если 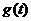 имеет
компактный носитель, то есть
имеет
компактный носитель, то есть 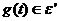 , то,
выражение
, то,
выражение 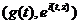 имеет смысл для любого
имеет смысл для любого 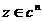 и
представляет собой целую аналитическую функцию. Она называется преобразованием
Лапласа обобщенной функции
и
представляет собой целую аналитическую функцию. Она называется преобразованием
Лапласа обобщенной функции 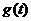 и
обозначается
и
обозначается 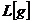 .
.
Определение.
Комплекснозначная функция 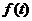 действительного переменного
действительного переменного 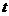 называется оригиналом, если:
называется оригиналом, если:
- 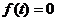 для
для 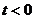 ;
;
- 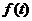 -
кусочно-дифференцируема;
-
кусочно-дифференцируема;
- 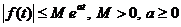 .
.
Тогда
функция 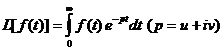 называется преобразованием Лапласа функции
называется преобразованием Лапласа функции 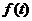 . Функция
. Функция 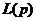 бесконечно
дифференцируема в полуплоскости
бесконечно
дифференцируема в полуплоскости 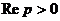 и для
нее справедливо следующее соотношение:
и для
нее справедливо следующее соотношение:
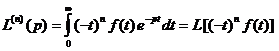 .
.
Если
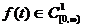 , то
, то 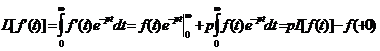 , где
, где 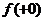 - скачок функции
- скачок функции 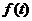 в начале
координат. Обратное преобразование Лапласа
в начале
координат. Обратное преобразование Лапласа 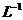 равно
равно 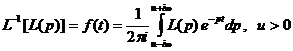 .
.
Приведем преобразование Лапласа некоторых функций:
- 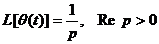 ;
;
- 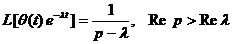 ;
;
- 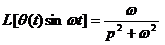 ;
;
- 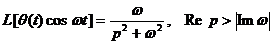 .
.
Определение.
Преобразование Лапласа обобщенной функции 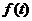 определяется
соотношением:
определяется
соотношением: 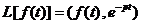 .
.
Свойства:
- 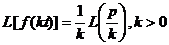 ;
;
- 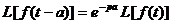 ;
;
- 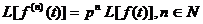 .
.
В данном случае производные нужно рассматривать как производные
обобщенных функций.
Заметно, что:
- 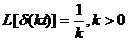 ;
;
- 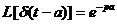 ;
;
- 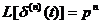 ;
;
- 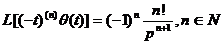 ;
;
- 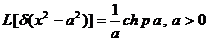 ;
;
Можно
найти преобразование Лапласа свертки обобщенных функций 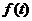 и
и 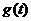 :
:
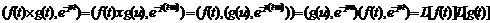 .
.
Получается:
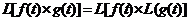 . Так как
. Так как 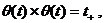 то
то 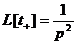 . Также можно написать
. Также можно написать
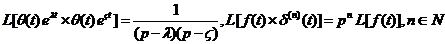 .
.
Преобразование
Лапласа часто используемых обобщенных функций:
- 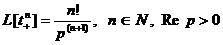 ;
;
- 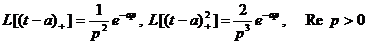 ;
;
- 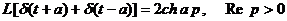 ;
;
- 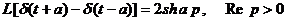 ;
;
- 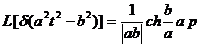 ;
;
- 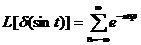 ;
;
- 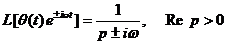 ;
;
- 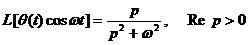 ;
;
- 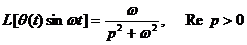 ;
;
- 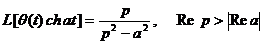 ;
;
-  ;
;
- 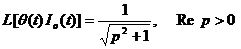 ,
,
где
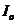 - функция Бесселя нулевого
порядка.
- функция Бесселя нулевого
порядка.
2.3 Преобразование Фурье обобщенных функций
Пусть
основное пространство 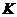 состоит из бесконечно дифференцируемых
комплекснозначных функций
состоит из бесконечно дифференцируемых
комплекснозначных функций 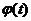 действительного переменного
действительного переменного 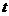 , равных нулю вне некоторого конечного интервала.
Преобразование Фурье функции
, равных нулю вне некоторого конечного интервала.
Преобразование Фурье функции 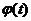 определяется
соотношением:
определяется
соотношением: 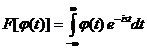 .
.
Если
рассматривать 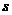 как комплексную переменную
как комплексную переменную  , то
, то
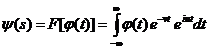
и
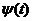 - бесконечно дифференцируемая функция (аналитическая)
во всей комплексной плоскости. Интегрируя по частям, получится:
- бесконечно дифференцируемая функция (аналитическая)
во всей комплексной плоскости. Интегрируя по частям, получится:
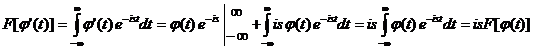 .
.
В
общем случае можно записать:
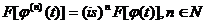 .
.
Далее,
если 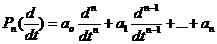 - дифференциальный полином с постоянными
коэффициентами
- дифференциальный полином с постоянными
коэффициентами 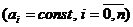 , то
, то 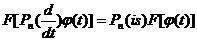 .
.
Определение.
Преобразование Фурье обобщенной функции 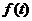 называется
обобщенная функция
называется
обобщенная функция 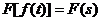 , определяемая соотношением:
, определяемая соотношением:
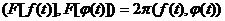 ,
,
которое
для регулярных функций называется равенством Парсеваля.
Свойства
преобразования Фурье:
- 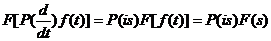 ;
;
- 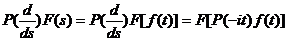 ;
;
- 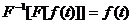 ,
,
где
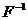 - оператор, обратный
- оператор, обратный 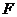 ,
удовлетворяющий соотношению
,
удовлетворяющий соотношению
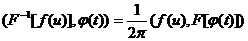 ;
;
-  ;
;
- 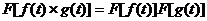 .
.
Преобразование Фурье от некоторых обобщенных функций:
- 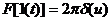 ;
;
-  ;
;
- 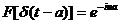 ;
;
- 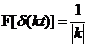 ;
;
- 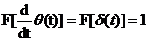 .
.
Пример. Найти преобразование Фурье обобщенной функции Дирака. По
определению:
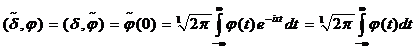 .
.
Заключение
Новые задачи физики и математики, появившиеся в XX столетии, привели к
появлению нового понятия функции - обобщенной функции или распределения.
Обобщенные функции получают сейчас все более широкое распространение в
различных разделах математики. В некоторой форме обобщенные функции по существу
уже давно применялись физиками.
Обычное
понятие функции, которое ставит в соответствие каждому значению 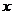 (из некоторой области определения этой функции)
соответствующее ему значение
(из некоторой области определения этой функции)
соответствующее ему значение 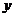 ,
оказалось абсолютно недостаточным.
,
оказалось абсолютно недостаточным.
Потребность
в подобном обобщении возникает во многих физических и математических задачах.
Обобщенные функции дают возможность выразить в математически корректной форме
такие идеализированные понятия, как плотность материальной точки, точечного
заряда, точечного диполя, (пространственную) плотность простого или двойного
слоя, интенсивность мгновенного источника и т.д.
В
понятии обобщенной функции находит отражение тот факт, что реально нельзя
измерить значение физической величины в точке, а можно измерять лишь ее средние
значения в малых окрестностях данной точки. Поэтому, техника обобщенных функций
служит удобным и адекватным средством для описания многих распределений
различных физических величин.
В
курсовой работе в качестве примера применения обобщенных функций на практике
была взята задача на нахождение решения уравнения изгиба балки 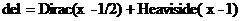 . Вычисления проводились в математическом пакете
Maple. В вычислениях применялись:
. Вычисления проводились в математическом пакете
Maple. В вычислениях применялись: 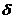 -функция
Дирака, функция Хевисайда
-функция
Дирака, функция Хевисайда 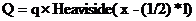 , их производные. Таким образом, было найдено решение
и построен график.
, их производные. Таким образом, было найдено решение
и построен график.
Приложение А
Нахождение
решения уравнения изгиба балки в математическом пакете Maple

Рисунок А.1 - Построение функции Хевисайда
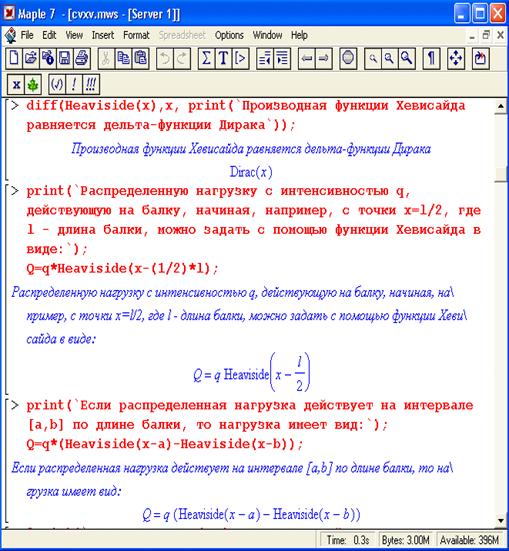
Рисунок А.2 - Описание уравнений нагрузки

Рисунок А.3 - Уравнение изгиба балки и его граничные условия