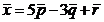Средства матричного исчисления уравнений и комплексных чисел
Контрольная
работа по линейной алгебре
Задание 1
Даны
комплексные числа 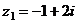 и
и 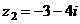 .
.
)
Вычислить 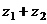 и
и 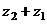 :
:
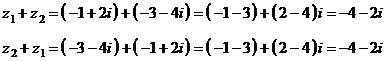
)
Вычислить 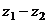 и
и 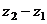 :
:
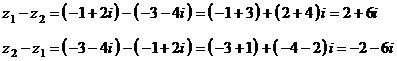
)
Вычислить 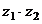 и
и 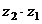 :
:
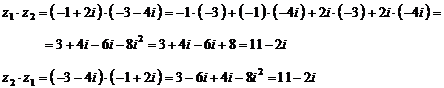
)
Вычислить 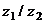 и
и 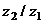 :
:
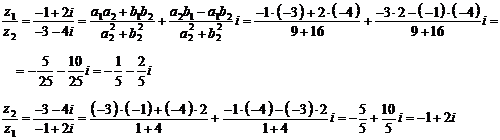
5)
Вычислить 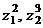 :
:
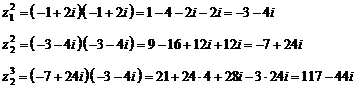
)
Вычислить корни третьей степени из числа 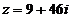 :
:
Найдем
модуль и аргумент числа 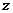 :
:
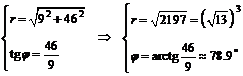
Тогда
модуль кубических корней будет равен:
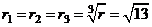
А
аргументы корней:
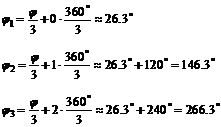
Таким
образом, корни 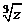 имеют вид:
имеют вид:
Или,
вычислив синусы и косинусы, в алгебраическом виде:
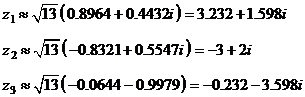
Задание
2
Вычислить
определитель:
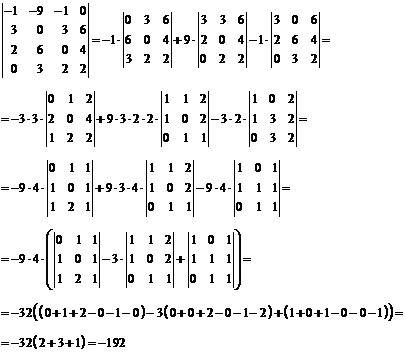
Ответ:
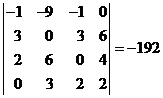
Задание
3
Даны
матрицы:
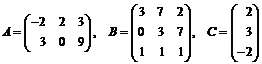
)
Вычислить 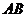 :
:
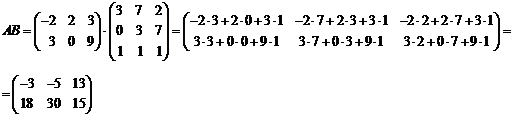
)
Вычислить 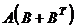 :
:
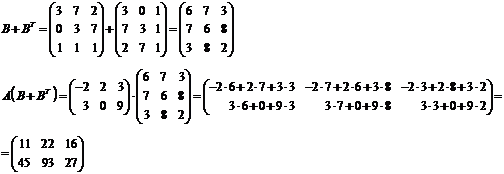
)
Вычислить 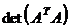 :
:
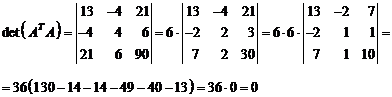
4)
Вычислить 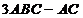 :
:
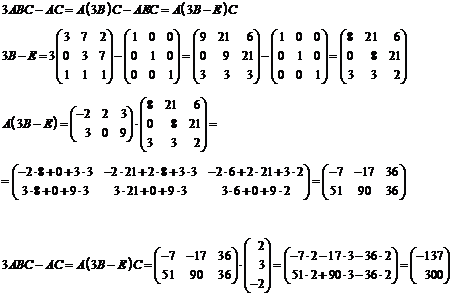
)
Вычислить 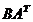 :
:
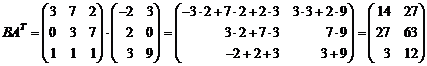

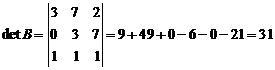
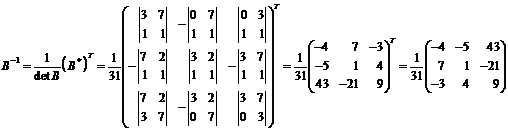
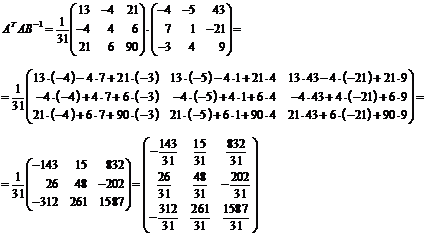
Задание
4
Решить
систему уравнений
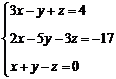
а)
С помощью формул Крамера:
Основной
определитель:
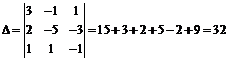
Вспомогательные
определители:
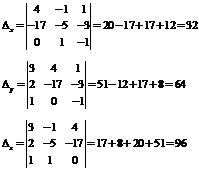
Тогда
решение системы уравнений:
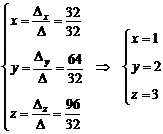
б)
Средствами матричного исчисления:
Матричная
запись системы имеет вид:
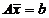 ,
,
где
комплексный алгебраический матричный
определитель
 .
.
А
ее решение:
Найдем
обратную матрицу:
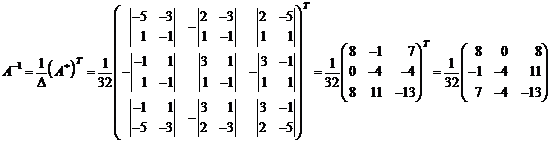
Тогда
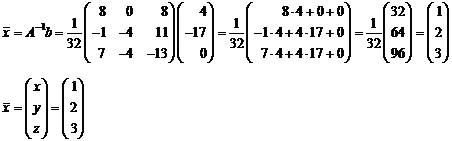
Задание
5
Найти
общее решение системы уравнений
а)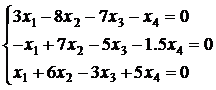
Запишем
правую часть системы в виде матрицы, для удобства вычислений переставив
предварительно уравнения местами (в обратном порядке). И приведем ее к
диагональному виду:
(запись
вида 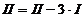 означает «от второй строки отнимаем утроенную первую
строку»)
означает «от второй строки отнимаем утроенную первую
строку»)


Таким образом, общее решение системы:
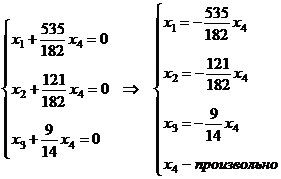
б)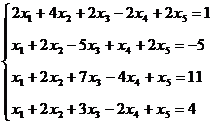
Как
и в предыдущем случае, преобразовываем систему к диагональному виду:
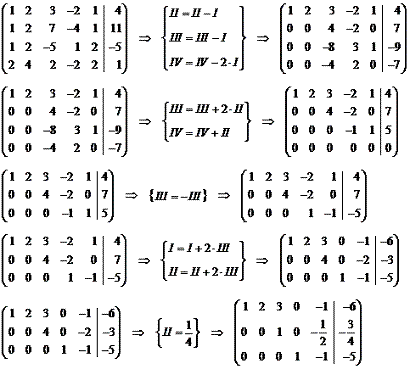

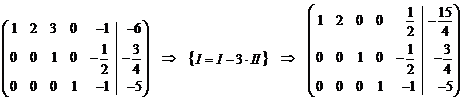
В
процессе преобразований одно уравнение оказалось линейно зависимым от
остальных. Таким образом, общее решение имеет вид:
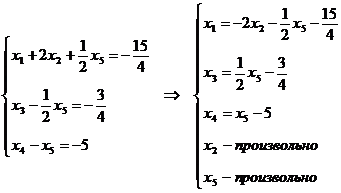
Найти
разложение вектора 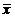 по векторам
по векторам 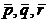 .
.
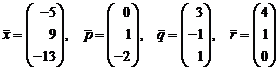
Будем искать вектор разложения в виде
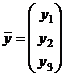
Тогда
разложение вектора 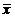 по векторам
по векторам 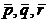 - это
решение системы уравнений:
- это
решение системы уравнений:
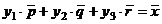
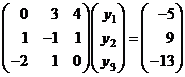
Решим
приведением матрицы к диагональному виду:
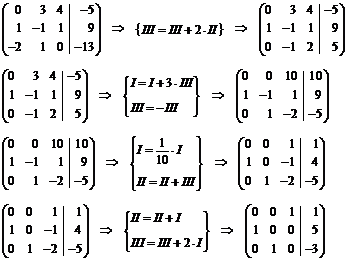
Т.е.
разложение вектора 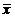 имеет вид:
имеет вид:

Или
в виде линейной комбинации: