Построение полного потока в транспортной сети. Нахождение корней уравнения
Министерство
образования Российской Федерации Международный институт «ИНФО-Рутения»
РГГРУ
Контрольная
работа
Дискретная
математика
Минина Н.В.
г.
Старая Русса
Контрольное задание №1
Задача №1. Дано одношаговое
рекуррентное соотношение 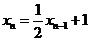 с начальным
условием
с начальным
условием 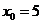 . Найти 7-й
член последовательности
. Найти 7-й
член последовательности 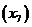
Решение. Чтобы найти 7-й член
последовательности по рекуррентному соотношению, нужно найти все предыдущие.
Нулевой член последовательности задан. Чтобы найти первый элемент, поставим 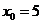 в правую
часть рекуррентного соотношения. Такая подстановка соответствует присваиванию
в правую
часть рекуррентного соотношения. Такая подстановка соответствует присваиванию 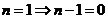 и можно
найти
и можно
найти 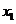 и т.д.
Следовательно:
и т.д.
Следовательно: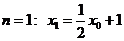 . Поставив
. Поставив 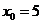 , получим
, получим 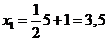 .
. 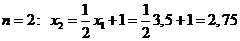 .
.
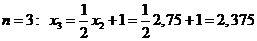 .
.
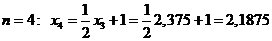 .
.
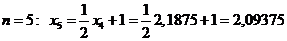 .
.
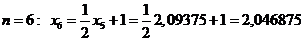 .
.
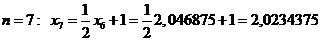 .
.
Ответ: 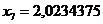 .
.
Задача №2. Вычислить 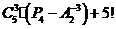
Решение.
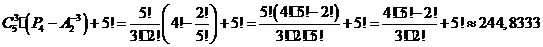 .
.
Задача №3. Решить уравнение 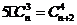
истинность логический карта карно
Решение.
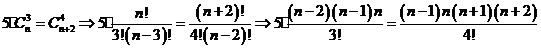 .
.
После сокращения получаем 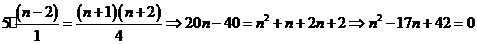 . Найдем
корни полученного уравнения:
. Найдем
корни полученного уравнения: 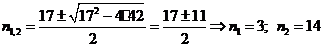 .
.
Ответ: 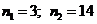 .
.
Задача №4. Сколькими способами можно
выбрать трех дежурных из группы в 20 человек
Решение. Поскольку порядок в выборке
из трех дежурных является не существенным, такая выборка будет неупорядоченной.
Поэтому, количество способов, которыми можно выбрать трех дежурных из группы в
20 человек определится сочетанием из 20 человек по 3 дежурным. В результате
получим 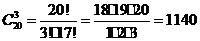 .
.
Ответ: 1140 способов.
Задача №5. Даны 2 множества: 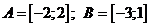 . Найти их
. Найти их
) Объединение
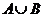 .Ответ:
.Ответ: 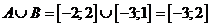 ;) Пересечение
;) Пересечение
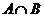 .Ответ:
.Ответ: 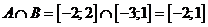 ;) Разность
;) Разность
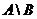 .Ответ :
.Ответ :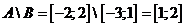 ;) Симметричную
разность
;) Симметричную
разность 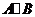 .Ответ:
.Ответ: 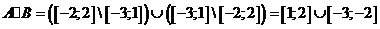 .
.
Контрольное задание №2
Задача №1. Построить полный поток в транспортной
сети G, приведенной на рисунке (цифрами даны пропускные способности дуг)
Решение. Начинаем с нулевого потока,
пологая 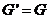 .
.
При нулевом потоке отсутствуют
насыщенные дуги. Выделим в G простую цепь 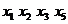 и увеличим потоки по дугам на 3 до
насыщения дуги (
и увеличим потоки по дугам на 3 до
насыщения дуги (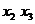 ). В
результате получим поток
). В
результате получим поток 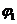 , содержащий
одну насыщенную дугу.. Пометим ее крестиком и удалим из орграфа, который снова
обозначим
, содержащий
одну насыщенную дугу.. Пометим ее крестиком и удалим из орграфа, который снова
обозначим 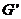 .
.
Выделим в 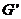 простую
цепь
простую
цепь 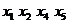 и увеличим
потоки по дугам этой цепи на 3 до насыщения дуги (
и увеличим
потоки по дугам этой цепи на 3 до насыщения дуги (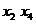 ). В
результате получим поток
). В
результате получим поток 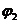 , величина
которого равна
, величина
которого равна 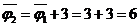 и который
содержит насыщенную дугу
и который
содержит насыщенную дугу 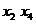 . Удалим эту
насыщенную дугу из
. Удалим эту
насыщенную дугу из 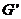 и
оставшийся орграф обозначим
и
оставшийся орграф обозначим 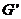 .
.
Выделим в 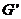 простую
цепь
простую
цепь 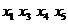 и увеличим
потоки по дугам этой цепи на 2 до насыщения дуги (
и увеличим
потоки по дугам этой цепи на 2 до насыщения дуги (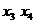 ). В
результате получим поток
). В
результате получим поток 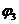 , величина
которого равна
, величина
которого равна 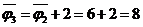 и который
содержит насыщенную дугу
и который
содержит насыщенную дугу 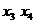 . Удалим эту
насыщенную дугу из
. Удалим эту
насыщенную дугу из 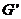 и
оставшийся орграф обозначим
и
оставшийся орграф обозначим 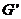 .
.
Выделим в 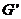 простую
цепь
простую
цепь 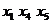 и увеличим
потоки по дугам этой цепи на 3 до насыщения дуги (
и увеличим
потоки по дугам этой цепи на 3 до насыщения дуги (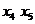 ). В
результате получим поток
). В
результате получим поток 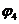 , величина
которого равна
, величина
которого равна 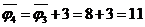 и который
содержит насыщенную дугу
и который
содержит насыщенную дугу 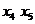 . Удалим эту
насыщенную дугу из
. Удалим эту
насыщенную дугу из 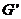 и
оставшийся орграф обозначим
и
оставшийся орграф обозначим 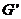 .
.
Выделим в 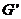 простую
цепь
простую
цепь 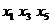 и увеличим
потоки по дугам этой цепи на 2 до насыщения дуги (
и увеличим
потоки по дугам этой цепи на 2 до насыщения дуги (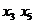 ). В
результате получим поток
). В
результате получим поток 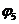 , величина
которого равна
, величина
которого равна 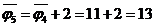 и который
содержит насыщенную дугу
и который
содержит насыщенную дугу 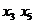 . Удалим эту
насыщенную дугу из
. Удалим эту
насыщенную дугу из 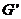 и
оставшийся орграф обозначим
и
оставшийся орграф обозначим 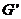 .
.
В оставшемся 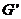 не
существует пути их
не
существует пути их 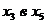 , который не
содержал бы насыщенных дуг, т.е. поток
, который не
содержал бы насыщенных дуг, т.е. поток 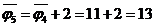 является полным и его величина
равна 13.
является полным и его величина
равна 13.
Задача №2. По данному логическому
выражению построить таблицу истинности без предварительного упрощения функции
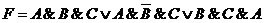 .
.
Построим таблицу истинности по
частям, предварительно построив таблицу истинности для каждой конъюнкции, а
затем в последнем столбце запишем логическую сумму (дизъюнкцию) соответствующих
значений трех конъюнкций 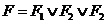 .
.
|
А
|
В
|
С
|
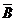 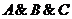 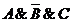 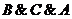 F F
|
|
|
|
|
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
Логические переменные А, В и С
принимают всего 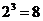 значений,
причем в таком порядке, что если перевести приведенные триады из двоичной
системы в десятичную то получим числа от 0 до 7. В столбцах 5, 6 и 7 приведены
элементарные конъюнкции, значения которых определяются перемножение
соответствующих логических переменных. Значения дизъюнкций, приведенное в 8
столбце таблицы, определяется суммой соответствующих конъюнкций.
значений,
причем в таком порядке, что если перевести приведенные триады из двоичной
системы в десятичную то получим числа от 0 до 7. В столбцах 5, 6 и 7 приведены
элементарные конъюнкции, значения которых определяются перемножение
соответствующих логических переменных. Значения дизъюнкций, приведенное в 8
столбце таблицы, определяется суммой соответствующих конъюнкций.
Задача №3. Функция задана
десятичными эквивалентами единичных значений. Представить эту функцию в виде
СДНФ или в виде СКНФ.
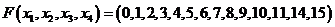 .
.
Поскольку в списке 14 чисел, т.е. 14
эквивалентов единичных значений, следовательно нулевых значений два (16-14=2).
Поэтому по таблице истинности целесообразней строить СКНФ.
Построим таблицу истинности. В
первом столбце укажем десятичные эквиваленты соответствующих наборов.
|
N
|
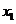 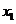 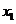 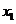 F F
|
|
|
|
|
|
|
1
|
0
|
0
|
0
|
1
|
0
|
|
|
2
|
0
|
0
|
1
|
0
|
0
|
|
|
3
|
0
|
0
|
1
|
1
|
0
|
|
|
4
|
0
|
1
|
0
|
0
|
0
|
|
|
5
|
1
|
0
|
1
|
0
|
|
|
6
|
0
|
1
|
1
|
0
|
0
|
|
|
7
|
0
|
1
|
1
|
1
|
0
|
|
|
8
|
1
|
0
|
0
|
0
|
0
|
|
|
9
|
1
|
0
|
0
|
1
|
1
|
|
|
10
|
1
|
0
|
1
|
0
|
1
|
|
|
11
|
1
|
0
|
1
|
1
|
0
|
|
|
*
|
12
|
1
|
1
|
0
|
0
|
0
|
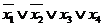
|
|
*
|
13
|
1
|
1
|
0
|
1
|
0
|
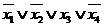
|
|
14
|
1
|
1
|
1
|
0
|
1
|
|
|
15
|
1
|
1
|
1
|
1
|
1
|
|
В таблице звездочками отмечены строчки, в
которых расположены наборы значений переменных, на которых функция равна нулю.
Справа напротив этих строк показаны полные
элементарные функции, которые на соответствующих наборах равны нулю. СКНФ
находится как конъюнкция этих дизъюнкций и будет иметь вид:
Задача №4. Упростить логические
выражения с помощью карты Карно
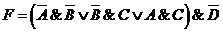 .
.
Известно, что конъюнкции
соответствует пересечение областей карты Карно, соответствующих сомножителям, а
дизъюнкции соответствует объединение областей, соответствующих слагаемым.
Конъюнкции второго ранга на карте Карно соответствует 4 клеточки. Затененная
область на рис. 1,2,3 соответствует конъюнкциям 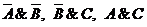 соответственно. На рис.4 показано
пересечение областей, соответствующих множителям
соответственно. На рис.4 показано
пересечение областей, соответствующих множителям 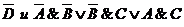 . В соответствующих клетках
пересечения областей стоят единицы и штриховкой показана область клеток для
переменной
. В соответствующих клетках
пересечения областей стоят единицы и штриховкой показана область клеток для
переменной 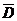 .
.
|
В
|
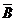 В В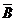
|
|
|
|
|
|
А 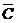
А
|
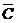
|
|
|
|
|
|
|
|
|
|
|
|
|
С
|
|
|
|
|
|
С
|
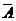
Рис.1. Область 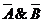 Рис.2.
Область
Рис.2.
Область 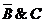
Клетки имеющие затенение и штриховку
одновременно соответствуют исходной функции. Объединив эти три единицы в две
пары, получим представление исходной функции в виде дизъюнкции двух конъюнкций
третьего ранга 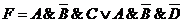 .
.
|
В
|
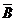 В В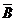
|
|
|
|
|
|
А 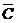
А
|
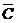
|
|
|
|
|
|
|
|
|
|
|
|
|
С
|
|
1
|
|
|
1
|
С
|
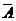
Рис.3. Область 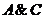 Рис.4.
Заполнение карты Карно
Рис.4.
Заполнение карты Карно