Множинна регресія
Вступ
Актуальність. Множинна регресія широко використовується у вирішенні проблем
попиту, прибутковості акцій, при вивченні функції витрат виробництва, в
макроекономічних розрахунках і цілому ряду інших питань економетрії. В даний
час множинна регресія - один з найбільш поширених методів в економетрії.
Мета: побудувати економетричну модель з великим числом факторів,
визначивши при цьому вплив кожного з них окремо, а також сукупну їх дію на
модельований показник.
Для досягнення мети були
поставлені такі завдання:
знайти і
опрацювати літературу з даної теми;
систематизувати
опрацьований матеріал;
освоїти методи
побудови рівняння множинної регресії;
побудувати
модель множинної регресії методом найменших квадратів;
зробити
висновки.
Предмет. Методи побудови та дослідження рівняння множинної регресії.
Об’єкт. Економетрична модель множинної регресії.
Методи дослідження. Методи найменших квадратів.
Короткий зміст
матеріалу.
1. У вступі визначено актуальність, мета, предмет, об’єкт, методи
дослідження всієї роботи.
2. В першій частині курсової роботи розглядаються основні теоретичні
відомості: поняття економетричної моделі множинної регресії та побудова
рівняння множинної регресії методом найменших квадратів.
3. В другій частині наведено приклад задачі побудованої на основі
методу найменших квадратів.
1. Загальна лінійна
економетрична модель
.1 Поняття моделі
та етапи її побудови
Економетрична модель - це функція чи система функцій, що описує
кореляційно-регресійний зв’язок між економічними показниками, один чи кілька з
яких є залежною змінною, інші - незалежними.
У загальному вигляді
економетрична модель запишеться так:

де y -
залежна змінна; 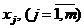 -
незалежні змінні; u - стохастична складова, або
-
незалежні змінні; u - стохастична складова, або
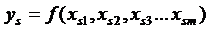 ,
,
де 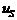 -
стохастична складова s-го рівняння,
-
стохастична складова s-го рівняння, 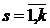 , тобто ця економетрична
модель складається з k функцій. [8, с. 84]
, тобто ця економетрична
модель складається з k функцій. [8, с. 84]
У загальному
матричному вигляді економетрична модель для фактичних даних записується так:
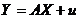 ,
,
де А -
матриця параметрів моделі розміром  (т - кількість
незалежних змінних, п - число спостережень); Y - матриця значень
залежної змінної; Х - матриця незалежних змінних u - матриця
випадкової складової.
(т - кількість
незалежних змінних, п - число спостережень); Y - матриця значень
залежної змінної; Х - матриця незалежних змінних u - матриця
випадкової складової.
Незалежні
фактичні змінні Х
(пояснювальні змінні) найчастіше бувають детермінованими і вони є наперед
заданими змінними, або вхідними показниками для економічної системи.
Випадкові
складові u називають ще стохастичними
складовими, помилками або частіше залишками. Вони є наслідками помилок
спостережень, містять у собі вплив усіх випадкових факторів, а також факторів,
які не входять у модель.
З огляду того, що
залежні фактичні змінні Y (пояснювані змінні), які є результативними
показниками, залежать від випадкової складової u, то вони також є
стохастичними (випадковими). Звідси і економетрична модель є стохастичною.
У ряді випадків
економетричні моделі можуть бути описані методами кореляційно-регресійного
аналізу. Задачею регресійного аналізу є встановлення виду залежності
між змінними та вивчення залежності між ними. Основною задачею кореляційного
аналізу є виявлення зв’язку між змінними та оцінка її тісноти та
значущості. Але на застосування кореляційно - регресійного аналізу накладаються
такі вимоги:
1. Необхідність
достатньо великої сукупності спостережень;
. Забезпечення
однорідної сукупності спостережень;
. Наявність
нормального закону розподілення сукупності вивчаючих одиниць, на якому
побудовані всі положення кореляційно-регресійного аналізу. [6, с. 103]
1.2 Класична
нормальна лінійна модель множинної регресії
Загальна множинна
регресійна модель має наступний вигляд:
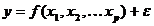 (1.1)
(1.1)
де y - залежна
змінна;
x1, x2,…,
xp - фактори (незалежні
змінні).
Якщо множинна регресійна
модель є лінійною (ЛМР), то вона подається у вигляді:
 (1.2)
(1.2)
Позначимо i-е
спостереження змінної y через yi, а факторів - xi1,
xi2,…, xip. Відтоді модель (1.2) можна подати у
вигляді:
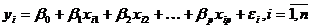 , (1.3)
, (1.3)
або у матричній формі:
 ,
,
де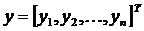 -
вектор (матриця-стовпець) значень залежної змінної;
-
вектор (матриця-стовпець) значень залежної змінної;
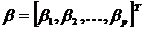 - вектор (матриця-стовпець)
коефіцієнтів регресійної моделі;
- вектор (матриця-стовпець)
коефіцієнтів регресійної моделі;
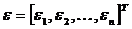 - вектор
(матриця-стовпець) похибок;
- вектор
(матриця-стовпець) похибок;
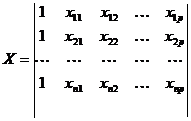 - матриця значень
факторів.
- матриця значень
факторів.
Відмітимо основні
припущення регресійного аналізу:
. В моделі
(1.3) похибка 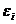 (або
залежна змінна
(або
залежна змінна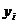 )
є випадковою величиною, а фактори
)
є випадковою величиною, а фактори  невипадкові величини (
невипадкові величини (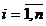 ).
).
. Математичне
сподівання похибки 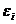 дорівнює
нулю:
дорівнює
нулю:
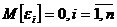 .
.
. Дисперсія
похибки 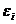 (або
залежної змінної
(або
залежної змінної 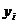 )
постійна дія будь-якої i:
)
постійна дія будь-якої i:
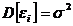 .
.
тобто виконується
умова гомоскедастичності.
. Похибки 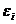 та
та
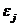 не
корельовані:
не
корельовані:
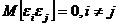 ,
,
. Похибка 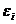 (або
залежна змінна
(або
залежна змінна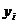 )
є нормально розподіленою випадковою величиною.
)
є нормально розподіленою випадковою величиною.
. Матриця
значень факторів невироджена, тобто її ранг дорівнює  .
.
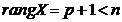 .
.
Модель (1.1), для
якої виконуються припущення 1-6, називається класичною нормальною лінійною
моделлю множинної регресії (CNLMR-model).
Оцінкою цієї
моделі за вибіркою є рівняння регресії:
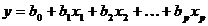 , (1.4)
, (1.4)
де 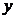 -
оцінка математичного сподівання залежної змінної
-
оцінка математичного сподівання залежної змінної 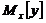 ;
;
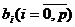 - оцінка коефіцієнтів
- оцінка коефіцієнтів  регресійної
моделі (або коефіцієнти регресії).
регресійної
моделі (або коефіцієнти регресії).
Коефіцієнт (індекс)
множинної кореляції R
використовується для оцінки тісноти спільного впливу факторів на залежну
змінну:
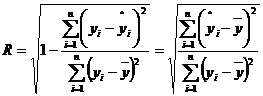 . (1.5)
. (1.5)
Властивості коефіцієнта
множинної кореляції R:
1. Коефіцієнт
множинної кореляції приймає значення на відрізку,  тобто
тобто /
/
. При R=1
кореляційний зв’язок є лінійною функціональною залежністю.
. При R=0
лінійний кореляційний зв’язок відсутній.
1.3 Оцінка значущості
множинної регресії. Коефіцієнт детермінації
Оцінка значущості
лінійної множинної регресії (ЛМР).
Значущість рівня ЛМР у
цілому оцінюється за допомогою F-критерія Фішера:
 (1.6)
(1.6)
із зрівнянням його з
табличним значенням
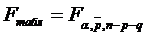 (1.7)
(1.7)
-критерій Фішера.
Якщо 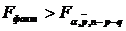 ,
то рівняння ЛМР признається статистично значущим на рівні значущості
,
то рівняння ЛМР признається статистично значущим на рівні значущості 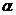 (зазвичай,
(зазвичай,
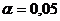 ).
).
Якщо 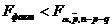 ,
то рівняння ЛМР признається статистична незначущість ЛМР на рівні значущості
,
то рівняння ЛМР признається статистична незначущість ЛМР на рівні значущості 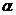 .
.
Оцінка
значущості коефіцієнтів рівняння ЛМР.
Оцінка значущості
коефіцієнтів рівняння ЛМР здійснюються за допомогою t-критерію
Ст’юдента:
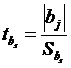 (1.8)
(1.8)
із зрівнянням його з
табличним значенням
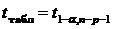 , (1.9)
, (1.9)
де  -
середньоквадратичне відхилення (стандартна похибка) коефіцієнта регресії
-
середньоквадратичне відхилення (стандартна похибка) коефіцієнта регресії 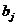 ;
;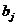 - коефіцієнт чистої регресії при факторі
- коефіцієнт чистої регресії при факторі  .
.
 - оцінка
середньоквадратичного відхилення похибок;
- оцінка
середньоквадратичного відхилення похибок;
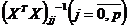 - відповідний
діагональний елемент матриці
- відповідний
діагональний елемент матриці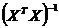 .
.
t-критерій
Якщо 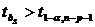 ,
то коефіцієнт
,
то коефіцієнт 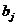 признається
статистично значущим; якщо
признається
статистично значущим; якщо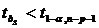 ,
то
,
то 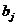 -
статистично незначущий на рівні значущості
-
статистично незначущий на рівні значущості 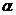 .
.
Другий варіант:
при 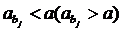 -
-
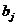 -
статистично значущий (незначущий) на рівні значущості
-
статистично значущий (незначущий) на рівні значущості 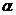 .
.
Коефіцієнт
(індекс) множинної детермінації R2
Для оцінки
адекватності регресії моделі, мірою якості рівняння регресії використовують
коефіцієнт детермінації, який визначається, як і раніше, за формулою:
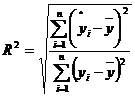 . (1.10)
. (1.10)
Нагадаємо, що R2
характеризує частку варіації залежної змінної, що обумовлена варіаціями
факторів.
Властивості коефіцієнта
множинної детермінації R2:
1. Коефіцієнт
множинної детермінації приймає значення на відрізку ,
тобто
,
тобто  .
.
Чим ближче R2
до одиниці, тим краще регресія апроксимує емпіричні дані.
. Якщо R2=1,
між змінними y та x1, x2,…, xp
існує лінійна функціональна залежність.
. Якщо R2=0,
то варіація залежної змінної повністю обумовлена виливом випадкових та
неврахованих факторів.
Для оцінки ступеня
апроксимації емпіричних даних рівнянням ЛМР можна керуватись аналогічними
емпіричними правилами, як і для випадку ЛПР.
Недоліком
коефіцієнта множинної детермінації R2 являється те, що він,
взагалі, збільшується при додаванні нових факторів, хоча це не обов’язково
означає поліпшення якості регресійної моделі. Тому є сенс використовувати
скоригований (адаптований, виправлений) коефіцієнт детермінації ,
який визначається за формулою:
,
який визначається за формулою:
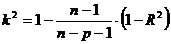 . (1.11)
. (1.11)
На відміну від R2
скоригований коефіцієнт  може
зменшуватись при введенні у модель нових факторів, які не чинять істотного
впливу на залежну змінну.
може
зменшуватись при введенні у модель нових факторів, які не чинять істотного
впливу на залежну змінну.
1.4 Визначення
довірчих інтервалів для функції регресії та її параметрів
Прогнозне
значення 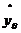 визначається
за шляхом підстановки у рівняння регресії (1.4) відповідних значень факторів
визначається
за шляхом підстановки у рівняння регресії (1.4) відповідних значень факторів 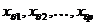 :
:
 . (1.12)
. (1.12)
Довірчий інтервал
прогнозу обчислюється за слідуючими формулами:
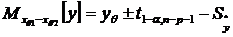 , (1.13)
, (1.13)
де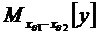 - умовне математичне сподівання залежної змінної в точці прогнозу;
- умовне математичне сподівання залежної змінної в точці прогнозу;
 - оцінка стандартної
похибки прогнозу, яка обчислюється за формулою
- оцінка стандартної
похибки прогнозу, яка обчислюється за формулою
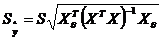 ; (1.14)
; (1.14)
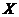 - матриця значень
факторів;
- матриця значень
факторів;
 - вектор
(матриця-стовпець) значень факторів для прогнозу.
- вектор
(матриця-стовпець) значень факторів для прогнозу.
Довірчі
інтервали для коефіцієнтів регресійної моделі:
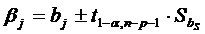 ,
,  , (1.15)
, (1.15)
Важливою економічною
характеристикою моделі є сумарна еластичність:
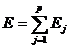 (1.19)
(1.19)
1.5 Специфікація
моделі. Відбір факторів при побудові рівняння множинної регресії
Побудова рівняння
множинної регресії починається з розв’язання питання про специфікацію моделі.
Він включає два круга питань:
· відбір
факторів
· вибір
виду рівняння регресії.
Включення в рівняння
множинної регресії того або іншого набору факторів пов'язане перш за все з
уявленням дослідника про природу взаємозв'язку модельованого показника з іншими
економічними явищами. Фактори, що включаються в множинну регресію, повинні
відповідати наступним вимогам.
1. Вони повинні
бути кількісно вимірні. Якщо необхідно включити в модель якісний фактор,
що не має кількісного вимірювання, то йому потрібно надати кількісну
визначеність.
2. Фактори не
повинні бути інтеркорельовані і тим більше знаходитися в точному
функціональному зв'язку.
Включення в модель
факторів з високою інтеркореляцією, може привести до небажаних наслідків -
система нормальних рівнянь може виявитися погано визначеною і спричинити
нестійкість і ненадійність оцінок коефіцієнтів регресії.
Якщо між факторами існує
висока кореляція, то не можна визначити їх ізольований вплив на результативний
показник і параметри рівняння регресії виявляються такими, що не
інтерпретуються.
Фактори, що включаються
в множинну регресію, повинні пояснити варіацію незалежної змінної. Якщо
будується модель з набором m факторів, то для неї розраховується
показник детермінації, який фіксує частку поясненої варіації результативної
ознаки за рахунок m факторів, що розглядаються в регресії. Вплив
інших, не врахованих в моделі факторів, оцінюється як 1-R2 з
відповідною залишковою дисперсією S2зал.
При додатковому
включенні в регресію m+1-го фактора коефіцієнт
детермінації повинен зростати, а залишкова дисперсія зменшуватися:
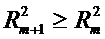 і
і 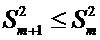 .
.
Якщо ж цього не
відбувається і дані показники практично не відрізняються один від одного, то
фактор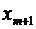 ,
що включається в аналіз, не покращує модель і практично є зайвим фактором.
,
що включається в аналіз, не покращує модель і практично є зайвим фактором.
Насичення моделі
зайвими факторами не тільки не знижує величину залишкової дисперсії і не
збільшує показник детермінації, але і приводить до статистичної незначущості
параметрів регресії згідно критерію Стьюдента.
Таким чином, хоча
теоретично регресійна модель дозволяє врахувати будь-яке число факторів,
практично в цьому немає необхідності. Відбір факторів проводиться на основі
якісного теоретико-економічного аналізу. Проте теоретичний аналіз часто не
дозволяє однозначно відповісти на питання про кількісний взаємозв'язок даних
ознак і доцільність включення фактора в модель.
Тому відбір
факторів зазвичай здійснюється в два етапи:
Ø на першому підбираються фактори виходячи з суті проблеми;
Ø на другому - на основі матриці показників кореляції визначають
статистики для параметрів регресії.
Коефіцієнти
інтеркореляції (тобто кореляції між пояснюючими змінними) дозволяють виключати
з моделі дублюючі фактори. Вважається, що дві змінні явно колінеарні, тобто
знаходяться між собою в лінійній залежності, якщо 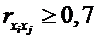 .
Якщо фактори явно колінеарні, то вони дублюють один одного і один з них
рекомендується виключити з регресії. Перевага при цьому віддається не фактору,
тісніше пов'язаному з результатом, а тому фактору, який при достатньо тісному
зв'язку з результатом має найменшу тісноту зв'язку з іншими факторами. У цій
вимозі виявляється специфіка множинної регресії як методу дослідження
комплексної дії факторів в умовах їх незалежності один від одного.
.
Якщо фактори явно колінеарні, то вони дублюють один одного і один з них
рекомендується виключити з регресії. Перевага при цьому віддається не фактору,
тісніше пов'язаному з результатом, а тому фактору, який при достатньо тісному
зв'язку з результатом має найменшу тісноту зв'язку з іншими факторами. У цій
вимозі виявляється специфіка множинної регресії як методу дослідження
комплексної дії факторів в умовах їх незалежності один від одного.
За величиною
парних коефіцієнтів кореляції виявляється лише явна колінеарність факторів.
Найбільші труднощі у використанні апарату множинної регресії виникають за
наявності мультиколінеарності факторів, коли більше ніж два фактори зв'язані
між собою лінійною залежністю, тобто має місце сукупна дія факторів один на
одного.
Суть мультиколінеарності
полягає в тому, що в багатофакторній регресійній моделі дві або більше
незалежних змінних пов'язані між собою лінійною залежністю або, іншими словами,
мають високий ступінь кореляції:
Наявність
мультиколінеарності факторів може означати, що деякі фактори завжди діятимуть в
унісон. В результаті варіація в початкових даних перестає бути повністю
незалежною і не можна оцінити дію кожного фактора окремо.
Для оцінки мультиколінеарності
факторів може використовуватися визначник матриці парних коефіцієнтів кореляції
між факторами.
Якби фактори не
корелювали між собою, то матриця парних коефіцієнтів кореляції між факторами
була б одиничною матрицею, оскільки всі недіагональні елементи 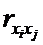
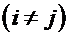 були б рівні нулю. Так,
для рівняння, що включає три пояснюючих змінних
були б рівні нулю. Так,
для рівняння, що включає три пояснюючих змінних
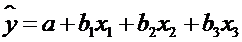
матриця
коефіцієнтів кореляції між факторами мала б визначника, рівного одиниці:
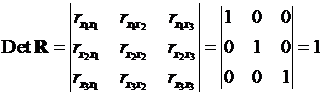 .
.
Якщо ж, навпаки, між
факторами існує повна лінійна залежність і всі коефіцієнти кореляції рівні
одиниці, то визначник такої матриці рівний нулю:
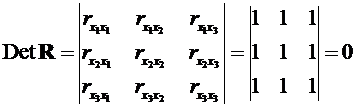 .
.
Чим ближче до
нуля визначник матриці міжфакторної кореляції, тим сильніше мультиколінеарність
факторів і ненадійніше результати множинної регресії. І, навпаки, чим ближче до
одиниці визначник матриці міжфакторної кореляції, тим менше мультиколінеарність
факторів.
Мультиколінеарність не є
проблемою, якщо єдиною метою регресійного аналізу є прогноз (оскільки
чим більше значення R2, тим точніший прогноз). Якщо метою
аналізу є не прогноз, а дійсне значення параметрів, то
мультиколінеарність перетворюється на проблему, оскільки її наявність призводить
до значних стандартних похибок оцінок параметрів.
2. Метод найменших
квадратів (МНК)
.1
Передумови застосування методу найменших квадратів
Нехай економетрична
модель у матричній формі має вигляд
 (2.1)
(2.1)
X - матриця незалежних змінних розміром  (n
- число спостережень, m - кількість незалежних змінних);
(n
- число спостережень, m - кількість незалежних змінних);
A - вектор оцінок параметрів моделі;
u - вектор залишків.
Щоб застосувати
1МНК для оцінки параметрів моделі, необхідне виконання таких умов:
1. математичне
сподівання залишків дорівнює нулю, тобто
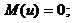 (2.2)
(2.2)
2. значення ui
вектора залишків u незалежні між собою і мають постійну дисперсію, тобто
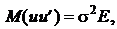 (2.3)
(2.3)
де Е - одинична
матриця;
. незалежні
змінні моделі не пов’язані із залишками:
 (2.4)
(2.4)
4. незалежні
змінні моделі утворюють лінійно незалежну систему векторів, або, іншими
словами, незалежні змінні не повинні бути мультиколінеарними, тобто 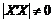 :
:
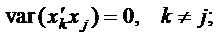 (2.5)
(2.5)
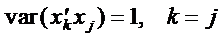 ,
,
де Xk
- k-й вектор матриці пояснювальних змінних; Xj - j-й
вектор цієї матриці пояснювальних змінних X, 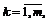
 .
.
Перша
умова, здавалося б, є очевидною. Адже коли математичне сподівання
залишків не дорівнює нулю, то це означає, що існує систематичний вплив на
залежну змінну, а до модельної специфікації не введено всіх основних незалежних
змінних. Якщо ця передумова не виконується, то йдеться про помилку
специфікації.
зауважимо, що
коли економетрична модель має вільний член, то майже завжди за рахунок його
значення можна скоригувати рівняння так, щоб математичне сподівання залишків
дорівнювало нулю. Отже, для таких моделей перша умова практично
виконуватиметься завжди.
Друга
умова передбачає наявність сталої дисперсії залишків. Цю властивість
називають гомоскедастичністю. Проте вона може виконуватись лише тоді,
коли залишки u є помилками вимірювання. Якщо залишки акумулюють
загальний вплив змінних, які не враховані в моделі, то звичайно дисперсія
залишків не може бути сталою величиною, вона змінюється для окремих груп
спостережень. У такому разі йдеться про явище гетероскедастичності, яке
впливає на методи оцінювання параметрів.
Третя
умова передбачає незалежність між залишками і пояснювальними змінними,
яка порушується насамперед тоді, коли економетрична модель будується на базі
одночасових структурних рівнянь або має лагові змінні. Тоді для оцінювання
параметрів моделі використовуються, як правило, дво - або трикроковий метод
найменших квадратів.
Четверта
умова означає, що всі пояснювальні змінні, які входять до економетричної
моделі, мають бути незалежними між собою. Проте очевидно, що в економіці дуже
важко вирізнити такий масив незалежних (пояснювальних) змінних, які були б
зовсім не пов’язані між собою. Тоді щоразу необхідно з’ясовувати, чи не
впливатиме залежність пояснювальних змінних на оцінку параметрів моделі.
Це явище
називають мультиколінеарністю змінних, що призводить до ненадійності
оцінки параметрів моделі, робить їх чутливими до вибраної специфікації моделі
та до конкретного набору даних. Знижується рівень довіри до результатів
верифікації моделей з допомогою МНК. Отже, це явище з усіх точок зору є дуже
небажаним. Але воно досить поширене. 8, c. 88]
2.2
Властивості оцінок на основі МНК
Можливі різні види
рівнянь множинної регресії: лінійні і нелінійні.
Зважаючи на чітку
інтерпретацію параметрів найширше використовується лінійна функція. У лінійній
множинній регресії
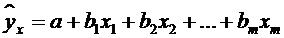
параметри при 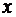 називаються
коефіцієнтами «чистої» регресії. Вони характеризують середню зміну результату
із зміною відповідного фактора на одиницю при незміненому значенні інших
факторів, закріплених на середньому рівні.
називаються
коефіцієнтами «чистої» регресії. Вони характеризують середню зміну результату
із зміною відповідного фактора на одиницю при незміненому значенні інших
факторів, закріплених на середньому рівні.
Розглянемо
лінійну модель множинної регресії
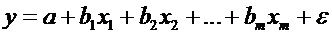 . (2.6)
. (2.6)
Класичний підхід
до оцінювання параметрів лінійної моделі множинної регресії заснований на
методі найменших квадратів (МНК). МНК дозволяє отримати такі оцінки параметрів,
при яких сума квадратів відхилень фактичних значень результативної ознаки 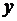 від
розрахункових
від
розрахункових 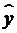 мінімальна:
мінімальна:
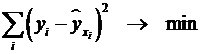 . (2.7)
. (2.7)
Як відомо з курсу
математичного аналізу, для того, щоб знайти екстремум функції багатьох змінних,
треба обчислити частинні похідні першого порядку по кожному з параметрів і
прирівняти їх до нуля.
Отже, маємо функцію
 аргументу:
аргументу:
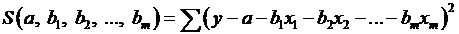 .
.
Знаходимо
частинні похідні першого порядку:
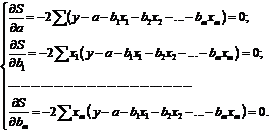
Після елементарних
перетворень приходимо до системи лінійних нормальних рівнянь для знаходження
параметрів лінійного рівняння множинної регресії (2.1):
 (2.8)
(2.8)
Для двохфакторної моделі
дана система матиме вигляд:
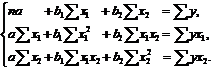
Метод найменших
квадратів застосовний і до рівняння множинної регресії в стандартизованому
масштабі:
 (2.9)
(2.9)
де 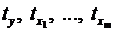 -
стандартизовані змінні:
-
стандартизовані змінні: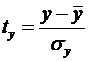 ,
,
 ,
для яких середнє значення рівне нулю:
,
для яких середнє значення рівне нулю: , а середнє квадратичне
відхилення рівне одиниці:
, а середнє квадратичне
відхилення рівне одиниці: 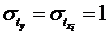 ;
;
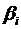 -
стандартизовані коефіцієнти регресії.
-
стандартизовані коефіцієнти регресії.
Стандартизовані
коефіцієнти регресії показують, на скільки одиниць зміниться в середньому
результат, якщо відповідний фактор 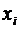 зміниться на одну
одиницю при незмінному середньому рівні інших факторів. Внаслідок того, що всі
змінні задані як центровані і нормовані, стандартизовані коефіцієнти регресії
зміниться на одну
одиницю при незмінному середньому рівні інших факторів. Внаслідок того, що всі
змінні задані як центровані і нормовані, стандартизовані коефіцієнти регресії 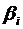 можна
порівнювати між собою. Порівнюючи їх один з одним, можна ранжирувати фактори по
силі їх дії на результат. У цьому основна перевага стандартизованих
коефіцієнтів регресії на відміну від коефіцієнтів «чистої» регресії, які
непорівнювані між собою.
можна
порівнювати між собою. Порівнюючи їх один з одним, можна ранжирувати фактори по
силі їх дії на результат. У цьому основна перевага стандартизованих
коефіцієнтів регресії на відміну від коефіцієнтів «чистої» регресії, які
непорівнювані між собою.
Застосовуючи МНК
до рівняння множинної регресії в стандартизованому масштабі, отримаємо систему
нормальних рівнянь вигляду
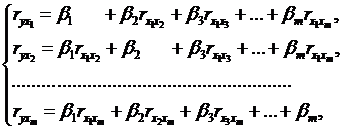 (2.10)
(2.10)
де 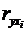 і
і
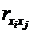 -
коефіцієнти парної і міжфакторної кореляції.
-
коефіцієнти парної і міжфакторної кореляції.
Коефіцієнти
«чистої» регресії 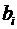 пов'язані
із стандартизованими коефіцієнтами регресії
пов'язані
із стандартизованими коефіцієнтами регресії 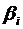 таким чином:
таким чином:
 . (2.11)
. (2.11)
Тому можна
переходити від рівняння регресії в стандартизованому масштабі (2.9) до рівняння
регресії в натуральному масштабі змінних (2.6), при цьому параметр 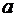 визначається
як
визначається
як 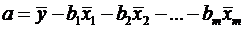 .
.
Розглянутий смисл
стандартизованих коефіцієнтів регресії дозволяє їх використовувати при відсіві
факторів - з моделі виключаються фактори з найменшим значенням 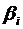 .
.
На основі
лінійного рівняння множинної регресії
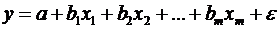 (2.12)
(2.12)
можуть бути знайдені
частинні рівняння регресії:
 (2.13)
(2.13)
тобто рівняння
регресії, які пов'язують результативну ознаку з відповідним фактором 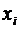 при
закріпленні решти факторів на середньому рівні. У розгорненому вигляді систему
(2.13) можна переписати у вигляді:
при
закріпленні решти факторів на середньому рівні. У розгорненому вигляді систему
(2.13) можна переписати у вигляді:
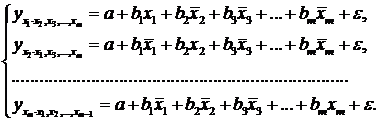
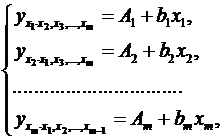 (2.14)
(2.14)

На відміну від парної
регресії частинні рівняння регресії характеризують ізольований вплив фактора на
результат, бо інші фактори закріплені на незмінному рівні. Ефекти впливу інших
факторів приєднані в них до вільного члена рівняння множинної регресії. Це
дозволяє на основі частинних рівнянь регресії визначати частинні коефіцієнти
еластичності:
 , (2.15)
, (2.15)
де 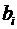 -
коефіцієнт регресії для фактора
-
коефіцієнт регресії для фактора 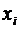 в рівнянні множинної
регресії,
в рівнянні множинної
регресії,  -
частинне рівняння регресії.
-
частинне рівняння регресії.
Разом з
частинними коефіцієнтами еластичності можуть бути знайдені середні по
сукупності показники еластичності:
 (2.16)
(2.16)
які показують на скільки
відсотків в середньому зміниться результат, при зміні відповідного фактора на
1%. Середні показники еластичності можна порівнювати один з одним і
відповідно ранжирувати фактори по силі їх дії на результат. [5, c. 130]
2.3
Перевірка значущості факторів і показники якості регресії
Практична значущість
рівняння множинної регресії оцінюється за допомогою показника множинної
кореляції і його квадрата - показника детермінації.
Показник множинної кореляції
характеризує тісноту зв'язку даного набору факторів з досліджуваною ознакою
або, інакше, оцінює тісноту спільного впливу факторів на результат.
Незалежно від форми
зв'язку показник множинної кореляції може бути знайдений як індекс множинної
кореляції:
 , (2.17)
, (2.17)
де 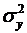 -
загальна дисперсія результативної ознаки;
-
загальна дисперсія результативної ознаки; 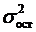 - залишкова дисперсія.
- залишкова дисперсія.
Межі зміни
індексу множинній кореляції від 0 до 1. Чим ближче його значення до 1, тим
тісніше зв'язок результативної ознаки зі всім набором досліджуваних факторів.
Величина індексу множинної кореляції повинна бути більше або рівна
максимальному парному індексу кореляції:
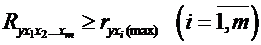 .
.
При правильному
включенні факторів в регресійну модель величина індексу множинної кореляції істотно
відрізнятиметься від індексу кореляції парної залежності.
Якщо ж додатково
включені в рівняння множинної регресії фактори малозначущі, то індекс множинної
кореляції може практично співпадати з індексом парної кореляції (відмінності в
третьому, четвертому знаках). Звідси ясно, що порівнюючи індекси
множинної і парної кореляції, можна зробити висновок про доцільність включення
в рівняння регресії того або іншого фактора.
Розрахунок
індексу множинної кореляції припускає визначення рівняння множинної регресії і
на його основі залишкової дисперсії:
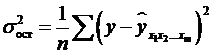 . (2.18)
. (2.18)
Можна користуватися
наступною формулою індексу множинної детермінації:
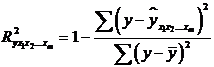 . (2.19)
. (2.19)
При лінійній залежності
ознак формула індексу множинної кореляції може бути представлена наступним
виразом:
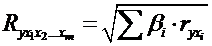 , (2.20)
, (2.20)
де 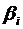 -
стандартизовані коефіцієнти регресії;
-
стандартизовані коефіцієнти регресії; 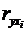 - парні коефіцієнти
кореляції результату з кожним фактором.
- парні коефіцієнти
кореляції результату з кожним фактором.
Формула індексу
множинної кореляції для лінійної регресії отримала назву лінійного коефіцієнта
множинної кореляції, або, що те ж саме, сукупного коефіцієнта кореляції.
Можливо також при
лінійній залежності визначення сукупного коефіцієнта кореляції через матрицю
парних коефіцієнтів кореляції:
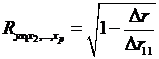 (2.21)
(2.21)
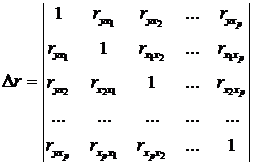
визначник матриці
парних коефіцієнтів кореляції;
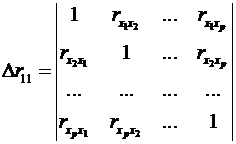
визначник матриці
міжфакторної кореляції.
Як бачимо,
величина множинного коефіцієнта кореляції залежить не тільки від кореляції
результату з кожним з факторів, але і від міжфакторної кореляції. Розглянута
формула дозволяє визначати сукупний коефіцієнт кореляції, не звертаючись при
цьому до рівняння множинної регресії, а використовуючи лише парні коефіцієнти
кореляції.
У розглянутих
показниках множинної кореляції (індекс і коефіцієнт) використовується залишкова
дисперсія, яка має систематичну помилку у бік зменшення, тим значнішу, чим
більше параметрів визначається в рівнянні регресії при заданому об'ємі
спостережень  .
Якщо число параметрів при
.
Якщо число параметрів при 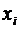 рівно
рівно
 і
наближається до об'єму спостережень, то залишкова дисперсія буде близька до
нуля і коефіцієнт (індекс) кореляції наблизиться до одиниці навіть при слабкому
зв'язку факторів з результатом. Для того,
щобнедопуститиможливогоперебільшеннятіснотизв'язку, використовуєтьсяскоректованийіндекс
(коефіцієнт) множинноїкореляції.
і
наближається до об'єму спостережень, то залишкова дисперсія буде близька до
нуля і коефіцієнт (індекс) кореляції наблизиться до одиниці навіть при слабкому
зв'язку факторів з результатом. Для того,
щобнедопуститиможливогоперебільшеннятіснотизв'язку, використовуєтьсяскоректованийіндекс
(коефіцієнт) множинноїкореляції.
Скоректований
індекс множинної кореляції містить поправку на число ступенів свободи, а саме
залишкова сума квадратів 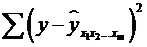 ділиться
на число ступенів свободи залишкової варіації, а загальна сума квадратів
відхилень
ділиться
на число ступенів свободи залишкової варіації, а загальна сума квадратів
відхилень 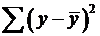 на
число ступенів свободи в цілому по сукупності
на
число ступенів свободи в цілому по сукупності 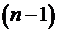 .
.
Формула
скоректованого індексу множинної детермінації має вигляд:
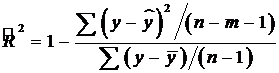 , (2.22)
, (2.22)
де  -
число параметрів при змінних
-
число параметрів при змінних 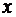 ;
; 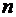 -
число спостережень.
-
число спостережень.
Оскільки 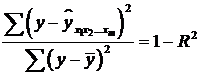 ,
то величину скоректованого індексу детермінації можна представити у вигляді:
,
то величину скоректованого індексу детермінації можна представити у вигляді:
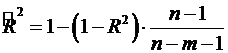 (2.22а)
(2.22а)
Чим більше
величина m, тим сильніша відмінність 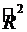 і
і
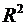 .
.
Як було показано
вище, ранжирування факторів, що беруть участь в множинній лінійній регресії,
може бути проведене через стандартизовані коефіцієнти регресії ( -
коефіцієнти). Ця ж мета може бути досягнута за допомогою частинних коефіцієнтів
кореляції (для лінійних зв'язків). Крім того, частинні показники кореляції
широко використовуються при розв’язанні проблеми відбору факторів: доцільність
включення того або іншого фактора в модель можна довести величиною показника
частинної кореляції.
-
коефіцієнти). Ця ж мета може бути досягнута за допомогою частинних коефіцієнтів
кореляції (для лінійних зв'язків). Крім того, частинні показники кореляції
широко використовуються при розв’язанні проблеми відбору факторів: доцільність
включення того або іншого фактора в модель можна довести величиною показника
частинної кореляції.
Частинні
коефіцієнти кореляції характеризують тісноту зв'язку між результатом і
відповідним фактором при усуненні впливу інших факторів, включених в рівняння
регресії.
Показники частинної
кореляції є відношенням скорочення залишкової дисперсії за рахунок додаткового
включення в аналіз нового фактора до залишкової дисперсії, що мала місце до
введення його в модель.
У загальному
вигляді за наявності  факторів
для рівняння
факторів
для рівняння

коефіцієнт
частинної кореляції, що вимірює вплив на 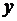 фактора хі
при незмінному рівні інших факторів, можна визначити за формулою:
фактора хі
при незмінному рівні інших факторів, можна визначити за формулою:
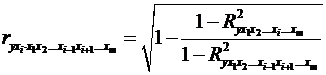 , (2.23)
, (2.23)
де 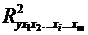 -
множинний коефіцієнт детермінації всіх
-
множинний коефіцієнт детермінації всіх  факторів з результатом;
факторів з результатом;
 -
той же показник детермінації, але без введення в модель фактора
-
той же показник детермінації, але без введення в модель фактора 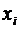 .
.
При двох факторах
формула (2.23) матиме вигляд:
 ;
;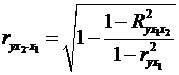 . (2.23а)
. (2.23а)
Порядок
частинного коефіцієнта кореляції визначається кількістю факторів, вплив яких
виключається. Наприклад, 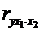 -
коефіцієнт частинної кореляції першого порядку. Відповідно коефіцієнти парної
кореляції називаються коефіцієнтами нульового порядку. Коефіцієнти частинної
кореляції вищих порядків можна визначити через коефіцієнти частинної кореляції
нижчих порядків за рекурентною формулою:
-
коефіцієнт частинної кореляції першого порядку. Відповідно коефіцієнти парної
кореляції називаються коефіцієнтами нульового порядку. Коефіцієнти частинної
кореляції вищих порядків можна визначити через коефіцієнти частинної кореляції
нижчих порядків за рекурентною формулою:
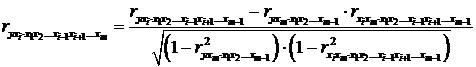 . (2.24)
. (2.24)
При двох факторах дана
формула матиме вигляд:
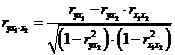 ;
; 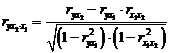 . (2.24а)
. (2.24а)
Для рівняння регресії з
трьома факторами частинні коефіцієнти кореляції другого порядку визначаються на
основі частинних коефіцієнтів кореляції першого порядку. Так, для рівняння
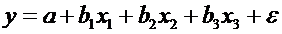
можливе
обчислення трьох частинних коефіцієнтів кореляції другого порядку:
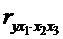 ,
,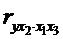 ,
, ,
,
кожний з яких
визначається за рекурентною формулою. Наприклад, при  маємо
формулу для розрахунку
маємо
формулу для розрахунку  :
:
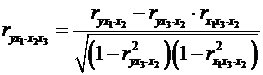 . (2.25)
. (2.25)
Розраховані за
рекурентною формулою частинні коефіцієнти кореляції змінюються в межах від -1
до +1, а за формулами через множинні коефіцієнти детермінації - від 0 до 1.
Порівняння їх один з одним дозволяє ранжирувати фактори по тісноті їх зв'язку з
результатом. Частинні коефіцієнти кореляції дають міру тісноти зв'язку кожного
фактора з результатом в чистому вигляді. Якщо із стандартизованого рівняння
регресії 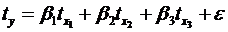 виходить,
що
виходить,
що 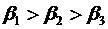 ,
тобто за силою впливу на результат порядок факторів такий:
,
тобто за силою впливу на результат порядок факторів такий: ,
, ,
, ,
то цей же порядок факторів визначається і по співвідношенню частинних
коефіцієнтів кореляції
,
то цей же порядок факторів визначається і по співвідношенню частинних
коефіцієнтів кореляції
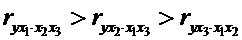 .
.
У економетрії
частинні коефіцієнти кореляції зазвичай не мають самостійного значення. Їх
використовують на стадії формування моделі. Так, будуючи багатофакторну модель,
на першому кроці визначається рівняння регресії з повним набором факторів і
розраховується матриця частинних коефіцієнтів кореляції. На другому кроці
відбирається фактор з найменшою і незначущою за t-критерієм Стьюдента величиною
показника частинної кореляції. Виключивши його з моделі, будується нове
рівняння регресії. Процедура продовжується до тих пір, поки не виявиться, що
всі частинні коефіцієнти кореляції істотно відрізняються від нуля. Якщо
виключений неістотний фактор, то множинні коефіцієнти детермінації на двох
суміжних кроках побудови регресійної моделі майже не відрізняються один від
одного,
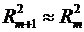 , де
, де  -
число факторів.
-
число факторів.
З наведених вище
формул частинних коефіцієнтів кореляції видно зв'язок цих показників з сукупним
коефіцієнтом кореляції. Знаючи частинні коефіцієнти кореляції (послідовно
першого, другого і більш високого порядку), можна визначити сукупний коефіцієнт
кореляції за формулою:
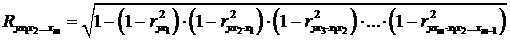 (2.26)
(2.26)
Зокрема, для
двохфакторного рівняння формула (2.21) матиме вигляд:
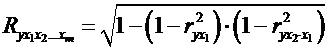 . (2.27)
. (2.27)
При повній залежності результативної
ознаки від досліджуваних факторів коефіцієнт сукупного їх впливу рівний
одиниці. Від одиниці віднімається частка залишкової варіації результативної
ознаки, обумовлена послідовно включеними в аналіз факторами. В результаті
підкореневий вираз характеризує сукупну дію всіх досліджуваних факторів.
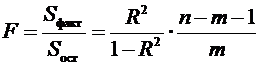 , (2.28)
, (2.28)
де 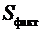 -
сума фактора квадратів на одну ступінь свободи;
-
сума фактора квадратів на одну ступінь свободи; 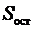 - залишкова сума
квадратів на одну ступінь свободи;
- залишкова сума
квадратів на одну ступінь свободи; 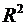 - коефіцієнт (індекс)
множинної детермінації;
- коефіцієнт (індекс)
множинної детермінації;  -
число параметрів при змінних
-
число параметрів при змінних 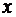 (у лінійній регресії
співпадає з числом включених в модель факторів);
(у лінійній регресії
співпадає з числом включених в модель факторів); 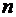 - число спостережень.
- число спостережень.
Оцінюється
значущість не тільки рівняння вцілому, але і фактора, додатково включеного в
регресійну модель. Необхідність такої оцінки пов'язана з тим, що не кожен
фактор, що увійшов до моделі, може істотно збільшувати частку поясненої
варіації результативної ознаки. Крім того, за наявності в моделі декількох
факторів, вони можуть вводитися в модель в різній послідовності. Зважаючи на
кореляцію між факторами, значущість одного і того ж фактора може бути різною
залежно від послідовності його введення в модель. Мірою для оцінки включення
фактора в модель служить частинний 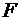 -критерій, тобто
-критерій, тобто  .
.
Частинний 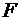 -критерій
побудований на порівнянні приросту факторної дисперсії, обумовленого впливом
додатково включеного фактора, із залишковою дисперсією на одну ступінь свободи
по регресійній моделі вцілому. У загальному вигляді для фактора
-критерій
побудований на порівнянні приросту факторної дисперсії, обумовленого впливом
додатково включеного фактора, із залишковою дисперсією на одну ступінь свободи
по регресійній моделі вцілому. У загальному вигляді для фактора 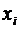 частинний
F-критерій визначиться як
частинний
F-критерій визначиться як
 , (2.29)
, (2.29)
де 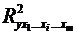 -
коефіцієнт множинної детермінації для моделі з повним набором факторів,
-
коефіцієнт множинної детермінації для моделі з повним набором факторів, 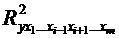 -
той же показник, але без включення в модель фактора хі,
-
той же показник, але без включення в модель фактора хі,
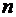 -
число спостережень,
-
число спостережень,  -
число параметрів в моделі (без вільного члена).
-
число параметрів в моделі (без вільного члена).
Фактичне значення
частинного F-критерію порівнюється з табличним при рівні значущості 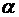 і
числі ступенів свободи: 1 і
і
числі ступенів свободи: 1 і  . Якщо фактичне значення
. Якщо фактичне значення
 перевищує
перевищує
 ,
то додаткове включення фактора
,
то додаткове включення фактора 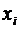 в модель статистично
виправдано і коефіцієнт чистої регресії
в модель статистично
виправдано і коефіцієнт чистої регресії 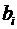 при фактору
при фактору 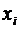 статистично
значущий. Якщо ж фактичне значення
статистично
значущий. Якщо ж фактичне значення  менше табличного, то
додаткове включення в модель фактора
менше табличного, то
додаткове включення в модель фактора 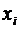 не збільшує істотно
частку поясненої варіації ознаки у, отже, недоцільне його
включення в модель; коефіцієнт регресії при даному факторі в цьому випадку
статистично незначущий.
не збільшує істотно
частку поясненої варіації ознаки у, отже, недоцільне його
включення в модель; коефіцієнт регресії при даному факторі в цьому випадку
статистично незначущий.
Для
двохфакторного рівняння частинні F-критерії мають вигляд:
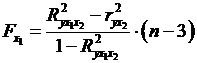 ,
,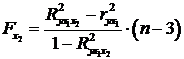 . (2.29а)
. (2.29а)
За допомогою
частинного F-критерію можна перевірити значущість всіх коефіцієнтів регресії в
припущенні, що кожен відповідний фактор 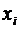 вводився в рівняння
множинної регресії останнім.
вводився в рівняння
множинної регресії останнім.
Частинний F-критерій
оцінює значущість коефіцієнтів чистої регресії. Знаючи величину ,
можна визначити і
,
можна визначити і 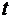 -критерій
для коефіцієнта регресії при і-му фактору,
-критерій
для коефіцієнта регресії при і-му фактору,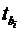 ,
а саме:
,
а саме:
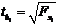 . (2.30)
. (2.30)
Оцінка значущості
коефіцієнтів чистої регресії по 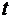 -критерію Стьюдента може
бути проведена і без розрахунку частинних
-критерію Стьюдента може
бути проведена і без розрахунку частинних 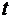 -критеріїв. В цьому
випадку, як і в парній регресії, для кожного фактора використовується формула:
-критеріїв. В цьому
випадку, як і в парній регресії, для кожного фактора використовується формула:
 , (2.31)
, (2.31)
де 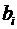 -
коефіцієнт чистої регресії при фактору,
-
коефіцієнт чистої регресії при фактору,  - середня квадратична
(стандартна) помилка коефіцієнта регресії
- середня квадратична
(стандартна) помилка коефіцієнта регресії 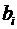 .
.
Для рівняння
множинної регресії 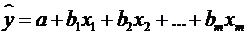 середня
квадратична похибка коефіцієнта регресії може бути визначена за наступною
формулою:
середня
квадратична похибка коефіцієнта регресії може бути визначена за наступною
формулою:
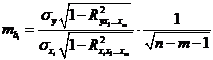 , (2.32)
, (2.32)
де 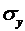 -
середнє квадратичне відхилення для ознаки у,
-
середнє квадратичне відхилення для ознаки у, 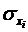 -
середнє квадратичне відхилення для ознаки хі,
-
середнє квадратичне відхилення для ознаки хі, 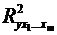 -
коефіцієнт детермінації для рівняння множинної регресії,
-
коефіцієнт детермінації для рівняння множинної регресії, 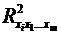 -
коефіцієнт детермінації для залежності фактора
-
коефіцієнт детермінації для залежності фактора 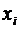 зі всіма іншими
факторами рівняння множинної регресії;
зі всіма іншими
факторами рівняння множинної регресії;  - число ступенів свободи
для залишкової суми квадратів відхилень.
- число ступенів свободи
для залишкової суми квадратів відхилень.
Як бачисо, щоб
скористатися даною формулою, необхідні матриця міжфакторної кореляції і
розрахунок по ній відповідних коефіцієнтів детерміації 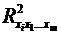 .
Так, для рівняння
.
Так, для рівняння 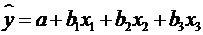 оцінка
значущості коефіцієнтів регресії
оцінка
значущості коефіцієнтів регресії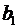 ,
, 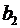 ,
,
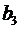 ,
припускає розрахунок трьох міжфакторних коефіцієнтів детерміації:
,
припускає розрахунок трьох міжфакторних коефіцієнтів детерміації: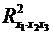 ,
,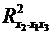 ,
,
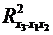 .
.
Взаємозв'язок
показників частинного коефіцієнта кореляції, частинного F-критерія і t-критерія
Стьюдента для коефіцієнтів чистої регресії може використовуватися в процедурі
відбору факторів. Відсів факторів при побудові рівняння регресії методом
виключення практично можна здійснювати не тільки по частинних коефіцієнтах
кореляції, виключаючи на кожному кроці фактор з найменшим незначущим значенням
частинного коефіцієнта кореляції, але і по величинах 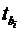 і
і
 .
Частинний F-критерiй широко використовується і при побудові моделі
методом включення.
.
Частинний F-критерiй широко використовується і при побудові моделі
методом включення.
Висновки
економетричний кореляція регресія інтервал
Дана курсова робота присвячена
дослідженню економічних процесів і явищ, а саме визначення рівняння множинної
регресії методом найменших квадратів та впливу на ньго мультиколінеарності.
В процесі роботи
виконано такі завдання:
. Розглянуто
теоретичні відомості про поняття економетричної моделі. Освоєно методи побудови
й оцінки параметрів, що характеризують кількісні взаємозв'язки в економічних
процесах з метою їхнього аналізу й прогнозування.
. Було наведено
приклад на основі реальних статистичних даних, за допомогою методів найменших
квадратів побудовано рівняння множинної регресії, а також досліджено фактори на
мультиколінеарність.
Список використаної
літератури
1. Ачкасов
І.А., Воронков О.О., Воронкова Т.Б. Конспект лекцій з курсу «Економетрія». -
Харків: ХНАМТ, 2009. - 120 с.
. Єлейно В.
Основи економетрії. - Львів:» Марка Лтд», 1995. - 191 с.
. Корольов
О.А. Економетрія: Навч. посібник. - К.: КНТЕУ, 2000. - 660 с.
. Лещинский
О.Л. Економетрія: Навч. посібник для студ. вищ. навч.
закл. - К.: МАУП,
2003. - 208 с.
. Лугінін
О.Є. Економетрія: Навч.посібник 2-ге видання, перероб. та доп. - К.: Центр
учбової літератури, 2008. - 278 с.
. Лугінін
О.Є., Білоусова С.В. Економетрія: Навч. посібник - К.: ЦНЛ, 2005. - 252 с.
. Лук’яненко
І.Г., Краснікова Л.І. Економетрика: Підручник. - К.: «Знання», КОО, 1998. - 493
с.
. Наконечний
С.І., Терещенко Т.О., Романюк Т.П. Економетрія: Навч. посібник. - К.: КНЕУ,
1998. - 276 с.
. Наконечний
С.І., Терещенко Т.О., Водзянова Н.К., Роскач О.С. Практикум з економетрії:
Навчальний посібник. - К.: КНЕУ, 1998. - 176 с.
. Магнус
Я.Р., Катышев П.К., Переседский А.А. Эконометрика: Начальний курс. - М.: Дело,
2001. - 400 с.
. Ставицький
А.В. Навчально-методичний комплекс з курсу «Економетрика». - К., 2004. - 112 с.