|
x
|
-0,037
|
0,27
|
-0,136
|
0,894
|
-0,625
|
0,552
|
-0,62485
|
0,551522
) Т.к. 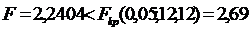 , то нет
оснований отвергать Н0 об отсутствии гетероскедастичности. , то нет
оснований отвергать Н0 об отсутствии гетероскедастичности.
Тест Глейзера
Тест Глейзера основывается на более
общих представлениях о зависимости стандартной ошибки случайного члена от
значений объясняющей переменной. Предположение о пропорциональности 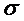 и Х снимаем
и хотим проверить, может ли быть более подходящей какая-либо другая
функциональная форма, например, и Х снимаем
и хотим проверить, может ли быть более подходящей какая-либо другая
функциональная форма, например, 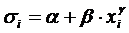 . Чтобы использовать этот метод: . Чтобы использовать этот метод:
оценивают регрессию Y по Х и
вычисляют 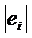 -
абсолютные значения остатков; -
абсолютные значения остатков;
оценивают регрессию 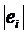 по по 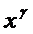 для нескольких
значений для нескольких
значений 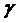 : :
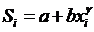 ; ;
1) если
Н0: b = 0
отклоняется (т.е. b значим), то
гипотеза об отсутствии гетероскедастичности будет отклонена.
Если при оценивании более чем одной функции получается
значимая оценка b, то
ориентиром при определении характера гетероскедастичности может служить лучшая
из них.
Пример. Воспользуемся расчетами предыдущего
примера и проверим наличие гетероскедастичности с помощью теста Глейзера.
Решение
1) Рассчитаем
уравнения регрессии еi от 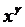 при при
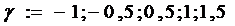
|
х
|
ABS(e)
|
x^(-1)
|
x^(-0,5)
|
x^0,5
|
x^1,5
|
|
25,5
|
3,459461
|
0,039216
|
0,19803
|
5,049752
|
128,7687
|
|
26,5
|
0,102578
|
0,037736
|
0,194257
|
5,147815
|
136,4171
|
|
27,2
|
3,39276
|
0,036765
|
0,191741
|
5,215362
|
141,8578
|
|
29,6
|
1,48376
|
0,033784
|
0,183804
|
5,440588
|
161,0414
|
|
35,7
|
0,859253
|
0,028011
|
0,167365
|
5,974948
|
213,3056
|
|
38,6
|
3,195708
|
0,025907
|
0,160956
|
6,21289
|
239,8175
|
|
39
|
0,758461
|
0,025641
|
0,160128
|
6,244998
|
243,5549
|
|
39,3
|
4,605526
|
0,025445
|
0,159516
|
6,268971
|
246,3706
|
|
40
|
3,015344
|
0,025
|
0,158114
|
6,324555
|
252,9822
|
|
41,9
|
0,286578
|
0,023866
|
0,154487
|
6,473021
|
271,2196
|
|
42,5
|
1,192448
|
0,023529
|
0,153393
|
6,519202
|
277,0661
|
|
44,2
|
2,374253
|
0,022624
|
0,150414
|
6,648308
|
293,8552
|
|
44,8
|
7,431617
|
0,022321
|
0,149404
|
6,69328
|
299,859
|
|
45,5
|
3,378201
|
0,021978
|
0,14825
|
6,745369
|
306,9143
|
|
45,5
|
0,378201
|
0,021978
|
0,14825
|
6,745369
|
306,9143
|
|
48,3
|
1,382526
|
0,020704
|
0,143889
|
6,94982
|
335,6763
|
|
49,5
|
3,394266
|
0,020202
|
0,142134
|
7,035624
|
348,2634
|
|
52,3
|
3,854994
|
0,01912
|
0,138277
|
7,231874
|
378,227
|
|
55,7
|
0,521591
|
0,017953
|
0,13399
|
7,463243
|
415,7026
|
|
59
|
1,203877
|
0,016949
|
0,130189
|
7,681146
|
453,1876
|
|
61
|
5,70989
|
0,016393
|
0,128037
|
7,81025
|
476,4252
|
|
61,7
|
0,619708
|
0,016207
|
0,127309
|
7,854935
|
484,6495
|
|
62,5
|
6,345214
|
0,016
|
0,126491
|
7,905694
|
494,1059
|
|
64,7
|
6,590357
|
0,015456
|
0,124322
|
8,043631
|
520,4229
|
|
69,7
|
11,02523
|
0,014347
|
0,11978
|
8,348653
|
581,9011
|
|
71,2
|
10,0101
|
0,014045
|
0,118511
|
8,438009
|
600,7863
|
|
73,8
|
4,317994
|
0,01355
|
0,116405
|
8,590693
|
633,9931
|
|
74,7
|
3,040812
|
0,013387
|
0,115702
|
8,642916
|
645,6258
|
|
75,8
|
7,16824
|
0,013193
|
0,114859
|
8,70632
|
659,939
|
|
76,9
|
0,895669
|
0,013004
|
0,114035
|
8,769265
|
674,3564
|
|
79,2
|
0,334838
|
0,012626
|
0,112367
|
8,899438
|
704,8355
|
|
81,5
|
1,374006
|
0,01227
|
0,11077
|
9,027735
|
735,7604
|
|
82,4
|
9,032812
|
0,012136
|
0,110163
|
9,077445
|
747,9814
|
|
82,8
|
2,729942
|
0,012077
|
0,109897
|
9,099451
|
753,4345
|
|
83
|
3,438682
|
0,012048
|
0,109764
|
9,110434
|
756,166
|
|
85,9
|
1,483721
|
0,011641
|
0,107896
|
9,268225
|
796,1406
|
|
86,4
|
2,294721
|
0,011574
|
0,107583
|
9,29516
|
803,1018
|
|
86,9
|
6,973162
|
0,011507
|
0,107273
|
9,322017
|
810,0833
|
|
88,3
|
6,392799
|
0,011325
|
0,106419
|
9,396808
|
829,7381
|
|
89
|
6,297383
|
0,011236
|
0,106
|
9,433981
|
839,6243
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,347879
|
|
|
|
|
|
|
R-квадрат
|
0,12102
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,097889
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,732943
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
39,07716
|
39,07716
|
5,23193
|
0,027833
|
|
|
Остаток
|
38
|
283,8211
|
7,468976
|
|
|
|
|
Итого
|
39
|
322,8983
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
8,7119
|
2,294002
|
3,797686
|
0,000512
|
4,067936
|
13,35586
|
|
x^(-0,5)
|
-37,7515
|
16,50452
|
-2,28734
|
0,027833
|
-71,1631
|
-4,33981
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,35414
|
|
|
|
|
|
|
R-квадрат
|
0,125415
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,1024
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,726101
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
40,49641
|
40,49641
|
5,449198
|
0,024963
|
|
|
Остаток
|
38
|
282,4019
|
7,431628
|
|
|
|
|
Итого
|
39
|
322,8983
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
-2,15816
|
2,486641
|
-0,8679
|
-7,1921
|
2,875785
|
|
x^0,5
|
0,754429
|
0,323186
|
2,334352
|
0,024963
|
0,100174
|
1,408685
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,351385
|
|
|
|
|
|
|
R-квадрат
|
0,123472
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,100405
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,729129
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
39,8688
|
39,8688
|
5,35285
|
0,026194
|
|
|
Остаток
|
38
|
283,0295
|
7,448144
|
|
|
|
|
Итого
|
39
|
322,8983
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
0,58244
|
1,356838
|
0,429263
|
0,670156
|
-2,16433
|
3,329215
|
|
х
|
0,050274
|
0,02173
|
2,313623
|
0,026194
|
0,006285
|
0,094263
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,345728
|
|
|
|
|
|
|
R-квадрат
|
0,119528
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,096358
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,735261
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
38,59537
|
38,59537
|
5,158668
|
0,02888
|
|
|
Остаток
|
38
|
284,3029
|
7,481655
|
|
|
|
|
Итого
|
39
|
322,8983
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
1,504832
|
1,002367
|
1,501278
|
0,141548
|
-0,52435
|
3,534019
|
|
x^1,5
|
0,004324
|
0,001904
|
2,27127
|
0,02888
|
0,00047
|
0,008178
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,338157
|
|
|
|
|
|
|
R-квадрат
|
0,11435
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,091044
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,743292
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
36,92349
|
36,92349
|
4,906351
|
0,032827
|
|
|
Остаток
|
38
|
285,9748
|
7,525652
|
|
|
|
|
Итого
|
39
|
322,8983
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
5,973455
|
1,173304
|
5,091141
|
9,98E-06
|
3,598226
|
8,348684
|
|
x^(-1)
|
-124,996
|
56,43102
|
-2,21503
|
0,032827
|
-239,235
|
-10,7577
|
2) Т.к. коэффициент b
статистически значим во всех уравнениях, то гетероскедастичность доказана.
Наилучший коэффициент детерминации (R2 = 0,1254)
при 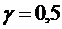 , поэтому
примем зависимость: , поэтому
примем зависимость:
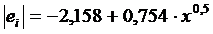 (см. далее). (см. далее).
Тест Парка
Тест относится к формализованным
тестам гетероскедастичности. Предполагается, что дисперсия остатков связана со
значениями факторов функцией
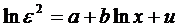
Данная регрессия строится для
каждого фактора в условиях многофакторной модели. Проверяется значимость
коэффициента регрессии b по t-критерию
Стьюдента. Если коэффициент регрессии окажется статистически значимым, то, следовательно,
имеет место гетероскедастичность.
Пример. По данным предыдущего
примера построим регрессию
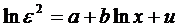
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,343033
|
|
|
|
|
|
|
R-квадрат
|
0,117672
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,094453
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,097694
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
22,30024
|
22,30024
|
5,067869
|
0,030238
|
|
|
Остаток
|
38
|
167,2121
|
4,400319
|
|
|
|
|
Итого
|
39
|
189,5124
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
-6,49359
|
3,634358
|
-1,78672
|
0,081962
|
-13,851
|
0,863782
|
|
lnx
|
2,027965
|
0,90084
|
2,251193
|
0,030238
|
0,204309
|
3,851621
|
Так как коэффициент регрессии статистически
значим, то гетероскедастичность доказана.
Тест Уайта. Предполагается, что
дисперсия ошибок регрессии представляет собой квадратичную функцию от значений
факторов, т.е. при наличии одного фактора 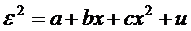 , или при р факторах , или при р факторах
 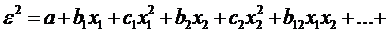
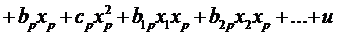 . .
О наличии или отсутствии
гетероскедастичности остатков судят по величине F-критерия
Фишера. Если фактическое значение критерия выше табличного, то, следовательно,
существует корреляционная связь дисперсии ошибок от значений факторов, и имеет
место гетероскедастичность остатков.
Пример. Определим квадратичную
функцию для нашего примера
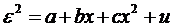
Пусть х1 = х, х2
= х2, построим уравнение множественной регрессии
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,353257
|
|
|
|
|
|
|
R-квадрат
|
0,12479
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,077482
|
|
|
|
|
|
|
Стандартная
ошибка
|
27,61916
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
2
|
4024,315
|
2012,157
|
2,637794
|
0,084932
|
|
|
Остаток
|
37
|
28224,27
|
762,8181
|
|
|
|
|
Итого
|
39
|
32248,59
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
-38,76
|
44,00045
|
-0,8809
|
0,384058
|
-127,913
|
50,39338
|
|
х
|
1,674985
|
1,618236
|
1,035069
|
0,307355
|
-1,60387
|
4,953843
|
|
х^2
|
-0,01017
|
0,013621
|
-0,74683
|
0,459886
|
-0,03777
|
0,017426
|
Так как уравнение статистически не значимо по F-критерию,
то гетероскедастичность остатков отсутствует.
. Методы смягчения проблемы гетероскедастичности
При наличии гетероскедастичности 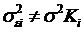 и величина Ki может
меняться от одного значения фактора к другому. При наличии гетороскедастичности
вместо обычного МНК используют обобщенный МНК (взвешенный). Суть метода
заключается в уменьшении вклада данных наблюдений, имеющих большую дисперсию в
результате расчета. и величина Ki может
меняться от одного значения фактора к другому. При наличии гетороскедастичности
вместо обычного МНК используют обобщенный МНК (взвешенный). Суть метода
заключается в уменьшении вклада данных наблюдений, имеющих большую дисперсию в
результате расчета.
случай. Если дисперсии возмущений
известны 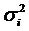 , то
гетероскедастичность легко устраняется. Вводят новые переменные: , то
гетероскедастичность легко устраняется. Вводят новые переменные:
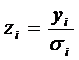 ; ; 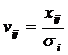 ; ; 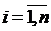 , , 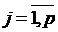
Регрессионная модель в векторной
форме
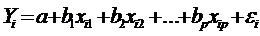 (*) /: (*) /: 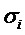
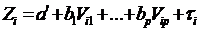 , , 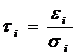 . .
При этом
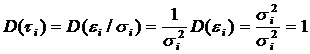 , ,
т.е. модель гомоскедастична.
случай. Если дисперсии возмущений
неизвестны, то делают реалистические предположения о значениях 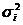 . .
Например:
а) дисперсии 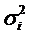 пропорциональны
xi: пропорциональны
xi: 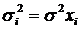 . Уравнение
регрессии (*) делят . Уравнение
регрессии (*) делят
на 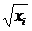 - в случае одной переменной; - на - в случае одной переменной; - на 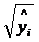 - в случае
множественной регрессии. - в случае
множественной регрессии.
б) дисперсии 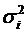 пропорциональны пропорциональны
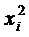 , т.е. , т.е.
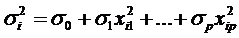 , ,
Уравнение регрессии (*) делят на хi.
Пример. Воспользовавшись характером
зависимости, полученным при использовании теста Глейзера
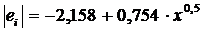 , разделим обе части уравнения на , разделим обе части уравнения на 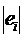
Уравнение регрессии примет вид
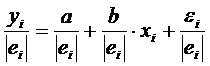 . .
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный
R
|
0,964
|
|
|
|
|
|
|
R-квадрат
|
0,929
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,927
|
|
|
|
|
|
|
Стандартная
ошибка
|
5,502
|
|
|
|
|
|
|
Наблюдения
|
40
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
15105
|
15105
|
498,9
|
2E-23
|
|
|
Остаток
|
38
|
1150,5
|
30,28
|
|
|
|
|
Итого
|
39
|
16255
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
-1,408
|
1,0935
|
-1,288
|
-3,622
|
0,806
|
|
x/e
|
0,337
|
0,0151
|
22,34
|
2E-23
|
0,3064
|
0,367
|
Получены новые оценки параметров линейного
уравнения, в котором смягчена гетероскедастичность.
Литература
1.
Айвазян С.А., Иванова С.С. Эконометрика. Краткий курс: учеб. пособие / С.А.
Айвазян, С.С. Иванова. - М.: Маркет ДС, 2007. - 104 с.
.
Бородич С.А. Вводный курс эконометрики: Учебное пособие. - Мн.: БГУ, 2009. -
354 с.
.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. - М.: Финансы и
статистика, 2008. - 480 с.
.
Доугерти Кристофер. Введение в эконометрику: Учебник для экон. спец. вузов /
Пер. с англ. Е.Н. Лукаш и др. - М.: ИНФРА-М, 2007. - 402 с.
.
Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы:
Учебник. - М.: Финансы и статистика, 2009. - 352 с.
.
Дуброва Т.А. Прогнозирование социально-экономических процессов. Статистические
методы и модели: учеб. пособие / Т.А. Дуброва. - М.: Маркет ДС, 2007. - 192 с.
Похожие работы на - Обобщенная линейная модель множественной регрессии. Гетероскедастичность
|