Расчетно-теоретический анализ поведения одиночной поры при воздействии расходящейся ударной волны
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
«Национальный
исследовательский ядерный университет «МИФИ»»
Саровский
физико-технический институт-филиал НИЯУ-МИФИ
Физико-технический
факультет
Кафедра
теоретической и экспериментальной механики
Пояснительная
записка
к курсовой
работе по дисциплине
«Электрические
измерения неэлектрических величин»
на тему:
«Расчетно-теоретический анализ поведения одиночной поры при воздействии
расходящейся ударной волны»
Саров
Реферат
Курсовая работа : 14 страниц, 4 рисунка, 2
источника.
ОДИНОЧНАЯ ПОРА, ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ,
УДАРНО-ВОЛНОВОЕ НАГРУЖЕНИЕ, ИССЛЕДУЕМЫЙ МАТЕРИАЛ, РАДИУС ПОРЫ.
В данной курсовой работе представлен
расчетно-теоретический анализ поведения одиночной поры при воздействии
расходящейся ударной волны. Рассмотрено изменение радиуса поры в зависимости от
амплитуды прикладываемого давления. Получены аналитические кривые, описывающие
зависимость конечного радиуса поры от величины прикладываемого давления.
Обозначения и
сокращения
МСС - механика сплошной среды,
УП - упругопластика,
УРС - уравнение состояния.
Содержание
Введение
. Постановка задачи
. Результаты численного моделирования
Заключение
Список используемых источников
Введение
Одной из характеристик отклика материалов на
динамическое нагружение является их сопротивление действию импульсных
растягивающих напряжений, возникающих при взаимодействии встречных волн
разрежения, - так называемая откольная прочность.
В современной трактовке откольное разрушение
представляет собой многостадийный, протекающий во времени процесс, в котором
могут быть выделены следующие стадии /1/:
· зарождение микродефектов (микропор
или микротрещин);
· рост микропор и микротрещин под
действием растягивающих напряжений;
· слияние соседних развитых дефектов;
· расслоение и разделение материала с
образованием одной или более свободных поверхностей (магистральные трещины) или
дробление (образование густой сетки трещин и осколков).
Экспериментальные результаты, полученные для
различных по структуре и свойствам материалов (алюминий, armco-железо,
стали, медь, кварц, поликарбонат), свидетельствуют, что концепция
многостадийности процесса откольного разрушения имеет универсальный характер.
Вопрос корректного описания каждой из стадий и
их взаимного влияния на сегодняшний день остается открытым. Предложенные на
сегодняшний день аналитические выражения созданы на основе совокупности
экспериментальных данных или теоретических исследований. В последнем случае
чаще всего рассматривается поведение одиночных или групповых идеальных дефектов
(поры или трещины), находящихся в «модельном» материале, под действием
разнообразных усилий. В качестве последних используются сжимающие и
растягивающие нагрузки.
В настоящей работе рассмотрены закономерности
роста одиночной поры в сфере определенного радиуса под действием расходящихся
ударных волн. Целью настоящей работы являлось выявление зависимости скорости
роста поры от амплитуды прикладываемого к ее поверхности давления.
1.Постановка
задачи
Расчетно-теоретический анализ поведения
одиночной поры выполнен путем численного моделирования ее отклика на
ударно-волновое воздействие в комплексе «KPD-1D»,
являющемся развитием программы УП для численного решения уравнений МСС в
одномерном приближении. Файлы начальных данных создаются с помощью комплекса Indigo.
Рассматривается пора различного начального
радиуса Rнач в сфере с
внешним радиусом Rсф =5 мм. На границу поры (внутренний диаметр сферы)
действует импульс давления (расходящаяся ударная волна) определенной амплитуды
и длительности. В качестве материала сферы выбрана медь.
Тип симметрии - сферический. Ось симметрии -
слева. Выбрано время расчета - 10 мкс.
Граничные условия: правое - свободная
поверхность;
левое - давление (в табличном виде)
|
Время,
10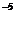 сДавление, ГПа
сДавление, ГПа
|
|
|
0
|
0
|
|
0,001
|
0,5(1;1,5;2;2,5;3)
|
|
0,5
|
0,5(1;1,5;2;2,5;3)
|
|
0,501
|
0
|
В таблице в скобках перечислены использованные
стационарные уровни давлений.
Задание давления в указанном виде соответствует
воздействию на левую границу прямоугольного импульса сжатия длительностью t=5
мкс. Вариацией величины давления в таком импульсе, например, в диапазоне от 0.5
до 3 ГПа, возможно получение различных конечных состояний одиночной поры.
Разбиение области: 500 точек. В заданной системе
«устанавливаются» лагранжевы датчики. Для радиуса - в точках 1, 2, 499 и 500
(например, для случая, когда Rнач=0,05).
Для давления и нормального напряжения - в точках 2, 250 и 499 (R=0,05).
Шаг по времени составляет 0,05 мкс.
Для описания поведения меди в условиях
высокоскоростного деформирования в настоящей работе использованы УРС в форме
Ми-Грюнайзена с переменным коэффициентом Гр для шаровой составляющей тензора
напряжений и модель ФМП [2] для описания сдвиговой прочности исследуемого
материала. Основные уравнения этих моделей записываются в виде:
Шаровая составляющая
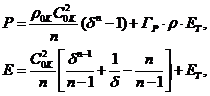
где r0k, С0k - плотность
и скорость звука при Т=0
°К, ГP -
коэффициент Грюнайзена, 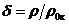 -
относительное сжатие. Коэффициент Грюнайзена считается зависящим только от
сжатия:
-
относительное сжатие. Коэффициент Грюнайзена считается зависящим только от
сжатия:
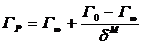 ,
,
где Г0 - величина ГP при r =r0k и Г¥=ГP при d®¥.
Коэффициент Пуассона в рассматриваемой
модели зависит от температуры:
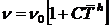
где C, h - константы
и n=n0 при Т=0 К.
Модель деформирования
(ФМП)
[2]
давление радиус сопротивление
напряжение
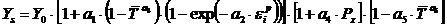
где Ys -
стационарный предел текучести; a1 …a6 -
параметры, определяемые в процессе верификации модели, 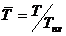 , Тпл -
температура плавления в заданном напряженно-деформированном состоянии,
вычисляемая по закону Линдемана; Pх - холодная составляющая давления;
, Тпл -
температура плавления в заданном напряженно-деформированном состоянии,
вычисляемая по закону Линдемана; Pх - холодная составляющая давления; 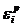 -
интенсивность пластических деформаций.
-
интенсивность пластических деформаций.
Параметры определяющих уравнений
взяты из [2] и сведены в таблицах 2,3.
Таблица 2. Параметры шаровой
составляющей [2]
|
r0, г/см3
|
С0K, км/с
|
n
|
Г0
|
Г¥
|
М
|
СV,
Дж/гК
|
Т0пл,
К
|
r0пл, г/см3
|
|
8.93
|
9.0632
|
3.95
|
4.3
|
1.96
|
0.7
|
1.2
|
0.391
|
1356
|
8.36
|
Таблица 3. Параметры девиаторной составляющей
[2]
|
Y0, ГПа
|
а1
|
а2
|
а3
|
а4,
1/ГПа
|
А5
|
а6
|
n0
|
С
|
h
|
|
0.077
|
9.66
|
1.5
|
5.0
|
0.11
|
1.0
|
1.0
|
0.347
|
0.44
|
1.0
|
2. Результаты
численного моделирования
В качестве иллюстрации возникающего в материале
сферы течения на рисунке 1 приведены временные истории напряжения,
реализующиеся в середине рассматриваемой счетной области (R0=0,275см).

а) Рстац=3ГПа;
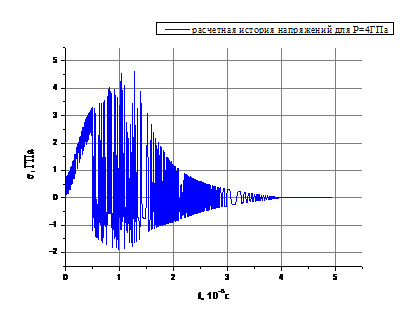
б) Рстац=4ГПа.
Рисунок 1 - Расчетные истории
напряжения для случая Rнач=0,05 см.
Из представленных графиков следует,
что материал сферы подвергается многократному ударно-волновому сжатию во время
действия нагрузки. Затем наблюдаются колебательный процесс относительно
нулевого значения напряжения (после окончания действия импульса сжатия). Как
видно из рисунка 1б происходит затухание колебаний.
В качестве отклика одиночной поры на
действующее давление целесообразно рассматривать зависимость ее конечного
радиуса от уровня давления в стационарной части расходящегося импульса.
Полученные в расчетах истории
изменения радиуса поры при вариации максимального давления приведены на рисунке
2. Рассмотрим графики зависимости поведения радиуса поры во времени R(t) во всех
расчетах. В каждом случае (в зависимости от начального давления) наблюдается
рост радиуса поры, а затем в определенный момент происходит «насыщение» и рост
поры останавливается. При этом время выхода на насыщение в каждом случае свое и
оно больше, чем время окончания действия нагрузки. Этот момент времени
обусловлен сдвиговой прочностью материала.
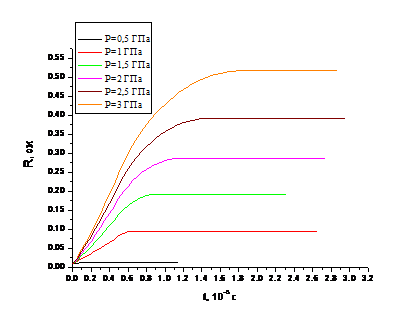
а) Rнач =0,01
см;
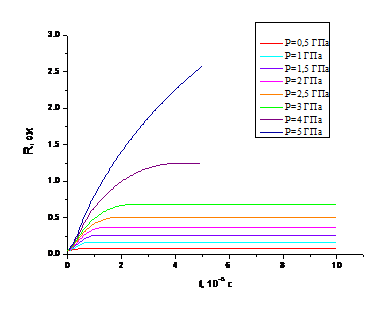
б) Rнач =0,05
см;
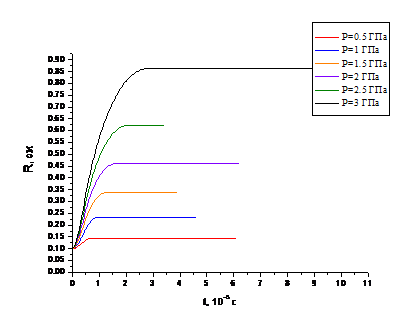
в) Rнач =0,1 см.
Рисунок 2. Изменение радиуса поры в
зависимости от амплитуды прикладываемого давления.
При дальнейшем увеличении давления
Р=4ГПа, 5ГПа (для серии задач при Rнач =0,05
см) - см. рисунок 2б - радиус поры начинает расти неограниченно и не наблюдается
его остановки. Как видно из рисунка 3а, на котором представлена история
движения внутреннего и внешнего радиуса сферы для двух типичных случаев, в
случае высокого начального давления наблюдается катастрофический рост поры, но
нет выхода ее радиуса на насыщение: реализуется сильное сжатие материала сферы,
Rнач
стремится к Rсф.
Напротив, из рисунка 3б следует, что в случае низкого уровня прикладываемого
давления радиус поры начинает расти, а затем выходит на насыщение в то время,
как радиус сферы практически не изменяется.
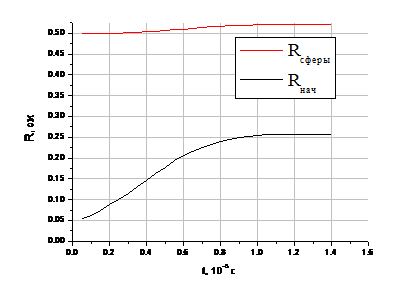
а) при Рстац=1,5ГПа;
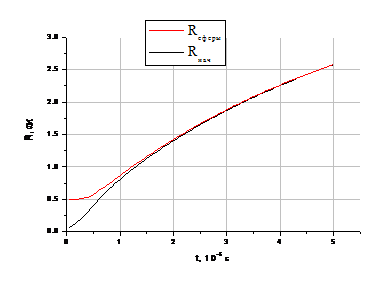
б) при Рстац =5ГПа.
Рисунок 3. Поведение сферы радиусом R=0,05см в
зависимости от величины прикладываемого давления.
На рисунке 4 представлены зависимости конечного
радиуса поры от амплитуды прикладываемого давления. Полученные восходящие
кривые располагаются близко друг к другу, несмотря на изменение начального
радиуса поры в 10 раз.
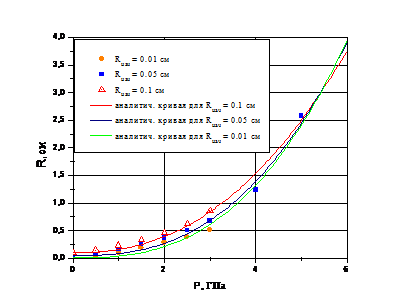
Рисунок 4. Зависимость конечного
радиуса поры от прикладываемого давления.
На рисунке 4 также представлены
аналитические кривые, описывающие зависимость конечного радиуса поры от
величины прикладываемого давления. Эти кривые описываются выражением:
Rпоры= Rнач
+А*((Рстац /Р*)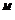 ),
),
где А=2,4 см, М=2,3÷2,7 и Р*=5ГПа -
постоянные величины.
Можно предположить, что величина Р*
- это минимальное давление, при котором в расчетах уже не фиксируется выхода
радиуса поры на насыщение. Постоянная А - это максимальный радиус остановки
поры, регистрируемый при воздействии импульса сжатия заданной длительности.
Заключение
Рассматривается пора различного начального
радиуса Rнач в сфере с
внешним радиусом Rсф =5 мм. На границу поры (внутренний диаметр сферы)
действует стационарный импульс давления (расходящаяся ударная волна)
определенной амплитуды и длительности.
Получены графики временных историй напряжений.
Из них видно, что материал сферы подвергается многократному ударно-волновому
сжатию, затем происходит колебательный процесс и постепенное затухание
импульса.
Также рассмотрено изменение радиуса поры в
зависимости от амплитуды прикладываемого давления - наблюдается рост радиуса
поры, а затем выход его на насыщение и остановка.
Получены аналитические кривые, описывающие
зависимость конечного радиуса поры от величины прикладываемого давления.
Необходимо отметить, что представленные результаты получены в рамках
моделирования с использованием определенной модели деформирования, а также при
воздействии импульса сжатия фиксированной длительности. Очевидно, что изменение
условий нагружения и тем более определяющего уравнения может привести к
существенной модификации получаемых результатов.
Список используемой
литературы
1. Огородников
В.А., Пушков В.А., Тюпанова О.А. Основы физики прочности и механики разрушения
// Учебное издание. 2-е изд., испр. и доп. 2009. 387 с.
2. Влияние
интенсивной пластической деформации и ударно-волнового нагружения на прочность меди
// Межд. конф. VII
Харитоновские тематические научные чтения. Саров. 2005. Большаков А.П., Глушак
Б.Л, Игнатова О.Н., и др. С. 421-425.