Разработка математической модели и приложения для реализации проверки признака совместимости ограничений

Разработка математической модели и приложения для реализации проверки признака совместимости ограничений

Введение

Под моделью понимают упрощенное, упакованное знание, несущее вполне определенную, ограниченную информацию о предмете отражающее те или иные его отдельные свойства. Модель можно рассматривать как специальную форму кодирования информации. Можно сказать, что модель содержит в себе потенциальное знание, которое человек, исследуя ее, может приобрести. [7] Модель необходима для того, чтобы:

понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром;

научиться управлять объектом (процессом или явлением) и определять наилучшие способы управления при заданных целях и критериях (оптимизация);

прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект

Модель представляет собой абстрактное описание системы (объекта, процесса, проблемы, понятия) в некоторой форме, отличной от формы их реального существования. [1]

Моделирование - исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.

Математика необходима в повседневной жизни, следовательно, определенные математические навыки нужны каждому человеку. В жизни приходится считать (например, деньги), используем (часто не замечая этого) знания о величинах, характеристиках протяженности, площади, объемы, промежутки времени. Все это пришло на уроках арифметики и геометрии и используется для ориентации в окружающем мире. Математические знания и навыки нужны практически во всех профессиях, прежде всего, конечно, в тех, которые связаны с естественными науками и экономикой. Математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику.

Математические методы и модели, которые будем рассматривать, хорошо известны и используются в различных контекстах - математические методы в принятии решений, методы исследования операций, методы оптимального управления. Построение математической модели процесса включает в себя следующие этапы:

) выбор переменных задачи.

) составление системы ограничений.

) выбор целевой функции. [2]

Компьютерное моделирование - это метод решения задач анализа или синтеза сложной системы на основе использования ее компьютерной модели.

Компьютерное моделирование можно рассматривать как:

− математическое моделирование;

− имитационное моделирование;

− стохастическое моделирование.

Под термином “компьютерная модель” понимают условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью уравнений, неравенств, логических соотношений, взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и отображающих структуру и взаимосвязи между элементами объекта.

Классификация моделей:

) Статические модели - предполагается, что переменные ее состояния на изучаемом отрезке времени остаются неизменными.

) Динамические модели - изменяются во времени.

) Аналитические модели. Представляют собой математические соотношения, предполагающие аналитический метод решения, поиски максимума. Для исследования аналитических моделей достаточно ручки и бумаги.

) Вычислительные модели. Предполагают использование вычислительных средств для решения аналитических моделей высокой размерности или с использованием функций, которые удобнее представлять в табличной форме. В данном случае чаще используют численные методы (интегрирования дифференциальных уравнений, поиска экстремумов и пр.)

) Имитационные модели. Это реализация наиболее сложных и громоздких алгоритмов описания сложных систем, включающих случайные процессы, дифференциальные, интегральные и рекурсивные уравнения. Фактически это экспериментальный метод изучения объекта с помощью ЭВМ. Процесс имитации заключается в следующем: сначала строится математическая модель изучаемого объекта, затем эта модель преобразуется в программу для ЭВМ., вводятся необходимые данные и ведется наблюдение за тем, как изменяются интересующие показатели.

Имитация применяется в тех случаях, когда модель слишком сложна, чтобы можно было использовать обычные аналитические методы. [3]

Целью курсовой работы является разработка математической модели и приложения для реализации проверки признака совместимости ограничений.

1. Разработка алгоритма

.1 Описание метода

Линейной называют модель, в которой переменные входят в целевую функцию и ограничения в первой степени. Математическая модель линейной задачи включает в себя: целевую функцию, ограничения и граничные условия.

Одним из основных методов решения задач линейного программирования является симплекс-метод. [9]

В 1947 году американский ученый Дж. Данциг описал один из основных методов решения задач линейного программирования, получивший название «симплексный».

Симплекс-метод - алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан советским математиком Канторовичем Л. В. в 1937 году. Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

Следует, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение

(x) = c,

где W(x) - максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку - требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.

Последовательность вычислений симплекс-методом можно разделить на две основные фазы:

) нахождение исходной вершины множества допустимых решений,

) последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

.2 Алгоритм симплекс-метода

Математическое программирование

Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи математического программирования формулируются следующим образом: найти экстремум некоторой функции многих переменных f ( x1, x2, ... , xn ) при ограничениях gi ( x1, x2, ... , xn ) * bi , где gi - функция, описывающая ограничения, * - один из следующих знаков £ , = , ³ , а bi - действительное число, i = 1, ... , m. f называется функцией цели ( целевая функция ).

Линейное программирование - это раздел математического программирования, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями, которым должны удовлетворять искомые переменные.[7]

Задачу линейного программирования можно сформулировать так . Найти max

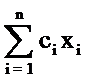
при условии: a11 x1 + a12 x2 + . . . + a1n xn £ b1;x1 + a22 x2 + . . . + a2n xn £ b2;

. . . . . . . . . . . . . . . . . . . . . . . . . . . .x1 + am2 x2 + . . . + amn xn £ bm;³ 0, x2 ³ 0, . . . , xn ³ 0 .

Эти ограничения называются условиями неотрицательности. Если все ограничения заданы в виде строгих равенств, то данная форма называется канонической.

В матричной форме задачу линейного программирования записывают следующим образом. Найти max cT x

при условии

x £ b;³ 0 ,

где А - матрица ограничений размером ( m´n), b(m´1) - вектор-столбец свободных членов, x(n ´ 1) - вектор переменных, сТ = [c1, c2, ... , cn ] - вектор-строка коэффициентов целевой функции.

Решение х0 называется оптимальным, если для него выполняется условие сТ х0 ³ сТ х , для всех х Î R(x).

Поскольку min f(x) эквивалентен max [ - f(x) ] , то задачу линейного программирования всегда можно свести к эквивалентной задаче максимизации.

Для решения задач данного типа применяются методы:

) графический;

) табличный (прямой, простой ) симплекс - метод;

) метод искусственного базиса;

) модифицированный симплекс - метод;

) двойственный симплекс - метод.

Табличный симплекс-метод

Для его применения необходимо, чтобы знаки в ограничениях были вида “ меньше либо равно ”, а компоненты вектора b - положительны.

Алгоритм решения сводится к следующему:

Приведение системы ограничений к каноническому виду путём введения дополнительных переменных для приведения неравенств к равенствам.

Если в исходной системе ограничений присутствовали знаки “ равно ” или “ больше либо равно ”, то в указанные ограничения добавляются

искусственные переменные, которые так же вводятся и в целевую функцию со знаками, определяемыми типом оптимума.

Формируется симплекс-таблица.

Рассчитываются симплекс-разности.

Принимается решение об окончании либо продолжении счёта.

При необходимости выполняются итерации.

На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса. Таблица пересчитывается по методу Жордана-Гаусса или каким-нибудь другим способом. [4]

В контрольных примерах надо проверить случай, когда признак выполняется и когда не выполняется.

Составляем первый контрольный пример. Исходные данные записаны в симплекс-таблице 1.1. Требуется проверить выполнение признака совместимости ограничений.

Таблица 1.1 - Исходные данные

Просматриваем коэффициенты в столбце свободных членов, за исключением первого элемента:-6, 5, 7, 4, 6. Так как в столбце свободных членов имеется отрицательный коэффициент -6, проверяем строку Y1 и находим в ней отрицательный элемент -2. Значит, что ограничения совместимы.

Составляем второй контрольный пример. Исходные данные записаны в симплекс-таблице 1.2.

Таблица 1.2 - Исходные данные

Требуется проверить выполнение признака совместимости ограничений.

Просматриваем коэффициенты в столбце свободных членов, за исключением первого элемента:8, -5, 3, 7, 4. Так как в столбце свободных членов имеется отрицательный коэффициент -5, проверяем строку Y2 и не находим в ней других отрицательных элементов. Значит, что ограничения не совместимы.

1.4 Разработка алгоритма решения задачи

При запуске программы выводится главная форма, на ней расположены: таблица (без шапок), кнопка для заполнения шапки таблицы, пять текстовых полей для вывода совместимости на определенной строчке Y, кнопка для поиска ограничений совместимости.

Исходные данные вводятся в поля формы, переводятся из строкового типа в целый формат и записываются в двумерный массив. Для этого используется вложенный цикл: первый по строкам, второй по столбцам матрицы.

В первом столбце выполняется поиск отрицательного элемента.

Если после просмотра всех элементов в строке найден отрицательный элемент, выдается сообщение у конкретной строки Y «признак выполняется».

В случае, если после просмотра всех элементов в строке не найден отрицательного элемента, выдается сообщение, у конкретной строки Y «признак не выполняется».

Блок-схема алгоритма приводится в приложении А.

2. Разработка программы

.1 Выбор языка программирования

линейный задача программа листинг

Для составления программы выбрана интегрированная среда разработки Delphi, в которой используется язык программирования Pascal. Главной частью приложения является файл проекта (.dpr), содержащий код на языке Object Pascal, с которого начинается выполнение программы и который обеспечивает инициализацию других модулей. Информация о формах хранится в двух файлах. В бинарном файле с расширением .dfm хранится информация о внешнем виде формы и ее свойствах. В текстовом файле с расширением .pas хранится код модуля, соответствующего данной форме.

При проектировании пользовательского интерфейса Delphi предоставляет возможность выбора отдельных компонентов из палитры с последующим размещением их в нужном месте. Проектирование начинается с создания формы, в которую вставляются с палитры компонентов нужные элементы: надписи, текстовые поля, кнопки. Элементам настраиваются свойства, такие как имена, количество строк и столбцов, количество столбцов с постоянными значениями, возможность редактировать данные в полях, наличие линейки прокрутки и т.д.[10] Внешний вид среды программирования Delphi отличается от многих других из тех, что можно увидеть в Windows. К примеру, Borland Pascal for Windows 7.0, Borland C++ 4.0, Word for Windows, Program Manager - это все MDI приложения и выглядят по-другому, чем Delphi. MDI (Multiple Document Interface) - определяет особый способ управления нескольких дочерних окон внутри одного большого окна.

Среда Delphi же следует другой спецификации, называемой Single Document Interface (SDI), и состоит из нескольких отдельно расположенных окон. Это было сделано из-за того, что SDI близок к той модели приложений, что используется в Windows 95.

Если использовать SDI приложение типа Delphi, то перед началом работы лучше минимизировать другие приложения, чтобы их окна не загромождали рабочее пространство. Если нужно переключиться на другое приложение, необходимо щелкнуть мышкой на системную кнопку минимизации Delphi. Вместе с главным окном свернутся все остальные окна среды программирования, освободив место для работы других программ. Выбранный объект появится на проектируемом окне и им можно манипулировать с помощью мыши. Палитра Компонент использует постраничную группировку объектов. Внизу Палитры находится набор закладок - Standard, Additional, Dialogs и т.д. Если щелкнуть мышью на одну из закладок, то можно перейти на следующую страницу Палитры Компонент. Принцип разбиения на страницы широко используется в среде программирования Delphi и его легко можно использовать в своей программе.[6] Для доступа к этому инструменту нужно просто выбрать в системном меню пункт Help и затем Contents. На экране появится Справочник. Справочник является контекстно-зависимым, при нажатии клавиши F1, всплывает подсказка, соответствующая текущей ситуации. [5]

.2 Входные и выходные данные

Входными данными являются элементы симплекс-таблицы размером шесть столбцов на шесть строк (6x6), целые числа любого знака или ноль.

коэффициенты целевой функции, которые записываются в верхней строчке таблицы;

свободные члены, записываются в первом столбце таблицы;

остальные элементы таблицы вводятся построчно: вначале для первого

Коэффициенты целевой функции, свободные члены и остальные элементы таблицы должны быть целыми любого знака.

Выходные данные:

диалоговое окно с текстом 'В строке Y признак выполняется', если ограничения совместимы;

диалоговое окно с текстом 'В строке Y признак не выполняется, если ограничения не совместимы;

2.3 Разработка пользовательского интерфейса

В программе используется текстовый интерфейс.

Основу графического интерфейса составляет форма, на которой размещаются визуальные компоненты. Компоненты выбираются из набора, имеющегося в библиотеках Delphi на странице Standard. Макет формы показан на рисунке 2.1.

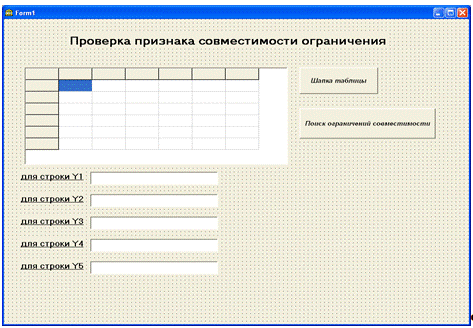
Рисунок 2.1 - Макет формы

При создании формы использовались следующие визуальные компоненты

надписи: «Проверка признака совместимости ограничения», «для строки Y1», «для строки Y2», «для строки Y3», «для строки Y4», «для строки Y5»;

кнопки с надписями: «Шапка таблицы», «Поиск ограничений совместимости»;

таблица для ввода - вывода размером 6*6 без заголовка.

пять окон редактирования, - в которых описывается: «признак выполняется» или «признак не выполняется».

2.4 Описание программы по листингу

В программе используются две процедуры:

procedure Button1Click(Sender: TObject) - процедура заполнения шапки таблицы, вызывается щелчком по кнопке «Шапка таблицы»;

procedure Button2Click(Sender: TObject) - процедура выполнения вычислений, вызывается щелчком по кнопке «Поиск ограничения совместимости».

StringGrid1.Cols[0].Strings[1]:='E';

StringGrid1.Cols[0].Strings[2]:='y1';

StringGrid1.Cols[0].Strings[3]:='y2';

StringGrid1.Cols[0].Strings[4]:='y3';.Cols[0].Strings[5]:='y4';.Cols[0].Strings[5]:='y5'.

Заполнение первой строки таблицы:

StringGrid1.Cols[1].Strings[0]:='Своб. член';

StringGrid1.Cols[2].Strings[0]:='x1';

StringGrid1.Cols[3].Strings[0]:='x2';

StringGrid1.Cols[4].Strings[0]:='x3';

StringGrid1.Cols[5].Strings[0]:='x4';

StringGrid1.Cols[6].Strings[0]:='x5'.

Для занесения данных из строковых полей формы в двумерный массив mas используется вложенный цикл for. Предварительно данные должны быть из строкового типа переведены в целый тип:

− for i:=1 to 6 do

− for j:=1 to 6 do[i,j]:=StrToint(StringGrid1.Cols[j].Strings[i])- переводит строковый тип, в целый и записывает массив..Text:='Признак выполняется'; - выводит сообщение о совместимости ограничения..Text:='Признак выполняется';.Text:='Признак выполняется';.Text:='Признак выполняется';.Text:='Признак выполняется';i:=2 to 6 do - цикл по строке.:=0; fl2:=0; -флаг.(mas[i,1]<0) then - ищет элемент меньше нуля, по строке в первом столбце.:=1; fl2:=0; - приравнивается к флагу 1, если больше то к флагу 2.j:=2 to 6 domas [i,j]<0 then fl2:=1; - ищет строке и столбце элемент меньше нуля , то флаг приравнивается единицы.;(fl1=1) and (fl2<>1) then -если возведен первый флаг и не возведен второй, то….(i=2) then Edit1.Text:=' Признак не выполняется'; - проверяет вторую строку и выводит сообщение о не совместимости ограничения.(i=3) then Edit2.Text:=' Признак не выполняется'; - проверяет третью строку и выводит сообщение о не совместимости ограничения.(i=4) then Edit3.Text:=' Признак не выполняется'; - проверяет четвертую строку и выводит сообщение о не совместимости ограничения.(i=5) then Edit4.Text:=' Признак не выполняется'; - проверяет пятую строку и выводит сообщение о не совместимости ограничения.(i=6) then Edit5.Text:=' Признак не выполняется'; - проверяет шестую строку и выводит сообщение о не совместимости ограничения.;;;.

Листинг программы приводится в приложении Б.

2.5 Тестирование и отладка программы

После создания формы, размещения в ней компонентов и создания обработчиков событий запускаем программу командой Run из меню. Для тестирования программы введем данные контрольного примера, который решен ранее.

Запустили программу на выполнение (Рисунок 2.4)

Рисунок 2.2 - Программа на исполнении

Нажимаем кнопку «Шапка таблицы». Выводится шапка таблицы, как показано на рисунке 2.3.

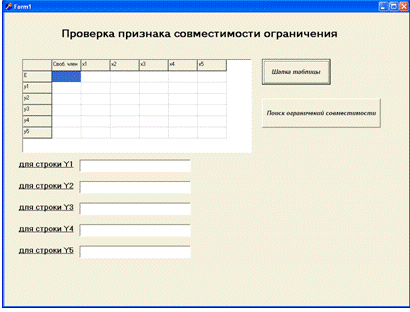
Рисунок 2.3 - Шапка таблицы

Вводим данные в таблицу (рисунок 2.4).

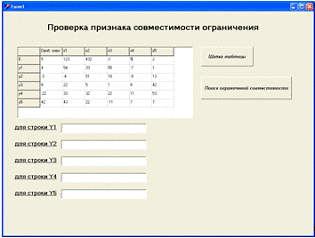
Рисунок 2.4 - Ввод исходных данных

Нажимаем кнопку «Поиск ограничений совместимости». В форме производится по строковый расчет выполнимости признака, как показано на рисунке 2.5.

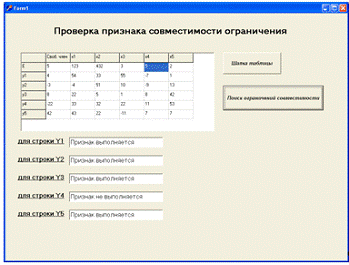
Рисунок 2.5 - Вывод результата

Тестирование показало, что результаты решения задачи на компьютере совпали с решением контрольного примера. Программа работает в соответствии с заданием.

2.6 Инструкция по применению программы

Запустить с рабочего стола файл Project1.exe. На экран выводится окно формы (рисунок 2.6).

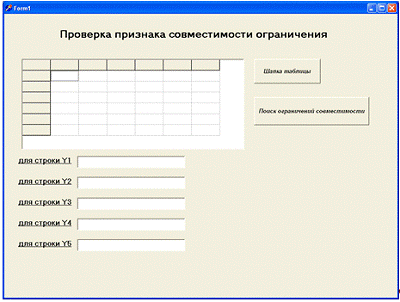
Рисунок 2.6 - Окно стартовое

После запуска выводится таблица без шапки. Вначале требуется ввести шапку таблицы нажав на кнопку с надписью «Шапка таблицы», после этого выведутся заголовки таблицы, как показано на рисунке 2.7.

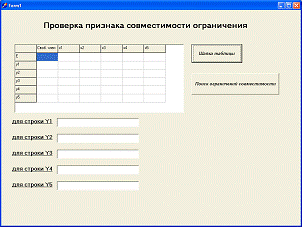
Рисунок 2.7 - Вывод шапки таблицы

Теперь необходимо ввести исходные данные в таблицу и нажать на кнопку с надписью « Поиск ограничения совместимости» и произвести расчет совместимости или не совместимости признака, как показано на рисунке 2.8.

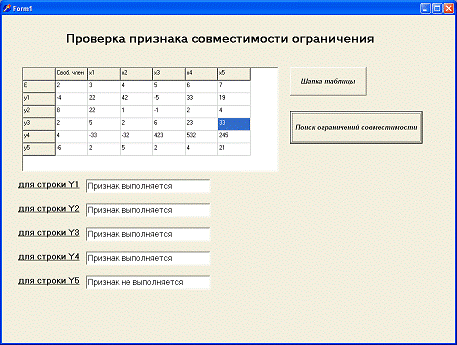
Рисунок 2.8 - Расчет совмести признака

В полях можно увидеть результат поиска совместимости ограничения, для конкретной строки, от Y1 до Y5. В поле будет указанно - «признак выполняется» или «признак не выполняется».

Заключение

В курсовой работе используется симплекс - метод, целью которого является поиск оптимального решения линейных задач. В курсовой работе разрабатывается алгоритм поиска ограничений совместимости. В работе приведено решение контрольного примера, словесный алгоритм и алгоритм в виде блок-схемы. Дано описание пользовательского интерфейса, где приведено описание основной формы программы, а так же перечислены все элементы, используемы для создания этой формы. Так же приведено описание входных и выходных данных, где указано, в каком виде необходимо задавать параметры и в каком виде выводятся данные.

Для реализации программы выбрана интегрированная среда разработки Delphi. Программа отлажена и протестирована. Приведено описание программы по листингу, где описаны отдельно каждые команды программы. Программа имеет графический интерфейс. Программа позволяет выполнить проверку в таблицах размером от 6х6. Таблица должна быть заполнена целыми числами с любым знаком.

Результаты расчета на компьютере совпали с данными контрольного примера, программа работает в соответствии с заданием.

Приложение

Листинг программы

Unit1;, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,, Grids;= class(TForm): TLabel;: TStringGrid;: TButton;: TButton;: TEdit;: TLabel;: TLabel;: TEdit;: TLabel;: TEdit;: TLabel;: TEdit;: TLabel;: TEdit;Button1Click(Sender: TObject);Button2Click(Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm1;

{$R *.DFM}

procedure TForm1.Button1Click(Sender: TObject);

begin.Cols[0].Strings[1]:='E';.Cols[0].Strings[2]:='y1';.Cols[0].Strings[3]:='y2';.Cols[0].Strings[4]:='y3';.Cols[0].Strings[5]:='y4';.Cols[0].Strings[6]:='y5';.Cols[1].Strings[0]:='Своб. член';.Cols[2].Strings[0]:='x1';.Cols[3].Strings[0]:='x2';.Cols[4].Strings[0]:='x3';.Cols[5].Strings[0]:='x4';.Cols[6].Strings[0]:='x5';;TForm1.Button2Click(Sender: TObject);:array[1..6,1..6] of integer;,j,fl1,fl2:integer;i:=1 to 6 do[i,j]:=StrToint(StringGrid1.Cols[j].Strings[i]);.Text:='Признак выполняется';.Text:='Признак выполняется';.Text:='Признак выполняется';.Text:='Признак выполняется';.Text:='Признак выполняется';i:=2 to 6 do:=0; fl2:=0;(mas[i,1]<0) then:=1; fl2:=0;j:=2 to 6 domas [i,j]<0 then fl2:=1;;(fl1=1) and (fl2<>1) then begin(i=2) then Edit1.Text:='Признак не выполняется';(i=3) then Edit2.Text:='Признак не выполняется';(i=4) then Edit3.Text:='Признак не выполняется';(i=5) then Edit4.Text:='Признак не выполняется';(i=6) then Edit5.Text:='Признак не выполняется';;;;.