Общая структура алгоритма Rijndael (AES)
Министерство образования и науки Российской
Федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
КУБАНСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ (КубГТУ)
Кафедра компьютерных технологий и информационной
безопасности
Факультет ИИТиБ
КУРСОВАЯ РАБОТА
по
дисциплине: «Математические основы криптологии»
на
тему: Общая структура алгоритма Rijndael (AES)
Выполнил
студент группы: 09-Б-КЗ1
Власов
Константин Александрович
ЗАДАНИЕ
на курсовое проектирование
студенту Власову Константину Александровичу группы 09-Б-КЗ1 факультета ИИТиБ
специальности 090104 Комплексная защита объектов информатизации.
Тема работы Общая структура
алгоритма Rijndael (AES)
Содержание задания Программная
реализация общей структуры алгоритма Rijndael
(AES) с длинами ключа
128, 192 и 256 бит
Объем работы:
а) пояснительная записка к работе 30 стр.
б) графическая часть листа формата А1
Рекомендуемая литература: 1) С.Г. Баричев, В.В.
Гончаров, Р.Е. Серов, Основы современной криптографии, 2-е издание, Москва,
"Горячая линия - Телеком", 2002.
) Осипенко Л. П., Васильченко А. А.
Математические основы криптологии. Методические указания для выполнения
курсовой работы. - Краснодар: Изд-во КубГТУ, 2009.
Реферат
В данной курсовой работе рассмотрен алгоритм
шифрования AES (Rijndael).
Рассмотрены основные математические операции на полях Галуа. Были разобраны и
реализованы процедуры AddRoundKey, SubBytes,
ShiftRows, MixColumns, играющие главную роль в работе алгоритма. Изучен принцип
расширения ключа (Key
Expansion) для увеличения
криптостойкости. С помощью полученных знаний AES
был реализован в среде программирования C#
с помощью Microsoft
Visual Studio
2010 в режиме шифрования ECB
(ELECTRONIC
CODEBOOK) для шифрования и
расшифрования текстовой информации.
Введение
Целью проведения конкурса AES
был поиск нового стандарта шифрования на замену таких алгоритмов как DES
и IDEA, криптостойкость
которых была подвергнута сомнению, а впоследствии и вовсем признали эти
алгоритмы ненадежными. В результате проведения конкурса был выбран новый
стандарт шифрования Advanced Encryption Standard (AES), также известный как
Rijndael - симметричный алгоритм блочного шифрования с переменной длиной блока
и переменной длиной ключа. Длина блока и длина ключа могут быть независимо
установлены в 128, 192 или 256 бит. Обычно длина блока составляет 128 бит,
поэтому в данной работе рассматривался именно этот размер. Алгоритм использует
линейно-подстановочные преобразования и состоит из 10, 12 или 14 раундов в
зависимости от длины ключа (соответственно 128, 192 и 256 бит). Блок данных,
обрабатываемый с использованием алгоритма Rijndael, делится на массивы байтов,
и каждая операция шифрования является байт-ориентированной.
Преобразование раунда алгоритма Rijndael не
имеет структуру сети Фейстеля, а использует структуру типа SP-сеть
(Substitution-Permutation network, подстановочно-перестановочная сеть) -
разновидность блочного шифра, предложенная в 1971 году Хорстом Фейстелем.
Ппреобразование каждого раунда состоит из четырех различных преобразований,
называемых слоями. Каждый слой разрабатывался с учетом противодействия
линейному и дифференциальному криптоанализу. В основу каждого слоя положена
своя собственная функция.
Алгоритм Rijndael очень хорошо выполняется как в
программной, так и в аппаратной реализации в широком диапазоне окружений, имеет
небольшие требования к памяти, что делает его пригодным для окружений с
ограниченными ресурсами. В этом случае он также демонстрирует отличное
выполнение.
1. Математические
основы алгоритма
В основе алгоритма AES
лежит математика на полях Галуа 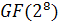 .
.
Поле же образуется из кольца, обладающего
некоторыми свойствами, которые рассмотрены ниже.
1.1 Основные
определения и свойства колец и полей
Непустое множество R называется кольцом, если в
нем определены две алгебраические операции: сложение, ставящее в соответствие
каждым двум элементам 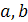 элемент
элемент 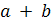 ,
называемый их суммой, и умножение, ставящее в соответствие каждым двум
элементам
,
называемый их суммой, и умножение, ставящее в соответствие каждым двум
элементам 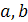 элемент
элемент 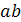 ,
называемый их произведением, причем эти операции обладают следующими
свойствами:. (Коммутативность сложения) a + b = b + a;. (Ассоциативность
сложения) a + (b + c) = (a + b) + c;. (Обратимость сложения) Для любых a и b из
R уравнение a + x = b имеет (по крайней мере, одно) решение, т. е. существует
элемент такой, что a + c = b;. (Коммутативность умножения) ab = ba;
,
называемый их произведением, причем эти операции обладают следующими
свойствами:. (Коммутативность сложения) a + b = b + a;. (Ассоциативность
сложения) a + (b + c) = (a + b) + c;. (Обратимость сложения) Для любых a и b из
R уравнение a + x = b имеет (по крайней мере, одно) решение, т. е. существует
элемент такой, что a + c = b;. (Коммутативность умножения) ab = ba;
Термин "кольцо" применяется также к
множествам с некоммутативным или даже неассоциативным умножением. Формулировки
других свойств также меняются.. (Ассоциативность умножения) a(bc) = (ab)c;.
(Дистрибутивность умножения относительно сложения) (a + b)c = ac + bc.
При обычных операциях сложения и умножения
кольцом является:
. Множество целых чисел.
. Множество рациональных чисел.
. Множество действительных чисел.
. Множество рациональных чисел.
. Множество, состоящее лишь из одного
числа 0.
. Множество четных чисел и вообще
множество целых чисел, кратных некоторому числу n.
. Множество комплексных чисел 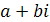 с
целыми
с
целыми 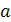 и
и
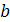 (так
называемое кольцо целых комплексных чисел).
(так
называемое кольцо целых комплексных чисел).
. Множество действительных чисел 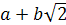 ,
где a и b - целые числа.
,
где a и b - целые числа.
Множество натуральных чисел, а также множество
всех положительных рациональных чисел кольцами не являются, так как не
выполняется аксиома III.
. Большую роль в алгебре играет кольцо
многочленов с одним или несколькими неизвестными и коэффициентами из некоторого
кольца R. При этом за операции сложения и умножения принимаются обычные
действия над многочленами, известные из школьной алгебры. Эти действия имеют
смысл, так как они сводятся к сложению и умножению коэффициентов многочленов, а
последние принадлежат к кольцу R, где указанные действия определены
. Пары (a, b) целых чисел образуют
кольцо, если операции определены по формулам
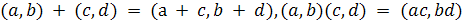 .
.
Примеры колец показывают, что в отношении
обратной операции для умножения (в отличие от сложения) различные кольца
обладают совершенно различными свойствами. Так, в кольце целых чисел деление
выполняется лишь в исключительных случаях, причем все элементы кольца делятся
на +1 и -1. В кольце же рациональных чисел деление всегда возможно (кроме
деления на 0). Желая изучить свойства обратной операции для умножения, приходим
к важнейшему частному случаю кольца - полю.
Полем называется кольцо P,
обладающее следующими свойствами:
VII.
(Обратимость умножения) Для любых
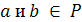 ,
,
где 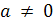 ,
уравнение
,
уравнение 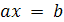 имеет (по крайней
мере одно) решение, т. е. существует элемент
имеет (по крайней
мере одно) решение, т. е. существует элемент 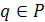 такой,
что
такой,
что 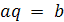 .
.
VIII. 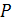 содержит
по крайней мере один элемент, отличный от нуля.
содержит
по крайней мере один элемент, отличный от нуля.
Из примеров 1-10 колец только 2, 3 и 4, т. е.
рациональные, действительные и комплексные числа, являются полями. В примере 5
свойство VII выполнено, так как вообще нет элемента a ≠ 0, но не
выполнено свойство VIII. В остальных примерах не выполняется свойство VII.
1.2 Основные теоремы
колец и полей
Для операции сложения и умножения в кольце
справедливы все следствия, полученные из законов ассоциативности и
коммутативности в предыдущем параграфе. В частности, можно определить сумму и
произведение любого конечного числа элементов, для которых верны правила
оперирования, аналогичные и которые не зависят от порядка данных элементов.
Свойства I - III показывают, что кольцо
относительно операции сложения является коммутативной группой. Поэтому во
всяком кольце существует элемент 0, называемый нулем кольца, со свойством
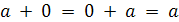
для любого a. Далее, для любого a существует
противоположный элемент -a такой, что
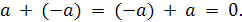
Из законов сложения I - III следует (как для
всякой коммутативной группы) существование в любом кольце операции вычитания,
обратной сложению. Умножение может и не обладать обратной операцией, как,
например, в кольце целых чисел или в кольце многочленов.
Следствие закона дистрибутивности. Прежде всего
из VI и IV следует, очевидно, вторая форма закона дистрибутивности:
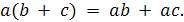
Далее, обе формы закона дистрибутивности
оказываются верными также и для разности, т. е.
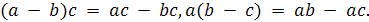
Для доказательства первого равенства надо проверить,
что элемент (a - b)c удовлетворяет определению разности элементов ac и bc. Но
действительно
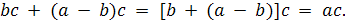
Второе равенство доказывается аналогично.
Теорема 1. Если один из сомножителей равен нулю,
то и все произведение равно нулю, т. е.
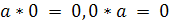 , для любого a.
, для любого a.
Докажем лишь первое из равенств, так как второе
вытекает из первого при помощи IV. По определению нуля и разности 0 = b - b для
любого b.
Отсюда
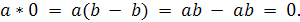
Однако теорема, обратная теореме 1, верная для
чисел, уже не сохраняется для любых колец, иными словами, если произведение
двух элементов кольца равно нулю, то нельзя утверждать, что хотя бы один из них
равен нулю. Так, в приведенном выше примере 10 кольца, составленного из пар (a,
b) целых чисел, нулем является, очевидно, пара (0, 0). Если взять целые числа и
, то пары (a, 0) и (0, b) отличны от нуля кольца, но (a, 0)(0, b) = (0, 0).
Определение 1. Элементы  кольца,
для которых, но
кольца,
для которых, но 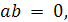 называются
делителями нуля. Кольцо без делителей нуля называется также областью
целостности.
называются
делителями нуля. Кольцо без делителей нуля называется также областью
целостности.
Теорема 2. Из 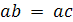 следует
следует
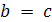 ,
если только
,
если только 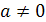 и не является
делителем нуля.
и не является
делителем нуля.
Теорема 3. (Свойства разности) В любом кольце
разность элементов обладает следующими свойствами:
а) 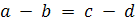 тогда
и только тогда, когда
тогда
и только тогда, когда 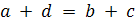 ;
;
б) 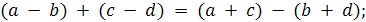
в) 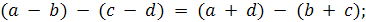
г) 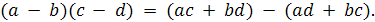
Подмножество M
кольца R называется
подкольцом, если оно само является кольцом при тех эе операциях сложения и
умножения, которые определены в кольце R.
Так, кольцо четных чисел является подкольцом
кольца целых чисел, а последнее в свою очередь - подкольцом кольца рациональных
чисел.
При выяснении того, является ли данное множество
кольца подкольцом, нет надобности проверять справедливость всех свойств кольца.
Большинство из них автоматически переходит с кольца на любое его подмножество.
Удобнее всего пользоваться для этого такой теоремой:
Теорема 4. Для того чтобы непустое подмножество M
кольца R было его
подкольцом, необходимо и достаточно, чтобы сумма, разность и произведение любых
двух элементов из M снова
принадлежали M.
Все теоремы из раздела Кольца, выведенные для
колец, остаются верными, в частности, для полей.
Как всякое кольцо, поле является группой
относительно операции сложения. Все элементы поля, не равные нулю, образуют группу
относительно операции умножения. Группа по сложению всех элементов поля
называется аддитивной, а группа по умножению всех его элементов, отличных от
нуля, - мультипликативной группой поля. Поле вполне определяется заданием двух
этих групп, заданием произведений нуля на все элементы и требованием
дистрибутивного закона для любых его элементов, включая нуль. Отсюда уже
следует, что произведение любого элемента на нуль равно нулю.
Из свойств мультипликативной группы следует, что
в поле существует единица, т. е. такой элемент e,
что 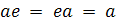 для
любого
для
любого 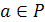 .
.
Теорема 5. Поле не имеет делителя нуля, т. е.
если ab = 0, то
либо a = 0, либо b
= 0.
Теорема 6. Всякое конечное кольцо без делителей
нуля, содержащее более одного элемента, является полем.
Теорема 7. (Свойства частного)
а) Если 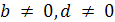 ,
то
,
то 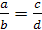 ,
тогда и только тогда, когда
,
тогда и только тогда, когда 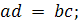 б) Если
б) Если 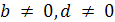 ,
то
,
то 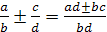 ;
;
в) Если 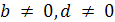 ,
то
,
то 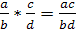 ;
;
г) Если 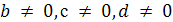 ,
то
,
то 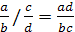 .
.
Существуют поля, содержащие элементы a ≠ 0
такие, что na = 0 при целом n, отличном от нуля. Так, в поле из двух элементов
0 и e имеем: 2e = e + e = 0. Справедливо утверждение:
Теорема 8. Для любого поля P имеет место один из
двух случаев:
а) для любого элемента a ≠ 0 и любого
целого числа n ≠ 0 кратное na также отлично от нуля;
б) существует единственное простое число p
такое, что pa = 0 для любого элемента a. (Под простым числом понимается
натуральное число, отличное от 1 и не делящееся ни на какое натуральное число,
кроме 1 и самого себя)
Характеристикой поля P называется число 0, если
na ≠ 0 для любого элемента a ≠ 0 и любого целого числа n ≠ 0
и простое число p такое, что pa = 0 для любого элемента a в противном случае.
Так как для числа 1 и любого целого n будет n · 1 = n, то все числовые поля
имеют характеристику 0.
1.3 Конечное поле
Конечное поле или поле Галуа - поле, состоящее
из конечного числа элементов. Конечное поле обычно обозначается 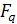 или
GF(q),
где q - число элементов
поля.
или
GF(q),
где q - число элементов
поля.
Свойства:
- Характеристика конечного поля
является простым числом;
- Число элементов любого конечного
поля есть его характеристика в натуральной степени
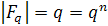 ;
;
Для каждого простого числа p
и натурального n существует
конечное поле из 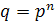 элементов,
единственное с точностью до изоморфизма. Это поле изоморфно полю разложения
многочлена
элементов,
единственное с точностью до изоморфизма. Это поле изоморфно полю разложения
многочлена
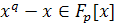 ;
;
- Мультипликативная группа 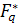 конечного
поля
конечного
поля 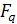 является
циклической группой порядка
является
циклической группой порядка 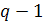 ;
;
o В частности, в конечном поле всегда
существует примитивный элемент 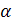 , порядок которого
равен
, порядок которого
равен 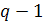 ,
то есть
,
то есть 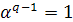 и
и
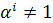 для
для
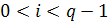 ;
;
o Любой ненулевой элемент 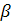 является
некоторой степенью примитивного элемента
является
некоторой степенью примитивного элемента
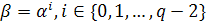 ;
;
- Поле 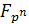 содержит
в себе в качестве подполя
содержит
в себе в качестве подполя 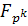 тогда и только
тогда, когда
тогда и только
тогда, когда 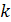 является делителем
является делителем
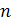 .
.
Построение поля
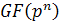
где p
- простое число, n -
натуральное число, начинается с построения его простого подполя (которое
совпадает со всем полем при n=1).
- Простое поле 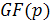 строится
как кольцо
строится
как кольцо 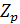 вычетов по модулю p,
которое в виду простоты не имеет делителей нуля и является полем.
вычетов по модулю p,
которое в виду простоты не имеет делителей нуля и является полем.
Элементы 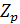 -
числа
-
числа 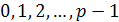 .
Операции проводятся как с обычными целыми числами с приведением результата по
модулю p;
.
Операции проводятся как с обычными целыми числами с приведением результата по
модулю p;
- Поле 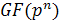 при
n>1 строится как
факторкольцо
при
n>1 строится как
факторкольцо
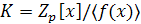
где 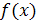 -
неприводимый многочлен степени n
над полем
-
неприводимый многочлен степени n
над полем 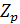 .
.
Таким образом, для построения поля из 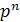 элементов
достаточно отыскать многочлен степени n,
неприводимый над полем
элементов
достаточно отыскать многочлен степени n,
неприводимый над полем 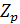 ;
;
Элементами поля K
являются все многочлены степени меньшей n
с коэффициентами из 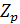 . Арифметические
операции (сложение и умножение) проводятся по модулю многочлена
. Арифметические
операции (сложение и умножение) проводятся по модулю многочлена 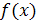 ,
то есть, результат соответствующей операции - это остаток от деления на
,
то есть, результат соответствующей операции - это остаток от деления на 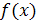 с
приведением коэффициентов по модулю p.
с
приведением коэффициентов по модулю p.
Для алгоримта AES
(Rijndael) были разработаны
собственные неприводимые полиномы в поле 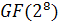 ,
а также операции сложения и умножения, рассмотренные в следующих разделах.
,
а также операции сложения и умножения, рассмотренные в следующих разделах.
2. Основные определения
и процедуры алгоритма
.1 Ключ шифра
является симметричным алгоритмом шифрования с
ключем. Ключ может иметь длину 128, 192 и 256 бит. Алгоритмы с ключем длиной
128, 192 и 256 бит обозначаются соответственно как AES-128, AES-192, AES-256.
2.2 Блоки данных
Алгоритм AES оперирует блоками по 16 байт,
представленными матрицами 4х4. В процессе обработки блоки в промежуточных
состояниях обозначаются как “текущие”.
2.3 Ключи раундов
Алгоритм AES (AES-128, AES192, AES-256)
расширяет ключ шифра и получает 10, 12 или 14 ключей раундов. Каждый ключ
раунда имеет длину 128 бит. Алгоритм получения ключа раунда называется “расширением
ключа” (KeyExpansion).
2.4 AddRoundKey
AddRoundKey(ref
byte[,] state,
byte[,] Key,
int round)
является 128-битным преобразованием, которое заключается в побитовой операции
XOR двух аргументов state
и Key, которые выступают
в качестве “текущего” блока и ключа раунда. Операция XOR
применяется для каждого байта state.
алгоритм key expansion кольцо
2.5 SubBytes
и InvSubBytes
SubBytes
- это 8-битное преобразование, которое определяется как аффинная функция 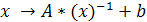 ,
где A - двоичная матрица
8х8, а b - 8-битный вектор, как показано на рисунке 1.
,
где A - двоичная матрица
8х8, а b - 8-битный вектор, как показано на рисунке 1.
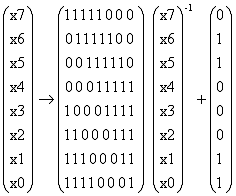
Рисунок 1 - Преобразование SubBytes
Здесь 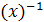 обозначает
инверсию над полем Галуа (конечным полем)
обозначает
инверсию над полем Галуа (конечным полем) 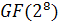 ,
которое определяется полиномом
,
которое определяется полиномом 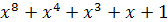 (для краткости
0x11b).SubBytes
является обратным преобразованием по отношению к SubBytes
и определяется как
(для краткости
0x11b).SubBytes
является обратным преобразованием по отношению к SubBytes
и определяется как 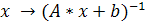 . Схематически
изображено на рисунке 2.
. Схематически
изображено на рисунке 2.
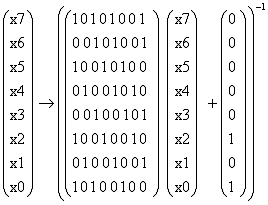
Рисунок 2 - Преобразование InvSubBytes
Преобразования SubBytes
и InvSubBytes
применяются независимо для каждого байта текущего блока.
2.6 Таблицы подстановки
S-Box и InvS-Box
Преобразования SubBytes
и InvSubBytes
могут быть представлены в виде таблиц подстановки S-Box и InvS-Box. Если на
входе имеется байт B [7-0], а x и y - его старшая и младшая часть (x [3-0] = B
[7-4], y [3-0] = B [3-0]), то на выходе байт получается кодированным в две
шестнадцатиричные цифры. Например, применение таблицы подстановки S-Box для
числа 85 (x=8; y=5 в шестнадцатиричном виде) дает на выходе шестнадцатиричное
97. А применение таблицы InvS-Box для 97 дает 85. Таблицы подстановки S-Box и InvS-Box
отображены в таблицах 1 и 2 соответственно.
Таблица 1 - Таблица подстановки S-Box
|
X,
Y
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
|
0
|
63
|
7C
|
77
|
7B
|
F2
|
6B
|
6F
|
C5
|
30
|
01
|
67
|
2B
|
FE
|
D7
|
AB
|
76
|
|
1
|
CA
|
82
|
C9
|
7D
|
FA
|
59
|
47
|
F0
|
AD
|
D4
|
A2
|
AF
|
9C
|
A4
|
72
|
C0
|
|
2
|
B7
|
FD
|
93
|
26
|
36
|
3F
|
F7
|
CC
|
34
|
A5
|
E5
|
F1
|
71
|
D8
|
31
|
15
|
|
3
|
04
|
C7
|
23
|
C3
|
18
|
96
|
05
|
9A
|
07
|
12
|
80
|
E2
|
EB
|
27
|
B2
|
75
|
|
4
|
09
|
83
|
2C
|
1A
|
1B
|
6E
|
5A
|
A0
|
52
|
3B
|
D6
|
B3
|
29
|
E3
|
2F
|
84
|
|
5
|
53
|
D1
|
00
|
ED
|
20
|
FC
|
B1
|
5B
|
6A
|
CB
|
BE
|
39
|
4A
|
4C
|
58
|
CF
|
|
6
|
D0
|
EF
|
AA
|
FB
|
43
|
4D
|
33
|
85
|
45
|
F9
|
02
|
7F
|
50
|
3C
|
9F
|
A8
|
|
7
|
51
|
A3
|
40
|
8F
|
92
|
9D
|
38
|
F5
|
BC
|
B6
|
DA
|
21
|
10
|
FF
|
F3
|
D2
|
|
8
|
CD
|
0C
|
13
|
EC
|
5F
|
97
|
44
|
17
|
C4
|
A7
|
7E
|
3D
|
64
|
5D
|
19
|
73
|
|
9
|
60
|
81
|
4F
|
DC
|
22
|
2A
|
90
|
88
|
46
|
EE
|
B8
|
14
|
DE
|
5E
|
0B
|
DB
|
|
A
|
E0
|
32
|
3A
|
0A
|
49
|
06
|
24
|
5C
|
C2
|
D3
|
AC
|
62
|
91
|
95
|
E4
|
79
|
|
B
|
E7
|
C8
|
6D
|
8D
|
D5
|
4E
|
A9
|
6C
|
56
|
F4
|
EA
|
65
|
7A
|
AE
|
08
|
|
C
|
BA
|
78
|
25
|
2E
|
1C
|
A6
|
B4
|
C6
|
E8
|
DD
|
74
|
1F
|
4B
|
BD
|
8B
|
8A
|
|
D
|
70
|
3E
|
B5
|
66
|
48
|
03
|
F6
|
0E
|
61
|
35
|
57
|
B9
|
86
|
C1
|
1D
|
9E
|
|
E
|
E1
|
F8
|
98
|
11
|
69
|
D9
|
8E
|
94
|
9B
|
1E
|
87
|
E9
|
CE
|
55
|
28
|
DF
|
|
F
|
8C
|
A1
|
89
|
0D
|
BF
|
E6
|
42
|
68
|
41
|
99
|
2D
|
0F
|
B0
|
54
|
BB
|
16
|
Таблица 2 - Таблица подстановки InvS-Box
|
X,
Y
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
|
0
|
52
|
09
|
6A
|
D5
|
30
|
36
|
A5
|
38
|
BF
|
40
|
A3
|
9E
|
81
|
F3
|
D7
|
FB
|
|
1
|
7C
|
E3
|
39
|
82
|
9B
|
2F
|
FF
|
87
|
34
|
8E
|
43
|
44
|
C4
|
DE
|
E9
|
CB
|
|
2
|
54
|
7B
|
94
|
32
|
A6
|
C2
|
23
|
3D
|
EE
|
4C
|
95
|
0B
|
42
|
FA
|
C3
|
4E
|
|
3
|
08
|
2E
|
A1
|
66
|
28
|
D9
|
24
|
B2
|
76
|
5B
|
A2
|
49
|
6D
|
8B
|
D1
|
25
|
|
4
|
72
|
F8
|
F6
|
64
|
86
|
68
|
98
|
16
|
D4
|
A4
|
5C
|
CC
|
5D
|
65
|
B6
|
92
|
|
5
|
6C
|
70
|
48
|
50
|
FD
|
ED
|
B9
|
DA
|
5E
|
15
|
46
|
57
|
A7
|
8D
|
9D
|
84
|
|
6
|
90
|
D8
|
AB
|
00
|
8C
|
BC
|
D3
|
0A
|
F7
|
E4
|
58
|
05
|
B8
|
B3
|
45
|
06
|
|
7
|
D0
|
2C
|
1E
|
8F
|
CA
|
3F
|
0F
|
02
|
C1
|
AF
|
BD
|
03
|
01
|
13
|
8A
|
6B
|
|
8
|
3A
|
91
|
11
|
41
|
4F
|
67
|
DC
|
EA
|
97
|
F2
|
CF
|
CE
|
F0
|
B4
|
E6
|
73
|
|
9
|
96
|
AC
|
74
|
22
|
E7
|
AD
|
35
|
85
|
E2
|
F9
|
37
|
E8
|
1C
|
75
|
DF
|
6E
|
|
A
|
47
|
F1
|
1A
|
71
|
1D
|
29
|
C5
|
89
|
6F
|
B7
|
62
|
0E
|
AA
|
18
|
BE
|
1B
|
|
B
|
FC
|
56
|
3E
|
4B
|
C6
|
D2
|
79
|
20
|
9A
|
DB
|
C0
|
FE
|
78
|
CD
|
5A
|
F4
|
|
C
|
1F
|
DD
|
A8
|
33
|
88
|
07
|
C7
|
31
|
B1
|
12
|
10
|
59
|
27
|
80
|
EC
|
5F
|
|
D
|
60
|
51
|
7F
|
A9
|
19
|
B5
|
4A
|
0D
|
2D
|
E5
|
7A
|
9F
|
93
|
C9
|
9C
|
EF
|
|
E
|
A0
|
E0
|
3B
|
4D
|
AE
|
2A
|
F5
|
B0
|
C8
|
EB
|
BB
|
3C
|
53
|
99
|
61
|
|
F
|
17
|
2B
|
04
|
7E
|
BA
|
77
|
D6
|
26
|
E1
|
69
|
14
|
63
|
55
|
21
|
0C
|
7D
|
2.7 Преобразование
ShiftRows и InvShiftRows
ShiftRows
является побайтовой перестановкой. Пример работы отображен в таблице 3.
Таблица 3 - Преобразование ShiftRows
|
a00
|
a01
|
a02
|
a03
|
àà
|
a00
|
a01
|
a02
|
a03
|
|
a10
|
a11
|
a12
|
a13
|
|
a11
|
a12
|
a13
|
a10
|
|
a20
|
a21
|
a22
|
a23
|
|
a22
|
a23
|
a20
|
a21
|
|
a30
|
a31
|
a32
|
a33
|
|
a33
|
a30
|
a31
|
a32
|
Название ShiftRows обозначает сдвиг строк в
двумерном массиве на различные смещения и происходит от представления
“текущего” блока в виде матрицы 4х4 байта. Первая строка массива остается без
изменений, вторая циклично сдвигается влево на одну позицию (один байт), третья
циклично сдвигается влево на две позиции, четвертая циклично сдвигается влево
на три позиции.является обратной функцией по отношению к ShiftRows. Пример работы
отображен в таблице 4.
Таблица 4 - Преобразование InvShiftRows
|
a00
|
a01
|
a02
|
a03
|
àà
|
a00
|
a01
|
a02
|
a03
|
|
a11
|
a12
|
a13
|
a10
|
|
a10
|
a11
|
a12
|
a13
|
|
a22
|
a23
|
a20
|
a21
|
|
a20
|
a21
|
a22
|
a23
|
|
a33
|
a30
|
a31
|
a32
|
|
a30
|
a31
|
a32
|
a33
|
2.8 Преобразование
MixColumns и InvMixColumns
является 128-битным преобразованием, работающим
со столбцами матрицы 4х4 байта, имеющейся на входе.
Преобразование воспринимает каждый столбец
матрицы как полином третьей степени с коэффициентами на поле AES-GF256. Над
каждым столбцом матрицы “текущего” блока производится умножение в 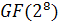 по
модулю
по
модулю 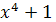 на
фиксированный многочлен:
на
фиксированный многочлен:
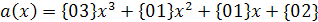 ,
,
где {--} обозначает элемент поля AES-GF256.
InvMixColumns
является 128-битным преобразованием, работающим со столбцами матрицы 4х4 байта,
поданной на вход.
Преобразование воспринимает каждый столбец
матрицы как полином третьей степени с коэффициентами на поле AES-GF256. Над
каждым столбцом матрицы “текущего” блока производится умножение в 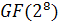 по
модулю
по
модулю 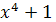 на
фиксированный многочлен:
на
фиксированный многочлен:
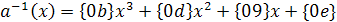 .
.
2.9 Преобразование
SubWord
является функцией, используемой в процедуре Key
Expansion, которая берет на входе 4-х байтное слово и, применяя S-box к каждому
из четырёх байтов, выдаёт выходное слово, а конкретно:
SubWord (X) = [S-Box(X[31-24]),
S-Box(X[23-16]), S-Box(X[15-8]), S-Box(X[7-0])]
2.10 Преобразование
RotWord
- это функция, использующаяся в процедуре Key
Expansion, которая берет 4-х байтное слово и производит над ним циклическую
перестановку, например, используется в качестве входного слова [a0,a1,a2,a3],
а возвращается слово [a1,a2,a3,a0].
2.11 Round Constant
(RCON)
Процедура расширения ключа использует 10
констант, называющихся Константами Раунда (в дальнейшем именуемых RCON).
Константы определяются как 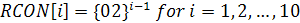 , операции
производятся над полем AES-GF256.
, операции
производятся над полем AES-GF256.
Каждое значение RCON представляется в виде
байта. Все десять констант в шестнадцатиричном виде представляются следующим
образом:
RCON [1] = 01, RCON [2] = 02, RCON
[3] = 04, RCON [4] = 08, RCON [5] = 10,[6] = 20, RCON [7] = 40, RCON [8] = 80,
RCON [9] = 1B, RCON [10] = 36.
2.12 Расширение ключа
(Key Expansion)
Стандарт AES использует ключи длиной 128, 192
или 256 бит. Ключи расширяются соответственно в 10, 12 или 14 ключей раундов, с
помощюю алгоритма расширения ключа. Каждый ключ раунда имеет длину 128 бит.
Расширение ключа зависит только от ключа шифра и не зависит от шифруемых
данных, следовательно, расширение ключа может производиться независимо от фазы
шифрованиф/дешифрования. В основе алгоритма расширения ключа лежит набор
преобразований SubWord(RotWord(temp))
и SubWord(temp) с
использованием констант RCON.
3 Общий алгоритм работы
AES
Рисунок 3 - Общий алгоритм работы AES
Общий алгоритм работы AES
представлен на рисунке 3. Число раундов Round
определяется длиной ключа. На вход поступает открытый текст, на выходе имеется
совокупность зашифрованных блоков (Ciphertext).
Код программы, разработанной исходя из общих
определений и процедур, представлен в приложении Б.
4. Используемые
математические операции
Все математические операции производятся в поле
Галуа 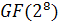 .
.
В процедурах AddRoyndKey
и KeyExpansion в основе лежат операции сложения байт по модулю 2 (XOR).
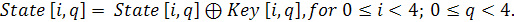
В AddRoyndKey
в сложении участвуют только текущий блок и ключ раунда, а в KeyExpansion в
сложении участвуют результат SubWord(RotWord(temp)),
предыдущий ключ раунда и Round Constant.
На языке C#
для 256 битного ключа данный алгоритм (KeyExpansion) запишется следующим
образом:
AKey = new byte[4, 60];ch = 0;(int i
= 0; i < 4; i++)
{(int q = 0; q < 8; q++)
{[i, q] = key[ch];++;
}
}(int i = 8; i < 60; i++)
{[] temp = new byte[4];(int q = 0; q
< 4; q++)
{[q] = AKey[q, i - 1];
}((i % 8) == 0)
{= SubWord(RotWord(temp), SBox);(int
q = 0; q < 4; q++)
{[q] ^= RCon[q];
}
}if (i % 8 == 4)
{= SubWord(temp,SBox);
}(int q=0; q<4; q++)[q,i] =
Convert.ToByte(AKey[q,i - 8] ^ temp[q]);
}
В процедурах SubBytes
и MixColumn при умножении байтов
используется неприводимый многочлен
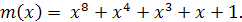
Вычисление произведения М байтов {b1}
на {b2} здесь
выполняется согласно следующему алгоритму
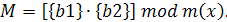
В этом случае обратная величина байта равна:
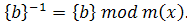
Как уже было сказано выше, в процедуре SubBytes
используется следующая формула умножения и сложения байт 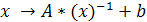 ,
где A - двоичная матрица
8х8, а b - 8-битный вектор, как показано на рисунке 4.
,
где A - двоичная матрица
8х8, а b - 8-битный вектор, как показано на рисунке 4.

Рисунок 4 - Формула в преобразовании SubBytes.
Для умножения полубайтов (коды длиной 4 бита)
используется неприводимый полином
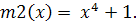
Вычисление произведения М полубайтов {a}
на {b} здесь выполняется
следующим образом
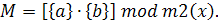
M представляет собой
полубайт d. Операцию
умножения полубайтов {a}
на {b} можно записать в
матричном виде
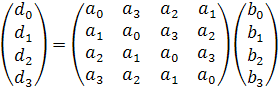
В процедуре MixColumn
общую формулу умножения можно представить в виде
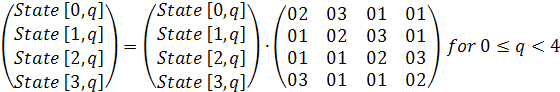
В обратной процедуре InvMixColumn
общая формула имеет вид
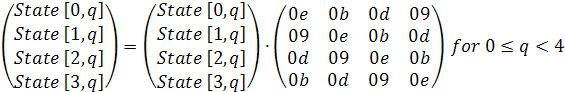
Заключение
В результате работы над данным проектом были
освоены современные методы шифрования, а в частности Rijndael,
написана программа, позволяющая шифровать текстовую информацию различными
длинами ключей (128, 192, 256 бит).
Приобретенные навыки активно использовались для
оценки эффективности и скорости работы других симметричных алгоритмов
шифрования.
Все поставленные цели и задачи выполнены.
Для реализации поставленной задачи
использовалась среда программирования Microsoft
Visual Studio
2010. Программа реализована в виде Windows
Forms Application
на языке C#.
Рекомендации по развитию программы
В данной программной реализации каждый блок
шифруется независимо от остальных, то есть используется простейший режим работы
ELECTRONIC
CODEBOOK (ECB),
что упрощает криптоанализ полученного шифра. Поэтому рекомендуется реализовать
остальные режимы работ алгоритма для повышения криптостойкости. Особенно важно
реализовать поддержку русского языка. Также можно было бы сделать поддержку
шифрования файлов различного формата.
Список используемых
источников
1. С.Г.
Баричев, В.В. Гончаров, Р.Е. Серов, Основы современной криптографии, 2-е
издание, Москва, "Горячая линия - Телеком", 2002.
2. Осипенко
Л. П., Васильченко А. А. Математические основы криптологии. Методические
указания для выполнения курсовой работы. - Краснодар: Изд-во КубГТУ, 2009.
. Кнут
Д. Искусство программирования. Т. 2. Получисленные алгоритмы. третье издание.
М.: МЦНМО, 1999.
Приложение А
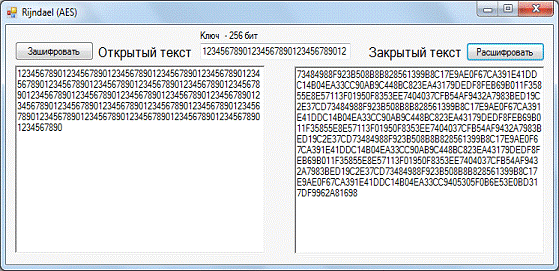
Рисунок 5 - Скриншот программы
Приложение Б
Листинг программы
using
System;System.Collections.Generic;System.ComponentModel;System.Data;System.Drawing;System.Linq;System.Text;System.Windows.Forms;
CryptoAES
{partial class Form1 : Form
{Form1()
{();
}
//public static string[,]
Tabl;static string ByteToHex(byte a)
{hex="";b = a / 16;c = a %
16;(b)
{0:+= '0';;1:+= '1';;2:+= '2';;3:+=
'3';;4:+= '4';;5:+= '5';;6:+= '6';;7:+= '7';;8:+= '8';;9:+= '9';;10:+=
'A';;11:+= 'B';;12:+= 'C';;13:+= 'D';;14:+= 'E';;15:+= 'F';;
}(c)
{0:+= '0';;1:+= '1';;2:+= '2';;3:+=
'3';;4:+= '4';;5:+= '5';;6:+= '6';;7:+= '7';;8:+= '8';;9:+= '9';;10:+=
'A';;11:+= 'B';;12:+= 'C';;13:+= 'D';;14:+= 'E';;15:+= 'F';;
}hex;
}static byte HexToByte(string hex)
{a=0;(hex[1])
{'0':= 0;;'1':= 1;;'2':= 2;;'3':=
3;;'4':= 4;;'5':= 5;;'6':= 6;;'7':= 7;;'8':= 8;;'9':= 9;;'A':= 10;;'B':=
11;;'C':= 12;;'D':= 13;;'E':= 14;;'F':= 15;;
}(hex[0])
{'0':+= 0;;'1':+= 16;;'2':+=
32;;'3':+= 48;;'4':+= 64;;'5':+= 80;;'6':+= 96;;'7':+= 112;;'8':+= 128;;'9':+=
144;;'A':+= 160;;'B':+= 176;;'C':+= 192;;'D':+= 208;;'E':+= 224;;'F':+= 240;;
}a;
}void button1_Click(object sender,
EventArgs e)
{[] input;(richTextBox1.Text.Length%16==0)=
new byte[richTextBox1.Text.Length];= new
byte[((richTextBox1.Text.Length/16)+1)*16];(int i = 0; i <
richTextBox1.Text.Length; i++)[i] = Convert.ToByte(richTextBox1.Text[i]);(int i
= richTextBox1.Text.Length; i < input.Length; i++)[i] = 0;
//------------------------------------[]
key = new byte[1];(textBox1.Text.Length <= 16)= new
byte[16];(textBox1.Text.Length > 16 && textBox1.Text.Length
<=24)= new byte[24];(textBox1.Text.Length > 24)= new byte[32];
(int i = 0; i < textBox1.Text.Length;
i++)[i] = Convert.ToByte(textBox1.Text[i]);(int i = textBox1.Text.Length; i
< key.Length; i++)[i] = 0;
//------------------------------------.Encrypt(ref
input, key);
/*TablLeng.ColumnCount =
16;.RowCount = 16;(int q = 0; q <= 15; q++)
{.Columns[q].Width =
40;.Columns[q].Name = Convert.ToString(q);
}oi = 0;(int l = 0; l < 16; l++)
{(int q = 0; q < 16; q++)
{[q, l].Value = Tabl[q, l];++;
}
}*/txt="";[] HexTable =
new string[256];(int i = 0; i < 256; i++)
{[i] = ByteToHex(Convert.ToByte(i));
}(int i = 0; i < input.Length;
i++)
{+= HexTable[input[i]];
}.Text = txt;
}
void button2_Click(object sender,
EventArgs e)
{[] input = new
byte[richTextBox2.Text.Length/2];txt="";(int i = 0; i <
richTextBox2.Text.Length; i+=2)
{=Convert.ToString(richTextBox2.Text[i])+Convert.ToString(richTextBox2.Text[i+1]);[i/2]
= HexToByte(txt);
}
//------------------------------------[]
key = new byte[1];(textBox1.Text.Length <= 16)= new
byte[16];(textBox1.Text.Length > 16 && textBox1.Text.Length <=
24)= new byte[24];(textBox1.Text.Length > 24)= new byte[32];
(int i = 0; i <
textBox1.Text.Length; i++)[i] = Convert.ToByte(textBox1.Text[i]);(int i =
textBox1.Text.Length; i < key.Length; i++)[i] = 0;
//------------------------------------
.Decrypt(ref input, key);
/*TablLeng.ColumnCount =
16;.RowCount = 16;(int q = 0; q <= 15; q++)
{.Columns[q].Width =
40;.Columns[q].Name = Convert.ToString(q);
}oi = 0;(int l = 0; l < 16; l++)
{(int q = 0; q < 16; q++)
{[q, l].Value = Tabl[q, l];++;
}
}*/= "";(int i = 0; i <
input.Length; i++)+= Convert.ToChar(input[i]);.Text = txt;
}
void textBox1_TextChanged(object
sender, EventArgs e)
{(textBox1.Text.Length <=
16).Text = "- 128 бит";(textBox1.Text.Length
> 16 && textBox1.Text.Length <= 24).Text = "- 192 бит";(textBox1.Text.Length
> 24).Text = "- 256 бит";
}
}AES
{
#region Create S-Box or
InvS-Boxstatic void Create_InvSBox(ref byte[] InvSBox)
{[] SBox = new byte[256];(int i = 0;
i <= 255; i++)
{result = Convert.ToByte(i);(int q =
1; q < 7; q++)= AES.PolynomsMult(AES.PolynomsMult(result, result, 0x11b),
Convert.ToByte(i), 0x11b);= AES.PolynomsMult(result, result, 0x11b);=
AES.PolynomsMult(0x1f, result, 0x101);[i] = Convert.ToByte(result ^ 0x63);
}(int i = 0; i <= 255; i++)
{[SBox[i]] = Convert.ToByte(i);
}
}static void Create_SBox(ref byte[]
SBox)
{(int i = 0; i <= 255; i++)
{result = Convert.ToByte(i);(int q =
1; q < 7; q++)= AES.PolynomsMult(AES.PolynomsMult(result, result, 0x11b),
Convert.ToByte(i), 0x11b);= AES.PolynomsMult(result, result, 0x11b);=
AES.PolynomsMult(0x1f, result, 0x101);[i] = Convert.ToByte(result ^ 0x63);
}
}
#endregion
#region Multiply Polynomsstatic byte
PolynomsMult(byte a, byte b, ushort mod)
{mult = 0;temp = b;(a > 0)
{((a & 0x01) == 1) mult ^=
temp;>>= 1;<<= 1;
}(byte i = 14; i >= 8; i--)((mult
>> i) == 1) mult = Convert.ToUInt16(mult ^ (mod << (i -
8)));Convert.ToByte(mult);
}
#endregion
#region Key schedule
static byte[,] KeyExpansion(byte[]
key, byte[] SBox)
{[] RCon= new byte[] { 0x01, 0x02,
0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36 };[,] AKey = new byte[4,60];(int
i = 0; i < 60; i++ )
{(int q = 0; q < 4; q++)[q, i] =
0;
}(key.Length == 16)
{= new byte[4, 44];ch = 0;(int i =
0; i < 4; i++)
{(int q = 0; q < 4; q++)
{[i, q] = key[ch];++;
}
}(int i = 4; i < 44; i++)
{[] temp = new byte[4];(int q = 0; q
< 4; q++)
{[q] = AKey[q, i - 1];
}((i % 4) == 0)
{= SubWord(RotWord(temp), SBox);[0]
^= RCon[(i / 4) - 1];
}(int q = 0; q < 4; q++)[q, i] =
Convert.ToByte(AKey[q, i - 4] ^ temp[q]);
}
}(key.Length == 24)
{= new byte[4, 52];ch = 0;(int i =
0; i < 4; i++)
{(int q = 0; q < 6; q++)
{[i, q] = key[ch];++;
}
}(int i = 6; i < 52; i++)
{[] temp = new byte[4];(int q = 0; q
< 4; q++)
{[q] = AKey[q, i - 1];
}((i % 6) == 0)
{= SubWord(RotWord(temp), SBox);(int
q = 0; q < 4; q++)
{[q] ^= RCon[q];
}
}if (i % 6 == 3)
{= SubWord(temp, SBox);
}(int q = 0; q < 4; q++)[q, i] =
Convert.ToByte(AKey[q, i - 6] ^ temp[q]);
}
}(key.Length == 32)
{= new byte[4, 60];ch = 0;(int i =
0; i < 4; i++)
{(int q = 0; q < 8; q++)
{[i, q] = key[ch];++;
}
}(int i = 8; i < 60; i++)
{[] temp = new byte[4];(int q = 0; q
< 4; q++)
{[q] = AKey[q, i - 1];
}((i % 8) == 0)
{= SubWord(RotWord(temp), SBox);(int
q = 0; q < 4; q++)
{[q] ^= RCon[q];
}
}if (i % 8 == 4)
{= SubWord(temp,SBox);
}(int q=0; q<4; q++)[q,i] = Convert.ToByte(AKey[q,i
- 8] ^ temp[q]);
}
}AKey;
}
static byte[] SubWord(byte[] W,
byte[] SBox)
{[] temp = new byte[4];(int i = 0; i
< 4; i++)[i] = SBox[W[i]];temp;
}
static byte[] RotWord(byte[] W)
{[] temp = new byte[4];(int i = 0; i
< 4; i++)[i] = W[(i + 1)%4];temp;
}
#endregion
#region Block_Encrypt or
Block_Decryptstatic void Cipher(ref byte[,] state, byte[,] AKey, byte[] SBox,
byte length)
{(ref state, AKey, 0);(int round =
1; round <= 9+length*2; round++)
{(ref state, SBox);(ref state);(ref
state);(ref state, AKey, round*4);
}
(ref state,SBox);(ref state);(ref
state, AKey, 40+length*8);
}static void InvCipher(ref byte[,]
state, byte[,] AKey, byte[] InvSBox, byte length)
{(ref state, AKey, 40 + length *
8);(ref state);(ref state, InvSBox);(int round = 9 + length * 2; round >= 1;
round--)
{(ref state, AKey, round * 4);(ref
state);(ref state);(ref state, InvSBox);
}(ref state, AKey, 0);
}static void MixColumns(ref byte[,]
state)
{[,] new_state = new byte[4, 4];(int
c = 0; c < 4; c++)
{_state[0, c] =
(byte)(PolynomsMult(2, state[0, c], 283) ^ PolynomsMult(3, state[1, c], 283) ^
state[2, c] ^ state[3, c]);_state[1, c] = (byte)(state[0, c] ^ PolynomsMult(2,
state[1, c],283) ^ PolynomsMult(3, state[2, c], 283) ^ state[3, c]);_state[2,
c] = (byte)(state[0, c] ^ state[1, c] ^ PolynomsMult(2, state[2, c],283) ^
PolynomsMult(3, state[3, c],283));_state[3, c] = (byte)(PolynomsMult(3,
state[0, c],283) ^ state[1, c] ^ state[2, c] ^ PolynomsMult(2, state[3,
c],283));
}= new_state;;
}static void InvMixColumns(ref
byte[,] state)
{[,] new_state = new byte[4, 4];(int
c = 0; c < 4; c++)
{_state[0, c] =
(byte)(AES.PolynomsMult(14, state[0, c], 283) ^ AES.PolynomsMult(11, state[1,
c], 283) ^ AES.PolynomsMult(13, state[2, c], 283) ^ AES.PolynomsMult(9,
state[3, c], 283));_state[1, c] = (byte)(AES.PolynomsMult(9, state[0, c], 283)
^ AES.PolynomsMult(14, state[1, c], 283) ^ AES.PolynomsMult(11, state[2, c],
283) ^ AES.PolynomsMult(13, state[3, c], 283));_state[2, c] =
(byte)(AES.PolynomsMult(13, state[0, c], 283) ^ AES.PolynomsMult(9, state[1,
c], 283) ^ AES.PolynomsMult(14, state[2, c], 283) ^ AES.PolynomsMult(11,
state[3, c], 283));_state[3, c] = (byte)(AES.PolynomsMult(11, state[0, c], 283)
^ AES.PolynomsMult(13, state[1, c], 283) ^ AES.PolynomsMult(9, state[2, c],
283) ^ AES.PolynomsMult(14, state[3, c], 283));
}= new_state;
}
static void ShiftRows(ref byte[,]
state)
{[,] temp = new byte[4,4];(int i =
0; i < 4; i++)
{(int q = 0; q < 4; q++)[i, q] =
state[i, (q + i) % 4];
}= temp;
}static void InvShiftRows(ref byte[,]
state)
{[,] temp = new byte[4, 4];(int i =
0; i < 4; i++)
{(int q = 0; q < 4; q++)[i, q] =
state[i, (q + 4 - i) % 4];
}= temp;
}
static void SubBytes(ref byte[,]
state, byte[] SBox)
{(int i = 0; i < 4; i++)
{(int q = 0; q < 4; q++)
{[i, q] = SBox[state[i,q]];
}
}
}
static void AddRoundKey(ref byte[,]
state, byte[,] AKey, int round)
{(int i = 0; i < 4; i++)
{(int q = 0; q < 4; q++)
{[i, q] ^= AKey[i,q+round];
}
}
}
#endregion
#region Encrypt or Decrypt text
static void Encrypt(ref byte[]
array, byte[] key)
{[,] temp = new byte[4,4];[] SBox =
new byte[256];_SBox(ref SBox);
/*Form1.Tabl = new string[16, 16];oi
= 0;(int l = 0; l < 16; l++)
{(int q = 0; q < 16; q++)
{.Tabl[q, l] =
Form1.ByteToHex(SBox[oi]);++;
}
{(int k = 0; k < 4; k++)
{(int q = 0; q < 4; q++)
{[k, q] = array[16 * i + j];++;
}
}= 0;(ref temp, AKey, SBox,
Convert.ToByte((key.Length - 16) / 8));(int k = 0; k < 4; k++)
{(int q = 0; q < 4; q++)
{[16 * i + j] = temp[k,q];++;
}
}= 0;
}= output;.Clear(AKey, 0,
AKey.Length);
}
static void Decrypt(ref byte[]
array, byte[] key)
{[,] temp = new byte[4,4];[] InvSBox
= new byte[256];[] SBox = new byte[256];_SBox(ref SBox);_InvSBox(ref InvSBox);
/*Form1.Tabl = new string[16, 16];oi
= 0;(int l = 0; l < 16; l++)
{(int q = 0; q < 16; q++)
{.Tabl[q, l] =
Form1.ByteToHex(InvSBox[oi]);++;
}
}*/[,] AKey = KeyExpansion(key,
SBox);len = (uint)(array.Length / 16);[] output = new byte[len * 16];j = 0;(int
i = 0; i < len; i++)
{(int k = 0; k < 4; k++)
{(int q = 0; q < 4; q++)
{[k, q] = array[16 * i + j];++;
}
}= 0;(ref temp, AKey, InvSBox,
Convert.ToByte((key.Length - 16) / 8));(int k = 0; k < 4; k++)
{(int q = 0; q < 4; q++)
{[16 * i + j] = temp[k, q];++;
}
}= 0;
}= output;.Clear(AKey, 0,
AKey.Length);
}
#endregion
#region Teststatic void test()
{[,] state = new byte[4, 4];[0, 0] =
0x32;[0, 1] = 0x88;[0, 2] = 0x31;[0, 3] = 0xe0;[1, 0] = 0x43;[1, 1] = 0x5a;[1,
2] = 0x31;[1, 3] = 0x37;[2, 0] = 0xf6;[2, 1] = 0x30;[2, 2] = 0x98;[2, 3] =
0x07;[3, 0] = 0xa8;[3, 1] = 0x8d;[3, 2] = 0xa2;[3, 3] = 0x34;[] key = new
byte[16];[0] = 0x2b;[1] = 0x28;[2] = 0xab;[3] = 0x09;[4] = 0x7e;[5] = 0xae;[6]
= 0xf7;[7] = 0xcf;[8] = 0x15;[9] = 0xd2;[10] = 0x15;[11] = 0x4f;[12] =
0x16;[13] = 0xa6;[14] = 0x88;[15] = 0x3c;[] SBox = new byte[256];[] InvSBox =
new byte[256];.Create_SBox(ref SBox);.Create_InvSBox(ref InvSBox);[,] AKey =
AES.KeyExpansion(key, SBox);.Cipher(ref state, AKey, SBox, 0);.InvCipher(ref
state, AKey, InvSBox, 0);
}
#endregion
}
}