Методика навчання диференціальних рівнянь майбутніх вчителів математики в педагогічних університетах
МІНІСТЕРСТВО ОСВІТИ І НАУКИ,
МОЛОДІ ТА СПОРТУ УКРАЇНИ
ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ
ПЕДАГОГІЧНИЙ
УНІВЕРСИТЕТ імені Г.С. СКОВОРОДИ
МАГІСТЕРСЬКА РОБОТА
“МЕТОДИКА НАВЧАННЯ ДИФЕРЕНЦІАЛЬНИХ
РІВНЯНЬ МАЙБУТНІХ ВЧИТЕЛІВ МАТЕМАТИКИ В ПЕДАГОГІЧНИХ УНІВЕРСИТЕТАХ”
Науковий керівник:
Док. п. н., професор.
Моторіна В.Г.
Харків - 2012
ЗМІСТ
ВСТУП
РОЗДІЛ І. ТЕОРЕТИЧНІ ОСНОВИ МЕТОДИКИ НАВЧАННЯ
ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ В ПЕДАГОГІЧНИХ УНІВЕРСИТЕТАХ
1.1 Диференціальні рівняння
як складова вивчення математики в педагогічних вищих навчальних закладах
1.2 Психолого-педагогічні
основи вивчення диференціальних рівнянь
.3 Теоретичні основи вивчення
диференціальних рівнянь
РОЗДІЛ ІІ. МЕТОДИКА НАВЧАННЯ ДИФЕРЕНЦІАЛЬНИХ
РІВНЯНЬ В ПЕДАГОГІЧНИХ УНІВЕРСИТЕТАХ
2.1 Розробка лекцій,
практичних робіт, опорних конспектів
.2 Контроль та корекція
ВИСНОВКИ
ВИКОРИСТАНА ЛІТЕРАТУРА
ВСТУП
Сучасний етап розвитку системи освіти в Україні визначається
тенденціями до інтеграції у світовій системі освіти, до збереження та зміцнення
інтелектуального потенціалу країни, підвищенням рівня конкуренції
інтелектуальної продукції. Це зумовлює її подальшу демократизацію, гуманізацію
і гуманітаризацію, диференціацію і орієнтацію на всебічний розвиток
особистості. Досягнення цього неможливе без застосування сучасних педагогічних
та інформаційних технологій, що вимагає подальших глибоких досліджень процесу
навчання.
Різке падіння соціального статусу і престижу знань серед молоді поступово
змінюється прагненням до одержання такого рівня освіти, яка б забезпечила
гідний статус молодої людини у сучасному суспільстві. Така ситуація сприяє
росту пізнавальної активності учнів, потягу їх до знань, бажанню працювати над
собою. Система освіти України має забезпечити можливості для всебічного
розвитку молодої людини як цілісної особистості, повинна сприяти розвитку
здібностей і обдарувань, збагачуючи цим самим інтелектуальний потенціал людини,
її духовність та культуру [30].
Оновлення змісту освіти у напрямку задоволення сучасних потреб
особистості та суспільства вимагає подальшого вдосконалення процесу навчання.
Концепція базової математичної освіти в Україні визначає пріоритетність методів
активного навчання і новітніх інформаційних технологій навчання [42].
Перетворення знань у переконання досягається лише тоді, коли учні
всебічно усвідомлюють навчальний матеріал, коли засвоєні знання є результатом
не тільки їхніх розумових зусиль, але й позитивних емоційних переживань. Все це
можливе лише за умов високого рівня професійної культури вчителя.
Професійна культура вчителя математики як сукупність його практичних,
матеріальних і духовних надбань, що визначають якість його професійної
діяльності, тісно пов’язана з його математичною культурою, загальною
педагогічною і психологічною, методичною і інформаційною, мовною і моральною
культурою. Вона передбачає допитливість і працьовитість, творчий підхід до
справи, вміння постійно вчитися, підвищувати свою кваліфікацію, орієнтуватися у
величезному потоці інформації, яка стосується, зокрема і сфери його професійної
діяльності [56, с. 10-18].
Фундамент професійної культури вчителя математики закладається під час
його навчання у педагогічному вищому навчальному закладі, зокрема, і в процесі
навчання фахових дисциплін, до яких відноситься і курс диференціальних рівнянь. Від міцності цього фундаменту залежить, як швидко і
наскільки надійно молодий педагог зможе створити себе як вчителя, щоб бути
бажаною персоною не тільки у школі загального профілю, але й у навчальних
закладах нового типу (гімназіях, ліцеях, коледжах тощо). Тому проблема
удосконалення професійної підготовки вчителя математики в сучасних умовах
набуває особливої актуальності.
Питанню професійної підготовки вчителя (зокрема і вчителя математики)
присвячена величезна кількість праць. Незважаючи на це, важко стверджувати, що
ця проблема повністю розв’язана чи, принаймні, близька до розв’язання. Такого
роду проблеми є вічними, оскільки життя ставить все нові задачі, в тому числі і
в галузі освіти. Зміни, які відбуваються у сучасній школі, висувають значно
вищі вимоги до професійної культури вчителя, а існуюча система навчання і
виховання людини не зможе задовольнити ці вимоги, якщо не будуть неперервно
удосконалюватися зміст освіти, розроблятися нові методичні системи навчання,
створюватися нові програми, підручники, навчальні посібники, дидактичні
матеріали, і все це на базі сучасних інформаційно-комунікаційних технологій, з
урахуванням досягнень людства у науці, техніці, організації суспільного життя.
Проблема формування професійної культури вчителя математики завжди була в
центрі уваги провідних вчених: педагогів, психологів, математиків. Значний
науково-теоретичний і практичний досвід розв’язання цієї проблеми знайшов своє
відображення у численних публікаціях, серед яких слід виділити роботи Ж.
Адамара [2], Г.О. Атанова [6] - [8], Ю.К. Бабанського [9], Г.П. Бевза [11] - [14], М.І. Бурди [21] - [22], М.І. Жалдака [32] -
[38], Г.С. Костюка [43] - [44], З.І. Слєпкань [64] -
[67], М.І. Шкіля [82] - [83] та багатьох інших.
Роботи З.І. Слєпкань [64] -
[67] присвячено психолого-педагогічним
основам навчання математики та загальним питанням методики навчання математики.
Проблемі формування математичної культури присвячено численні підручники,
посібники, задачники, адресовані як майбутнім, так і працюючим учтелям
математики. Серед них особливе місце посідають книги авторів, які є
професійними математиками, що активно досліджують суто математичні проблеми,
зокрема, серед цих підручників та посібників є книги П.С. Александрова, Б.В.
Гнєденка, М.О. Давидова, В.К Дзядика, А.М. Колмогорова, Л.Д. Кудрявцева, М.М.
Лузіна, І.П. Натансона, Д.А. Райкова, Г.М. Фіхтенгольца, М.І. Шкіля та багатьох
інших.
Тому ми й звернули увагу на те, що майбутні вчителі,
викладачі природничо-математичних спеціальностей повинні бути підготовлені до
професійної діяльності в конкретному середовищі, в якому кожна ситуація вимагає
творчого підходу.
В навчальній, методичній, науково-популярній літературі
недостатньо розроблена методика навчання диференціальних рівнянь майбутніх
вчителів математики в педагогічних університетах. Це і обумовило вибір теми
магістерської роботи: «Методика навчання диференціальних рівнянь майбутніх
вчителів математики в педагогічних університетах».
В даній роботі розглянуті методичні рекомендації щодо
вивчення одного (першого) змістовного модуля курсу «Диференціальні рівняння».
Цей матеріал містить розробки планів-конспектів лекцій, практичних та
індивідуальних занять, модульних контрольних робіт. Також наявні завдання для
самостійної та індивідуальної роботи, розроблені модульні контрольні роботи.
Мета дослідження:
Розробити методику навчання диференціальних рівнянь майбутніх
вчителів математики в педагогічних університетах.
Завдання дослідження:
1. Проаналізувати навчальну, методичну,
науково-популярну літературу з педагогічного дослідження.
2. Проаналізувати навчальну програму з метою вивчення
диференціальних рівнянь у ВУЗах.
. Теоретично обґрунтувати цілі, зміст, форми, методи і
засоби методики навчання диференціальних рівнянь.
. Розробити та експериментально обґрунтувати методику
навчання диференціальних рівнянь майбутніх вчителів математики в педагогічних
університетах.
Об’єкт дослідження:
Процес вивчення диференціальних рівнянь у педагогічних вищих
навчальних закладах (ВУЗах).
Предмет дослідження:
Цілі, зміст, форми, методи, засоби, контроль та корекція
навчання диференціальних рівнянь.
РОЗДІЛ
І. ТЕОРЕТИЧНІ ОСНОВИ МЕТОДИКИ НАВЧАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ В ПЕДАГОГІЧНИХ
УНІВЕРСИТЕТАХ
1.1 Диференціальні рівняння як складова вивчення
математики в педагогічних вищих навчальних закладах
Теорія диференціальних рівнянь є одним з найбільших розділів
сучасної математики. Щоб охарактеризувати її місце в сучасній математичній
науці, перш за все, необхідно підкреслити основні особливості теорії
диференціальних рівнянь, математики, що складається з двох областей: теорії
звичайних диференціальних рівнянь і теорії рівнянь з частковими похідними.
Перша особливість - це безпосередній зв'язок теорії диференціальних
рівнянь з їх
широким спектром застосування. Характеризуючи математику як метод проникнення в таємниці природи,
можна сказати, що основним шляхом застосування цього методу є формування і
вивчення математичних моделей реального світу. Вивчаючи будь-які фізичні явища, дослідник, перш за все,
створює його математичну ідеалізацію або, іншими словами, математичну модель,
тобто, нехтуючи другорядними характеристиками явища, він записує основні закони в математичній формі. Дуже часто ці закони можна виразити у
вигляді диференціальних рівнянь. Такими виявляються моделі різних явищ механіки
суцільного середовища, хімічних реакцій, електричних і магнітних явищ і ін.
Досліджуючи отримані диференціальні рівняння разом з
додатковими умовами, які, як правило, задаються у вигляді початкових і
граничних умов, математик отримує відомості про явище, що відбувається, іноді
може дізнатися його минуле і майбутнє. Вивчення математичної моделі
математичними методами дозволяє не тільки отримати якісні характеристики
фізичних явищ і розрахувати із заданим ступенем точності хід реального процесу,
але і дає можливість проникнути в суть фізичних явищ, а іноді передбачити і
нові фізичні ефекти. Буває, що сама природа фізичного явища
підказує і підходи, і методи математичного дослідження. Критерієм правильності
вибору математичної моделі є практика, зіставлення даних математичного
дослідження з експериментальними даними.
Для складання математичної моделі у вигляді диференціальних рівнянь
потрібно, як правило, знати тільки локальні зв'язки і не потрібна інформація
про все фізичне явище в цілому. Математична модель дає можливість вивчати явище
в цілому, передбачити його розвиток, робити кількісні оцінки змін, що
відбуваються з часом. Нагадаємо, що на основі аналізу диференціальних рівнянь так були відкриті електромагнітні хвилі,
і лише після експериментального підтвердження Герцем фактичного існування
електромагнітних коливань стало можливим розглядати рівняння Максвела як
математичну модель реального фізичного явища.
Як відомо, теорія звичайних диференціальних рівнянь почала
розвиватися в XVII столітті одночасно з
виникненням диференціального і інтегрального числення. Можна сказати, що необхідність
вирішувати диференціальні рівняння для потреб механіки, тобто знаходити
траєкторії рухів, в свою чергу,
з'явилася поштовхом для створення Ньютоном нового числення. Органічний зв'язок
фізичного і математичного ясно виявилася в методі флюксій Ньютона. Закони
Ньютона є математичною моделлю механічного руху. Так вдалося вирішити завдання, які протягом довгого часу
не піддавалися рішенню. У небесній механіці виявилося можливим не тільки
отримати і пояснити вже відомі факти, але і зробити нові відкриття (наприклад,
відкриття Льоверье в 1846 році планети Нептун на основі аналізу диференціальних рівнянь).
Звичайні диференціальні рівняння виникають тоді, коли
невідома функція залежить лише від однієї незалежної змінної. Співвідношення
між незалежною змінною, невідомою функцією і її похідними до деякого порядку
складає диференціальне рівняння. В даний час теорія звичайних диференціальних рівнянь є
багатою, широко розгалуженою теорією.
Рівняння з частковими похідними почали вивчатися значно
пізніше. Потрібно підкреслити, що теорія рівнянь з частковими похідними виникла на основі
конкретних фізичних завдань, що приводять до дослідження окремих рівнянь з частковими похідними, які отримали назву
основних рівнянь математичної фізики. Вивчення математичних моделей конкретних
фізичних завдань привело до створення в середині XVIII століття нової гілки
аналізу - рівнянь математичної фізики, яку можна розглядати як науку про
математичні моделі фізичних явищ.
Основи цієї науки були закладені працями Д'аламбера, Ейлера, Бернуллі, Лагранжа і інших учених. Цікаве те, що
багато хто з них був не тільки математиками, але і астрономами, механіками,
фізиками. Розроблені ними при дослідженні конкретних завдань математичної фізики
ідеї і методи виявилися застосовними до вивчення широких класів диференціальних
рівнянь, що і послужило в кінці XIX століття основою для розвитку загальної
теорії диференціальних рівнянь.
Найважливішими рівняннями математичної фізики є: рівняння Лапласа, рівняння
теплопровідності,
хвилеві рівняння.
Важливо відзначити, що для перевірки правильності
математичної моделі дуже важливі теореми існування вирішень відповідних
диференціальних рівнянь, оскільки математична модель не завжди адекватна
конкретному явищу і з існування рішення реальної задачі (фізичною, хімічною,
біологічною) не виходить існування рішення відповідної математичної задачі.
В даний час важливу роль в розвитку теорії диференціальних рівнянь грає
застосування сучасних електронних обчислювальних машин. Дослідження
диференціальних рівнянь часто полегшує можливість провести обчислювальний
експеримент для виявлення тих або інших властивостей їх рішень, які потім
можуть бути теоретично обгрунтовані і стануть фундаментом для подальших теоретичних досліджень.
Отже, перша особливість теорії диференціальних рівнянь - її
тісний зв'язок із їхніми застосуваннями. Іншими словами, можна сказати, що теорія диференціальних
рівнянь народилася із застосувань. У
цьому своєму розділі - теорії диференціальних рівнянь - математика перш за все
виступає як невід'ємна частина природознавства, на якій грунтується вивід і
розуміння кількісних і якісних закономірностей, складового змісту наук
про природу.
Саме природознавство є для теорії диференціальних рівнянь
чудовим джерелом нових проблем, воно значною мірою визначає напрям їх
досліджень, дає правильну орієнтацію цим дослідженням.
Вивчення рівнянь з частковими похідними в загальному випадку
- таке складне завдання, що якщо хто-небудь навмання напише яке-небудь, навіть
лінійне диференціальне рівняння з частковими похідними, то з великою
вірогідністю жоден математик не зможе про нього сказати що-небудь і, зокрема,
з'ясувати, чи має це рівняння хоч би одне рішення.
Ф. Клейн в книзі "Лекції про розвиток математики в XIX сторіччі" писав, що
"математика супроводжувала по п'ятах фізичне мислення і, назад, отримала
найбільш могутні імпульси з боку проблем, що висувалися фізикою".
Другою особливістю теорії диференціальних рівнянь є її
зв'язок з іншими розділами математики, такими, як функціональний аналіз,
алгебра і теорія ймовірності. Теорія диференціальних рівнянь і, особливо теорія
рівнянь з частковими похідними, широко використовують основні поняття, ідеї і
методи цих областей математики і, більш того, впливають на їх проблематику і
характер досліджень. Деякі великі і важливі розділи математики були викликані
до життя завданнями теорії диференціальних рівнянь. Класичним прикладом такої взаємодії з
іншими областями математики є дослідження коливань струни, що проводилися в середині
XVIII століття.
При вивченні конкретних диференціальних рівнянь, що виникають в процесі
вирішення фізичних завдань, часто створювалися методи, що володіють великою
спільністю і застосовувалися без строгого математичного обгрунтування до
широкого круга математичних проблем. Такими методами є, наприклад, метод Фурье,
метод Рітца, метод Галеркіну та інші.
У перший період розвитку теорії звичайних диференціальних
рівнянь одним з основних завдань було знаходження загального розв’язку в
квадратурі, тобто через інтеграли від відомих функцій (цим займалися Ейлер,
Ріккаті, Лагранж, Д'аламбер і ін.). Завдання інтеграції диференціальних рівнянь
з постійними коефіцієнтами зробили великий вплив на розвиток лінійної алгебри.
Таким чином, диференціальні рівняння знаходяться якби на перехресті
математичних доріг. З одного боку, нові важливі досягнення в топології,
алгебрі, функціональному аналізі, теорії функцій і інших областях математики
відразу ж приводять до прогресу в теорії диференціальних рівнянь і тим самим знаходять
шлях до застосувань. З іншого боку, проблеми фізики,
сформульовані на мові диференціальних рівнянь, викликають до життя нові напрями
в математиці, приводять до необхідності вдосконалення математичного апарату,
дають початок новим математичним теоріям, що мають внутрішні закони розвитку,
свої власні проблеми.
1.2 Психолого-педагогічні основи навчання вивчення
диференціальних рівнянь
Навчання фахових математичних дисциплін, і в частності диференціальних рівнянь, відіграє вирішальну роль у
формуванні математичної культури вчителя математики. Менш очевидна їх роль у формуванні інших компонентів
професійної культури вчителя математики, проте провідні вчені - і педагоги, і
математики - давно зрозуміли, що успішне вирішення задачі формування основ
професійної культури вчителя математики можливе лише за умови професійно
спрямованого навчання цих дисциплін. Так, видатний німецький математик Фелікс
Клейн у своїй праці “Елементарна математика з точки зору вищої”, обґрунтовуючи
необхідність професійно спрямованого навчання майбутнього вчителя математики,
писав: “Вступаючи до вищої школи, молодий студент стикається з такими
завданнями, які зовсім не нагадують йому те, чим він займався раніше; природно,
що все це він швидко і ґрунтовно забуває. Коли ж він закінчує університет і
стає викладачем, він повинен як учитель викладати традиційну математику і часто
не в змозі самостійно пов’язати це завдання з тим, що він чув у вищій школі,
тому він швидко засвоює стару традицію, а університетська освіта залишається у
нього тільки у вигляді приємного спогаду, який не має впливу на викладання ним
математики” [41, с. 15].
Схожа ситуація мала (і, на жаль, ще часто має) місце і у сучасних педагогічних вузах. Пом’якшенню цієї
ситуації сприяють численні праці, присвячені дослідженню проблеми професійної
спрямованості або так званій “педагогізації” навчання фахових математичних
дисциплін майбутніх вчителів математики.
Мабуть, уперше в Україні термін “педагогізація” було введено
у 1955 році І.Є. Шиманським, який у своїй роботі [81, с. 123] писав, що
педагогізація курсу диференціальних рівнянь полягає в тому, щоб пов’язати його
вивчення з профілем майбутнього фахівця, і це повинно здійснюватися так: 1) усі
питання програми, які мають безпосереднє відношення до шкільного курсу математики,
повинні розглядатися так, щоб студент - майбутній учитель - міг використати цей
матеріал (хоча б неповністю) у своїй педагогічній роботі; 2) потрібно
ознайомлювати студентів з тими застосуваннями теоретичних питань курсу
диференцільних рівнянь, які відносяться до політехнізації середньої школи; 3) нарешті, потрібно вказувати
студентам на той матеріал, який доцільно розглядати на заняттях шкільного
математичного гуртка.
Таким чином, у перших роботах, присвячених навчанню фахових
математичних дисциплін майбутніх вчителів математики, під професійною
спрямованістю цього навчання розуміли, в основному, формування математичної
культури саме вчителів математики, тобто ґрунтовне засвоєння ними основ
шкільного курсу математики у процесі навчання фахових математичних дисциплін.
З часом з’являється розуміння того, що навчання фахових
математичних дисципліни, і в частості диференціальних рівнянь, дуже важливе для
формування інших компонентів професійної культури вчителя математики. Так, у
роботі Г.І. Саранцева [62] міститься ідея про можливість формування методичної
культури вчителя математики за рахунок педагогізації, яка повинна здійснюватися
і в напрямку вдосконалення методики читання лекцій і проведення практичних
занять із спеціальних математичних дисциплін.
Цілісну концепцію професійної спрямованості навчання вчителя математики
розробив А.Г. Мордкович [52]. В
основі цієї концепції лежать принципи, які покладені в основу побудови
методичної системи навчання диференціальних рівнянь майбутніх учителів математики:
) принцип диференційованої фундаментальності (фундаментальна математична
підготовка повинна бути не тільки метою, а й засобом підготовки вчителя
математики);
) принцип “узагальнення для полегшення”, згідно з яким перехід до
загальніших об’єктів часто робить теорію значно прозорішою і легшою для
сприймання, ніж розгляд цієї теорії на менш загальних об’єктах;
) принцип мінімізації часу на вивчення курсу за умови досить повільного
зростання рівня абстракції матеріалу, починаючи з рівня абстракції шкільного
курсу математики;
) принцип інтегрованості (вивчення багатьох фактів одночасно для так
званих дійсних і комплексних випадків; звертати увагу на поєднання
математичної, методичної, педагогічної, психологічної, інформаційної, мовної і
моральної ліній);
) принцип провідної ідеї (тісний взаємозв’язок між курсом диференціальних рівнянь та шкільним курсом математики і
вплив одного курсу на інший);
) принцип “навчаючи, навчай навчати”;
) принцип неперервності (професійна
культура вчителя математики формується протягом його життя).
Надалі розумітимемо під професійною спрямованістю навчання
вчителя таке навчання, яке забезпечує формування максимально можливої кількості
компонентів професійної культури вчителя.
Незважаючи на значну кількість праць, в яких досліджується
проблема формування професійної культури вчителя математики у процесі навчання
фахових математичних дисциплін, ця проблема потребує подальшої розробки,
оскільки високотехнологічна цивілізація, яка вступила в
інформаційно-комп’ютерне XXI століття, вимагає усунення
невідповідності між її потребами та змістом, методами, формами і засобами
навчання та виховання.
Так, потребують подальшого дослідження проблема визначення
поняття “професійна культура вчителя математики” і пов’язані з нею проблеми
створення нормативної і предметної моделей (коли предметом є диференціальні
рівняння) майбутнього вчителя математики, які передбачають, зокрема, визначення
та конкретизацію конструктивних цілей курсу диференціальних рівнянь, визначення
змісту, методів, засобів і організаційних форм навчання курсу, які забезпечили
б формування основ професійної культури вчителя математики.
Педагогічна культура вчителя математики. Педагогічну культуру вчителя
математики визначають такі його знання та уміння:
► знання: 1) поняття сутності процесу навчання, функцій
цього процесу, його суперечностей, етапів опанування знаннями, мотивів учіння;
2) основних дидактичних принципів навчання і розвиваючого навчання
математики; 3) системного, комплексного та діяльнісного підходів
до організації навчального процесу; 4) мети і завдань навчання
математики у різних типах навчальних закладів; 5) основних форм
організації процесу навчання; 6) основних методів і засобів
навчання математики, зокрема, методів активного навчання; 7)
загальних педагогічних вимог до навчального матеріалу і засобів навчання
математики; 8) загальних прийомів роботи з математичними
текстами; 9) основних шляхів і форм індивідуального та
диференційованого навчання математики; 10) основних видів
контролю та самоконтролю навчально-пізнавальної діяльності та форм їх
проведення; 11) основних педагогічних видань, пов’язаних з
професійною діяльністю вчителя.
► уміння: 1) реалізовувати функції процесу навчання на кожному
етапі опанування знанням, враховуючи протиріччя процесу навчання та мотиви
учіння; 2) враховувати основні дидактичні принципи навчання; 3)
застосовувати системний, комплексний і діяльнісний підходи до організації
навчального процесу; 4) ставити мету і розв’язувати завдання навчання
математики, враховуючи тип навчального закладу; 5) застосовувати різні
форми організації та проведення класної і позакласної навчально-виховної
діяльності; 6) застосовувати різні методи і засоби навчання, віддаючи
перевагу активним методам навчання; 7) добирати навчальний матеріал і
засоби навчання для проведення відповідних занять, враховуючи поставлену мету;
8) володіти загальними прийомами роботи з математичними текстами і
застосовувати їх у навчальному процесі; 9) обирати шляхи і форми
індивідуального та диференційованого навчання; 10) організовувати і проводити
контроль та самоконтроль навчально-пізнавальної діяльності; 11)
систематично працювати над педагогічною літературою, використовувати знайдені
там нові ідеї у навчальному процесі.
Психологічна культура вчителя математики. Зміст психологічної культури
вчителя математики визначається такими його знаннями та уміннями:
► знання: 1) психологічних механізмів навчально-пізнавальної
діяльності людини; 2) психологічних трактувань загальних розумових дій
та прийомів розумової діяльності; 3) психологічних принципів
розвиваючого навчання; 4) основних психологічних принципів взаємодії між
учителем і учнем; 5) психолого-педагогічних умов мотивації та
активізації пізнавальної діяльності людини; 6) основних залежностей між
інформаційними і психологічними явищами; 7) рекомендацій психологічних
теорій щодо продукування ідей, розвитку уявлень і мислення людини, її
пізнавальної активності; 8) психологічних аспектів теорії проблемного
навчання та інших теорій активного навчання; 9) психологічних, вікових
та індивідуальних особливостей учнів; 10) основних психологічних видань,
пов’язаних з професійною діяльністю вчителя.
► уміння: 1) застосовувати у навчальному процесі
психологічні закономірності навчально-пізнавальної діяльності людини; 2)
використовувати у навчальному процесі психологічну сутність загальних
розумових дій та прийомів розумової діяльності; 3) враховувати
основні психологічні принципи розвиваючого навчання; 4) будувати
навчальний процес на основі психологічних принципів організації взаємодії
між учителем і учнем; 5) створювати психолого-педагогічні
умови активізації пізнавальної діяльності учнів; розкривати учням відповідні
психологічні механізми, що сприяють досягненню високих результатів навчання;
6) враховувати залежності між інформаційними і психологічними явищами;
7) застосовувати рекомендації психологічних теорій щодо
продукування ідей, розвитку уявлень і мислення; 8)
враховувати психологічні аспекти теорії проблемного навчання та інших теорій
активного навчання; 9) враховувати психологічні, вікові та
індивідуальні особливості учнів; 10) систематично
працювати над психологічною літературою і використовувати знайдені там нові
ідеї у навчальному процесі.
Математична культура вчителя математики. Математичну культуру вчителя
математики визначають такі його знання та уміння:
► знання: 1) основних фактів з фахових
математичних дисциплін; 2) загальних методів розв’язування
математичних задач, включаючи і методи доведення тверджень; 3)
сутності математичного моделювання і методів побудови математичних моделей; 4)
прикладів важливих застосувань математики у різних галузях науки, техніки і
життя; 5) найяскравіших фактів з історії математики; 6) шкільного
курсу математики та його особливостей у різних типах середніх навчальних
закладів; 7) логічних прогалин шкільного курсу математики, причин їх
виникнення та можливі засоби їх усунення; 8) основних математичних
видань (підручники, посібники, монографії, журнали тощо), пов’язаних з
професійною діяльністю вчителя математики.
► уміння: 1) використовувати знання з фахових математичних
дисциплін у своїй роботі в школі; 2) розв’язувати математичні задачі,
зокрема, і доводити твердження різного рівня складності, демонструючи зразок
логічного мислення, обґрунтованості кожного кроку міркувань, гнучкість думки,
творчий підхід, широкий математичний кругозір, математичну інтуїцію, яскравість
уявлень; 3) розвивати прикладну спрямованість математики, будувати
математичні моделі процесів і явищ, пов’язаних з матеріалом шкільного курсу
математики та доступних учням середніх шкіл; 4) використовувати
практично значущі задачі для підвищення рівня мотивації вивчення
математики; 5) використовувати факти з історії математики для підвищення
інтересу учнів до математики та активізації процесу навчання математики; 6)
використовувати різні підходи та різні методи введення найважливіших понять і
різні методи доведень тверджень; 7) при необхідності пояснювати учням
сутність логічних прогалин шкільного курсу математики та розкривати можливі
шляхи їх усунення; 8) систематично працювати над математичною літературою
і навчати цього своїх учнів, виховуючи критичність мислення, вміння виявляти
помилки і неповноту міркувань, будувати контрприклади, узагальнювати; розвивати
нахили учнів до творчої діяльності.
Методична культура вчителя математики. Названі нижче знання та уміння
вчителя математики визначають зміст його методичної культури:
► знання: 1) програм шкільного курсу математики, змісту та
структури шкільних підручників і посібників для різних типів середніх
навчальних закладів; 2) форм календарних і тематичних планів та
планів-конспектів уроків математики і методів їх складання з чітко виділеними
метою та завданнями навчання відповідної теми та окремого уроку; 3) типів
уроків з математики, їх структури і методики проведення; 4) видів
математичних понять (тверджень), їх систематизації та класифікації, основних
методів і прийомів навчання для введення математичних понять і “відкриття” та
доведення математичних тверджень; 5) поняття математичної задачі, видів
математичних задач, методів навчання учнів умінню розв’язувати математичні
задачі, зокрема, задачі на доведення; 6) внутрішньопредметних і
міжпредметних зв’язків математики та методики використання цих зв’язків для
активізації процесу навчання математики; 7) методики застосування
сучасних засобів навчання математики; 8) специфіки навчання математики у
школах і класах різної спрямованості: гуманітарної, математичної, економічної,
технічної тощо; 9) основних методичних видань, пов’язаних з професійною
діяльністю вчителя математики.
► уміння: 1) аналізувати програми, підручники й посібники з
точки зору їх науковості та доступності, добирати найкращі підручники і
посібники та ефективно їх використовувати для формування у своїх учнів
необхідних знань, навичок і вмінь з основних тем шкільного курсу математики; 2)
складати календарні і тематичні плани та плани-конспекти уроків і адекватно їх
реалізовувати у процесі навчання математики своїх учнів; 3) обирати тип
уроку, який дозволяв би ефективно досягати поставлених цілей і завдань,
проводити уроки різних типів, пояснювати відповідний матеріал науково, але
доступно й цікаво для учнів, заохочуючи їх до активної співпраці; 4)
добирати ефективні методи і прийоми навчання для введення математичних понять і
“відкриття” й доведення математичних тверджень та застосовувати їх в процесі
навчання; 5) ефективно формувати в учнів уміння розв’язувати математичні
задачі, зокрема і задачі на доведення; 6) використовувати
внутрішньопредметні і міжпредметні зв’язки математики для активізації процесу
пізнання, реалізовувати прикладну спрямованість навчання; 7) добирати
методи застосування сучасних засобів навчання згідно з метою, завданням і типом
уроку та ефективно їх використовувати у процесі навчання математики; 8)
враховувати специфіку навчання математики у школах і класах різної спрямованості;
9) систематично працювати над науково-методичною літературою,
використовувати знайдені там нові ідеї у навчальному процесі.
Майбутній учитель математики у процесі свого навчання повинен
постійно діставати підтвердження того, що любов і довіра вчителя до учня не
виключає регулярного контролю за його роботою, розумної вимогливості і
строгості в оцінці результатів цієї роботи. При цьому справедлива і об’єктивна оцінка знань
учня разом з доброзичливим відношенням до нього вчителя є надзвичайно
важливим для ефективності навчання і виховання.
Широкі можливості для формування у майбутніх учителів математики високих
моральних якостей (чесності, порядності, поваги до оточуючих людей, тактовності
і об’єктивності, наполегливості, відповідальності і сумлінного ставлення до
своїх обов’язків, скромності і самокритичності, бадьорості духу) викладач має
на практичних заняттях, на яких студенти можуть явно побачити прояв цих
якостей, правильно оцінити допомогу товаришів, роль довіри викладача,
дискомфорт від дій, несумісних з високими моральними якостями, відчути, як
важко повернути загублену довіру до себе і яким святом може бути повернення
цієї довіри після того, як визнав свою помилку і справою довів свою чесність і
безкорисливість, порядність і принципове ставлення до людей.
Для майбутніх учителів математики повинні бути взірцем уміння викладача
створити на практичних заняттях атмосферу доброзичливості і взаємної довіри,
коли студенти знаходяться у стані духовної розкутості, не соромлячись ні
викладача, ні товаришів, запитують, коли їм щось незрозуміло, діляться своїми
припущеннями, гіпотезами, сумнівами. Саме така атмосфера гарантує успішність
процесу навчання. Досягти мистецтва створювати таку атмосферу важко, проте
можливо завдяки вдумливому і самокритичному відношенню викладача до своїх
обов’язків, зацікавленості в успіхах своїх студентів, завдяки досвіду власного
і своїх колег, завдяки поступовому опануванню методами роботи з колективом
індивідуумів, що мають різні здібності і різні підготовленості до навчання,
різні характери і темпераменти. До цього викладачеві слід докласти чимало
зусиль, не обмежуючись колективними заняттями і заходами, а звертаючи також
велику увагу на індивідуальні контакти із студентами під час консультацій та
особистих бесід, коли викладач може надати студентові відповідну допомогу, дати
корисну пораду, позитивно морально вплинути на нього. Саме у процесі
спілкування з викладачами майбутній учитель математики звикає до коректного
звертання (на “ви”), до розумної психологічної дистанції, яка виключає
панібратські стосунки, але в залежності від обставин може змінюватися,
сигналізуючи про певні незадоволення або задоволення сторін спілкування; тут
він вчиться розрізняти різні стилі спілкування (авторитарний, демократичний і
ліберальний), формує переконання, що стиль спілкування може змінюватися залежно
від ситуації, проте повинен залишатися природним і невимушеним, що можливо лише
за умов взаємоповаги і взаємодопомоги сторін, які спілкуються.
Отже, у процесі навчання майбутнього вчителя слід прагнути до формування
у нього переконання у тому, що успіх процесів навчання і виховання залежить
перш за все від того, хто навчає і виховує. Лише власним прикладом можна
виховати доброту, великодушність, гуманізм та інші високі моральні
якості. Лише той має право навчати і виховувати, і буде це успішно робити, хто
відчуває відповідальність за свою роботу, захоплений нею, хвилюється за
її результати, переконаний у правильності своїх дій і принципів, якими він
керується; той, хто тактичний до інших, вміє уважно вислуховувати думку інших,
враховувати її, коли вона слушна, і ненав’язливо відстоювати власну думку, коли
опонент помиляється; той, хто дістає задоволення від спілкування з учнями, щиро
радіючи їхнім успіхам.
1.3 Теоретичні основи вивчення диференціальних
рівнянь
Навчальна програма вивчення курсу «Диференціальні рівняння»
для студентів фізико-математичного факультету вищих навчальних педагогічних
закладів
I. Загальні відомості
Дисципліна «Диференціальні рівняння» є однією з основних
дисциплін циклу природничо-наукової (фундаментальної) підготовки студентів.
II. Перелік дисциплін, знання яких необхідне для вивчення курсу
Для оволодіння курсом студент повинен опонувати розділами диференціального і
інтегрального числення з курсу математичного аналізу, алгеброю та геометрією.
III. Цілі і завдання дисципліни
Основні цілі вивчення дисципліни:
- оволодіння студентами основними поняттями, методами теорії звичайних
диференціальних рівнянь, варіаційного числення та технікою розв’язання
прикладних задач;
систематично викласти основи теорії диференціальних рівнянь та
варіаційного числення під кутом їхнього практичного застосування;
виробити у студентів логічне й алгоритмічне мислення, необхідне для
розв’язання теоретичних та практичних задач за фахом;
прищепити
навички дослідження динамічних математичних моделей практичних задач, їх
розв’язання та вміння аналізувати отримані результати.
Головна задача вивчення навчальної дисципліни:
опанувати сучасними математичними методами диференціальних рівнянь і
варіаційного числення, які дозволяють розв’язувати теоретичні та практичні
задачі;
навчити формалізувати прикладну задачу і приводити її до типових сучасних
задач теорії диференціальних рівнянь і варіаційного числення.
Після вивчення курсу:
Ø студент повинен знати формулювання основних означень,
понять, теорем, та їх доведення в межах програми, основні методи розв’язування диференціальних рівнянь;
Ø студент повинен вміти застосовувати теоретичний
матеріал до розв'язання задач і прикладів, які пропонуються як у даному курсі,
так і в процесі подальшого навчання.
Набуті знання використовуються в чисельних методах, чисельних
методах системного аналізу, методах оптимізації, теорії керування, основах
системного аналізу.
Знання з даного курсу будуть використовуватися при вивченні рівнянь із
частинними похідними, варіаційного числення, спеціальних курсів, написання
курсових, кваліфікаційних та дипломних робіт.
IV. Методи навчання та інформаційно-методичне забезпечення
Основними методами навчання є лекції та практичні заняття, на яких
закріплюються та відпрацьовуються основні теоретичні положення та вміння їх
застосовувати до розв’язання практичних та прикладних задач.
V. Форми
оцінювання
Іспит,
залік, колоквіум, контрольні роботи
VI. Зміст
дисципліни
|
№ п/п
|
Зміст програмного
матеріалу
|
Літе-ратура
|
Кількість годин
|
Кален-дарні
строки
|
|
|
|
Лекції
|
Прак-тичні
заня-ття
|
Самос-тійна робота
|
|
|
ЗМІСТОВНИЙ МОДУЛЬ І
|
|
1.
|
Основні означення.
Задачі, які приводять до звичайних диференціальних рівнянь. Геометричний
зміст диференціального рівняння першого порядку. Диференціальні рівняння
першого порядку з відокремлюючими змінними.
|
[3, 2, 9, 12]
|
4
|
2
|
2
|
|
|
2.
|
Однорідні рівняння
першого порядку. Рівняння, які зводяться до однорідних.
|
[3, 4, 5, 12]
|
2
|
2
|
2
|
|
|
3.
|
Лінійні
диференціальні рівняння першого порядку. Метод варіації довільної змінної.
Рівняння Бернуллі. Метод Бернуллі.
|
[3, 4, 5, 12]
|
2
|
2
|
2
|
|
|
4.
|
Диференціальне
рівняння у повних диференціалах. Інтегруючий множник.
|
[3, 4, 9, 11]
|
2
|
2
|
2
|
|
|
ЗМІСТОВНИЙ МОДУЛЬ ІІ
|
|
5.
|
Диференціальні
рівняння, які не розв’язуються відносно похідної. Рівняння Лагранжа. Рівняння
Клеро.
|
[2, 3, 4, 5, 9,
11, 12]
|
2
|
2
|
2
|
|
|
6.
|
Диференціальні
рівняння вищих порядків. Методи пониження порядків.
|
[2, 3, 4, 5, 9,
11, 12]
|
2
|
2
|
2
|
|
|
ЗМІСТОВНИЙ МОДУЛЬ ІІІ
|
|
7.
|
Лінійні
диференціальні рівняння вищих порядків. Однорідні лінійні рівняння. Основні
властивості однорідних лінійних рівнянь.
|
[2, 3, 4, 5, 9, 11, 12]
|
2
|
2
|
2
|
|
|
8.
|
Лінійно залежні
функції. Вронскіан. Властивості Вронскіана.
|
[2, 3, 4, 5, 9,
11, 12]
|
2
|
2
|
2
|
|
9. Лінійні однорідні рівняння 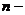 ого порядку. Характеристичне рівняння. Корені
характеристичного рівняння: 1) дійсні різні; 2) дійсні кратні; 3) комплексні.
Загальні розв'язки рівнянь.
ого порядку. Характеристичне рівняння. Корені
характеристичного рівняння: 1) дійсні різні; 2) дійсні кратні; 3) комплексні.
Загальні розв'язки рівнянь.
[2, 3, 4, 5, 9, 11, 12]
10. Лінійні неоднорідні рівняння 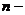 ого порядку з постійними коефіцієнтами. Метод варіації
довільних постійних.
ого порядку з постійними коефіцієнтами. Метод варіації
довільних постійних.
[2, 3, 4, 5, 9, 11, 12]
11. Лінійні неоднорідні рівняння 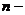 ого порядку із постійними коефіцієнтами. Метод
невизначених коефіцієнтів.
ого порядку із постійними коефіцієнтами. Метод
невизначених коефіцієнтів.
[2, 3, 4, 5, 9, 11, 12]
|
ЗМІСТОВНИЙ
МОДУЛЬ ІV
|
|
12.
|
Системи звичайних
лінійних рівнянь. Зведення лінійних рівнянь до лінійних рівнянь вищого
порядку.
|
[2, 3, 4, 5, 9, 11, 12]
|
2
|
2
|
2
|
|
|
13.
|
Системи звичайних
лінійних однорідних рівнянь. Характеристичне рівняння. Корені
характеристичного рівняння: 1) дійсні різні; 2) дійсні кратні; 3) комплексні.
|
[2, 3, 4, 5, 9, 11, 12]
|
2
|
4
|
2
|
|
|
14.
|
Системи звичайних
лінійних неоднорідних рівнянь. Метод невизначених коефіцієнтів.
|
[2, 3, 4, 5, 9,
11, 12]
|
2
|
2
|
2
|
|
|
|
|
|
|
|
|
|
ВСЬОГО
|
|
30
|
32
|
28
|
|
. Література до курсу:
1. Арнольд В.И. Обыкновенные дифференциальные уравнения.
2. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
. Ляшко И.И. и др. Дифференциальные уравнения.
. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных
уравнений.
. Степанов В.В. Курс дифференциальных уравнений.
. Кисилев А.И., Краснов М.А., Макаренко Т.И. Сборник задач по
обыкновенным дифференциальным уравнениям.
. Пономарев К.К. Составление дифференциальных уравнений.
. Самойленко Ф.М., Кривошея С.А., Перестюк Н.А. Дифференциальные
уравнения, примеры и задачи.
. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного.
. Матвеев Н.М. Сборник задач и упражнений по обыкновенным
дифференциальным уравнениям.
. Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным
уравнениям.
12. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations
Дидактичні
і методичні вимоги до академічної лекції
Лекція є найкращим засобом для викладення інформації певній кількості людей
(особливо великим групам). Цей метод гнучкий і може включати поєднання кількох
методів - бесіду чи промову, наочні посібники, опитування чи обговорювання. Цей
спосіб викладання добре відповідає ситуаціям, коли треба дати певну інформацію
для підготовки підґрунтя для подальшої роботи.
Коли йдеться про лекцію у вищому навчальному закладі, то
мається на увазі академічна лекція, яка відповідає навчальному завданню
конкретної дисципліни і спрямована на реалізацію відповідної програми. Це ставить певні вимоги до змісту,
структури, технології і методики підготовки та читання лекції.
Структура академічної лекції: план - основні питання лекції;
вступна частина - зв´язок з минулою лекцією, введення в тему; виклад
основних положень з акцентованими висновками за кожним окремо; підбиття
підсумків - загальний висновок.
Академічна лекція будується на принципах системності,
інформативності, наочності, зрозумілості (доступності). Кожна лекція є логічно
завершеною ланкою єдиної замкненої системи - курсу лекцій. У її тексті мають
бути чітко пов´язані між собою структурно-логічні дидактичні блоки.
Проектується графічний текст, планується, де, коли, скільки і які схеми,
рисунки, графіки, формули подаються як підтвердження вербальної інформації.
Принцип наочності реалізується засобами візуалізації (ТЗН, роздатковий
матеріал, схеми, планшети тощо). Лекція має читатися зрозумілою для студентів
мовою, незнайомі слова і терміни роз´яснюються, не варто перенасичувати
лекцію "наукоподібними" термінами і модними іноземними словами. Текст
лекції має бути логічним, простим і зрозумілим.
Зміст навчального матеріалу означеної теми має великі можливості для
інтелектуального розвитку студентів. Включення в лекцію низки проблемних
ситуацій, виокремлення завдань сприятиме активізації мислення студентів, а
отже, і розвитку їхнього інтелекту. Широка
палітра для реалізації вимог виховної функції міститься у темі про розвиток і
формування особистості. Необхідно виділити низку загальнодидактичних вимог
до лекції у вищій школі:
зміст лекції має відповідати робочій навчальній програмі,
відображати найновіші досягнення науки, висвітлювати перспективи подальшого
розвитку наукових пошуків;
в лекції мають реалізовуватись вимоги загальнодидактичних
принципів навчання: науковості, систематичності і послідовності, свідомості,
активності й самостійності, наочності, зв´язку змісту навчального
матеріалу з професійною діяльністю, доступності, емоційності;
має бути забезпечена логічно доцільна структура лекції відповідно до
змісту навчального матеріалу;
- лекція
має сприяти активізації мисленнєвої діяльності студентів з метою їх інтелектуального
розвитку;
- в
лекції доцільно виокремлювати певні компоненти змісту для самостійного
опрацювання студентами з належним методичним забезпеченням.
Щодо методичних вимог до лекції, то вони наступні:
лекцію
треба викласти так, щоб студенти зрозуміли, зацікавилися її змістом, осмислено
законспектували і при цьому не перевтомилися. Важливою умовою цього є
ораторська і педагогічна майстерність лектора, його мовленнєва культура. Треба
вміло користуватися текстом лекції, не допускаючи неперервного монотонного
читання і не відриваючись далеко від теми, захопившись окремими подробицями і
деталями. Необхідно створювати оптимальні умови для конспектування. Це особливо
важливо на молодших курсах. Значущі моменти, дидактичні одиниці доцільно
виділяти інтонацією, зміною темпу, повторенням. Корисними під час лекції будуть
рекомендації викладача типу: "Цю тезу підкресліть особливо",
"Виділіть це поняття певним позначенням", "Це можна не
записувати, послухайте, а рука відпочине". Зберігаючи оптимальний темп
викладу, лектор має бути впевненим, що студенти встигають конспектувати,
розуміють і осмислюють почуте, не перенапружуючи свої зусилля до стресового
стану.
Який би не був досвідчений викладач, він повинен завчасно підготувати
повний текст лекції, постійно удосконалювати, поліпшувати її, доповнювати,
додавати новий матеріал, проектувати хід, подумки тренуватися. Підготовка і
читання лекцій, якщо підходити до цього серйозно і відповідально, - складна,
тяжка і затратна в часі робота. К.Д. Ушинський писав, що мистецтво класної
розповіді зустрічається у викладачеві не часто, - не тому, що це рідкісний
дарунок природи, а тому, що й обдарованій людині треба багато попрацювати, щоб
виробити у собі здатність якісної педагогічної розповіді.
Шкідливими і небезпечними є поради окремих, як правило слабких, лекторів
молодим типу: "Будь переконаним у тому, що ти в аудиторії найрозумніший,
що студенти все сприймуть, що б ти не говорив". Треба кожного разу
ретельно готуватися до лекції, продумувати її сценарій стосовно конкретної аудиторії,
бути вимогливим до себе, самокритичним.
Однією з важливих вимог лекції є її емоційність. Але не варто
перенасичувати лекцію емоціями. Раціональний і емоційний компоненти мають бути
збалансованими. Ніяка емоційність, вишукані прийоми педагогічної техніки не
замінять і не закриють змістової пустоти, наукової неспроможності,
непідготовленості викладача.
Необхідно враховувати особливості студентської аудиторії. Одну й ту саму
лекцію треба подавати по-різному залежно від профілю ВНЗ, факультету, курсу, форми
навчання. Особливо уважно треба підходити до читання лекцій першокурсникам,
враховувати їх недостатню адаптованість. Певна специфіка властива і викладу
лекцій студентам заочної форми навчання.
Лекція не повинна мати характеру дослівного, текстового, письмового
стилю. Жива, імпровізована усна мова набагато легше сприймається і засвоюється
студентами ніж письмова, книжна. Вона має бути літературно правильною,
виразною, ясною, простою, образною, доступною. Стиль - лаконічний,
конкретизований, предметний. Не треба "лити воду" і витрачати дорогоцінний час на елементарні речі. Доцільно
дотримуватися принципу: "Немає часу, щоб витрачати час даремно".
При читанні лекції не повинно бути другорядних елементів, дрібниць.
Найважливіший компонент лекції - її зміст. Але досить важливими є манера
викладу, інтонація, жести, міміка, то нальність, гучність голосу. Говорити слід
достатньо гучно, щоб чули, і достатньо тихо, щоб слухали; ясно, просто,
виразно, дохідливо, не монотонно, але й не "хвилеподібно".
Не рекомендується заучувати зміст лекції напам´ять, а також читати всуціль, не
відриваючись від тексту. Найкраще сприймається студентами імпровізаційний
виклад матеріалу з періодичним умілим користуванням планом-конспектом лекції.
Педагогічна парадигма співробітництва вимагає ставлення до студентів як
до партнерів, рівних співрозмовників. Треба уміти вести себе розкуто,
невимушено, але й не чванливо, не розв´язно. Лектор має бути доброзичливим,
атракційним, емпатичним.
Необхідно пам´ятати, що студенти не тільки слухають зміст лекції, а
й уважно спостерігають і оцінюють самого лектора. Треба бути належно і охайно
одягненим, дотримуватися природних, невимушених поз, поводити себе щиро,
доброзичливо, впевнено.
Основні вимоги до практичних та семінарських занять
Практичне заняття використовується при опануванні навиків, включаючи ментальні
навички, фізичні або соціальні навички.
Цей метод може використовувати такі самі засоби, як і лекція, та
застосовуватися для більшості видів діяльності з чіткими правилами та добре
відлагодженими процесами.
. Відповідність змісту практичних і семінарських занять до типової і робочої навчальних програм, відображення
у них розділів дисципліни.
. Підготовленість викладача до проведення семінарських і практичних
занять.
. Зміст: Мета та спрямованість практичного заняття, його місце в темі курсу;
професійна спрямованість семінарських і практичних занять, яка забезпечує
відображення особливостей відповідній спеціальності; використання наукових
методів пізнання суті явищ, що вивчаються, і положень науки; розкриття на
конкретних прикладах органічної єдності теорії і практики; наявність
понятійного апарату, висновків з кожного питання та зв’язку з матеріалом, що
вивчається.
. Структура: Раціональне використання дидактичних доцільних форм і
методів навчання, спрямованих на найбільш ефективне здійснення навчальної мети
семінарських і практичних занять і забезпечуючих логічну послідовність їх
побудови, використання проблемного та інших методів навчання, які формують у
студентів самостійний творчий підхід.
. Стиль: Вміння точно і обгрунтовано висловлювати свої думки мовою
конкретної науки. Розвиток продуктивного мислення студентів у перебігу
обговорення проблем, що розглядаються, залучення їх у колективну пізнавальну
діяльність. Створення безпосереднього контакту викладача зі студентами, вміння
залучити студентів до дискусії.
. Забезпеченість семінарських і практичних занять методичними розробками,
пакетами візуального супроводження, використання технічних засобів навчання.
Основні вимоги до контролю та корекції
Функції контролю знань студентів. Система навчання у вищій школі -
багатогранний процес, який складається з цілого ряду взаємопов’язаних
елементів. Серед них важливе місце посідає контроль та корекція знань, тобто організація зворотного
зв'язку як засобу управління навчально-виховним процесом. Ця проблема особливо
актуальна у наш час у зв'язку з тим, що вся система вищої освіти в Україні
підлягає повній організаційній перебудові.
Посилення уваги до проблеми контролю занять викликано не тільки бажанням
визначити ступінь підготовленості студентів, але і потягом до удосконалення
всієї системи навчання. Перевірка і оцінка знань виконують, принаймні, шість
функцій: контрольну, навчальну, виховну, організаторську, розвиваючу і
методичну.
Для визначення рівня сформованості знань та умінь з даної дисципліни, необхідно спроектувати фонд тестових
завдань,
контрольних.
Тестові завдання слугують базою для формування критеріально
орієнтовних тестів досягнень, які належать до психо-діагностичних методик,
спрямованих на оцінку досягнутого рівня розвитку здібностей, знань та умінь.
Основними канонічними формами тестових завдань, які
рекомендовані розроблювачами, вважаються такі: 1) завдання (задачі) закритої
форми із запропонованими відповідями; 2) завдання (задачі) відкритої форми із
вільно конструйованими відповідями. Тестові завдання (задачі) закритої форми
мають складатися з трьох компонентів: а) інструкція до їх виконання; б)
запитальної (змістовної) частини; в) відповіді (ей).
Тестові завдання закритої форми
Тестові завдання закритої форми розрізняються за принципом побудови
відповіді.
.1. Альтернативні тестові завдання, які передбачають наявність двох
варіантів організації відповіді тестового завдання (типів "так" -
"ні"; "вірно" - "невірно") тощо. Як правило, їх
використовують для грубої перевірки правильності вибору або прийняття рішення у
згорненій формі.
.2. Тестові завдання з множинним вибором. Вони передбачають принаймні три
можливі відповіді (але не більше п’яти). Цей тип тестових завдань
використовується у тих випадках, коли із запропонованих декількох відповідей
лише одна є правильною
Тестові запитання відкритого типу
Тестові запитання відкритого типу передбачають вільні відповіді тих, хто
тестується, по суті завдання без запропонованих варіантів відповідей. Той, хто
тестується, має виконувати завдання згідно з власним баченням, яке має являти
собою твердження з невідомою змінною.
РОЗДІЛ
ІІ. МЕТОДИКА НАВЧАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ В ПЕДАГОГІЧНИХ УНІВЕРСИТЕТАХ
2.1 Розробка лекцій, практичних робіт, опорних конспектів
В цьому пункті другого розділу розроблені лекції, практичні
роботи, опорні конспекти до змістовного модуля I «Основні поняття теорії
диференціальних рівнянь. Рівняння з відокремлюючими змінними».
Методичні особливості вивчення змістовного модуля I «Основні поняття теорії
диференціальних рівнянь. Рівняння з відокремлюючими змінними»
Основна мета вивчення модуля:
оволодіння студентами основними поняттями теорії диференціальних рівнянь,
методами теорії звичайних диференціальних рівнянь першого порядку, однорідних,
лінійних та рівнянь у повних диференціалах;
вироблення у студентів логічного й алгоритмічного мислення,
необхідного для розв’язання задач, які пов’язані з теорією звичайних
диференціальних рівнянь першого порядку, однорідних, лінійних та рівнянь у
повних диференціалах;
- прищеплення навичків
дослідження динамічних математичних моделей практичних задач, їх розв’язання та
вміння аналізувати отримані результати.
Теми лекцій, практичних занять та завдання для самостійної
роботи для
змістовного модуля I
Лекція 1.Диференціальні рівняння, основні визначення.
Звичайне диференціальне рівняння, рівняння в частинних
похідних, порядок диференціального рівняння. Задачі, які приводять до звичайних
диференціальних рівнянь.
Завдання для самостійної роботи: самостійне вивчення матеріалу з теми
«Перспективи застосування диференціальних рівнянь у механіці і техніці» -
2 год. Література: [1-4].
Лекція 2.Диференціальні рівняння першого порядку.
Диференціальні рівняння першого порядку (загальні відомості).
Розв’язок диференціального рівняння, загальний інтеграл і частинний розв’язок
рівняння. Диференціальні рівняння із відокремлюючими змінними. Диференціальні
рівняння із змінними, які відокремлюються.
Практичне заняття 1.
Диференціальні рівняння з відокремлюючими змінними.
Завдання для самостійної роботи: самостійне вивчення матеріалу з теми
«Теорема Пікара. Варіанти теореми Пікара»- 2 год. Література: [1,3].
Лекція 3.Однорідні рівняння першого порядку.
Однорідна функція n-го порядку. Однорідні рівняння першого
порядку.
Практичне заняття 2. Однорідні рівняння та рівняння, що зводяться до них.
Завдання для самостійної роботи: самостійне вивчення
матеріалу «Геометрична інтерпретація рівнянь, розв’язаних відносно похідної»
- 2 год. Література: [2-4].
Лекція 4. Лінійні диференціальні рівняння першого порядку.
Лінійні однорідні рівняння. Лінійні неоднорідні рівняння.
Метод Лагранжа (метод варіації довільної змінної). Рівняння Бернуллі.
Практичне заняття 3. Лінійні диференціальні рівняння
першого порядку та рівняння, що зводяться до них (рівняння Бернуллі, метод
Міндінг-Дарбу, рівняння Ріккаті).
Завдання для самостійної роботи: самостійне вивчення матеріалу лекції,
інтегрування рівнянь, не розв’язаних відносно похідної - 2 год. Література: [1,3].
Лекція 5. Рівняння в повних диференціалах.
Загальні відомості про рівняння в
повних диференціалах. Інтегруючий множник.
Практичне заняття 4. Рівняння в повних диференціалах (1)
рівняння, які задані в повних диференціалах; 2) рівняння, які неявно задані в
повних диференціалах.
Завдання для самостійної роботи: самостійне вивчення матеріалу з теми
«Теорема Коші» - 2 год. Література: [1,2,5].
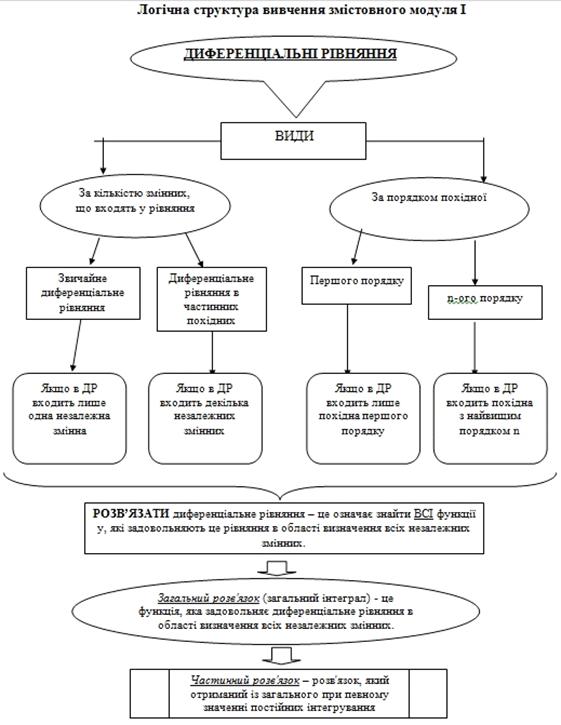

Короткий довідник з теми «Диференціальні рівняння I порядку»
|
Тип рівняння
|
Стандартна форма запису
|
Особливості
|
Метод розв’язування
|
З відокремлюючими змінними 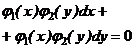 При диференціалах
- похідна функції, яка
залежить одна
При диференціалах
- похідна функції, яка
залежить одна
|
від x, інша - від y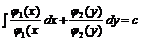
|
|
|
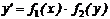 Права частина - добуток функцій, які
залежать одна
Права частина - добуток функцій, які
залежать одна
Розробка лекцій до змістовного модуля І
Лекція 1
Тема: «Диференціальні рівняння, основні визначення»
Мета:
– вивчення основних положень та визначень з теми
«Диференціальні рівняння»;
– ознайомлення із виникненням та застосуванням
диференціальних рівнянь;
– поглиблення, розширення знань, отриманих раніше при
вивченні розділів диференціального і інтегрального
числення з курсу математичного аналізу, алгебри та геометрії.
– розвиток наукового мислення та пам’яті;
– виховання культури математичного запису і мовлення.
При вивченні теми студенти повинні:
знати: означення диференціального рівняння та основні поняття, які
його стосуються (види, порядок, степінь, розв'язок);
уміти: визначати диференціальне рівняння з переліку рівнянь,
складати рівняння за умовою задачі, що приводить до диференціального рівняння;
здатні: знаходити невизначений інтеграл (з курсу математичного
аналізу).
Основні поняття: диференціальне рівняння (ДР), звичайне ДР, ДР у
частинних похідних, порядок ДР, степінь, розв'язок.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські
матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Поняття диференціального рівняння і його розв'язку.
2. Приклади задач, які приводять до диференціального
рівняння.
Список літератури
1. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
2. Пономарев К.К. Составление дифференциальных уравнений.
3. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations.
4. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
Текст лекції
1.Поняття диференціального рівняння і його розв'язку.
В диференціальному численні за заданою функцією одного чи
більшого числа змінних вивчались властивості цієї функції (монотонність,
випуклість і ін.). Однак більшість задач практичного застосування мають
характер обернених: треба знайти функцію, яка б мала наперед задані
властивості.
При вивченні фізичних явищ часто не вдається безпосередньо
знайти закон, який зв’язує розглядувані величини, але в той же час порівняно
легко встановлюється залежність між тими ж величинами і їх похідними або
диференціалами.
І ті і другі задачі приводять до рівнянь, що містять невідомі
функції під знаками похідних і диференціалів.
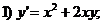
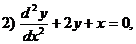
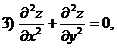
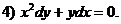
Означення 2. Якщо в диференціальному рівнянні невідома функція є функцією однієї
незалежної змінної, то таке диференціальне рівняння називається звичайним.
У загальному випадку його можна записати у вигляді
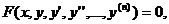 (1)
(1)
де 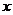 - незалежна змінна,
- незалежна змінна, 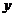 -
функція від
-
функція від 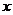 , яка підлягає визначенню,
, яка підлягає визначенню, 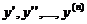 - її похідні.
- її похідні.
Означення 3. Якщо невідома функція, яка входить у диференціальне рівняння, є функцією
двох і більшого числа незалежних змінних, то таке диференціальне рівняння
називається рівнянням у частинних похідних.
Рівняння 1), 2) і 4) є звичайними диференціальними рівняннями, а 3) -
рівняння в частинних похідних.
Означення 4. Порядком диференціального рівняння називається максимальний порядок
похідної (або диференціала), що входить у нього.
Рівняння 1) і 4) є рівняннями першого порядку. Рівняння (1) - звичайне
диференціальне рівняння 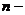 ого порядку.
ого порядку.
Означення 5. Якщо ліва частина рівняння (1) є многочленом відносно похідної
максимального порядку від невідомої функції, то степінь цього многочлена
називається степенем даного диференціального рівняння. Наприклад, рівняння
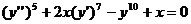
- п’ятого степеня другого порядку, а рівняння
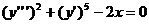
- другого степеня третього порядку.
У диференціальному рівнянню (1) 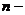 ого
порядку незалежна змінна
ого
порядку незалежна змінна 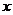 , шукана функція
, шукана функція 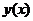 і
її похідні до
і
її похідні до 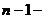 ого порядку включно в явному вигляді можуть бути, але
можуть окремо або всі разом бути відсутніми. Наявність же в явному вигляді
похідної
ого порядку включно в явному вигляді можуть бути, але
можуть окремо або всі разом бути відсутніми. Наявність же в явному вигляді
похідної 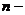 ого порядку необхідна, щоб це рівняння було
диференціальним. Наприклад,
ого порядку необхідна, щоб це рівняння було
диференціальним. Наприклад, 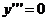 є
диференціальним рівнянням третього порядку, хоча в ньому в явному вигляді й
відсутні
є
диференціальним рівнянням третього порядку, хоча в ньому в явному вигляді й
відсутні 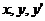 і
і 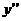 .
.
Означення 6. Розв’язком диференціального рівняння (1) називається 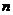 разів диференційована функція
разів диференційована функція 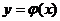 в інтервалі
в інтервалі 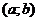 ,
яка, будучи підставленою в це рівняння, перетворює його в інтервалі
,
яка, будучи підставленою в це рівняння, перетворює його в інтервалі 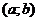 в тотожність
в тотожність
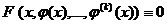 .
.
Наприклад, функція 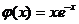 є
розв’язком рівняння
є
розв’язком рівняння
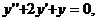
оскільки для всіх 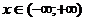 вона перетворює це рівняння в тотожність.
вона перетворює це рівняння в тотожність.
Справді, знайшовши похідні 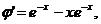
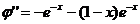 і підставивши функцію
і підставивши функцію  її
похідні в рівняння, дістанемо тотожність
її
похідні в рівняння, дістанемо тотожність
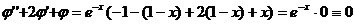 ,
,
правильну для 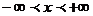 .
.
Розв’язати диференціальне рівняння - означає знайти всі його розв'язки.
Ці розв'язки найчастіше приводять до обчислення невизначених інтегралів. Тому
операція знаходження розв’язків диференціального рівняння називається
інтегруванням цього рівняння. Задача інтегрування диференціального рівняння
вважається розв’язаною, якщо цю задачу звести до більш простої і вже вивченої в
курсі інтегрального числення задачі обчислення невизначених інтегралів.
2. Приклади задач, які приводять до диференціального
рівняння.
Задача 1. Знайти криві, які мають ту властивість, що відрізок
дотичної (проведеної в будь-якій її точці), який міститься між осями координат,
ділиться точкою дотику навпіл.
Розв’язання. Нехай 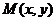 -
довільна точка шуканої кривої
-
довільна точка шуканої кривої 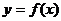 (мал.
1). Тоді
(мал.
1). Тоді 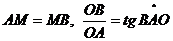 . Оскільки
. Оскільки 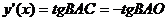 ,
,
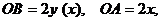 то маємо співвідношення
то маємо співвідношення
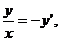 (2)
(2)
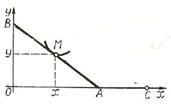


Мал. 1 Мал. 2
яке зв’язує незалежну змінну 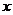 ,
шукану функцію
,
шукану функцію 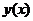 і її похідну
і її похідну 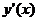 ,
тобто дістали звичайне диференціальне рівняння першого порядку. Переписавши (2)
у вигляді
,
тобто дістали звичайне диференціальне рівняння першого порядку. Переписавши (2)
у вигляді 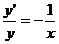 , а це останнє - у вигляді
, а це останнє - у вигляді 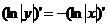 , маємо рівність
, маємо рівність 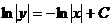 .
Звідси
.
Звідси 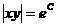 , і, отже,
, і, отже,
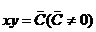 ,(3)
,(3)
де 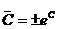 . Шукані криві (3) є сім'єю гіпербол, для яких осі
координат виконають роль асимптот.
. Шукані криві (3) є сім'єю гіпербол, для яких осі
координат виконають роль асимптот.
Задача 2. Відомо, що швидкість розпаду радію пропорційна наявній його
кількості.
Знайти закон, який виражає зміну кількості радію протягом часу, якщо
відомо, що через 1600 років залишиться половина кількості радію.
Розв’язання. Нехай 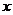 -
кількість радію в момент часу
-
кількість радію в момент часу 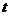 (час
у роках). Оскільки швидкість зміни є похідною від
(час
у роках). Оскільки швидкість зміни є похідною від 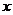 за часом
за часом 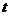 ,
то, згідно з умовою задачі,
,
то, згідно з умовою задачі,
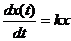 .
(4)
.
(4)
Тут задача привела до звичайного диференціального рівняння першого
порядку.
Переписавши (4) у вигляді 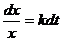 .
А останнє у вигляді
.
А останнє у вигляді 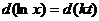 , маємо рівність
, маємо рівність
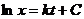 ,
(5)
,
(5)
де 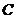 - стала.
- стала.
Нехай у початковий момент 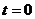 кількість
радію дорівнює
кількість
радію дорівнює 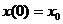 . Підставляючи замість
. Підставляючи замість 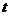 і
і
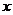 в (5) відповідно
в (5) відповідно 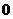 і
і
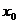 , дістанемо
, дістанемо 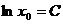 .
Таким чином,
.
Таким чином, 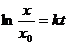 або
або 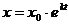 .
.
Коефіцієнт 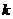 знаходимо з умови, що
знаходимо з умови, що  при
при
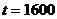 :
:

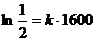 .
.
Звідси 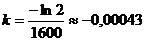 .
.
Отже, кількість радію в момент часу 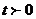 визначається
за формулою
визначається
за формулою
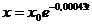 .
.
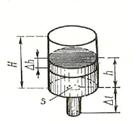
Задача 3. З циліндричної посудини висотою 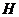 і
радіусом
і
радіусом 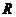 , повністю заповненою водою, через отвір площі
, повністю заповненою водою, через отвір площі 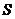 , що міститься в його дні, витікає вода. За яким
законом буде знижуватися рівень води в посудині протягом часу, якщо відомо, що
швидкість
, що міститься в його дні, витікає вода. За яким
законом буде знижуватися рівень води в посудині протягом часу, якщо відомо, що
швидкість 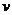 витікання рідини з отвору залежить від висоти
витікання рідини з отвору залежить від висоти  (Мал.3) стовпа рідини за формулою
(Мал.3) стовпа рідини за формулою
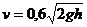 ,
,
де 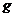 - прискорення вільного падіння.
- прискорення вільного падіння.
Розв’язання. За проміжок часу від 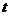 до
до
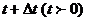 висота рівня води в посудині знизиться з висоти
висота рівня води в посудині знизиться з висоти 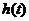 до
до 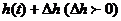 .
За цей час
.
За цей час 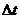 з посудини витікає об’єм води, що дорівнює -
з посудини витікає об’єм води, що дорівнює - 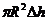 . Такий же об’єм води витікає з отвору. Він дорівнює
. Такий же об’єм води витікає з отвору. Він дорівнює 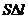 , де
, де 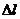 -
довжина шляху, пройденого частинкою рідини з моменту
-
довжина шляху, пройденого частинкою рідини з моменту 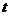 до
до 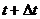 :
:
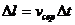 , де
, де 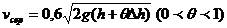 -
середня швидкість руху рідини за час
-
середня швидкість руху рідини за час 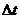 .
.
Таким чином,
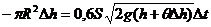 ,
,
звідси 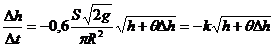 ; де
; де 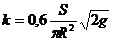 .
.
Переходячи до границі при  ,
дістанемо диференціальне рівняння
,
дістанемо диференціальне рівняння
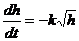 ,
,
яке зв’язує 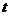 і
і 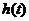 .
.
З (6) маємо
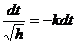 або
або
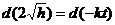 .
.
Звідси 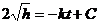 , де
, де 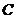 -
довільна стала. Оскільки в момент
-
довільна стала. Оскільки в момент 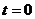 рівень
рівень
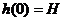 , то
, то 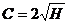 .
Отже,
.
Отже, 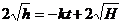 або
або 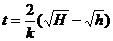 .
Такий закон витікання рідини з отвору в дна посудини. Взявши
.
Такий закон витікання рідини з отвору в дна посудини. Взявши 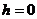 , дістанемо
, дістанемо
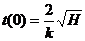
- час, протягом якого з посудини витікає вся рідина.
Лекція 2
Тема: «Диференціальні рівняння першого порядку»
Мета:
– вивчення основних положень та визначень з теми
«Диференціальні рівняння першого порядку»;
– ознайомлення із видами диференціальних рівнянь
першого порядку та методами їх розв'язування;
– розвиток візуального мислення та пам’яті;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення та види диференціальних рівнянь першого порядку;
уміти: визначати диференціальне рівняння першого порядку з
переліку рівнянь, знаходити загальний та частинний інтеграл рівняння з
відокремлюючими змінними за допомогою теореми Коші;
здатні: використовувати алгоритм розв'язування рівняння з
відокремлюючими змінними.
Основні поняття: диференціальне рівняння першого порядку, загальний
та частинний інтеграл, особливий розв'язок, рівняння з відокремлюючими
змінними.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські
матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Загальні відомості про диференціальні рівняння першого
порядку.
2. Диференціальні рівняння із відокремлюючими змінними.
. Диференціальні рівняння із змінними, які відокремлюються.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations.
2. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
3. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных
уравнений.
Текст лекції
1. Загальні відомості про диференціальні рівняння першого
порядку.
Означення 1. Диференціальне рівняння першого порядку має вигляд
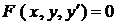 .
.
Якщо це рівняння можна розв'язати відносно 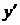 , то його можна записати у вигляді
, то його можна записати у вигляді
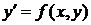 .
.
Для такого рівняння справедлива наступна теорема, яка називається
теоремою існування і одиничності розв'язку диференціального рівняння.
Теорема 1. Якщо в рівнянні 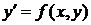 функція
функція 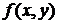 і
її частинна похідна
і
її частинна похідна 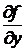 по у неперервні в деякій області D на
площині 0ху, яка містить деяку точку
по у неперервні в деякій області D на
площині 0ху, яка містить деяку точку 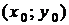 ,
то існує єдиний розв'язок цього рівняння
,
то існує єдиний розв'язок цього рівняння 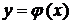 ,
який задовольняє умові
,
який задовольняє умові 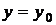 при
при 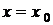 .
.
Геометричний зміст теореми полягає в тому, що існує і притім єдина
функція 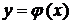 , графік якої проходить через точку
, графік якої проходить через точку 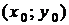 .
.
Означення 2. Умова, що при 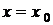 функція у повинна дорівнюватися заданому числу
функція у повинна дорівнюватися заданому числу
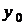 , називається початковою умовою, або умовою
Коші. Вона записується у вигляді
, називається початковою умовою, або умовою
Коші. Вона записується у вигляді
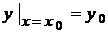 або
або
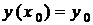 .
.
Означення 3. Задача, у якій потрібно знайти частинний розв'язок рівняння 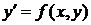 , який задовольняє початковій умові
, який задовольняє початковій умові 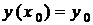 , називається задачею Коші.
, називається задачею Коші.
Означення 4. Загальним розв'язком диференціального рівняння першого порядку
називається функція
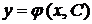 ,
,
яка залежить від однієї довільної сталої С і задовольняє наступним
умовам:
а) вона задовольняє диференціальному рівнянню при будь-якому
конкретному значенні сталої С;
б) яка б не була початкова умова 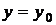 при
при
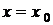 , тобто
, тобто 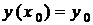 ,
можна знайти таке значення
,
можна знайти таке значення 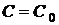 ,
що функція
,
що функція 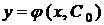 задовольняє даній початковій умові. При цьому
передбачається, що значення
задовольняє даній початковій умові. При цьому
передбачається, що значення 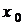 і
і
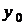 належать до тієї області зміни змінних х і у,
у якій виконуються умови теореми існування й одиничності розв'язку.
належать до тієї області зміни змінних х і у,
у якій виконуються умови теореми існування й одиничності розв'язку.
У процесі знаходження загального розв'язку диференціального рівняння ми
приходимо до співвідношення вигляду
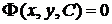 ,
,
не розв'язаному відносно у. Розв'язавши це співвідношення
відносно у, одержуємо загальний розв'язок. Однак не завжди удається
виразити у в елементарних функціях; у таких випадках загальний розв'язок
залишається в неявному вигляді.
Означення 5. Рівність вигляду 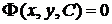 ,
яка неявно задає загальний розв'язок, називається загальним інтегралом диференціального
рівняння.
,
яка неявно задає загальний розв'язок, називається загальним інтегралом диференціального
рівняння.
Означення 6. Частинним розв'язком називається будь-яка функція 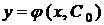 , яка утворюється з загального розв'язку
, яка утворюється з загального розв'язку 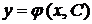 , якщо в останньому довільної сталої С придати
визначене значення
, якщо в останньому довільної сталої С придати
визначене значення 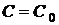 . Співвідношення
. Співвідношення 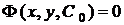 називається
в цьому випадку частинним інтегралом рівняння.
називається
в цьому випадку частинним інтегралом рівняння.
З геометричної точки зору загальний інтеграл являє собою сімейство
кривих на координатній площині, яке залежить від однієї довільної сталої С.
Ці криві називаються інтегральними кривими даного диференціального
рівняння. Частинному інтегралу відповідає одна крива цього сімейства, яка
проходить через деяку задану точку площини.
Вирішити або проінтегрувати диференціальне рівняння - значить:
а) знайти його загальний розв'язок або загальний інтеграл (якщо початкові
умови не задані) або
б) знайти той частинний розв'язок рівняння, який задовольняє заданим
початковим умовам (якщо такі є).
Означення 7. Особливим розв'язком називається такий розв'язок, у всіх
точках якого умова одиничності не виконується, тобто в будь-якому околі кожної
точки 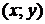 особливого розв'язку існують принаймні дві
інтегральні криві, які проходять через цю точку.
особливого розв'язку існують принаймні дві
інтегральні криві, які проходять через цю точку.
Особливі розв'язки не утворюються з загального розв'язку
диференціального рівняння ні при яких значеннях довільної сталої С (у
тому числі і при 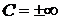 ).
).
2. Диференціальні рівняння із відокремлюючими змінними
Означення 8. Диференціальне рівняння типу

називають рівнянням із відокремлюючими змінними, тому що
в цьому рівнянні змінні відокремлені, тобто при 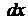 знаходиться
тільки функція від х, а при
знаходиться
тільки функція від х, а при 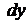 -
тільки функція від у.
-
тільки функція від у.
Інтегруючи обидві частини цього рівняння, одержимо співвідношення, яке
зв'язує розв'язок у, незалежну змінну х і довільну сталу С,
тобто одержимо загальний інтеграл рівняння
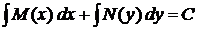 .
.
Приклад.
Знайти загальний розв'язок рівняння
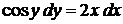 .
.
Розв'язок. 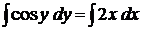 ,
, 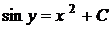 ,
,
 .
.
. Диференціальні рівняння із змінними, які
відокремлюються.
Означення 9. Диференціальні рівняння, у яких змінні можна відокремити за допомогою
множення або ділення обох частин рівняння на той самий вираз, називаються диференціальними
рівняннями із змінними, які відокремлюються.
Це рівняння виду
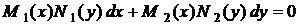 .
.
Воно може бути приведене до рівняння із відокремленими змінними шляхом
ділення обох його частин на вираз 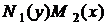 :
:
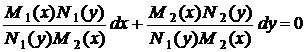 ,
або
,
або
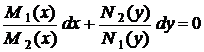 .
.
Приклад.
Знайти загальний розв'язок рівняння
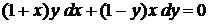 .
.
Розв'язок. Відокремлюючи змінні, знаходимо:
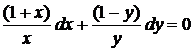 ,
,
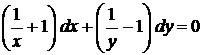 .
.
Інтегруючи, отримаємо: 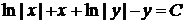 або
або
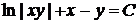 .
.
Останнє співвідношення є загальний інтеграл даного рівняння.
Приклад.
Розв'язати задачу Коші
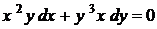 ,
,
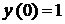 .
.
Розв'язок. Відокремлюючи змінні, знаходимо:
 .
.
Інтегруючи, отримаємо: 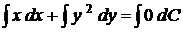 ,
,
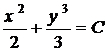 .
.
Одержали загальний інтеграл вихідного рівняння.
Розв'язавши останнє рівняння відносно у, знайдемо загальний
розв'язок вихідного рівняння
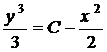 ,
,
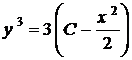 ,
, 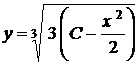 .
.
Знайдемо частинний розв'язок, який задовольняє початковій умові 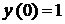 .
.
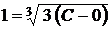 ,
,
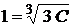 ,
, 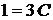 ,
,
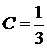 .
.
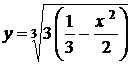 -
розв'язок задачі Коші.
-
розв'язок задачі Коші.
Лекція 3
Тема: «Однорідні рівняння першого порядку»
Мета:
– вивчення основних положень та визначень з теми
«Однорідні диференціальні рівняння першого порядку»;
– ознайомлення із методами розв'язування однорідних
рівнянь першого порядку;
– поглиблення, розширення знань, отриманих раніше при
вивченні диференціальних рівнянь, для розв'язування однорідних рівнянь;
– розвиток наукового мислення та пам’яті;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення та види однорідних рівнянь першого порядку,
означення однорідної функції;
уміти: визначати однорідне рівняння першого порядку з переліку рівнянь,
знаходити загальний та частинний розв'язок однорідного рівняння;
здатні: використовувати алгоритм розв'язування однорідних рівнянь
першого порядку.
Основні поняття: однорідна функція, однорідне рівняння першого
порядку.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські
матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Однорідна функція.
2. Однорідні рівняння першого порядку.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations.
2. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного.
3. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
4. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
5. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных
уравнений.
Текст лекції
1. Однорідна функція.
Означення 1. Функція 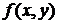 називається однорідною функцією n-го порядку
щодо змінних х і у, якщо при будь-якому t справедлива
тотожність
називається однорідною функцією n-го порядку
щодо змінних х і у, якщо при будь-якому t справедлива
тотожність
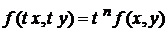 .
.
Приклад.
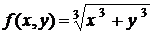 - однорідна функція першого порядку, тому що
- однорідна функція першого порядку, тому що
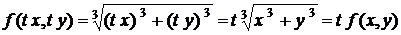 .
.
Приклад.
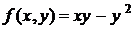 - однорідна функція другого порядку, тому що
- однорідна функція другого порядку, тому що
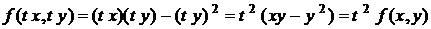 .
.
Приклад.
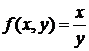 - однорідна функція нульового порядку, тому що
- однорідна функція нульового порядку, тому що
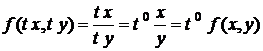 .
.
2. Однорідні рівняння першого порядку.
Означення 2. Рівняння виду 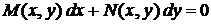 називається однорідним, якщо функції при
називається однорідним, якщо функції при 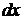 і
і 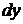 є
однорідними однакового порядку.
є
однорідними однакового порядку.
Однорідне рівняння зводиться до вигляду 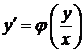 і
за допомогою заміни змінних
і
за допомогою заміни змінних 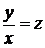 ,
де
,
де 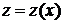 ,
, 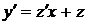 ,
або
,
або 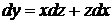 зводиться до рівняння із змінними, які
відокремлюються.
зводиться до рівняння із змінними, які
відокремлюються.
Приклад.
Розв'язати задачу Коші
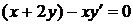 ,
,
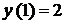 .
.
Розв'язок. 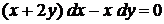
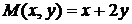
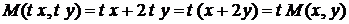
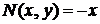
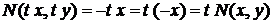
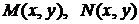 -
однорідні функції першого порядку
-
однорідні функції першого порядку
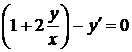
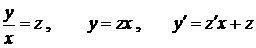
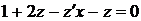 ,
,
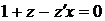 ,
, 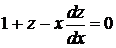 ,
,

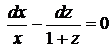 ,
,
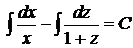 ,
,
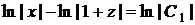 ,
,
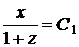 ,
,
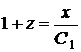 ,
, 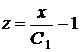 ,
,
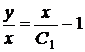 ,
,
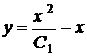 -
загальний розв'язок.
-
загальний розв'язок.
Знайдемо частинний розв'язок, який задовольняє початковій умові 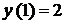 :
: 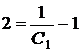 ,
,
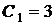 .
.
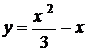 -
розв'язок задачі Коші.
-
розв'язок задачі Коші.
Лекція 4
Тема: «Лінійні диференціальні рівняння першого
порядку»
Мета:
– вивчення основних положень та визначень з теми «Лінійні
диференціальні рівняння першого порядку»;
– ознайомлення із видами лінійних рівнянь першого
порядку та методами їх розв'язування;
– поглиблення, розширення знань, отриманих раніше при
вивченні диференціальних рівнянь, для розв'язування лінійних рівнянь;
– розвиток візуального мислення та пам’яті;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення та види лінійних рівнянь першого порядку, методи
їх розв'язування;
уміти: визначати лінійне рівняння першого порядку з переліку
рівнянь, знаходити загальний та частинний розв'язок лінійного рівняння як
однорідного, так і неоднорідного;
здатні: використовувати алгоритм розв'язування лінійних рівнянь
першого порядку.
Основні поняття: лінійне рівняння першого порядку (лінійне однорідне,
лінійне неоднорідне), підстановка та рівняння Бернуллі, метод Лагранжа.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські
матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Загальні відомості про лінійні рівняння першого порядку.
. Рівняння Бернуллі.
3. Метод Лагранжа (метод варіації довільної змінної) для
розв'язку лінійних рівнянь першого порядку.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations.
2. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного.
3. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
4. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных
уравнений.
Текст лекції
1. Загальні відомості про лінійні рівняння першого порядку.
Означення 1. Лінійним рівнянням першого порядку називається
рівняння, що має вигляд
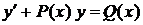 ,
(1)
,
(1)
де 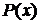 і
і 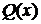 -
задані неперервні функції від х (або сталі).
-
задані неперервні функції від х (або сталі).
Якщо 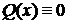 , то рівняння називається лінійним однорідним.
, то рівняння називається лінійним однорідним.
Якщо 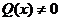 , то рівняння називається лінійним неоднорідним.
, то рівняння називається лінійним неоднорідним.
Шукаємо розв'язок рівняння (1) у вигляді добутку двох функцій від х:
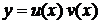 ,
(2)
,
(2)
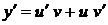 .
(3)
.
(3)
Підставивши у і 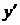 в
(1), маємо:
в
(1), маємо:
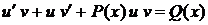 ,
,
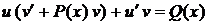 .
(4)
.
(4)
Виберемо функцію 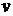 такою, щоб
такою, щоб
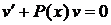 ,
(5)
,
(5)
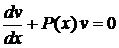 ,
,
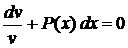 ,
, 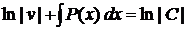 ,
,
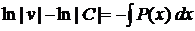 ,
,
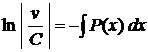 ,
,
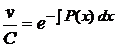 ,
,
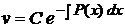 .
.
Так як нам досить якого-небудь відмінного від нуля розв'язку рівняння
(5), то за функцію 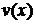 візьмемо
візьмемо 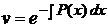 .
.
Підставляючи знайдене значення 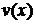 в
(4), одержимо:
в
(4), одержимо:
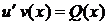 ,
,
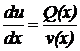 ,
, 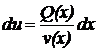 ,
,
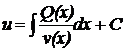 .
.
Підставляючи 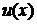 й
й 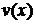 у
(2), одержуємо розв'язок неоднорідного рівняння:
у
(2), одержуємо розв'язок неоднорідного рівняння:
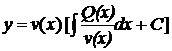 ,
,
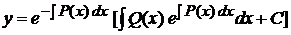 .
(6)
.
(6)
Розв'язок однорідного рівняння можна записати у вигляді:
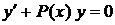 ,
,
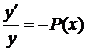 ,
, 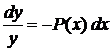 ,
,
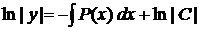 ,
,
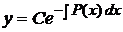 .
.
Приклад.
Розв'язати рівняння
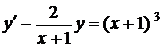 .
.
Розв'язок. Скориставшись (2), (3) 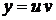 ,
,
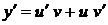 , маємо:
, маємо:
навчання диференціальний рівняння конспект
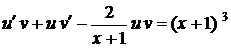 ,
,
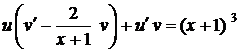 .
.
Згідно методу виберемо функцію 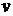 такою,
щоб
такою,
щоб 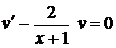 , тоді
, тоді
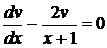 ,
,
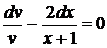 ,
,
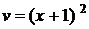 .
.
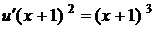 ,
,
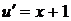 ,
,  ,
,
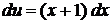 ,
,
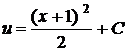 .
.
Підставляючи 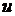 й
й 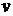 ,
одержуємо загальний розв'язок рівняння:
,
одержуємо загальний розв'язок рівняння:
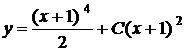 .
.
2.
Рівняння Бернуллі
Означення 2. Рівнянням Бернуллі називається рівняня
виду 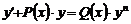 або
або 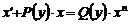 .
.
Рівняння Бернуллі
відрізняється від лінійного
правою частиною і зводиться до послідовності рівнянь з відокремлюючими змінними
за тією ж схемою, що і лінійне, з підстановкою 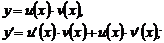
або
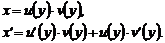
Приклад 1. Знайти загальний розв'язок диференціального рівняння 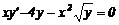 .
.
. Визначаємо тип диференціального рівняння (таблиця 1):
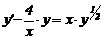 - рівняння
Бернуллі, де
- рівняння
Бернуллі, де 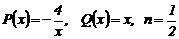 .
.
. Запишемо підстановку:
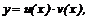
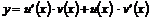 .
.
. Здійснимо підстановку в дане рівняння:
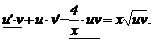
.
Запишемо послідовність
рівнянь відносно функцій 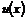 та
та 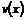 . Згрупуємо перший і третій члени рівняння:
. Згрупуємо перший і третій члени рівняння:
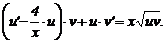
Виберемо
функцію 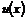 так, щоб вона перетворювалася
в нуль дужку, отримаємо
послідовність функцій:
так, щоб вона перетворювалася
в нуль дужку, отримаємо
послідовність функцій:
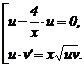
. Знайдемо функції 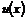 та
та 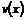 . Кожне з рівнянь послідовності є рівнянням з
відокремлюючими змінними:
. Кожне з рівнянь послідовності є рівнянням з
відокремлюючими змінними:
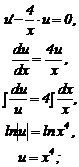
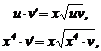
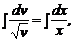
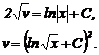
.
Запишемо загальний
розв'язок диференціального рівняння:
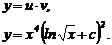
. Метод Лагранжа (метод варіації довільної змінної)
для розв'язку лінійних рівнянь першого порядку
Суть методу полягає в тому, що спочатку знаходимо загальний розв'язок
відповідного лінійного однорідного рівняння 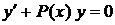
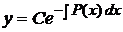 .
.
Потім, вважаючи в цьому розв'язку сталу С функцією від х,
шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:
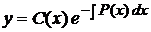 .
(7)
.
(7)
Розв'язок (7) повинен задовольняти рівняння (1). Диференціюючи і
підставляючи (7) в (1), маємо:
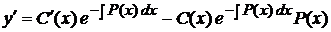 ,
,
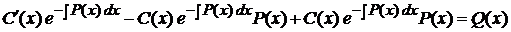 ,
,
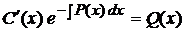 ,
,
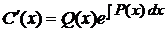 ,
,
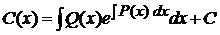 ,
,
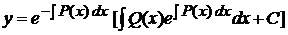 .
(8)
.
(8)
Він співпадає з розв'язком (6).
Приклад.
Розв'язати рівняння методом Лагранжа
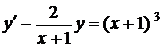 .
.
Розв'язок. Розв'яжемо відповідне однорідне рівняння
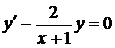 ,
,
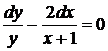 ,
, 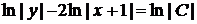
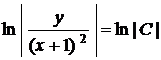 ,
,
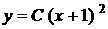 .
.
Вважаючи в цьому розв'язку сталу С функцією від х,
шукаємо розв'язок лінійного неоднорідного рівняння у вигляді:
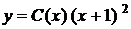 ,
,
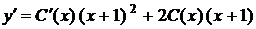 .
.
Підставимо у вихідне рівняння у, 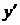 і
з отриманого диференціального рівняння знайдемо функцію
і
з отриманого диференціального рівняння знайдемо функцію 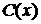 :
:
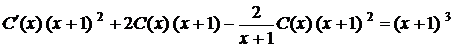 ,
,
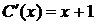 ,
,
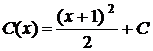 .
.
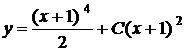 -
загальний розв'язок.
-
загальний розв'язок.
Тому що 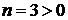 , то
, то 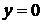 -
теж розв'язок вихідного рівняння.
-
теж розв'язок вихідного рівняння.
Лекція
5
Тема: «Диференціальні рівняння в повних диференціалах»
Мета:
– вивчення основних положень та визначень з теми
«Диференціальні рівняння в повних диференціалах»;
– ознайомлення із видами рівнянь в повних диференціалах
та методами їх розв'язування;
– поглиблення, розширення знань, отриманих раніше при
вивченні диференціальних рівнянь, для розв'язування рівнянь в повних
диференціалах;
– розвиток наукового мислення та пам’яті;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення інтегруючого множника, означення та види рівнянь
в повних диференціалах, методи їх розв'язування;
уміти: визначати рівняння в повних диференціалах з переліку
рівнянь, знаходити інтегруючий множник для рівняння, яке зводиться до рівняння
в повних диференціалах;
здатні: використовувати алгоритм розв'язування рівнянь в повних
диференціалах.
Основні поняття: рівняння в повних диференціалах, інтегруючий
множник.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські
матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
1. Загальні відомості про рівняння в повних диференціалах.
2. Інтегруючий множник
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations.
2. Арнольд В.И. Обыкновенные дифференциальные уравнения.
3. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного.
4. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
5. Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
6. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных
уравнений.
Текст лекції
1. Загальні відомості про рівняння в повних диференціалах.
Означення 1. Рівняння 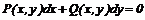 називається рівнянням в повних диференціалах , якщо
його ліва частина - повний диференціал деякої функції
називається рівнянням в повних диференціалах , якщо
його ліва частина - повний диференціал деякої функції 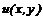 , тобто
, тобто
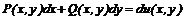 .
.
Необхідною і достатньою умовою повного диференціала є рівність частинних
похідних 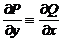 .
.
Де функція 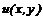 може
бути знайдена за однією із формул:
може
бути знайдена за однією із формул:
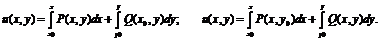
Приклад 1. Вказати
рівняння в повних диференціалах:
а)
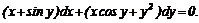
.
Диференціальне рівняння записано в симетричній формі, де
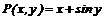 ,
, 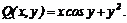
. Знайдемо частинні похідні:
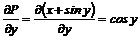 ,
, 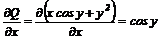 .
.
. Порівняємо частинні похідні. Так як 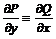 , то рівняння є рівнянням
в повних
диференціалах.
, то рівняння є рівнянням
в повних
диференціалах.
б)
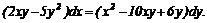
.
Диференціальне рівняння записано в симетричній формі, де
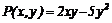 ,
, 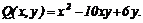
. Знайдемо частинні похідні:
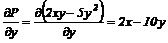 ,
, 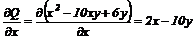 .
.
. Порівняємо частинні похідні. Так як 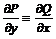 , то рівняння є рівнянням
в повних
диференціалах.
, то рівняння є рівнянням
в повних
диференціалах.
Приклад 2. Знайти загальний інтеграл
диференціального рівняння
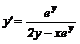 .
.
. Визначаємо тип рівняння (таблиця 1):
Запишемо рівняння в симетричній формі
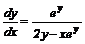 ,
,
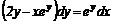 ,
, 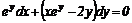 ,
,
тоді
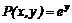 ,
,
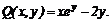
.2. Знайдемо частинні похідні:
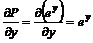 ,
,
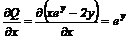 .
.
.3. Порівняємо частинні похідні. Так
як 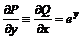 , то рівняння
є рівнянням в повних
диференціалах.
, то рівняння
є рівнянням в повних
диференціалах.
.
Запишемо формулу загального
інтеграла:
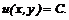
30.
Виберемо формулу для відшукання функції
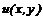 :
:
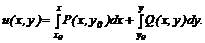
. Знайдемо
функцію 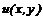 :
:
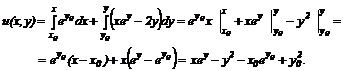
.
Запишемо загальний інтеграл рівняння:
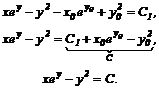
Приклад 3. Знайти загальний інтеграл диференціального рівняння 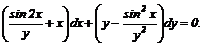
Відповідь: 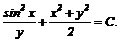
Приклад 4. Серед рівнянь вказати те, яке є
одночасно однорідним і в повних диференціалах:
а)
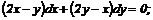
б)
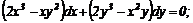
в)
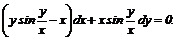
. Інтегруючий множник
Нехай функції 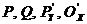 неперервні в області
неперервні в області 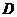 вигляду
вигляду
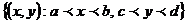 . Якщо для рівняння
. Якщо для рівняння
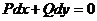 (1)
(1)
умова 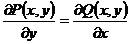 не виконується в області
не виконується в області 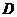 , то це рівняння не буде рівнянням у повних
диференціалах у цій області.
, то це рівняння не буде рівнянням у повних
диференціалах у цій області.
В цьому разі виникає питання, чи не можна підібрати функцію 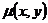 так, щоб після множення на неї рівняння (1) дістали
рівняння
так, щоб після множення на неї рівняння (1) дістали
рівняння
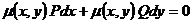 (1’)
(1’)
в повних диференціалах. Така функція називається інтегруючим множником
диференціального рівняння (1).
Щоб функція 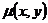 , неперервна в однов’язній області
, неперервна в однов’язній області  разом зі своїми частинними похідними
разом зі своїми частинними похідними 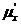 і
і 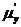 ,
була інтегруючим множником рівняння (1), необхідно і достатньо, щоб для всіх
точок
,
була інтегруючим множником рівняння (1), необхідно і достатньо, щоб для всіх
точок 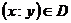 виконувалась рівність
виконувалась рівність
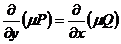 ,
,
тобто
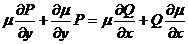 .
(2)
.
(2)
Рівність (2) містить невідому функцію  під
знаком частинних похідних, тобто (2) є диференціальне рівняння в частинних
похідних. Його розв’язання є задачею складнішою, ніж розв’язання рівняння (1).
Однак задача по знаходженню інтегруючого множника значно спрощується, коли
відомо, що він залежить від однієї незамкненої змінної
під
знаком частинних похідних, тобто (2) є диференціальне рівняння в частинних
похідних. Його розв’язання є задачею складнішою, ніж розв’язання рівняння (1).
Однак задача по знаходженню інтегруючого множника значно спрощується, коли
відомо, що він залежить від однієї незамкненої змінної 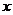 або
або 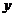 .
.
Припустимо, що рівняння (1) має інтегруючий множник, залежний тільки
від 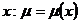 . В цьому разі рівняння (2) набере вигляду
. В цьому разі рівняння (2) набере вигляду
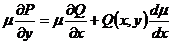 ,
,
або 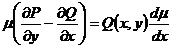 ,
,
звідки 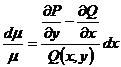 . (3)
. (3)
Оскільки 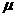 є функцією однієї незалежної змінної
є функцією однієї незалежної змінної 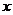 , то вираз
, то вираз
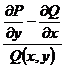 (4)
(4)
не повинен залежати від 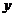 .
Позначивши його через
.
Позначивши його через 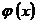 і припускаючи, що
і припускаючи, що 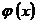 -
неперервна функція в інтервалі
-
неперервна функція в інтервалі 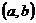 ,
з (3) дістанемо
,
з (3) дістанемо

і, таким чином,
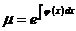 ,
де
,
де 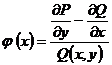 . (5)
. (5)
Покажемо, що коли вираз (4) справді не залежить від  і є неперервною функцією від
і є неперервною функцією від 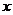 на інтервалі
на інтервалі 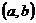 ,
то функція
,
то функція 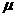 , задана рівністю (5), є інтегруючим множником
рівняння (1).
, задана рівністю (5), є інтегруючим множником
рівняння (1).
Справді, для цього достатньо переконатись у справедливості рівності
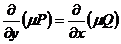 (6)
(6)
для всіх точок 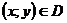 . Маємо
. Маємо
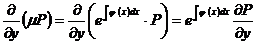 ,
,
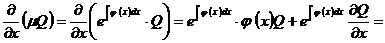
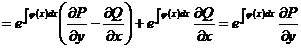 ,
,
тобто рівність (6) дійсно виконується в області 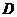 .
.
В аналогічній спосіб можна показати, що коли вираз
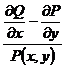
не залежить від 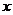 і є неперервною в інтервалі
і є неперервною в інтервалі 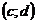 , то рівняння (1) має інтегруючий множник, незалежний
від
, то рівняння (1) має інтегруючий множник, незалежний
від 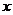 , який знаходиться за формулою
, який знаходиться за формулою
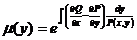 .
.
Розглянемо питання про еквівалентність рівнянь (1) і (1’). Якщо
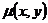 є інтегруючий множник рівняння (1), то рівняння
є інтегруючий множник рівняння (1), то рівняння
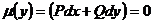 (7)
(7)
є рівнянням в повних диференціалах, тобто існує функція 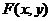 , повний диференціал якої дорівнює лівій частині цього
рівняння:
, повний диференціал якої дорівнює лівій частині цього
рівняння:
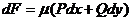 .
(8)
.
(8)
Загальний інтеграл рівняння (7) має вигляд
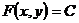 .
.
З (8) дістанемо
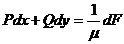 (9)
(9)
і, отже, ліва частина (9) може перетворитись у нуль не тільки при 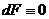 , але й при
, але й при 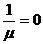 .
(10)
.
(10)
Якщо рівняння (10) задає 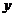 як
деяку функцію від
як
деяку функцію від  або
або 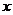 як
деяку функцію від
як
деяку функцію від 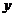 , то вона є розв’язком рівняння
, то вона є розв’язком рівняння
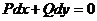 (11)
(11)
що не міститься в загальному інтегралі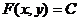 рівняння (7).
рівняння (7).
Крім того, якщо рівняння
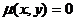 (12)
(12)
задає деяку функцію 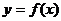 або
або
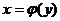 , то з (7), видно, що ця функція ввійде в загальний
інтеграл рівняння (5), однак може виявитись побічним розв’язком рівняння (11).
, то з (7), видно, що ця функція ввійде в загальний
інтеграл рівняння (5), однак може виявитись побічним розв’язком рівняння (11).
Таким чином, щоб дістати загальний інтеграл рівняння (11), треба взяти
загальний інтеграл рівняння (7) і з нього вилучити ті розв'язки рівняння (12),
які не є розв'язками рівняння (11), і додати ті розв'язки рівняння (10), які не
є розв'язками рівняння (7).
Приклад 1. Розв’язати рівняння
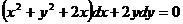 (13)
(13)
Розв’язання. Тут 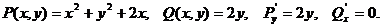 Функції
Функції 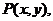
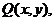
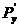 і
і 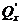 неперервні
в усій площині
неперервні
в усій площині 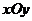 , однак умова
, однак умова 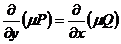 не
виконана і, отже, рівняння (13) не є рівнянням у повних диференціалах. Вираз
(4)
не
виконана і, отже, рівняння (13) не є рівнянням у повних диференціалах. Вираз
(4) 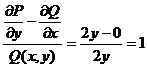 не залежить від
не залежить від 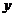 і
являє собою неперервну функцію від
і
являє собою неперервну функцію від 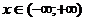 .
Тому інтегруючий множник визначається за формулою (5)
.
Тому інтегруючий множник визначається за формулою (5)
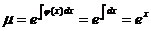 .
.
Помноживши на цей множник праву і ліву частини рівняння (13), дістанемо
рівняння в повних диференціалах 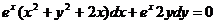
Функцію 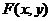 , повний диференціал якої дорівнює лівій частині
останнього рівняння, знаходимо з рівнянь
, повний диференціал якої дорівнює лівій частині
останнього рівняння, знаходимо з рівнянь

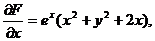
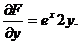
З першого рівняння маємо
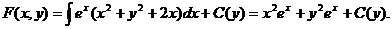
Звідси і з другого рівняння знаходимо
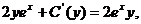
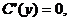
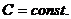
Таким чином, загальний інтеграл рівняння (13) має вигляд
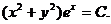
Опорні конспекти лекцій змістовного модуля I
Лекція 1. Диференціальні рівняння, основні визначення
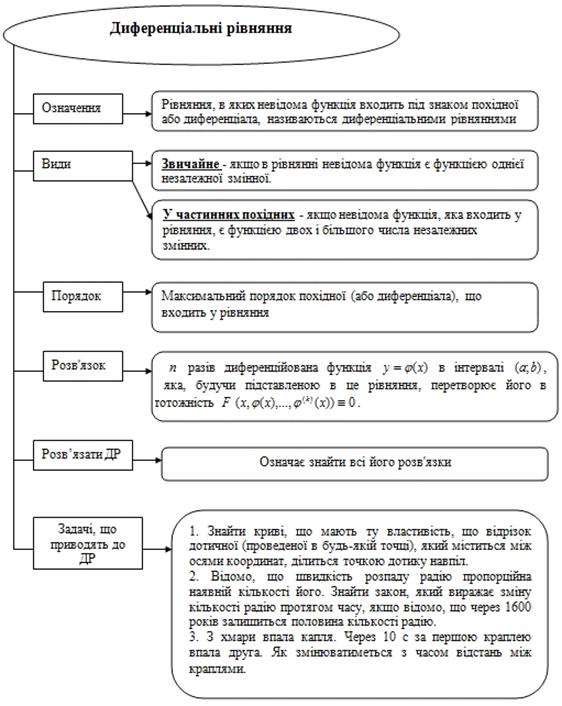
Лекція 2. Диференціальні рівняння першого порядку
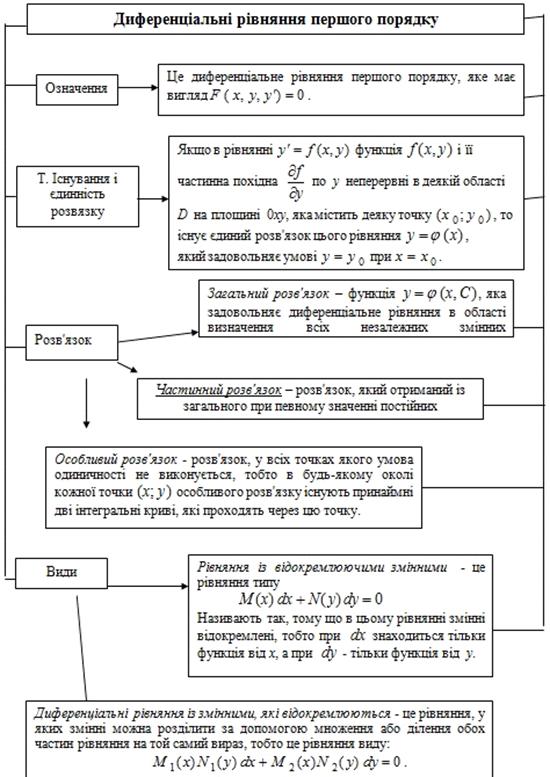
Лекція 3. Однорідні рівняння першого порядку


Лекція 4. Лінійні диференціальні рівняння першого порядку

Лекція 5. Диференціальні рівняння в повних диференціалах
Розробка практичних занять для змістовного модуля І
Практичне заняття 1
Тема: «Диференціальні рівняння з відокремлюючими змінними»
Мета:
– вироблення вмінь та удосконалення навичок розв’язувати
загальні диференціальні рівняння з відокремлюючими змінними;
– вироблення вмінь зводити диференціальне рівняння до
рівняння з відокремлюючими змінними;
– розвиток продуктивного мислення;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення диференціального рівняння з відокремлюючими
змінними, методи їх розв'язування;
уміти: застосовувати знання для розв'язування рівняння з
відокремлюючими змінними, зводити рівняння до рівняння з відокремлюючими
змінними;
здатні: розв'язувати загальні рівняння з відокремлюючими змінними.
Обладнання: підручники, дидактичний матеріал (таблиці), картки із
самостійною роботою, мультимедійний проектор, комп’ютер.
Час: 2 год.
План заняття
I. Організаційний момент.
II. Актуалізація опорних знань (термінологічний диктант).
III. Вироблення вмінь та навичок.
IV. Контроль.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
2. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
3. Матвеев Н.М. Сборник задач и упражнений по обыкновенным
дифференциальным уравнениям.
4. Самойленко Ф.М., Кривошея С.А., Перестюк Н.А. Дифференциальные
уравнения, примеры и задачи.
. Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным
уравнениям.
Хід заняття
I. Привітання із студентами,
повідомлення мети й завдань заняття, перевірка присутніх.
II. Мета етапу: визначення рівня засвоєння теоретичного матеріалу
студентами та рівня підготовки до практичного заняття.
Термінологічний диктант. Викладач називає терміни, які
студенти вивчали на першій та другій лекції, вони записують відповіді. Після
закінчення - взаємоперевірка (сусід перевіряє у сусіда), правильні відповіді на
проекторі.
|
Перший варіант 1. Яке рівняння називається диференціальним?
2. Записати загальний вид диференціального рівняння першого порядку. 3. Що
називається інтегральною кривою диференціальне рівняння у' =F (х;
у)? 4. Що називається загальним розв'язком диференціального рівняння у' =F (х;
у)?
|
Другий варіант 1. Яке диференціальне рівняння називається
рівнянням першого порядку? 2. Записати загальний вид диференціального
рівняння. 3. Що називається розв'язком диференціального рівняння у' =F (х;
у)? 4. Як із загального розв'язку одержати частинний розв'язок?
|
|
5. Яке
диференціальне рівняння називається рівнянням з відокремлюючими змінними?
|
III. Мета етапу: вироблення вмінь та удосконалення навичок
розв’язувати загальні диференціальні рівняння з відокремлюючими змінними.
Розв'язування задач та вправ.
1. Знайти загальний розв'язок рівняння: 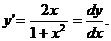
Розв'язування. 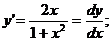
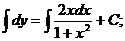
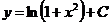 -
загальний розв'язок рівняння.
-
загальний розв'язок рівняння.
. Знайти сім’ю розв’язків рівняння 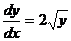 .
.
Розв'язування. Розглянемо рівняння
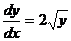 (1)
(1)
Його права частина f (х0; у0) 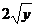 неперервна
при у
неперервна
при у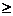 0, тобто
у верхній півплощині, включаючи вісь, Ох (область D'1).
Функція
0, тобто
у верхній півплощині, включаючи вісь, Ох (область D'1).
Функція 
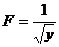 неперервна
при у>0, тобто у верхній півплощині, виключаючи вісь Ох
(область D1). Рівняння (1) має сім'ю розв'язків:
неперервна
при у>0, тобто у верхній півплощині, виключаючи вісь Ох
(область D1). Рівняння (1) має сім'ю розв'язків:
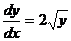 ,
,
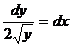 ,
, 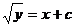 ,
(2)
,
(2)
де С - довільна стала. Формула (2) називається загальним розв'язком
рівняння (1). Тоді у = (х+с)2, при чому х+с>Q. В півплощині у>0 функція у = (х+с)2 є розв'язком початкового
рівняння.
. Знайти загальний інтеграл диференціального рівняння (відповідь
представити у вигляді 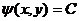 )
)
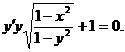
Розв'язування. 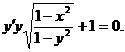
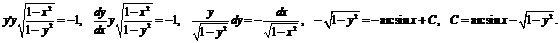
. Знайти загальний інтеграл диференціального рівняння. 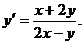
Розв'язування. 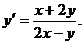
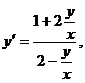
Вводимо заміну 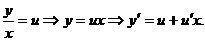
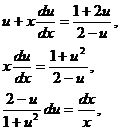
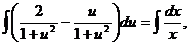
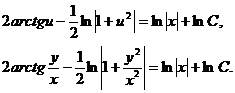
6. Знайти загальний інтеграл диференціального рівняння 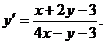
Розв'язування.
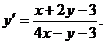
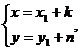
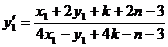
Нехай 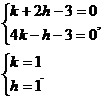
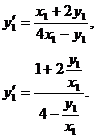
Вводимо заміну 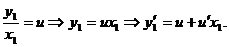
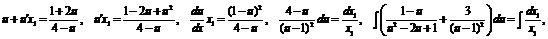
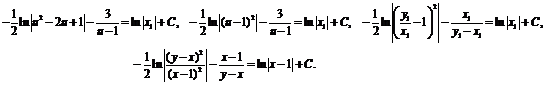
IV. Мета етапу: перевірка базових вмінь та навичок студентів
знаходити загальний інтеграл функції (з курсу математичного аналізу).
Самостійна робота (за варіантами). Перевіряється викладачем,
результати оголошуються на наступному занятті.
1. Обчислити
невизначені інтеграли: А)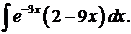
Б)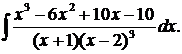
2. Знайти площу фігури, яка обмежена графіками
функцій.
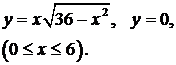 1. Обчислити
невизначені інтеграли:
1. Обчислити
невизначені інтеграли:
А) 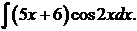
Б) 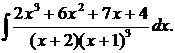
2. Знайти площу фігури, яка обмежена графіками
функцій.
Домашнє завдання: за підручником [1] розв’язати на ст. 11 (P.L. 1.1.) № 1 (10-15), № 2 (9-12).
Практичне заняття 2
Тема: «Однорідні рівняння та рівняння, що зводяться до них»
Мета:
– вироблення вмінь та удосконалення навичок розв’язувати
загальні однорідні диференціальні рівняння та рівняння, що зводяться до них;
– вироблення вмінь зводити диференціальне рівняння до
однорідного рівняння;
– розвиток продуктивного мислення;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення диференціального однорідного рівняння, методи
його розв'язування;
уміти: застосовувати знання для розв'язування однорідного рівняння
та рівняння, що зводиться до нього;
здатні: розв'язувати загальні однорідні рівняння.
Обладнання: підручники, дидактичний матеріал (таблиці), картки із
самостійною роботою, мультимедійний проектор, комп’ютер.
Час: 2 год.
План заняття
I. Організаційний момент.
II. Актуалізація опорних знань (тестові завдання).
III. Вироблення вмінь та навичок.
IV. Контроль.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
2. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
3. Матвеев Н.М. Сборник задач и упражнений по обыкновенным
дифференциальным уравнениям.
4. Самойленко Ф.М., Кривошея С.А., Перестюк Н.А.Дифференциальные
уравнения, примеры и задачи.
. Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным
уравнениям.
Хід заняття
I. Привітання із студентами,
повідомлення мети й завдань заняття, перевірка присутніх, оголошення й аналіз
результатів самостійної роботи.
II. Мета етапу: визначення рівня засвоєння теоретичного матеріалу
студентами та рівня підготовки до практичного заняття.
Студенти разом з викладачем обговорюють наступну задачу.
Задача 1. Серед даних рівнянь вказати однорідні
диференціальні рівняння:
а)
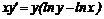 ;в)
;в) 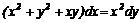 ;
;
б)
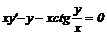 ;г)
;г) 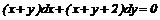 .
.
Розв’язуємо перше рівняння:
а)
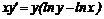 .
.
. Перетворюємо диференціальне рівняння.
Розділимо обидві частини рівняння на 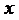 ; для виразу в дужках застосовуємо властивість, отримаємо:
; для виразу в дужках застосовуємо властивість, отримаємо:
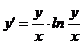 .
.
.
Права частина перетвореного
диференціального рівняння

є функцією нульового порядку однорідності так, як
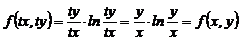 ,
,
то
диференціальне рівняння є
однорідним.
б)
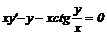 .
.
. Перетворюємо диференціальне рівняння.
Розділимо обидві частини рівняння на 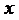 ; виразимо
; виразимо 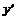 , отримаємо:
, отримаємо:
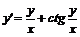 .
.
.
Права частина перетвореного
диференціального рівняння
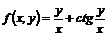
є функцією нульового порядку однорідності так, як
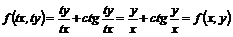 ,
,
то
диференціальне рівняння є
однорідним.
в)
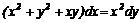 .
.
. Перетворюємо диференціальне рівняння.
Розділимо обидві частини рівняння на 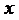 ; виразимо
; виразимо 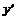 , отримаємо:
, отримаємо:
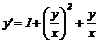 .
.
.
Права частина перетвореного
диференціального рівняння
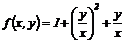
є функцією нульового порядку однорідності так, як
 ,
,
то
диференціальне рівняння є
однорідним.
г)
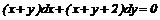 .
.
. Перетворюємо диференціальне рівняння.
Розділимо обидві частини рівняння на 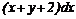 ; виразимо
; виразимо 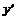 , отримаємо:
, отримаємо:
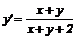 ,
, 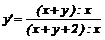 ,
, 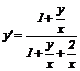
.
Права частина перетвореного
диференціального рівняння
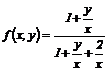
не
є функцією нульового порядку
однорідності так, як
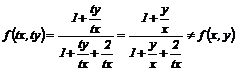 ,
,
то
диференціальне рівняння не є
однорідним.
Так отримали відповідь: а), б), в).
Цим самим студенти не лише актуалізують знання, але й
вироблять алгоритм зведення рівняння до однорідного.
III. Мета
етапу: вироблення вмінь та удосконалення навичок розв’язувати загальні
однорідні диференціальні рівняння та рівняння, що зводяться до них.
Розв'язування задач та вправ.
Задача 1 (розв’язують всі разом): розв’язати рівняння 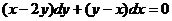
Розв'язування. Перевіряємо чи є дане рівняння однорідним:
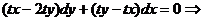
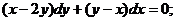
Як бачимо, дане рівняння - однорідне.
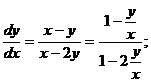
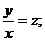 тоді
тоді 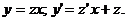
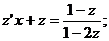
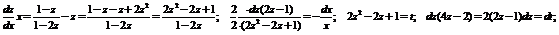
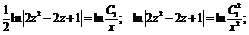
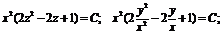
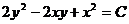 -
загальний розв'язок.
-
загальний розв'язок.
Особливих розв’язків не має.
Далі викладач розділяє студентів на дві групи, кожна з яких розв’язує
одне рівняння, але розв’язує досить детально, розписуючи кожен крок. Після чого
викладач навмання викликає одного студента з підгрупи, який доповідає по
розв’язуванню. Оцінюється робота за виступом доповідача та зробленою роботою
кожного учасника.
|
Завдання і
розв’язання першої групи
|
Завдання і
розв’язання другої групи
|
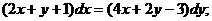
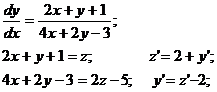
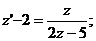
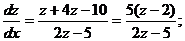
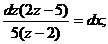

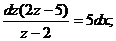
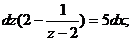
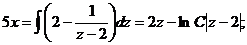
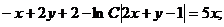
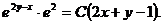
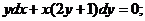
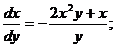
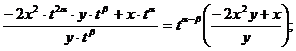
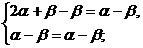
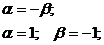
Робимо заміну:
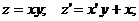
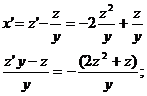
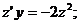
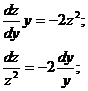
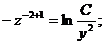
IV. Мета етапу: перевірка вмінь та навичок студентів розв’язувати
рівняння з відокремлюючими змінними.
Самостійна робота (за варіантами). Перевіряється викладачем,
результати оголошуються на наступному занятті.
Перший варіант 1.Розв’язати диференціальне рівняння: 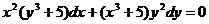
. Знайти загальний інтеграл рівняння: 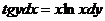 при
при 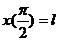 .Другий
варіант
.Другий
варіант
1.Розв’язати диференціальне рівняння: 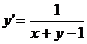
|
2. Знайти загальний
інтеграл рівняння: 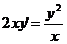
|
|
Домашнє завдання: за підручником [1] розв’язати на ст. 27 (P.L.1.3) №1(13-20).
Практичне заняття 3
Тема: «Рівняння, що зводяться до лінійних»
Мета:
– вироблення вмінь та удосконалення навичок на основі
лінійних рівнянь розв’язувати загальні диференціальні рівняння, що зводяться до
лінійних (рівняння Бернуллі, Ріккаті, Міндінг-Дарбу);
– вироблення вмінь зводити диференціальне рівняння до
лінійного рівняння;
– розвиток продуктивного мислення;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення диференціального лінійного рівняння та рівняння,
що зводиться до нього, методи їх розв'язування;
уміти: застосовувати знання для розв'язування лінійних рівнянь та
рівнянь, що до них зводяться;
здатні: розв'язувати загальні рівняння, що зводяться до лінійних.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські
матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План заняття
I. Організаційний момент.
II. Вироблення вмінь та навичок (виступи із заздалегідь підготовлені
доповідями).
III. Контроль.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
2. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
3. Матвеев Н.М. Сборник задач и упражнений по обыкновенным
дифференциальным уравнениям.
4. Самойленко Ф.М., Кривошея С.А., Перестюк Н.А. Дифференциальные
уравнения, примеры и задачи.
. Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным
уравнениям.
Хід заняття
I. Привітання із студентами,
повідомлення мети й завдань заняття, перевірка присутніх, оголошення й аналіз
результатів самостійної роботи.
II. Мета етапу: вироблення вмінь та удосконалення навичок
розв’язувати загальні диференціальні рівняння, що зводяться до лінійних.
Заздалегідь студенти були розділені на три групи, кожна з
яких готувала доповіді про види рівнянь, які зводяться до лінійних. Виступ
повинен містити: загальний вид рівняння та приклади розв'язування. Оцінювання
включає в себе: зміст виступу (оцінка - «4») та відповіді на додаткові
запитання групи та викладача (оцінка - «5»).
Виступ групи №1. «Рівняння Бернуллі»
Рівняння Бернуллі має вид: 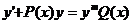
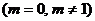
Розв'язування задач.
Задача 1. 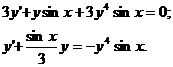
При розв’язуванні рівняння Бернуллі краще зразу використати підстановку
Бернуллі:
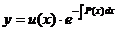
Отож, 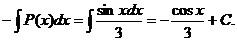
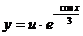 .
.
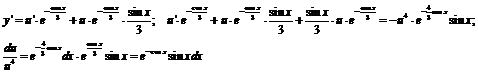
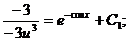
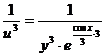
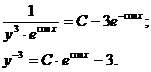
Задача 2. 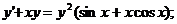
Застосовуємо підстановку Бернуллі:
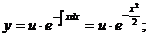
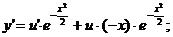
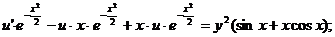
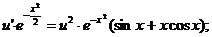
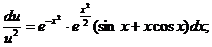
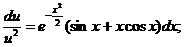
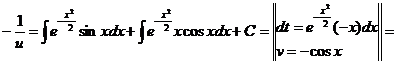
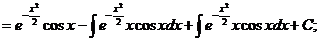
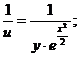
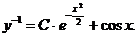
Виступ групи №2. «Рівняння Міндінг-Дарбу»
Рівняння Міндінг-Дарбу має вид 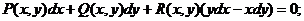 де
де
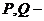 виміру
виміру  ,
,
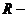 виміру
виміру 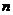 .
При розв’язуванні роблять заміну
.
При розв’язуванні роблять заміну 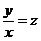 і
розв’язують як однорідне диференціальне рівняння.
і
розв’язують як однорідне диференціальне рівняння.
Розв'язування задач.
Задача 1. 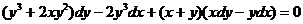
Робимо заміну: 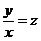 . Звідки
. Звідки 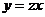 ,
,
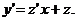
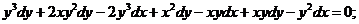
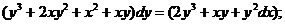
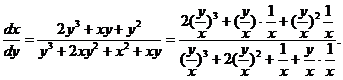
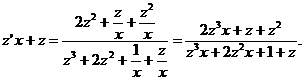
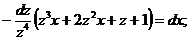
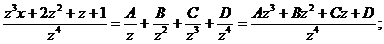
Методом невизначених коефіцієнтів знайшли невідомі:
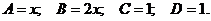
Задача 2. 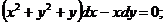
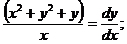
Робимо заміну: 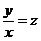 . Звідки
. Звідки 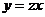 ,
,
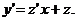
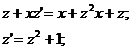
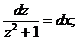
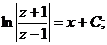 або
або
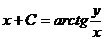 .
.
1. Виступ групи №2. «Рівняння Ріккаті»
Рівняння Ріккаті має загальний вид 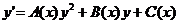 .
.
Звернути увагу!!!! 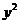 - обов’язковий елемент рівняння.
- обов’язковий елемент рівняння.
Для кожного виду рівняння Ріккаті існує своя підстановка:
або 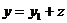 , або
, або 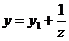 .
.
Щоб визначити, яку підстановку вибирати - треба перевіряти.
Розв'язування задач.
Задача 1. 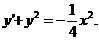
Вибираємо підстановку: 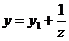 .
.
Тоді 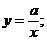
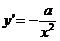 .
. 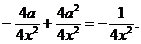
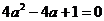
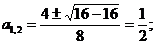
Тому 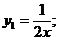 звідки:
звідки: 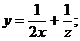
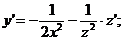
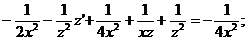
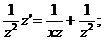
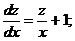
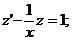
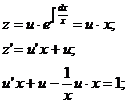
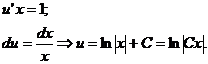
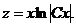
Підставляємо: 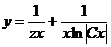
III. Мета
етапу: перевірка вмінь та навичок студентів розв’язувати однорідні
диференціальні рівняння та рівняння з відокремлюючими змінними.
Самостійна робота (за варіантами). Перевіряється викладачем, результати
оголошуються на наступному занятті.
Перший варіант 1.Розв’язати диференціальне рівняння: 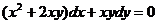
. Знайти загальний інтеграл рівняння: 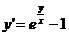 Другий
варіант
Другий
варіант
1.Розв’язати диференціальне рівняння: 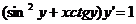
|
2. Знайти загальний
інтеграл рівняння: 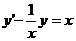
|
|
Домашнє завдання: за підручником [1] розв’язати на ст. 35 (P.L.1.4.) №1(15-21)
Практичне заняття 4
Тема: «Рівняння в повних диференціалах»
Мета:
– вироблення вмінь та удосконалення навичок розв’язувати
рівняння в повних диференціалах та рівняння, що зводяться до них;
– вироблення вмінь зводити диференціальне рівняння до
рівняння в повних диференціалах за допомогою інтегруючого множника;
– розвиток продуктивного мислення;
– виховання математичної культури.
При вивченні теми студенти повинні:
знати: означення інтегруючого множника, означення рівняння в
повних диференціалах, методи його розв'язування;
уміти: застосовувати знання для розв'язування рівняння в повних
диференціалах та рівняння, що зводиться до нього за допомогою інтегруючого
множника;
здатні: розв'язувати рівняння в повних диференціалах.
Обладнання: підручники, дидактичний матеріал (таблиці), картки із
самостійною роботою, мультимедійний проектор, комп’ютер.
Час: 2 год.
План заняття
I. Організаційний момент.
II. Вироблення вмінь та навичок.
III. Контроль.
Список літератури
1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
2. Давидов М.О. Курс математичного аналізу: Підручник: У
3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. - 2-ге вид.,
перероб. і допов. - К.: Вища школа, 1991 - 336 с.
3. Матвеев Н.М. Сборник задач и упражнений по обыкновенным
дифференциальным уравнениям.
4. Самойленко Ф.М., Кривошея С.А., Перестюк Н.А. Дифференциальные
уравнения, примеры и задачи.
. Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным
уравнениям.
Хід заняття
I. Привітання із студентами,
повідомлення мети й завдань заняття, перевірка присутніх, оголошення й аналіз
результатів самостійної роботи.
II. Мета етапу: вироблення вмінь та удосконалення навичок
розв’язувати рівняння в повних диференціалах та рівняння, що зводяться до них.
Розв’язування вправ.
Задача 1. Знайти загальний інтеграл диференціального рівняння
першого порядку:
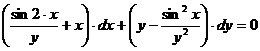
а) Перевіримо чи є це рівняння рівнянням в повних
диференціалах вигляду P(x; y)dx + Q(x; y)dy = 0.
Якщо 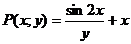 , а
, а 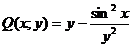 ,
то
,
то
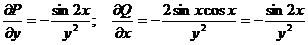 ,
тобто
,
тобто 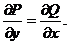
Таким чином, рівняння є рівнянням в повних диференціалах, де ліва
частина представляє собою повний диференціал деякої функції F(х;у):
dF(х; у) = 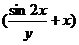 dx +
dx + 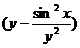 dy.
Тобто
dy.
Тобто 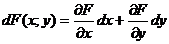 , то
, то
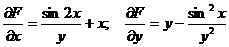 .
.
Із першого рівняння знайдемо: 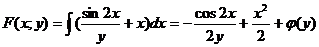 .
.
Диференціюємо по y та підставляємо в друге рівняння:
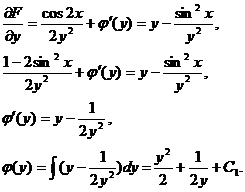
Тоді остаточно отримаємо:
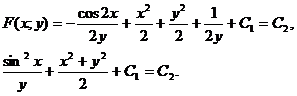
Задача 2. Знайти загальний розв'язок диференціального
рівняння.
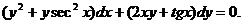
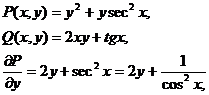
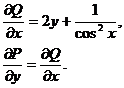

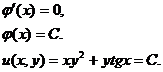
Задача 3. Розв’язати методом інтегрувального множника.
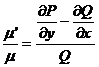 ,
коли функція залежить від
,
коли функція залежить від 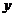 , то навпаки.
, то навпаки.
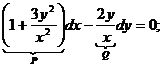
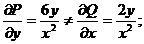
Умова не виконується. Робимо припущення, що існує множник 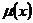 .
.
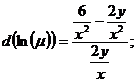
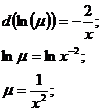
Множимо на 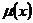 ліву та праву частини:
ліву та праву частини:
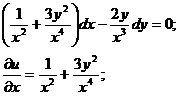
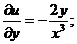
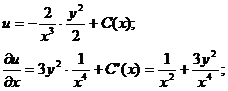
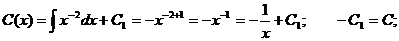
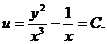
III. Мета
етапу: перевірка вмінь та навичок студентів розв’язувати диференціальні
однорідні та лінійні рівняння, рівняння з відокремлюючими змінними.
Самостійна робота (за варіантами). Перевіряється викладачем, результати
оголошуються на здачі модуля (практичної частини).
Перший варіант 1.Розв’язати диференціальні рівняння: А) 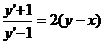 ;
;
Б) 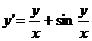 ,
,
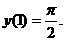
. Знайти загальний інтеграл рівняння: 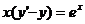 Другий варіант
Другий варіант
1.Розв’язати диференціальні рівняння:
А) 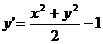 ;
;
Б) 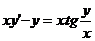 ,
,
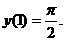
|
2. Знайти загальний
інтеграл рівняння: 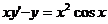
|
|
Домашнє завдання: за підручником [1] розв’язати на ст. 43 (P.L.1.5.) №1 (16-26)
Семантичний конспект до змістовного модуля I
Диференціальні рівняння, основні визначення
ü рівняння, в яких невідома функція
входить під знаком похідної або диференціала, називаються диференціальними
рівняннями;
ü якщо в диференціальному рівнянні невідома функція є функцією однієї
незалежної змінної, то таке диференціальне рівняння називається звичайним:  ;
;
ü якщо невідома функція, яка входить у диференціальне рівняння, є
функцією двох і більшого числа незалежних змінних, то таке диференціальне
рівняння називається рівнянням у частинних похідних;
ü порядком диференціального рівняння називається максимальний порядок
похідної (або диференціала), що входить у нього;
ü розв’язком диференціального рівняння називається 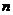 разів диференційована функція
разів диференційована функція 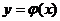 в інтервалі
в інтервалі 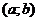 ,
яка, будучи підставленою в це рівняння, перетворює його в інтервалі
,
яка, будучи підставленою в це рівняння, перетворює його в інтервалі 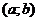 в тотожність
в тотожність 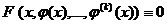 ;
;
ü розв’язати диференціальне рівняння - означає знайти всі його розв'язки;
ü операція знаходження розв’язків диференціального рівняння називається
інтегруванням цього рівняння;
ü задача інтегрування диференціального рівняння вважається розв’язаною,
якщо цю задачу звести до більш простої і вже вивченої в курсі інтегрального
числення задачі обчислення невизначених інтегралів.
Диференціальні рівняння першого порядку
ü диференціальне рівняння першого порядку має вигляд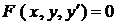 ;
;
ü якщо в рівнянні 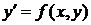 функція
функція 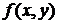 і
її частинна похідна
і
її частинна похідна 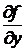 по у неперервні в деякій області D на
площині 0ху, яка містить деяку точку
по у неперервні в деякій області D на
площині 0ху, яка містить деяку точку 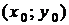 ,
то існує єдиний розв'язок цього рівняння
,
то існує єдиний розв'язок цього рівняння 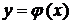 ,
який задовольняє умові
,
який задовольняє умові 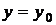 при
при 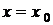 ;
;
ü умова, що при 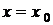 функція у повинна дорівнюватися заданому числу
функція у повинна дорівнюватися заданому числу
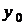 , називається початковою умовою, або умовою Коші:
, називається початковою умовою, або умовою Коші: 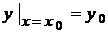 або
або 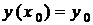 ;
;
ü задача, у якій потрібно знайти частинний розв'язок рівняння 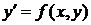 , який задовольняє початковій умові
, який задовольняє початковій умові 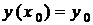 , називається задачею Коші;
, називається задачею Коші;
ü загальним розв'язком диференціального рівняння першого порядку
називається функція 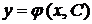 ;
;
ü рівність вигляду 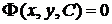 , яка неявно задає загальний розв'язок, називається
загальним інтегралом диференціального рівняння;
, яка неявно задає загальний розв'язок, називається
загальним інтегралом диференціального рівняння;
ü частинним розв'язком називається будь-яка функція 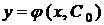 , яка утворюється з загального розв'язку
, яка утворюється з загального розв'язку 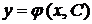 , якщо в останньому довільної сталої С придати
визначене значення
, якщо в останньому довільної сталої С придати
визначене значення 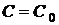 ;
;
ü співвідношення 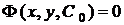 називається в цьому випадку частинним інтегралом
рівняння;
називається в цьому випадку частинним інтегралом
рівняння;
ü вирішити або проінтегрувати диференціальне рівняння - значить:
а) знайти його загальний розв'язок або загальний інтеграл
(якщо початкові умови не задані) або
б) знайти той частинний розв'язок рівняння, який задовольняє
заданим початковим умовам (якщо такі є);
ü особливим розв'язком називається такий розв'язок, у всіх точках якого
умова одиничності не виконується, тобто в будь-якому околі кожної точки 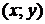 особливого розв'язку існують принаймні дві
інтегральні криві, які проходять через цю точку.
особливого розв'язку існують принаймні дві
інтегральні криві, які проходять через цю точку.
Диференціальні рівняння із відокремлюючими змінними
ü диференціальне рівняння типу  називають
рівнянням із відокремлюючими змінними, в цьому рівнянні змінні відокремлені,
тобто при
називають
рівнянням із відокремлюючими змінними, в цьому рівнянні змінні відокремлені,
тобто при 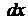 знаходиться тільки функція від х, а при
знаходиться тільки функція від х, а при 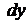 - тільки функція від у;
- тільки функція від у;
ü диференціальні рівняння, у яких змінні можна розділити за допомогою
множення або ділення обох частин рівняння на той самий вираз, називаються
диференціальними рівняннями із змінними, які відокремлюються: 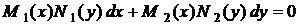 .
.
Однорідні рівняння першого порядку
ü функція 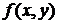 називається однорідною функцією n-го порядку щодо
змінних х і у, якщо при будь-якому t справедлива
тотожність
називається однорідною функцією n-го порядку щодо
змінних х і у, якщо при будь-якому t справедлива
тотожність 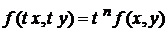 ;
;
ü рівняння виду 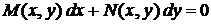 називається однорідним, якщо функції при
називається однорідним, якщо функції при 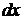 і
і 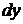 є
однорідними однакового порядку.
є
однорідними однакового порядку.
Лінійні диференціальні рівняння першого порядку
ü лінійним рівнянням першого порядку називається рівняння, що має вигляд 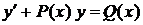 , де
, де 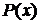 і
і
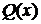 - задані неперервні функції від х (або сталі);
- задані неперервні функції від х (або сталі);
ü якщо 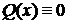 , то рівняння називається лінійним однорідним;
, то рівняння називається лінійним однорідним;
ü якщо 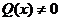 , то рівняння називається лінійним неоднорідним;
, то рівняння називається лінійним неоднорідним;
ü рівнянням Бернуллі
називається рівняня виду 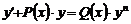 або
або 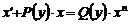 ;
;
ü суть методу Лагранжа полягає в тому, що спочатку знаходимо загальний
розв'язок відповідного лінійного однорідного рівняння 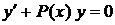
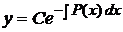 . Потім, вважаючи в цьому розв'язку сталу С
функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у
вигляді
. Потім, вважаючи в цьому розв'язку сталу С
функцією від х, шукаємо розв'язок лінійного неоднорідного рівняння у
вигляді 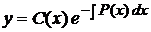 .
.
Диференціальні рівняння в повних диференціалах
ü рівняння 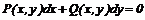 називається рівнянням в повних диференціалах, якщо
його ліва частина - повний диференціал деякої функції
називається рівнянням в повних диференціалах, якщо
його ліва частина - повний диференціал деякої функції 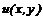 , тобто
, тобто 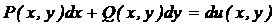 ;
;
ü необхідною і достатньою умовою повного диференціала є рівність
частинних похідних 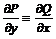 ;
;
ü загальний інтеграл рівняння в повних диференціалах має вигляд 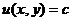 ;
;
ü щоб функція 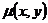 , неперервна в однов’язній області
, неперервна в однов’язній області 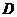 разом зі своїми частинними похідними
разом зі своїми частинними похідними 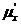 і
і 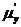 ,
була інтегруючим множником диференціального рівняння, необхідно і достатньо,
щоб для всіх точок
,
була інтегруючим множником диференціального рівняння, необхідно і достатньо,
щоб для всіх точок 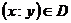 виконувалась рівність
виконувалась рівність 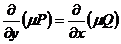 .
.
2.2 Контроль та корекція
Індивідуальні творчі завдання до змістовного модуля I
1. Скласти бібліографію з питань вивчення диференціальних
рівнянь першого порядку. До кожного джерела скласти анотацію.
. Розробити особистісну траєкторію вивчення матеріалу з теми
(за варіантами).
|
Номер варіанта
|
Тема
|
Номер варіанта
|
Тема
|
|
1.
|
Теорема Коші -
Пеано
|
6.
|
Єдиність розв’язку
задачі Коші.
|
|
2.
|
Початкова умова.
Задача Коші.
|
7.
|
Теорема Пеано.
|
|
3.
|
Поле напрямів.
Узагальнені інтегральні криві.
|
8.
|
Звичайні і особливі
точки диференціального рівняння.
|
|
4.
|
Ізокліни. Ламані
Ейлера.
|
9.
|
Теорема Коші.
|
|
5.
|
Відшукання
особливих інтегральних кривих диференціального рівняння за його загальним
інтегралом.
|
10.
|
Неперервна
залежність розв'язку диференціального рівняння від початкових умов і
параметра.
|
. Скласти семантичний конспект з диференціальних рівнянь на
відповідну тему (за варіантами).
|
Номер варіанта
|
Тема
|
Номер варіанта
|
Тема
|
|
1.
|
Диференціальне рівняння
першого порядку, його загальний розв'язок.
|
6.
|
Рівняння Ріккаті.
|
|
2.
|
Рівняння з
відокремлюючими змінними.
|
7.
|
Диференціальні
рівняння, що зводяться до однорідних.
|
|
3.
|
Однорідні
диференціальні рівняння.
|
8.
|
Задачі, що
приводять до диференціальних рівнянь.
|
|
4.
|
Поняття лінійного
рівняння, існування і єдиність розв'язку задачі Коші.
|
9.
|
Рівняння Бернуллі.
|
|
5.
|
Рівняння в повних
диференціалах.
|
10.
|
Рівняння Міндінг -
Дарбу.
|
. Розробити алгоритм розв’язування задачі, в якій
пропонується знайти загальний інтеграл диференціального рівняння.
|
Номер варіанта
|
Умова задачі
|
|
1.
|
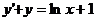
|
|
2.
|
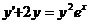
|
|
3.
|
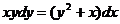
|
|
4.
|
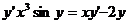
|
|
5.
|
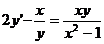
|
|
6.
|
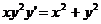
|
|
7.
|
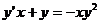
|
|
8.
|
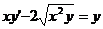
|
|
9.
|
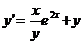
|
|
10.
|
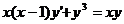
|
. Розв’язати задачі. Знайти загальний розв'язок
диференціального рівняння.
|
Номер варіанта
|
Умова задач
|
|
1.
|
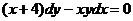 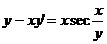
|
|
|
2.
|
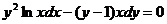 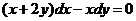
|
|
|
3.
|
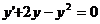 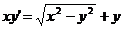
|
|
|
4.
|
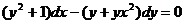 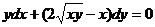
|
|
|
5.
|
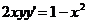 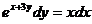
|
|
|
6.
|
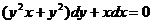 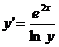
|
|
|
7.
|
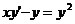 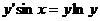
|
|
|
8.
|
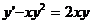 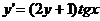
|
|
|
9.
|
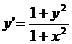 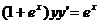
|
|
|
10.
|
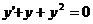 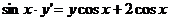
|
|
6. Розв’язати задачу.
|
Номер варіанта
|
Умова задачі
|
|
1.
|
Знайти рівняння
кривої, що проходить через точку М (1;2), якщо кутовий коефіцієнт проведеної
до нього дотичної дорівнює 4x3.
|
|
2.
|
Моторний човен
рухається в стоячій воді зі швидкістю 5 м/с. На повному ходу її мотор був
вимкнутий; через 4 с її швидкість стала рівної 1 м/с. Вважаючи, що сила опору
води пропорційна швидкості руху човна, визначити, через скільки секунд після
вимкнення мотора швидкість зменшиться до 4 см/с?
|
|
3.
|
Є М0 радіоактивної
речовини. Якщо за 30 років розпадається 50% його, те через скільки часу
залишиться 25% первісної кількості?
|
|
4.
|
Десятиметровий шар
води поглинає 40% світла ,що падає на її поверхню. На якій глибині денне
світло буде по яскравості таким же, як місячне світло на поверхні води, якщо
яскравість місячного світла складає 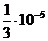 яскравості
денного світла? яскравості
денного світла?
|
|
5.
|
Є судина ємністю
а л, наповнений водним розчином солі. В судину вливається вода зі
швидкістю b л в хвилину, перемішується, і розчин ,що одержується однорідної
концентрації виходить з судини з тією ж швидкістю. Скільки солі буде
міститися в розчині в момент часу t, якщо в початковий момент (t=0) її було в
розчині A0 кг? Обчислити відповідь, якщо а=100 л, A0=10 кг, b=3 л в хвилину,
t=1 година.
|
|
6.
|
Металева деталь,
нагріта до 500°С, охолоджується в, повітрі при температурі 20 °С. Через 10
хвилин після початку охолодження температура на поверхні деталі понизилася до
100°С. Який буде температура на поверхні деталі через 20 хвилин?
|
|
7.
|
Послідовно
ввімкнені джерело струму з ЕРС Е, В, котушка з індуктивністю L, Гн (L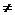 0) і активний опір R, Ом. Знайти закон зміни сили струму I(t) в ланцюгу, вважаючи, що в початковий момент
часу (t=0) вона
дорівнює нулю. Розглянути випадок коли ЕРС постійна - E(t)=E. 0) і активний опір R, Ом. Знайти закон зміни сили струму I(t) в ланцюгу, вважаючи, що в початковий момент
часу (t=0) вона
дорівнює нулю. Розглянути випадок коли ЕРС постійна - E(t)=E.
|
|
8.
|
Знайти швидкість v
(t) руху тіла, що падає в повітрі на землю, вважаючи силу опору повітря прямо
пропорційною швидкості руху і початкову швидкість рівної v0 м/с.
|
|
9.
|
Знайти швидкість v
(t) руху тіла, що падає в порожнечі на землю, вважаючи початкову швидкість
руху рівної v0.
|
|
10.
|
Через 12 годин
після початку досліду кількість бактерій зросла втроє. Вимога задачі: у
скільки разів збільшиться кількість бактерій через 3 доби?
|
Модульна контрольна робота змістовного модуля I
1. Серед
даних рівнянь вказати звичайне диференціальне рівняння першого порядку:
а)
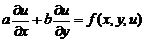 ; б)
; б) 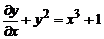 ;
;
в)
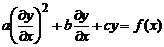 ; г)
; г) 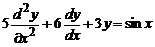 ;
;
д)
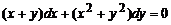 ; е)
; е)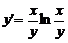 .
.
Відповідь: б); в); д); е).
.
Серед даних рівнянь вказати
рівняння з відокремлюючими змінними:
а)
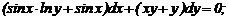 б)
б) 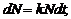
в)
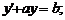 г)
г) 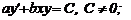
д)
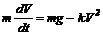 .
.
Відповідь: а); б); в); д).
. Серед рівнянь вказати лінійне:
а)
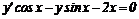 ; б)
; б) 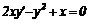 ;
;
в)
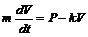 ; г)
; г) 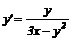 .
.
Відповідь: а), в), г).
. Серед рівнянь вказати те, яке одночасно є однорідним, в повних
диференціалах та лінійним:
а)
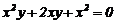 ; б)
; б) 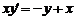 .
.
Відповідь: а); б).
. Серед рівнянь вказати те, яке одночасно є рівнянням з відокремлюючими
змінними, в повних диференціалах та лінійним:
а)
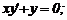 ; б)
; б) 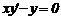 .
.
Відповідь: а).
. Серед інтегральних кривих, що задовольняють рівняння 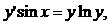 знайти ту, яка проходить через точку
знайти ту, яка проходить через точку 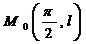
Відповідь: 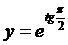 .
.
. Знайти загальний розв'язок диференціального рівняння:
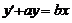 .
.
Відповідь: 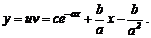
8. Знайти загальний інтеграл диференціального рівняння:
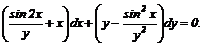
Відповідь: 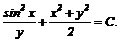
9. Знайти загальний розв'язок диференціального рівняння:
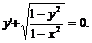
Вказівка: застосувати формулу
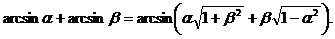
Відповідь: 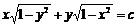 .
.
. Знайти загальний розв'язок диференціального рівняння:
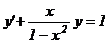 .
.
Відповідь: 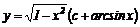 .
.
ВИСНОВКИ
На основі аналізу навчальної, методичної, науково-популярної
літератури було теоретично обґрунтувано цілі, зміст, форми, методи і засоби
методики навчання диференціальних рівнянь, розроблено та експериментально
обґрунтувано методику навчання диференціальних рівнянь майбутніх вчителів
математики в педагогічних університетах, проаналізовано навчальну програму з
метою вивчення диференціальних рівнянь в ВУЗах.
В роботі також створено і теоретично обґрунтовано основні компоненти
методичної системи навчання диференціальних рівнянь майбутніх учителів математики.
При цьому розв’язано такі задачі:
• визначено конструктивні цілі навчання диференціальних рівнянь, які відповідають загальним цілям
підготовки вчителя математики;
• розроблено навчальну програму курсу диференціальних рівнянь, спрямовану на професію вчителя
математики;
• визначено структуру і зміст курсу диференціальних рівнянь, розроблено і апробовано методику навчання одного (першого) модуля цього курсу, яка орієнтована на підготовку вчителя математики для різних типів навчальних
закладів;
• розкрито напрями удосконалення змісту навчального матеріалу курсу диференціальних рівнянь та методів навчання цієї дисципліни
для формування не тільки математичної культури
вчителя математики, а й інших основних компонентів
його професійної культури. Для даного модуля курсу диференціальних рівнянь визначено, чому цей розділ потрібен
майбутньому вчителю математики, на що він повинен
звертати особливу увагу (і як учитель математики,
і як математик), що з цього розділу вчитель може використати у своїй роботі безпосередньо, а що опосередковано;
• досліджено можливості різних форм навчання студентів у професійній
підготовці майбутніх учителів математики; розкрито можливості використання проблемних методів навчання для формування професійної культури
вчителя математики;
• проаналізовано особливості організаційних форм, методів, прийомів і
засобів навчання майбутніх учителів математики, в тому числі, можливості
використання сучасних інформаційно-комунікаційних технологій навчання та звернено увагу на можливі помилки, які можуть бути допущені,
якщо буде
недостатнім рівень математичної культури вчителів.
У даній роботі розглянуті методичні рекомендації щодо
вивчення одного (першого) змістовнго модуля курсу «Диференціальні рівняння» у
педагогічних вищих навчальних закладах. Ця робота належить до тієї невеликої
групи видань, які містять розробки планів-конспектів лекцій, практичних та
індивідуальних занять, модульних контрольних робіт. Також наявні завдання для
самостійної та індивідуальної роботи, розроблені модульні контрольні роботи.
Також досить цікавим виявиться те, що в роботі кожен бажаючий
зможе знайти опорний конспект до кожної лекції, короткий довідник модуля,
семантичний конспект теми. Це все подано в доступній, розгорнутій формі і стане
у нагоді як викладачам, так і студентам.
Матеріал роботи дозволяє виробити практичні навички в
розв’язуванні та дослідженні диференціальних рівнянь та їх систем, що описують
еволюційні процеси в різних областях.
Зміст диплому повністю охоплює програму з курсу звичайних
диференціальних рівнянь для вищих педагогічних навчальних закладів.
ВИКОРИСТАНА
ЛІТЕРАТУРА
1. Pudy A.E., Rakov S.A. Mathematical Analysis.
Differential Equations.
2. Адамар Ж. Исследования психологии изобретения в
области математики: Пер. с франц. / Ж. Адамар. - М.: Сов. радио, 1972. - 152
с.
. Аксёнов А.П. Математический анализ (Ряды
Фурье. Интеграл Фурье. Суммирование расходящихся рядов). / А.П. Аксёнов. - СПб:
НЕСТОР, 1999. - 87 с.
. Араманович И.Г. Уравнения математической
физики. / И.Г. Араманович, В.И. Левин. - М.: Наука, 1964. - 286 с.
5. Арнольд В.И. Обыкновенные дифференциальные уравнения. / В.И. Арнольд. - М.: Наука, 1966. - 456 с.
6. Атанов Г.А. Возрождение дидактики - залог развития высшей
школы. / Г.А. Атанов. - Донецк: ДОУ, 2003. - 180 с.
7. Атанов Г.А. Деятельностный подход в обучении. / Г.А. Атанов. - Донецк: ДОУ, 2001. -160 с.
8. Атанов Г.А. Обучение и искусственный интеллект или основы
дидактики высшей школы. / Г.А. Атанов, И.Н. Пустынникова. - Донецк: ДОУ, 2002. -
504 с.
9. Бабанский Ю.К. Оптимизация процесса обучения. / Ю.К. Бабанский. - М.: Педагогика, 1977. - 348 с.
. Бацевич О.Ф. Диференціальні рівняння. Курс лекцій
для студентів базового напряму «Електромеханіка». / О.Ф. Бацевич. - Львів:
Львівська політехніка, 2007. 40 с.
. Бевз В.Г. Геометрія: 10 - 11 класи. / В.Г. Бевз,
Г.П. Бевз, Н. Г. Владімірова. - К.: Вежа, 2002. - 224 с.
12. Бевз Г.П. Алгебра: 7 - 9 класи. / Г.П. Бевз. - К.: Освіта, 2001. - 304 с.
13. Бевз Г.П. Математика: 11 клас. / Г.П. Бевз. - К.: Освіта, 1995. - 192 с.
14. Бевз Г.П. Про числа // Математика в школі. / Г. П. Бевз. - 2001. № 1. - С. 6 - 9, - № 2.
- С. 2 - 3.
15. Бейтмен Г. Таблицы интегральных преобразований.
Преобразование Фурье, Лапласа, Меллина. Том 1. / Г. Бейтмен, А. Эрдейн.
- М.: Наука, 1969. - 344с.
16. Босс В. Лекции по математике: Дифференциальные
уравнения. / В. Босс. - М.: Едиториал УРСС, 2004. -
208 с.
17. Бохан К.А. Курс математического анализа. т. І-ІІ. / К.А. Бохан, И.А. Егорова, К.В. Лащенов.
- М.: Просвещение, 1972. - 392 с.
. Бронштейн И.Н. Справочник по математике. / И.Н. Бронштейн. - М., 1980. - 974 с.
19. Бугров Я.С. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного. / Я.С. Бугров, С.М. Никольский. - М.: Наука, 1968. - 564 с.
. Будак Б.М. Сборник задач по математической физике. / Б.М. Будак, А.А. Самарский, А.Н. Тиханов.
- М.: Наука, 1980. - 686 с.
21. Бурда М.І. Методичні основи диференційованого
формування геометричних умінь учнів основної школи: Автореф. дис. д-ра пед.
наук: 13.00.02. / М.І. Бурда. - К., 1994. - 36 с.
22. Бурда М.І. Математика: 10-11 класи. / М.І. Бурда, О.С. Дубінчук, Ю.І. Мальований.
- К.: Освіта, 1997. - 224 с.
23. Бутузов В.Ф. Математический анализ в вопросах и
задачах: Учебн. пособие. - 4-е изд., исправ. / В.Ф. Бутузов. - М.: Физико-математическая литература, 2001.
- 480 с.
24. Власова Б.А. Приближенные методы математической
физики: Учеб. для вузов / Б.А. Власова,
В.С. Зарубин, В.Н. Кувыркин. - М.:
Изд-во МГТУ им. Н.Э. Баумана, 2001. - 700
с.
25. Выгодский М.Я. Справочник по высшей математике. / М.Я. Выгодский. - М., 1957. - 783 с.
26. Гахов В.Д. Краевые задачи. / В.Д. Гахов. - М.: Государственное издательство физико-математической
литературы, 1958. - 543 с.
27. Годунов С.К. Уравнения математической физики. / С.К. Годунов. - М.: Наука, 1979. - 392 с.
. Давидов М.О. Курс математичного аналізу:
Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. /
М.О. Давидов. - 2-ге вид., перероб. і допов. - К.: Вища шк., 1991. - 366 с.
. Данко П.Е. Высшая математика в упражнениях и
задачах в двух частях: Ч. 1. / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.:
Высшая школа, 1986. - 416 с.
30. Державна національна програма “Освіта” (Україна ХХІ
століття). - К.: Райдуга, 1994. - 64 с.
31. Еругин Р.П. Курс обыкновенных дифференциальных
уравнений. /
Р.П. Еругин. - М.:
Наука, 1966. - 656 с.
. Жалдак М.И. Система подготовки учителя к использованию информационной технологии в учебном процессе: Автореф. дис.
докт. пед. наук. /
М.И. Жалдак. - М.: НИИ СИМО АПН СССР, 1989. - 48 с.
33. Жалдак М.І. Гуманітарний потенціал
інформатизації навчального процессу // Проблеми інформатизації освіти: Зб.
наук. праць. / М.І. Жалдак. - К.: УДПУ, 1994. - С. 3 - 20.
. Жалдак М.І. Гуманітарний потенціал
інформатизації освіти // Рідна школа / М.І. Жалдак. - 1990. - № 7 - 8. - С. 61
- 64.
35. Жалдак М.І. Комп’ютер на уроках математики. / М.І. Жалдак. - К.: Техніка, 1997. - 304с.
. Жалдак М.І. Педагогічний потенціал
інформатизації навчального процессу // Наукові записки Тернопільського
державного пед. університету імені В. Гнатюка. Серія: Педагогіка. / М.І.
Жалдак. - 2002. - № 6. - С. 143 - 154.
. Жалдак М.І. В. Комп’ютер на уроках геометрії.
/ М.І. Жалдак, О.В. Вітюк. - К.: НПУ імені М.П. Драгоманова, 2000. - 160 с.
. Жалдак М. І. Комп’ютер і елементи стохастики
в шкільному курсі математики // Комп’ютер в школі та сім’ї. / М.І. Жалдак, Ю.В.
Горошко. - 1998. - № 3.
- С. 5 - 8, № 4. - С. 4 - 7.
40. Кисилев А.И. Сборник задач по обыкновенным
дифференциальным уравнениям. / А.И. Кисилев, М.А. Краснов, Т. И. Макаренко. - М.: Наука, 1976. - 346с.
. Клейн Ф. Элементарная математика с точки
зрения высшей: Пер. с нем. - / Ф. Клейн. - М.: Наука, 1987.- 432 с.
42. Концепція математичної освіти 12-річної школи. Проект.
// Математика в школі. - 2002. - № 2. - С. 12 - 17.
43. Костюк Г.С. Актуальні психологічні питання
програмованого навчання // Психологія
навчання і виховання. / Г. С. Костюк. - К.: , 1964. - 124 с.
44. Костюк Г.С. Навчально-виховний процес і психічний
розвиток особистості. / Г.С. Костюк. - К.: Рад. школа, 1984. - 608 с.
45. Кудрявцев Л.Д. Курс математического анализа. /
Л.Д. Кудрявцев. - М.: Дрофа, 1996. - 350с.
46. Кузнецов Д.С. Специальные функции. Издание второе,
перераб. и допол. / Д.С. Кузнецов. - М.: Высшая школа, 1956. - 424 с.
47. Ладыженская О.А. Краевые задачи математической физики.
/ О.А. Ладыженская. - М.: Наука, 1973. - 408
с.
48. Ляшко И.И. Основы классического и современного
математического анализа. / И.И. Ляшко, В.Ф. Емельянов, А.К. Боярчук. - К.: Выща
шк. Главное изд-во, 1988. - 591 с.
49. Маркушевич А.И. Введение в теорию аналитических
функций. Учебн. Пособие для студентов физ-мат. фак. пед. ин-том. / А.И. Маркушевич, Л.А.
Маркушевич. - М.: Просвещение, 1977. - 320 с.
50. Матвеев Н.М. Методы интегрирования обыкновенных
дифференциальных уравнений. /Н.М.
Матвеев. - М.: Наука, 1966. - 656 с.
. Матвеев Н.М. Сборник задач и упражнений по
обыкновенным дифференциальным уравнениям. /Н.М. Матвеев. - М.: Наука, 1786. -
452 с.
52. Мордкович А.Г. Профессионально-педагогическая
направленность специальной подготовки учителя математики в педагогическом
институте: Дис. док. пед. наук: 13.00.02. / А.Г.
Мордкович. - М., 1986. - 380 с.
53. Мышкис А.Д. Лекции по высшей математике. / А.Д.
Мышкис. - М.: Наука, 1967. - 640 с.
54. Мэтьюз Дж. Математические методы физики. / Дж. Мэтьюз, Р. Уокер. - М: Атомиздат, 1976. - 400 с.
55. Никифоров А.Ф. Специальные функции математической
физики. / А.Ф. Никифоров, В.Б. Уваров. - М.: Наука, 1978. - 319 с.
56. Николенко Д.Ф. Становление учителя. / Д.Ф. Николенко,
Н. И. Шкиль. - К.: Знание, 1986. - 48 с.
. Никольский С.М. Курс математического анализа. Т. 1. - 3-е изд.,
перераб. и доп. / С.М. Никольский. - М.:
Наука, Главная редакция физико-математической литературы, 1983. - 464 с.
58. Очан Ю.С. Методы математической физики. / Ю.С. Очан. - М.: Высшая школа, 1965. - 383 с.
59. Пономарев К.К. Составление дифференциальных уравнений. / К.К. Пономарев. - М.: Наука, 1966. - 656
с.
. Попов И.Ю. Лекции по математической физике. / И.Ю. Попов. - СПб.: СПбГИТМО (ТУ), 1998. - 57 с.
. Самойленко А.М. Дифференциальные уравнения:
примеры и задачи. Учеб. пособие. - 2-е изд., перераб. / А.М. Самойленко, С.А.
Кривошея, Н.А. Перестюк. - М.: Высшая школа, 1989. - 383 с.: ил.
62. Саранцев Г.И. Общие вопросы методической подготовки
учителя математики в пединституте // Проблемы подготовки учителя математики в
пединститутах: Сб. тр. 51. / Г.И. Саранцев. - М. - 1977.- Вып. 4. - С. 20 - 29.
63. Свешников А.Г. Теория функций комплексной переменной.
/ А.Г. Свешников. - М.: Наука, 1970. - 304.
64. Слепкань З.И. Методика преподавания алгебры и начал
анализа. / З.И. Слепкань. - К.: Рад. школа,
1978. - 224 с.
65. Слепкань З.И. Методическая система реализации
развивающей функции обучения математике в средней школе: Дис. докт. пед. наук: 13.00.02. /
З.И. Слепкань. - М., 1987. - 47 с.
66. Слепкань З.И. Психолого-педагогические основы обучения
математике. / З.И. Слепкань. - К.: Рад. школа,
1983. - 192 с.
67. Слєпкань З.І. Про державний освітній стандарт з
математики // Математика в школі. / З.І. Слепкань.- 1998. - № 1. - С. 4 - 19.
68. Смирнов В.И. Курс высшей математики. Т. ІІ. / В.И. Смирнов. - М.: Наука, 1974. - 655
с.
69. Смирнов М.М. Дифференциальные уравнения в частных
производных второго порядка. / М.М. Смирнов. -
М.: Наука, 1964. - 206 с.
70. Смирнов М.М. Задачи по уравнениям математической
физики. / М.М. Смирнов. - М.: Наука, 1975. - 127 с.
. Соболев С.Л. Уравнения математической физики.
/ С.Л. Соболев. - М.: Наука, 1966. - 443 с.
72. Степанов В.В. Курс дифференциальных уравнений. / В.В.
Степанов. - М.: Наука, 1976. - 438 с.
. Стрижак Т.Г. Математичний аналіз: приклади і задачі.
Навч. посібник. / Т.Г. Стрижак, Н.Р. Коновалова. - К.: Либідь, 1995. - 240 с.
74. Тихонов А.Н. Уравнения математической физики. / А.Н. Тихонов, А.А. Самарский. - М.: Наука, 1977. - 735 с.
. Толстов Г.П. Ряды Фурье. / Г.П. Толстов. - М.: Государственное издательство технико-теоретической
литературы, 1981.
- 396 с.
76. Толстов Г.П. Элементы математического анализа. Том II.
/ Г. П. Толстов. - М.: Наука, 1966. - 464 с.
77. Филиппов А.Ф. Сборник задач по обыкновенным
дифференциальным уравнениям. / А.Ф. Филиппов. - М.: Наука, 1976. - 456 с.
. Фихтенгольц Г.М. Курс дифференциального и
интегрального исчисления. Том III. / Г.М. Фихтенгольц. - М.: Наука, 1966. - 656
с.
79. Флоров Н.А. Дифференциальное и интегральное
исчисление. / Н.А. Флоров. - М.:
Государственное учебно-педагогическое издательство, 1955. - 337 с.
. Черненко В.Д. Высшая математика в упражнениях
и задачах: Учебное пособие для вузов. В 3 т.: Т. 3. / В.Д. Черненко. - СПб:
Политехника, 2003. - 476 с.: ил.
81. Шиманський І.Є. До питання педагогізації
викладання математичних дисциплін в педагогічних інститутах // Наукові записки
Київського педінституту, 1955. / І.Є. Шиманський. - Т. XVII. - Пед. серія № 1. - С. 121 - 127.
82. Шкиль Н.И. Об опыте методической подготовки студентов
математиков в педагогических институтах УССР //
Совершенствование методической подготовки учителей математики в пединститутах
СССР: Материалы Всесоюзной научной
конференции. / Н.И. Шкиль. - К.: КГПИ, 1985. - С. 79 - 86.
83. Шкиль Н.И. Профессия - преподаватель математики //
Советская педагогика. / Н.И. Шкиль. - 1986. - № 2. - С. 72 - 75.