Расчет параметров нестационарного теплообмена
Расчётные данные
Исходные данные:
Стальная пластина (алюминий)
δ = 2S
= 0,3 [м] (толщина пластины)
l1 =
l2 =
0,8 [м] (длина и высота пластины)
Тf
=
600 [К] (температура среды)
Т0 = 300 [К] (температура пластины)
Тw
= 500 [К] (средняя по объёму температура пластины после нагрева «охлаждения»)
Величины, заданные в некотором интервале,
зависящие от температуры необходимо интерполировать.
Интерполяция (от лат. Interpolatio
- изменение, переделка), в математике и статистике, отыскание промежуточных
значений величины по некоторым её значениям.
Например отыскание значений x , лежащей в
интервале от от 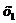 до
до 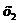
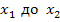 , по известным интервалам значения y1 и y2.
, по известным интервалам значения y1 и y2.
Пример определения теплоёмкости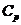 при
температуре Т0.
при
температуре Т0.
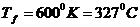
Пусть при 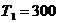
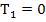 (0С);
(0С); 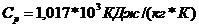
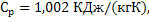 ,а при
,а при
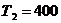 (
(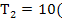 0С );
0С ); 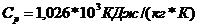
Определить 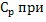
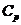 при Т0:
при Т0:
[400-300]=100 ед.
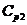 -
-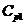
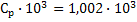 =
=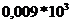
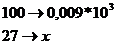
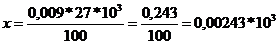
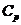 =
=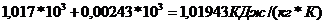
В данной работе нужно рассчитать
параметры нестационарного теплообмена.
Для этого необходимо рассчитать:
тепловой поток Qизл,
передаваемый в виде излучения (или отводимый от неё);
коэффициент теплоотдачи излучением 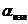 ;
;
критерии подобия (Pr, Gr, Nu);
коэффициент теплоотдачи конвекцией 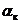 ;
;
суммарный коэффициент теплоотдачи 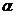 ;
;
коэффициент температуропроводности а;
критерии подобия (Bi, Fo),
корни характеристического уравнения 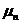 ,
,
среднюю по объёму безразмерную
температуру Θm через
интервал времени, выбранный произвольно;
среднюю по объёму температуру
заготовки Tm;
значение отклонения полученного
результата от заданного (не более 5 %);
искомый период времени с начала
процесса τ;
безразмерную температуру Θ не менее чем
для пяти значений относительной координаты X (0; 0,25; 0,5; 0,75, 1).
(Для построения графиков
распределения температур по толщине расчёт безразмерной температуры Θ следует
повторить для периодов времени 0,5τ, τ, 1,5τ.)
Тепловой поток излучения 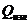
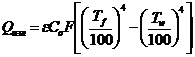 [Вт]
[Вт]
где ε - степень
черноты материала заготовки;
Со - коэффициент
излучения абсолютно чёрного тела, Со=5,67 Вт/(м2 К4);
F - площадь
поверхности излучения (торцы не учитывать) , (м2);
Тf -
температура охлаждающей жидкости или стенок нагревательной печи, (К);
Тw - текущая
температура заготовки, К. Предположим, что Тw= Т0.
Так как 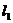 =
=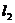 :
: 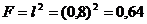 (м2)
(м2)
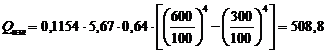 [Вт]
[Вт]
Коэффициент теплоотдачи излучения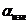
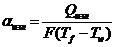 , [Вт/м2 К];
, [Вт/м2 К];
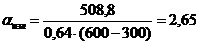 [Вт/м2 К]
[Вт/м2 К]
Число Прандтля 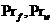

Следует рассчитывать Prf
- при температуре нагревающей (охлаждающей) среды, и Prw - при
температуре заготовки.
При 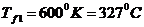 ,
,
коэффициент динамической вязкости 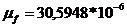 (
(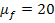
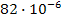 Па
Па
 );
);
теплоёмкость 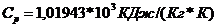
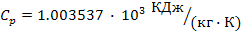 ;
;
Теплопроводность 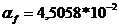 (
(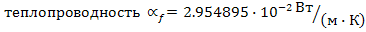 Вт/м2
К) ;
Вт/м2
К) ;
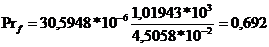
При 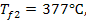
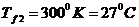
коэффициент динамической вязкости 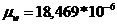 (
(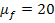
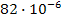 Па
Па
 )
)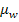 ;
;
теплоёмкость 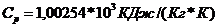 ;
;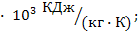
теплопроводность
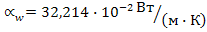 (Вт/м2 К );
(Вт/м2 К );
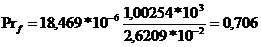
Число Грасгофа Gr
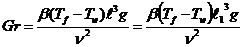
где 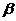 - коэффициент объёмного расширения;
- коэффициент объёмного расширения; 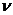 -
кинематическая вязкость;
-
кинематическая вязкость; 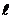 - линейный
размер; g - ускорение
свободного падения (9,81);
- линейный
размер; g - ускорение
свободного падения (9,81); 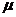 - коэффициент динамической вязкости;
- коэффициент динамической вязкости;
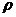 - плотность.
- плотность.
Определяющим линейным размером для
тел, расположенных вертикально, является высота, 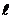 =
= 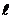 1.
1.
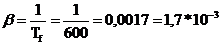
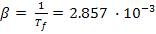 ;
;
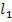
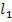 = 0.8 м; g=9.81м/
= 0.8 м; g=9.81м/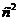 ;
;
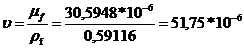 м/
м/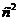 ;
;
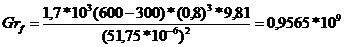 ;
;
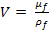

где В , n -
поправочный коэффициент и показатель степени для вертикальных и горизонтальных
поверхностей,
Таблица 3
|
вертикальные
|
горизонтальные
|
|
Grf Prf
|
103…109
|
>109
|
103…108
|
|
В
|
0,76
|
0,15
|
0,5
|
|
n
|
0,25
|
0,33
|
0,25
|
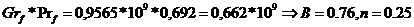 ;
;
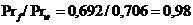 ;
;
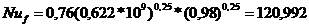
Коэффициент теплоотдачи конвекцией 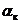
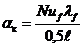 (Вт/м2 К);
(Вт/м2 К);
δ = 2S = 0,3 [м]
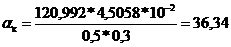 (Вт/м2 К).
(Вт/м2 К).
Тепловой поток 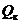
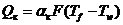 (Вт);
(Вт);
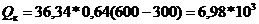 (Вт).
(Вт).
Суммарный коэффициент теплоотдачи 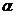
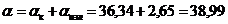 , (Вт/м2 К)
, (Вт/м2 К)
теплоемкость температура
излучение конвекция
Число Био Bi
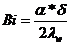 ,
,
где α- суммарный
коэффициент теплоотдачи, Вт/(м2·К);
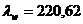
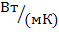
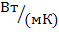 коэффициент
теплопроводности твёрдого тела;
коэффициент
теплопроводности твёрдого тела;
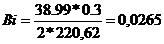 .
.
Коэффициент температуропроводности а
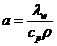 , (м2/ с)
, (м2/ с)
где 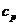 - удельная
теплоёмкость, Дж/(кг·К);
- удельная
теплоёмкость, Дж/(кг·К); 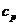 = 938,31
= 938,31
ρ - плотность материала, кг/м3;
ρ = 2784,45
При температуре Тw ,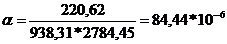 (м2/
с).
(м2/
с).
Критерий Фурье 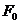
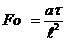
где а - коэффициент
температуропроводности, м2/ с;
ℓ - характерный линейный
размер, для случая симметричного нагрева равен половине толщины, м;
τ - период времени с начала
процесса, с.
В предварительном расчёте период
времени τ
принимается
произвольно.
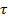
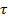 = 15000;
= 15000;
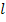
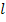 =
=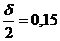
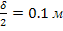 м;
м;
 =
= 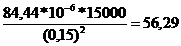
Безразмерная температура 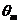
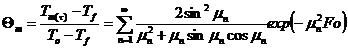 ,
,
Тm(τ)- средняя по
объёму температура заготовки, К;
То- начальная температура
заготовки, К.
Поскольку ряд быстро сходится, будем
учитывать три корня характеристического уравнения. При 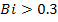
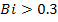 можно ограничимся первым членом
можно ограничимся первым членом
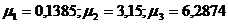
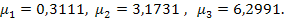
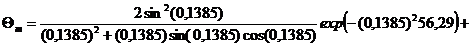
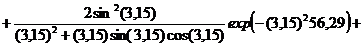
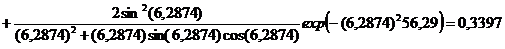
Средняя температура 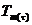
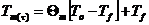 ,[К];
,[К];
Тm(τ) = 0,228 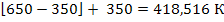
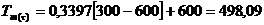 К;
К;
Тm=500 К.
Отклонение 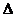
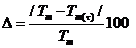
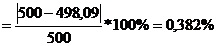
Безразмерная температура  в i-той точке
в i-той точке
i=хi/ℓ
(например, Х1=0; X2=0,25; X3=0,5; X4=0,75, X5=1)
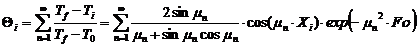
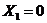
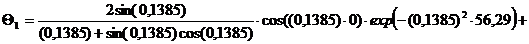
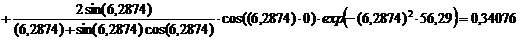
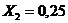
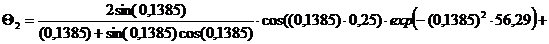
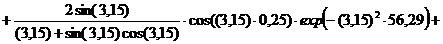
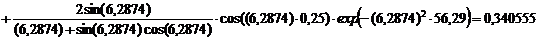
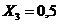
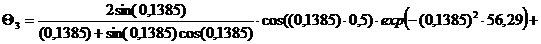
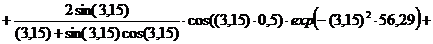
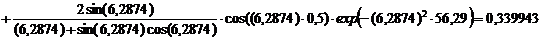

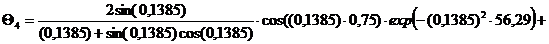
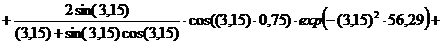
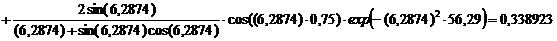
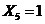
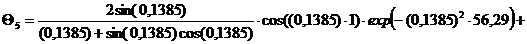
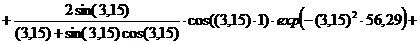
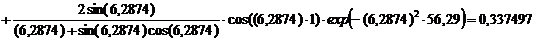
Текущие координаты 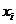
хi = Xi 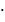
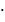 ℓ м;
ℓ м; 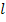
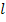 =
=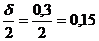
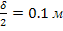 м;
м;
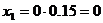 (м);
(м);
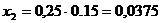 (м);
(м);
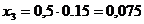 (м);
(м);
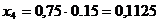 (м);
(м);
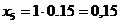 (м);
(м);
Температура в i-той точке 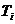
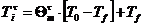 , (К) ;
, (К) ;
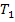
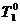 = 0,34076(300-600)+600=497,772 (K);
= 0,34076(300-600)+600=497,772 (K);
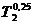 = 0,340555(300-600)+600=497,8335
(К);
= 0,340555(300-600)+600=497,8335
(К);
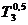 = 0,339943(300-600)+600=498,0171
(К);
= 0,339943(300-600)+600=498,0171
(К);
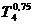 = 0,338923(300-600)+600=498,3231
(К);
= 0,338923(300-600)+600=498,3231
(К);
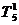 = 0,337497(300-600)+600=498,7509
(К).
= 0,337497(300-600)+600=498,7509
(К).
Безразмерная температура и средняя
температура для периода времени 0,5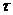 ;
;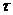 ;1,5
;1,5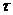
Для построения графика распределения
температур 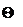 и
и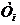 по толщине
для периодов времени
по толщине
для периодов времени 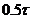 и
и 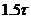 расчёт с
пункта 1.11 следует повторить.
расчёт с
пункта 1.11 следует повторить.
Для 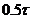
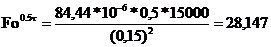
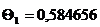
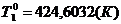
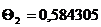
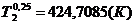
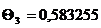
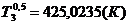
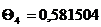
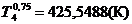
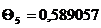
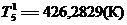
Для 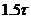
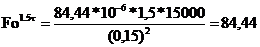
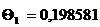
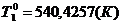
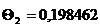
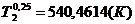
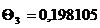
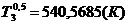
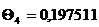
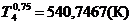
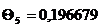
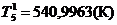
Расчётно-графический метод
Для получения значений температуры
по толщине заготовки можем так же использовать графический метод. С этой целью
воспользуемся данными представленными на диаграмме 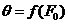 для числа
для числа 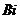 ,
соответствующим условиям задачи. В таблице 1 представлены координаты для точек
на поверхности и в средней плоскости пластины.
,
соответствующим условиям задачи. В таблице 1 представлены координаты для точек
на поверхности и в средней плоскости пластины.
Таблица 1.
На поверхности 1-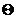 =0,66
=0,66
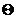 =0,14
=0,14
В средней пл.
-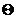 =0,5
=0,5
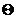 =0,5На поверхности
=0,5На поверхности
-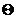 =0,92
=0,92
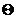 =0,08
=0,08
В средней пл.
-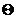 =0,84
=0,84
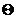 =0,16На поверхности
=0,16На поверхности
-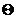 =1
=1
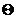 =0
=0
В средней пл.
-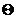 =0,92
=0,92
|
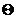 =0,08 =0,08
|
|
|
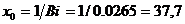 .
.
Список использованной литературы
. Теплотехника: учебник для Втузов/
А.М. Архаров, И. А. Кожинов, В. И. Исаев и др. Под общей редакцией В. И
Крутова.: Машиностроение 1986
. Теплотехника: учеб. Для вузов /
А.П. Баскаков, Б.В. Берг, О.К. Витт и др.; Под ред. Баскакова А.П.-М.: -2-е
изд., перераб. - М.: Энергоатомиздат, 1991.-224 с.