Расчет осесимметричных оболочек и толстостенных цилиндров

Расчет осесимметричных оболочек и толстостенных цилиндров

1. ОСЕСИММЕТРИЧНЫЕ ТОНКОСТЕННЫЕ ОБОЛОЧКИ

Напомним, что оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина оболочки) есть величина малая по сравнению с двумя другими размерами. Поверхность, равноудалённая от ограничивающих поверхностей называется срединной поверхностью. Оболочки могут иметь переменную толщину, однако мы будем рассматривать только оболочки постоянной толщины.

Оболочки имеют весьма широкое распространение в технике: корпуса судов, летательных аппаратов и ракет: сосуды для хранения жидкостей и газов; трубы; детали машин и приборов; оболочки покрытий в строительстве и т.д. Достоинством оболочек является то обстоятельство, что они обладают выгодными упругими свойствами: при малой толщине они способны выдерживать значительные нагрузки. Это позволяет создавать прочные и лёгкие конструкции, незаменимые в тех случаях, когда необходимо минимизировать массу изделия.

Будем рассматривать тонкие оболочки, у которых толщина мала по сравнению с радиусом кривизны поверхности. Если допустить обычную для технических расчётов относительную погрешность 5%, то тонкими оболочками можно считать такие оболочки, у которых: h / R < 1/20, где h - толщина, а R - радиус кривизны срединной поверхности оболочки. Приведенная граница, конечно, является условной, и, иногда, теорию тонких оболочек используют для расчёта более толстостенных конструкций, допуская при этом большие погрешности.

Наиболее распространённый вариант теории оболочек основан на гипотезе Кирхгофа - Лява:

1)   элемент, прямолинейный и нормальный к срединной поверхности до деформации, остаётся прямолинейным и нормальным к деформированной срединной поверхности;

2)   нормальными напряжениями на площадках, параллельных срединной поверхности, можно пренебречь.

Эти допущения совершенно аналогичны тем, что приняты для балок (гипотеза плоских сечений), и позволяют задачу трёхмерную свести к задаче двухмерной. Как при расчёте балок исследование сводится к изучению объекта одномерного - оси балки, так и в случае оболочек рассматривается только срединная поверхность.

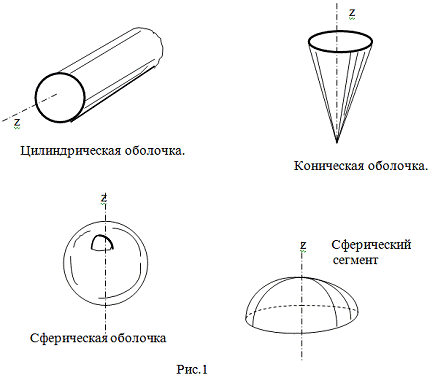
Нами будет рассматриваться лишь один тип оболочек - осесимметричные оболочки. Это оболочки вращения, срединная поверхность которых образована вращением некоторой кривой (в частном случае прямой) относительно оси симметрии. К этому классу относятся, например, цилиндрические, конические и сферические оболочки, столь часто встречающиеся в практике проектирования конструкций.

Мы будем придерживаться так называемой безмоментной теории оболочек, т.е. полагать, что нормальные напряжения по толщине оболочки распределяются равномерно и изгибающие моменты отсутствуют. Условия существования безмоментного напряжённого состояния следующие:

. Срединная поверхность оболочки должна быть достаточно плавной, так, чтобы радиус кривизны резко не изменялся и нигде не обращался бы в нуль;

1. Нагрузки, действующие на оболочку, должны быть так же достаточно гладкими и не должно быть сосредоточенных сил.

2. Условия закрепления краёв оболочки должны быть такими, чтобы по ним не возникали изгибающие моменты и поперечные силы.

Безмоментное напряжённое состояние чрезвычайно выгодно, т.к. приводит к равномерному, т.е. очень выгодному распределению напряжений и экономии материала.

Уравнение Лапласа.

Рассмотрим осесимметричную оболочку. Положение точки на срединной поверхности задаётся как пересечение двух координатных линий: параллели и меридиана.

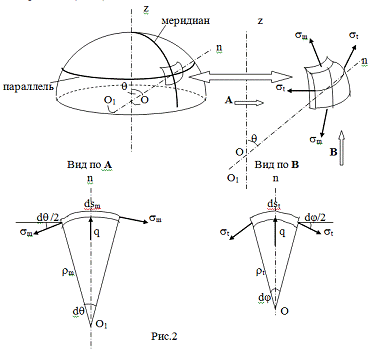
Радиус кривизны меридиана - r_m ; радиус кривизны параллели - r_t; внешняя нормаль к срединной поверхности в данной точке - n. Нагрузку, действующую на оболочку, будем считать осесимметричной, т.е. не меняющейся в пределах одной параллели, и нормальной к срединной поверхности оболочки. Такой, например, является гидростатическая нагрузка. Интенсивность нагрузки (нагрузка, приходящаяся на единицу площади) - q.

Выделим в окрестности произвольной точки малый элемент и исследуем его равновесие (Рис.2). Ввиду малости углов положим:

Sin(dq/2) » dq/2; Sin(dj/2) » dj/2.

Спроектируем силы, действующие на элемент, на направление норма- ли n.

-2s_mds_th(dq /2) - 2s_tds_mh(dj /2) + qds_mds_t = 0.

Учтём, что dq = ds_m/r_m; dj = ds_t/r_t, тогда получим:

s_m/r_m + s_t/r_t = q / h (1)

Это и есть уравнение Лапласа. Оно содержит две неизвестные: меридиональное и окружное напряжения. Второе уравнение мы получим, рассматривая равновесие части оболочки, отсечённой по той параллели, где мы ищем напряжения (Рис.3).

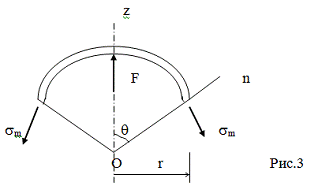
Пусть F - равнодействующая внешней нагрузки, приложенной к отсечённой части оболочки. В силу осевой симметрии она направлена по оси z. Проектируя силы, действующие на отсечённую часть, на ось z, получим:

s_m×2prh×Sinq = F . (2)

Определив из (2) s_m и подставив его выражение в (1), Найдём s_t.

Пример 1. Цилиндрический резервуар находится под действием внутреннего давления p (Рис.4). Определить напряжения в цилиндрической части резервуара, в местах достаточно удалённых от примыкания днищ. Последняя оговорка имеет тот смысл, что в тех местах, где днища соединяются с цилиндрической частью, напряжённое состояние не будет безмоментным, т.к. здесь радиус кривизны претерпевает резкое изменение.

Рассечём оболочку и составим уравнение равновесия для отсечённой части (Рис.4). Равнодействующая внешних сил, приложенных к отсечённой части, независимо от формы днища ( [1], стр.299 ), равняется:

F = pR²×p

Проектируя на ось z, имеем:

s_m×2pRh = pR²×p Þ s_m = pR /2h .

Обратимся к уравнению Лапласа: r_m® ¥; r_t=R; q = p Þ s_t = pR/h.

Главные напряжения равны: s₁ = s_t; s₂ = s_m; s₃ » 0.

Пример 2. Сферический замкнутый резервуар находится под действием внутреннего давления p. Найти напряжения, возникающие в оболочке. Радиус срединной поверхности оболочки R, толщина h. p Ввиду центральной симметрии s_m = s_t = s.

Из уравнения Лапласа следует: s = pR/2h.

Главные напряжения: s₁ = s₂ = s; s₃ » 0.

Обратим внимание на тот факт, что наибольшие напряжения в сферической оболочке в два раза меньше, чем в цилиндрической оболочке того же радиуса.

Пример 3. Замкнутая сферическая оболочка (Рис.6) с радиусом кривизны срединной поверхности R=100мм, толщиной h = 2мм, находящаяся под действием внутреннего давления p₁ = 54МПа, помещена в резервуар с давлением p₂ = 50МПа. Материал сталь: s_yt= 250МПа, s_yc = 300МПа.

Проанализировать напряжённое состояние и определить коэффициент запаса по текучести.

Решение

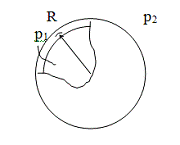
Разложим внутреннее давление p₁ на две составляющие: р₂ и р₁ - р₂ . Первая из них уравновешивает внешнее давление и вызывает в оболочке напряжённое состояние всестороннего сжатия, а вторая будет растягивать оболочку внутренним давлением (см. предыдущий пример).

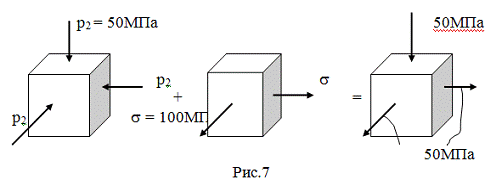
При всестороннем сжатии по всем трём направлениям возникают напряжения, равные - р₂ = - 50МПа. От действия избыточного давления р₁-р₂=2МПа, в оболочке возникают растягивающие напряжения (см.предыдущий пример):

s = (р₁-p₂)R/2h = 4МПа×100/(2×2) = 100МПа.

Складывая эти два напряжённые состояния, получим следующие значения главных напряжений:

s₁ = s₂ = 50МПа; s₃ = - 50МПа.

Т.к. материал имеет разные значения пределов текучести при растяжении и сжатии, то следует применить теорию Мора. Эквивалентные напряжения будут равны:

s_экв = s₁ - ks₃ , где k = s_yt/s_yc = 250/300 » 0,833; s_экв= 50 - 0,833(-50) =

= 91,7МПа.

Коэффициент по текучести n_y = s_yt/s_экв= 250/91,7 = 2,73.

Пример 4. Тонкостенная замкнутая оболочка R = 50мм, h = 1мм, подвергается действию внутреннего давления р = 2МПа и закручивается моментом m = 1кН×м (Рис.8). Проанализировать напряжённое состояние и найти коэффициент запаса по текучести, если: s_yt = s_yc = 300МПа.

Решение.

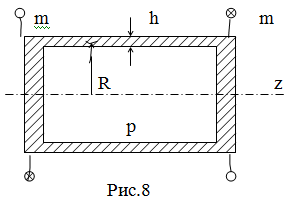
Данная конструкция работает под действием давления, как цилиндрическая R z оболочка (Пример 1) и , как тонкостенный стержень на кручение.

От действия давления в оболочке возникают окружные и меридиональные напряжения:

s_t = pR/h = 2МПа×50/1 = 100МПа; s_m = pR/2h = 50МПа (см.пример 1).

При кручении появляются касательные напряжения

t_tm = t_max = T/W_k,

где крутящий момент Т = m = 1кН×м = 100кН×см, а геометрическая характеристика

W_k = 2pR²h » 2×3,14×5²×0,1 = 15,7см³.

Таким образом касательные напряжения равны:

t_tm = 100/15,7 = 6,37кН/см² = 63,7МПа.

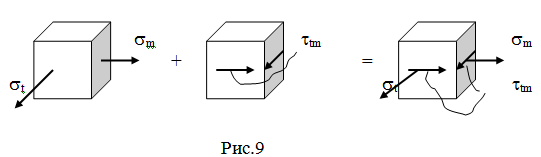
Напряжённое состояние будет двухосным. Главные напряжения найдутся:

s¢¢ = ½(s_m+ s_t) - ½Ö(s_m- s_t)² + 4t_tm²

Подставляя сюда найденные значения напряжений, найдём главные напряжения:

s¢ = 143,4МПа; s¢¢ = 6,6МПа.

Учитывая, что ещё одно главное напряжение равно нулю, поучим;

s₁ = 143,4МПа; s₂ = 6,6МПа: s₃ = 0.

Используем теорию наибольших касательных напряжений (критерий пластичности Треска - Сен-Венана):

s_экв = s₁ - s₃ = 143,4МПа.

Коэффициент запаса по текучести будет равен

n_y = s_yt/s_экв = 300/143,4 = 2,09.

Заметим, что согласно оговорке Примера 1, мы рассматривали точки цилиндрической части, достаточно удалённые от примыкания к днищам.

Пример 5. Резервуар для жидкости, показанный на Рис.10, доверху налит водой. Определить напряжения, возникшие в резервуаре. Материал - малоуглеродистая сталь с пределом текучести 240МПа. Толщина стенок резервуара

z d = 5мм; H = 9,93м; H₁ = 6,93м; R = 4м;

R a =p/6.

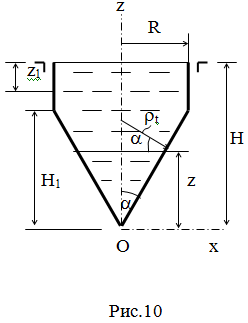
Плотность жидкости r=1000кг/м³.

Будем рассматривать только точки, достаточно удалённые от вершины конуса и от примыкания конической части резервуара к цилиндрической, т.к. в этих местах напряжённое состояние не будет безмоментным. Здесь возникнет так называемый краевой эффект - зона повышенных напряжений, простирающаяся на расстояние в несколько толщин оболочки.

Если материал оболочки достаточно пластичен, то напряжения перераспределяются и краевой эффект существенной роли не играет.

Решение.

1)   Коническая часть. Т.к. r_m ® ¥ то из уравнения Лапласа следует:

s_t = qr_t/d ,

где q = rg(H - z); g - ускорение силы тяжести,

r_t = z×tga/ cosa = z×sina/cos²a.

Тогда получим:

          rg×sina(Hz - z²)

s_t = ¾¾¾¾¾¾¾¾¾ (2)

          d×cos²a

Проанализируем полученную зависимость. В вершине конуса (с учётом приведенной выше оговорки) окружные напряжения равны нулю. При z=6,93м:

          10³кг/м³×9,8м/с²×0,5(9,93×6,93 - 6.93²)

s_t = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = 27,6×10⁶Па = 27,6МПа.

          5×10^-3м×0,866²

Найдём максимальное значение окружных напряжений:

ds_t/dz =0 Þ z = H/2, подставив в (2), получим:

          rgH²×sina 10³×               9,8×9,93²×0,5s_t = ¾¾¾¾¾¾ = ¾¾¾¾¾¾¾¾   = 32,2×10⁶Па = 32,2МПа.

          4d×cos²a 4×                     5×10^-3×0,866²

Определим меридиональные напряжения. Рассечём оболочку по параллели с координатой z и рассмотрим равновесие отсечённой части (Рис.11).

åF_z = 0 Þ(s_m×2pztga)cosa = G,

Где G = rgV; V - объём столба жидкости, приходящийся на отсечённую часть конуса: 

V = p(ztga)²z/3 + p(ztga)²z (H - z).

Учитывая это, получим:

          a z rg×sina( Hz - (2/3)×z²)

s_m = ¾¾¾¾¾¾¾¾¾¾¾ .

          O 2dcos²a

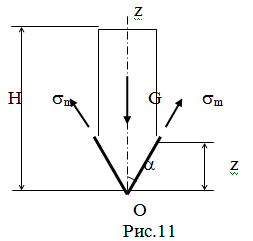
Закон распределения меридиональных напряжений - параболический, как и в случае окружных напряжений. Найдём экстремальное значение s_m:

ds_m/dz = 0 Þ z = 3H/4 = 7,45м > H₁ ,

т.е. внутреннего экстремума нет и наибольшее значение будет достигнуто при z = 6,93м. Подставляя это значение в формулу для меридиональных напряжений, получим: max s_m = 24МПа

2)   Цилиндрическая часть резервуара. Координату z₁ будем отсчитывать от уровня верха жидкости (Рис.10). Гидростатическая нагрузка равна:

q = rgz₁,

тогда, учитывая, что r_m ® ¥ , а r_t = R, из уравнеия Лапласа получим:

s_t = rgRz₁/d.

Закон распределения линейный. Наибольшие напряжения имеют место при z₁ = H - H₁ = 3м и равны:

max s_t = 23,5МПа.

Меридиальные напряжения не зависят от координаты z₁ и определятся, как результат деления веса жидкости всего резервуара площадь поперечного сечения цилиндра: s_m = 20,8МПа.

На Рис.12 показаны эпюры напряжений.

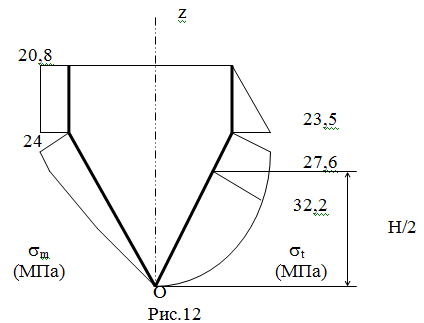
Обратим внимание на то обстоятельство, что несмотря на большие размеры резервуара и его малую толщину, напряжения в нём незначительны. Этим потверждается факт, что оболочки способны при малом расходе материала выдерживать большие нагрузки.

2. ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ

Рассмотрим цилиндр (Рис.13), у которого на соотношение между внутренним и наружным радиусом не наложено никаких ограничений. Нагрузку, действующую на цилиндр, будем считать осесимметричной и постоянной в направлении оси z.

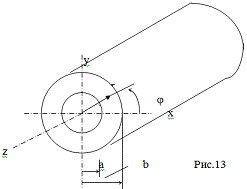
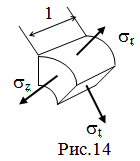
Введём цилиндрические координаты z, r, j. В силу осевой симметрии цилиндра и нагрузки, все искомые функции не зависят от j, а т.к. нагрузка постоянна вдоль оси, то и от z. Единственной независимой переменной будет полярный радиус r. Опять же по причине осевой симметрии, элемент, выделенный радиальными и цилиндрическими сечениями (Рис.14), не испытывает сдвига и касательные напряжения по его граням 1 отсутствуют. Т.е. площадки, образующие главные.

Поставим себе задачей найти закономерности распределения напряжений.

Приложим к элементу, размер которого в направлении оси z будем считать единичным, усилия и составим уравнение равновесия, проектируя силы на радиус (Рис.15).

s_r rdj + (d/dr)(s_r rdj)dr

s_r rdj + (d/dr)(s_r rdj)dr - s_r rdj - 2s_tdr(dj/2) = 0 Þ

(d/dr)(s_r r) - s_t = 0 Þ (ds_r/dr)×r + s_r - s_t = 0.s_r/dr + (s_r - s_t)/r = 0. (1)

оболочка осесимметричный толстостенный цилиндр

Выражение (1) представляет собой дифференциальное уравнение равновесия.

Рассмотрим геометрическую сторону задачи. Ввиду осевой симметрии перемещение любой точки направлено по радиусу и зависит только от радиальной координаты: u = u(r). Перемещение точек с полярным радиусом r: kk¢ = u, a точки с радиусом r + dr: mm¢ = u + (du/dr)dr (Рис.16).

Относительное удлинение в радиальном m¢ n¢ направлении:

m n e_r = (m¢k¢ - mk)/mk = (mm¢ - kk¢)/mk = k¢ l¢ = (u + (du/dr)dr - u)/dr Þ l

e_r =du/dr (2)

r dj

Относительное удлинение в окружном направлении:

s_t = (k¢l¢ - kl )/kl = ((r + u)dj - rdj)/(rdj) Þ

e_t = u /r (3)

Т.к. деформации e_r и e_t выражаются через одну и ту же функцию перемещение u, то они не могут быть независимыми и они связаны между собой соотношением, называемым уравнением совместности деформаций.

Из (3) Þ u = e_tr; du/dr = (d/dr)(e_tr), сопоставляя с (2), имеем:

(d/dr)(de_tr) = e_r Þ (de_t/dr)r + e_t - e_r = 0 Þe_t/dr + (e_t - e_r)/r = 0 (4)

Обратим внимание на структуру уравнения совместности деформаций. Уравнение (4) аналогично дифференциальному уравнению равновесия (1).

Обратимся к физической стороне задачи. Будем считать, что материал линейно-упругий и следует закону Гука:

e_r = (1/E)[s_r - n(s_t + s_z)],

e_t = (1/E)[s_t - n(s_z + s_r)],

e_z = (1/E)[s_z - n(s_r + s_t)]. (5)

Из последнего уравнения выразим осевые напряжения:

s_z = Ee_z + n(s_r + s_t),

подставив это в два первых, имеем:

e_r = ((1 - n²)/E)[s_r - (n/(1 - n))s_t],

e_t = ((1 - n²)/E)[s_t - (n/(1 - n))s_r]. (5a)

Введём функцию напряжений F = F(r), такую, что радиальное и окружное напряжение через неё выражаются:

s_r = F/r; s_t = F¢ = dF/dr. (6)

Легко убедится в том , что функция напряжений тождественно удовлетворяет дифференциальному уравнению равновесия (1). Таким образом, отпадает необходимость привлекать к решению уравнение (1), а надо лишь решить уравнение совместности (4), выразив в нём деформации через функцию напряжений. Подставим (6) в (5а):

e_r = ((1 - n²)/E)[F/r - (n/(1 - n))F¢],

e_t = ((1 - n²⁾/E)[F¢ - (n/(1 - n)(F/r]. (7)

Производная от окружной деформации:

de_t/dt = ((1 - n²)/E)[F¢¢ - (n/(1 -n))(F¢/r - F/r²)]. (8)

Подставив (7) и (8) в (4), получим следующее дифференциальное уравнение:

F¢¢ + F¢/r - F/r² = 0. (9)

Этого уравнения будем искать в форме F = Crⁿ, где С - произвольная постоянная, а n Î Z.

F¢ = Cnr^n-1; F¢¢ = Cn(n - 1)r^n-2,

подставив всё это в (9), и учитывая, что С¹0 и r¹0, произведём сокращения и получим:

n(n - 1) + n - 1 = 0 Þ (n - 1)(n + 1) = 0 Þ n₁ = 1; n₂ = -1.

Каждому значению n соответствует частное решение уравнения (9), а общее решение получится, как с умма линейно-независимых решений:

F = C₁r + C₂/r (10)

Радиальные и окружные напряжения определятся

s_r = F/r = C₁ + C₂/r², (11)

s_t = F¢ = C₁ + C₂ / r². (12)

Это и есть уравнения Ламе для определения напряжений в толстостенном цилиндре. Постоянные интегрирования определяются из граничных условий, т.е. из условий нагружения цилиндра.

Рассмотрим различные случаи нагружения цилиндра.

) Нагружение цилиндра внутренним давлением.

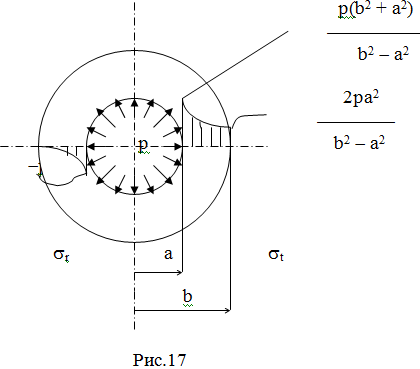
Пусть на цилиндр действует внутреннее давление р (Рис.17). Запишем граничные условия:

1)   при r = a: s_r = -p;

2)   при r = b: s_r = 0.

Подставляя это в (11), получим систему из двух алгебраических уравнений, из решения которой получим значения произвольных постоянных:

C₁ = pa²/(b² - a²); C₂ = - pa²b²/(b² - a²).

Подставив это в (11) и (12) получим:

          pa²

s_t/s_r = ¾¾¾ (1 ± (b/r)²). (13)

          b² - a²

Мы видим, что окружные и радиальные напряжения меняются по гиперболическому закону. Эпюры напряжений показаны на рис.17.

Обратимся к осевым напряжениям. Подставим (13) в выражение для s_z, полученное из последнего уравнения (5):

s_z = Ee_z + n(s_r + s_t) = Ee_z + 2npa²/(b² - a²).

Оказывается, что осевое напряжение по сечению цилиндра постоянно. Возможнны два различных случая:

) Цилиндр имеет днище (Рис.18).

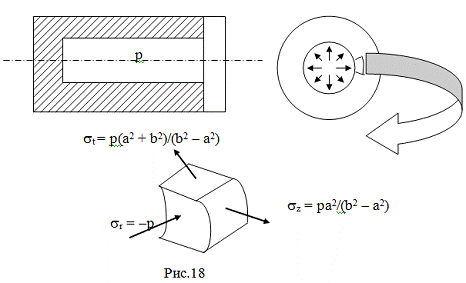
s_t = p(a² + b²)/(b² - a²)

s_z = pa²/(b² - a²)

s_r = -p

Сила, растягивающая цилиндр, равна произведению давления на площадь днища. Тогда осевые напряжения равны:

s_z = ppa²/p(b² - a²) = pa²/(b² - a²). (14)

Наиболее опасными являются точки внутреннего контура. Напряжённое состояние в них показано на Рис.18. Если использовать теорию наибольших касательных напряжений (критерий пластичности Треска - Сен-Венана), то эквивалентные напряжения найдутся:

s_экв = s₁ - s₃ = p(a² + b²)/(b² - a²) - (-p) Þ

s_экв=2pb²/(b² - a²) (15)

2) цилиндр открыт (например, ствол орудия). Осевые напряжения в этом случае равны нулю. На Рис.19 показано напряжённое состояние в наиболее опасной - внутренней точке. Т.к. эквивалентное напряжение не зависит от осевого напряжения, то оно определяется по той же формуле (15).

s_t = p(a² + b²)/(b² - a²)

s_r = - p

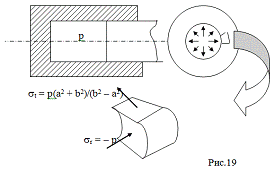
3)   Нагружение цилиндра внешним давлением.

Граничные условия запишутся:

1)   при r = a: s_r = 0;

2)   при r = b: s_r = - p.

Используя граничные условия, получим формулы для окружного и радиального напряжений.

                   pb²

s_t/s_r = - ¾¾¾ (1 ± (a/r)²). (16)

                   b² - a²

Закономерности распределения напряжений показаны на Рис.20. Эквивалентные напряжения определяются той же формулой (15).

Пример. Замкнутый толстостенный цилиндр (Рис.21) подвергается действию внутреннего давления р = 50МПа и растягивается внецентренно приложенной силой F = 400кН. Материал сталь: s_yt = s_yc = 300МПа. Размеры: а = =50м: b = 100мм. Проанализировать напряжённое состояние и определить коэффициент запаса по текучести.

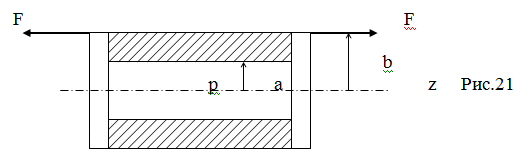
От внутреннего давления в цилиндре возникают напряжения:

r = a: s_t = p(a² + b²)/(b² - a²) = 50МПа×(5² + 10²)/(10² - 5²) =

= 83,3МПа; s_r = - p = - 50МПа;

при r = b: s_t = 2pa²/(b² - a²) = 2×50МПа×5²/(10² - 5²) = 33,3МПа; s_r = 0.

Осевые напряжения s¢_z = pa²/(b² - a²) = 16,7МПа.

От внецентренного растяжения нормальные напряжения равны:

s_z¢¢ = F/A + Fby/I_x, где А = p(b² - a²) = 3,14(10² - 5²) = 235,5см² ;_x = p(2b)⁴ (1 - (a/b)⁴ /64 = 3,14×20⁴ (1 - 0,5⁴)/64 = 7359см⁴;

- координата точки, в которой вычисляются напряжения. Вычислим напряжения в следующих точках (Рис.22):

1)   точка 1: y = 10см, s_z¢¢= 400/235,5 + 400×10×10/7359 = 7,14кН/см² =

= 71,7МПа;

2)   точка 2: y = 5см, s_z¢¢= 1,69 + 2,72 = 4,41кН/см² = 44,1МПа;

3)   точка 3: y = - 5см, s_z¢¢= 1,69 - 2,72 = 1,03кН/см² = -10,3МПа;

4)   точка 4: y = -10см, s_z¢¢= 1,69 - 5,44 = - 3,75кН/см² = -37,5МПа.

Если сложить эти напряжения с s_z¢ = 16,7МПА, то мы получим значения s_z = s_z¢ + s_z¢¢ соответственно равные: 88,4МПа, 60,8МПа, 6,4МПа, -20,8МПа.

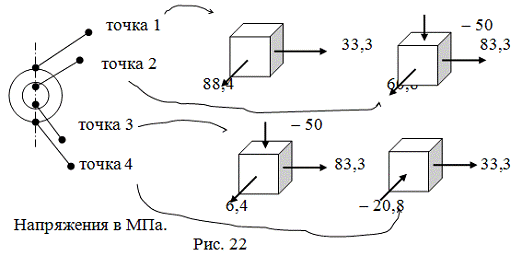
Эквивалентные напряжения по теории наибольших касательных определятся:

в точке 1 - s_экв = 88,4 - 0 = 88,4МПа;

в точках 2 и 3 - s_экв = 83,3 - (-50) = 133,3МПа;

в точке 4 - s_экв = 33,3 - (-20,8) =54,1МПа.

Наиболее опасными являются точки внутреннего контура. Коэффициент запаса по текучести равен:

n_y = s_yt/s_экв = 300/133,3 = 2,25.

Список литературы

1.Барташевич А.А. Материаловедение. - Ростов н/Д.: Феникс, 2008.

.Вишневецкий Ю.Т. Материаловедение для технических колледжей: Учебник. - М.: Дашков и Ко, 2008.

.Заплатин В.Н. Справочное пособие по материаловедению (металлообработка): Учеб. пособие для НПО. - М.: Академия, 2007.

.Материаловедение: Учебник для ВУЗов. / Под ред. Арзамасова Б.Н. - М.: МГТУ им. Баумана, 2008.

.Материаловедение: Учебник для СПО. / Адаскин А.М. и др. Под ред. Соломенцева Ю.М. - М.: Высш. шк., 2006.

.Материаловедение: Учебник для СПО. / Под ред. Батиенко В.Т. - М.: Инфра-М, 2006.

.Моряков О.С. Материаловедение: Учебник для СПО. - М.: Академия, 2008.

.Основы материаловедения (металлообработка): Учеб. пособие для НПО. / Заплатин В.Н. - М.: Академия, 2008.

.Ржевская С.В. Материаловедение: Учебник для ВУЗов. - М.: Университетская книга Логос, 2006.

.Солнцев Ю.П. Материаловедение: Учебник для СПО. - М.: Академия, 2008.

.Солнцев Ю.П. Материаловедение: Учебник для СПО. - М.: Академия, 2007.

.Справочник по конструкционным материалам. / Под ред. Арзамасова Б.Н. - М.: МГТУ им. Баумана, 2009.

.Черепахин А.А. Материаловедение: Учебник для СПО. - М.: Академия.

.Чумаченко Ю.Т. Материаловедение и слесарное дело: Учеб. пособие. - Ростов н/Д.: Феникс, 2009.

.Чумаченко Ю.Т. Материаловедение: Учебник для СПО. - Ростов н/Д.: Феникс, 2009.