Исследование и компьютерная визуализация движения диска по шероховатой поверхности

1. Теоретическая часть

1.1 Описание модели

.1.1 Твердое плоское тело круглой формы

Рассматривается задача о движении однородного плоского тела круглой формы в пространстве по наклонной плоскости, в конкретном смысле будем иметь в виду диск. Под однородным твердым диском подразумевается система одинаковых по своему составу материальных точек, которая целиком заполняет определенный объем пространства, и при этом расстояние между любыми двумя ее точками остается неизменным с течением времени. Поскольку диск круглый, то он динамически симметричен относительно центра масс, имеет конечный радиус и, соответственно, ограничен краем, имеющим форму окружности.

Диск осуществляет поступательное и вращательное движение. При этом на него действует сила тяжести:

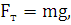
а также сила и момент трения, которые определяются в зависимости от используемого закона распределения давления: закона Герца или закона Галина.

1.1.2 Поверхность движения и место контакта тела с поверхностью

Поверхность, по которой происходит движение, абсолютно шероховатая, располагается в наклонной плоскости - под углом α к горизонту (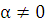).Диск соприкасается с плоскостью движения своей наибольшей по площади стороной (круглым основанием) и, таким образом, можно конкретизировать движение как скольжение с сухим трением. Таким образом, «пятном» контакта является вся плоская сторона диска, радиус «пятна» контакта равен радиусу самого диска. При этом, учитывая, что движение происходит безотрывное, возникает нормальная реакция опоры плоскости в области контакта:

.

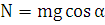1.2 Постановка задачи

Целью данной работы является визуализация движений диска по шероховатой поверхности, описываемых законами Герца и Галина соответственно, на основании численных экспериментов. В задаче рассматривается однородный твердый диск массы 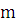и радиуса  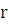и наклонная плоскость с трением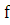, угол между плоскостью движения и горизонтальной плоскостью - 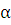. Возьмем массу и радиус за единицу массы и длины, соответственно (т.е. 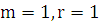). Пусть  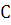- центр диска, тогда  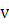- его линейная скорость, а 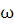 - угловая. Во время движения образуется угол, между линией наибольшего ската наклонной плоскости и направлением оси 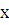. Обозначим его φ. Уравнения движения диска имеют вид:

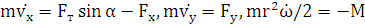. (1.1)

При этом ось 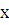 лежит в наклонной плоскости и направлена вдоль вектора скорости 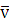, ось 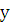также лежит в наклонной плоскости, но направлена ортогонально вектору скорости 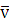, а ось 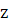- вдоль нормали к плоскости движения диска. Формулы для силы трения 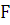 и момента трения  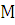определяются, в зависимости от выбранных законов распределения давления на диск. Во всех случаях это распределение будет радиально-симметричное, в отличие от работы [6].

Давление распределено по закону Герца.

Рассмотрим движения диска по наклонной плоскости в случае, когда давление на него распределено по следующему закону:

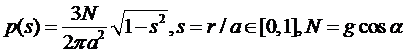
Если попытаться обосновать словами данный закон, то можно сказать, что в этом случае давление в центре диска невероятно большое (стремиться к бесконечности), а вдоль окружности, ограничивающий диск, т.е. «на краю» давление очень мало (стремиться к нулю). В этом случае уравнения силы и момента на диск выражаются следующими формулами:

При :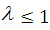

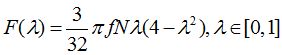
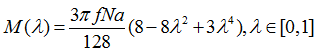
При :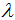

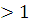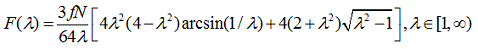
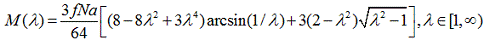
В этих формулах, как обычно обозначено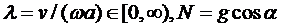

Здесь все зависит от коэффициента .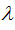

Давление распределено по закону Галина.

Рассмотрим случай, когда давление на диск распределено по закону Галина:

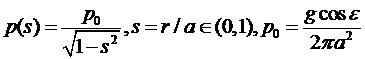
В этом случае можно сказать, что закон действует по обратному принципу, нежели закон Герца: давление на границе у края диска стремиться к бесконечности, а в центре - к нулю. Тогда сила трения и момент выражаются формулами:

При :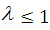

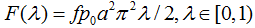
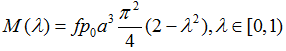
При :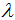

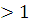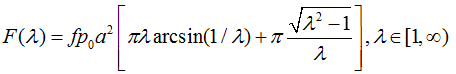
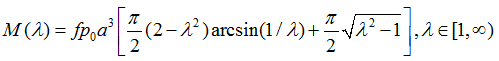
Здесь, как обычно, обозначено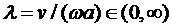

Уравнения движения.

Для нахождения траекторий движения диска, необходимых для построения визуализации, а также угла собственного поворота диска 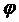, воспользуемся следующими дифференциальными уравнениями:

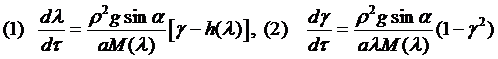
где обозначено

Функции 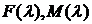 определены соответствующими формулами для соответствующего закона нормальных напряжений (Герца и Галина).

Также введем уравнение:

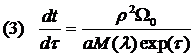
Наконец, к вышеуказанным дифференциальным уравнениям присоединим нужные нам уравнения для координат 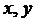 центра масс диска и угла  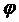его собственного поворота:

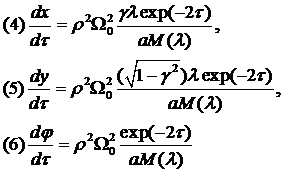
Решая систему из 6 данных уравнений, найдем искомые функции. Построим их графики и на основании графиков создадим наглядную визуализацию процесса движения диска.

В описанной модели под диском можно подразумевать монету, которая движется по наклонной плоскости своим круглым основанием, именуемым аверс / реверс. В качестве поверхности можно выбрать крышку стола, установленную в наклонной плоскости. Таким образом, наша модель находит реальное обоснование и может быть без труда воссоздана в реальных условиях.

Оба случая, описанные выше, будут разобраны с практической стороны в ГЛАВЕ II. Мы построим траектории движения диска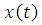и 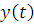, с помощью них создадим визуализацию движения диска при различных начальных условиях. Попытаемся прокомментировать полученные результаты, обосновать их.

2. Практическая часть

2.1 Предисловие к практической части

В этой главе приведены результаты решения систем, описанных в ГЛАВЕ I, а также их наглядная визуализация.

Все расчеты и графики будут сделаны в математическом пакете Maple 11. Для визуализации движения диска воспользуемся программой Macromedia Flash 8, как наиболее подходящей в данном случае. Для удобного просмотра, в зависимости от выбранных начальных условий и сравнения движения при разных законах в реальный момент времени, была написана программа на языке C#. Код программ можно увидеть в Приложении «Программный код».

2.2 Исследование динамики диска, результаты, обоснование

.2.1 Динамика диска при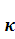>1

Итак, рассмотрим программную реализацию модели движения плоского диска по шероховатой поверхности. Под этим в данной работе подразумевается решение системы дифференциальных уравнений, описывающей движение диска. В зависимости от закона распределения давления, значения для силы трения и момента, используемые в системе, будут изменяться, но сама система постоянна. Будем приводить два графика для каждой величины - первый показывает результаты при законе Герца, второй - при законе Галина. Такой способ группировки результатов представляется наиболее удобным для сравнения и оценки. Масса и радиус всегда единичные, как и было решено. Отношение коэффициента трения к тангенсу угла наклона 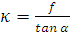больше единицы.

Начальные данные: 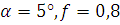, следовательно, ,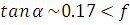

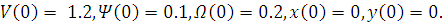
Остальные данные, такие как: ускорение свободного падения, вес и пр. можно увидеть в программном коде в Приложении. Вариация угла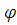 не влияет в целом на общие результаты, поэтому здесь не будет этого отображено. Данный угол будет всегда постоянным.

Поступательное и вращательное движение заканчиваются одновременно, как и должно быть.

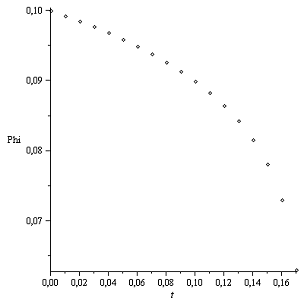
Получили интересные результаты. Они очень схожи с предыдущими. Остановка диска при законе Галина вновь происходит через 0.5 сек после начала движения, а при законе Герца - 0.16 сек. Графики совсем немного отличаются друг от друга. График при законе Галина немного более выпуклый. Можно говорить об их схожести.

Очевидно, что при законе Герца ситуация схожа с предыдущим случаем: угол между линией наибольшего ската и направлением скорости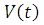сначала изменяется медленно (около 0.1 сек), а затем - довольно быстро. Как показывают графики скоростей - линейная скорость в это точке (t=0.1) начинает изменяться медленнее, а угловая - немного быстрее.

Здесь ситуация различная. При законе Герца график вполне характерен, так как график скорости изменяется почти равномерно. А вот при законе Галина график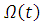довольно вогнутый, а график  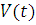в начале движения слегка выпуклый. Логично, что линейная скорость всегда больше угловой - получаем соответствующий график. Однако, кажется подозрительной немного резкая остановка диска, но учитывая большой коэффициент трения и довольно малые (к этому моменту) скорости - вероятной.

Траектории, как уже было сказано, вполне характерные и будут такими всегда, поскольку напрямую зависят лишь от линейной скорости движения.

Итак, теперь попробуем уменьшить коэффициент трения, поскольку он довольно много больше тангенса угла наклона. Уменьшим его вдвое. Остальные начальные данные оставим без изменений.

Итак: 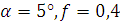, следовательно, ,

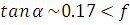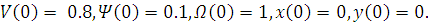
Время движения увеличилось, что логично, поскольку коэффициент трения стал меньше. Однако вновь при законе Галина диск останавливается за большее время, 1.3 сек. При законе Герца - за 0.4 сек. Графики немного схожи по форме, но при законе Герца график совсем немного вогнут, а при законе Галина - наоборот. Под «схожей формой» понимается схожий характер движения, т.е. с одинаковым числом экстремумов, без резких убываний или возрастаний и пр.

При законе Галина график вогнут немного сильнее. Изменение рассматриваемой скорости при законе Герца для невооруженного взгляда представляется равномерным (при численном анализе выясняется, что это не совсем так - график слегка выпуклый).

График Φ(t):

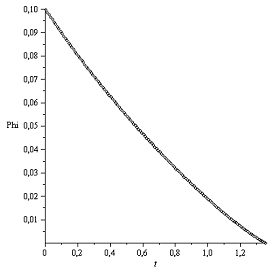
Закон Герца Закон Галина

Угол между линией наибольшего ската и направлением линейной скорости при законе Герца вновь подчиняется такой же закономерности, что и ранее. В другом случае распределения давления на диск график данного угла вогнут.

График k(t)

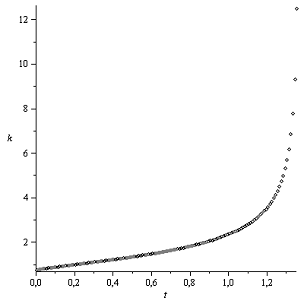
Закон Герца Закон Галина

Аналогично предыдущему случаю, здесь график коэффициента 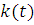 при законе Галина возрастает потому, что график линейной скорости при этом законе слегка выпуклый, а угловой скорости - вогнутый, потому коэффициент, равный отношению линейной скорости к угловой, всегда возрастает. Момент остановки диска почти аналогичен предыдущему случаю.

Траектории - график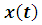ии: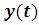

Закон Герца

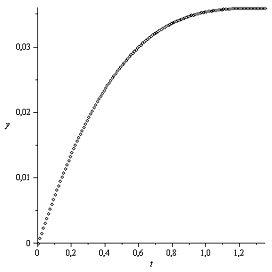
Закон Галина

Вывод (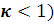: При распределении давления по закону Герца характерной чертой является: быстрая остановка диска, медленное изменение угла 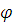 в первой половине движения, и резкое его уменьшение во второй. Напомним, что закон Герца и закон Галина представляют собой две противоположности распределения давления (хотя оба распределения осесимметричные): в первом случае давление сосредоточено в центре, а во втором - по краю диска. Получается, что если осуществлять давление только на центр диска, то сила трения будет действовать сильнее на объект, и он будет скользить медленнее. А вот распределение давления по краям диска почти не отличается от равномерного распределения. Попробуем, для уверенности, сравнить полученные результаты для закона Галина с другими работами. Например, в [8] рассматривается аналогичная модель, при этом давление на диск распределено по закону Галина. В качестве примера практической реализации взята следующая начальная модель: линейная скорость больше угловой (причем во много раз), угол наклона плоскости движения равен нулю, поэтому диск останавливается за конечное время. Полученные в [8] графики для 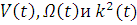 (см. Приложение «Графики других работ») имеют такую же «форму», как графики, полученные в данной работе с аналогичной начальной ситуацией (только лишь линейная скорость не так превосходит угловую - см. стр. 21).

2.2.2 Динамика диска при 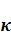<1

Рассмотрим динамку диска в случае, когда отношение коэффициента трения к тангенсу угла наклона 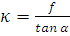меньше единицы.

Начальные данные: 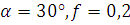, следовательно, ,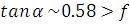

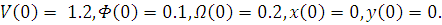
Соответственно, линейная скорость больше угловой.

График V(t):

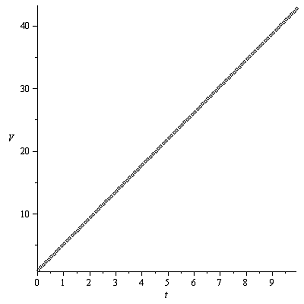
Закон Герца Закон Галина

Графики показывают, что диск не останавливается (по крайней мере, в течение десяти секунд, но можно быть уверенным, что не останавливается никогда). Графики равномерно растут, при этом в случае распределения давления по закону Герца - диск движется немного медленнее, но также равномерно.

График Ω(t):

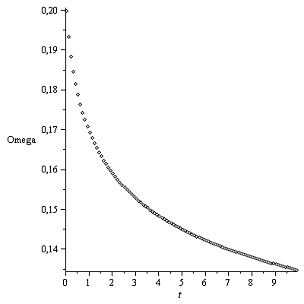
Закон Герца Закон Галина

Рассмотрим графики угловых скоростей. Наблюдается интересный эффект: через, приблизительно, семь секунд после начала движения угловая скорость при законе Герца начинает немного «колебаться», движение якобы перестает быть равномерным. При этом коэффициент трения взят 0.2. Аналогичная ситуация наблюдается при меньшем значении коэффициента, но при большем (хотя бы на несколько сотых) этого не происходит. Возможно, здесь «виноваты» рекуррентные формулы Рунге-Кутты. Как видно на графиках, приблизительно, через десять секунд от начала процесса, движение становится исключительно поступательным. Верчение диска останавливается.

График Φ(t):

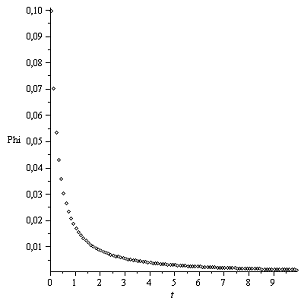
Закон Герца Закон Галина

Угол между линией наибольшего ската и направлением линейной скорости движения диска в первые секунды времени уменьшается быстро, затем довольно медленно, в обоих случаях распределения. Ситуация кажется логичной, поскольку угловая скорость начинает затухать, а линейная неуклонно растет, мешая диску приблизиться к линии наибольшего ската.

График k(t)

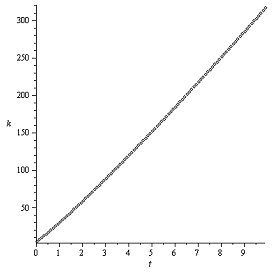
Закон Герца Закон Галина

Как и следовало ожидать, график функции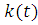 при законе Герца начинает немного «колебаться» после, приблизительно, семи секунд движения (как и график угловой скорости). Оба графика возрастают, имея легкую вогнутость, поскольку угловая скорость уменьшается, и отношение линейной скорости к угловой становиться больше с каждым шагом. После, приблизительно, десяти секунд движения графики должны стать равномерно возрастающими, копируя график линейной скорости (ведь верчение остановиться к этому времени).

Траектории - график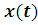и и: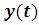

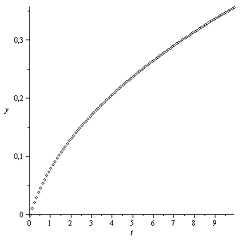
Закон Герца

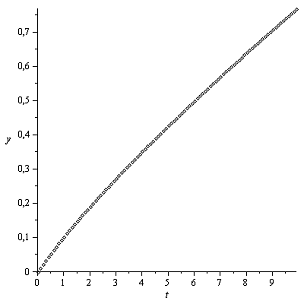
Закон Галина

Графики траекторий весьма характерные. Вогнутость графиков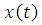и выпуклость графиков  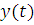объясняется увеличением скорости 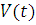 и приближением диска к линии наибольшего ската.

Рассмотрим другие начальные данные:

Оставим без изменений: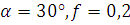. Изменим начальные скорости:

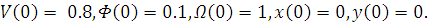
Получается, что в этом случае угловая скорость больше линейной.

График V(t):

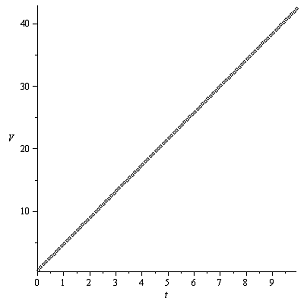
Закон Герца Закон Галина

Ситуация, аналогичная предыдущей. Причем, скорость к концу рассматриваемого интервала времени, для невооруженного глаза кажется такой же, как ранее. (Если сравнивать численные показатели, то в данном случае скорость на 0.37511506 меньше, чем в предыдущем).

График Ω(t):

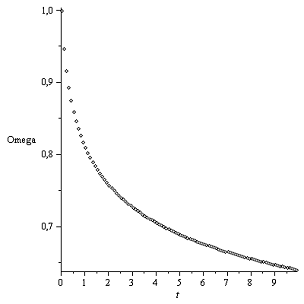
Закон Герца Закон Галина

Графики почти похожи.

График Φ(t):

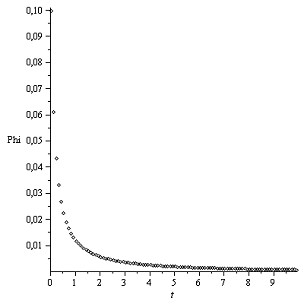
Закон Герца Закон Галина

График k(t)

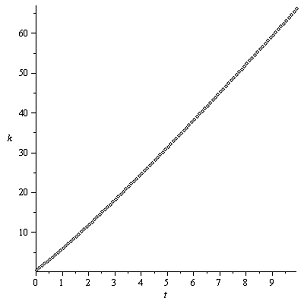
Закон Герца Закон Галина

Траектории - график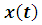ии: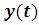

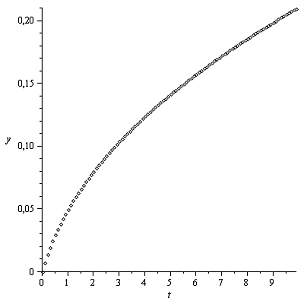
Закон Герца

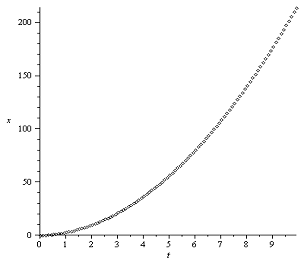
Закон Галина

Все приведенные графики вполне характерные для рассматриваемого случая, схожи с предыдущим и особых комментариев не требуют.

Вывод (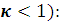Ситуация, при которой коэффициент трения меньше тангенса угла наклона плоскости движения, является наиболее простой из всех трех и поддается логическому рассуждению. Вполне вероятно, что существует такой момент времени, в который движение диска становится исключительно поступательным, а верчение заканчивается. Что вполне видно на графиках, приведенных выше. Также напрашивается вывод, что оба закона распределения давления довольно схоже влияют на движение диска в рассматриваемом случае. Стоит отметить, что если начальное значение функции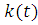 будет больше единицы, то таким оно будет на протяжении всего движения.

2.2.3 Динамика диска при 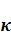=1

Рассмотрим теперь случай, когда коэффициент трения равен тангенсу угла наклона. Предположительно, диск может, как остановиться, так и нет, в зависимости от начальных данных. В работе [5] аналитически выявлено, что если начальное значение 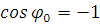, то диск остановится за конечное время, при этом его скольжение и верчение закончатся одновременно. В противном случае, когда 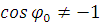, движение диска происходит на бесконечном интервале времени, и при этом существует момент времени, в который это движение превращается в исключительно поступательное, без верчения.

Начальные данные: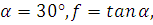

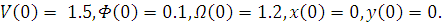
График V(t):

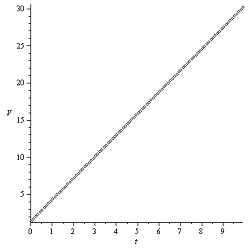
Закон Герца Закон Галина

Итак, при законе Галина, диск не останавливается, график схожи с графиком, полученным для случая 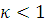. А вот при законе Герца скорость в определенный момент времени начинает расти очень медленно (она не постоянна, как показывает численный анализ) и через, приблизительно, шесть секунд после начала процесса движение начинает быть исключительно поступательным.

График Ω(t):

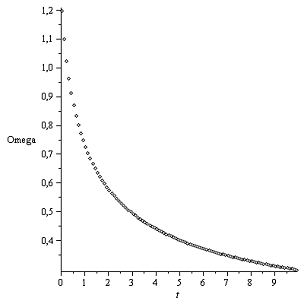
Закон Герца Закон Галина

Графики вполне характерные. При законе Герца верчение останавливается после, приблизительно, шести секунд от начала движения.

График Φ(t):

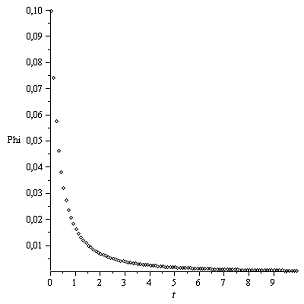
Закон Герца Закон Галина

При законе Галина диск начинает двигаться вдоль линии наибольшего ската гораздо раньше.

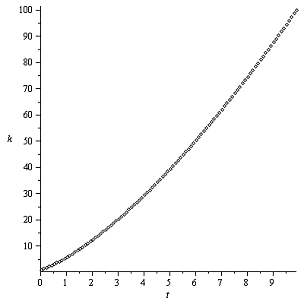
Закон Герца Закон Галина

Здесь наблюдается некоторое «блуждание» точек графика при законе Герца. Но это происходит не в тот же момент времени, когда линейная скорость начинает расти очень медленно. И можно с уверенностью сказать, что значение функции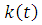всегда больше единицы, значит дело не в смене используемых формул для момента и силы трения. На данный момент можно сделать вывод, что при концентрировании давления на диск в одной точке (центре), силы трения действуют на диск так, что он начинает двигаться довольно медленно.

Графики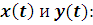

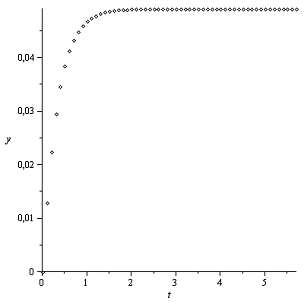
Закон Герца

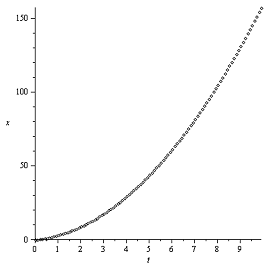
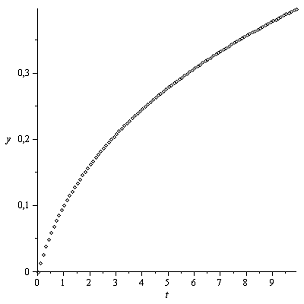
Закон Галина

Вывод (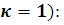в случае распределения давления на диск по закону Галина динамика диска предсказуема и укладывается в рамки аналитических рассуждений и выводов. Диск не останавливается, но в какой-то момент движение начинает быть исключительно поступательным, верчение останавливается. Графики функций довольно схожи с графиками, полученными в случае, когда отношение коэффициента трения к тангенсу угла наклона плоскости движения меньше единицы. В случае распределения давления на диск по закону Герца ситуация не столь ясная и очевидная. В определенный момент времени диск начинает набирать линейную скорость очень медленно, затем движение переходит в исключительно поступательное, но по-прежнему скорость «нарастает» довольно медленно, особенно в сравнении с другим законом распределения давления.

2.3 Создание визуализации

На основании полученных результатов, построим визуализацию движения диска. Для удобства выберем программу Macromedia Flash 8. Нарисуем диск с отсечкой поворота вокруг собственной оси.

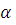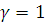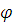Выберем начальные условия движения, например: закон Герца, угол = 30, f = 0.3, . Найдем необходимые для построения данные: x(t), y(t) и (t) для каждой 0.1 секунды. По ним построим траекторию движения (координаты центра масс диска) и внесем её в программу.

Используя доказанные факты из части 2.2 и основываясь на посекундно полученных данных, построим покадровое движение.

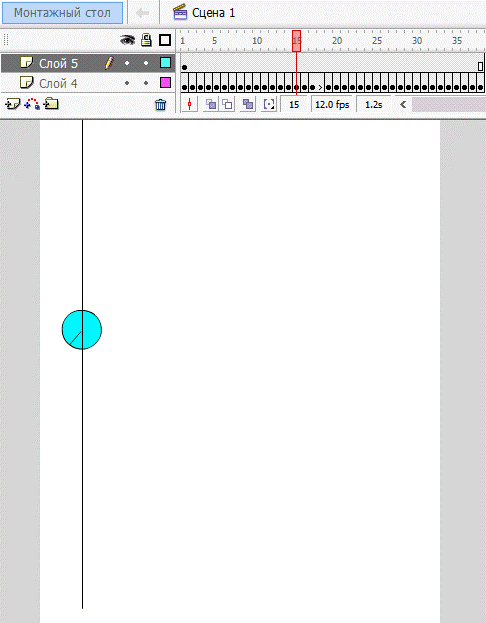
Аналогично поступим с остальными роликами

2.4 Разработка программы «Визуализация Движений Диска»

Для удобства использования полученных видеороликов было принято решение разработать программу, позволяющую выбирать начальные условия и просматривать требуемое видео. При реализации была выбрана среда разработки Microsoft Visual Studio 2010, язык C#, как один из самых современных языков программирования. При разработке был использован компонент Windows Media Player, благодаря которому был осуществлен вывод видео на экран. Также были установлены 3 ListBox’а для выбора начальных условий и кнопка «Визуализация», по нажатию которой начинал проигрываться видеоролик.

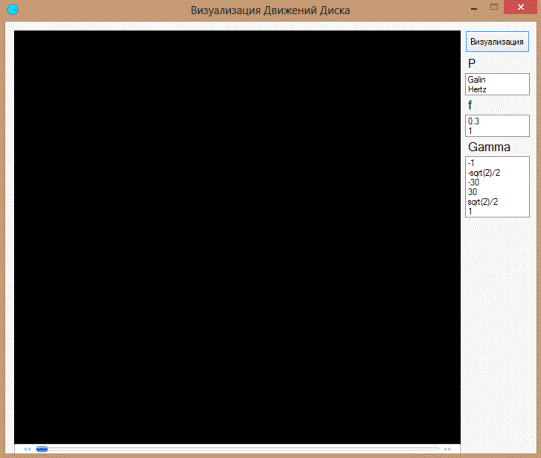
Был запрограммирован элементарный алгоритм выбора с помощью оператора if.

В процессе разработки появилась необходимость просмотра двух видео различных законов одновременно для возможности их сравнения. Для этого были добавлены 2 кнопки: «Сравнение» и «Pause» для одновременной остановки обоих видео.

Также был размещен второй компонент Windows Media Player. Для компактности программы было принято решение сделать его выезжающим. С этой целью было запрограммировано 3 основных таймера и 1 вспомогательный. Первый таймер отвечает за плавный выезд компонента Windows Media Player, второй за паузу для проигрывания видео, третий для обратного заезда компонента.

В процессе тестирования программы были выявлены следующие баги (англ. Bug - жаргонное слово, обозначающее ошибку в программе):

.        Не выбрав начальные условия, панель со вторым компонентом уверенно выезжала.

.        При обратном заезде второго компонента Windows Media Player, нажимая на кнопку «Визуализация», нарушалась работа 3 таймера, в связи с чем заезд зацикливался.

.        На некоторых компьютерах видео не воспроизводилось, и программа завершалась аварийно.

Все ошибки были успешно устранены обработкой исключений, более жесткими условиями выбора и запретом одновременного нажатия нескольких кнопок. Также, для уменьшения веса программы, она была загружена в компактный установщик.

В итоге была получена удобная программа с интуитивно понятным интерфейсом.

Заключение

В данной работе рассматривалась модель движения плоского тела - диска по абсолютно-шероховатой поверхности, представляющей собой наклонную плоскость. Был проведен качественный анализ динамики диска при различных случаях взаимосвязи коэффициента трения и тангенса угла наклона плоскости движения. При этом для каждого случая рассматривалось два способа распределения давления на диск (распределение всегда осесимметричное). Результатом данной работы являются графики, представляющие собой решение системы дифференциальных уравнений движения диска по шероховатой плоскости, их компьютерная анимация и специальная программа для просмотра полученных визуализаций. Некоторые результаты были подвергнуты сравнению с работами, выполненными ранее. Также можно сделать вывод, что случай распределения давления на диск по закону Герца представляет собой более отличительную модель. Графики функций, полученные для этого закона, показывают, что если осуществлять большое давление на одну точку в центре диска (в остальных точках давление стремиться к нулю), то силы трения будут действовать сильнее на диск, нежели при других законах распределения давления. В зависимости от рассматриваемого случая, диск либо довольно быстро останавливается, либо его движение вскоре после начала процесса переходит в скольжение (диск движется поступательно), а верчение диска заканчивается. При этом рассматриваемый объект быстрее приближается к линии наибольшего ската и начинает двигаться вдоль нее, нежели при законе распределения давления Галина. Все это было отражено в графических визуализациях.

В ходе выполнения задачи было показано, что в случае, когда коэффициент трения больше тангенса угла наклона плоскости, диск останавливается за конечное время, причем его скольжение и верчение заканчиваются одновременно. Такие результаты наблюдались в обоих случаях распределения давления на плоское тело. Целью данной работы было получение практических результатов при моделировании рассматриваемой системы и наглядная демонстрация движения диска.

Литература

[1] Журавлев В.Ф. О модели сухого трения в задачах качения твердых тел. // ПММ, 1998, т. 62, №5, с. 762-767.

[2] Ишлинский Ю.А., Соколов Б.Н., Черноусько Ф.Л. О движении плоских тел при наличие сухого трения. // Изв. АН СССР, МТТ, 1981, т. 4, с. 17-28

[3] Неймарк Ю.И. и Фуфаев Н.А. Динамика неголономных систем. // «Наука», 1967 г.

[4] Розенблат Г.М Об интегрировании уравнений движения диска по шероховатой плоскости. // Изв. РАН, МТТ, №1, 2022, с. 60-67

[5] Карапетян А.В., Русинова А.М., Качественный анализ динамики диска на наклонной плоскости с сухим трением. // Прикладная математика и механика, 2011, т. 75, вып. 5

[6] Трещев Д.В., Сальникова Т.В., Галлямов С.Р. Движение свободной шайбы по шероховатой горизонтальной плоскости. // Нелинейная динамика, 2012, т. 8, №1, с. 83-101

[7] Розенблат Г.М Динамические системы с сухим трением. // Москва - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2006 г.

[8] О.Б. Федичев, П.О. Федичев. Приближенное решение задачи плоского движения твердых тел по шероховатой горизонтальной поверхности. // Нелинейная динамика, 2010, т. 6, №2, с. 359-364

[9] Галин Л.А. Развитие теории контактных задач в СССР. // М., 1978

[10] Журавлев В.Ф. Закономерности трения при комбинации скольжения и верчения. // Изв. РАН, МТТ, №4, 2003, с. 81-88

Приложение

Программный код

1. Движение диска по шероховатой поверхности в случае распределения давления на объект по закону Герца. (Maple 11)

>

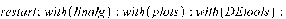
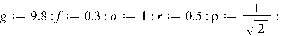
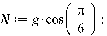
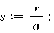
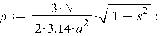
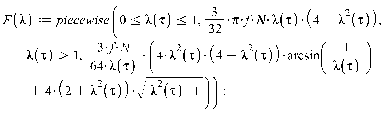
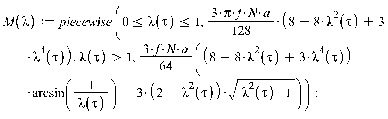
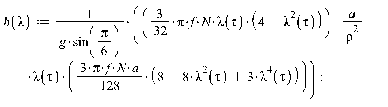
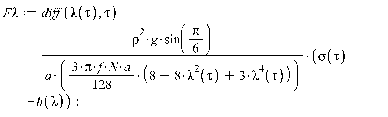
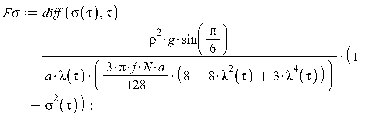
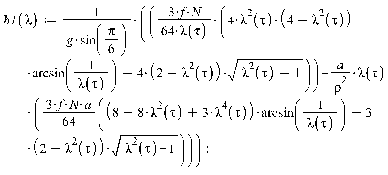
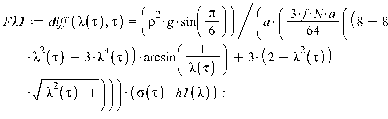
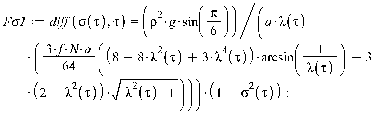
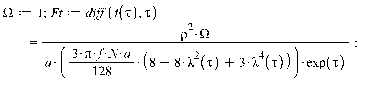
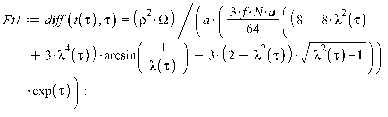
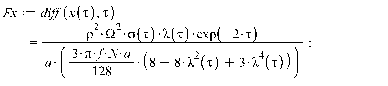
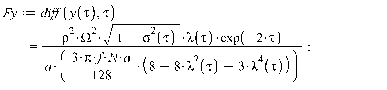
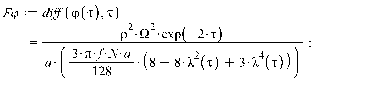
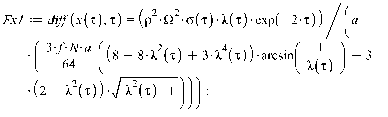
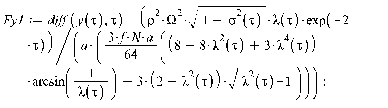
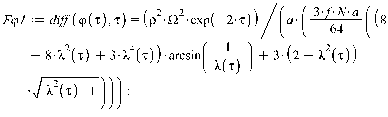
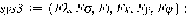
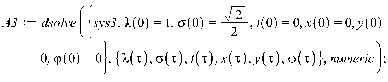
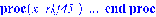
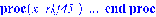
2. Движение диска по шероховатой поверхности в случае распределения давления на объект по закону Галина. (Maple 11)

>

>

>

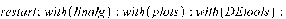
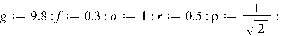
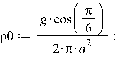
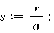
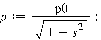
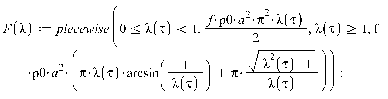
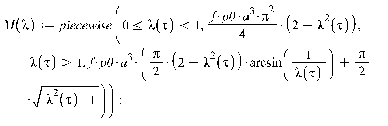
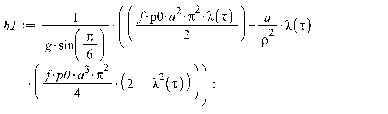
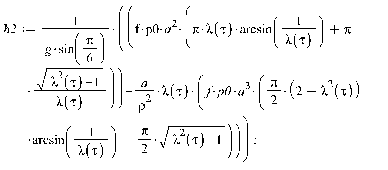
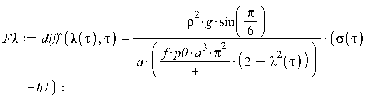
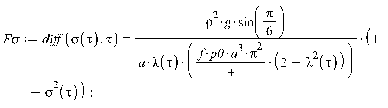
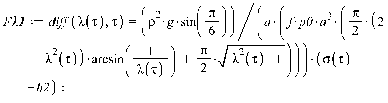
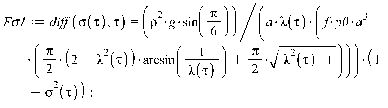
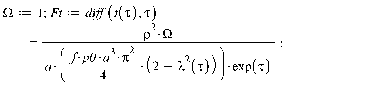
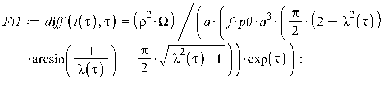
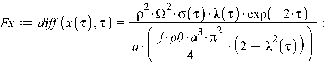
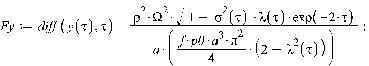
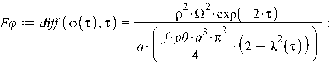
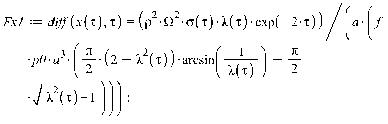
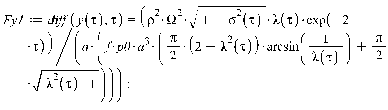
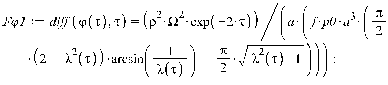
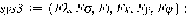
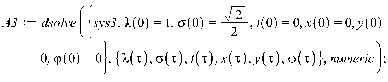
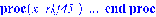
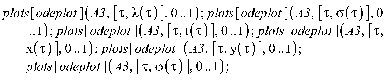
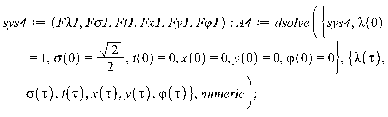
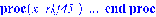
. Программа «Визуализация Движений Диска». (Microsoft Visual Studio)

using System;System. Collections. Generic;System. ComponentModel;System. Data;System. Drawing;System. Linq;System. Text;System. Windows. Forms;WindowsFormsApplication2

{partial class Form1: Form

{Form1 ()

{();= 720;

}void Сhoose_Click_1 (object sender, EventArgs e)

{

{(fBox. SelectedItem!= null && gammaBox. SelectedItem!= null && PBox. SelectedItem!= null)

{(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 0 && PBox. SelectedIndex == 0).URL = @ «Video\G-1.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 1 && PBox. SelectedIndex == 0).URL = @ «Video\G-sqrt2.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 2 && PBox. SelectedIndex == 0).URL = @ «Video\G-30.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 3 && PBox. SelectedIndex == 0).URL = @ «Video\G30.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 4 && PBox. SelectedIndex == 0).URL = @ «Video\Gsqrt2.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 5 && PBox. SelectedIndex == 0).URL = @ «Video\G1.03.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 0 && PBox. SelectedIndex == 0).URL = @ «Video\G-1.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 1 && PBox. SelectedIndex == 0).URL = @ «Video\G-sqrt2.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 2 && PBox. SelectedIndex == 0).URL = @ «Video\G-30.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 3 && PBox. SelectedIndex == 0).URL = @ «Video\G30.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 4 && PBox. SelectedIndex == 0).URL = @ «Video\Gsqrt2.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 5 && PBox. SelectedIndex == 0).URL = @ «Video\G1.1.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 0 && PBox. SelectedIndex == 1).URL = @ «Video\H-1.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 1 && PBox. SelectedIndex == 1).URL = @ «Video\H-sqrt2.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 2 && PBox. SelectedIndex == 1).URL = @ «Video\H-30.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 3 && PBox. SelectedIndex == 1).URL = @ «Video\H30.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 4 && PBox. SelectedIndex == 1).URL = @ «Video\Hsqrt2.03.avi»;(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 5 && PBox. SelectedIndex == 1).URL = @ «Video\H1.03.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 0 && PBox. SelectedIndex == 1).URL = @ «Video\H-1.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 1 && PBox. SelectedIndex == 1).URL = @ «Video\H-sqrt2.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 2 && PBox. SelectedIndex == 1).URL = @ «Video\H-30.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 3 && PBox. SelectedIndex == 1).URL = @ «Video\H30.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 4 && PBox. SelectedIndex == 1).URL = @ «Video\Hsqrt2.1.avi»;(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 5 && PBox. SelectedIndex == 1).URL = @ «Video\H1.1.avi»;

}. Show («Выберите начальные условия», «Ошибка», MessageBoxButtons.OK);

}

{. Show («Обновите необходимые компоненты!», «Ошибка», MessageBoxButtons.OK);

}

}void button1_Click (object sender, EventArgs e)

{(fBox. SelectedItem!= null && gammaBox. SelectedItem!= null && PBox. SelectedItem!= null)

{. Interval = 10000;. Enabled = true;. Visible = true;. Interval = 50;. Visible = true;. Enabled = true;. Enabled = true;

Сhoose. Enabled = false;

}. Show («Выберите начальные условия», «Ошибка», MessageBoxButtons.OK);

}i = 0;void button2_Click (object sender, EventArgs e)

{(i == 0)

{. Ctlcontrols.pause();. Ctlcontrols.pause();. Enabled = false;. Enabled = false;= 1;

}

{. Ctlcontrols.play();. Ctlcontrols.play();. Enabled = true;= 0;

}

}void timer1_Tick (object sender, EventArgs e)

{. Enabled = true;. Enabled = false;

}void button3_Click (object sender, EventArgs e)

{. Interval = 50;. Visible = true;. Enabled = true;

}void timer2_Tick (object sender, EventArgs e)

{(Width < 1320)

{= Width + 10;. Enabled = false;

}

{= 1325;. Enabled = false;

{(PBox. SelectedIndex == 0)

{(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 0)

{.URL = @ «Video\G-1.03.avi»;.URL = @ «Video\H-1.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 1)

{.URL = @ «Video\G-sqrt2.03.avi»;.URL = @ «Video\H-sqrt2.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 2)

{.URL = @ «Video\G-30.03.avi»;.URL = @ «Video\H-30.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 3)

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 4)

{.URL = @ «Video\Gsqrt2.03.avi»;.URL = @ «Video\Hsqrt2.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 5)

{.URL = @ «Video\G1.03.avi»;.URL = @ «Video\H1.03.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 0)

{.URL = @ «Video\G-1.1.avi»;.URL = @ «Video\H-1.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 1)

{.URL = @ «Video\G-sqrt2.1.avi»;.URL = @ «Video\H-sqrt2.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 2)

{.URL = @ «Video\G-30.1.avi»;.URL = @ «Video\H-30.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 3)

{.URL = @ «Video\G30.1.avi»;.URL = @ «Video\H30.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 4)

{.URL = @ «Video\Gsqrt2.1.avi»;.URL = @ «Video\Hsqrt2.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 5)

{.URL = @ «Video\G1.1.avi»;.URL = @ «Video\H1.1.avi»;

}

}(PBox. SelectedIndex == 1)

{(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 0)

{.URL = @ «Video\H-1.03.avi»;.URL = @ «Video\G-1.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 1)

{.URL = @ «Video\H-sqrt2.03.avi»;.URL = @ «Video\G-sqrt2.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 2)

{.URL = @ «Video\H-30.03.avi»;.URL = @ «Video\G-30.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 3)

{.URL = @ «Video\H30.03.avi»;.URL = @ «Video\G30.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 4)

{.URL = @ «Video\Hsqrt2.03.avi»;.URL = @ «Video\Gsqrt2.03.avi»;

}(fBox. SelectedIndex == 0 && gammaBox. SelectedIndex == 5)

{.URL = @ «Video\H1.03.avi»;.URL = @ «Video\G1.03.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 0)

{.URL = @ «Video\H-1.1.avi»;.URL = @ «Video\G-1.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 1)

{.URL = @ «Video\H-sqrt2.1.avi»;.URL = @ «Video\G-sqrt2.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 2)

{.URL = @ «Video\H-30.1.avi»;.URL = @ «Video\G-30.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 3)

{.URL = @ «Video\H30.1.avi»;.URL = @ «Video\G30.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 4)

{.URL = @ «Video\Hsqrt2.1.avi»;.URL = @ «Video\Gsqrt2.1.avi»;

}(fBox. SelectedIndex == 1 && gammaBox. SelectedIndex == 5)

{.URL = @ «Video\H1.1.avi»;.URL = @ «Video\G1.1.avi»;

}

}

}

{. Show («Обновите необходимые компоненты!», «Ошибка», MessageBoxButtons.OK);

}

}

}void timer3_Tick (object sender, EventArgs e)

{(Width > 730)

{= Width - 10;. Enabled = false;

}

{= 720;. Enabled = true;

Сhoose. Enabled = true;. Visible = false;. Enabled = false;

}

}void timer4_Tick (object sender, EventArgs e)

{. Enabled = true;. Enabled = false;

}

визуализация движение диск поверхность

}

}