Аппаратно-программный комплекс для идентификации объектов управления на основе вещественного интерполяционного метода
Министерство образования и науки
Российской Федерации
Государственное образовательное
учреждение
высшего профессионального образования
"НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Институт: Институт кибернетики
Специальность: "Автоматизация и
управление" 220200
Кафедра: Интегрированных компьютерных
систем управления
АППАРАТНО-ПРОГРАММНЫЙ КОМПЛЕКС ДЛЯ
ИДЕНТИФИКАЦИИ ОБЪЕКТОВ УПРАВЛЕНИЯ НА ОСНОВЕ ВЕЩЕСТВЕННОГО ИНТЕРПОЛЯЦИОННОГО
МЕТОДА
Выпускная квалификационная работа
(на соискание академической степени
"магистр")
Студент Н.С. Николаева
Руководитель В.А. Рудницкий
Нормоконтроль Е.И. Громаков
Томск - 2011
Задание
. Тема выпускной квалификационной работы:
Аппаратно-программный комплекс для идентификации объектов управления на основе
вещественного интерполяционного метода (утверждена приказом ректора
(распоряжением декана) от 07.06.2011 №2671/с).
. Срок сдачи студентом готовой работы: 10.06.2011 г.
. Исходные данные к работе: модельные примеры и
экспериментальные временные характеристики объекта управления, алгоритм
параметрической идентификации на основе вещественного интерполяционного метода.
. Содержание текстового документа (перечень подлежащих
разработке вопросов):
.1 Введение.
4.2 Идентификация объектов.
4.3 Аппаратно-программный комплекс идентификации.
.3.1 Аппаратная часть микропроцессорной системы управления и
сбора информации.
.3.2 Программная часть.
.4 Анализ работоспособности аппаратно-программного комплекса.
.4.1 Идентификация на модельных примерах.
.4.2 Пример идентификации реального объекта управления.
.5 Заключение.
. Перечень графического материала (с точным указанием
обязательных чертежей):
.1 ФЮРА.425430.001 ТЧ - Блок-схемы алгоритмов.
.2 ФЮРА.425430.001 ТБ - Сводные данные модельных примеров.
.3 ФЮРА.425430.001 ТБ - Графики зависимостей первого узла.
. Дата выдачи задания на выполнение выпускной
квалификационной работы: 01.03.2010 г.
Реферат
Выпускная квалификационная работа содержит _______ с., 86
рис., 16 табл., 27 источников, 3 л. графич. материала.
Ключевые слова: ИДЕНТИФИКАЦИЯ, ВЕЩЕСТВЕННЫЙ ИНТЕРПОЛЯЦИОННЫЙ
МЕТОД, АППАРАТНО-ПРОГРАММНЫЙ КОМПЛЕКС.
Целью работы является разработка
аппаратно-программного комплекса, предназначенного для осуществления
идентификации объектов управления на основе вещественного интерполяционного
метода [1].
Для проверки разработанного алгоритма в качестве объекта
управления был взят малогабаритный вентильный двигатель, который применяется в
воздушно-охладительных системах ПК, однако это не означает, что идентификация
ОУ ограничивается только этим типом двигателей.
Спроектирован опытный образец устройства сопряжения,
реализован алгоритм идентификации ОУ. Разработан и реализован пользовательский
интерфейс программы. Проведена проверка работоспособности АПК идентификации ОУ.
Достигнутые результаты позволяют разработать на их основе
эффективное программное обеспечение для решения задач идентификации, которое
может быть использовано в рамках организации концепции аппаратно-программного
комплекса на производстве.
Разработанные алгоритмы и программы применимы для
идентификации структуры и параметров моделей объектов управления.
Пояснительная записка к дипломному проекту выполнена в
текстовом редакторе Microsoft Word 2007 и представлена вместе с проектными
файлами на диске (в конверте на обороте обложки).
Содержание
Задание
Реферат
Определения, обозначения и сокращения
Введение
1. Идентификация объектов
1.1 Алгоритмическая основа для аппаратно-программного комплекса
1.2 Идентификация объектов на основе вещественного
интерполяционного метода
2. Аппаратно-программный комплекс идентификации
2.1 Аппаратная часть комплекса
2.1.1 Выбор микроконтроллера
2.1.2 Сопряжение с персональным компьютером
2.1.3 Устройство сопряжения с объектом управления
2.2 Программная часть комплекса
2.2.1 Алгоритм идентификации объектов управления вещественным
интерполяционным методом
2.2.2 Основные функции программы
2.2.3 Интерфейс программы
2.2.4 Выбор структуры модели объекта управления
2.2.5 Формирование интерполяционной сетки
2.2.6 Нахождение коэффициентов ПФ модели объекта управления
2.2.7 Проверка адекватности модели ОУ
2.2.8 Итерационный поиск
3. Анализ работоспособности аппаратно-программного комплекса
3.1 Идентификация на модельных примерах
3.2 Пример идентификации реального объекта управления
Заключение
Список использованных источников
Приложения
Определения,
обозначения и сокращения
В данной работе применены следующие термины с
соответствующими определениями:
Аппаратно-программный комплекс - это продукт, в состав
которого входят технические средства и программное обеспечение, совместно
применяемые для решения задач определенного типа [2].
В данной дипломной работе используются следующие
аббревиатуры:
· АПК - аппаратно-программный комплекс;
· САУ - система автоматического управления;
· ВИМ - вещественный интерполяционный метод;
· ОУ - объект управления;
· СЛАУ - система линейных алгебраических
уравнений;
· ПФ - передаточная функция;
· ЧХ - численная характеристика.
Введение
Актуальность работы. В настоящее время
проблемы, связанные с получением математических моделей объектов
технологических процессов, экономики и живой природы, формируют одно из
основных направлений науки и техники - моделирование. Это объясняется тем, что
математические модели объектов широко применяются как при создании систем
управления этими объектами, так и при их эксплуатации [3].
На сегодняшний день уровень развития техники характеризуется
многообразием различных по своей структуре, выполняемым функциям и сложности
объектов управления. Часто возникают ситуации, когда отсутствует достаточно
четкое математическое описание объекта. Для осуществления эффективного
управления объектами необходимо знание законов, которым они подчиняются.
Поэтому задача идентификации объектов занимает значимое место в теории
управления.
Решение задач идентификации объекта управления требует
эффективных средств, позволяющих оперативно получать его математическую модель,
в связи с этим становиться актуальным создание мобильного АПК для осуществления
идентификации объектов управления.
Существует большое количество методов [3,4], позволяющих
решать данную задачу, поэтому при выборе алгоритмов идентификации необходимо
ограничиться теми, которые могут быть и действительно были использованы в тех
классах, к которым принадлежит рассматриваемая задача.
Специфика практических задач регламентирует ограничения,
которые следует учитывать при разработке алгоритмической составляющей, т.е.
алгоритмы, на основе которых в дальнейшем будет строиться управляющая
программа, должны быть адаптированными к последующей интеграции в контроллер.
Отмеченные обстоятельства определяют практическую и
теоретическую ценность разработки АПК для осуществления идентификации объектов
управления. Таким образом, актуальность темы выпускной квалификационной работы
вряд ли вызывает сомнение.
Цель выпускной квалификационной работы - разработка АПК для
осуществления идентификации объектов управления.
Для достижения поставленной цели необходимо было
выполнить следующие задачи:
- изучить существующий алгоритм решения
задач идентификации на основе на ВИМ;
- спроектировать опытный образец устройства
сопряжения;
- разработать программу получения данных об
ОУ от устройства сопряжения;
- провести анализ разработанных алгоритмов и
программ.
Методы исследования. Для достижения
сформулированной цели и связанных с нею задач в работе использованы методы
теории автоматического управления, вещественный интерполяционный метод и методы
численного и компьютерного моделирования.
Достоверность и обоснованность полученных в выпускной
квалификационной работе теоретических результатов и формулируемых на их основе
выводов подтверждена моделированием на ПК.
Новизна работы заключается в следующем:
- применение ВИМ в качестве алгоритмической
основы АПК для осуществления идентификации объектов управления;
- реализован алгоритм итерационного поиска
расположения первого узла интерполирования, при котором ошибка идентификации
минимальна;
- реализована возможность построения графика
зависимости переходной характеристики от расположения первого узла
интерполяционной сетки.
Публикации. Результаты, проделанной работы, были
опубликованы и представлены на конференциях:Всероссийская научно-практическая
конференция студентов, аспирантов и молодых учёных "Молодёжь и современные
информационные технологии" с международным участием (МСИТ-2010), Томск,
2010.
Первая Международная научно-техническая интернет-конференция
"Автоматизация, мехатроника, информационные технологии" (АМИТ), Омск,
2010.
Научно-технический журнал "Автоматика-информатика"
1-2 (2627), Караганда, 2010.Х Всероссийская научно-практическая конференция
студентов, аспирантов и молодых учёных "Молодёжь и современные
информационные технологии" с международным участием (МСИТ-2011), Томск,
2011.
Опубликовано 4 печатные работы.
идентификация программный управление объект
1.
Идентификация объектов
Классическое определение идентификации дал Л. Заде в 1962
году: "Идентификация состоит в отыскании по входным и выходным сигналам
некоторой системы эквивалентной ей системы из некоторого заданного
класса". Хоть с момента появления понятия "идентификация" прошло
немало лет, оно не утратило свою актуальность и остается достаточно сложной
задачей, включающей трудоемкие теоретические расчеты, неоднозначные выбор
критерия оценки и алгоритма реализации.
Более формализовано, идентификация - определение параметров и
структуры математической модели, обеспечивающих наименьшее несовпадение
выходных координат модели и процесса при одинаковых входных воздействиях [4].
При изучении любых объектов основной задачей является построение их моделей по
результатам экспериментального исследования входных и выходных переменных
объекта без изучения его физической сущности. Этот подход широко используется
на практике, так как позволяет обойтись минимумом априорных сведений об объекте
при построении его модели. Реализация входа формируется исследователем путем
подачи на вход объекта испытательного сигнала желаемой формы (скачкообразного
сигнала, импульсного сигнала, сигнала в виде гармонических, прямоугольных,
трапецеидальных, треугольных колебаний и др.). Реализацией выхода объекта является
его реакция на испытательный сигнал. На рисунке 1 показана идентификация
объекта.
Проектирование АПК для осуществления идентификации в большей
степени зависит от наличия математического обеспечения, благодаря которому
возможно получить сравнительно точную модель объекта управления, поэтому
реализация связана с выбором наиболее подходящих методов, а так же построения
на их основе, алгоритмов для решения задачи идентификации объекта управления.
1.1
Алгоритмическая основа для аппаратно-программного комплекса
Создание технических средств, предназначенных для получения
математических моделей объектов, связано с выбором наиболее подходящих методов
и алгоритмов. При этом полагают, что наиболее целесообразный путь решения
задачи состоит в сочетании теоретического и численного подходов, когда
структура объекта принимается на основе теоретических знаний, а численные
значения ее параметров вычисляются. В этих случаях полагают структуру модели
известной, а задачу идентификации рассматривают в параметрической постановке.
В литературе представлено большое количество подходов к
решению данной задачи. Это как классические методы идентификации, так и
относительно новые и перспективные, такие как аппарат нейронных сетей и
нечетких моделей [4-7, 11]. Самым распространенным из методов идентификации
является метод, основанный на представлении нелинейной характеристики в виде
рядов Вольтерра. Данный метод позволяет интерпретировать линейный объект, как
подкласс нелинейных объектов, что существенно упрощает дальнейший анализ, но
метод имеет существенный недостаток, связанный с вычислительными трудностями,
которые влекут за собой затруднения в его использовании при создании АПК [8].
Одним из наиболее выгодных методов идентификации является
ВИМ, который в силу своих особенностей, предъявляет невысокие требования к
аппаратной части, что делает его применение целесообразным для решения
различных задач, в том числе и задач идентификации. В работе [9], было
показано, что ВИМ позволяет снизить вычислительные затраты, например, по сравнению
с частотным методом - примерно вдвое.
Основой ВИМ является вещественное интегральное
преобразование, когда мнимая часть приравнивается к нулю
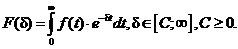
На начальном этапе, для того чтобы использовать ВИМ в целях
идентификации нелинейных объектов управления, необходимо заменить в уравнении
функцию f (t) на y (x), а затем для обеспечения
сходимости конечного предела нужно ввести сомножитель δ
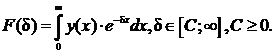
Для последнего уравнения, в общем случае разработанная
процедура идентификации включает следующие этапы:
) выбор узлов интерполирования и получение модели звена в
непараметрической форме;
) получение модели звена в области изображений в виде
дробно-рациональной функции;
) получение модели объекта в области оригиналов и оценивание
погрешности;
) выполнение при необходимости итеративного улучшения модели
путем изменения расположения узлов интерполирования.
Получение математической модели объекта на основе ВИМ
обладает рядом следующих преимуществ.
. Функция F (δ) не содержит мнимой
составляющей, что позволяет сократить объем вычислений при выполнении операций
с выражениями такого вида;
2. Для функций f (x) и F (δ), справедливо так называемое "перекрестное свойство",
состоящее в том, что при больших значениях δ изображение F (δ) характеризует поведение функции-оригинала на начальном участке
времени. И, наоборот, при малых значениях δ функция F (δ) характеризует поведение функции-оригинала f (x) преимущественно
на конечном интервале x. При решении приближенных задач данное свойство
оказывается очень важным, т.к. позволяет перераспределять погрешность в области
оригиналов, используя интерполяционный механизм;
. Функцию F (δ) можно получить не
только прямым путем, но по изображению Лапласа F (p). В этом случае функция F (δ) находится путем формальной замены переменной p на δ, что позволяет использовать широкий спектр справочных материалов
по преобразованию Лапласа, что важно с практической точки зрения [1, 12].
Также хотелось бы отметить, что использование ВИМ в качестве
метода параметрической идентификации позволит избавиться от ряда недостатков и
даст возможность осуществить процедуру идентификации:
) путем подачи на ОУ детерминированных сигналов различной
формы (ступенчатого, трапецеидального, пилообразного и т.д.), что позволяет
учитывать различные особенности функционирования объекта управления для
осуществления наиболее рационального и безопасного исследования;
) на основе простых расчетных формул, не требующих
значительных временных и вычислительных затрат при практической реализации;
) с возможностью коррекции полученных результатов за счет
привлечения итерационной процедуры настройки на требуемый уровень точности.
Выше перечисленные качества указывают на преимущества
использования ВИМ в качестве основы алгоритмического обеспечения АПК.
1.2
Идентификация объектов на основе вещественного интерполяционного метода
Получение ЧХ - важный момент, так как для корректной
идентификации, необходимо для начала снять значения с идентифицируемого объекта
и представить их в виде таблицы, содержащей значения времени переходного
процесса и значения выходной величины.
Рассмотрим задачу формирования численных характеристик
объекта на основе экспериментальных данных на примере линейного непрерывного
объекта, относящегося к классу одномерных, стационарных, детерминированных.
Условное представление показано на рисунке 2.
Задача идентификации заключается в получении математического
описания объекта по известному входному воздействию x (t) и
реакции объекта y (t). При разработке алгоритма будем полагать,
что сигналы входа и выхода являются детерминированными и не сопровождаются
погрешностями измерения. Они удовлетворяют условиям существования d-изображений, что
позволяет найти их по формуле прямого d-преобразования
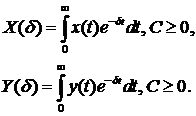
Откуда можно найти вещественную передаточную функцию
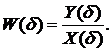
Для систем с сосредоточенными параметрами и сигналов, выражаемых
через элементарные функции, вещественная передаточная функция 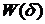 будет дробно-рациональной [16, 17] вида:
будет дробно-рациональной [16, 17] вида:
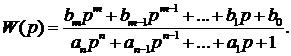 (1)
(1)
В этом случае задача параметрической идентификации заключается в
следующем: по известным сигналам x (t) и у (t)
необходимо определить параметры, 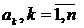 и
и 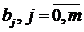 , при известных значениях степеней m
и n полиномов числителя и знаменателя этой ПФ (1).
, при известных значениях степеней m
и n полиномов числителя и знаменателя этой ПФ (1).
Схему решения задачи можно представить в виде последовательности
нескольких этапов. На первом этапе осуществляется переход от функций x (t),
у (t) к вещественным изображениям X (d), Y (d). Затем выполняется этап перехода к
машинно-ориентированной форме представления информации об этих функциях - к
форме численных характеристик. Затем следует заключительный и в тоже время
наиболее важный этап решения задачи - определение искомых коэффициентов ПФ
вида, оценивание результата и, если это необходимо, повышение точности решения
[18].
Первый шаг преобразований базируется на связи переходной
характеристики с вещественной передаточной функцией 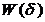 , которая имеет вид
, которая имеет вид
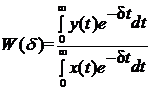 ,
, 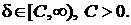
На основе этого выражения найдется ЧХ 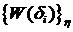 :
:
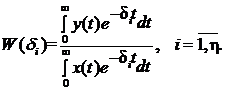 (2)
(2)
В условиях идентификационного эксперимента сигналы 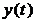 и
и 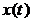 обычно получают в виде последовательности значений
обычно получают в виде последовательности значений 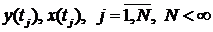 . Поэтому для нахождения элементов
. Поэтому для нахождения элементов 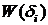 необходим переход от выражения (2) к
дискретным представлениям и численным операциям, в частности, к численному
интегрированию. Метод интегрирования может быть выбран практически любой, но с
минимальным числом операций, поскольку алгоритм ориентирован на работу в
реальном времени. При использовании метода прямоугольников получим расчетную
формулу
необходим переход от выражения (2) к
дискретным представлениям и численным операциям, в частности, к численному
интегрированию. Метод интегрирования может быть выбран практически любой, но с
минимальным числом операций, поскольку алгоритм ориентирован на работу в
реальном времени. При использовании метода прямоугольников получим расчетную
формулу
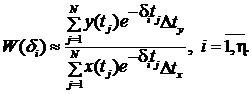
Данную формулу можно применять для получения ЧХ объекта по
экспериментальным отсчетам 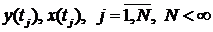 . Исследования [19] показали, что в первом приближении можно
принять
. Исследования [19] показали, что в первом приближении можно
принять 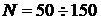 , при условии, что на интервале времени
, при условии, что на интервале времени 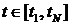 проявятся существенные свойства объекта идентификации.
проявятся существенные свойства объекта идентификации.
В работе [20] проведены исследования по выбору метода
интегрирования и сделано заключение о некоторых преимуществах метода средних
прямоугольников. Поэтому в дальнейшем будем ориентироваться на этот результат.
Следующий шаг заключается в выборе узлов интерполирования 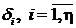 . Данный выбор оказывает влияние на
точность решения задачи параметрической идентификации.
. Данный выбор оказывает влияние на
точность решения задачи параметрической идентификации.
Формирование системы узлов 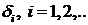 включает в себя две задачи - определение интервала расположения
узлов и закона их распределения. В общем случае эти задачи не имеют точного
решения, поэтому приходиться использовать эмпирические сведения и рекомендации
[12]:
включает в себя две задачи - определение интервала расположения
узлов и закона их распределения. В общем случае эти задачи не имеют точного
решения, поэтому приходиться использовать эмпирические сведения и рекомендации
[12]:
Интервал 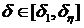 находится итерационным путем. Сначала по
предлагаемым формулам вычисляется узел
находится итерационным путем. Сначала по
предлагаемым формулам вычисляется узел 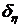
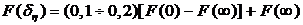 . (3)
. (3)
В отношении закона распределения узлов также имеются рекомендация
- использовать равномерное расположение узлов, которое обеспечивает приемлемую
точность и простоту решения задачи
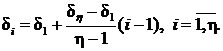 (4)
(4)
Для равномерной сетки расположения узлов удобно пользоваться
выражениями (3) и (4), хотя выбор лучшего, в смысле удовлетворения заданной
точности, закона распределения узлов является нетривиальной задачей и в ряде
случаев (объекты с распределенными параметрами, синтез регуляторов,
компенсаторов и др.) приходится отступать от указанных рекомендаций [1].
Далее необходимо получить коэффициенты передаточной функции по
найденной ЧХ. Эта процедура достаточно хорошо разработана в [21]. Следуя
имеющимся алгоритмам, составим СЛАУ вида
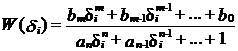 ,
, 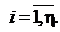
В левой части СЛАУ - найденные элементы ЧХ. В правой части
содержатся известные узлы интерполирования di. Неизвестными остаются лишь коэффициенты передаточной
функции объекта идентификации 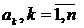 и
и 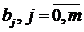 , которые входят в СЛАУ. Можно показать,
что подобные системы имеют решение и оно единственно при выполнении несложных
условий [11]. Для решения системы можно использовать стандартные методы.
Найденные таким образом значения
, которые входят в СЛАУ. Можно показать,
что подобные системы имеют решение и оно единственно при выполнении несложных
условий [11]. Для решения системы можно использовать стандартные методы.
Найденные таким образом значения 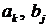 являются коэффициентами вещественной передаточной функции, что
означает получение модели объекта в виде аналитического выражения.
являются коэффициентами вещественной передаточной функции, что
означает получение модели объекта в виде аналитического выражения.
После нахождения математической модели объекта необходимо оценить
насколько близко полученная модель отражает реальные свойства объекта. Поэтому
проводится проверка точности результата.
Оценку полученного на основе ВИМ решения задачи можно
осуществлять: в вещественной области и во временной области. Первый вариант
может давать удовлетворительные результаты в области изображений, тогда как в
области времени результаты моделирования и экспериментальной переходной
характеристики могут быть далеки друг от друга. Из критериев в области времени
можно отметить широко используемый критерий среднеквадратичного отклонения
(СКО) и минимаксный критерий. Однако СКО обладает существенным недостатком,
который заключается в том, что при общей удовлетворительной оценке по этому
критерию могут иметь место значительные локальные отклонения на промежутках
переходных характеристик. В случае, когда эти отклонения вызваны случайной
помехой, это дает положительный эффект, в случае, когда эти отклонения отражают
особенности объекта управления, теряется информация об этих свойствах.
В общем случае считается предпочтительным оценивать близость
функций по критерию абсолютного максимального отклонения
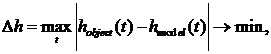 (5)
(5)
где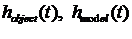 - точная переходная характеристика и ее
модельное представление.
- точная переходная характеристика и ее
модельное представление.
Если величина погрешности 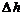 оказывается меньше заданной
оказывается меньше заданной 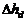 , то задача считается решенной. Если данное условие не
выполняется, то необходимо изменить узлы интерполирования, если же и это не
улучшает степень приближения модели и реального объекта, то необходимо
увеличить степень передаточной функции или поменять ее.
, то задача считается решенной. Если данное условие не
выполняется, то необходимо изменить узлы интерполирования, если же и это не
улучшает степень приближения модели и реального объекта, то необходимо
увеличить степень передаточной функции или поменять ее.
Еще одним достоинством данного критерия является возможность его
использования в тех задачах идентификации, когда точное решение вообще не
существует. При этом речь идет в первую очередь не о влиянии погрешности
вычислений, но о классе задач, в которых эта особенность является
принципиальной [12].
Выше были приведены основные этапы параметрической идентификации
средством ВИМ. При такой идентификации считают, что структура объекта известна,
определению подлежат только коэффициенты принятой модели. В случае описания
объектов в форме ПФ в качестве параметров, характеризующих структурные
особенности модели объекта, выступают степени n и m полиномов
знаменателя числителя. Как показали исследования, указанный путь поиска
математических моделей объектов является эффективным не только по достигаемой
точности, но и объему вычислительных операций [20-22].
В работе [23] предлагается идентифицировать структуру передаточной
функции методом направленного перебора. На начальном этапе порядок модели
объекта выбирается исходя из условия минимальной сложности. Так, если
переходная характеристика объекта носит апериодический характер, то
предпочтительно выбрать ПФ первого порядка; если переходная характеристика
имеет колебательный вид - целесообразно принять ПФ второго порядка. Затем
алгоритм идентификации структуры ПФ сводится к увеличению степеней полиномов
знаменателя и числителя, которые наращиваются до тех пор, пока точность
восстановления временной характеристики не достигнет заданного уровня [12].
Данный подход эффективен, так как сокращается объем вычислений, поскольку
уменьшается количество перебираемых вариантов. В разработанной программе учтено
данное достоинство направленного перебора.
2.
Аппаратно-программный комплекс идентификации
В аппаратно-программный комплекс идентификации (рисунок 3)
входит устройство портативного исполнения, оснащенное необходимыми функциями,
подключаемое к ПК с предустановленной операционной системой семейства Windows,
по средствам USB, позволяющее получать необходимую информацию об объекте
управления для решения задачи идентификации объекта управления представляющего
собой черный ящик.
Таким образом, основными составляющими АПК являются: ПК,
портативное устройство и непосредственно сам исследуемый объект управления.
На ПК устанавливается разработанное специализированное
программное обеспечение, которое позволяет провести идентификацию ОУ по
полученной информации от портативного устройства. Требования и минимальные
характеристики ПК обозначены в руководстве пользователя (Приложение А).
Портативное устройство представляет собой микропроцессорную
систему управления и сбора информации, а так же является связующим звеном между
ОУ и ПК.
ОУ следует выбирать с учетом наличия в них систем управления
с возможностью пуска по внешнему сигналу малой мощности, поскольку
разработанное портативное устройство является тестовым образцом.
Для тестирования работоспособности комплекса, в качестве ОУ
для проведения исследований был взят малогабаритный вентильный двигатель с
открытым коллектором, оснащенный датчиком Холла. Двигатель предназначен для
преобразования электрической энергии постоянного тока в механическую энергию
вращательного движения. Основная часть момента, создаваемого ротором (якорем)
двигателя, используется для управления внешней нагрузкой.
Двигатели постоянного тока широко применяются в
роботах-манипуляторах, лентопротяжных механизмах, дисководах, в машиностроении
и исполнительных устройствах следящих систем, благодаря высокому вращающему
моменту, возможности регулирования скорости в широком диапазоне, компактности,
хорошим нагрузочным характеристикам и возможности быть использованными в
различных системах управления.
Однако это не означает, что идентификация ОУ ограничивается
только этим типом двигателей.
Схема взаимодействия АПК представлена на рисунке 4.
Процесс получения переходной характеристики ОУ управляется
оператором. После подачи команды старта с ПК на портативное устройство подается
команда пуска, затем происходит подача ступенчатого сигнала на ОУ. В этот
момент с датчика положения, в портативное устройство начинает поступать
информация о его состоянии, которая обрабатывается в режиме реального времени и
передается на ПК, где и происходит ее визуализация в виде графика переходной
характеристики ОУ. Далее сам процесс идентификации ОУ реализуется
специализированным программным обеспечением, установленным на ПК. Данное
программное обеспечение разработано на базе пакета прикладных программ MATLab и
позволяет оперировать априорной информацией об ОУ, полученной при помощи
портативного устройства, при помощи которого можно провести тест и получить
переходную характеристику ОУ. При этом легко осуществить контроль процесса
идентификации ОУ на всех его стадиях и наглядно представить всю необходимую
наладчику информацию, как в графическом, так и текстовом виде [10].
2.1
Аппаратная часть комплекса
При выборе аппаратной части будем учитывать, какие функции
должно выполнять портативное устройство в составе АПК.
На начальном этапе будем исходить из того, что выходным
сигналом будет являться характеристика скорости вращения объекта управления,
например, двигателя постоянного тока, как ответная реакция на входное
возмущение, заданное с целью идентификации параметров объекта управления.
Для фиксирования скорости вращения вала двигателя
целесообразно применять датчик Холла, основные его преимущества заключаются в
отсутствии механических движущихся частей и высоком быстродействии (до 100
кГц). Благодаря этому датчики Холла отличаются высокой надежностью,
долговечностью и не требуют физического контакта с измеряемой средой [11].
.1.1 Выбор
микроконтроллера
Для получения частоты вращения вала, в необходимом виде,
нужно применять датчик Холла совместно с микропроцессорной системой, основанной
на базе микроконтроллеров AVR, отличающийся малой стоимостью и по своим
техническим характеристикам данные микроконтроллеры подходят к разработанному
алгоритму и позволяют осуществить поставленную задачу с наименьшими трудозатратами
и потерями.
Выбор типа микроконтроллера произведем с учетом потребностей,
а так же необходимой разрядности, быстродействия, экономичности потребления,
температурного диапазона работы, наличия на кристалле необходимых интерфейсных
средств. В таблице 1 представлены микросхемы семейства Mega, основное различие
между которыми состоит в реализации памяти программ [13].
Таблица 1 - Параметры микроконтроллеров
|
Микросхема
|
ПЗУ программ, кбайт
|
ОЗУ
|
ЭСПЗУ
|
Таймеры
|
Посл. порты
|
АЦП
|
Корпус, кол-во выводов
|
|
ATtiny26/L
|
2
|
128 Б
|
128 Б
|
2
|
USI
|
11 вх.
|
20
|
|
ATmega8/L
|
8
|
1 KБ
|
512 Б
|
3
|
USART
|
6/8 вх.
|
28,32
|
|
ATmega8515/L
|
8
|
512 Б
|
512 Б
|
2
|
USART
|
нет
|
40,44
|
|
ATmega8535/L
|
8
|
512 Б
|
512 Б
|
2
|
USART
|
8 вх.
|
40,44
|
|
ATmega16/L
|
16
|
1 KБ
|
512 Б
|
3
|
USART
|
8 вх.
|
40,44
|
|
ATmega162L/V
|
16
|
1 KБ
|
512 Б
|
4
|
2 USART
|
нет
|
40,44
|
|
ATmega169L/V
|
16
|
1 KБ
|
512 Б
|
3
|
USART
|
8 вх.
|
40,44
|
Все микроконтроллеры семейства Mega имеют возможность
самопрограммирования, т.е. самостоятельного изменения содержимого своей памяти
программ. Эта особенность позволяет создавать на их основе очень гибкие
системы, алгоритм работы которых будет меняться самим микроконтроллером в
зависимости от каких-либо внутренних условий или внешних событий.
Гарантированное число циклов перезаписи Flash-памяти у
микроконтроллеров AVR второго поколения составляет не менее 10 тыс. циклов при
типовом значении 100 тыс. циклов. Выбор сделан в пользу ATmega8, так как по
всем параметрам это оптимальный вариант.
Отличительные особенности ATmega8:
) 8-разрядный высокопроизводительный AVR микроконтроллер с малым
потреблением;
) 130 высокопроизводительных команд, большинство команд
выполняется за один тактовый цикл;
) 32 8-разрядных рабочих регистра общего назначения;
) полностью статическая работа;
) встроенный 2-цикловый перемножитель;
) энергонезависимая память программ и данных: 8 Кбайт
внутрисистемно программируемой Flash памяти;
) дополнительный сектор загрузочных кодов с независимыми
битами блокировки;
) режим одновременного чтения/записи (Read-While-Write);
) 512 байт EEPROM, который обеспечивает 100000 циклов
стирания/записи;
) 1 Кбайт встроенной SRAM;
) 16-разрядный таймер/счетчик с отдельным предварительным
делителем и режимами захвата и сравнения;
) счетчик реального времени с отдельным генератором;
) программируемый последовательный USART.
Специальные микроконтроллерные функции ATmega8:
) сброс по подаче питания и программируемый детектор
кратковременного снижения напряжения питания;
) встроенный калиброванный RC-генератор;
) внутренние и внешние источники прерываний;
) пять режимов пониженного потребления: Idle, Power-save,
Power-down, Standby и снижения шумов ADC.
Расширенная система команд обеспечивает побайтовую и
побитовую адресацию. Отдельные программно доступные биты могут быть
установлены, сброшены, могут пересылаться, проверяться и использоваться в
логических вычислениях. Структурная схема микроконтроллера представлена на
рисунке 5.
2.1.2
Сопряжение с персональным компьютером
Рассмотрим возможные варианты сопряжения портативного
устройства и ПК.
Самый общеизвестный это универсальный последовательный
интерфейс - UART. Практически все микроконтроллеры поддерживают его полностью
аппаратно. Единственное, что требуется учитывать при сопряжении это разницу
между логическими уровнями TTL микроконтроллера и логическими уровнями
интерфейса RS-232 ПК.
Еще одним, не менее известным последовательным интерфейсом
передачи данных, является Universal Serial Bus или же просто USB. К сожалению
не все микроконтроллеры имеют его аппаратную поддержку, поэтому часто для
организации последовательного обмена данными через шину USB используют
высоко-интегрированные микросхемы являющиеся переходником USB - COM.
Для тех микроконтроллеров, которые поддерживают USB,
требуется написание специального драйвера для операционной системы, только
после этого с ними можно будет работать как с полноценными USB устройствами.
В связи с тем, что во многих современных компьютерах
отсутствует выход СОМ-порта (на современных ноутбуках практически на всех)
проблема соединения устройств на микроконтроллерах с ПК встает очень остро.
Решить данную проблему помогают микросхемы серии FT232x [15].
В семействе FT232x особый интерес вызывает FT232R. Эта
микросхема представляет собой практически готовое решение, подключаемое к ПК по
USB и имеющее на выходе сигналы UART. Данные сигналы понятны для любого
микроконтроллера. Для простого подключения вполне достаточно двух линий - TX и
RX.
Схема включения FT232R представлена на рисунке 6.
После подключения к порту USB модуля на основе FT232R,
операционная система ПК опознает его как "FT232R USB UART" - виртуальный
СОМ-порт. Информационный обмен по которому осуществляется так же как и через
обычный СОМ-порт.
2.1.3
Устройство сопряжения с объектом управления
Устройство сопряжения обеспечивает получение переходной
характеристики реального объекта. Изначально данные поступают в буферную зону в
виде набора значений времени t переходного процесса и снятых с объекта
соответствующих им значений выходного сигнала h (t). Впоследствии на ПК
формируется текстовый файл "Charect. txt", по которому уже на ПК, воссоздается
по этим данным график переходного процесса.
Принципиальная схема аппаратной части устройства сопряжения
приведена в приложении, а перечень элементов в спецификации. Чертежи корпуса
устройства сопряжения приведены в приложении.
Основной алгоритм управляющей программы контроллера
устройства сопряжения, представлен на рисунке 7.
Ниже приведено описание основных функций и кодов операций
управляющей программы.
Используемый внешний файл sysio. c, содержит следующие
основные функции:
init_IO (void) - функция инициализирующая
приемник и передатчик USART, устанавливающая скорость обмена данными и формат
передаваемых данных (8 битов данных и два стоповых бита без паритета);
getchar (void) - функция получения данных
из буфера ресивера
Файл главной программы МК Main. c:
_C_task void main (void) - основная функция
программы инициализирует со 2 по 5 биты портов C и D, устанавливает начальную
частоту прерывания по совпадению таймера, разрешает глобальные прерывания и
запускает бесконечный цикл получения команд с помощью функции get_command
(void).
get_command (void) - функция, возвращающая код
команды считанной из массива. В массив команда попадает из буфера ресивера.
2.2
Программная часть комплекса
2.2.1
Алгоритм идентификации объектов управления вещественным интерполяционным
методом
Первым шагом необходимо выбрать, как будут заданы значения
идентифицируемого объекта. Это могут быть либо характеристики моделей, заданных
в форме передаточных функций, либо переходные характеристики, полученные с
реального объекта управления.
Затем необходимо по полученным значениям восстановить график
переходного процесса.
Следующим шагом необходимо задать структуру идентифицирующей
модели из списка.
Далее происходит идентификация модели объекта выбранной
структурой:
- учитывая порядок идентифицирующей модели,
производится расчет необходимого количества узлов интерполирования;
- производится расчет значения первого узла
по известным формулам;
- происходит расчет значений переходной
функции в зависимости от значения первого узла интерполирования;
- составляется СЛАУ;
- производится решение СЛАУ относительно
неизвестных коэффициентов передаточной функции.
В итоге получается передаточная функция, все параметры
которой известны.
Далее следует оценка полученного результата: вычисляется
погрешность идентификации, и если полученный результат не приемлем, то
начинается итерационный поиск, благодаря которому находится оптимальный первый
узел интерполирования.
Затем опять происходит идентификация модели и оценка
полученного результата. Последние пункты повторяются до тех пор, пока не будет
достигнут приемлемый результат.
Алгоритм идентификации объектов в виде блок-схемы представлен
на рисунке 8.
.2.2 Основные
функции программы
Листинг программы представлен на электронном носите, в
приложении Б приведены только основные функций.
Главный модуль программы Object_Identification содержит
следующие основные функции:
Function inObjectData=Transfer_ch_cr
(inObjectData) - функция расчета табличных значений переходной характеристики для
модельных примеров.- структура входных данных с информацией об объекте
исследования, состоящая из:
- TimeResponse - временя установления (время
переходного процесса);
- TimePointNumbers - количество временных
точек;
- коэффициенты ПФ имитационной модели
объекта.
Выходным параметром функции является сама входная структура,
в которую дописываются следующие параметры:
- rTimeSliceNumbers - количество временных
приращений;
- rTimeArray - массив временных точек;
- rTimeSliceArray - массив значений
приращений;
- rCharacteristicArray - массив значений
переходной характеристики.
Function inObjectData=Transfer_ch_frfile
(FullName) - функция считывания переходной характеристики реального объекта из
файла. Входной параметр: строка с полным именем и путем
Function NumericalResponse=ObjNumericalResponse
(inObjectData, DeltaArray) - функция нахождения численной характеристики
объекта по его временной характеристике и массиву узлов.
Function ModelData=Identification
(inObjectData,vec_delta,mExpDen,mExpNum) - функция расчета коэффициентов модели объекта
по его переходной характеристики.- структура входных данных с информацией об
объекте исследования;_delta - массив значений интерполяционной сетки;- старшая
степень полинома знаменателя искомой модели объекта;- старшая степень полинома
числителя искомой модели объекта.
Function Numerical_Delta_Derivation - функция итерационного
поиска наилучшего решения.
Function ErrorGraphData (ModelData,ObjectData) - функция расчета
абсолютной и относительной ошибки.- структура входных данных с информацией об
объекте исследования, состоящая из:
- rCharacteristicArray - массив значений
переходной характеристики.
- ModelData - структура входных данных с
информацией о модели объекта, состоящая из массива значений переходной
характеристики mHt.
Step (Model, Time) - функция нахождения
реакции системы на единичный скачек входного воздействия.- передаточная функция
модели объекта;- значение времени переходного процесса.
Функция описана в [26].
2.2.3
Интерфейс программы
Главное окно программы для получения ПХ с реального ОУ, имеет
следующий вид (рисунок 9):
Работа с программой начинается с первой вкладки Объект, в
которой осуществляется подключение к устройству сопряжения с реальным объектом.
На следующей вкладке оператору предоставляется возможность визуально
контролировать процесс получения переходной характеристики объекта управления
(рисунок 10).
Если возникли какие-либо помехи, процесс получения переходной
характеристики можно повторить неограниченное число раз, до получения
удовлетворительного результата. График переходного процесса может быть увеличен
(рисунок 11) по клику на соответствующем графике.
Вследствие некачественной установки датчиков Холла, а так же
ряда других причин, получаемая характеристика является зашумленной и не может
быть использована в таком виде для идентификации. Поэтому ее нужно пропустить
через сглаживающий фильтр, после работы, которого характеристика примет
следующий вид (рисунок 11).
Снятые значения с идентифицируемого объекта сохраняются в
файл в виде таблицы, содержащей значения времени переходного процесса и
значения выходной величины. После чего характеристику можно восстановить и
принять для идентификации объекта.
2.2.4 Выбор
структуры модели объекта управления
При осуществлении идентификации пользователю требуется
выбрать структуру модели, для которой и будет происходить поиск решения.
В основе созданного программного модуля идентификации лежит
ВИМ [12]. Разработанный интерфейс пользователя, показан на рисунке 12.
Главной трудностью при программировании обратного
преобразования Лапласа, является то, что не существует открытого кода в
свободном доступе, хотя данная задача легко решается специализированными
прикладными программами.
В разработанном модуле идентификации использование обратного
преобразования Лапласа происходит без дополнительной установки
специализированных программных продуктов (объем занимаемого места, на жестком
диске которых может достигать до 5 Гб), а за счет установки только библиотеки
MATLAB Component Runtime. Данная среда исполнения свободно распространяется
вместе с легально созданным компонентом, использование которого регулируется
лицензионным соглашением для конечного пользователя. Академическая лицензия для
студентов, вузов, некоммерческих организаций предоставляется бесплатно [14].
Поскольку АПК позиционирует себя как мобильный, то при
переносе исходной программы на другой ПК, время на установку ПО а так же
занимаемый объем на жестком диске должны быть минимальными.
.2.5
Формирование интерполяционной сетки
Согласно методике, изложенной в [1,12], в большинстве случаев используется
наиболее простой вариант, когда расположение узлов формируют по правилу
равномерной сетки. В процессе применения выяснилось, что область существенных
изменений и значений функции 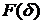 должна лежать в интервале
должна лежать в интервале 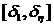 , т. е определение интервала расположения узлов заключается в
выборе значений первого
, т. е определение интервала расположения узлов заключается в
выборе значений первого 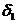 и последнего
и последнего 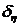 узлов [12].
узлов [12].
Процесс выбора узлов необходимо максимально формализовать с тем,
чтобы показать возможные стартовые условия, остановившись на которых можно
решить задачу или же проводить поиск альтернативных решений и исследовать
возможность оптимизации по формированию интерполяционной сетки [25].
Если же выбор первого по порядку узла 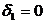 является неприемлемым, то за
является неприемлемым, то за 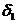 , выбирается узел
, выбирается узел
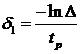 , (6)
, (6)
где 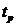 - время установления переходного
процесса, равное абсциссе точки входа переходной характеристики в
- время установления переходного
процесса, равное абсциссе точки входа переходной характеристики в 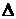 % трубку;
% трубку;
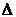 - малая величина, до которой уменьшится подынтегральное выражение
по окончании времени регулирования
- малая величина, до которой уменьшится подынтегральное выражение
по окончании времени регулирования 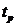 [1].
[1].
Данные рекомендации были учтены в разработанном модуле
идентификации (рисунок 13), где предоставляется возможность задания первого
узла. Все остальные узлы располагаются согласно правилу равномерной сетки.
2.2.6
Нахождение коэффициентов ПФ модели объекта управления
Данная методика подробно изложена в [12], откуда взяты
основные выводы и формулы для созданного программного модуля идентификации.
На рисунке 14 представлено рабочее окно программы с
полученным решением: выводом результата в виде переходной характеристики и в
виде ПФ модели идентифицируемого объекта.
2.2.7
Проверка адекватности модели ОУ
После того как математическая модель объекта найдена
необходимо убедиться в ее соответствии реальному объекту. Критерий (5)
позволяет оценить погрешность моделирования в локальных точках ПХ. Он является
относительно простым и на достаточном уровне отражает степень соответствия
модели и реального объекта [12, 24].
Для наглядности в программе строятся графики абсолютной и
относительной ошибок (рисунок 15).
2.2.8
Итерационный поиск
Если в первом полученном приближенном решении ошибка превышает
допустимое заданное отклонение, то можно воспользоваться итерационным поиском
для ее минимизации.
Допустим в ходе проведения первой итерации, для решения какой-либо
приближенной задачи получен результат, характеризующийся значительной величиной
ошибки на начальном (конечном) интервале 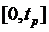 , что позволяет предположить на основании перекрестного свойства
значительную величину ошибки и на конечном участке функции
, что позволяет предположить на основании перекрестного свойства
значительную величину ошибки и на конечном участке функции 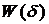 . Для ее уменьшения необходимо увеличить
интервал расположения узлов
. Для ее уменьшения необходимо увеличить
интервал расположения узлов 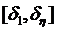 за счет смещения узла
за счет смещения узла 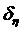 в сторону больших (меньших) значений. Необходимо проводить n-ое
количество итерационных смещений узлов до тех пор, пока не установиться
примерное на начальном и конечном участках интервала
в сторону больших (меньших) значений. Необходимо проводить n-ое
количество итерационных смещений узлов до тех пор, пока не установиться
примерное на начальном и конечном участках интервала 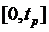 равенство погрешностей [12]:
равенство погрешностей [12]:
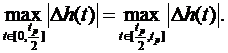
Блок-схема алгоритма итерационного поиска приведена на рисунках
16-17.
3. Анализ
работоспособности аппаратно-программного комплекса
Для проверки работоспособности комплекса было проведено
исследование, которое заключалось в тестировании программы при различных
переходных характеристиках ОУ и различных структурах модели объекта.
В качестве переходных характеристик ОУ были использованы:
характеристики моделей, заданных в форме передаточных
функций;
переходные характеристики, полученные с реального ОУ.
3.1
Идентификация на модельных примерах
Для проведения анализа рассмотрим
несколько следующих примеров:
Пример с использованием апериодического звена второго
порядка, [16], заданного в виде ПФ:
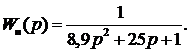
График переходного процесса представлен на рисунке 18.
Для идентификации использовались структуры модели, заложенные в
программе (рисунок 19).
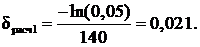
Проведем идентификацию, используя модель структуры 1:
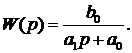
Найденные программой коэффициенты:
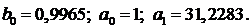
Полученное решение представлено на рисунке 20.
В данном случае абсолютная ошибка составляет 0,08, графики
абсолютной и относительной ошибок приведены на рисунке 21.
График переходного процесса, полученный после идентификации,
представляет плавную кривую, совпадающую на начальном и конечном участках с
исходным графиком, расхождения и максимальная ошибка приходиться на средний
участок. Уменьшить ее возможно путем дальнейшего перебора узлов. Воспользуемся
итерационным поиском первого узла, чтобы уменьшить ошибку первого приближения.
Для этого необходимо задать интервал поиска 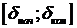 , а так же шаг поиска.
, а так же шаг поиска.
Установленные значения: интервал поиска 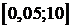 с шагом равным 0,05. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки
с шагом равным 0,05. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки 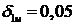 , при котором абсолютная ошибка минимальна
и равна 0,012. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 22. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска
, при котором абсолютная ошибка минимальна
и равна 0,012. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 22. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска 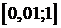 , увеличив частоту шага. Первый узел
интерполирования будет найден более точно
, увеличив частоту шага. Первый узел
интерполирования будет найден более точно 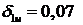 , а абсолютная ошибка при этом составит 0,01.
, а абсолютная ошибка при этом составит 0,01.
Найденные программой коэффициенты:
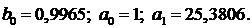
Полученное решение представлено на рисунке 23.
Из рисунка 23 видно, что график переходного процесса, полученный
после идентификации, представляет плавную кривую, практически совпадающую с
исходным графиком. Графики абсолютной и относительной ошибок приведены на
рисунке 24.
Исходные и полученные данные сведены в таблицу 2.
Таблица - 2 Данные идентификации структурой 1 для примера 1
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,021
|
b0=0,99654 b1= b2=0 a0=1 a1=31,2283 a2= a3=0
|
0,08
|
0,05
|
10
|
0,05
|
0,05
|
b0=0,99654 b1= b2=0 a0=1 a1=25,3806 a2= a3=0
|
0,01
|
Проведем идентификацию, используя модель структуры 2:
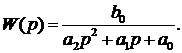
Найденные программой коэффициенты, при 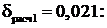
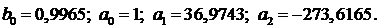
Значение коэффициента 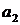
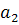 является отрицательным, что соответствует неустойчивой системе,
поэтому полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей.
является отрицательным, что соответствует неустойчивой системе,
поэтому полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей.
Интервал поиска 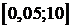 с шагом равным 0,05. как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен
с шагом равным 0,05. как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен 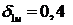 , при котором абсолютная ошибка минимальна
и равна 0,0032. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 25. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска
, при котором абсолютная ошибка минимальна
и равна 0,0032. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 25. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска 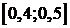 , увеличив частоту шага. Первый узел
интерполирования будет найден более точно
, увеличив частоту шага. Первый узел
интерполирования будет найден более точно 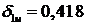 , а абсолютная ошибка при этом составит 0,0031.
, а абсолютная ошибка при этом составит 0,0031.
Найденные программой коэффициенты:
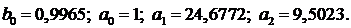
Полученное решение представлено на рисунке 26.
Из рисунка 26 видно, что график переходного процесса, полученный
после идентификации, представляет плавную кривую, практически совпадающую с
исходным графиком. На рисунке 27 показаны графики абсолютной и относительной
ошибок.
Исходные и полученные данные сведены в таблицу 3.
Таблица - 3 Данные идентификации структурой 2 для примера 1
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,021
|
b0=0,99654 b1= b2=0 a0=1 a1=36,9743 a2= -
273,6165 a3=0
|
529
|
0,05
|
10
|
0,05
|
0,05
|
b0=0,99654 b1= b2=0 a0=1 a1=24,6772 a2=9,5923
a3=0
|
0,0032
|
Проведем идентификацию, используя модель структуры 3:
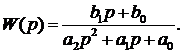
Найденные программой коэффициенты, при 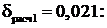
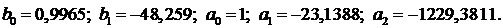
Значение коэффициентов 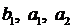 отрицательные, что соответствует неустойчивой системе. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей. Интервал
поиска
отрицательные, что соответствует неустойчивой системе. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей. Интервал
поиска 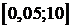 с шагом равным 0,05, как и для случая
первой структуры модели. При данных начальных условиях итерационного поиска
первый узел интерполяционной сетки равен
с шагом равным 0,05, как и для случая
первой структуры модели. При данных начальных условиях итерационного поиска
первый узел интерполяционной сетки равен 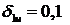 , при котором абсолютная ошибка минимальна и равна 0,0034. График
зависимости ошибки от расположения первого узла интерполяционной сетки приведен
на рисунке 28. Из графика видно, что минимальная ошибка лежит в области нуля.
Следовательно, можно изменить интервал поиска
, при котором абсолютная ошибка минимальна и равна 0,0034. График
зависимости ошибки от расположения первого узла интерполяционной сетки приведен
на рисунке 28. Из графика видно, что минимальная ошибка лежит в области нуля.
Следовательно, можно изменить интервал поиска 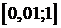 , увеличив частоту шага. Первый узел интерполирования будет найден
более точно
, увеличив частоту шага. Первый узел интерполирования будет найден
более точно 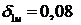 , а абсолютная ошибка при этом составит
0,003.
, а абсолютная ошибка при этом составит
0,003.
Найденные программой коэффициенты:
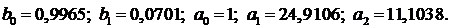
Полученное решение представлено на рисунке 29.
Графики абсолютной и относительной ошибок (рисунок 30).
Исходные и полученные данные сведены в таблицу 4.
Таблица 4 - Данные идентификации структурой 3 для примера 1
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,021
|
b0=0,9965 b1= - 48,259 b2=0 a0=1 a1=-23,1388
a2= - 1229,3811 a3=0
|
326
|
0,05
|
10
|
0,05
|
0,1
|
b0=0,9965 b1=0,0168 b2=0 a0=1 a1=24,8699
a2=9,6057 a3=0
|
0,0034
|
Проведем идентификацию, используя модель структуры 4:
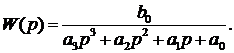
Найденные программой коэффициенты, при 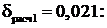
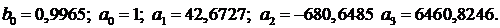
Полученное решение представлено на рисунке 31.
Значение коэффициента 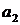 является отрицательным, что соответствует неустойчивой системе,
поэтому полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей.
является отрицательным, что соответствует неустойчивой системе,
поэтому полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей.
Интервал поиска 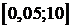 с шагом равным 0,05. как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен
с шагом равным 0,05. как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен 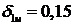 , при котором абсолютная ошибка минимальна
и равна 0,0033. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 32. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска
, при котором абсолютная ошибка минимальна
и равна 0,0033. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 32. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска 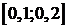 , увеличив частоту шага. Первый узел
интерполирования будет найден более точно
, увеличив частоту шага. Первый узел
интерполирования будет найден более точно 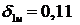 , а абсолютная ошибка при этом составит 0,0032.
, а абсолютная ошибка при этом составит 0,0032.
Найденные программой коэффициенты:
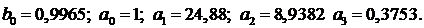
Полученное решение представлено на рисунке 33.
Графики абсолютной и относительной ошибок (рисунок 34).
Из рисунка 33 видно, что график переходного процесса, полученный
после идентификации, представляет плавную кривую, практически совпадающую с
исходным графиком.
Исходные и полученные данные сведены в таблицу 5.
Таблица 5 - Данные идентификации структурой 4 для примера 1
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,021
|
b0=0,9965 b1= b2=0 a0=1 a1=42,6727 a2= -
680,6485 a3=6460,8246
|
1000
|
0,05
|
10
|
0,05
|
0,05
|
b0=0,9965 b1= b2=0 a0=1 a1=24,88 a2=8,9382
a3=0,3752
|
0,0033
|
Проведем идентификацию, модель структуры 5:
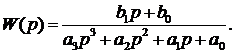
Найденные программой коэффициенты, при 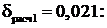
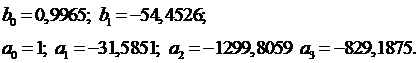
График переходного процесса, полученный после идентификации,
представляет плавную кривую, совпадающую на начальном и среднем участках с
исходным графиком, расхождения и максимальная ошибка приходиться на конечный
участок. Полученное решение представлено на рисунке 35. Значение коэффициентов 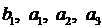 отрицательные, что соответствует
неустойчивой системе, поэтому полученные значения коэффициентов являются неудовлетворительными.
Для нахождения оптимальных значений необходимо воспользоваться итерационным
поиском первого узла интерполирования, при котором ошибка будет наименьшей.
отрицательные, что соответствует
неустойчивой системе, поэтому полученные значения коэффициентов являются неудовлетворительными.
Для нахождения оптимальных значений необходимо воспользоваться итерационным
поиском первого узла интерполирования, при котором ошибка будет наименьшей.
Интервал поиска 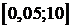 с шагом равным 0,05, как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен
с шагом равным 0,05, как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен 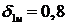 , при котором абсолютная ошибка минимальна
и равна 0,011. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 35.
, при котором абсолютная ошибка минимальна
и равна 0,011. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 35.
Из графика 35 видно, что минимальная ошибка лежит в области нуля.
Следовательно, можно изменить интервал поиска 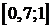 , увеличив шаг. Первый узел интерполирования будет найден более
точно
, увеличив шаг. Первый узел интерполирования будет найден более
точно 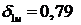 .
.
Найденные программой коэффициенты:
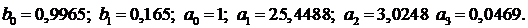
Полученное решение представлено на рисунке 36.
Графики абсолютной и относительной ошибок (рисунок 37).
Исходные и полученные данные сведены в таблицу 6.
Таблица 6 - Данные идентификации структурой 5 для примера 1
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,021
|
b0=0,9965 b1= - 54,4526 b2=0 a0=1 a1=-31,5851
a2= - 1299,8059 a3=-829,1875
|
0,1
|
0,05
|
10
|
0,05
|
0,05
|
b0=0,9965 b1=0,165 b2=0 a0=1 a1=25,4488
a2=3,0248 a3=0,0469
|
0,011
|
Проведем идентификацию, модель структуры 6:
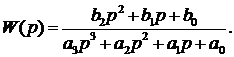
Найденные программой коэффициенты, при 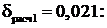
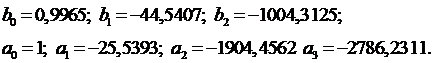
Значение коэффициентов 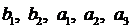 отрицательные, что соответствует неустойчивой системе, поэтому
полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей.
отрицательные, что соответствует неустойчивой системе, поэтому
полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей.
Интервал поиска 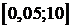 с шагом равным 0,05, как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен
с шагом равным 0,05, как и для случая первой структуры модели. При
данных начальных условиях итерационного поиска первый узел интерполяционной
сетки равен 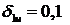 , при котором абсолютная ошибка минимальна
и равна 0,0032. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 38. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска
, при котором абсолютная ошибка минимальна
и равна 0,0032. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 38. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска 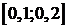 , увеличив частоту шага. Первый узел
интерполирования остался без изменений.
, увеличив частоту шага. Первый узел
интерполирования остался без изменений.
Найденные программой коэффициенты:
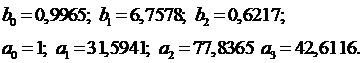
График переходного процесса, полученный после идентификации,
представляет плавную кривую, совпадающую на начальном, среднем и конечном
участках с исходным графиком идентифицируемого ОУ. Полученное решение
представлено на рисунке 39.
Графики абсолютной и относительной ошибок (рисунок 40).
Исходные и полученные данные сведены в таблицу 7.
Таблица 7 - Данные идентификации структурой 6 для примера 1
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,021
|
b0=0,9965 b1= - 44,5407 b2=-1004,3125 a0=1
a1=-25,5393 a2= - 1904,4562 a3=-2786,2311
|
0,1
|
0,05
|
10
|
0,05
|
0,05
|
b0=0,9965 b1=6,7578 b2=0,6217 a0=1 a1=31,5941
a2=77,8365 a3=42,6116
|
0,0032
|
Проанализируем полученные результаты. Для этого объединим в
сводную таблицу 8 данные по итерационному поиску, для всех шести структур.
Таблица 8 - Сводные данные
|
№
|
Структура
|
Решение
|
Ошибка
|
|
1
|
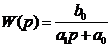 b0=0,99654; b1= b2=0;
a0=1; a1=25,3806; a2= a3=00,01 b0=0,99654; b1= b2=0;
a0=1; a1=25,3806; a2= a3=00,01
|
|
|
|
2
|
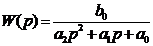 b0=0,99654; b1= b2=0;
a0=1; a1=24,6772; a2=9,5923; a3=00,0032 b0=0,99654; b1= b2=0;
a0=1; a1=24,6772; a2=9,5923; a3=00,0032
|
|
|
3 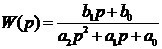 b0=0,9965; b1=0,0168; b2=0; a0=1
b0=0,9965; b1=0,0168; b2=0; a0=1
|
a1=24,8699; a2=9,6057; a3=00,0034
|
|
|
|
|
4
|
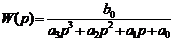 b0=0,9965; b1= b2=0;
a0=1; a1=24,88; a2=8,9382; a3=0,37520,0033 b0=0,9965; b1= b2=0;
a0=1; a1=24,88; a2=8,9382; a3=0,37520,0033
|
|
|
5 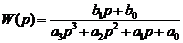 b0=0,9965; b1=0,165 b2=0; a0=1
b0=0,9965; b1=0,165 b2=0; a0=1
|
a1=25,4488; a2=3,0248; a3=0,04690,011
|
|
|
6 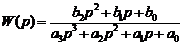 b0=0,9965; b1=6,7578; b2=0,6217;=1; a1=31,5941; a2=77,8365;
b0=0,9965; b1=6,7578; b2=0,6217;=1; a1=31,5941; a2=77,8365;
Поскольку идентифицируемая переходная характеристика объекта
соответствует апериодическому звену второго порядка, то предпочтительно
начинать перебор с ПФ первого порядка, увеличивая степень полиномов знаменателя
и числителя до тех пор, пока точность восстановления временной характеристики
не достигнет заданного уровня.
Из таблицы видно, что оптимальный результат получается, если
проводить идентификацию структурой 2, так как в данном случае не будет
избыточных коэффициентов, что снижает время работы программы.
Следующим примером для анализа выберем апериодическое звено
первого порядка [16], заданного в виде ПФ:
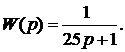
График переходного процесса представлен на рисунке 40.
Согласно формуле (6) рассчитаем  :
:
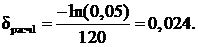
Проведем идентификацию, используя модель структуры 1:
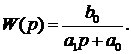
Найденные программой коэффициенты:
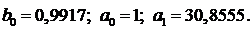
Полученное решение представлено на рисунке 41.
График переходного процесса, полученный после идентификации,
представляет плавную кривую, совпадающую на начальном и конечном участках с
исходным графиком, расхождения и максимальная ошибка приходиться на средний
участок. Уменьшить ее возможно путем дальнейшего перебора узлов. Графики
абсолютной и относительной ошибок приведены на рисунке 42.
Установленные значения: интервал поиска 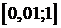 с шагом равным 0,01. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки
с шагом равным 0,01. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки 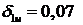 , при котором абсолютная ошибка минимальна
и равна 0,011. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 43.
, при котором абсолютная ошибка минимальна
и равна 0,011. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 43.
Найденные программой коэффициенты:
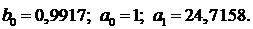
Полученное решение представлено на рисунке 44.
Из рисунка 44 видно, что график переходного процесса, полученный
после идентификации, представляет плавную кривую, практически совпадающую с
исходным графиком. Графики абсолютной и относительной ошибок приведены на
рисунке 45.
Исходные и полученные данные сведены в таблицу 9.
Таблица 9 - Данные идентификации структурой 1 для примера 2
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,024
|
b0=0,9917 b1= b2=0 a0=1 a1=30,8555 a2= a3=0
|
0,07
|
0,01
|
1
|
0,01
|
0,07
|
b0=0,9917 b1= b2=0 a0=1 a1=24,7158 a2= a3=0
|
0,007
|
Проведем идентификацию, используя модель структуры 2:
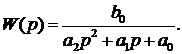
Найденные программой коэффициенты, при 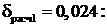
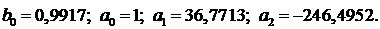
Значение коэффициента 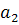
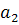 является отрицательным, что соответствует неустойчивой системе,
поэтому полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей (рисунок
46). Интервал поиска
является отрицательным, что соответствует неустойчивой системе,
поэтому полученные значения коэффициентов являются неудовлетворительными. Для
нахождения оптимальных значений необходимо воспользоваться итерационным поиском
первого узла интерполирования, при котором ошибка будет наименьшей (рисунок
46). Интервал поиска 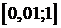 с шагом равным 0,01, как и для случая
первой структуры модели. При данных начальных условиях итерационного поиска
первый узел интерполяционной сетки равен
с шагом равным 0,01, как и для случая
первой структуры модели. При данных начальных условиях итерационного поиска
первый узел интерполяционной сетки равен 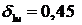 , при котором абсолютная ошибка минимальна и равна 0,0068.
, при котором абсолютная ошибка минимальна и равна 0,0068.
Найденные программой коэффициенты:
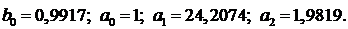
Полученное решение представлено на рисунке 47.
Из рисунка 47 видно, что график переходного процесса, полученный
после идентификации, представляет плавную кривую, практически совпадающую с
исходным графиком. На рисунке 48 представлены графики абсолютной и
относительной ошибок.
Исходные и полученные данные сведены в таблицу 10.
Таблица 10 - Данные идентификации структурой 2 для примера 2
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,024
|
b0=0,9917 b1= b2=0 a0=1 a1=36,7713 a2= -
246,4952 a3=0
|
247
|
0,01
|
1
|
0,01
|
0,45
|
b0=0,9917 b1= b2=0 a0=1 a1=24, 2074 a2=1,9819
a3=0
|
0,0068
|
Для структур 3 и 4 зависимости переходной характеристики от
расположения первого узла интерполирования, оптимальные графики переходного
процесса, полученные после идентификации, а так же графики ошибок приведены на
рисунках 49-54. В данном примере в качестве модели объекта была взята ПФ
апериодического звена первого порядка, поэтому идентификация структурами 5 и 6
не проводилась, поскольку были получены оптимальные результаты при
использовании структур с меньшими значениями степеней полиномов.
Данные полученные при идентификации с использованием 3 и 4
структур представлены в таблице 11.
Таблица 11 - Данные идентификации структурами 3 и 4 для
примера 2
|
Структура
|
Решение
|
dнач
|
dкон
|
Шаг
|
d1и
|
Ошибка
|
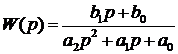 b0=0,9917; b1=0,965; b2=0; a0=1
b0=0,9917; b1=0,965; b2=0; a0=1
|
a1=25,6; a2=25,1887; a3=00,0110,010,080,007
|
|
|
|
|
|
|
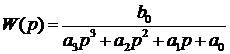 b0=0,9917;
b0=0,9917;
|
b1= b2=0; a0=1; a1=24,6477; a2=0,9107;
a3=0,01260,0110,010,10,0075
|
|
|
|
|
|
|
Оптимальный результат получается, если проводить
идентификацию любой из 1-4 структур, разница ошибки составляет тысячные доли,
поэтому целесообразно проводить идентификацию при помощи первой структуры, так
как сокращается объем вычислений, поскольку процедура идентификации происходит
за два-три шага.
Следующим примером для анализа выберем звено с
колебательностью [16], заданное в виде ПФ:
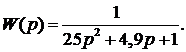
График переходного процесса представлен на рисунке 55.
Согласно формуле (6) рассчитаем 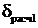 :
:
Исходя из условия минимальной сложности, так как переходная
характеристика имеет колебательный вид - целесообразно начинать перебор
структур со второй.
Проведем идентификацию, используя модель структуры 2:
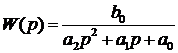 .
.
Найденные программой коэффициенты, при 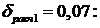
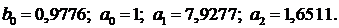
Полученное решение представлено на рисунке 56.
В данном случае абсолютная ошибка составляет 0,3, графики
абсолютной и относительной ошибок приведены на рисунке 57.
График переходного процесса, полученный после идентификации,
представляет плавную кривую, совпадающую на конечном участке с исходным
графиком, расхождения и максимальная ошибка приходиться на начальный и средний
участок. Уменьшить ее возможно путем дальнейшего перебора узлов. Воспользуемся
итерационным поиском первого узла, чтобы уменьшить ошибку первого приближения.
Для этого необходимо задать интервал поиска  , а так же шаг поиска.
, а так же шаг поиска.
Установленные значения: интервал поиска  с шагом равным 0,05. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки
с шагом равным 0,05. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки 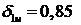 , при котором абсолютная ошибка минимальна
и равна 0,02. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 58. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска
, при котором абсолютная ошибка минимальна
и равна 0,02. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 58. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска  , увеличив частоту шага. Первый узел интерполирования
остался точно таким же.
, увеличив частоту шага. Первый узел интерполирования
остался точно таким же.
Найденные программой коэффициенты:
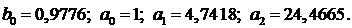
Полученное решение представлено на рисунке 59.
Из рисунка 59 видно, что график переходного процесса, полученный
после идентификации, представляет плавную кривую, практически совпадающую с
исходным графиком, за исключением последнего участка. На рисунке 60 приведены
графики абсолютной и относительной ошибок.
Исходные и полученные данные сведены в таблицу 12.
Таблица 12 - Данные идентификации структурой 2 для примера 3
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
0,07
|
b0=0,9776 b1= b2=0 a0=1 a1=1,6511 a2=7,9277
a3=0
|
0,3
|
0,01
|
1
|
0,01
|
0,85
|
b0=0,9776 b1= b2=0 a0=1 a1=4,7418 a2=24,4665
a3=0
|
0,02
|
Для структур 3-6 зависимости переходной характеристики от
расположения первого узла интерполирования, оптимальные графики переходного
процесса, полученные после идентификации, а так же графики ошибок приведены на
рисунках 61-72.
Данные полученные при идентификации с использованием 3-6
структур представлены в таблице 13.
Таблица 13 - Данные идентификации структурами 3-6 для примера
3
|
Структура
|
Решение
|
dнач
|
dкон
|
Шаг
|
d1и
|
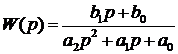 b0=0,9776; b1=0,0088; b2=0; a0=1;
b0=0,9776; b1=0,0088; b2=0; a0=1;
|
a1=4,6408; a2=24,8218; a3=00,0110,010,740,02
|
|
|
|
|
|
|
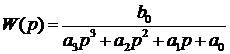 b0=0,9776;
b0=0,9776;
|
b1= b2=0; a0=1; a1=4,7543; a2=24,4384;
a3=0,01290,0110,010,740,029
|
|
|
|
|
|
|
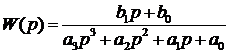 b0=0,9776; b1=192,9972;=0; a0=1
b0=0,9776; b1=192,9972;=0; a0=1
|
a1=197,9387; a2=969,3639;
a3=4825,68780,0110,010,250,004
|
|
|
|
|
|
|
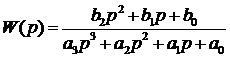 b0=0,9776; b1=15,4538; b2=0,0081;=1; a1=20,0915; a2=100, 5456;
b0=0,9776; b1=15,4538; b2=0,0081;=1; a1=20,0915; a2=100, 5456;
|
a3=385,8570,0110,010,250,02
|
|
|
|
|
|
|
Наименьшая ошибка получается, если проводить идентификацию
структурой 5. При идентификации другими структурами разница ошибки составляет
тысячные доли, следовательно, порядок структуры выбирается исходя из условия
минимальной сложности, так оптимальным решением может быть вторая и третья
структуры.
3.2 Пример
идентификации реального объекта управления
Пример 4. Снятые с объекта значения времени t переходного
процесса и соответствующие им значения выходного сигнала h (t) представлены в
виде таблицы и сведены в текстовый файл "Charect. txt" на электронном
носителе.
Таблица 14 иллюстрирует часть данных, из текстового файла.
Таблица 14 - Значения, снятые с реального ОУ
|
t
|
0
|
0.115167
|
0.230334
|
0.2766165
|
0.3419725
|
0.361046
|
0.379166
|
|
h (t)
|
0
|
90.13
|
324.835
|
580.455
|
691.5
|
738.97
|
807.12
|
|
t
|
0.41384
|
0.461657
|
0.5077245
|
0.536491
|
0.5643795
|
0.578306
|
0.5915425
|
|
h (t)
|
866.97
|
916.44
|
960.805
|
1004.045
|
1043.775
|
1075.7
|
1105.165
|
|
t
|
0.618107
|
0.6441545
|
0.6696825
|
0.69475
|
0.719398
|
0.743669
|
0.618107
|
|
h (t)
|
1129.35
|
1152.365
|
1175.205
|
1197.34
|
1217.17
|
1236.58
|
1129.35
|
|
t
|
0.7675975
|
0.8030015
|
0.826359
|
0.8491715
|
0.871984
|
0.894264
|
0.916544
|
|
h (t)
|
1253.78
|
1269.55
|
1284.465
|
1299.675
|
1315.13
|
1331.39
|
1346.565
|
|
t
|
0.9273545
|
0.9491545
|
0.9707345
|
0.9921005
|
1.013271
|
1.044478
|
1.06529
|
|
h (t)
|
1361.9
|
1376.245
|
1390.655
|
1404.21
|
1417.53
|
1429.795
|
1441.91
|
|
t
|
1.0757095
|
1.1064685
|
1.126808
|
1.136735
|
1.156798
|
1.1767335
|
1.1965445
|
|
h (t)
|
1453.435
|
1464.735
|
1475.11
|
1485.695
|
1495.445
|
1505.29
|
1514.47
|
|
t
|
1.216241
|
1.235827
|
1.2553065
|
1.27469
|
1.3036965
|
1.322898
|
1.341941
|
|
h (t)
|
1523.515
|
1531.905
|
1540.525
|
1547.925
|
1555.465
|
1562.595
|
1550.335
|
|
t
|
1.360984
|
1.3703705
|
1.3893805
|
1.408299
|
1.4271265
|
1.455359
|
1.474059
|
|
h (t)
|
1556.57
|
1577.28
|
1578.355
|
1586.21
|
1593.64
|
1598.305
|
1604.485
|
Исходной информацией будет являться воссозданный по этим
данным график переходного процесса приведенный на рисунке 73.
Проведем идентификацию, используя модель структуры 1:
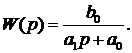
Найденные программой коэффициенты:
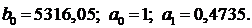
Полученное решение представлено на рисунке 74.
График переходного процесса, полученный после идентификации,
представляет плавную кривую, совпадающую на начальном и среднем участках с
исходным графиком, расхождения и максимальная ошибка приходиться на средний
участок. Уменьшить ее возможно путем дальнейшего перебора узлов. Воспользуемся
итерационным поиском первого узла, чтобы уменьшить ошибку первого приближения.
Для этого необходимо задать интервал поиска  , а так же шаг поиска.
, а так же шаг поиска.
Установленные значения: интервал поиска 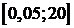 с шагом равным 0,05. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки
с шагом равным 0,05. При данных начальных
условиях итерационного поиска был найден первый узел интерполяционной сетки 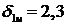 , при котором абсолютная ошибка минимальна
и равна 300. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 75. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска
, при котором абсолютная ошибка минимальна
и равна 300. График зависимости ошибки от расположения первого узла
интерполяционной сетки приведен на рисунке 75. Из графика видно, что
минимальная ошибка лежит в области нуля. Следовательно, можно изменить интервал
поиска 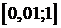 , увеличив частоту шага. Первый узел
интерполирования будет найден более точно
, увеличив частоту шага. Первый узел
интерполирования будет найден более точно 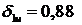 , а абсолютная ошибка при этом составит 219.
, а абсолютная ошибка при этом составит 219.
Найденные программой коэффициенты:
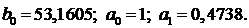
Полученное решение представлено на рисунке 76.
Графики абсолютной и относительной ошибок (рисунок 77).
Исходные и полученные данные сведены в таблицу 15.
Таблица 15 - Данные идентификации структурой 1 для примера 4
|
Первое приближение
|
Итерационный поиск
|
|
d1р
|
Решение
|
Ошибка
|
dнач
|
dкон
|
Шаг
|
d1и
|
Решение
|
Ошибка
|
|
2,3
|
b0=5316,05 b1= b2=0 a0=1 a1=0,4735 a2= a3=0
|
300
|
0,01
|
1
|
0,01
|
0,88
|
b0=5316,05 b1= b2=0 a0=1 a1=0,4738 a2= a3=0
|
219
|
Для структур 2-4 зависимости переходной характеристики от
расположения первого узла интерполирования, оптимальные графики переходного
процесса, полученные после идентификации, а так же графики ошибок приведены на
рисунках 78-86.
Данные полученные при идентификации с использованием 2-4
структур представлены в таблице 16.
Таблица 16 - Данные идентификации структурами 2-4 для примера
4
|
Структура
|
Решение
|
dнач
|
dкн
|
Шаг
|
d1и
|
Ошибка
|
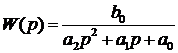 b0=5316,05;= b2=0; a0=1;
b0=5316,05;= b2=0; a0=1;
|
a1=0,4341; a2=0,0153; a3=00,0120,011,0295,8
|
|
|
|
|
|
|
|
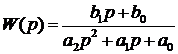 b0=5316,05; b1=85,8272;
b2=0; a0=1; a1=0,4302; a2=0,0161; a3=00,0120,011,1178,9 b0=5316,05; b1=85,8272;
b2=0; a0=1; a1=0,4302; a2=0,0161; a3=00,0120,011,1178,9
|
|
|
|
|
|
|
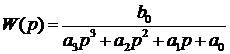 b0=5316,05;
b0=5316,05;
|
b1= b2=0; a0=1; a1=0,4184; a2=0,022;
a3=0,0040,0120,011,1190,5
|
|
|
|
|
|
|
Из таблицы видно, что наименьшая ошибка получается, если
проводить идентификацию 2 структурой, так как в данном случае не будет
избыточных коэффициентов.
Заключение
В процессе выполнения выпускной квалификационной работы был
изучен вещественный интерполяционный метод и разработан аппаратно-программный
комплекс, предназначенный для осуществления идентификации объектов управления.
Решение задачи идентификации с помощью вещественного
интерполяционного метода, позволяет получать математическую модель объекта, при
этом вычислительные затраты достаточно малы, а вмешательство в режим его
нормального функционирования - минимально.
В рамках выполнения работы был спроектирован опытный образец
устройства сопряжения, реализован алгоритм идентификации ОУ, разработан
пользовательский интерфейс программы. Данное программное обеспечение позволяет
идентифицировать математическую модель объекта управления по исходным данным в
виде переходной характеристики, получаемой непосредственно с объекта
управления. Анализ работоспособности АПК идентификации ОУ, позволяет сделать
вывод, что на основе достигнутых результатов можно разработать эффективное
программное обеспечение для решения задач идентификации, которое может быть
использовано в рамках организации концепции аппаратно-программного комплекса на
производстве.
Данная выпускная квалификационная работа выполнена в полном
объеме в соответствии с техническим заданием.
Работы в данном направлении не потеряют своей актуальности,
поскольку процедура идентификации, базирующаяся на анализе экспериментальных
характеристик систем, эффективна для решения задач оперативной диагностики САУ.
Список
использованных источников
1. Гончаров
В.И. Синтез электромеханических исполнительных систем промышленных роботов. -
Томск: Изд-во ТПУ, 2002. - 100 с.
2. Электронный
ресурс - Электрон. дан. - Режим доступа: http://www.philosoft.ru/apks. zhtml
. Методы
классической и современной теории автоматического управления: синтез
регуляторов и теория оптимизации систем автоматического управления / под ред
Н.Д. Егупова. - М.: МГТУ им Баумана, 2000. - 736 с.
. Эйкхофф
П. Основы идентификации систем управления. - М.: Изд-во "Мир", 1975.
- 683 с.
. Sage
A. P. System identification / A. P. Sage, J. L. Melsa. - N. Y.: Academic press,
1974. - 532 p.
. Способ
оптимальной автоматической настройки системы управления - патент РФ
№2001103023, МПК G05B13/00 - опубл.10.02.2003.
. Еремин
Д.М. Идентификация динамических объектов управления с применением нейронных
сетей // Автоматическое управление и интеллектуальные системы: межвуз. сб.
научн. тр. МИРЭА. - М.: 1996. - с.77 - 82.
. Замятин
С.В., Плотников Д.А., Гончаров В.И. Идентификация нелинейных объектов на основе
вещественного интерполяционного метода // Известия Томского политехнического
университета. 2008. Т312. - № 5.
. Рудницкий
В.А. Разработка и исследование алгоритмического и программного обеспечения
идентификатора на основе вещественного интерполяционного метода: автореф. дис.
канд. техн. наук - Томск, 2002. - 20 с.
. Nikolaeva
N. S., Shilnikova A. A., Yurova M. V. Application of the real interpolation
method for identification of nonlinear objects // Автоматизация, мехатроника,
информационные технологии: материалы I Международной научно-технической
интернет-конференции молодых ученых. - Омск: ОмГТУ, 2010. - 200 с.
. Справочник
по теории автоматического управления / Под редакцией А.А. Красовского. - М.:
Наука, 1987. - 712 с.
. Алексеев
А.С. Вещественный интерполяционный метод в задачах автоматического управления /
А.С. Алексеев, А.А. Антропов, В.И. Гончаров, С.В. Замятин, В.А. Рудницкий. -
Томск: Изд-во Томского политехнического университета, 2010. - 227 с.
. Электронный
ресурс - Электрон. дан. - Режим доступа: www.atmel.ru
. Электронный
ресурс - Электрон. дан. - Режим доступа:
http://www.mathworks.com/help/toolbox/compiler/f12-999353.html
. Электронный
ресурс - Электрон. дан. - Режим доступа: http://www.ftdichip.com
. Бесекерский
В.А., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука,
1975.
. Ким
Д.П. Теория автоматического управления. Линейные системы. - М.: Физматлит,
2007. - 310 с.
. Алексеев
А.С. Самонастройка регуляторов исполнительных подсистем мехатронных устройств:
автореф. дис. канд. техн. наук - Томск, 2010. - 20 с.
. Гончаров
В.И., Лиепиньш А.В., Рудницкий В.А. Получение машинноориентированных моделей
объектов управления в адаптивных системах // Компьютерные технологии в науке,
проектировании и производстве: тезисы докладов II Всероссийской
научно-технической конференции, часть VIII - 3-4 февраля 2000 г, Нижний
Новгород. - Нижний Новгород: Нижегородский государственный технический
университет, 2000. - с.39.
. Морозов,
Е.А. Каноническое интегрирование в проектировании динамических систем. -
Екатеринбург, Ижевск: ИЭ УрО РАН, 2006. - 197 с.
. Goncharov
V. System identification based of the real interpolation method / V. Goncharov,
A. Liepinsh, W.rudnicki. - Wroclaw: Oficyna Wydawnicza Politechniki
Wroclawskies, 2001. - 234-239 p.
. Иванова
Е.Н., Рудницкий В.А. Применение аппарата обусловленности при решении задач
идентификации на основе вещественного интерполяционного метода // Молодежь и
современные информационные технологии: сборник трудов VI Всероссийской
научно-практической конференции студентов, аспирантов и молодых ученых - Томск,
26-28 февраля 2008. - Томск: СПб Графикс, 2008. - с.400 - 402.
. Антропов
А.Т., Удод А.С. Идентификация объектов с помощью вещественного
интерполяционного метода // Проектирование инженерных и научных приложений в
MATLAB: сборник трудов II научной конференции - М., 2004. - с.784 - 796.
. Богомолов
Е.Н., Николаева Н.С., Шильникова А.А. Программное обеспечение для идентификации
объектов управления // Молодежь и современные информационные технологии. Сборник
трудов IX Всероссийской научно-практической конференции студентов, аспирантов и
молодых ученых "Молодежь и современные информационные технологии".
Томск, 11-13 мая 2011, ч.2. Томск: СПБ Графикс, 2011. - 247 с.
. Богомолов
Е.Н., Николаева Н.С., Шильникова А.А. Вещественный интерполяционный метод
идентификации объектов // Автоматика Информатика. Караганда: КарГТУ, 2010. - №
1-2 (26-27).
. Лазарев
Ю.Ф. Начало программирования в среде MatLAB. - К.: НТУУ "КПИ", 2003.
- 424 с.
Приложение Б.
Основные функции программы (справочное)
Основные функции
программыinObjectData=Transfer_ch_cr (inObjectData)
b0=inObjectData. b0;=inObjectData. b1;=inObjectData.
b2;=inObjectData. a0;=inObjectData. a1;=inObjectData. a2;=inObjectData.
a3;=inObjectData. TimeResponse;. rTimeSliceNumbers=inObjectData.
TimePointNumbers-1;=inObjectData. rTimeSliceNumbers;=Tp/TSN;. rTimeArray=0:
TTS: Tp;i=1: 1: TSN. rTimeSliceArray (i) =TTS;=tf ([b2 b1 b0], [a3 a2 a1
a0]);_temp=step (Wm, inObjectData. rTimeArray);. rCharacteristicArray=Hdt_temp.
';
function inObjectData=Transfer_ch_frfile
(FullName)
F=fopen (FullName,'rt');=0;feof (F) ==0=k+1;(F);(F);=zeros
(1,k);=zeros (1,k);i=1: k(i) = fscanf (F,'%g',1);(i) = fscanf
(F,'%g',1);;(F);=length (Time);=zeros (1,Npoints);=Time (Npoints);_state=Rpm
(Npoints);=Npoints;i=1: 1: Npoints-1(i) =Time (i+1) - Time (i);.
rCharacteristicArray=Rpm;. TimePointNumbers=length (Time);.
rTimeSliceNumbers=length (Time) - 1;. rTimeArray=Time;. rTimeSliceArray=D;
function NumericalResponse = ObjNumericalResponse
(inObjectData, DeltaArray)
b0 =inObjectData. rCharacteristicArray (inObjectData.
TimePointNumbers);=inObjectData. rCharacteristicArray;=inObjectData.
rTimeSliceNumbers;=inObjectData. TimePointNumbers;=inObjectData.
rTimeArray;=inObjectData. rTimeSliceArray;=length (DeltaArray);=zeros (1,
iend);_compearData. iend=iend;_compearData. SpaceNumbers=SpaceNumbers;i=1: 1:
iend=0;=0;j=1: 1: SpaceNumbers_compearData. Hdt (i,j) =Hdt (j);_compearData. D
(i,j) =D (j);_compearData. DeltaArray (i) =DeltaArray (i);_compearData. dt
(i,j) =dt (j);=sum+ (.
(Hdt (j)) *D (j).
*exp (-DeltaArray (i) *dt (j)));_compearData. sum=sum;(i)
=b0*exp (-DeltaArray (i) *dt (SpaceNumbers));_compearData. Rsum (i) =Rsum
(i);(i) =sum+Rsum (i);_compearData. dh (i) =dh (i);=dh;
function ModelData = Identification
(inObjectData, vec_delta,mExpDen, mExpNum)
Npoints = inObjectData. TimePointNumbers;=inObjectData.
rTimeArray;
[mNumAr,mDenAr] =Identification_koef (mExpNum,mExpDen,
inObjectData,vec_delta);. mNumAr=mNumAr;. mDenAr=mDenAr;=zeros (1,Npoints);count=1:
1: Npoints(count) =MyILaplaceII ([mDenAr 0], mNumAr, rTimeArray (count));.
mHt=Ht;
function Numerical_Delta_Derivation (hObject,
eventdata, handles)
global inObjectData ModelData M N=str2num (get (handles.
Edit_Delta,'string'));_start=str2num (get (handles.
Edit_delta_start,'string'));_step=str2num (get (handles.
Edit_delta_step,'string'));_end=str2num (get (handles.
Edit_delta_end,'string'));_iter=delta_start: delta_step: delta_end;=length
(delta_iter);=1;_delta=zeros (1,5);i=1: 1: iend=1: 1: 5;_delta (j) =delta_iter
(i) *j;
[ModelData] =Identification (inObjectData,vec_delta,N,M);all
(ModelData. mDenAr>=0) %ita1 (i) >=0&&ita2 (i)
>=0&&ita3 (i) >=0(k) =Maximum_deviation (ModelData,
inObjectData);_iter_mass (k) =delta_iter (i); %*10;=k+1;=1;
[min_Derivation,n] =min
(Derivation);_Der_delta=Delta_iter_mass (n);(handles.
Edit_min_Derivation,'string',num2str (min_Derivation));(handles.
Edit_min_Der_Delta1,'string',num2str (min_Der_delta));(handles.
Edit_Delta1,'string',num2str (min_Der_delta));=figure ('Name','Гафик
зависимости погрешности от расположения первого
узла');(Delta_iter_mass,Derivation);('\delta1','FontSize',12,'FontWeight','Bold');('\Deltah
(\delta1) ','FontSize',12,'FontWeight','Bold');
function [AbsErr,LimY1,RelErr,LimY2] =
ErrorGraphData (ModelData, ObjectData)
Hdt=ObjectData. rCharacteristicArray;=ModelData.
mHt;=0;=0;=0;=0;=0;=0;=length (Ht);=zeros (1,count);=zeros (1,count);i=1:
count(i) = Hdt (i) - Ht (i);=sum1+AbsErr (i);i=1: count(Hdt (i) ==0) &&
(Ht (i) ==0)(i) =0;(i) = ( (Hdt (i) - Ht (i)) /Hdt (i)) *100;RelErr (i)
==-inf(i) =-realmax;RelErr (i) ==inf(i) =realmax;=sum2+RelErr (i);=abs
(sum1/count);average1==0=1;=average1+average1*1.5;=abs
(sum2/count);average2==0=1;=average2+average2*1.5;