Matroid maps
Matroid maps
A.V. Borovik, Department of Mathematics, UMIST
1. Notation
This paper continues the works [1,2] and uses, with some
modification, their terminology and notation. Throughout the paper W is a
Coxeter group (possibly infinite) and P a finite standard parabolic subgroup of
W. We identify the Coxeter group W with its Coxeter complex and refer to
elements of W as chambers, to cosets with respect to a parabolic subgroup as
residues, etc. We shall use the calligraphic letter 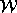 as a notation for the
Coxeter complex of W and the symbol
as a notation for the
Coxeter complex of W and the symbol 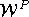 for the set of left cosets of
the parabolic subgroup P. We shall use the Bruhat ordering on
for the set of left cosets of
the parabolic subgroup P. We shall use the Bruhat ordering on 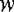 in its
geometric interpretation, as defined in [2, Theorem 5.7]. The w-Bruhat ordering
on
in its
geometric interpretation, as defined in [2, Theorem 5.7]. The w-Bruhat ordering
on 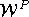 is denoted by the same symbol
is denoted by the same symbol 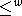 as the w-Bruhat ordering on
as the w-Bruhat ordering on 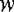 . Notation
. Notation 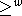 , <w,
>w has obvious meaning.
, <w,
>w has obvious meaning.
We refer to Tits [6] or Ronan [5] for definitions of chamber
systems, galleries, geodesic galleries, residues, panels, walls,
half-complexes. A short review of these concepts can be also found in [1,2].
2. Coxeter matroids
If W is a finite Coxeter group, a subset 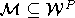 is called a Coxeter
matroid (for W and P) if it satisfies the maximality property: for every
is called a Coxeter
matroid (for W and P) if it satisfies the maximality property: for every 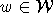 the set
the set 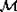 contains a
unique w-maximal element A; this means that
contains a
unique w-maximal element A; this means that 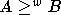 for all
for all 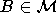 . If
. If 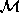 is a Coxeter
matroid we shall refer to its elements as bases. Ordinary matroids constitute a
special case of Coxeter matroids, for W=Symn and P the stabiliser in W of the
set
is a Coxeter
matroid we shall refer to its elements as bases. Ordinary matroids constitute a
special case of Coxeter matroids, for W=Symn and P the stabiliser in W of the
set 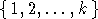 [4]. The maximality property in this case is nothing else but the
well-known optimal property of matroids first discovered by Gale [3].
[4]. The maximality property in this case is nothing else but the
well-known optimal property of matroids first discovered by Gale [3].
In the case of infinite groups W we need to slightly modify the
definition. In this situation the primary notion is that of a matroid map

i.e. a map satisfying the matroid inequality
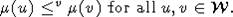
The image 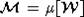 of
of 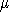 obviously satisfies
the maximality property. Notice that, given a set
obviously satisfies
the maximality property. Notice that, given a set 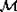 with the maximality
property, we can introduce the map
with the maximality
property, we can introduce the map 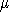 by setting
by setting 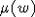 be equal to
the w-maximal element of
be equal to
the w-maximal element of 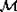 . Obviously,
. Obviously, 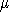 is a matroid
map. In infinite Coxeter groups the image
is a matroid
map. In infinite Coxeter groups the image 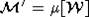 of the matroid map associated
with a set
of the matroid map associated
with a set 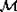 satisfying the maximality property may happen to be a proper subset
of
satisfying the maximality property may happen to be a proper subset
of 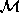 (the set of all `extreme' or `corner' chambers of
(the set of all `extreme' or `corner' chambers of 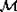 ; for
example, take for
; for
example, take for 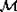 a large rectangular block of chambers in the affine Coxeter group
a large rectangular block of chambers in the affine Coxeter group 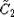 ). This
never happens, however, in finite Coxeter groups, where
). This
never happens, however, in finite Coxeter groups, where 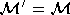 .
.
So we shall call a subset 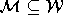 a matroid if
a matroid if 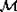 satisfies
the maximality property and every element of
satisfies
the maximality property and every element of 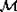 is w-maximal in
is w-maximal in 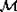 with respect
to some
with respect
to some 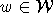 . After that we have a natural one-to-one correspondence between
matroid maps and matroid sets.
. After that we have a natural one-to-one correspondence between
matroid maps and matroid sets.
We can assign to every Coxeter matroid 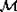 for W and P the
Coxeter matroid for W and 1 (or W-matroid).
for W and P the
Coxeter matroid for W and 1 (or W-matroid).
Теорема
1. [2, Lemma 5.15] A map
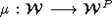
is a matroid map if and only if the map

defined by 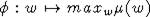 is also a matroid map.
is also a matroid map.
Recall that 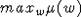 denotes the w-maximal element
in the residue
denotes the w-maximal element
in the residue 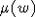 . Its existence, under the assumption that the parabolic subgroup P
is finite, is shown in [2, Lemma 5.14].
. Its existence, under the assumption that the parabolic subgroup P
is finite, is shown in [2, Lemma 5.14].
3. Characterisation of matroid maps
Two subsets A and B in 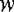 are called adjacent if there
are two adjacent chambers
are called adjacent if there
are two adjacent chambers 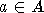 and
and 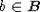 , the common panel of
a and b being called a common panel of A and B.
, the common panel of
a and b being called a common panel of A and B.
Лемма 1. If A and B are two adjacent convex subsets of 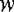 then all
their common panels belong to the same wall
then all
their common panels belong to the same wall  .
.
We say in this situation that  is the common wall of A and B.
is the common wall of A and B.
For further development of our theory we need some structural
results on Coxeter matroids.
Теорема 2. A map 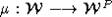 is a matroid map if and only if
the following two conditions are satisfied.
is a matroid map if and only if
the following two conditions are satisfied.
(1) All the fibres 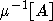 ,
, 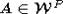 , are convex subsets
of
, are convex subsets
of 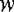 .
.
(2) If two fibres 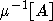 and
and 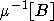 of
of 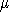 are adjacent
then their images A and B are symmetric with respect to the wall
are adjacent
then their images A and B are symmetric with respect to the wall  containing the
common panels of
containing the
common panels of 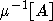 and
and 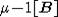 , and the residues A and B lie on the opposite sides of the wall
, and the residues A and B lie on the opposite sides of the wall  from the sets
from the sets 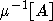 ,
, 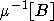 ,
correspondingly.
,
correspondingly.
Доказательство. If 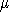 is a matroid map then the satisfaction of conditions (1) and (2) is
the main result of [2].
is a matroid map then the satisfaction of conditions (1) and (2) is
the main result of [2].
Assume now that 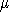 satisfies the conditions (1)
and (2).
satisfies the conditions (1)
and (2).
First we introduce, for any two adjacent fibbers 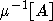 and
and 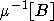 of the map
of the map 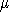 , the wall
, the wall 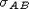 separating
them. Let
separating
them. Let 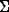 be the set of all walls
be the set of all walls 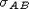 .
.
Now take two arbitrary residues 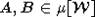 and chambers
and chambers 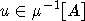 and
and 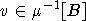 . We
wish to prove
. We
wish to prove 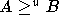 .
.
Consider
a geodesic gallery
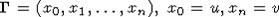
connecting the chambers u and v. Let now the chamber x moves along 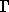 from u to v,
then the corresponding residue
from u to v,
then the corresponding residue 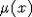 moves from
moves from 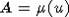 to
to 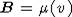 . Since the
geodesic gallery
. Since the
geodesic gallery 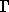 intersects every wall no more than once [5, Lemma 2.5], the chamber
x crosses each wall
intersects every wall no more than once [5, Lemma 2.5], the chamber
x crosses each wall  in
in 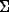 no more than once and, if it crosses
no more than once and, if it crosses  , it moves from the same side
of
, it moves from the same side
of  as u to the opposite side. But, by the assumptions of the theorem, this
means that the residue
as u to the opposite side. But, by the assumptions of the theorem, this
means that the residue 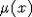 crosses each wall
crosses each wall  no more than
once and moves from the side of
no more than
once and moves from the side of  opposite u to the side
containing u. But, by the geometric interpretation of the Bruhat order, this
means [2, Theorem 5.7] that
opposite u to the side
containing u. But, by the geometric interpretation of the Bruhat order, this
means [2, Theorem 5.7] that 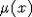 decreases, with respect to the
u-Bruhat order, at every such step, and we ultimately obtain
decreases, with respect to the
u-Bruhat order, at every such step, and we ultimately obtain 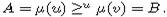
Список литературы
Borovik A.V., Gelfand I.M. WP-matroids and thin Schubert cells on
Tits systems // Advances Math. 1994. V.103. N.1. P.162-179.
Borovik A.V., Roberts K.S. Coxeter groups and matroids, in Groups of
Lie Type and Geometries, W. M. Kantor and L. Di Martino, eds. Cambridge
University Press. Cambridge, 1995 (London Math. Soc. Lect. Notes Ser. V.207)
P.13-34.
Gale D., Optimal assignments in an ordered set: an application of
matroid theory // J. Combinatorial Theory. 1968. V.4. P.1073-1082.
Gelfand I.M., Serganova V.V. Combinatorial geometries and torus
strata on homogeneous compact manifolds // Russian Math. Surveys. 1987. V.42.
P.133-168.
Tits J. A local approach to buildings, in The Geometric Vein
(Coxeter Festschrift) Springer-Verlag, New York a.o., 1981. P.317-322.
Для
подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/