|
Критерий
|
Показатель
надежности
|
Определение
|
|
Безотказность
|
Вероятность
безотказной работы (вероятность своевременного выполнения работ)
|
Вероятность
того, что в пределах заданного периода функционирования потока отказ не
возникнет. Вероятность того, что запланированный объем работ будет выполнен в
заданный срок.
|
|
Средняя
наработка на отказ
|
Математическое
ожидание наработки процесса (потока) до отказа. Отношение наработки потока к
математическому ожиданию числа отказов в течение этой наработки.
|
|
Средняя
наработка между отказами
|
Математическое
ожидание наработки объекта между отказами. Случайная продолжительность,
выполненная строительным подразделением до наступления некоторого события или
момента времени окончания объема работ, ввода объекта в эксплуатацию.
|
|
Интенсивность
отказов
|
Плотность
распределения наработки потока до отказа, определяемая при условии, что до
рассматриваемого момента отказ не возник.
|
|
Ведущая
функция потока отказов
|
Математическое
ожидание числа отказов строительного потока в течение заданной наработки.
|
|
Параметр
потока
|
Первая
производная ведущей функции потока отказов
|
|
Ремонто-
пригодность
|
Вероятность
восстановления
|
Вероятность
того, что фактическая продолжительность работ по восстановлению
работоспособности строительного потока не превысит заданной
|
|
Среднее
время простоя
|
Математическое
ожидание времени вынужденного нерегламентированного пребывания строительного
потока в состоянии неработоспособности.
|
|
Среднее
время восстановления
|
Математическое
ожидание времени восстановления работоспособности строительного потока.
|
|
Интенсивность
восстановления
|
Плотность
вероятности момента окончания восстановления строительного потока,
определяемая при условии, что до данного момента восстановление завершено.
|
|
Безотказность
и ремонто- пригодность
|
Коэффициент
готовности
|
Доля
времени, в течении которого строительный поток находится в работоспособности
состоянии в установившемся стационарном процессе производства работ.
|
|
Коэффициент
простоя
|
Доля
времени, в течении которого строительный поток находится в неработоспособном
состоянии в установившемся процессе производства работ.
|
|
Коэффициент
технического использования
|
Отношение
средней наработки строительного потока в единицах времени за некоторый период
функционирования потока к сумме средних значений наработки; времени простоя,
обусловленного техническим обслуживанием, и времени ремонтов за этот же
период функционирования потока.
|
|
Коэффициент
оперативной готовности
|
Вероятность
того, что строительный поток, окажется работоспособным в заданный момент
времени в процессе производства работ и, начиная с этого момента времени,
будет работать безотказно в течение заданного интервала времени.
|
.3 Классификация видов надежности
Надежность - свойство объекта сохранять во
времени в установленных пределах значения всех параметров, характеризующих
способность выполнять требуемые функции в заданных режимах и условиях
применения, технического обслуживания, реставрации, модернизации, ремонтов,
хранения и транспортировки.
Надежность является сложным свойством, которое в
зависимости от значения объекта и условий его использования состоит из
сочетаний безотказности, долговечности, ремонтопригодности и сохранности.
Надежность технологических
решений должна обеспечивать бесперебойное функционирование строительного
процесса, выбор способа производства, позволяющему строительному потоку
функционировать с заданными параметрами, в первую очередь с заданной
интенсивностью, таким образом, чтобы отклонения, вызванные случайными
производственными факторами, не превышали определенных пределов.
Указанный принцип взаимосвязи
различных видов надежности можно представить на рисунке 1.3.

Рис.1.3.Взаимосвязь различных
видов надежности
В процессе проектирования
организации строительства объектов, представляющего собой сложную вероятностную
систему, одним из важных условий принятия целесообразных решений является
системный подход. Это следует учитывать при рассмотрении различных параметров и
характеристик проектирования строительства, изготовления конструкций, их
транспортировки, возведения зданий и сооружений, в том числе и показателей
надежности.
Системный подход особенно важен
при проектировании организации работ, так как требования, предъявляемые к
строительной системе при проектировании, зачастую являются противоречивыми.
Поэтому приходится постоянно
анализировать взаимосвязь отдельных параметров системы в процессе составления
математической модели, соответствующей организационно-технологической модели
для строительной системы в целом. Процесс постановки задачи фактически
осуществляется на этапе предварительного проектирования (при формировании
годовой программы, разработке ПОС), хотя многие производственные
взаимоотношения, существующие, в строительном объединении, проявляются в
процессе составления первоначальных графиков производства работ.
Основная задача теории
надежности на этапе организационно-технологического проектирования - помочь
разработчику принять обоснованные решения, касающиеся выбора структуры потока,
последовательности возведения объектов и комплексов, необходимость
использования резервов времени, фронта работ, материально-технических и других
ресурсов, вариантов организационно-технологических моделей строения системы
оперативного планирования и управления и т.д.
Основной задачей теории
надежности на этапе реализации проекта строительства объектов годовой программы
строительного подразделения является оперативное планирование производства
строительно-монтажных работ и управления им, обеспечивающее предупреждение
возникновения отказов; ликвидация отказов и их последствий; расчет и создание
страховых запасов ресурсов; сбор статистических данных о причинах, продолжительности
и последствиях отказов и их анализ; разработка организационно-технологических
мероприятий по повышению надежности с оценкой целесообразности их реализации.
Важная проблема - это прогноз
отказов и сравнение вариантов организационных решений для получения
максимального экономического эффекта при обеспечении запланированного ввода
объектов в эксплуатацию, а также расчет уровня надежности в условиях конкретной
строительно-монтажной организации. Решение этих задач связанно с использованием
теории управляемых случайных процессов. В условиях реализации проектно -
производственных систем в строительстве, создания проектно-строительных фирм и
стабильной надежности функционирования всего инвестиционного процесса
организационно-технологическую надежность можно сформулировать, как способность
проектно-производственно-строительной системы обеспечивать функционирование
всех элементов и участков инвестиционного процесса с отклонениями в заданных
пределах.
.4 Вероятностный характер
строительства. Влияние случайных факторов
Вероятностный характер строительства заключается
в том, что на ход работ все время воздействуют различные случайные факторы. Эти
воздействия трудно предвидеть и оценить. Случайные факторы имеют весьма
многообразную природу, и последствия их воздействия весьма многообразны.
Случайные факторы можно классифицировать по
следующим категориям:
1. Случайные факторы технического порядка:
всевозможные поломки машин, механизмов, деталей, транспортных средств, низкое
качество материалов, конструкций, не позволяющее применить их по назначению;
изменение проектных решений в процессе строительства.
2. Случайные факторы технологического
порядка: устранение брака, переделка недоброкачественно выполненных работ;
появление непредвиденных работ.
. Случайные факторы организационного
порядка: нарушение по поставкам материалов, конструкций, срыв согласованных
сроков работ, отсутствие рабочих требуемой специальности или квалификации.
. Случайные факторы климатического
порядка.
. Случайные факторы социального порядка: невыход
работника на производство, невыполнение производственного задания при полном
обеспечении работ, умышленная порча или хищение материалов, оборудования.
Очень важно оценить воздействие случайных
факторов, предвидеть их наступление.
Влияние случайных факторов конкретно выражается
в том, что при самом разнообразном сочетании случайных величин и при различной
их природе совокупное воздействие, в конечном счете, выражается, в основном,
следующим образом: фактическая продолжительность работ и фактические затраты
ресурсов на выполнение этих работ отклоняются от значений, принятых в исходных
планах и графиках.
1.5 Использование метода
резервирования для повышения надежности
Рассмотрим использование метода
резервирования при восстановлении. Чрезвычайные ситуации (ЧС) на железных
дорогах приводят к сложным процессам при восстановительных строительных
работах. Если имеет место резервный фонд машин, конструкций, бригад и т.д., то
при ЧС восстановительный процесс облегчается.
Надежность строительного
объекта увеличивается в случае, когда некоторые части объекта можно
восстанавливать в процессе работы объекта. Восстановление есть мощное средство
повышения надежности при наличии резервного фонда. Уменьшая время
восстановления отказавших объектов, имеющих резервный фонд, можно существенно
повысить как готовность, так и безотказность объекта.
Особенности восстановления
объектов, имеющих резервный фонд, рассмотрим на примере дублированной системы,
в которой имеются две одинаковые строительные единицы (бригада, машина, конструкция
и т.д.) - основная и резервная.
Предположим, что во время
восстановления в строительный единицах (СЕ) не могут возникнуть вторичные
отказы. Тогда дублированная система может находиться в одном из трех состояний,
которые обозначим цифрами:
О - строительная система
работоспособна (СЕ работоспособны);
- строительная система
работоспособна, но одна СЕ отказала (система стала нерезервированной);
- строительная система
неработоспособна (отказала).
Обозначим вероятности
перечисленных выше состояний через P0(t),
P1(t),
P2(t).
Отметим, что эти вероятности зависят от начального состояния системы, в котором
она находилась при t = 0. В
зависимости от назначения резервного фонда к нему могут предъявляться различные
требования:
. С начала производства
строительных работ (строительства или реконструкции железной дороги)
строительная система должна безотказно функционировать заданное время; перерывы
в работе недопустимы. При этом необходимо знать вероятность непрерывной
безотказной работы системы (вероятность первый раз не оказаться в состоянии 2).
Вычисляем условные вероятности безотказной работы на интервале (0, t)
при условии, что при t
= 0 основная и резервная СЕ работоспособны.
. Необходимо, чтобы вероятность
застать строительную систему работоспособной в любой заданный момент времени t
была достаточно высока (перерывы в работе всей строительной системы не играют
существенной роли). При этом рассматриваем готовность строительной системы и ее
характеристики: функцию готовности Г(t)
или коэффициент готовности k2.
Иначе говоря, находиться вероятность не оказаться в состоянии 2. Этот случай
отличается от предыдущего тем, что имеется возможность перехода из состояния 2
в состояние 1.
Найдем формулы для функции
готовности и вероятности безотказной работы с восстановлением. Предположим, что
основная и резервная СЕ равнонадежны, имеют показательные распределения времени
безотказной работы и времени восстановления, λ1
= λ2 = λ, μ1
= μ2 = μ, неработающих
СЕ невозможны, отказы обнаруживаются мгновенно. Вначале рассмотрим случаи, где
отказы допустимы. На рис.1.5. приведены графы состояний четырёх возможных
вариантов восстанавливаемой строительной системы, имеющей резервный фонд:
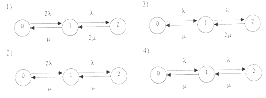
Рис.1.5. Графы состояния различных вариантов
восстанавливаемого строительного объекта, имеющего резервный фонд
1. Нагруженный резервный фонд - при отказах СЕ
они могут приводиться в готовность как отдельно, по одному, так и одновременно
(восстановление без ограничений);
2. Нагруженный резервный фонд -
отказавшие СЕ могут восстанавливаться лишь по одному (ограниченное
восстановление);
. Ненагруженный резервный фонд
- восстановление производиться без ограничений;
. Ненагруженный резервный фонд
- восстановление производиться по одной СЕ.
Дифференциальное уравнение для
вероятности состояний в соответствии с графами состояний (см. рис.1.5.) имеют
вид:
для первого варианта
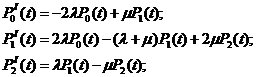 (1)
(1)
для второго варианта
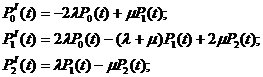 (2)
(2)
для третьего варианта
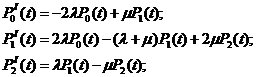 (3)
(3)
для четвертого варианта
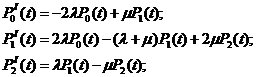 (4)
(4)
Для всех четыре вариантов эти
уравнения должны быть дополнены нормирующим условием:
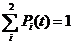 (5)
(5)
Решив уравнения (1)-(5) при
начальных условиях Р0(0) = 1; P1(0)
= Р2(0) = 0, найдем зависимости Рi(t)
для i = 0,1,2.
Для рассматриваемых систем
функция готовности
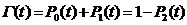 (6)
(6)
Функция готовности
рассмотренных выше четырех вариантов резервированных систем с восстановлением
имеют вид:
для первого варианта
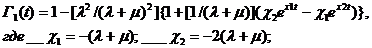 (7)
(7)
для второго варианта
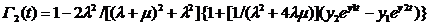 (8)
(8)
для четвертого варианта
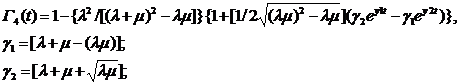 (10)
(10)
На рис.1.6 приведены
зависимости Г(t), вычисленные по
формулам (7)-(10) для λ=0,01, 1/ч;
μ=0,1,
1/ч
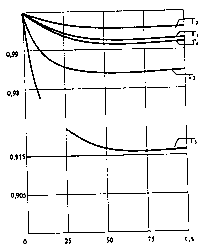
Рис. 1.6. График функции готовности для четырех
вариантов восстанавливаемого строительного объекта, имеющего резервный фонд
Для сравнения на графике
показана функция готовности Г5(t)
строительной системы, не имеющей резервного фонда, с теми же значениями λ
и
μ.
Обозначив Р = λ
/ μ из формул (7)-(10) получим:
k21=(1
+ 2ρ)/(1 + ρ)2;(11)
k22=(1
+ 2 ρ)/[(1 + ρ)2+
ρ 2];(12)
k23=2(1
+ 2 ρ)/[(1 + ρ)2+1];(13)
k24=(1
+ 2 ρ)/[(1 + ρ)2-
ρ].(14)
При ρ
= 0,1 соответствующие
значения k2
равны 0,992; 0,984; 0,995; 0,991.
Г5(t)
- функция готовности соответствующего строительного объекта, не имеющего
резервного фонда.
Таким образом, для повышения
готовности восстанавливаемой строительной системы, имеющей резервный фонд,
необходимо стремиться к созданию условий, обеспечивающих осуществление
ненагруженного резервного фонда и восстановление без ограничений.
Для определения условий
вероятности безотказной работы составим дифференциальных уравнений при условии,
что состояние 2 является поглощающим, т. е. Отсутствуют переходы из состояния 2
в состояние 1. При этом в соответствии с графами состояний (см. рис.1.6)
получим:
для первого и второго вариантов
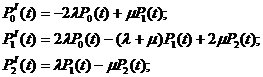 (15)
(15)
для третьего и четвертого
вариантов
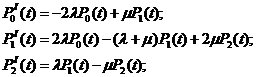 (16)
(16)
При начальных условиях Р0(0)
= 1, Р1(0) = Р2(0) = 0 в результате решения систем
уравнений (15) и (16) совместно с нормировочным условием (5) получим выражение
для условной вероятности безотказной работы:
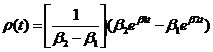 (17)
(17)
где для первого и второго
вариантов:
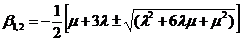 (18)
(18)
для третьего и четвертого
вариантов:
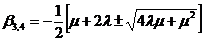 (19)
(19)
Зависимости p(t),
вычисленные по формулам (17)-(19) для λ=0,01, 1/ч;
μ=0,1,
1/ч
приведены на рис.1.7.
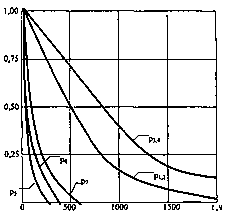
Рис.1.7. График функции надежности различных
строительных систем при ненагруженном резервном фонде в зависимости от среднего
времени безотказной работы
На рисунке для сравнения
приведены графики функций надежности невосстанавливаемых систем: без резервного
фонда p5(t),
с нагруженным резервным фондом без восстановления p6(t)
и ненагруженным резервным фондом без восстановления р7(t).
Если в начальный момент времени
(t= 0) все СЕ
системы, имеющей резерв, работоспособны, то время безотказной работы есть время
перехода из начального состояния в подмножество неработоспособных состояний.
Предположим, что нет
ограничений на число ремонтных бригад, отказы обнаруживаются мгновенно,
аппаратура контроля безотказна, основная и резервная СЕ равнонадежны и имеют
показательные распределения времени безотказной работы и времени
восстановления. Применяя известные методы, получаем выражения для среднего
времени безотказной работы системы с резервным фондом, состоящей из одной
основной и k-1 запасных СЕ: При
нагруженном резервном фонде
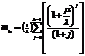 (20)
(20)
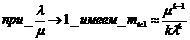 (21)
(21)
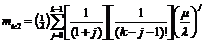 (22)
(22)
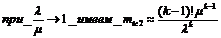 (23)
(23)
В реальных строительных
системах могут существовать ограничения по числу ремонтных бригад, общему
допустимому числу восстановлений и др. Поэтому значения mtc,
вычисленные по формулам (20)-(23), приходится считать верхним пределом среднего
времени безотказной работы восстанавливаемой системы, имеющей резервный фонд.
Выражения для при г = 1 получены путем составления и решения системы
дифференциальных уравнений, соответствующей графу состояний при г = 1.
Сопоставив выражение для
среднего времени безотказной работы дублированной восстанавливаемой
строительной системы с нагруженным резервным фондом при идеальном контроле
согласно (20), со значением среднего времени безотказной работы
невосстанавливаемой системы с нагруженным резервом mtc
=3/2λ, найдем
mtc
/ m"tc
= 1+μ/3λ
= 1+1/3ρ (24)
Таким образом, при ρ
= λ/μ
= 0,01 - 0,001 применение восстановления повышает среднее время безотказной
работы строительной системы, имеющей резервный фонд, в 30-300 раз.
Строительство железных дорог,
как и любое другое производство, требует больших объемов поставок различных
материалов, конструкций, изделий, топлива и т.п. Для обеспечения ритмичности
выполнения работ по сооружению объектов железнодорожного строительства
необходимо не только выдерживать определенный темп поставок, но и обеспечивать
комплектацию поставляемых конструкций и изделий.
В большинстве случаев трудно
обеспечить необходимую ритмичность строительного процесса только за счет
регулярности поставок исходных компонентов. Их доставка сопровождается, как
правило, сбоями, возникающими по разным причинам: погодные факторы, технические
- поломки машин, социальные - невыход на работу и др. Следствием этих сбоев
являются срывы плановых или договорных сроков строительства.
Для компенсации возможных
отклонений темпа поставки от исходного темпа, определяемого темпом
строительства, используют накопление прибывающих материалов, изделий,
конструкций и т.п. на складах.
Склады могут быть
приобъектными, рассчитанными на хранение относительно небольших объемов
материалов в течение срока строительства. Хранение осуществляется, как правило,
на открытых площадках, что допустимо для большинства крупногабаритных
строительных конструкций. Однако для материалов, требующих особых условий
хранения, необходимо предусматривать специальные помещения, что ведет к
удорожанию единицы хранения.
Накопление грузов для группы
объектов обычно осуществляется на производственных базах, имеющих капитальные
склады, что увеличивает допустимый срок хранения, но и удорожает его, Поэтому
решение задачи управления запасами должно обеспечить приемлемую стоимость
хранения при обеспечении ритмичного снабжения строительных объектов.
Графическая модель накопления и
расходования запасов на складе выглядит следующим образом:
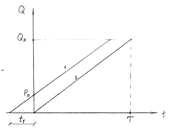
1 - график поставок на склад; 2 - график
расходования материалов со склада; Т - срок строительства;QК
- общий объем материалов, израсходованных за время строительства.
Рис.1.8. Графическая модель накопления и
расходования запасов на складе
Модель, представленная на рис, описывает
функционирование приобъектного склада, который завершает свое существование
вместе с окончанием строительства объекта или цикла поставок на склад
каких-либо материалов, изделий или конструкций. Началом этого цикла служит
момент первой поставки, а завершение происходит вместе с прекращением
потребности в данном виде материала.
Исходными параметрами модели являются:
Т - срок строительства;
QК
- объем материалов, изделий, конструкций, израсходованных за время
строительства объекта.
Рассчитаем количество рельсов длиной 25 м
необходимых для укладки рельсов:
nр=(619000/25)*2=45520
(шт)
Рассчитаем количество деревянных шпал, исходя из
того, что 20% длины строящегося участка приходится на кривые.
На 1 км на прямой укладывается 1840 шпал:
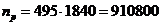 (шп.).
(шп.).
На 1 км на кривой укладывается 2000 шпал:
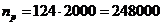 (шп.).
(шп.).
Тогда общий объем необходимых материалов равен:
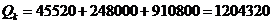 (шт.).
(шт.).
Имея эти исходные данные, можно определить
интенсивность расходования материалов со склада.
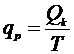 (25)
(25)
где T
= 59,71 сут. - время укладки рельсошпальной решётки краном ПБ-3.
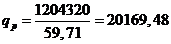
Обычно известна интенсивность потока поставок,
либо на нее можно воздействовать в требуемом направлении. Эту интенсивность
можно определить следующим образом:
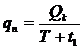 (26)
(26)
Если зафиксировать произвольный
момент времени tx,
то ему будут соответствовать ординаты Qхр
и Qхр,
которые, соответственно, покажут, сколько материала (Qхр)
к этому моменту было израсходовано и получено (Qхn,)
на склад. Разница между ними px
= Qxn - Qхп,,
покажет, сколько материала на данный момент находится на складе.
Одним из главных назначений
склада является выполнение буферной функции, то есть сглаживание
неравномерности потока поставок для обеспечения ритмичности снабжения объектов
строительства. Понятно, что, чем больше объем склада, тем лучше он будет
выполнять буферную функцию.
С другой стороны, увеличение
объема склада удорожает хранение. Кроме того, реальная ситуация может
накладывать ограничения на максимальный объем склада, Например, на 100 м пути
можно разместить три пакета звеньев путевой решетки длиной по 25 м; выделив
один станционный путь длиной 850 м под склад, мы тем самым ограничиваем его
объем девятью пакетами звеньев, что сопоставимо со сменной выработкой на
укладке пути.
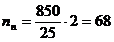 (шт.);
(шт.);
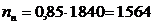 (шп.).
(шп.).
Общий объем необходимых
материалов:
Pо
= 68 + 1564 = 1632 (шт).
С точки зрения выполнения складом буферной
функции, важным является создание до начала строительства первоначального
запаса Р0 , который будет находиться на складе в момент времени Т0
начала строительства. Для обеспечения этого запаса поставки на склад необходимо
начать за t1
дней до начала строительства.
Определить срок t1
можно, зная режим поставок на склад. В приведенном на рис случае поставки
завершаются в момент завершения строительства. Поэтому время t1
можно определить как
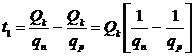 . (27)
. (27)
Однако работа склада в таком режиме, как на рис,
снижает надежность бесперебойного снабжения строительства по мере приближения к
его завершению за счет постоянного сокращения буферного запаса.
Для повышения надежности снабжения следует
ограничить объем склада так, чтобы не допустить его, снижения. Так как объем материалов,
прошедший через склад, должен быть равен израсходованному строителями, то
поставки на склад должны быть завершены до окончания строительства.
В данном случае удобно считать, что qn
= qp , и, зная Р0 как
минимально допустимый запас на складе, время начала поставок можно определить
как
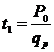 (28)
(28)
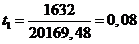 (сут.);
(сут.);
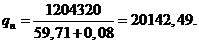
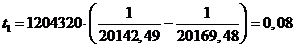 (сут.).
(сут.).
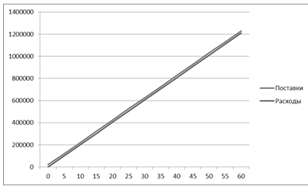
Рис.1.9. Диаграмма поступления и расходования
материала.
Наиболее сложной модель управления запасами
становится тогда, когда необходимо учесть сезонные колебания темпа строительства
и связанные с этим колебания расхода материалов со склада.
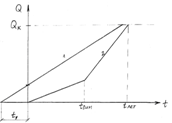
Рис. 1.10 Диаграмма поступления и расходования
материала в зимний период.
Будем считать, что зимний расход материала
меньше, а летом больше. Тогда модель будет выглядеть следующим образом. Эта
модель построена в предположении, что интенсивность потока поставок постоянна,
меняется только интенсивность расхода. При этом из чертежа видно, что
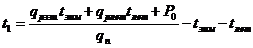 (29)
(29)
Максимальный объем склада при этом составит:
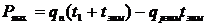 (30)
(30)
1.6 Использование метода
дублирования для повышения надежности
Надежность электрических схем
систем автоматического управления определяют такими показателями безотказности,
как вероятность безотказной работы в течение заданного отрезка времени; средняя
наработка до первого отказа.
Элементы схем считаются
невосстанавливаемыми, а сама схема - восстанавливаемой. Также полагают,
интенсивность отказов постоянной. Для таких допущений вероятность безотказной
работы любого элемента автоматики определяют в соответствии с показательным
законом:
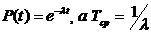 (31)
(31)
Поскольку, исходя из методов
построения схем, в электрических цепях элементы соединены последовательно
(основное соединение), то вероятность безотказной работы любой цепи схемы можно
определить по формуле:
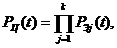 (32)
(32)
где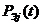 -
вероятность безотказной работы j-го
элемента электрической цепи схемы; k
- общее количество элементов в цепи.
-
вероятность безотказной работы j-го
элемента электрической цепи схемы; k
- общее количество элементов в цепи.
Если в цепи предусмотрено
дублирование какого-либо элемента (параллельное включение элементов,
выполняющих одни и те же функции и работающих одновременно - горячий резерв),
то вероятность безотказной работы такого участка цепи определится так:
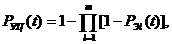 (33)
(33)
где 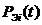 -
вероятность безотказной работы l-го
элемента; m - число элементов,
включённых параллельно.
-
вероятность безотказной работы l-го
элемента; m - число элементов,
включённых параллельно.
В любой схеме системы
автоматического управления каждая последующая цепь зависима от предыдущей.
Поэтому принимают, что цепи в электрических схемах соединены последовательно.
Тогда вероятность безотказной
работы всей схемы системы управления определяют так:
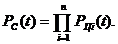 (34)
(34)
2. Формулировка и определение
отказов
.1 Отказ - важнейший критерий
оценки технологии строительства
Отказ представляет собой
событие, заключающееся в нарушении исправного состояния объекта или его
работоспособности. Применительно к строительному производству под объектом
понимается строительный процесс, организационно-технологические решения,
деятельность строительно-монтажного подразделения по возведению зданий и их
комплексов, по выполнению годовой программы строительно-монтажных работ.
При анализе функционирования
строительного потока можно отметить отклонения фактических параметров его
работы от детерминированных, установленных в технологической карте, графике или
проекте производства работ. Это отклонение представляет собой технологический
отказ.
Технологический отказ - полное
или частичное прекращение функционирования строительного процесса,
технологической линии, вызывающее отклонение параметров потока от заданных.
В отличие от технических систем
и изделий отказ в организации строительного производства не обязательно связан
с прекращением функционирования процесса. Характерным являются сбои (частичные
отказы), которые самоустраняются в процессе производства работ или
ликвидируются соответствующими службами строительно-монтажной организации. Если
эти отклонения существенно сказываются на результатах деятельности бригады,
такой сбой также может быть признан отказом.
Отказы в строительных процессах
появляются в результате возникновения многочисленных и разнообразных
организационно-технологических факторов, дестабилизирующих производство работ,
а также взаимодействия их между собой. Исследование таких воздействий связано с
изучением влияния каждого фактора на функционирование строительного процесса в
области организации строительства, изготовления конструкций, их
транспортировки, возведения сооружений и требует системного рассмотрения на
всех этапах деятельности строительной системы.
Сложность такого исследования
заставляет рассматривать отказы как изменение некоторого выходного параметра на
большую или меньшую величину, определяющую его функциональные свойства и
нарушающую работоспособность строительного процесса.
Организационный отказ -
событие, в результате которого нарушаются установленные сроки выполнения
запланированных объёмов строительно-монтажных работ или ввода объекта в
эксплуатацию.
Для каждого конкретного
строительства выбирают вариант технологии и организации производства работ,
учитывающий реальные средства механизации, численный и квалификационный состав
исполнителей, условия поставки изделий и материалов, интенсивность процессов,
которые определяют оптимальную для данных условий технологически целесообразную
продолжительность возведения объекта Топт. Разница между оптимальной
и минимальной продолжительностями строительства составит
организационно-технологический резерв времени
r
= Тоггт - Тmin.
Многообразие причин отказов,
случайных производственных факторов определяют разнообразный характер отказов в
строительном производстве, которые можно классифицировать по ряду признаков.
По области проявления отказа их
можно разделить на технологические, организационные и управленческие. Кроме
того, можно выделить проектные (или конструктивные) отказы.
По степени устойчивости
неработоспособности отказы можно разделить на устойчивые, сбои и
перемежающиеся.
Устойчивый отказ - стабильно
возникающий длительный отказ строительного потока или системы управления
строительством по одной и той же причине или на одном и том же процессе
(потоке).
Сбой - самоустраняющийся отказ,
приводящий к кратковременной утрате строительным потоком или строительным
подразделением работоспособности, кратковременному отклонению параметров
поточного строительства.
Перемежающийся отказ -
многократно возникающий сбой одного и того же характера, кратковременный часто
повторяющийся отказ.
По наличию внешних проявлений
различают очевидный (явный) и скрытый (неявный) отказ. Очевидный отказ вызывает
полную остановку строительного процесса (потока). Скрытый отказ происходит в
результате снижения интенсивности потока, выхода его параметров за допустимые
пределы под влиянием невидимых потерь рабочего времени.
.2 Закономерности распределения
вероятностей отказов
Отказы в строительном
производстве представляют собой случайные величины, которые могут быть
дискретными и непрерывными в зависимости от физического смысла исследуемого
явления, и характеризуются функциями распределения вероятностей.
Если 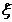 -
случайная величина, то вероятность того, что она примет значение, меньшее
некоторого числа х
-
случайная величина, то вероятность того, что она примет значение, меньшее
некоторого числа х
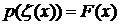 , (35)
, (35)
называется интегральной
функцией распределения вероятностей или законом распределения вероятностей
случайной величины отказов.
Для случайных дискретных
величин F(x)
есть неубывающая ступенчатая функция; для непрерывных случайных величин F(x)
непрерывная функция для всех значений х.
Производная от f(x)=F(x)
, если она существует, называется плотностью (или функцией) распределения
вероятностей отказов.
Изучение теоретических законов
распределения случайных величин и сфер их пригодности для различных
строительных процессов и методов организации строительного производства весьма
важно, так как позволяет резко сократить объем статистического материала и
продолжительность наблюдений для описания поведения числа и величины отказов.
Равномерное распределение
справедливо для тех случаев, когда случайное событие лежит в определенном
временном интервале, причем появление его в любой момент времени равновероятно.
Пусть благоприятное событие
распределено равномерно на временном интервале Т и плотность распределения
постоянна f(x)=const
на всем участке действия закона от 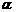 до
до
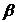 .
Вероятность события равна 1. Отсюда плотность распределения:
.
Вероятность события равна 1. Отсюда плотность распределения:
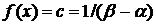 (36)
(36)
Интегральная функция
распределения:

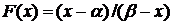 (37)
(37)
Математическое ожидание
случайной величины, имеющее равномерное распределение:
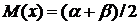 (38)
(38)
Дисперсия распределения:
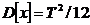 (39) , т.е. дисперсия равномерного распределения
растет пропорционально квадрату интервала, на котором возможно появление
отказов процесса.
(39) , т.е. дисперсия равномерного распределения
растет пропорционально квадрату интервала, на котором возможно появление
отказов процесса.
Показательное распределение
является одним из наиболее распространенных в строительном производстве
благодаря своей простоте и приблизительному соответствию распределению отказов
сложных многоэлементных систем. Накопление сведений о проведении разнообразных
взаимосвязанных строительных процессов деятельности
строительно-производственных подразделений приводит к другим законам, более
точно отражающим реальное распределение, но одновременно во много раз
усложняющим вычисления.
Функция распределения
показательного закона записывается следующим образом:
F(x)
= 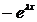 (40)
(40)
Закон справедлив для Х > 0 и
зависит только от одном параметра 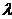 ,
характеризующего интенсивность (опасность) отказов.
,
характеризующего интенсивность (опасность) отказов.
Плотность распределения при
показательном распределении:
f(x)
= dF(x)/d(x}
= 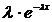 ,
(41)
,
(41)
т. е. представляет собой
монотонно убывающую функцию.
Математическое ожидание:
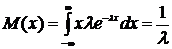 (42)
(42)
Дисперсия показательного
распределения:
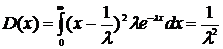 (43)
(43)
т.е. 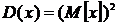 -
это свойство показательного распределения можно использовать при оценке
возможности его применения для описания экспериментальных данных.
-
это свойство показательного распределения можно использовать при оценке
возможности его применения для описания экспериментальных данных.
Распределением Вейбулла нередко
пользуются при определении надежности ряда процессов. Функция записывается в
следующем виде:
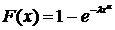 (44)
(44)
Это равенство справедливо для
х>0, но зависит от двух параметров 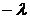 и
и
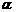 .
При
.
При 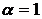 распределение
Вейбулла переходит в показательное.
распределение
Вейбулла переходит в показательное.
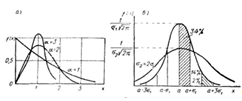
Рис. 2.2.1. Законы распределения вероятностей
Вейбулла (а), Гаусса (б)
Нормальное распределение широко
применяют в теории надежности для описания событий, зависящих от многих
факторов, каждый из которых слабо влияет на распределение случайного события.
По нормальному закону распределяются параметры выработки исполнителей и бригад
на строительных процессах, продолжительности технологических стадий и
строительства типовых объектов и др.
Плотность распределения
нормального закона записывается в следующем виде:
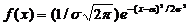 , (45)
, (45)
где 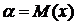 -
математическое ожидание;
-
математическое ожидание;
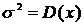 - дисперсия
распределения.
- дисперсия
распределения.
Чем больше дисперсия, тем более
плоской получается кривая распределения.
Вероятность попадания случайной
величины, распределенной по нормальному закону, на заданный интервал измерения
параметра х от 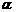 до
до 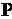 обычно
определяется интегрированием плотности распределения.
обычно
определяется интегрированием плотности распределения.
Распределение Пуассона наиболее
успешно используется для определения вероятности дискретных событий или
появления потока событий. Если независимые события следуют с конкретной средней
частотой, то расчет вероятности Рт , т.е. вероятности того, что за
какой-то отрезок времени t
произойдет ровно т событий, производится по закону Пуассона.
Закон Пуассона записывается в
следующем виде:
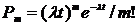 (46)
(46)
Распределение Пуассона имеет
следующее свойство: математическое ожидание и его дисперсия равны одной и той
же величине 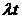 .
.
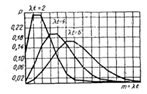
Рис. 2.2.2. Закон распределения вероятностей
Пуассона
Биноминальным называется такое
распределение, при котором его члены получаются в результате разложения бинома
(р + q)n,
где р и q - вероятности
появления и непоявления события в каждом из п опытов. Очевидно, что сумма всех
членов указанного разложения тождественно равна 1, поскольку (р + q)n=1
n,
а каждый член разложения представляет собой определенную вероятность,
рассчитанную по формуле:
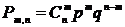 , (47)
, (47)
где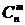 -
число сочетаний из n по m;
q = 1 - p.
-
число сочетаний из n по m;
q = 1 - p.
В курсовой работе для описания
возможных отказов для комплекса работ по балластировки участка пути было
принято нормальное распределение, т.к. при производстве работ на данную систему
влияет большое количество случайных факторов.
3. Практическая реализация положений
организационно-технологической надежности
.1 Организационная надежность и сетевые модели
Одной из моделей отражения вероятностных
производственных процессов является сетевая модель. На сетевом графике можно
отразить все технологические и организационные взаимосвязи между элементами
строительного процесса. Большим преимуществом сетевого графика является то, что
при его расчете из общего количества работ выделяется та цепочка
последовательно выполняемых работ, которая и определяет продолжительность
процесса в целом. Эта цепочка носит название критического пути. Принадлежащие
ей работы называют критическими, все прочие работы - некритическими.
Для анализа сетевой модели применим метод
статистических испытаний (метод Монте-Карло). Суть его заключается в
многократной реализации вероятностного процесса на модели. По каждой работе
сетевого графика определим предельные значения параметров (продолжительности
работ) и закон распределения вероятностей наступления значений параметров на
интервале предельных значений. Затем, выполняем математическое моделирование
вероятного значения параметра с помощью генерирования случайных чисел. Далее
сетевой график рассчитываем как детерминированный, определяем одно из значений
параметра строительного процесса в целом - продолжительность работ. В
результате получается эмпирическое распределение параметров процесса, которое
можно подвергнуть любому целенаправленному анализу при необходимости.
Методом статистических испытаний (Монте-Карло)
решаем задачу устойчивости критического пути при вероятностной сети.
Сроки работ определяются по формуле:
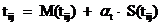 , (48)
, (48)
гдеαt
- случайное число, взятое из таблицы случайных чисел.
Таблица.3.1. Расчёт сроков работ
|
Код
работы
|
М
(t)
|
S
(Tкр)
|
A
|
t
ij
|
|
|
|
a1
|
a2
|
a3
|
t
1
|
t
2
|
t
3
|
|
1-2
|
10
|
2
|
0,2005
|
-0,5564
|
0,4043
|
10,401
|
8,88
|
10,80
|
|
1-3
|
32
|
3
|
1,1609
|
1,7981
|
0,4688
|
35,48
|
37,39
|
33,40
|
|
1-4
|
11
|
3
|
0,427
|
0,8115
|
12,75
|
12,28
|
13,45
|
|
2-5
|
38
|
2
|
0,1425
|
-0,7679
|
0,5405
|
38,28
|
36,46
|
39,08
|
|
2-6
|
14
|
2
|
0,9516
|
-0,0077
|
-1,1929
|
15,90
|
13,98
|
11,61
|
|
3-4
|
0
|
0
|
-0,5863
|
0,8115
|
0,0093
|
0,00
|
0,00
|
0,00
|
|
3-6
|
13
|
4
|
1,1572
|
0,0904
|
0,4167
|
17,62
|
13,36
|
14,66
|
|
4-6
|
16
|
4
|
-0,4428
|
1,2809
|
0,5154
|
14,22
|
21,12
|
18,06
|
|
4-7
|
12
|
3
|
-0,3934
|
2,8854
|
0,2005
|
10,81
|
20,65
|
12,60
|
|
5-8
|
10
|
2
|
0.8319
|
-0,5557
|
1,1603
|
11,66
|
8,08
|
12,32
|
|
6-5
|
0
|
0
|
-1,7708
|
1,4664
|
0,2005
|
0,00
|
0,00
|
0,00
|
|
6-7
|
8
|
1
|
1,1922
|
-0,5098
|
0,1425
|
9,19
|
7,49
|
8,14
|
|
6-8
|
13
|
4
|
-0,6690
|
0,6141
|
0,3516
|
10,32
|
15,45
|
16,80
|
|
6-9
|
35
|
4
|
-0,245
|
-0,8888
|
-0,5863
|
34,02
|
31,44
|
32,65
|
|
7-9
|
17
|
5
|
-0,2863
|
0,8960
|
1,1572
|
15,56
|
21,48
|
22,78
|
|
8-9
|
0
|
0
|
1,2809
|
-0,8513
|
-0,5863
|
0,00
|
0,00
|
0,00
|
|
8-10
|
26
|
2
|
0,8574
|
0,5816
|
-0,3954
|
27,71
|
27,16
|
25,21
|
|
9-10
|
17
|
3
|
0,9900
|
1,5068
|
0,8315
|
19,99
|
21,52
|
19,49
|
Сетевая модель 1-го варианта Ткр1=107,12ед.
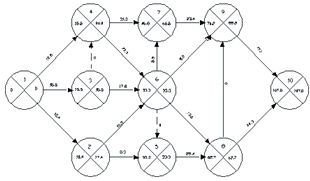
Рис. 3.1.1
Сетевая модель 2-го варианта Ткр2=111,47ед.
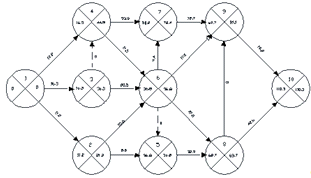
Рис.3.1.2
Сетевая модель 3-го варианта Ткр3=110,8ед
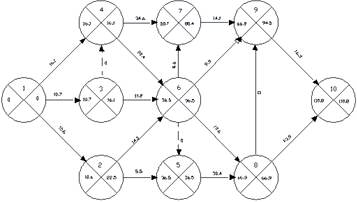
Рис.3.1.3
Ткр1 = 139,32
Ткр2 = 118,92
Ткр3 = 101,11
Ткр4 = 107,12
Ткр5 = 119,78
Ткр6 = 107,00
Ткр7=110,3
Ткр8=110,8
Доверительные границы критического пути, т.е.
устойчивость критического пути как статистической вероятности его прохождения
по определённым событиям при заданной вероятности p
= 0,98
, λ = 3,02 соответственно определяются по следующим
формулам:
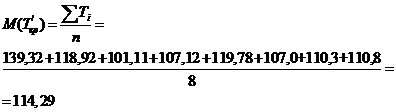
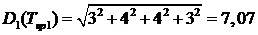
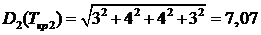
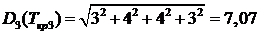
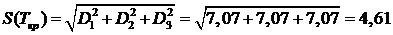
Далее находим максимальное и минимальное
значения критического пути при заданной вероятности p
= 0,98
, λ = 3,02
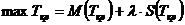 (49)
(49)
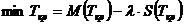 (50)
(50)
Tmax=114,29+3,02*4,61=128,21.
Tmin=114,29-3,02*4,61=100,36.
Все вычисленные величины наносим на график,
который представлен на рис.3.3.
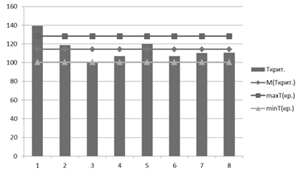
Рис. 3.3. График, с представленными на нем
значениями вычисленных критических путей и их максимальных и минимальных
вероятностных значений.
Вывод: в результате проведенных расчетов
величины критического пути получены результаты: все критические пути
удовлетворяют и попадают в диапазон между минимальным (Tmin=100,36)
и максимальным (Tmax=128,21)
критическим путем, следовательно, они надежны и могут являться основным
решением для строительства объекта.
.2 Организационная схема железнодорожного
строительства и транспортных объектов
Для начала укладки пути
необходимо, чтобы большая часть укладочного материала была доставлена на
материальные базы. Этот материал имеет большой объем, поэтому его доставка
обеспечивается железнодорожным или водным транспортом. При строительстве новых
железных дорог такие базы создают на опорных пунктах, от которых ведется
развертывание строительства. Опорные пункты располагают у станций примыкания к
действующей сети железных дорог или в местах пересечения с судоходными реками.
По месту в общем комплексе
строительства железной дороги, в технологической последовательности с другими
видами основных работ, укладка может быть нормальной, форсированной и
временной.
Нормальной называют укладку
пути, проводимую по полностью законченному земляному полотну. До начала
нормальной укладки пути строители, совместно с представителями заказчика,
составляют акт о готовности земляного полотна к укладке пути.
Форсированной иногда называют
укладку пути по "зеленым отметкам". Ее выполняют по поверхности земли
или по неполностью законченному земляному полотну. В этом случае инвентарный
железнодорожный путь используют как землевозный для завоза грунта, пригодного
для отсыпки в тело земляного полотна, из дальних карьеров поездной возкой. Чаще
всего такая ситуация встречается в северных и северо-восточных районах (в
вечной мерзлоте, болотистой местности).
Временную укладку пути ведут,
например, при сооружении обходов преградных сооружений, укладке инвентарного
пути на одной из полос движения притрассовой автомобильной дороги для завоза
грунта и конструкций водопропускных сооружений. После укладки пути на основной
трассе потребность в инвентарном пути отпадает и он разбирается.
По составу укладочных работ на
перегоне укладка делится на звеньевую, плетьевую и поэлементную.
Укладку пути производим
звеньевым способом. При звеньевой укладке пути процесс делится на сборку
звеньев на базе, на транспортировку готовых звеньев к месту укладки и на
укладку звеньев в путь с выправкой пути для пропуска рабочих поездов. Для того,
чтобы вся эта технологическая цепочка функционировала в рациональном режиме
необходима согласованная работа всех ее элементов.
Звеньевой способ нашел в нашей
стране наибольшее распространение. При его использовании повышается качество
сборки звеньев, собираемых на предприятии строительной продукции -
звеносборочной базе. Снижается стоимость и трудозатраты - на укладку 1 км пути
(вместе со сборкой) расходуется в среднем 140-150 чел.-дня.
Плетьевая укладка предполагает
сборку плетей рельсошпальной решетки длиной до 200 м на путях станции,
примыкающей к перегону, где ведется укладка пути; доставку плетей на тележках к
месту укладки в путь; опускание плети на катки и перемещение (с помощью
трактора) по земляному полотну. После полной надвижки на земляное полотно,
удаления катков и стыковки с ранее уложенной плетью, выполняется
"черный" ремонт пути.
Такой, его еще иногда называют
"звеньевой конвейерный", способ укладки пути в последнее время
практически не используется, поскольку при этом деформируется сливная призма
земляного полотна.
Поэлементную укладку пути
применяют при небольших объемах укладки на рассредоточенных объектах при
отсутствии в непосредственной близости от них звеносборочной базы. Это могут
быть отдельные приемоотправочные или тупиковые пути на станциях, подъездные
пути к предприятиям и т.д. При таком способе укладки на подготовленном земляном
полотне последовательно раскладывают шпалы, выполняют сверление и
антисептирование отверстий, раскладывают и пришивают обшивочными костылями
подкладки, надвигают и пришивают рельсы, ставят шпалы по меткам, устанавливают противоугоны.
Для раскладки шпал и рельсов используют автокран или кран на железнодорожном
ходу, - если рядом имеется железнодорожный путь. Затраты труда на поэлементную
укладку пути составляют 240-250 чел.-дней на 1 км.
При звеньевом способе укладки
звенья предварительно собираем на базе.
На полуавтоматических поточных
звеносборочных линиях (ППЗЛ) собирают звенья с рельсами Р50 и Р65 и деревянными
шпалами всех типов при эпюре их расположения 1440-2000 шпал/км с нераздельным
костыльным прикреплением рельсов к шпалам или с раздельными скреплениями.
Работы на базе выполняют в две
смены. В первую смену ведут сборку звеньев рельсошпальной решетки, а во вторую
смену выполняют погрузку готовых звеньев на подвижной состав; выгружают и
складируют поступающие на базу материалы верхнего строения пути. Для увеличения
производительности базы может быть организована работа на двух секциях. В этом
случае звеносборочную линию (она на рельсовом ходу) по завершении первой смены
перекатывают во вторую секцию. В это время первая секция пополняется
материалами, а изготовление звеньев ведется на второй секции. По завершении
второй смены звеносборочная линия снова перемещается на первую секцию и цикл
"сборка-пополнение" повторяется.
Последовательность операций по
сборке звеньев на ППЗЛ следующая:
1) подают краном пакет
шпал (100-120 шт.) на шпалопитатель. На нем отбраковывают шпалы по длине и
ширине, подбирают стыковые и предстыковые шпалы (отличающиеся несколько
увеличенными размерами), кантуют шпалы на нижнюю постель;
2) по наклонному рольгангу
шпала поступает на сверлильный станок. Здесь одновременно сверлят 8-10
отверстий и заливают их антисептиком; далее шпалы поштучно поступают на
сборочный стенд;
) на стенде с движущимся
цепным конвейером раскладывают на шпалы подкладки, взятые из контейнеров с
подкладками; наживляют обшивочные костыли; после заполнения всех ячеек
конвейера, краном на шпалы с подкладками устанавливают рельсы;
) перед поступлением на
сборочный станок наживляют пришивочные костыли, взятые из контейнеров; на сборочном
станке выполняют запрессовку наживленных костылей; звено постепенно опускается
на тележки;
) звено, полностью
вышедшее из сборочного станка, подхватывается краном и убирается на склад
готовой продукции.
Сборку звеньев на ППЗЛ -650
выполняет бригада, состоящая из 12 чел., включая двух операторов, машиниста
крана и девять монтеров пути. Работы по погрузке готовых звеньев, выгрузке
материалов верхнего строения пути во вторую смену выполняет бригада в составе
машиниста крана и четырех монтеров пути.
Транспортировка звеньев к месту
укладки производится на железнодорожных платформах, оборудованных роликами. При
подаче звеньев платформами локомотив на последнем раздельном пункте
переставляется с головы в хвост состава.
Платформы оборудованы
унифицированным съемным оборудованием УСО-1 для закрепления звеньев от
продольных и поперечных сдвигов. Перед погрузкой на роликовые транспортеры
укладывают специальные "лыжи", сваренные из прокатных профилей или
старогодных рельсов. Иногда вместо лыж нижнее звено переворачивают и головки
рельсов укладывают на ролики.
Укладку рельсового пути с
помощью путеукладчика ПБ-3 осуществляют в следующем порядке. После прибытия
поезда к месту работ кран подготавливают к работе и раскрепляют пакеты звеньев.
Затем производят протяжку первого пакета на платформу крана. Стропуя звено,
монтеры пути подводят под подошвы рельсов траверсы, звено поднимают с помощью
лебедки на высоту 0,6 м над пакетом, перемещают его по стреле крана до полного
выхода из портала крана и опускают на земляное полотно, где устанавливают
зазоры в стыках между уложенными и укладываемыми звеньями. Состыкованные звенья
фиксируют накладками с постановкой по два болта на стык. Цикл укладочных работ
повторяют. После выработки первого пакета на платформу крана перетягивают пакет
звеньев со следующего сцепа платформ состава.
С путеукладчиком работает
бригада, состоящая из 16 человек.
При укладке звеньев в путь
должны быть соблюдены следующие нормы допуска:
забег стыков рельсовых нитей
при временной эксплуатации на прямых участках пути не должен превышать 8 см., а
при постоянной - 3см.;
отступление размера стыковых
зазоров от расчетных значений в первом случае допускается ±3мм., а во втором
±2мм.
Длина участка, на котором
производится укладка пути: Lул = 619 км.
Срок строительства
железнодорожной линии:
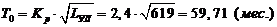
Кр =2,4-для
холмистой местности.
Время подготовительных работ tподг.
примем 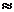 5%
от срока производства работ
5%
от срока производства работ 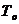 .
.
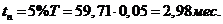
Земляные
работы:
Время производства земляных
работ определяется, исходя из вида местности, длины линии и производительности
механизированной колонны , рассчитанной на период (год):
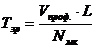 ; (51)
; (51)
где 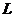 -
длина линии,
-
длина линии,
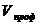 - профильный объем
земляных работ,
- профильный объем
земляных работ,
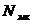 - годовая выработка
механизированной колонны.
- годовая выработка
механизированной колонны.
если Кр =2,4, то 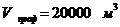 на
1 км .
на
1 км .
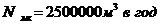 .
.
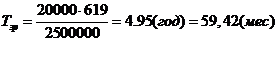
Если принять, что на площадке
работает 10 механизированных колонн, тогда Тзр=4,6(мес)
Время укладки рельсошпальной
решетки краном ПБ-3:
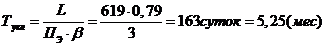
где 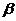 =3
- количество смен,
=3
- количество смен,
Пэ - производительность крана
ПБ-3 (Пэ=1/0,79),
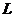 - длина линии.
- длина линии.
Время, необходимое для
балластировочных работ, рассчитывается из производительности балластировочной
машины:
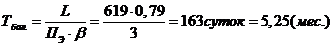
гдеПэ - производительность
балластировочной машины (Пэ = 1/0,79)
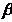 = 3 - количество смен,
= 3 - количество смен,
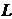 - длина линии.
- длина линии.
Время на отделку пути:
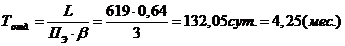 ,
,
где Пэ - производительность
работ (Пэ=1/0,64)
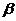 =3 - количество
смен.
=3 - количество
смен.
Строительство водопропускных
труб
Количество труб на участке
определяется, исходя из длины линии: на 1 км пути укладывается 4 трубы.
На производство одной трубы
требуется 6 дней. Соответственно, срок работ по укладке труб:
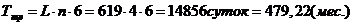
Время необходимое для
строительства одной бригадой. Для уменьшения срока строительства будет
задействованы 30 комплексных бригад. Срок строительства составит 15,97 (мес.)
где 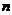 -
количество труб.
-
количество труб.
Строительство мостов:
К расчету примем, что на участке длиной 619км -
4 средних моста. Большие и внеклассные мосты отсутствуют. На 1 мост требуется
затратить 3 месяца. Таким образом, время, необходимое на строительство мостов -
12 (месяцев.)
Затем необходимо построить гистограммы для
определения частоты отказов, характеризующих виды работ на объектах.
.2.1 Расчёт гистограммы для определения частоты
отказов характеризующих виды работ на объектах
Гистограмма показывает вероятность попадания
результатов испытаний в определенные интервалы. Рассмотрим вероятность
попадания Ткр в определенные интервалы (Ткр - берется из
расчета сетевых моделей).
Число интервалов определяем по правилу
Старджесса:
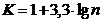 , (52)
, (52)
Где n - объем выборки для каждого вида работ.
К - число интервалов в гистограмме.
Частота попадания результата испытаний в
интервал:
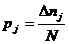 ; (53)
; (53)
где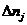 - количество попаданий в j-ый интервал;
- количество попаданий в j-ый интервал;
N - объем выборки.
.Для земляных работ:
K=1+3,3lg52=7
Δxi
- длина одного шага.
Δxi=(Xmax-Xmin)/K
Принимаем К=7, тогда Δxi=(24-3)/7=3
P1=1,5/52=0,028
P2=1,5/52=0,028
P3=3/52=0,259
P4=18,5/52=0,355
P5=22,5/52=0,0432
P6=3,5/52=0,067
P7=1,5/52=0,028
Высота столбца гистограммы определяется по
выражению:
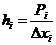
h1=0.028/3=0.006
h2=0.028/3=0.019
h3=0.259/3=0.067
h4=0.355/3=0.16
h5=0.432/3=0.027
h6=0.067/3=0.019
h7=0.028/3=0.013
Гистограмма земляных работ рис.3.1.
.Для труб:
K=1+3,3lg104=8
Δxi-
длина одного шага.
Принимаем К=7 тогда Δxi=(40-4)/8=4,5
P1=2/104=0,019
P2=4/104=0,019
P3=36/104=0,346
P4=29/104=0,278
P5=27/104=0,259
P6=4/104=0,038
P7=2/104=0,019
Р8=2/104=0,019
Высота столбца гистограммы определяется по
выражению:
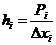
h1=0,019/4,5=0,004
h2=0,019/4,5=0,004
h3=0,346/4,5=0,076
h4=0,278/4,5=0,061
h5=0,259/4,5=0,057
h6=0,038/4,5=0.008
h7=0,019/4,5=0,004
h8=0,019/4,5=0,004
Гистограмма прокладки труб рис.3.2.
.Для мостов:
K=1+3,3lg57=7
Δxi-
длина одного шага.
Принимаем К=7, тогда Δxi=(29-5)/7=3.42
P1=2,5/57=0,043
P2=2,5/57=0.043
P3=5/57=0,087
P4=14,5/57=0,254
P5=24/57=0,421
P6=6/57=0,105
P7=2,5/57=0,043
Высота столбца гистограммы определяется по
выражению:
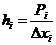
h1=0,043/3,42=0,012
h2=0,043/3,42=0.012
h3=0,087/3,42=0,025
h4=0,254/3.42=0,074
h5=0,421/3,42=0,123
h6=0,105/3,42=0,030
h7=0,043/3,42=0,012
Гистограмма строительства мостов рис3.3.
.Для укладки пути:
K=1+3,3lg69=8
Δxi-
длина одного шага.
Принимаем К=7, тогда Δxi=(39-7)/8=4
P1=3/69=0,043
P2=3/69=0,043
P3=4/69=0,057
P4=14/69=0,202
P5=33/69=0,478
P6=6/69=0,086
P7=3/69=0,043
P8=3/69=0,043
Высота столбца гистограммы определяется по
выражению:
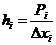
h1=0,043/4=0,010
h2=0,043/4=0,010
h3=0,057/4=0,014
h4=0,202/4=0,050
h5=0,478/4=0,119
h6=0,086/4=0,021
h7=0,043/4=0,010
h8=0,043/4=0,010
Гистограмма укладки пути рис.3.4.
.Для балластировки пути:
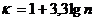 =1+3,3lg57=7
=1+3,3lg57=7
Принимаем К=7, тогда Δxi=(26-5)/7=3.00
P1=2/57=0.035
P2=3/57=0.053
P3=18/57=0,32
P4=24/57=0.42
P5=5/57=0.09
P6=3/57=0.053
P7=2/57=0.035
Высота столбца гистограммы определяется по выражению:
h1=0.035
/3=0.012
h2=0.053/3=0.018
h3=0.32/3=0.11
h4=0.42/3=0.14
h5=0.09/3=0.03
h6=0.053/3=0.018
h7=0.035/3=0.012
Гистограмма балластировки пути рис.3.5.
.Для отделки пути:
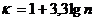 =1+3,3lg63=7
=1+3,3lg63=7
Принимаем К=7, Δxi=(20-9)/7=1,57
P1=4,5/63=0,071
P2=4,5/63=0,071
P3=15,5/63=0,246
P4=14,5/63=0,230
P5=10,5/63=0,166
P6=9/63=0,142
P7=4,5/63=0,071
Высота столбца гистограммы определяется по
выражению:
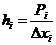
h1=0,071/1,57=0,045
h2=0,071/1,57=0,045
h3=0,246/1,57=0,156
h4=0,230/1,57=0,146
h5=0,166/1,57=0,105
h6=0,142/1,57=0.090
h7=0,071/1,57=0,045
.Для производственно-технических зданий:
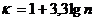 =1+3,3lg50=7
=1+3,3lg50=7
Принимаем К=7, Δxi=(20-4)/7=2,28
P1=2/50=0,04
P2=2/50=0,04
P3=5/50=0,1
P4=17/50=0,34
P5=18/50=0,36
P6=4/50=0,08
P7=2/50=0,04
Высота столбца гистограммы определяется по
выражению:
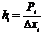
h1=0,04/2,28=0,017
h2=0,04/2,28=0,017
h3=0,1/2,28=0,043
h4=0,34/2,28=0,149
h5=0,36/2,28=0,157
h6=0,08/2,28=0.035
h7=0,04/2,28=0,017
.Для некатегорийного объекта:
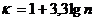 =1+3,3lg67=8
=1+3,3lg67=8
Принимаем К=7, Δxi=(36-5)/8=3,87
P1=2,5/67=0,037
P2=2,5/67=0,037
P3=9/67=0,134
P4=14,5/67=0,216
P5=31/67=0,462
P6=5/67=0,074
P7=2,5/67=0,037
P8=2,5/67=0,037
Высота столбца гистограммы определяется по выражению:
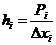
h1=0,037/3,87=0,009
h2=0,037/3,87=0,009
h3=0,134/3,87=0,034
h4=0,216/3,87=0,055
h5=0,462/3,87=0,119
h6=0,074/3,87=0,019
h7=0,037/3,87=0,009
h8=0,037/3,87=0,009
Таб.3.2 Расчетные параметры гистограмм.
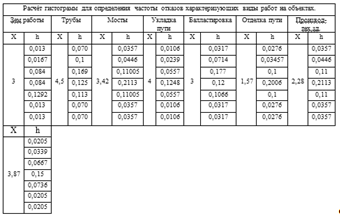
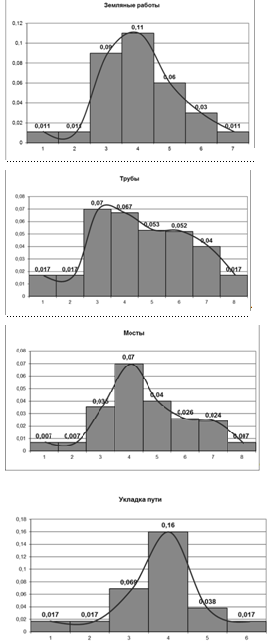
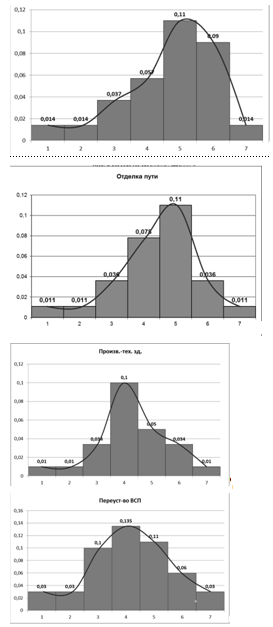
По полученным данным строим гистограммы каждой
из видов работ
3.2.2 Показатели организационно-технологической
надежности
Ритмичность производства характеризует выпуск
продукции в установленные сроки и определённого вида или номенклатура.
В проекте выполняется расчет следующих
коэффициентов:
) коэффициент ритмичности выпуска строительной
продукции
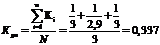 ,
,
где Кi
- коэффициенты по декадам,
N - число декад (N
= 3).
) коэффициент номенклатуры видов строительных
работ
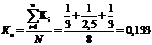
- число видов работ (N
= 8).
) коэффициент качества строительной продукции
Качество продукции - это совокупность
технических, эксплуатационных, экономических, эргономических и экологических
свойств для удовлетворения потребности производства и работников.
Система показателей качества продукции включает:
· показатели назначения,
· показатели надёжности,
· показатели экологичности,
· показатели технологичности,
· показатели эстетичности,
· показатели эргономичности и безопасности
использования,
· показатели стандартизации и
унификации,
· патентно-правовые показатели.
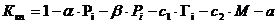 , (54)
, (54)
где Р - процент продукции, несданной с первого
предъявления,
α - показатель
технологичности,
β - показатель надёжности,
с1 - удельный показатель
эргономичности,
с2 - удельный показатель унификации,
Г - нарушение технической дисциплины в процентах
от количества проверочных операций;
М - процент брака сверх установленной нормы;
а - снижение коэффициента надёжности по причинам
упущений технологий и организации работ;
Для земляных работ:
Pi
= 0,22
α = 0,01
β = 0,025
с1 = 0,015
с2 = 0,05
Г=0,14
M=0,02
а=0,14
Кисп=1-0,01*0,22-0,025*0,22-0,015*0,14-0,05*0,02-0,14=0,8492.
Для труб:
Pi
= 0,22
α = 0,02
β = 0,05
с1 = 0,02
с2 = 0,04
Г=0,09
М=0,04
а= 0,18
Кисп=1-0,02*0,22-0,05*0,22-0,02*0,09-0,04*0,04-0,18=0,8012.
Для мостов:
Pi
= 0,24
α = 0,02
β = 0,05
с1 = 0,02
с2 = 0,05
Г=0,10
М=0,04
а= 0,18
Кисп=1-0,02*0,24-0,05*0,24-0,02*0,10-0,05*0,04-0,18=0,79992.
Для укладки пути:
Pi
= 0,21
α = 0,03
β = 0,05
с1 = 0,01
с2 = 0,04
Г=0,16
М=0,04
а=0,16
Кисп=1-0,03*0,21-0,05*0,21-0,01*0,16-0,04*0,04-0,16=0,8208.
Для балластировки пути:
Pi
= 0,26
α = 0,04
β = 0,07
с1 = 0,03
с2 = 0,05
Г=0,03
М=0,04
а=0,16
Кисп=1-0,04*0,26-0,07*0,26-0,03*0,03-0,05*0,04-0,16=0,8085.
Для отделки пути:
Pi
= 0,25
α = 0,04
β = 0,06
с1 = 0,03
с2 = 0,04
Г=0,06
М=0,03
а=0,18
Кисп=1-0,04*0,25-0,06*0,25-0,03*0,06-0,04*0,03-0,18=0,792
Для производственно-технических зданий
Pi=0,24
α=0,02
ß=0,07
c1=0,02
c2=0,04
Г=0,09
М=0,06
а=0,21
Kисп =
1-0,02*0,24-0,07*0,24-0,02*0,09-0,04*0,06-0,21=0,7642
Для переустройства ВСП
Р=0,26
α=0,04
ß=0,05
с1=0,04
с2=0,06
Г=0,09
М=0,04
а=0,22
Кисп=1-0,04*0,26-0,05*0,26-0,04*0,09-0,06*0,04-0,22=0,7506
) коэффициент использования основных фондов
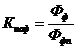 , (55)
, (55)
где Фф - фактическая фондоотдача,
Ффп - нормативная фондоотдача.
Для земляных работ:
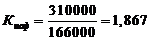 .
.
Для труб и мостов:
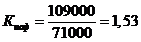 .
.
Для укладки пути:
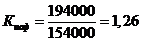 .
.
Для балластировки пути:
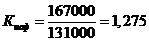 .
.
Для отделки пути:
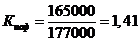 .
.
Для произ-тех. зданий
Киоф=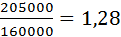
) коэффициент общего интегрального использования
при строительстве железной дороги и транспортных объектов:
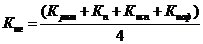 . (56)
. (56)
Для земляных работ:
Киг=(0,355+0,133+0,8475+1,24)/4=0,643
Для труб:
Киг=(0,355+0,133+0,8012+1,27)/4=0,6398
Для мостов:
Киг=(0,355+0,133+0,7992+1,27)/4=0,6393
Для укладки пути:
Киг=(0,355+0,133+0,8208+1,260)/4=0,6422
Для балластировки пути:
Киг=(0,355+0,133+0,8085+1,38)/4=0,6691
Для отделки пути:
Киг=(0,355+0,133+0,792+1,16)/4=0,6100
Для производственно-технических зданий:
Киг=(0,355+0,133+0,7642+1,94)/4=0,798
Для переустройства ВСП
Киг=(0,355+0,133+0,7506+1,28)/4=0,6296
) коэффициент качества выполнения управленческих
решений
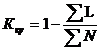 , (57)
, (57)
гдеΣL
- величина отказов, ΣL
= 11
ΣN
- общее количество отказов (принимается из задания)
Для земляных работ:
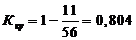
Для труб:
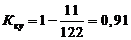
Для мостов:
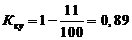
Для укладки пути:
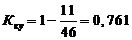
Для балластировки пути:
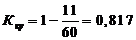
Для отделки пути:
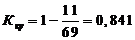
Для переустройства ВСП:
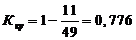
Для производственно
-технических зданий :
Кку=1-11/75=0,853
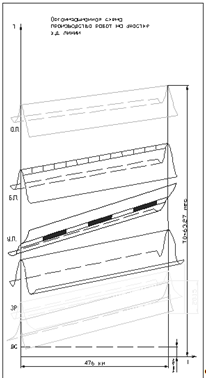
После расчета гистограмм по отдельным работам,
входящих в комплекс основных при строительстве участка железнодорожной линии,
составляется календарный график организации строительства железной дороги с
добавленной к организационной схеме вероятностных параметров, для работ,
полученных в гистограммах.
Заключение
Проблема организационно-технологической
надежности объединяет теоретические, методологические, практические пути и
решения многофакторных организационных задач на различных структурных уровнях
сооружения объектов и их эксплуатационного содержания. Надежность системы
управления на определенном уровне руководства определяется вероятностью
реализации этой системой выработанных решений по выполнению основных функций. В
строительстве основной функцией систем управления является обеспечение
директивной продолжительности строительства объектов и их комплексов. Но
следует учитывать, что на эффективность организационно-технологических систем
железнодорожного строительства влияет объединение в производственном процессе
не только технических (материалы, машины), но и социологических систем
(рабочие, специалисты). Взаимодействие этих систем между собой и с внешней
средой носит вероятностный характер. В данном курсовом проекте это
продемонстрировано на примере практической реализации положений организационной
надежности и расчета сетевых моделей.
Отказы в транспортном строительстве, являясь
случайными величинами, выражаются дискретно или непрерывно в зависимости от
физического смысла исследуемого явления и характеризуются функциями
распределения вероятностей, которые также представлены в курсовом проекте.
На основе расчетов, представленных в курсовом проекте
можно сделать вывод, что эффективность организационно-технологической
надежности строительства железных дорог базируется на комплексном подходе к
определению эффективности всех элементов системы, на моделировании и учете
связей между объектами строительства при его проектировании, возведении, на
учете вероятностного характера транспортного строительства, оценке и контроле
промежуточных решений в ходе строительства и эксплуатации объекта. Результаты
расчетов могут быть использованы в практической инженерной деятельности для
решения проблемы надежности организационных систем управления в двух
направлениях: исследование влияния на надежность систем их организации (состав,
количество, взаимосвязь и надежность элементов систем); исследование влияния на
надежность систем иерархической структуры управления.
надежность строительство железный
дорога
Литература
. Управление
железнодорожным строительством. Методы, принципы, эффективность. Спиридонов
Э.С., Шепитько Т.В. М.: ГОУ "УМЦ ЖДТ", 2008.
. Технология
железнодорожного строительства. Под ред. Э.С. Спиридонова, А.М. Призмазонова.
М.: Желдориздат, 2002.
. Железнодорожное
строительство. Технология и механизация. Под ред. С.П. Першина. М.: Транспорт,
1991.
. Справочник
проектировщика. Типовые железобетонные конструкции зданий и сооружений для
промышленного строительства . Под ред. Г.И. Бердичевского. М.: Стройиздат,1974.
. Железнодорожная
транспортная система. Эффективность. Надежность. Безопастность. Призмазонов
А.М., Сбитнев В.И. и др. М.:Желдортранс, 2002.
. Вопросы
информации и надежности в управлении транспортным строительством. Сборник
научных трудов кафедры "Строительное производство". Выпуск 991. М.:
МИИТ,1997
. Информационное
обеспечение технологии и управления строительством. Проблемы и решения. Сборник
научных трудов кафедры "строительное производство". Выпуск 920. М.:
МИИТ,1998.
. Менеджмент
в железнодорожном строительстве. Волков Б.А., Муджири Г.М., Прокудин И.В. М.:
Транспорт, 1998.
. Логика
оценки статистических гипотез. Дружинин Н.К.
. Новые
информационные технологии в создании устойчивых объектов инфраструктуры
отраслей и среды обитания человека. Иванов М.И., Мастаченко В.И. М.:МАИ,1996.
. Управление
проектами. Ильин Н.И. СПб.: "Два-Три", 1996.
. Выбор
организационно-технологических решений при переустройстве железных дорог. М.:
МИИТ, 2000.