Непрерывная случайная величина
Содержание
Непрерывная
случайная величина
Функция
распределения непрерывной случайной величины
Свойства
функции распределения
Регрессионный
анализ
Задача
Список
используемой литературы
Непрерывные случайные величины
Кроме дискретных случайных величин, возможные
значения которых образуют конечную или бесконечную последовательность чисел, не
заполняющих сплошь никакого интервала, часто встречаются случайные величины,
возможные значения которых образуют некоторый интервал. Примером такой
случайной величины может служить отклонение от номинала некоторого размера
детали при правильно налаженном технологическом процессе. Такого рода,
случайные величины не могут быть заданы с помощью закона распределения
вероятностей р(х). Однако их можно задать с помощью функции распределения
вероятностей F(х). Эта функция определяется точно так же, как и в случае
дискретной случайной величины:

Таким образом, и здесь функция F(х) определена
на всей числовой оси, и ее значение в точке х равно вероятности того, что
случайная величина примет значение, меньшее чем х.
Функция 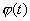 называется
плотностью распределения вероятностей, или кратко, плотностью распределения.
называется
плотностью распределения вероятностей, или кратко, плотностью распределения.
|
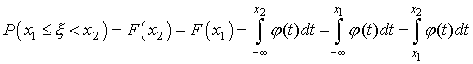 (2) (2)
|
Исходя из геометрического смысла интеграла как
площади, можно сказать, что вероятность выполнения неравенств 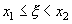 равна
площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой
равна
площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой
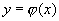 (рис.
1).
(рис.
1).
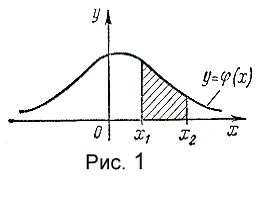
Рис. 1
Так как 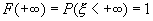 ,
а на основании формулы (1)
,
а на основании формулы (1)
 , то
, то
|
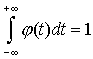 (3) (3)
|
Пользуясь формулой (1), найдем 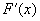 как
производную интеграла по переменной верхней границе, считая плотность
распределения
как
производную интеграла по переменной верхней границе, считая плотность
распределения 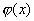 непрерывной**:
непрерывной**:
|
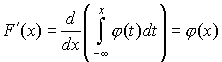 (4) (4)
|
Заметим, что для непрерывной случайной величины
функция распределения F(х) непрерывна в любой точке х, где функция 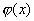 непрерывна.
Это следует из того, что F(х) в этих точках дифференцируема.
непрерывна.
Это следует из того, что F(х) в этих точках дифференцируема.
На основании формулы (2), полагая x1=x, 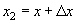 ,
имеем
,
имеем
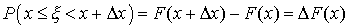
В силу непрерывности функции F(х) получим, что
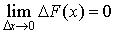
Следовательно
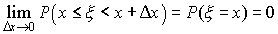
Таким образом, вероятность того, что непрерывная
случайная величина может принять любое отдельное значение х, равна нулю.
Отсюда следует, что события, заключающиеся в
выполнении каждого из неравенств 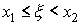 ,
,
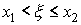 ,
,
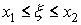 ,
,
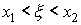
Имеют одинаковую вероятность, т.е.
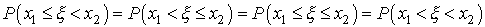
В самом деле, например,
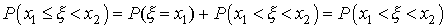
так как 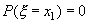
Замечание. Как мы знаем, если событие
невозможно, то вероятность его наступления равна нулю. При классическом
определении вероятности, когда число исходов испытания, конечно, имеет место и
обратное предложение: если вероятность события равна нулю, то событие
невозможно, так как в этом случае ему не благоприятствует ни один из исходов
испытания. В случае непрерывной случайной величины число возможных ее значений
бесконечно. Вероятность того, что эта величина примет какое-либо конкретное
значение x1 как мы видели, равна нулю. Однако отсюда не следует, что это
событие невозможно, так как в результате испытания случайная величина может, в
частности, принять значение x1. Поэтому в случае непрерывной случайной величины
имеет смысл говорить о вероятности попадания случайной величины в интервал, а
не о вероятности того, что она примет какое-то конкретное значение.
Так, например, при изготовлении валика нас не
интересует вероятность того, что его диаметр будет равен номиналу. Для нас
важна вероятность того, что диаметр валика не выходит из поля допуска.
Пример. Плотность распределения непрерывной
случайной величины задана следующим образом:
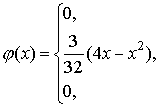
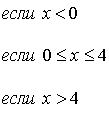
График функции 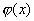 представлен
па рис. 7. Определить вероятность того, что случайная величина
представлен
па рис. 7. Определить вероятность того, что случайная величина 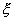 примет
значение, удовлетворяющее неравенствам
примет
значение, удовлетворяющее неравенствам 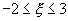 .Найти
функцию распределения заданной случайной величины.
.Найти
функцию распределения заданной случайной величины.
(Решение)
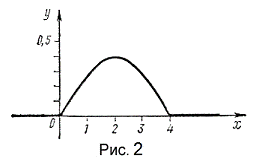
Рис. 2
Следующие два пункта посвящены часто
встречающимся на практике распределениям непрерывных случайных величин -
равномерному и нормальному распределениям.
Функция распределения непрерывной
случайной величины
Функцией распределения вероятностей F(x)
случайной величины Х в точке х называется вероятность того, что в результате
опыта случайная величина примет значение, меньше, чем х, т.е. F(x)=P{X < х}.
Рассмотрим свойства функции F(x).
. F(-∞)=lim(x→-∞)F(x)=0.
Действительно, по определению, F(-∞)=P{X
< -∞}. Событие (X < -∞) является невозможным событием:
F(-∞)=P{X < - ∞}=p{V}=0.
. F(∞)=lim(x→∞)F(x)=1,
так как по определению, F(∞)=P{X < ∞}.
Событие Х < ∞ является достоверным событием. Следовательно,
(∞)=P{X < ∞}=p{U}=1.
. Вероятность того, что случайная величина
примет значение из интервала [Α Β] равна
приращению функции распределения вероятностей на этом интервале.
P{Α ≤X<Β}=F(Β)-F(Α).
. F(x2)≥ F(x1), если x2, > x1, т.е.
функция распределения вероятностей является неубывающей функцией.
. Функция распределения вероятностей непрерывна
слева.
FΨ(xo-0)=limFΨ(x)=FΨ(xo) при
х→ xo
Различия между функциями распределения
вероятностей дискретной и непрерывной случайных величин хорошо иллюстрировать
графиками. Пусть, например, дискретная случайная величина имеет n возможных
значений, вероятности которых равны
{X=xk}=pk, k=1,2,..n.
Если x ≤ x1, то F(Х)=0, так как левее х
нет возможных значений случайной величины. Если x1< x ≤ x2 , то левее
х находится всего одно возможное значение, а именно, значение х1.
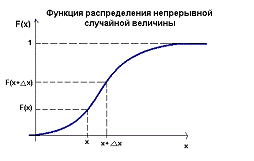
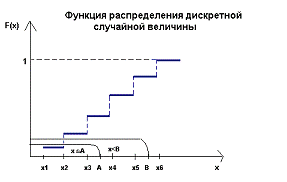
Рис. 3
Значит, F(x)=P{X=x1}=p1.При x2< x ≤ x3
слева от х находится уже два возможных значения, поэтому
F(x)=P{X=x1}+P{X=x2}=p1+p2. Рассуждая аналогично, приходим к выводу, что если
хk< x≤ xk+1, то F(x)=1, так как функция будет равна сумме вероятностей
всех возможных значений, которая по условию нормировки равна единице. Таким
образом, график функции распределения дискретной случайной величины является
ступенчатым. Возможные значения непрерывной величины располагаются плотно на
интервале задания этой величины, что обеспечивает плавное возрастания функции
распределения F(x), т.е. ее непрерывность.
Рассмотрим вероятность попадания случайной
величины в интервал
[x, x+Δx], Δx>0: P{x≤X<
x+Δx}=F(x+ Δx)-F(x).
Перейдем к пределу при Δx→0:
lim(Δx→0)P{x≤
X < x+Δx}=lim(Δx→0)F(x+Δx)-F(x).
Предел равен вероятности того, что случайная
величина примет значение, равное х. Если функция F(x) непрерывна в точке х, то
lim(Δx→0)F(x+Δx)=F(x),
т.е.
P{X=x}=0.
P{Α< X≤
Β},P{Α ≤
X< Β},P{Α< X< Β},P{Α ≤
X≤
Β}
равны, если Х - непрерывная случайная величина.
Для дискретных величин эти вероятности
неодинаковы в том случае, когда границы интервала Α
и(или)
Β
совпадают
с возможными значениями случайной величин. Для дискретной случайной величины
необходимо строго учитывать тип неравенства в формуле P{Α
≤X<Β}=F(Β)-F(Α).
Свойства функции распределения
Любая функция распределения обладает следующими
свойствами:
Она не убывает: если  ,
то
,
то  ;
;
Существуют пределы 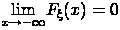 и
и
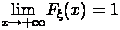 ;
;
Она в любой точке непрерывна слева:
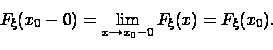
Доказательство свойства (1). Для любых чисел  событие
событие
 влечёт
событие
влечёт
событие  ,
т.е.
,
т.е.  .
Но вероятность - монотонная функция событий, поэтому
.
Но вероятность - монотонная функция событий, поэтому
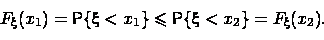
Для доказательства остальных свойств нам
понадобится свойство непрерывности вероятностной меры.
Доказательство свойства (2). Заметим сначала,
что существование пределов в свойствах (2), (3) вытекает из монотонности и ограниченности
функции 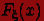 .
Остается лишь доказать равенства
.
Остается лишь доказать равенства
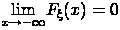 ,
, 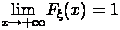 и
и
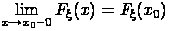 .
.
Для этого в каждом случае достаточно найти предел
по какой-нибудь подпоследовательности 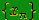 ,
так как существование предела влечёт совпадение всех частичных пределов.
,
так как существование предела влечёт совпадение всех частичных пределов.
Докажем, что  при
при
 .
Рассмотрим вложенную убывающую последовательность событий
.
Рассмотрим вложенную убывающую последовательность событий 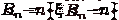 :
:
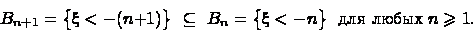
Пересечение 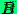 всех
этих событий состоит из тех и только тех
всех
этих событий состоит из тех и только тех  ,
для которых
,
для которых 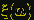 меньше любого
вещественного числа. Но для любого элементарного исхода
меньше любого
вещественного числа. Но для любого элементарного исхода  значение
значение
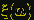 вещественно,
и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение
событий
вещественно,
и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение
событий 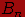 не
содержит элементарных исходов, т.е.
не
содержит элементарных исходов, т.е. 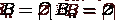 .
По свойству непрерывности меры,
.
По свойству непрерывности меры,  при
при  .
.
Точно так же докажем остальные свойства.
Покажем, что  при
при
 ,
т.е.
,
т.е. 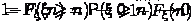 .
Обозначим через
.
Обозначим через 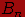 событие
событие 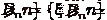 .
События
.
События 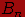 вложены:
вложены:
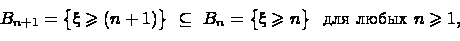
а пересечение 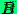 этих
событий снова пусто - оно означает, что
этих
событий снова пусто - оно означает, что  больше
любого вещественного числа. По свойству непрерывности меры,
больше
любого вещественного числа. По свойству непрерывности меры,
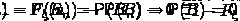 при
при  .
.
Доказательство свойства (3). Достаточно
доказать, что

при  .
Иначе говоря, доказать сходимость к нулю следующей разности:
.
Иначе говоря, доказать сходимость к нулю следующей разности:
вероятность распределение
регрессионный анализ
Регрессионный анализ
Регрессионный анализ - метод моделирования
измеряемых данных и исследования их свойств. Данные состоят из пар значений
зависимой переменной (переменной отклика) и независимой переменной (объясняющей
переменной). Регрессионная модель есть функция независимой переменной и
параметров с добавленной случайной переменной. Параметры модели настраиваются
таким образом, что модель наилучшим образом приближает данные. Критерием
качества приближения (целевой функцией) обычно является среднеквадратичная
ошибка: сумма квадратов разности значений модели и зависимой переменной для
всех значений независимой переменной в качестве аргумента. Регрессионный анализ
- раздел математической статистики и машинного обучения. Предполагается, что
зависимая переменная есть сумма значений некоторой модели и случайной величины.
Относительно характера распределения этой величины делаются предположения,
называемые гипотезой порождения данных. Для подтверждения или опровержения этой
гипотезы выполняются статистические тесты, называемые анализом остатков. При
этом предполагается, что независимая переменная не содержит ошибок.
Регрессионный анализ используется для прогноза, анализа временных рядов,
тестирования гипотез и выявления скрытых взаимосвязей в данных.
Регрессия - зависимость математического ожидания
(например, среднего значения) случайной величины от одной или нескольких других
случайных величин (свободных переменных), то есть 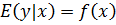 .
Регрессионным анализом называется поиск такой функции f, которая описывает эту
зависимость. Регрессия может быть представлена в виде суммы неслучайной и
случайной составляющих.
.
Регрессионным анализом называется поиск такой функции f, которая описывает эту
зависимость. Регрессия может быть представлена в виде суммы неслучайной и
случайной составляющих.
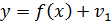
где f - функция регрессионной зависимости, а v -
аддитивная случайная величина с нулевым матожиданием. Предположение о характере
распределения этой величины называется гипотезой порождения данных. Обычно
предполагается, что величина v имеет гауссово распределение с нулевым средним и
дисперсией 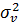 .
.
Задача нахождения регрессионной модели нескольких
свободных переменных ставится следующим образом. Задана выборка - множество 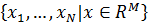 значений
свободных переменных и множество
значений
свободных переменных и множество 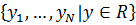 соответствующих
им значений зависимой переменной. Эти множества обозначаются как D, множество
исходных данных
соответствующих
им значений зависимой переменной. Эти множества обозначаются как D, множество
исходных данных 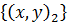 . Задана
регрессионная модель - параметрическое семейство функций f(w,x) зависящая от
параметров
. Задана
регрессионная модель - параметрическое семейство функций f(w,x) зависящая от
параметров 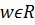 и свободных
переменных x. Требуется найти наиболее вероятные параметры
и свободных
переменных x. Требуется найти наиболее вероятные параметры 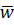 :
:
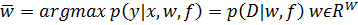
Функция вероятности p зависит от гипотезы
порождения данных и задается Байесовским выводом или методом наибольшего
правдоподобия.
Линейная регрессия предполагает, что функция f
зависит от параметров w линейно. При этом линейная зависимость от свободной
переменной x необязательна,
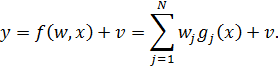
В случае, когда функция 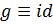 линейная
регрессия имеет вид
линейная
регрессия имеет вид

здесь 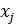 -
компоненты вектора x.
-
компоненты вектора x.
Значения параметров в случае линейной регрессии
находят с помощью метода наименьших квадратов. Использование этого метода
обосновано предположением о гауссовском распределении случайной переменной.
Разности 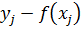 между
фактическими значениями зависимой переменной и восстановленными называются
регрессионными остатками (residuals). В литературе используются также синонимы:
невязки и ошибки. Одной из важных оценок критерия качества полученной
зависимости является сумма квадратов остатков:
между
фактическими значениями зависимой переменной и восстановленными называются
регрессионными остатками (residuals). В литературе используются также синонимы:
невязки и ошибки. Одной из важных оценок критерия качества полученной
зависимости является сумма квадратов остатков:
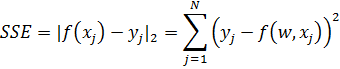
Здесь SSE - Sum
of Squared Errors.
Дисперсия остатков вычисляется по формуле
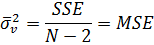
Здесь MSE - Mean Square Error,
среднеквадратичная ошибка.
Нелинейные регрессионные модели - модели вида 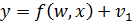 ,
которые не могут быть представлены в виде скалярного произведения
,
которые не могут быть представлены в виде скалярного произведения
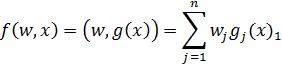
Где 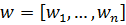 -
параметры регрессионной модели, x - свободная переменная из пространства Rn, y
- зависимая переменная, v - случайная величина и
-
параметры регрессионной модели, x - свободная переменная из пространства Rn, y
- зависимая переменная, v - случайная величина и 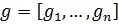 -
функция из некоторого заданного множества.
-
функция из некоторого заданного множества.
Задача
По двум независимым выборкам объемом
 n1=30 и
n2=15, извлеченным из нормальных генеральных совокупностей, найдены выборочные
средние
n1=30 и
n2=15, извлеченным из нормальных генеральных совокупностей, найдены выборочные
средние 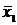 =25 и
=25 и 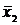 =27.
Дисперсии генеральных совокупностей известны
=27.
Дисперсии генеральных совокупностей известны 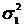 =1,3 и
=1,3 и 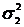 =1,6. На
уровне значимости
=1,6. На
уровне значимости 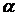 =0,1
проверить гипотезу Н0: μ1=
μ2 при
конкурирующей гипотезе Н1: μ1
=0,1
проверить гипотезу Н0: μ1=
μ2 при
конкурирующей гипотезе Н1: μ1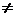 μ2.
μ2.
Решение
Найдем отношение большой
исправленной дисперсии к меньшей Fнабл=1.6/1.3=1.23.
По условию конкурирующая гипотеза
имеет вид μ1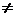 μ2 поэтому
критическая область - двусторонняя. В соответствии с правилом 2 при отыскании
критической точки следует брать уровень значимости вдвое меньше заданного.
μ2 поэтому
критическая область - двусторонняя. В соответствии с правилом 2 при отыскании
критической точки следует брать уровень значимости вдвое меньше заданного.
По таблице приложения 7, по уровню
значимости a/2=0.1/2=0.05 и числом степеней свободы k1=15-1=14 и k2=30-1=29,
находим критическую точку Fкр(0,05;14;29)=2,38.
Так как Fнабл>Fкр - нулевую
гипотезу о равенстве генеральных дисперсий отвергаем.
Список используемой литературы
1. Ахтямов
А.М. <http://ru.wikipedia.org/wiki/%D0%90%D1%85%D1%82%D1%8F%D0%BC%D0%BE%D0%B2,_%D0%90%D0%B7%D0%B0%D0%BC%D0%B0%D1%82_%D0%9C%D1%83%D1%85%D1%82%D0%B0%D1%80%D0%BE%D0%B2%D0%B8%D1%87>
«Теория вероятностей». - М.: Физматлит, 2009.
. Булдык
Г.М. «Теория вероятностей и математическая статистика», Мн., Высш. шк., 1989.
. Гнеденко
Б.В. «Курс теории вероятностей», УРСС. М.: 2001.
. Мацкевич
И.П., Свирид Г.П. «Высшая математика. Теория вероятностей и математическая
статистика», Мн.: Выш. шк., 1993.
. Севастьянов
Б.А. «Курс теории вероятностей и математической статистики», - М.: Наука, 1982.