Гамільтонові графи
Курсова робота
«Гамільтонові графи»
Вступ
Традиційно до дискретної математики відносять такі області
математики, як комбінаторика, теорія чисел, математична логіка, теорія систем
алгебри, теорія графів і мереж і так далі. Дискретна математика завжди
залишалася найбільш динамічною областю знань. Сьогодні найвагомішою областю
застосування методів дискретної математики є область комп'ютерних технологій.
Це пояснюється необхідністю створення і експлуатації електронно обчислювальних
машин, засобів передачі і обробки інформації, автоматизованих систем управління
і проектування. На грані дискретної математики і програмування з'являються нові
дисципліни, такі як розробка і аналіз обчислювальних алгоритмів, комбінаторні
алгоритми та алгоритмізація процесів. Дискретна математика і дисципліни, що є
суміжними з нею, вивчаються в всіх університетах і інститутах, де здійснюється
підготовка фахівців в області програмування, математики, а також по
економічних, технічних і гуманітарних напрямах.
Проблема
теорії графів є однією з актуальних проблем сучасної дискретної математики. Її
вирішення дозволить ефективно застосовувати отриманні знання в різних галузях
науки і техніки.
Теорія графів - молода область дискретної
дискретної математики. Порте методи теорії графів завоювали визнання не
тільки математиків, а й інженерів, економістів, психологів, біологів, хіміків.
Використання мови і методів теорії графів прискорює розв’язання практичних
задач, спрощує розрахунки. Теорія графів є однією з важливих частин математичного
апарату інформатики і кібернетики. У термінах теорії графів формулюють велику
кількість задач, пов’язних з дискретними об’єктами. Вивчення достатніх умов
існування в графі гамільтонового циклу - один із важливих напрямків у
теорії графів.
Мета курсової роботи - дослідити основні властивості
гамільтонових графів, розглянути приклади практичного застосування відшукання
гамільтонового циклу.
Об’єкт дослідження - теорія графів.
Методи дослідження - теоретичний аналіз
наукової літератури з проблеми, аналіз навчальних програм, підручників.
Завдання дослідженя:
1. Означити основні поняття теорії графів
(граф, маршрут, цикл і т.д.), проілюструвати їх на прикладах і навести зразки
задач, які зводяться до встановлення ти чи інших властивостей графів.
2. Дати означення гамільтонового та
напівгамільтонового графів, навести приклади.
. Довести теорему Дірака про достатні
умови гамільтоновості графа.
. Розглянути задачу побудови гамільтонових
циклів у графі.
1. Основні поняття теорії графів
.1 Історія виникнення графів
граф гамільтоновий цикл платоновий
Графи виникли у
вісімнадцятому сторіччі, коли відомий математик, Леонард Ейлер, намагався
вирішити тепер уже класичну задачу про Кенігсбергські мости. У той час в місті
Кенігсберг були два острови, сполучених сімома мостами з берегами річки Преголь
і один з одним так, як показано на мал. 1. Завдання полягає в наступному:
здійснити прогулянку по місту так, щоб, пройшовши рівно по одному разу по
кожному мосту, повернутися в те ж місце, звідки починалася прогулянка. Вирішуючи
цю задачу, Ейлер зобразив Кенігсберг у вигляді графа, ототожнивши його вершини
з частинами міста, а ребра - з мостами, якими зв'язані ці частини. Ейлерові
вдалося довести, що шуканого маршруту обходу міста не існує. Довгий час
дослідження Ейлера були єдиними результатами теорії графів. Нові результати
були отримані лише в середині ХІХ століття. Інтенсивно теорія почала
розвиватись лише в 50-60 роки в теорії автоматів, проектуванні, економіці.
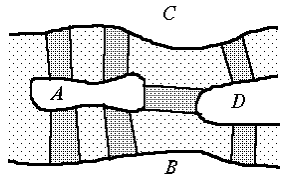
Рис. 1.1.1 Схема Кенігсберга
1.2 Основні поняття теорії графів
У завданні, до якого
звернувся Ейлер, запитується: чи можна знайти маршрут прогулянки, який
проходить рівно один раз по кожному з мостів і починається і закінчується в
одному і тому ж місці міста?
Модель завдання - це граф,
що складається з безлічі вершин і безлічі ребер, що
сполучають вершини. Вершини символізують береги річки і острова, а ребра
позначають сім мостів. Шуканий маршрут (якщо він існує) відповідає обходу ребер
графа таким чином, що кожне з них проходиться тільки один раз. Прохід ребра,
очевидно, відповідає перетину річки по мосту.
Означення 1.2.1 Графом
називається система, яка складається з непорожньої множини V і множини U,
деяких невпорядкованих пар елементів з множини V. Множина V називається вершинами,
U - ребрами.
Дві вершини U і V в простому
графові називаються суміжними, якщо вони з'єднуються будь-яким
ребром, про яке говорять, що воно інцидентне вершині u. Аналогічно
вводиться поняття суміжних ребер. Таким чином, ми можемо уявляти собі
множину ребер як множину пар суміжних вершин, визначаючи тим самим
нерефлексивне, симетричне відношення на множині V'. Відсутність
рефлексивності пов'язана з тим, що в простому графові немає петель, тобто
ребер, обидва кінці яких знаходяться в одній вершині. Симетричність же
відношення витікає з того факту, що ребро, що сполучає вершину U з V, (інакше кажучи,
ребра не орієнтовані, тобто не мають напряму).
Приведемо приклад задачі, яка може бути розв’язана, за
допомогою графів.
Задача 1.2.1:
На вечірку запрошено шестеро людей, чи може бути така
ситуація, що кожен знав тільки двох запрошених.
Розв’язання:
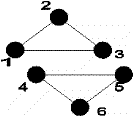
Кожного з цієї компанії зобразимо точкою, і пронумеруємо
їх. Якщо двоє знайомі, то з’єднаємо їх відрізком (ребром). Виявляється, що така
ситуація не тільки можлива, але й може описуватися декількома схемами.
Тобто можна сказати, що граф - це сукупність
об’єктів, зв’язками між якими служать ребра.
Приклади графів з декількома вершинами та
ребрами. На рис. 1.2.1 показаний граф з чотирма вершинами та п'ятьма ребрами На
рис. 1.2.2 зображено граф з п’ятьма вершинами та двома ребрами
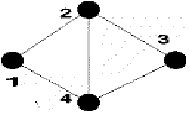
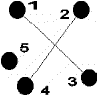
Рис. 1.2.1 Рис. 1.2.2
Прикладами графів можуть слугувати схеми метрополітенів, схеми
шосейних чи залізничних доріг, карти, які показують зв’язки між окремими
об’єктами.
Лема 1.2.1 (Про
рукостискання). Сума степенів всіх вершин графа є парним
числом.
Дійсно, кожне ребро
вносить у суму всіх вершин графа число 2, тобто
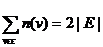
Якщо інтерпретувати кожне ребро як рукостискання двох
людей, то отримаємо, що при будь-якому числі рукостискань загальна кількість
потиснутих рук буде парною.
Наслідок 1.2.1 У будь-якому графі число вершин
непарного степеня парне. Дійсно, якби це було не так, то сума степенів всіх
вершин графа не могла б бути парним числом, що суперечить лемі про
рукостискання.
Графи зручно зображувати на площині або в просторі у
вигляді діаграм, які складаються з точок і відрізків, що з'єднують деякі з цих
точок. При цьому точки ототожнюються з вершинами графа, а відрізки - з його
ребрами.
Граф може містити декілька однакових ребер. Такі ребра
називаються кратними. Граф який містить кратні ребра називається мультиграфом.
Означення 1.2.2 Підграфом графа G
= (V, Е) називається граф G' = (V', Е'), у якому Е' з Е і V з V.
Якщо кінці ребра співпадають то він називається петлею.
Граф, який містить кратні ребра і петлі називається
псевдографом.
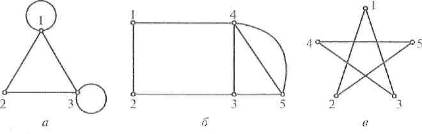
Рис. 1.2.3 Зображено а) псевдограф, б) мультограф, в) граф
.3 Різновиди графів
Розглянемо деякі
різновиди графів, які часто зустрічаються.
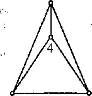
Рис. 1.3.1 Граф К4
Рис. 1.3.2 Граф К5
Повні графи
Означення 1.3.1.1 Граф, будь-які
дві вершини якого суміжні, називається повним графом. Отже, якщо G= (V, Е) - повний граф, то Е = V2. Повний граф з n вершинами
позначаємо Кn Графи К4 і К5
зображені на рис. 1.3.1 і 1.3.2 відповідно.
Регулярні графи
Більш загальними, ніж повні, є регулярні графи.
Означення 1.3.2.1 Граф називається
регулярним або однорідним, якщо всі його вершини мають один і той же степінь.
Якшо степінь кожної вершини дорівнює k, то граф називається регулярним графом
степеня k. Отже, повний граф n-го порядку є регулярним графом степеня n-1. Регулярні
графи степеня 3 називають також кубічними, або тривалентними графами (ці графи
викликають особливий інтерес у зв'язку із задачею розфарбування графів).
Відомим прикладом кубічного графа є граф Петерсена, який показано на рис.
1.3.2.1.
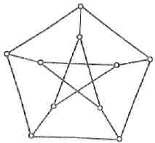
Рис. 1.3.2.1 Граф
Петерсена
Платонові графи
Означення 1.3.3.1. Платоновими
графами називаються графи, утворені вершинами і ребрами п'яти правильних
многогранників - платонових тіл: тетраедра, куба, октаедра, додекаедра та
ікосаедра.
Граф К4, зображений на рис. 1.3.1, відповідає
тетраедру, а графи, що відповідають кубу і октаедру, показані на рис. 1.3.3.1
відповідно.
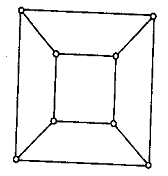
Рис. 1.3.3.1 Платонові
графи
Двочастинні графи
Означення 1.3.4.1 Граф називається двочастинним, якщо існує
таке розбиття множини його вершин на два класи, при якому кінці кожного ребра
лежать у різних класах.
Означення двочастинного графа можна подати іншим чином - в
термінах розфарбування його вершин двома кольорами, наприклад червоним і синім.
При цьому граф називається двочастинним, якщо кожну його вершину можна
пофарбувати синім або червоним кольором, так щоб кожне його ребро мало один
кінець червоний, а другий - синій.
Якщо в двочастинному
графі будь-які дві вершини з різних класів суміжні, то такий граф називається
повним двочастинним графом. Повний двочастинний граф, в якого один клас має m вершин, а другий
n - вершин
позначають Кm,n
Повний двочастинний граф
К1,n називається зірковим графом. На рис.
1.3.4.1 зображений граф К1,5.
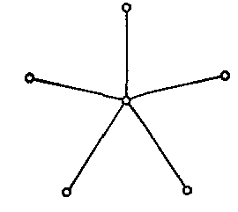
Рис. 1.3.4.1 Зірковий
граф
Аналогічно можна ввести k-частинні графи. Граф
називається k-частинним графом, якщо існує таке розбиття множини його
вершин на k класів, при якому будь-яке ребро графа з'єднує дві вершини з
різних класів.
.4 Маршрути, ланцюги і цикли
Маршрутом в графі
називається скінченна послідовність суміжних ребер. Кожне ребро маршрут.
Число ребер у маршруті
називається довжиною маршруту.
Маршрут у якого всі ребра
різні називається ланцюгом.
Циклом в графі прийнято
називати послідовність вершин, кожна пара яких є кінцями одного ребра, а
решта вершин (і ребра) не повторюється. Іншими словами, цикл - це замкнутий
маршрут, що проходить через кожну свою вершину і ребро тільки один раз.
Маршрут (цикл) у якого
всі ребра різні називається простим.
Відстанню від вершини А до
вершини В називається довжина найкоротшого маршруту, що з’єднує їх.
Граф називають зв'язним,
якщо будь-яку пару його вершин сполучає який-небудь маршрут. Будь-який
загальний граф можна розбити на підграфи, кожен з яких виявиться зв'язним.
Мінімальне число таких зв'язкових компонент називається числом зв'язності графа
і позначається через з(G)
1.5 Орієнтовані графи (орграфи)
Означення 1.5.1.1 Орієнтованим
графом (орграфом) G=(V, E), називаэться система, яка складається з
непорожньої множини V і непорожньої множини U впорядкованих пар елементів з
множини V. Елементи множини V називаються вершинами орграфа
G, а елементи множини Е - дугами орграфа G
=(V, E). Отже, дуга - це впорядкована пара
вершин. Відповідно, V називається множиною вершин і Е - множиною дуг
орграфа
G.
Якщо е= (v, w) - дуга, то вершина
v називається початком, а вершина w - кінцем дуги е.
Кажуть, що дуга е веде з вершини v у вершину
w або виходить з v і заходить у w. Дугу е і вершини
v та w називають інцидентними між собою, а вершини
v i w суміжними.
Дуга (v, v), в якій початок і кінець
збігаються називається петлею. Надалі розглядатимемо
тільки орграфи без петель.
Приклади орграфів
показані на рис. 1.5.1.
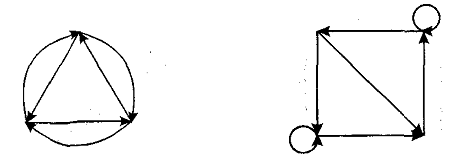
Рис. 1.5.1 Орієнтовані
графи
1.6 Представлення графів
Найбільш відомий і популярний спосіб
представлення графів полягає в геометричному
зображенні точок (вершин) і ліний (ребер) на папері. При чисельному вирішенні завдань на
обчислювальних машинах граф повинен бути представлений дискретним способом.
Існує досить багато способів такого роду представлення графів. Проте простота
використання представления графа, як і
ефективність алгоритму, в основі котрого він лежить, повною мірою залежить від конкретного вибору.
Один з напрямів теорії графів пов'язаний з їх матричним уявленням. Існують
різні види матриць, асоційовані з графами. Ці форми алгебри використовуються
для вирішення багатьох завдань теорії графів. Нижче розглядаються дві такі
матричні форми і декілька нестандартних уявлень, які найширше використовуються в
алгоритмах на графах.
Одним зі способів завдання графа G =(V,
E) є завдання кожної з множин V і E за допомогою переліку
їх елементів.
Приклад 1.6.1. Граф G1=(V1,
E1), V1={v1, v2,
v3, v4} і E1={(v1,
v3), (v1, v4), (v2,
v3), (v2, v4), (v3,
v4)} - це граф із чотирма вершинами і п’ятьма
ребрами.
Граф G =(V, E) зручно
зображати за допомогою рисунка на площині, який називають діаграмою
графа G. Вершинам графа G ставляться у бієктивну відповідність
точки площини; точки, що відповідають вершинам v i w, з’єднуються
лінією (відрізком або кривою) тоді і тільки тоді, коли v i w
суміжні вершини. Зрозуміло, що діаграма графа змінюватиме свій вигляд у
залежності від вибору відповідних точок на площині.
Приклад 1.6.2. На рисунку 3.1
зображені діаграми графів G1 i G2 з
попереднього прикладу.
G1 G2
Рис. 1.6.1
Матриця
суміжності графа
Означення 1.6.1.1 Матрицею
суміжності неорієнтованого графа
з n вершинами називається матриця n на m, елементи якої обчислюються за
правилом:
Аij=1, якщо Аi
суміжне Aj;
Aij=0, у протилежному випадку.
Приклад 1.6.1.1 Для графів G1
i G2 маємо відповідно:
A1=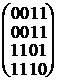 i A2=
i A2=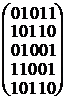
Очевидно, що матриці суміжності графів - симетричні.
Означення 1.6.1.2 Матрицею
суміжності орієнтованого графа з n вершинами називається матриця n на m,
елементи якої обчислюються за правилом.
Матриця суміжності однозначно визначає структуру
графа. Зазначимо, що петлі в матриці суміжності можуть бути представлені
відповідним одиничним діагональним елементом. Кратні ребра можна представити,
припустивши, що елемент матриці може бути більший 1, але зазвичай представляють
кожен елемент матриці одним двійковим розрядом.
Матриця інцидентності графа
Означення 1.6.2.1 Матрицею
інцидентності неорієнтованого графа з n вершинами m ребрами називається
матриця розмірності n на m елементи якої обчислюються за правилом:
Aij=1, якщо Ai інцидентне Aj;
Aij=0, у протилежному випадку.
Приклад 1.6.2.1. Для графів G1
і G2 маємо (ребра графів нумеруємо в тому порядку, в якому
вони виписані в прикладі 1.6.1).
B1=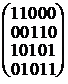 і B2=
і B2=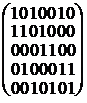
Означення 1.6.2.2 Матрицею
інцидентності орієнтованого графа з n вершинами m ребрами називається
матриця розмірності n на m елементи якої обчислюються за правилом:
, якщо вершина vi є початком
дуги ej;ij = -1, якщо вершина vi
є кінцем дуги ej;
, якщо вершина vi і дуга ej
неінцидентні.
1.7
Ейлерові графи
Означення 1.7.1. Граф, в якому
знайдеться маршрут, що починається і закінчується в одній вершині, і що
проходить по всіх ребрах графа рівно один раз, називається ейлеровим графом.
Означення 1.7.2. Послідовність
вершин (може бути і з повтореннями), через які проходить шуканий маршрут, як і
сам маршрут, називається ейлеровим циклом.
Крім того, Ейлерові
вдалося довести і протилежне твердження, так що граф, в якому будь-яка пара
вершин зв'язана деякою послідовністю ребер, є Ейлеровим тоді і тільки тоді,
коли всі його вершини мають парний ступінь. Ступенем вершини v називається
число ребер, інцидентних їй.
Теорема 1.7.1 (теорема
Ейлера). Зв’язний граф G є ейлеровим тоді і тільки тоді, коли
степені всіх його вершин парні.
Доведення. Необхідність. Нехай G - ейлерів граф.
Ейлерів цикл цього графа, проходячи через кожну вершину, заходить у неї по
одному ребру, а виходить - по іншому. Це означає,
що кожна вершина інцидентна парній кількості ребер ейлерового циклу, а оскільки
цей цикл містить усі ребра графа, то звідси випливає парність степенів усіх
вершин графа.
Достатність. Припустимо, що
степені всіх вершин графа G =(V, E) парні. Візьмемо деяку
вершину v1ÎV і розпочнемо з
неї обхід графа, кожен раз обираючи ребро, яке раніше не використовувалось.
Оскільки степінь кожної вершини парний і ненульовий, то цей шлях може
закінчитися тільки у вершині v1, утворивши таким чином цикл Z1.
Якщо в результаті описаного процесу використано всі ребра графа G, то
шуканий ейлерів цикл побудовано. Якщо ж Z1 містить не всі
ребра графа G, то вилучимо з G всі ребра, які входять у Z1.
Одержимо граф G1 - підграф графа G,
всі вершини якого також матимуть парні степені (це випливає з того, що і G,
i Z1 мають вершини тільки парних степенів). Крім того,
внаслідок зв’язності графа G Z1 i G1
мають принаймні одну спільну вершину v2. Відтак, починаючи з
вершини v2, побудуємо цикл Z2 у графі G1.
Позначимо через Z1¢ частину циклу Z1
від v1 до v2, а через Z1¢¢ - частину циклу Z1
від v2 до v1. Отримаємо новий цикл Z1¢, Z2,
Z1¢¢, що веде з v1
у v1. Якщо цей цикл ейлерів - процес
завершився. У противному разі продовжуємо аналогічні побудови ще раз і т.д. Цей
процес завершиться побудовою шуканого ейлерового циклу.
Теорема 1.7.2 Ланцюг Ейлера в псевдо
графові G існує тоді і тільки тоді, коли виконуються наступні умови:
· Граф зв'язний;
· Степені внутрішніх вершин
парні (внутрішні вершини не є початком і кінцем ланцюга);
· Якщо вершини а і b є
початком і кінцем ланцюга і то ступені їх непарні;
· Якщо вершини а і b є
початком і кінцем ланцюга, то ступені їх парні.
Тепер абсолютно очевидно, що в графові, що
моделює завдання про мости Кенігсберга, ейлерового циклу знайти не можна.
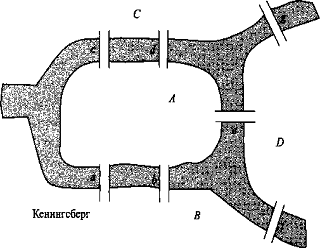
Рис. 1.7.1 Схема старого
Кенігсберга
Дійсно, ступені всіх його
вершин непарні: 6 (B) = 6 (C) - 6 (D) = 3 і 6 (A) =
5. З легкої руки Ейлера графи, подібні тому, який ми досліджували при вирішенні
задачі про мости, почали використовуватися при вирішенні багатьох практичних
завдань, а їх вивчення виросло в значну область математики.
Теорема 1.7.2 Щоб в зв'язаному
неорієнтованому графові G існував ейлеровий цикл, необхідно і достатньо, щоб
число вершин непарного ступеня було парним.
Наслідок 1.7.1 Для зв'язного
ейлерового графа G безліч ребер можна розбити на простих цикли.
Наслідок 1.7.2 Для того, щоб
зв'язний граф G покривався єдиним ейлеровим ланцюгом необхідно і достатньо, щоб
він містив рівно 2 вершини з непарним степенем. Тоді ланцюг починається в одній
з цих вершин і закінчується в інший.
Справедливі й зворотні твердження:
Якщо граф зв’язний і має тільки дві непарні
вершини, то він містить Ейлерів шлях, який починається в одній непарній
вершині, а закінчується в іншій.
Одним з найефективніших
методів відшукання ейлерового циклу в графі є алгоритм Флері.
Алгоритм Флері полягає в
наступному:
· Вибираємо довльну
вершину V0
· Йдемо по ребру
інцедентному цій вершині, позначивши його N1
· Прийшовши у
вершину V1 викреслюємо ребро N1
· Якщо на k-му кроці прийшли
у вершину Vk, то для наступного ходу вибирають будь-яке ребро
інцидентне цій вершині (при цьому ребро-міст вибирають лише тоді коли інших
можливостей немає).
2. Гамільтонові цикли у графах
.1 Означення гамільтонового та
напівгамільтонового графа
Означення 2.1.1. Шлях x0, x1,…,
xn-1, xn у зв'язному графі
G=(V, E) називають
гамільтоновим шляхом, якщо V={x0,x1,…,
xn-1, xn } і xі ≠ xj для 0≤i<j≤n.
Означення 2.1.2. Цикл x0, x1,…,
xn-1, xn, x0 (тут n>1) у
графі G=(V, E) називають гамільтоновим циклом, якщо x0, x1,…,
xn-1, xn - гамільтонів шлях.
Іншими словами, гамільтонів цикл і гамільтонів
шлях проходять через кожну вершину графа точно один раз (можливо, за
виключенням першої і останньої вершин). Зазначимо, що гамільтонові цикл і шлях,
якщо казати загалом, не містять усіх ребер графа.
Означення 2.1.3. Граф називається
гамільтоновим, якщо він містить гамільтонів цикл.
Означення 2.1.4. Граф називається
напівгамільтоновим, якщо він містить гамільтонів шлях.
.2 Достатні умови гамільтоновості графа
Пошук критерію гамільтоновості графа - це
одна з основних невирішених проблем теорії графів. Про гамільтонові графи
відомо ще зовсім мало.
Теорема 2.2.1 (Поша). Нехай G=(V,
Е), |V| ³ 3. Якщо для будь-якого n, 1£n<(|V|-1)/2 число
вершин зі степенями, що не перевищують n, менше ніж n, і для непарного |V|
число вершин ступеня (|V|-1)/2 не перевищує (|V|-1)/2, то G - гамільтонов граф.
Один із найбільш відомих результатів загального
характеру подається в такій теоремі.
Теорема 2.2.2 (Г. Дірак 1952 р.). Якщо
G - зв'язний простий граф з n≥3 вершинами і для кожної вершини v
виконується нерівність deg(v) ≥n/2, то граф G має гамільтонів цикл.
Доведення. Додамо до графа G k нових вершин і і
з’єднаємо ребром
кожну з цих вершин з кожною вершиною з G. Отриманий граф з n+k вершинами
позначимо через G'. Важатимемо, що k - найменша кілкість вершин, потрібних для того, щоб
у графі G з’явився
гамільтонів цикл. Покажемо, що припущення k≥1 призводить до суперечності.
Нехай v, p, w, …, v - гамільтонів цикл
у G', де v та w - вершини з G, p - одна з нових
вершин. Тоді w несуміжна з v, інакше могли б не використовувати вершину p, що
суперечить мінімальності k. Більше того, вершина w', суміжна з вершиною w, не може в
гамільтоновому циклі безпосередньо йти за вершиною v', суміжною з v. Дійсно,
якщо є гамільтонів цикл v, p, w, …, v', w', …, v, то ми можемо
замінити його на v, v', …, w, w', …, v, повертаючи частину циклу, що міститься
між w та v' - це знову суперечить мінімальності k.
Отже, кількість вершин графа G', які не суміжні з
w, не менша від
кількості вершин, суміжних з v (тобто дорівнює принаймні n\2+k). Натомість
очевидно, що кількість вершин графа G', суміжних з w, також дорівнює принаймні n\2+k. Але жодна з
вершин графа G' не може одночасно бути суміжною і несуміжною з вершиною w, так
що загальна кількість вершин графа G' дорівнює щонайменше n\2+k. Але це
суперечить тому, що кількість вершин графа G' дорівнює n+k.
Одержана суперечність доводить теорему.
Теорема 2.2.3 (Оре, 1960 р.).
Якщо у графі G з n вершинами (n≥3) сума степенів будь-яких двох вершин є не
меншою, ніж n,
то граф G
є гамільтоновим.
Теорема 2.2.4 (В.А. Перепелиця). Майже
усі повні графи - гамільтонові.
Теореми Оре і Дірака є наслідками до теореми
Поша.
Ці умови не є необхідними.
Як знайти гамільтонів цикл або переконатись, що
його немає? Очевидний алгоритм, який можемо застосувати - це «повний
перебір усіх можливостей», тобто n!. Перестановок всіх вершин графа і
перевірок. Зрозуміло, що такий спосіб практичного застосування не знаходить.
Для таких задач невідомий (і є вагомі підстави
вважати, що його не існує) ефективний алгоритм їхнього розв’язання.
Зв’язок між ейлеровими і гамільтоновими циклами
заданого графа G і відповідними циклами так званого реберного
графа L(G) встановлюється за допомогою нижченаведених тверджень.
Теорема 2.2.5 Якщо граф G
має ейлерів цикл, то граф L(G) має як ейлерів, так і гамільтонів
цикли.
Теорема 2.2.6 Якщо граф G
має гамільтонів цикл, то граф L(G) також має гамільтонів цикл.
.3 Задача побудови гамільтонових циклів у графі
Термін «гамільтонів» походить від імені відомого
ірландського математика У. Гамільтона (W. Hamilton), який 1857 р.
запропонував гру «Навколосвітня подорож». Кожній із двадцяти вершин додекаедра
(правильного дванадцятигранника, грані якого - п'ятикутники) приписана
назва одного з великих міст світу. Потрібно, починаючи з довільного міста,
відвідати решту 19 міст точно один раз і повернутись у початкове місто. Перехід
дозволений по ребрах додекаедра.
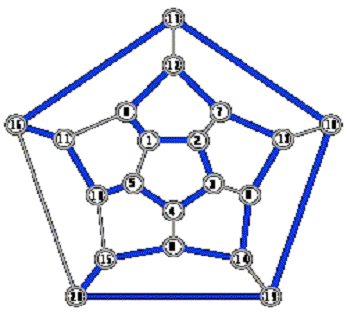
Рис. 2.3.1
Приклад 2.1.1. Ту саму задачу
можна зобразити і на площині (рис. 2.3.1).
Вона зводиться до відшукання на графі
гамільтонового циклу. Один із можливих розв'язків показано на рис. 2.3.1
потовщеними лініями.
Задача комівояжера
Вона полягає в
наступному: комівояжер повинен відвідати кожне із заданих n міст по одному
разу, виїхавши з якогось з цих міст і повернутися до нього ж. Потрібно знайти
найкоротший маршрут, знаючи відстані між кожною парою міст.
Математична постановка цієї задачі
виглядає так: у повному зваженому графі потрібно знайти гамільтонів цикл (чи
ланцюг) мінімальної ваги. Під вагою циклу розуміється сума ваг ребер, що
складають його.
До теперешнього часу для задачі
комівояжера відомі такі алгоритми:
динамічне програмування;
метод аналізу і відсівання варіантів;
метод гілок і границь
серед яких останній - найбільш популярний.
Ми познайомимося з одним алгоритмом
побудови гамільтонового циклу мінімальної ваги «йди в найближчий», що для
неповного графа дає наближене рішення.
Опис алгоритму «йди в найближчий» (a):
Алгоритм a виконується по
крокам S= 1,2,…, n. На кроці S=1 фіксується "u1ÎV і розглядається множина E(u1)ÌE усіх ребер, інцидентних u1. Серед них вибирається найкоротше, тобто таке е1 = (u1, u2), для якого вага 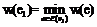
Після чого вважаємо, що на I кроці побудовано ланцюг L1=[u1,u2].
Нехай здійснено S£ n-1
кроків, у результаті S - го кроку побудовано елементарний ланцюг LS=[u1,u2,…,uS+1]…
Позначимо через Е (uS+1) - множину усіх таких ребер е=(uS+1,u)ÎE, що:
) інцидентні вершині uS+1;
) не інцидентні ніякій вершині u з ланцюга Ls,
тобто uÏLS
На кроці S+1 серед ребер множини E (uS+1)
вибираємо найкоротше ребро e+1, тобто таке, що задовольняє
умові 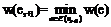
Після чого ребро es+1 приєднуємо до ls і
одержуємо простий ланцюг Ls+1=[u1,…,uS+1,uS+2]…
Алгоритм a закінчує
роботу на кроці S=n, перед початком якого, у результаті кроку S= n-1 виділений
гамільтонова ланцюг Ln-1=[u1,…,un]…
Тоді на кроці S=n, гамільтонів ланцюг Ln-1
замикається в гамільтонів цикл шляхом приєднання до цього ланцюга ребра е = (un, u1)ÎE де Е - множина ребер даного графа G=(V, E).
Цей процес виявиться безрезультатним, якщо не містить ребра e=(un, u1).
Робота алгоритму a
виявляється безрезультатною на якому-небудь кроці S також у тому випадку, коли
множина ребер E(uSH)=Æ
На повному графі алгоритм a завжди знаходить деяке припустиме рішення задачі комівояжера X =
(V, Ех)Î X, де X - це гамільтонів цикл даного повного
графа G = (V, Е).
2.4 Задача
Навести приклад графа, який має ейлерів цикл, але
не має гамільтонового циклу, а також графа, який має гамільтонів цикл, але не
має ейлеревого циклу.
Розв’язання:

Граф G1 має всі вершини
парні, тому він є ейлерів, але граф не є гамільтоновим.
Граф G2 має непарні
вершини, тому він не є ейлерів, але він є гамільтоновим.
Висновок
граф гамільтоновий цикл платоновий
Отже, проблема теорії графів є однією з
актуальних проблем сучасної дискретної математики. Її вирішення дозволить
ефективно застосовувати отриманні знання в різних галузях науки і техніки.
Даний процес є важливим, оскільки він сприяє спрощенню при передаванні
інформації по різним каналам зв’язку.
Багато найрізноманітніших завдань природно формулюється в термінах
точок і зв'язків між ними, тобто в термінах графів. Так, наприклад, можуть бути
сформульовані завдання складання розкладу, аналізу мереж в електротехніці, в
програмуванні, в проектуванні електронних схем, в економіці, в соціології і
т.д. Тому ефективні алгоритми вирішення завдань теорії графів мають велике
практичне значення.
Основна література
1. Нікольський
Ю.В. Дискретна математика: Підручник._Львів: Магнолія Плюс, 2005. - 608 с.
2. Акимов
О.Е. Дискретная математика: логика, группы, графы. 2-е узд., дополн. - М:
Лабораторія Базових Знаний, 2001. - 376 с.
. Андрійчук В. І., Комарницький М.Я. Вступ до дискретної
математики: Навч. Посіб., - К.:Центр, 2004. - 254 с.
. Бардачов Ю.М. та ін. Дискретна математика.: Підручник /
Ю.М. Бардачов, І. А. Соколова, В. Є. Ходакова. - К.:Вища школ, 2002. - 287 с.
. Капітонова Ю.В. та ін. Основи дискретної математики, -
К.:Наукова думка, 2002. - 578 с.
. Оре О. Теорія графов. - М.: Наука, 1968. - 352 с.
. Швай О.Л. Дискретна математика.: Навч. Посіб. Для вищ.
Навч. Зак. - Луцьк: РВВ «Вежа» Волин. нац. ун-ту ім. Лесі Українки,
2008. - 188 с.