Решение геодезических задач с помощью языка программирования Turbo Pascal и табличного процессора Excel
Федеральное агентство образования и
науки Российской Федерации
Санкт-Петербургский государственный
горный институт им. Г.В. Плеханова
(технический университет)
КУРСОВАЯ РАБОТА
По дисциплине: Информатика
Тема: Решение геодезических задач
с помощью языка программирования Turbo Pascal и табличного процессора Excel
Автор: студент гр. ГГ-04-1
Трущелёв А.В.
Проверил:
Руководитель проекта, доцент
Косовцева Т.Р.
Санкт-Петербург 2005
Аннотация
Пояснительная записка представляет собой отчёт по курсовой работе на
тему: решение геодезических задач с помощью языка программирования Turbo Pascal и табличного процессора Excel. Отчёт оформлен в текстовом процессоре Microsoft Word.
Страниц 48, рисунков 13.
The summary
The explanatory note represents the report on course work on
a theme: the decision of geodesic problems with the help of programming
language Turbo Pascal and tabulated processor Excel. The report is made out in
word-processor Microsoft Word. 48, figures 13.
Оглавление
Введение
.
«Обратная геодезическая задача»
.1
Теоретические сведения
.2
Постановка задачи
.3
Исходные данные
.4
Блок схема для Turbo Pascal
.5
Текст программы
.6
Результат программы
.8
Анализ
.
«Прямая угловая засечка»
.1
Теоретические сведения
.2
Постановка задачи
.3
Исходные данные
.4
Блок схема для Turbo Pascal
.5
Текст программы
.6
Результат программы
.7
Вычисления MS Excel
.8
Анализ
.
«Теодолитный ход»
.1
Теоретические сведения
.2
Постановка задачи
.3
Исходные данные
.4
Алгоритм для Turbo Pascal
.5
Текст программы
.6
Результат программы
.7
Анализ
.
«Решение СЛАУ методом Гаусса»
.1
Теоретические сведения
.2
Постановка задачи
.3
Исходные данные
.4
Блок-схема для Turbo Pascal
.5
Текст программы
.6
Результат программы
.7
Табличные вычисления MS Excel
.8
Анализ
Заключение
Библиографический
список
Введение
Задание:
Составить программы с помощью языка программирования Turbo Pascal для решения геодезических задач: решение обратной
геодезической задачи, нахождение прямой угловой засечки, вычисление координат
теодолитного хода, решение системы линейных уравнений методом Гаусса.
В настоящее время компьютерные технологии на основе программирования
внедряются в различные сферы деятельности человека. Исключением не является и
маркшейдерское дело. Основной задачей маркшейдерского дела является составление
планов горных выработок. Для их создания маркшейдерам необходимо получать
координаты точек опорной сети. Процесс обработки материалов (камеральные
работы) становится более быстрым и менее трудоемким с внедрением программ для
решения геодезических задач. С помощью языка программирования Turbo Pascal можно составить программы для
решения почти всех маркшейдерских задач.
В данной курсовой работе основной целью является закрепление полученного
опыта работы с системой Turbo Pascal с помощью создания программ для камеральных работ. Проверка программ
проводится в табличном процессоре MS Excel.
1.
«Обратная геодезическая задача»
.1
Теоретические сведения
Обратная геодезическая задача заключается в вычислении дирекционного угла
a и расстояния R = | AB
| по заданным на плоскости декартовым координатам x, y двух точек А и В. Дирекционный угол, в
конечном итоге, должен быть представлен в градусной мере, как это принято в
геодезии. Расстояние между точками определяется через найденный дирекционный
угол.
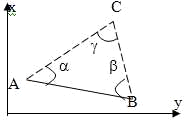
Рис. 1.1
Пусть
даны две точки А и В (рис.1.1), координаты которых соответственно
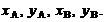
Согласно
схеме, показанной на рис. 1.1., приращения координат определяются:
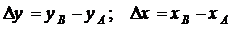 (1.1)
(1.1)
Затем
находят величину румба.
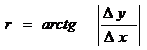 (1.2)
(1.2)
Далее
по знакам приращения координат находят название четверти, что, в свою очередь,
позволяет определить значение дирекционного угла (см. табл. 1.1).
Табл.
1.1
|
Знаки приращения координат
|
Название четверти
|
Формула дирекционного угла
|
|
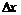 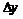
|
|
|
|
|
+
|
+
|
I
|
a
= r
|
|
-
|
+
|
II
|
a
= pr
|
|
-
|
-
|
III
|
a
= p + r
|
|
+
|
-
|
IV
|
a
= 2p - r
|
Горизонтальное расстояние между точками может быть определено по формуле:
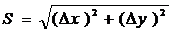 (1.3)
(1.3)
или
по формуле:
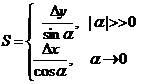 (1.4)
(1.4)
Перевод
вычисленного дирекционного угла в градусную меру может быть выполнен различными
способами. Один из возможных способов следующий:
Переводим
величину a в градусную меру
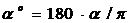 ;
;
Выделяем
целую часть 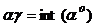 ;
;
Вычисляем
остаток и переводим его в минуты
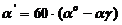 ;
;
Вычисляем
целое число минут
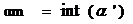 ;
;
Определяем
остаток минут, переводим в секунды и округляем до целого
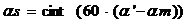 .
.
Значение
дирекционного угла в градусах, минутах и секундах дают, соответственно,
значения переменных ag, am, as.
.2
Постановка задачи
Даны координаты 2-х точек A(х,y) и B(x,y). Определить дирекционный угол
прямой AB
.3
Исходные данные
А) X1=5119.94 Y1=6157.33
X2=7182.27
Y2=4976.39
В) Х1=10932.84 Y1=6112.26
X2=9115.24
Y2=4903.68
1.4 Блок
схема для Turbo Pascal
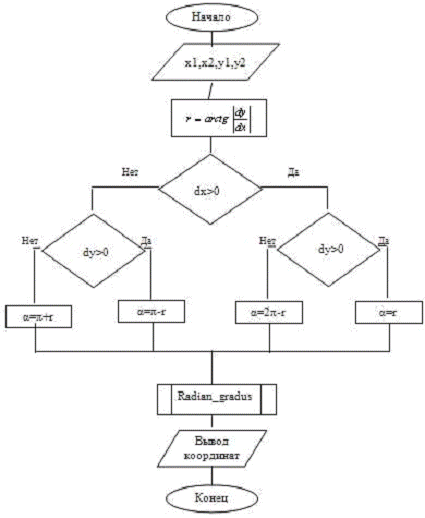
Рис. 1.2
var,x2,y1,y2,dir0,l,d,m,s,temp,r:real;RadToDeg(var
d,m,s,temp:real);:=(temp*180)/pi;:=int(temp);:=int((temp-d)*60);:=round((((temp-d)*60)-m)*60);;('Vvedite
koordinaty to4ek');('x1=');(x1);('y1=');(y1);('x2=');(x2);('y2=');(y2);:=arctan(abs((y2-y1)/(x2-x1)));((y2-y1)>0)and((x2-x1)>0)
then dir0:=r;((y2-y1)>0)and((x2-x1)<0) then
dir0:=pi-r;((y2-y1)<0)and((x2-x1)<0) then
dir0:=pi+r;((y2-y1)<0)and((x2-x1)>0) then dir0:=2*pi-r;(d,m,s,dir0);(d:3:0,m:3:0,'`',s:3:0,'"');:=sqrt(sqr(x2-x1)+sqr(y2-y1));('S=
',l:0:2);;.
1.6
Результат программы
A:
Vvedite koordinaty to4ek=5119.94=6157.33=7182.27=4976.39
12` 13"= 2376.52:koordinaty
to4ek=10932.84=6112.26=9115.24=4903.68
37` 16"= 2182.74
1.7
Вычисления MS Excel
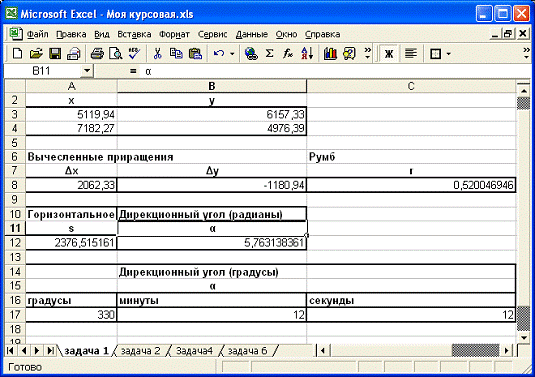
Рис. 1.3.a Excel - вычисления
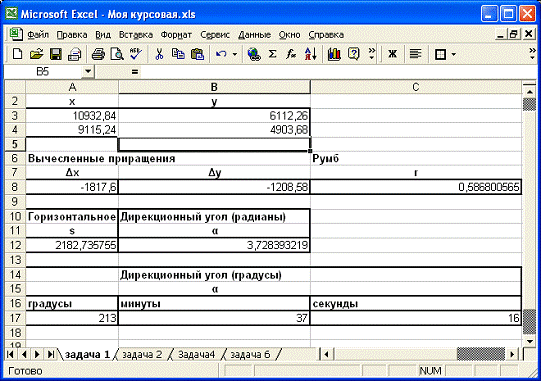
Рис. 1.3.б Excel - вычисления
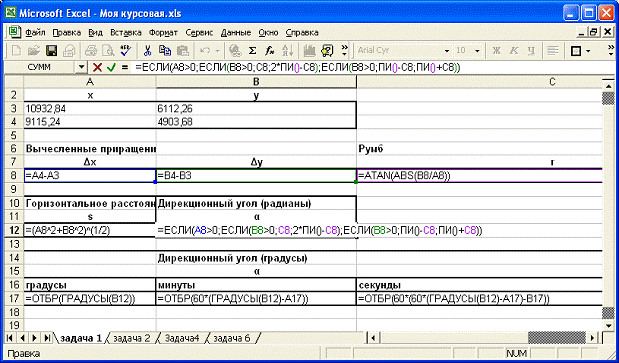
Рис. 1.4 Excel
с открытыми формулами
1.8 Анализ
Обратная геодезическая задача была решена с помощью языка
программирования Turbo Pascal и с помощью табличного процессора Excel. Ответы сошлись.
2. «Прямая
угловая засечка»
.1
Теоретические сведения
Прямая
угловая (геодезическая) засечка - такое название носит способ определения
координат точки местности Р, если на плоскости дана система точек
геодезической сети 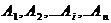 с известными координатами
с известными координатами 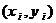 и на этих точках измерены горизонтальные углы
и на этих точках измерены горизонтальные углы 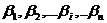 (рис.2.1.). Величины углов
(рис.2.1.). Величины углов 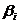 в геодезии принято задавать в градусной мере.
в геодезии принято задавать в градусной мере.
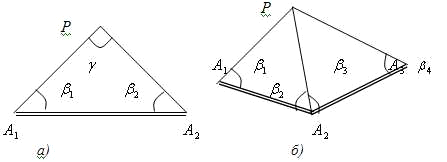
Рис.
2.1. Схемы прямой геодезической засечки.
Большое
значение имеет величина угла при вершине треугольника - угла засечки g, от которого во многом зависит точность определения
координат. В инструкциях по проведению геодезической съемки указывается, что
угол засечки не должен быть меньше 30о и больше 150о.
Для
определения координат точки Р можно использовать формулы Юнга или
формулы Гаусса. Чаще используются формулы Юнга, которые еще называют формулами
котангенсов внутренних углов треугольника.
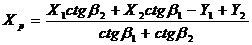 (2.1)
(2.1)
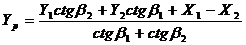 (2.2)
(2.2)
Широко
используются и формулы Гаусса. В этом случае исходными данными являются не
только координаты пунктов А1 и А2 и
измеренные горизонтальные углы b1, b2, но и вычисленный дирекционный угол a
стороны А1 А2.
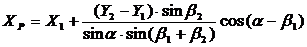 (2.3)
(2.3)
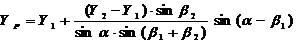 (2.4)
(2.4)
Если
пунктов геодезической сети более двух (рис.2.1 б), то исходные данные
являются избыточными, т.к. для определения искомых координат точки Р
достаточно знать координаты и углы двух точек одного треугольника. Однако
решение прямой засечки только из одного треугольника является бесконтрольным.
Достаточно, например, выписать из каталога координату исходной точки с ошибкой,
как результат окажется совершенно неверным. По этой причине инструкции по
выполнению геодезических работ требуют, чтобы координаты точки Р
определялись как минимум из двух треугольников (или был организован какой-либо
другой контроль)
Избыточность исходных данных позволяет повысить надежность определения
окончательных значений искомых величин за счет применения правила
арифметического среднего.
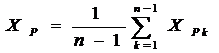 (2.5)
(2.5)
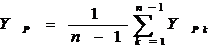 , (2.6)
, (2.6)
где
XP k,
YP k
координаты, определенные из k-того треугольника.
2.2
Постановка задачи
Определить координаты точки P по трем точкам с известными координатами и 4 углам. (2 треугольникам)
.3
Исходные данные
Вариант 9
|
№ п/п
|
X, м
|
Y, м
|
B1, DDD MM SS
|
B2, DDD MM SS
|
|
1
|
5935.51
|
5441.24
|
98 4 30
|
|
|
2
|
5687.41
|
5172.76
|
63 0 12
|
41 54 46
|
|
3
|
5142.93
|
5460.08
|
|
54 19 48
|
2.4 Блок
схема для Turbo Pascal

Рис. 2.2.
2.5 Текст
программы
Program Zadacha2;
Var x,y,x1,x2,x3,y1,y2,y3,b11g,b11m,b11s,b12g,b12m,b12s,
b21g,b21m,
b21s,b22g,m,b22s,b1,b2,b3,b4,xp1,xp2,yp1,yp2,rad:real;Gradus_radian(var
g,m,s,rad:real);:=(g+(m/60)+(s/3600))*Pi/180;;x_y(var
x1,x2,y1,y2,b1,b2,x,y:real);:=(x1*cos(b2)/sin(b2)+x2*cos(b1)/sin(b1)-y1+y2)/(cos(b1)/sin(b1)+cos(b2)/(b2));:=(y1*cos(b2)/sin(b2)+y2*cos(b1)/sin(b1)-x2+x1)/(cos(b1)/sin(b1)+cos(b2)/(b2));;
Begin('**Koordinati tochek**');
Writeln('Vvedite x1,y1');(x1,y1);('Vvedite
x2,y2');(x2,y2);('Vvedite x3,y3');(x3,y3);
Writeln('**Izmerennie ugli pervogo treugolnika**');('Pervij
ugol');('G');(b11g);('M');
Readln(b11m);('S');(b11s);('Vtoroj
ugol');('G');(b12g);('M');(b12m);('S');(b12s);
Writeln('**Izmerennie ugli vtorogo treugolnika**');
Writeln('Pervij
ugol');('G');(b21g);('M');(b21m);('S');(b21s);('Vtoroj
ugol');('G');(b22g);('M');(b22m);('S');(b22s);_radian(b11g,b11m,b11s,b1);_radian(b12g,b12m,b12s,b2);_y(x1,x2,y1,y2,b1,b2,xp1,yp1);_radian(b21g,b21m,b21s,b3);_radian(b22g,b22m,b22s,b4);_y(x2,x3,y2,y3,b3,b4,xp2,yp2);
Writeln('**Koordinati tochki P**');
x:=(xp1+xp2)/2;:=(yp1+yp2)/2;('x=',x:4:3);('y=',y:4:3);.
2.6
Результат программы
**Koordinati tochek**x1,y1
.51
.24x2,y2
.41
.76x3,y3
5142.93
.08
**Izmerennie ugli pervogo treugolnika**ugol
ugol
**Izmerennie ugli vtorogo treugolnika**ugol
G
**Koordinati tochki P**
x=5406.999=5932.281
2.7
Вычисления MS Excel
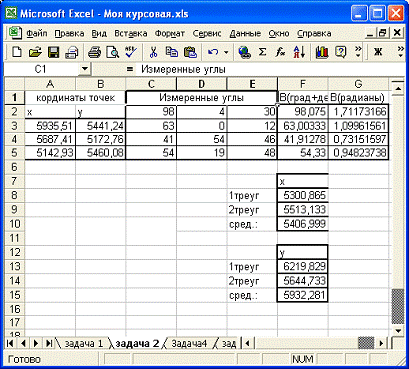
Рис. 2.3. Excel - вычисления
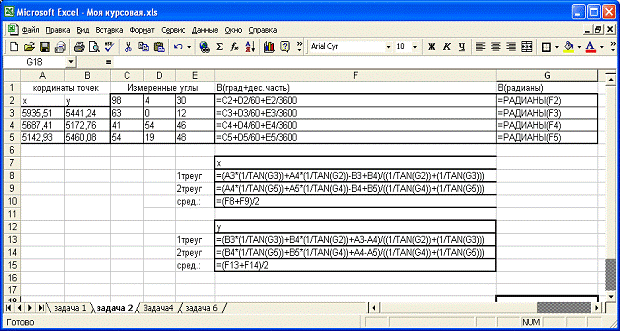
Рис. 2.4. Excel с открытыми
формулами
2.8 Анализ
Задача №2 (прямая угловая засечка) была решена с помощью языка
программирования Turbo Pascal и с помощью табличного процессора Excel. Ответы 2-х разных решений сошлись.
3.
«Теодолитный ход»
.1
Теоретические сведения
Теодолитная съемка относится к числу крупномасштабных и выполняется с
целью составления горизонтального плана равнинной местности, когда рельеф на
плане не отображается, или для составления кадастрового плана. Применяется при
картировании сравнительно небольших застроенных участков. Съемку выполняют с
точек геодезической сети, расположенных на участке, и точек съемочного
обоснования, координаты которых определяют путем проложения теодолитных ходов.
Теодолитный ход -
это полигон, представляющий собой систему ломаных линий, в котором
горизонтальные расстояния между всеми его смежными вершинами измеряются
стальными мерными лентами и рулетками, либо оптическими дальномерами, а
горизонтальные углы между смежными сторонами - техническими теодолитами
В зависимости от конструкции полигона, различают разомкнутый теодолитный
ход, начало и конец которого опираются на пункты геодезического обоснования (рис.3.1
а), замкнутый теодолитный ход (замкнутый многоугольник), примыкающий к
пункту геодезического обоснования (рис.3.1 б) и висячий (рис.3.1 в).



а)
б) в)
Рис.3.1. Схемы теодолитных ходов.
На рис. 3.1 точки опорной геодезической сети показаны квадратиками, а
точки, координаты которых требуется определить - черными кружочками. Отрезок
между опорными точками называется исходной (примычной) стороной, а угол между
ней и стороной теодолитного хода - примычным углом. На рисунке исходные стороны
показаны двойными линиями.
При создании съемочного обоснования теодолитной съемки, как правило,
используются разомкнутые ходы, начинающиеся и заканчивающиеся на разных опорных
точках. Замкнутые и, особенно, висячие ходы считаются ненадежными, так как
остаются незамеченными ошибки исходных данных и не контролируются
систематические ошибки линейных измерений.
Разомкнутый
теодолитный ход.
Создание съемочного обоснования заключается в закреплении на местности
новых точек и определении их координат. Если эти координаты определяются путем
проложения теодолитного хода, то работы состоят из нескольких последовательных
этапов. В данной курсовой работе будем рассматривать только последний этап -
вычисление координат искомых точек.
На
рис. 3.2 схематично представлен разомкнутый теодолитный ход. Заданы координаты
опорных точек баз AB и CD, длины сторон теодолитного хода 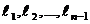 и углы при вершинах
и углы при вершинах 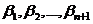 . Особо
подчеркнем, что все углы должны быть правыми.
. Особо
подчеркнем, что все углы должны быть правыми.

Рис.3.2 Схема разомкнутого теодолитного хода.
Когда определяются прямоугольные координаты некоторой точки по известным
координатам другой, горизонтальному расстоянию и дирекционному углу, задачу
называют прямой. В нашем случае, для решения прямой задачи необходимо вначале
вычислить дирекционные углы a1 ... an. Порядок вычисления дирекционного
угла был описан выше.
Из курса геодезии известно (и как следует из рис. 3.2), что
разность примычных углов должна быть равна разности дирекционных углов
примычных сторон. Однако, в силу ошибок измерения, это равенство практически
никогда не выполняется.
Разность между теоретическими положениями и результатами измерений
называется невязкой. В случае, когда она меньше допуска, в измеренные
величины вводят поправки таким образом, чтобы свести невязку к нулю. Сумма
поправок равна невязке по абсолютной величине и противоположна по знаку.
Формула для вычисления угловой невязки для левых по ходу углов
записывается следующим образом:
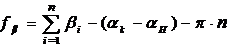 , (3.1)
, (3.1)
где
aн -
дирекционный угол базы AB, ak - дирекционный угол базы CD. Углы при
вершинах теодолитного хода представлены в радианах.
Для
правых по ходу углов дирекционные углы в формуле меняются местами.
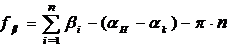 (3.2)
(3.2)
Угловую
невязку сравнивают с допустимой f доп,
определяют по формуле:
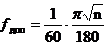 [рад.]
(3.3)
[рад.]
(3.3)
Если
угловая невязка в пределах допуска, то ее распределяют поровну во все
измеренные углы. По исправленным углам вычисляют дирекционные углы сторон
теодолитного хода. Для этого можно воспользоваться следующим соотношением:
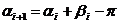 (3.4)
(3.4)
где
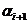 - дирекционный угол последующей стороны хода,
- дирекционный угол последующей стороны хода, 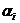 - дирекционный угол предыдущей стороны,
- дирекционный угол предыдущей стороны, 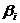 - левый по ходу угол между этими сторонами. Если углы
по ходу правые, то угол
- левый по ходу угол между этими сторонами. Если углы
по ходу правые, то угол 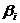 вычитается.
вычитается.
Далее
вычисляются приращения координат:
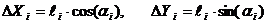 (3.5)
(3.5)
Приращения
координат суммируются и вычисляются абсолютные линейные невязки по
соответствующим осям f x и f y.
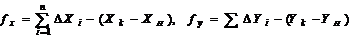 (3.6)
(3.6)
XH,YH и Xk, Yk - координаты начальной и конечной точек хода.
Общая
абсолютная невязка и общая относительная невязка теодолитного хода,
соответственно:
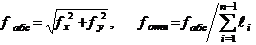 (3.7)
(3.7)
Величина
допустимой относительной невязки определяется в соответствии с инструкцией по
топографической съемке [5]. Если допуски выполняются, абсолютные невязки по
осям распределяют пропорционально длинам сторон теодолитного хода и далее
определяют искомые координаты новых точек по следующим формулам:
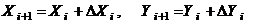 (3.8)
(3.8)
Подтверждением
правильности вычисления является совпадение координат вычисленного значения
опорной точки в конце теодолитного хода и заданного в исходных данных.
3.2
Постановка задачи
Теодолитный ход. По заданным координатам 4х точек опорной геодезической
сети, длинам сторон теодолитного хода и измеренным углам, определить координаты
точек теодолитного хода.
.3
Исходные данные
Вариант 9
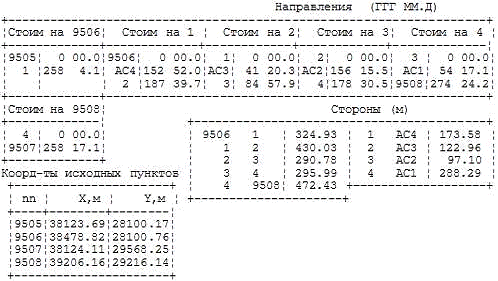
3.4
Алгоритм для Turbo Pascal
геодезический уравнение засечка теодолитный
1) Ввод координат известных точек (х1, х2, х3, х4, у1, у2, у3, у4.),
длин сторон и измеренных горизонтальных углов(вручную или из файла)
2) Вычисление дирекционных углов (процедура CoordToDirCorner)
) Перевод измеренных горизонтальных углов в радианы(Grad_to_rad)
) Вычисление углов хода и невязки хода
) Вычисление дирекционных углов
) Вычисление приращения координат
) Вычисление абсолютной линейной невязки и ее распределение
) Вывод х и у точек теодолитного хода
.5 Текст
программы
program teodxod;
var
sumx,sumy,fabs,fotn,sl,sx,sy,fx,fy,x1,x2,x3,x4,y1,y2,y3,y4,s1,s2,s3,s4,s5,AB,CD,dd,mm,ss,rad,fb :real;
i,j:integer;:string;:array[1..6,1..3] of real;:array[1..7]of
real;:array[0..5,1..2] of real;:array[1..5]of real;:text;
{Процедура перевода градусов в радианы}
procedure v_rad (var a,b,rad:real);:=(a+(b/60))*Pi/180;
end;
{Процедура вычисления дирекционных углов твердых сторон по их
координатам}
procedure dir_ugol(var
x1,x2,y1,y2,r:real);:=arctan((y2-y1)/(x2-x1));((y2-y1)>0)and((x2-x1)>0)
then r:=r;((y2-y1)>0)and((x2-x1)<0) then
r:=pi-r;((y2-y1)<0)and((x2-x1)<0) then
r:=pi+r;((y2-y1)<0)and((x2-x1)>0) then r:=2*pi-r;
end;
{Вводим данные с клавиатуры}
Writeln(‘Koordinaty tochek’);
Writeln('
koordinaty tochek 9505 "xxxxx.xx yyyyy.yy"');
Readln(x1,y1);
Writeln('
koordinaty tochek 9506 "xxxxx.xx yyyyy.yy"');
Writeln('
koordinaty tochek 9507 "xxxxx.xx yyyyy.yy"');
Readln(x3,y3);
Writeln('
koordinaty tochek 9508 "xxxxx.xx yyyyy.yy"');
Readln(x4,y4);('Vvedite dliny izvestnyh storon');('9506 -
1');(s[1]);('1 - 2');(s[2]);('2 - 3');(s[3]);('3 - 4');(s[4]);('4 -
9508');(s[5]);(‘Vvedite ugly');('Stoim na tochke 9506');
writeln(' na 9505 =');(dd,mm);_rad (dd,mm,rad);
dir[1,1]:=rad;(' na 1=');(dd,mm);
v_rad (dd,mm,rad);[1,2]:=rad;
Writeln(' Stoim na tochke 1');(' na 9506 =');(dd,mm);_rad
(dd,mm,rad);
dir[2,1]:=rad;('to 2=');(dd,mm);_rad
(dd,mm,rad);[2,2]:=rad;(' Stoim na tochke 2');(' на 1 =');(dd,mm);_rad (dd,mm,rad);[3,1]:=rad; writeln(' на 3=');(dd,mm);_rad (dd,mm,rad);
dir[3,2]:=rad;(Stoim na tochke 3');(' na 2 =');(dd,mm);_rad
(dd,mm,rad);
dir[4,1]:=rad;(' na 4=');(dd,mm);
v_rad (dd,mm,rad);[4,2]:=rad;
Writeln(‘Stoim na tochke 4');(' na 3 =');(dd,mm);_rad
(dd,mm,rad);
dir[5,1]:=rad;(' na 9508=');(dd,mm);
v_rad (dd,mm,rad);[5,2]:=rad;
Writeln(' Stoim na tochke 9508');(' na 4 =');(dd,mm);_rad
(dd,mm,rad);
dir[6,1]:=rad;('na 9507=');(dd,mm);
v_rad (dd,mm,rad);[6,2]:=rad;
{конец ввода данных с клавиатуры}
dir_ugol (x1,x2,y1,y2,AB);
dir_ugol (x3,x4,y3,y4,CD);[1]:=AB;
Corners[7]:=CD;
{вычисление углов и невязки хода}
for i:=1 to 6
do[i,3]:=dir[i,2]-dir[i,1];:=(dir[1,3]+dir[2,3]+dir[3,3]+dir[4,3]+dir[5,3]+dir[6,3])-(corners[7]-corners[1]);fb<((pi*sqrt(6))/(60*180))
then for i:=1 to 6 do dir[i,3]:=dir[i,3]-fb/6;
{Вычисление дирекционных углов сторон теодолитного хода}
for i:=1 to 5
do[i+1]:=corners[i]+dir[i,3]-pi;[0,1]:=x2;[0,2]:=y2;i:=1 to 5 do {Вычисление приращения координат}[i,1]:=s[i]*cos(corners[i+1]);:=sx+points[i,1];[i,2]:=s[i]*sin(corners[i+1]);:=sy+points[i,2];
end;
{Вычисление абсолютной линейной невязки}
fx:=sx-(x3-x2);:=sy-(y3-y2);i:=1 to 5
do:=sl+s[i];:=sqrt(sqr(fx)+sqr(fy));:=fabs/sl;
{распределение невязки пропорционально приращениям по осям}
for i:=1 to 5 do[i,1]:=points[i,1]-(points[i,1]*fx/sx);[i,2]:=points[i,2]-(points[i,2]*fy/sy);;
for i:=1 to 5 do {Вычисление координат искомых точек}
begin[i,1]:=points[i,1]+points[i-1,1];[i,2]:=points[i,2]+points[i-1,2];;(‘Iskomye
velichiny');i:=1 to 5 do(i,'-aya tochka x=',(points[i,1]):0:2,'
y=',(points[i,2]):0:2);;
end.
.6
Результат программы
Koordinaty tochek
koordinaty tochek 9505 "xxxxx.xx yyyyy.yy"
.69 28100.17
koordinaty tochek 9506 "xxxxx.xx yyyyy.yy"
.82 28100.76
koordinaty tochek 9507 "xxxxx.xx yyyyy.yy"
.11 29568.25
koordinaty tochek 9508 "xxxxx.xx yyyyy.yy"
392056.16 29216.14dliny izvestnyh storon
- 1
.93
- 2
.03
- 3
.78
- 4
.99
- 9508
.43ugly
Stoim na tochke 95069505 =
1=
.1na tochke 19506 =
2=
.7na tochke 21 =
3=
.9na tochke 32 =
4=
.5na tochke 43 =
9508=
.2na tochke 95084 =
9507=
.1velichiny
-aya tochka x=38446.33 y=28519.32
-aya tochka x=38431.07 y=29083.81
-aya tochka x=38291.15 y=29022.55
-aya tochka x=38149.37 y=28950.21
-aya tochka x=38124.11 y=29568.25
4.
«Решение СЛАУ методом Гаусса»
.1
Теоретические сведения
Рассмотрим один из наиболее известных и широко применяемых прямых методов
решения систем линейных уравнений. Обычно этот метод называют методом
исключения или методом Гаусса.
Чтобы проиллюстрировать этот метод, рассмотрим сначала систему из трех
уравнений с тремя неизвестными:
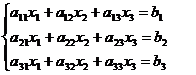 (4.1)
(4.1)
В
такой системе по крайней мере один из коэффициентов 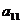 ,
,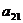 ,
,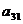 должен быть отличен от нуля, иначе бы мы имели бы дело
в этих трех уравнениях только с двумя неизвестными. Если
должен быть отличен от нуля, иначе бы мы имели бы дело
в этих трех уравнениях только с двумя неизвестными. Если 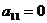 , то можно переставить уравнения так, чтобы
коэффициент при
, то можно переставить уравнения так, чтобы
коэффициент при 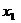 в первом уравнении был отличен от нуля. Очевидно, что
перестановка уравнений оставляет систему неизменной: ее решение остается
прежним.
в первом уравнении был отличен от нуля. Очевидно, что
перестановка уравнений оставляет систему неизменной: ее решение остается
прежним.
Теперь
введем множитель
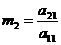 .
.
Умножим
первое уравнение системы (4.1) на 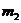 и вычтем
его из второго уравнения системы. («Первое» и «второе» уравнения берем уже
после перестановки, если она была необходима). Результат вычитания равен:
и вычтем
его из второго уравнения системы. («Первое» и «второе» уравнения берем уже
после перестановки, если она была необходима). Результат вычитания равен:
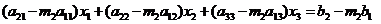
Так
как
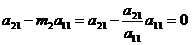 ,
,
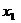 фактически
исключается из второго уравнения (именно для достижения такого результата и
было выбрано значение
фактически
исключается из второго уравнения (именно для достижения такого результата и
было выбрано значение 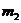 ).
).
Определим
теперь новые коэффициенты
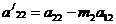
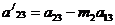
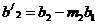 .
.
Тогда
второе уравнение системы приобретает вид
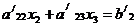 (4.2)
(4.2)
Заменим
второе из первоначальных уравнений уравнением (4.2) и введем множитель для
третьего уравнения
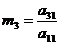 .
.
Умножим
первое уравнение на этот множитель и вычтем его из третьего. Коэффициент при 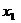 снова становится нулевым, и третье уравнение
приобретает вид
снова становится нулевым, и третье уравнение
приобретает вид
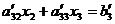 (4.3)
(4.3)
где
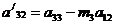
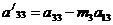
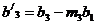 .
.
Если
теперь в исходной системе уравнений (4.1) заменить третье уравнение на (4.3),
то новая система выглядит так:
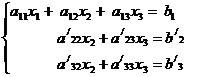 (4.4)
(4.4)
Эти
новые уравнения полностью эквивалентны исходным уравнениям с тем преимуществом,
что 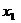 входит только в первое уравнение и не входит ни во
второе, ни в третье. Таким образом, два последних уравнения представляют собой
систему из двух уравнений с двумя неизвестными; если теперь найти решение этой
системы, т.е. определить
входит только в первое уравнение и не входит ни во
второе, ни в третье. Таким образом, два последних уравнения представляют собой
систему из двух уравнений с двумя неизвестными; если теперь найти решение этой
системы, т.е. определить 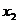 и
и 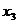 , то
результат можно подставить в первое уравнение и найти
, то
результат можно подставить в первое уравнение и найти 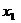 . Иначе говоря, задача сведена к решению системы из
двух уравнений с двумя неизвестными.
. Иначе говоря, задача сведена к решению системы из
двух уравнений с двумя неизвестными.
Попытаемся
теперь исключить 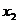 из двух последних уравнений. Если
из двух последних уравнений. Если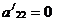 , то снова мы переставим уравнения так, чтобы
, то снова мы переставим уравнения так, чтобы 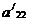 было отлично от нуля (если
было отлично от нуля (если 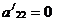 и
и 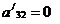 , то
система вырождена и либо вовсе не имеет решения, либо имеет бесчисленное
множество решений).
, то
система вырождена и либо вовсе не имеет решения, либо имеет бесчисленное
множество решений).
Введем
новый множитель
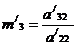 .
.
Умножим
второе уравнение полученной системы (4.4) на 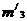 и вычтем
его из третьего. Результат вычитания равен
и вычтем
его из третьего. Результат вычитания равен
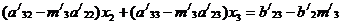
В
силу выбора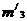
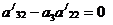 .
.
Полагая,
что
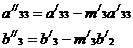
окончательно
получим
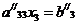 (4.5)
(4.5)
Третье
уравнение полученной системы (4.4) можно заменить уравнением (4.5), после чего
система уравнений приобретает следующий вид:
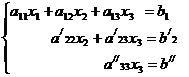 (4.6)
(4.6)
Такая
система уравнений (4.6) иногда называется треугольной из-за своего
внешнего вида.
Для
решения необходимо определить 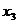 из
третьего уравнения системы (4.6), подставить этот результат во второе уравнение
и определить
из
третьего уравнения системы (4.6), подставить этот результат во второе уравнение
и определить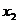 . Полученные значения
. Полученные значения 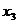 и
и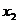 подставить в первое уравнение и определить
подставить в первое уравнение и определить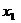 . Этот процесс, который обычно называется обратной
подстановкой (обратный ход), определяется формулами:
. Этот процесс, который обычно называется обратной
подстановкой (обратный ход), определяется формулами:
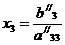
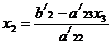 (4.7)
(4.7)
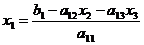 .
.
Необходимо
отметить, если 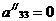 , то система уравнений вырождена.
, то система уравнений вырождена.
Пример.
Дана
система уравнений:
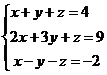
Найти
решение системы уравнений.
Решение.
Легко
убедиться, что множители для второго и третьего уравнений равны 2 и 1. После
исключения 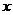 из второго и из третьего уравнений, новый множитель,
исключающий
из второго и из третьего уравнений, новый множитель,
исключающий 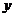 из третьего уравнения, равен -2. Треугольная система
уравнений имеет вид
из третьего уравнения, равен -2. Треугольная система
уравнений имеет вид
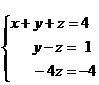
Из
последнего уравнения 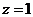 , из второго
, из второго 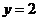 , из
первого
, из
первого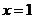 . Можно подставить эти значения в исходные уравнения и
убедиться, что они точно удовлетворяютcя. Теперь можно обобщить этот
метод на случай системы из n - уравнений с n-неизвестными.
Ниже записана система уравнений, приведенная к треугольному виду (4.8).
. Можно подставить эти значения в исходные уравнения и
убедиться, что они точно удовлетворяютcя. Теперь можно обобщить этот
метод на случай системы из n - уравнений с n-неизвестными.
Ниже записана система уравнений, приведенная к треугольному виду (4.8).
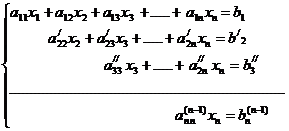 (4.8)
(4.8)
Формулы
для вычисления неизвестных (обратный ход) будут иметь вид:
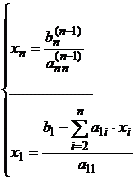 (4.9)
(4.9)
4.2
Постановка задачи
Решение системы линейных алгебраических уравнений методом Гаусса
.3
Исходные данные
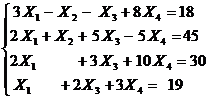
4.4
Блок-схема для Turbo Pascal

Рис.4.1
4.5 Текст программы
gauss;
uses crt;=4;:array[1..n,1..n+1] of
real=((4,-7,-5,-5,47),(14,-24,-6,-5,129),(0,1,4,2,-10), (2,-3,1,0,14));,i,j:integer;:real;:array[1..n]
of real;;('vvedite koefficienty uravnenii');i:=1 to n doj:=1 to n+1 do('
',a[i,j]:5:2);;;k:=1 to n doj:=k+1 to n+1 do[k,j]:=a[k,j]/a[k,k];i:=1 to n
doi<>k thenj:=k+1 to n+1 do
a[i,j]:=a[i,j]-a[i,k]*a[k,j];
end;;('rezultat');
for i:=1 to n do('x',i,'=',a[i,n+1]:8:3);;.
4.6
Результат программы
vvedite koefficienty uravnenii
1.00 -2.00 2.00 0.00 13.00
.00 2.00 5.00 5.00 29.00
.00 2.00 1.00 3.00 17.00= 3.000= -0.500= 4.500= 1.500
.7
Табличные вычисления MS Excel
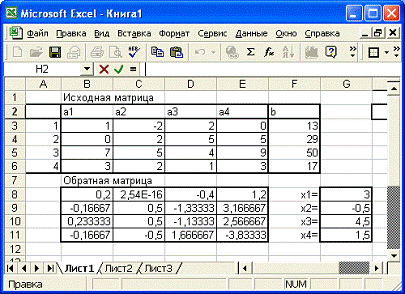
Рис. 4.2 Excel - вычисления
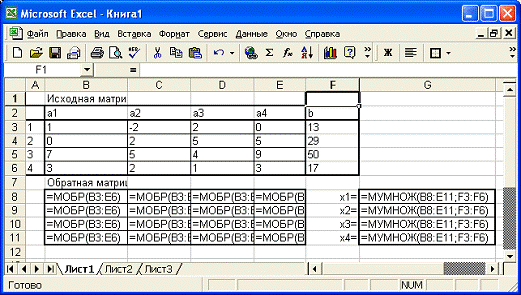
Рис. 4.3. Excel - с
открытыми формулами
4.8 Анализ
Задача №6 (решение СЛАУ методом Гаусса) решена с помощью языка
программирования Turbo Pascal, причем составленная программа
позволяет решать СЛАУ с любым количеством неизвестных (здесь до 30).
Заключение
В данной курсовой работе я решил с помощью языка программирования Turbo Pascal несколько задач, входящих в камеральные работы
маркшейдера. Попутно проверял правильность написания программ в табличном
процессоре Excel. В написании программ мне помогли
знания, полученные из курса информатики и геодезии.
Библиографический
список
1.
Информатика: Программа и методические указания по выполнению курсовой работы
для студентов специальности "Маркшейдерское дело" дневной формы
обучения / Санкт-Петербургский горный ин-т. Сост.: А.П. Кондрашов, Т.Р.
Косовцева, В.В. Петров, - СПб, 2004. 51 с.