Синтез устройства управления узлом ЭВМ в программе Electronics Workbench (EWB)

Синтез устройства управления узлом ЭВМ в программе Electronics Workbench (EWB)

Содержание

Введение

. Разработка структуры устройства управления узлом ЭВМ

.1 Теоретическое вступление

.2 Этап абстрактного синтеза

.3 Минимизация внутренних состояний

.4 Структурный синтез дискретного автомата

.5 Определение функций возбуждеиия

.6 Определение выходных функций

.7 Мультиплексор

. Синтез устройства управления узлом ЭВМ в программе Electronics Workbench (EWB)

.1 Первый этап. Синтез входного алфавита на базе мультиплексора

.2 Второй этап. Синтез состояний автомата на базе мультиплексора

.3 Третий этап. Синтез функций возбуждения на базе мультиплексора

.4 Четвёртый этап. Синтез выходного алфавита на базе мультиплексора

.5 Пятый этап. Синтез интерфейса с пользователем с использованием мультиплексоров

.6 Шестой этап. Отладка синтезируемого автомата в EWB

Заключение

Литература

Введение

мультиплексор интерфейс синтезируемый

Современные приборы и устройства сервиса представляют собой сложные технические системы, реализованные на базе средств вычислительной техники. Цифровые устройства и микропроцессоры являются важнейшей составной частью различных объектов бытовой техники: радиоэлектронной аппаратуры, стиральных и посудомоечных машин, холодильников и климатсистем, изделий оргтехники и других устройств.

Такой широкий диапазон применения цифровых устройств определяется их высокими техническими параметрами и технико-экономическими показателями. В частности - зто низкое энергопотребление, высокое быстродействие, высокая надежность и помехозащищенность, возможность реализации алгоритмов управления и обработки сигналов любой сложности, малые габариты,технологичность и низкая стоимость.

В данной курсовой работе произведён синтез устройства управления узлом ЭВМ согласно выданному заданию. Синтез проведём в программном продукте «ElectronicsWorkbench»фирмы «InteractiveImageTecnolgiesLtd.».

1. Разработка структуры устройства управления узлом ЭВМ

.1 Теоретическоевступление

Термин автомат (в переводе с греческого - самодействующий) как правило, используется в двух аспектах. С одной стороны, автомат - устройство, выполняющее некоторые функции без непосредственного участия человека. В этом смысле мы говорим, что ЭВМ - автомат, так как после загрузки программы и исходных данных ЭВМ решает заданную задачу без участия человека. С другой стороны, термин «автомат» как математическое понятие обозначает математическую модель реальных технических автоматов [3].

Цифровые устройства с точки зрения теории дискретных устройств представляется дискретными автоматами. Рассмотрим основные понятия, относящиеся к дискретным автоматам - математическим моделям цифровых устройств.

Автоматом конечным (дискретным) называется математическая модель устройства, обладающего конечным числом устойчивых состояний и осуществляющего преобразование дискретной информации

Так как дискретная информация может быть представлена в той иди иной системе счисления (представлена цифрами), то часто дискретные автоматы называют цифровыми автоматами.

С точки зрения взаимодействия с внешней средой дискретный автомат можно представить в виде "черного яшика", который обменивается информацией с внешней средой через входные и выходные каналы.

Реальные устройства работают но тактам. На каждом из тактов но окончанию переходного npoцeccaустанавливается определенное внутреннее состояние автомата и соответствующие этому состоянию выходные сигналы.

Закон функционирования автомата может быть задан двумя функциями - функцией переходовδ:Q×X→Y,связывающей пару «входной сигнал - состояние» и отображающей множествоQ×X вQ,а также функцией выходов λ:Q×X→Y,связывающей пару «выходная буква - состояние» и огоорожающей миожествоQ×Xв Y, соответственно.

Таким образом, характерной особенностью математического описания конечного автомата является дискретность математических моделей, а такжеконечность областей значений входных, выходных сигналов и состояний.

По способу формирования интервалов дискретности дискретные автоматы делят на двакласса - синхронные автоматы и асинхронные. В синхронных автоматах моменты времени, в которых фиксируются изменения состояний автомата, задаются специальным устройством - генератором синхросигналов, выдающим импульсы через равные промежутки времени (постоянный интервал дискретности). В асинхронных автоматах моменты перехода автомата из одного состояния в другое заранее не определены и зависят от каких-то событий, например, от темпа поступления входных сигналов. В таких автоматах интервал дискретности является переменным.

Общая теория автоматов при сделанных выше допущениях разбивается на две большие части - абстрактнуютеорию автоматов и структурную теорию автоматов. Различие между нимизаключается в том, что в абстрактной теории мы отвлекаемся от структуры, как самого автомата, так и его входных и выходных сигналов. Не интересуясь способом построения автомата, абстрактная теория изучает лишь те переходы, которые претерпевает автомат под воздействием входных сигналов, и те выходные сигналы, которые он при этом выдает. Абстрактная теория автоматовблизка теории алгоритмов, является ее дальнейшей детализацией.

В общем случае математической моделью цифрового устройства является дискретный автомат, заданный совокупностью шести объектов:

)        конечное множество X входных сигналов:

X ={x1(t), x2(t), …, xn(t)}.

)        конечное множество Y выходных сигналов:

={y1(t), y2(t), …, yk(t)}.

)        множество Q состояний автомата:

={q1(t), q2(t), …, qs(t)}.

)        начальное состояние автомата q0, как элемент множества Q:

(t)ϵ Q.

)        функция δ(q,x) (функция перехода автомата из одного состояния в другое);

)        функцияλ (q,x)(функция выходов автомата).

В начальный момент времени t0 автомат находится в начальном состоянии qo. В дискретные моменты времени t на автомат поступают входные сигналы х(t), автомат последовательно меняет внутренние состояния и генерирует соответствующие выходные сигналы y(t).

По объему памяти дискретные автоматы подразделяются на:

)        дискретные автоматы с большим объемом памяти;

)        дискретные автоматы с малым объемом памяти;

)        дискретные автоматы с одним состоянием (комбинационные или функциональные автоматы);

К дискретным автоматам с большим объемом памяти относятся модели различных запоминающих устройств.

К дискретным автоматам (цифровым устройствам) с малым объемом памяти относятся модели триггеров, счетчиков, регистров, распределителей импульсов, управляющих автоматов и др.

Комбинационным автоматом называется дискретный автомат (ДА), имеющий одно внутреннее состояние, определённое типами и характером соединения элементов схемы автомата.

Это частный случай ДА. Для комбинационных автоматов характерна однозначная зависимость между входными и выходными сигналами в каждый момент времени.

К комбинационным автоматом относятся преобразователи кодов, шифраторы, дешифраторы, мультиплексоры, комбинационные сумматоры и др.

В особый класс выделяют бесконечные автоматы, у которых Q, XиYмогут быть бесконечными. Такие автоматы являются моделями вычислительных машин, поведение которых определяется не только внутренней структурой, но и записанной программой.

По характеру функционирования автоматы могуг быть детерминированными и вероятностными. Функции переходов и выходов вероятностных автоматов, а также их структура зависят or случайного выбора.

По формированию выходного сигнала дискретные автоматы подразделяются на автоматы Мили и автоматы Мура.

Дискретный автомат, для которого выходной сигнал зависит от входного сигнала и состояния, то есть λ:Q×X→Y, называется автоматом Мили.

Дискретный автомат, для которого выходной сигнал зависит только от состояния и не зависит от входного сигнала, то есть λ:Q→Y, называется автоматом Мура.

1.2 Этап абстрактного синтеза

Согласно заданию требуется синтезировать асинхронный автомат Мура, начальное описание которого представлено вход-выходной последовательностью:

¾      входная последовательность: x0x1x2x3x2x1x0;

¾      выходная последовательность: y0y1y2y1y2y2y1y3y0.

Соответствие входных и выходных сигналов согласно исходным данных приведено втаблице1.

Таблица 1 - Соответствие входных и выходных сигналов

Определим мошность входного и выходного множеств (количество различных значений):

Автома Мура при поступлении входного сигнала сначала меняет своё состояние, а затем формирует выходной сигнал.

Построим первичную таблицу переходов-выходов автомата Мура (таблица 2), она имеет 4 строки по числу входных сигналов и 10 столбцов. При этом считаем, что каждому такту соответствует новое состояние автомата Si, которому ставитсяв соответствие выходной сигнал уk.

Таблица 2 - Первичная таблица переходов-выходов автомата Мура

Считаем, что автомат Мура перед подачей входной последовательности находится в начальном состоянии Sо, в котором выходной сигнал не формируется. Реальное устройство может переходить в такое состояние при подключении источника питания. Отсутствие сигнала выходного алфавита на выходах устройства, когда автомат находится в начальном состоянии, обозначим символом у*.При подаче входной последовательности автомат последовательно переходит в девять состояний, обозначенных S1…S9. Часть ячеек остается незаполненной. Для обеспечения устойчивой работы доопределяем автомат дополнительными переходами, в которых начальное и конечное состояния переходов совпадают (состояния в скобках).Первичный граф переходов-выходов представлен на рисунке 1.

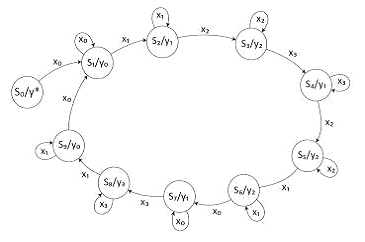
Рисунок 1 - Первичный граф переходов-выходов автомата Мура

1.3 Минимизация внутренних состояний

Задача минимизации автомата сводится к возможно максимальному уменьшению числа внутренних состояний без изменения закона их функционирования.

Решение этой задачи выполним методом Ауфенкампа и Хона, основанного на понятиях эквивалентных состояний.

Эквивалентными состояниями называются состояния Snи Sm, которым, во-первых, соответствуют одинаковые выходные сигналы y(t), а, во-вторых, переход из состояний Snи Sm под воздействием любого символа приводит к одному и тому же (или эквивалентному) состоянию.

Это означает, что автомат, находящийся вэтих состояниях под воздействием любой последовательности формирует одинаковые выходные последовательности.

Алгоритм оптимизации основан на разбиении множества состояний на непересекающиеся подмножества эквивалентных состояний и замена каждого подмножества эквивалентных состояний одним из его представителей.

Алгоритм минимизации:

а)      методом последовательного разбиения выделяем все попарно эквивалентные состояния;

б)      объединяем эквивалентные состояния в одинаковые классы γ1, γ2, …и выделяем в каждом классе по одному состоянию для выполнения последующих этапов, при разбиении на классы пустые клетки во внимание не принимаются;

в)      строим вторичную таблицу переходов-выходов, в которой каждый класс состояний представляем только одним эквивалентным состоянием.

Первое разбиение состояний на классы выполняем по выходным сигналам (таблица 3).

Таблица 3 - Первое разбиение на классы состояний автомата Мура

Анализ таблицы 3 показывает, что в классе γ2состояниеS4 не является эквивалентным состоянию S7 этого класса, так какпри поступлении входного сигнала х3автомат из состояния S7переходит в классγ4, а находясь в состоянии S4 - остаётся в классе γ2. . Поэтому состояние S4вынесем в отдельный классγ5.

Аналогично в классе γ1состояниеS9 не является эквивалентным состоянию S1 этого класса, так как при поступлении входного сигнала х1автомат из состояния S1переходит в классγ2, а находясь в состоянии S9 - остаётся в классе γ1.. Поэтому состояние S9вынесем в отдельный классγ6.

Таким образом, на основании вышеизложенного добавим в таблицу 3 дополнительные классы (таблица 4)

Таблица 4 - Второе разбиение на классы состояний автомата Мура

На основании таблица 4 строим вторичную таблицу переходов-выходов автомата Мура, эквивалентного исходному автомату но содержащей семь состояний вместо десяти (таблица 5).

Таблица 5 - Вторичная таблица переходов-выходов автомата Мура

Теперь определим мошность состояний автомата:

Вторичный граф переходов-выходов автомата Мура представлен на рисунке 2.

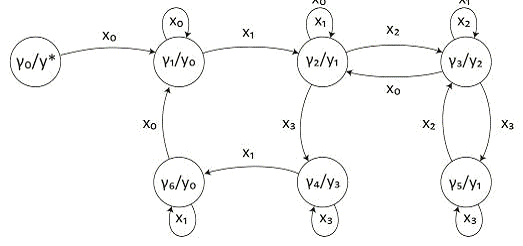
Рисунок 2- Вторичный граф переходов-выходов автомата Мура

1.4 Структурный синтез дискретного автомата

Структурный синтез начинается с кодированиявходного и выходного алфавитов и состояний автомата.

Количество разрядов для входных, выходных сигналов и состояний определяется в соответствие с формулой:

= [log2M]

гдеМ - мощность множества соответствующего алфавита;

[i] - означает минимальное целое, не меньшее числа i.

Используя (1), (2) и (3), определим количество разрядов, необходимых для кодирования входного и выходного алфавитов и состояний автомата

= log24 = 2 (приMx = 4);= log25 = 3 (приMy = 5);= log27 = 3 (при Mq = 7).

Кодирование входного алфавита синтезируемого автомата представлено в таблице 6

Таблица 6 - Кодирование входного алфавита синтезируемого автомата

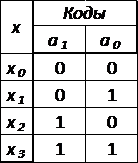
Кодирование выходного алфавита синтезируемого автомата представлено в таблице7

Таблица 7 - Кодирование выходного алфавита

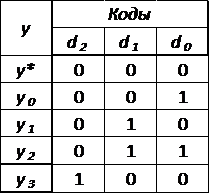
В соответствии с таблицей7 для кодирования синтезируемого автомата требуется три триггера

Выполним кодирование состояний синтезируемого автомата с учётом необходимости обеспечения единичного кодового расстояния между кодами смежных узлов графа, изображённого на рисунке 2 (таблица8). Это нужно для исключения возможных проявлений состязания элементов памяти.

Таблица 8 - Кодирование состояний синтезируемого автомата

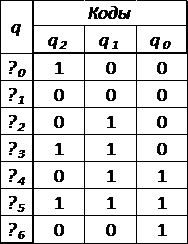
Структурный граф синтезируемого автомата Мура представлен на рисунке 3. Все смежные вершины графа обозначены кодовыми комбинациями с кодовым расстояниемрасстоянием, равным единице.

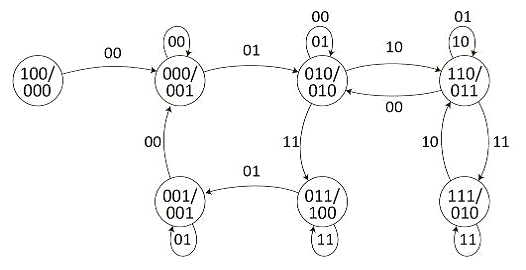
Рисунок 3 - Структурный графавтомата Мура

Таблица 9 - Структурная таблица синтезируемого автомата Мура

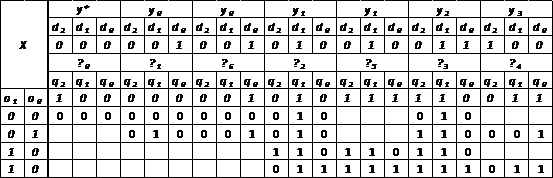
1.5 Определение функций возбуждеиия

Следующим этапом структурного синтеза является определение функций возбуждения элементов памяти и выходных функций автомата.

Согласно заданию, автомат Мура требуется реализовать на RS-триггерах. На рисунке 4 изображено условное графическое обозначение RS-триггера.

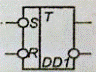
Рисунок 4 - Условное графическое обозначение RS-триггера

Триггеры - элементарные автоматы, содержащие элемент памяти и схемы управления им. При подаче на управляющие входы триггерасоответствующих сигналов он устанавливается, как правило, в одно из двух устойчивых состояний, которое сохраняется в течение заданного времени после окончания действия входных сигналов. Состояние триггера определяется значением выходного сигнала на прямом выходе (Q). Обычно триггер имеет и инверсный выход.

Триггеры RS-типа имеют два входа раздельной установки в нулевое и единичное состояние. Воздействие по входу S (англ. set-установка) переводит триггер в единичное состояние, а воздействие по входу R (англ. Reset - сброс) - в нулевое. Одновременная подача сигналов Rи Sне допускается.

Блок памяти синтезируемого автомата Мура должен содержать три RS-триггера, выходные сигналы которых кодируют состояние автомата - γ0…γ6.

Зависимость состояния RS-триггера от логических сигналов на его входах представлена в таблице 10.

Таблица 10 - Таблица входов RS-триггера

Составим структурную таблицу переходов-выходов автомата Мура (таблица 11).

Таблица 11 - Структурная таблицупереходов-выходов синтезаруемого автомата Мура

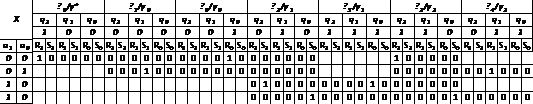
Строки таблицы возбуждения элементов памяти отмечаются кодовыми комбинациями входных сигналов, а столбцы - кодовыми комбинациями состояний триггеров, кодирующих состоянияавтомата в соответствии со структурной таблицей переходов. На пересечениях j-й строкии i-го столбца ставятся входные сигналы триггеров, состояния которых соответствуют переходуδ(qi, xj).

На её основании (На основании таблицы возбуждения) формируем шесть функций возбуждения:R2, S2, R1, S1, R0, S0.

Таблица возбуждения показывает, что функции возбуждения зависят от пяти логических переменных и являются частично определенными. Так как каждая функция возбуждения имеет не более двух единичных состояний, и активным сигналом возбуждения тригге рассчитается сигнал логической единицы, то целесообразно доопределить эти функции нулевыми значениями. В результате получим, что каждая из этих функция является конституентой единицы (минтермом). Поэтому функции возбуждения удобно представить в дизъюнктивной нормальной форме в виде конъюнкций пяти переменных:

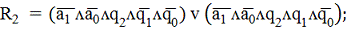
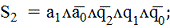
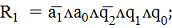
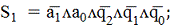
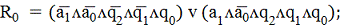
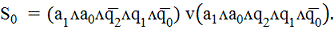
На данном этапе необходимость минимизации функций отсутствует.

Следует отметить, что в начальное состояние автомат обычно переводится при включении питания сигналом одновибратора. В начальное состояние, определённое кодом 100, автомат можно перевести подачей сигнала сброса (reset) на входы S2, R1иR0 триггера (логическое сложение функций с переменной, отображающей сигнал одновибратора).

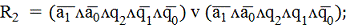
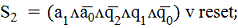
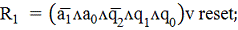
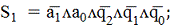
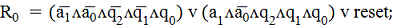
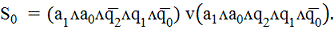
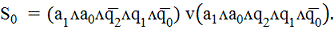
1.6 Определение выходных функций

Выходные функции d2,d1 иd0 автомата Мура, являясь функциями состояний зависят только от трех переменных q2,q1 иq0. Пользуясь структурной таблицей переходов-выходов синтезаруемого автомата (таблица 11), построим таблицу истинности для выходных функций d2,d1 иd0(таблица 12). Выходные функции также являются частично опредёнными, доопределим выходные их нулевыми значениями (значения в скобках).

Таблица 12 - Структурная таблица переходов-выходов синтезаруемого автомата Мура

Выходные функции также как и функции возбуждения являются минтермом (конъюнкця трёх переменных), поэтому их также представим в дизъюнктивной нормальной форме.

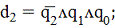
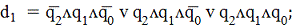
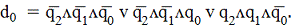
.7 Мультиплексор

Согласно задания необходимо синтезировать автомат на базе мультиплексоров.

Мультиплексором называется функциональный узел, осуществляющий передачу информации с одного из 2n информационных входов (n - число адресных входов) на один выход, т.е. выполняет функцию, обратную демультиплексору.

Графическое изображение мультиплексора с тремя адресными входами и восемью информационными в программе ElectronicsWorkbench (EWB)приведено на рисунке 5, где:

¾      A, B, C - адресные входы;

¾      D0 - D7 - информационные входы;

¾      G’ - инверсный выход;

¾      Y - прямой выход;

¾      W - стробирующий вход.

Рисунок 5 - Графическое изображение мультиплексора в программе ElectronicsWorkbench.

Структурная схема мультиплексора представлена на рисунке 6.

Рассмотрим работу мультиплексора, изображенного на рисунке 6. В зависимости от состояния входов A, B, C выбирается один из элементов «И», т.е. на двух его входах формируется логическая единица. В это время на входах остальных элементов «И» присутствует хотя бы один ноль. Наличие трёх единиц на входах выбранного элемента позволяет передать информацию с информационного входа Diна выход. Помимо адресных и информационных входов каждый элемент «И» имеет стробирующий вход W (при подаче логической единицы на W, на выходе мультиплексора всегда будет логический ноль).

Рисунок 6 - Структурная схема мультиплексора

В таблице 13 представлено соответствие входных и выходных сигналов мультиплексора.

Таблица 13 - Таблица истинности мультиплексора

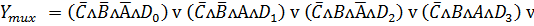
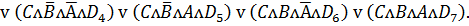(1)

Мультиплексор можно использовать в качестве универсального логического элемента (ЛЭ) для реализации любой функции от числа аргументов, равных числу адресных входов мультиплексора.

Для осуществленя на базе мультиплексора логического сложения необходимо на информационные входы подать аргументы (на A и B при двух аргументах и на A, B, C - при трёх), а на информационные входы логическую единицу (на D₁…D₃ при двух аргументах и на D₁…D₇ - при трёх).

Для осуществленя на базе мультиплексора логического умножения необходимо на информационные входы подать аргументы (на A и B при двух аргументах и на A, B, C - при трёх), а на информационный вход - логическую единицу (на D₃ при двух аргументах и на D₇ - при трёх).

2. Синтез устройства управления узлом ЭВМ в программе Electronics Workbench (EWB)

.1 Первый этап. Синтез входного алфавита на базе мультиплексора

На первом этапе синезируем входные сигналы на базе мультиплексора, используя таблицу 6 и функцию (1) (рисунок 7).

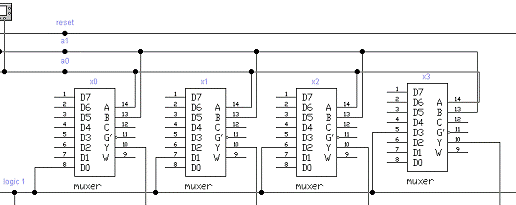
Рисунок 7 - Синез входного алфавита на базе мультиплексора

На адресные входы мультиплексора подаются неинвертированные сигналы с генератора, а на соответствующий (таблицу 6) информационный вход подаётся логическая единица.

2.2 Второй этап. Синтез состояний автомата на базе мультиплексора

На втором этапе синезируем состояния автомата на базе мультиплексора, используя таблицу 8 и функцию (1) (рисунок 9).

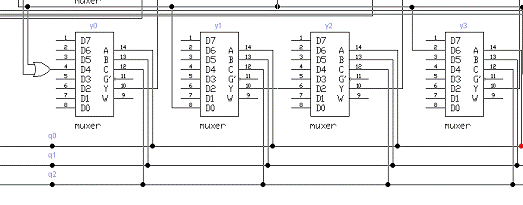
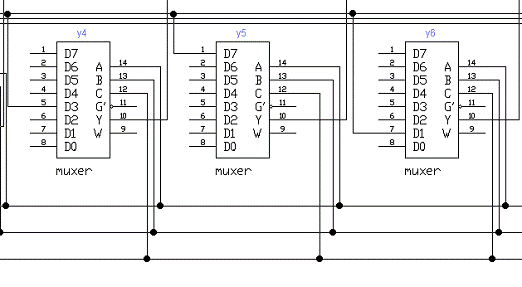
Рисунок 8 - Синез состояний автомата на базе мультиплексора

Для перехода триггеров при включении схемы в состояние γ₀, на информационный вход мультиплексора γ₀ через элемент «ИЛИ» подаётся сигналы логической единицы и reset.

2.3 Третий этап. Синтез функций возбуждения на базе мультиплексора

Запишем функции возбуждения синезируемого автомата через входные сигналы и состояния автомата

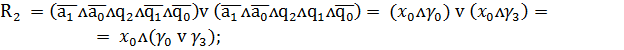
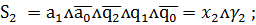
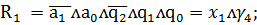
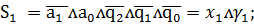
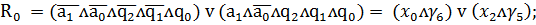
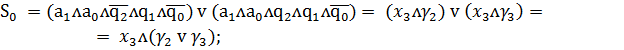
Итак

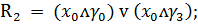
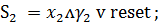
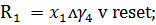
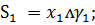
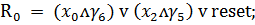
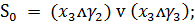
(2)

Теперь необходимо синезировать девять минтермов (конъюнкций):

¾ x₀ᴧγ₀, x₀ᴧγ₃, x₀ᴧγ₆,

¾ x₁ᴧγ₁, x₁ᴧγ₄,

¾ x₂ᴧγ₂, x₂ᴧγ₅,

¾ x₃ᴧγ₂, x₃ᴧγ₃.

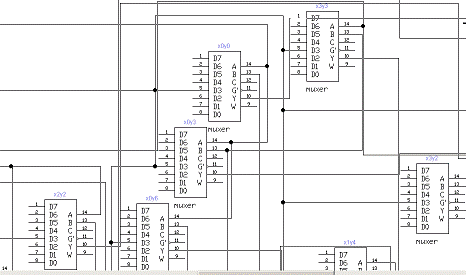
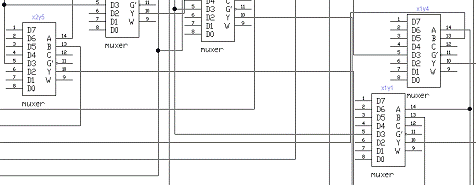
Рисунок 9 - Синез конъюнкций входных сигналов и состояний автомата на базе мультиплексора

Используя таблицу 13 (таблица истинности мультиплексора) и функции (2), синтезируем функции возбуждения автомата (рисунок 10).

Для перехода триггеров при включении схемы в состояние γ₀, на информационный вход мультиплексора (в зависимости от того, на какой из адресных входов был подан сигнал reset) через элемент «ИЛИ» подаётся сигналы логической единицы и reset.

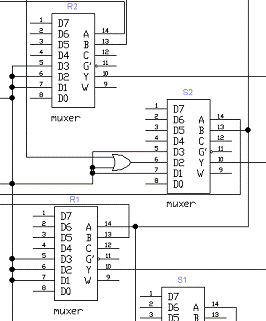
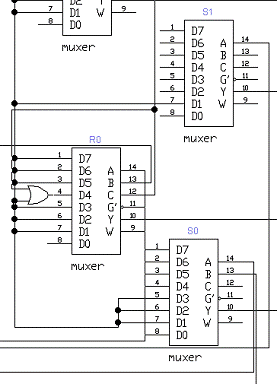
Рисунок 10 - Синез функций возбуждения на базе мультиплексора

С выходов мультиплексоров R₂, S₂, R₁, S₁, R₀, S₀ сигналы подаются триггеры, которые кодируют текущее состояние автомата (рисунок 11).

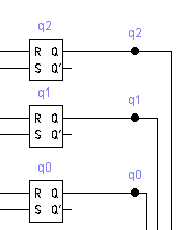
Рисунок 11 - RS-триггеры в синтезаруемом автомате Мура

2.4 Четвёртый этап. Синтез выходного алфавита на базе мультиплексора

На данном этапе синезируем выходные сигналы на базе мультиплексора, используя структурную таблицу переходов-выходов (таблица 12) и функцию (1) (рисунок 11).

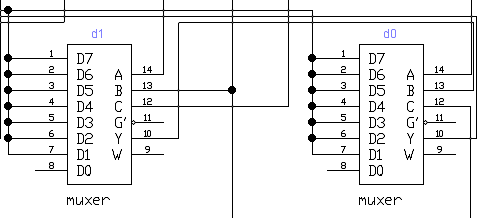
Рисунок 12 - Синез функций возбуждения на базе мультиплексора

Так как функция d₂ принимает единичное значение только при γ₄, то для неё можно подать сигнал напрямую с мультиплексора γ₄.

2.5 Пятый этап. Синтез интерфейса с пользователем с использованием мультиплексоров

Для удобства отладки и проверки работоспособности синтезируемогоавтомата необходимо обеспечить удобный интерфейс с ползователем (насколько это позволяют средства EWB).

Соответствия входных и выходных сигналов и промежуточных состояний синтезаруемого автомата в различные временные интермалы (такты) представлены в таблицае 14.

Таблица 14 - Таблица соответствия входных и выходных сигналов и промежуточных состояний синтезаруемого автомата

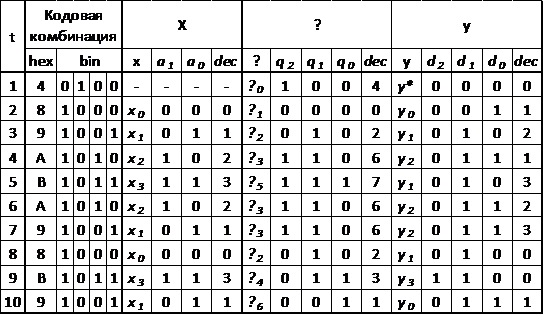
Необходимо отобразить порядковые номера входных и выходных сигналов и промежуточных состояний автомата в десятичной форме. Входные сигналы можно непосредственно подать на табло в EWB, т.к. их представление в двоичной форме соответствует порядковому номеру в десятичной системе счисления. А выходные сигналы и промежуточных состояния необходимо закодировать. Для этого составим таблицы кодирования выходных сигналов (таблица 15) и промежуточных состояний (таблица 16) автомата Мура.

Таблица 15 - Таблица кодирования выходных сигналов автомата

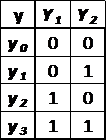
Таблица 16 - Таблица кодирования промежуточных состояний автомата

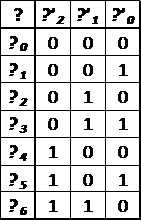
На основании таблицы 16 запишем функции функции γ'₂, γ'₁ и γ'₀.

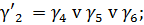
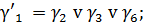
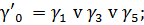
(3)

Используя таблицу 14 и таблицу 15 запишем функции Y₁ и Y₀ через промежуточные состояния автомата.

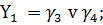
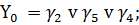
(4)

Синтез функций (3) и (4) в EWB представлен на рисунке 13.

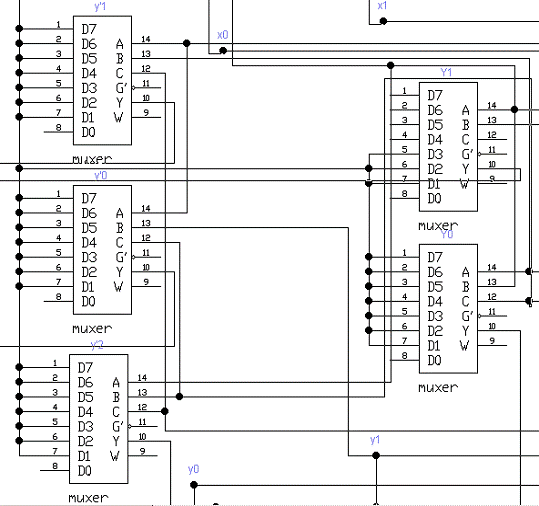
Рисунок 13 - Реализация выходных сигналов и промежуточных состояний синтезаруемого автомата Мура

.6 Шестой этап. Отладка синтезируемого автомата в EWB

Для генерации входных сигналов в EWB воспользуемся «генератором слов» (рисунок 14) и сконфигарируем его согласно таблице 14 (рисунок 15).

Рисунок 14 - Графическое изображение генератора слов в программе Electronics Workbench.

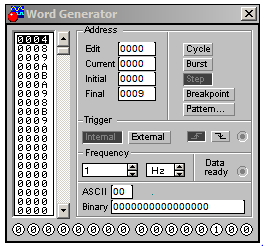
Рисунок 15 - Графическое изображение интерфейса управления генератором слов в программе Electronics Workbench

Проверку работы синтезированного автомата будем проверять посредством отображения входных и выходных сигналов и промежуточных состояний синтезарованного автомата на реализиванном интерфейсе пользователя в EWB (рисунок 16). Где цифровые табло расположены в порядке, соответствующем таблице 14, что облегчает процесс отладки и проверки работоспособности.

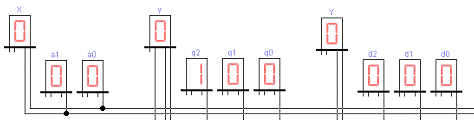
Рисунок 16 - Интерфейс пользователя автомата

При отладке автомата удобно пользоваться таблицей 14.

Согласно рисунку 16 автомат находится в начальном состоянии (сразу после включения) - о чём можно судить по цифре «0» на табло «γ» (посередине в верхнем ряду), отображающем состояние автомата.

Для проверки правильности работы автомата приведё ещё раз таблицу соответствия входных и выходных сигналов (таблица 17).

Таблица 17 - Соответствие входных и выходных сигналов

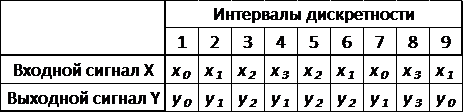
Входные на интерфейсе пользователя автомата отображаются на табло «X» (слева в верхнем ряду), и выходные сигналы - на табло «Y» (справа в верхнем ряду).

Проверим работу автомата в соответствии с заданием (рисунок 17 - рисунок 26).

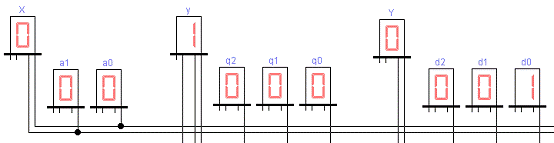
Рисунок 17 - Первый такт работы автомата

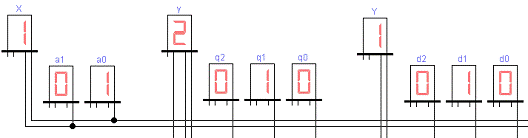
Рисунок 18 - Второй такт работы автомата

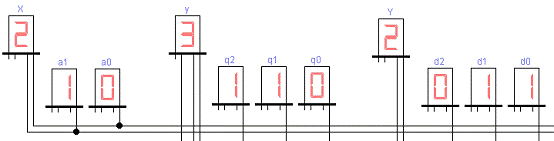
Рисунок 19 - Третий такт работы автомата

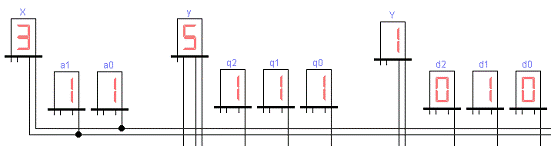
Рисунок 20 - Четвёртый такт работы автомата

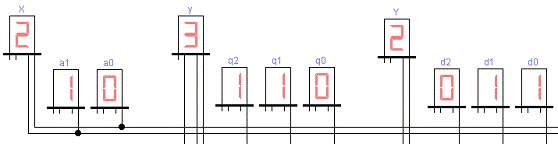
Рисунок 21 - Пятый такт работы автомата

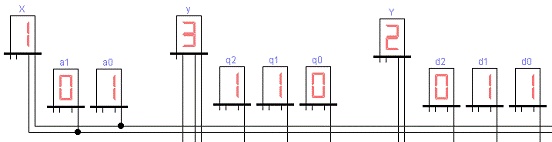
Рисунок 22 - Шестой такт работы автомата

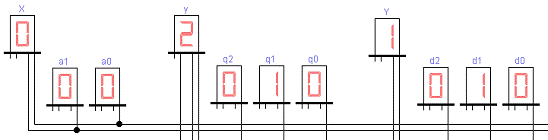
Рисунок 23 - Седьмой такт работы автомата

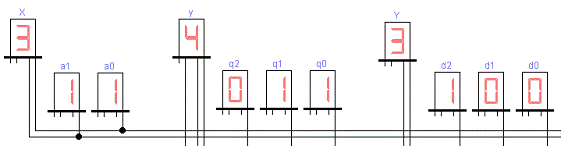
Рисунок 24 - Восьмой такт работы автомата

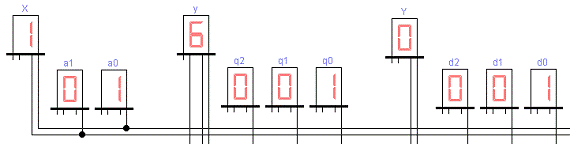
Рисунок 25 - Девятый такт работы автомата

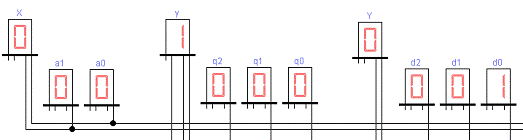
Рисунок 26 - Десятый такт работы автомата

После девятого такта (последний входной сигнал заданной последовательности) (рисунок 25) при поступлении первого входной сигнал заданной последовательности автомат перешёл в состояние γ₁ и сформировал выходной сигнал y₀ (рисунок 26), что означает обеспечение цикличной работы автомата.

Итак, видно, что автомат выполняет требуемые операции и функционирует согласно поставленной задаче.

На рисунке 27 представлена общая схема синтезированного автомата в EWB на базе мультиплексоров.

На рисунке 28 представлена схема того же автомата в EWB на базе мультиплексоров с применением логических элементов «И», «ИЛИ» и «НЕ» в выходном каскаде и при формировании функций возбуждения элементов памяти.

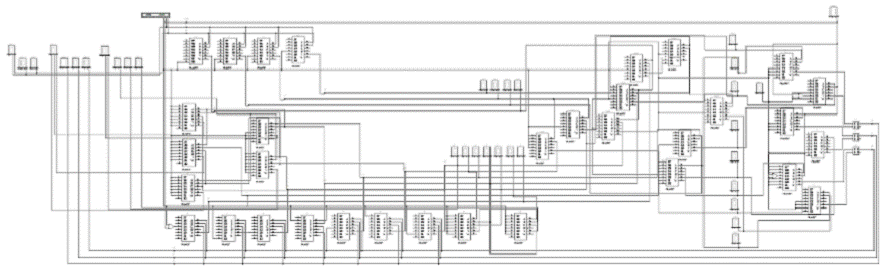
Рисунок 27 - Схема автомата в EWB на базе мультиплексоров

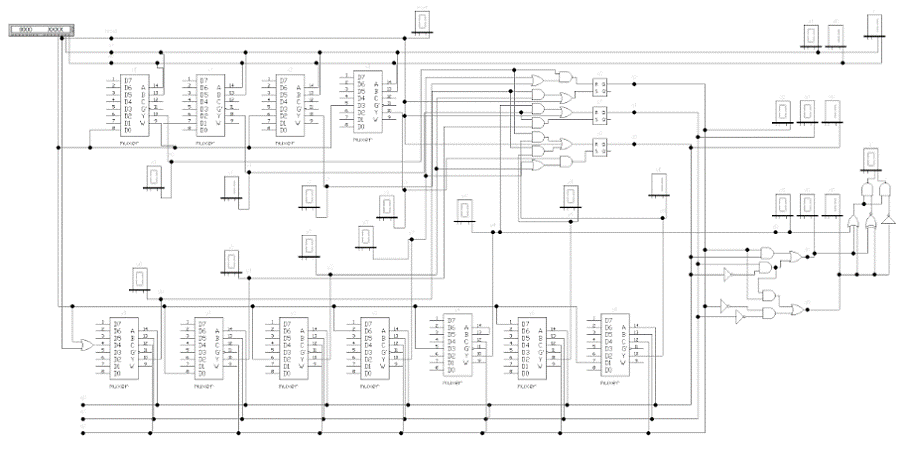
Рисунок 28 - Схема автомата в EWB на базе различных логических элементов

Заключение

В ходе выполнения курсовой работы был разработан и и реализован в программе Electronics Workbench дискретный автомат согласно поставленной задаче. Проверена работоспособность созданного автомата и соответствие режима его работы исходным данным.

Синтезированный дискретный автомат соответствует заданию.

Литература

1       Трофименко В. Н, Трофименко Е. Н. Цифрые устройства и микропроцессоры: Синтез дискретных автоматов: Учебное пособие. Ростов-на-Дону.: РИС ЮРГУЭС. 2005. 46 с.

         Горелик, В. Ю. Схемотехника ЭВМ: Учеб. пособие для вузов ж.-д. транспорта. / Горелик В. Ю., Ермаков А. Е., Ермакова О.П. - М. ГОУ «Учебно-меггодпческий центр по образованию на железнодорожном транспорте», 2007. - 174 с .

         Энциклопедия кибернетики / Под ред. В. М. Глушкова. - Киев: Главная редакция украинской советской энциклопедии, 1974 г.