Развитие речи дошкольников
Содержание
Введение
Глава
I. Теоретические основы изучения моделирования текста задачи как средства
развития математического мышления младших школьников
.1
Мышление как психический процесс
.2
Особенности математического мышления младших школьников
Глава
II. Методология математики
2.1
Основные методы и приемы работы с задачей в начальной школе
.2
Модель текста задачи как основа наглядно-образного мышления младших школьников
Заключение
Список
использованной литературы
математическое мышление задача школа
Введение
Математика сегодня - это одна из жизненно важных
областей знания современного человечества, необходимая для существования
человека в цивилизованном обществе. Широкое использование техники, в том числе
и компьютерной, требует от индивида определенного минимума математических
знаний и представлений. Существуют различные взгляды на объем и качество этого
необходимого для социализации минимума. Проблема создания оптимального курса
математики для общеобразовательной школы более чем актуальна. На сегодняшний
день существует не менее пятнадцати учебников по математике для начальных
классов, и почти все они рекомендованы Министерством образования и науки РФ к
использованию в учебном процессе.
Последнее десятилетие XX в. характеризуется
значимыми изменениями в подходах к определению целей начального математического
образования. Эти изменения были порождены сменой приоритетных целей обучения:
их обусловленностью на современном этапе проблемой воспитания личности ребенка
на основе личностно-ориентированного деятельностного подхода [21]. С этой
позиции целесообразным будет тот курс математики для младших школьников,
который позволял бы средствами данного предмета реализовать идею развивающего
обучения, и в то же время обеспечивал усвоение соответствующих знаний и умений,
готовил и позволял бы уже с первых шагов творчески использовать их при решении
разнообразных задач как практического, так и теоретического характера.
Базовым положением концепции является положение
о том, что начальное звено в системе школьного образования обладает своей
собственной непреходящей ценностью, и поэтому обязано предоставить ребенку
возможность и условия самореализации в тех видах деятельности, которые являются
ведущими в этом возрасте. Одной из неотложных задач педагогики является проблема
качественного усовершенствования математического образования вообще, как в
средней, так и в начальной школе. Судьба математической подготовки прежде всего
зависит от того, как будет поставлено это дело именно в первые четыре года
обучения в школе. Тому имеются серьезные психологические основания. По
действующим ныне программам на изучение математики в начальной школе отводится
около 800 уроков, что составляет почти 40% времени, отводимого на эту
дисциплину за всю среднюю школу.
Обучение решению текстовых задач является
ключевой проблемой в течение всего курса обучения математики, и это
подтверждается результатами Единого Государственного Экзамена по математике.
Менее 50% детей справляются с решением текстовых задач. Тем более важно начать
обучение решению текстовых задач в начальных классах [3].
Актуальность исследования обусловлена
необходимостью определения оптимальных условий эффективного усвоения знаний и
развития мышления школьников. Одним из направлений в решении этой проблемы
является разработка и внедрение в учебный процесс новых методов обучения,
основанных на изучении психологических закономерностей взаимосвязи процессов
усвоения знаний и развития мышления с учетом специфики конкретных учебных
дисциплин. В настоящее время в педагогической психологии достаточно глубоко
изучены общие механизмы мышления в процессе усвоения, такие как анализ, синтез,
обобщение, абстрагирование и другие мыслительные операции [17]. В то же время
существует сравнительно мало исследований, направленных на выявление особенностей
и механизмов мыслительной деятельности учащихся при изучении ими конкретных
учебных дисциплин, что является важным для решения проблемы совершенствования
методов обучения, разработки новых методов, построенных в соответствии с
психологическими закономерностями мышления и его особенностями, определяемыми
спецификой учебного предмета.
Вопросами изучения и развития мышления младших
школьников занимались Выготский Л.С., Леонтьев А.Н., Немов Р.С., Никольская
И.Л. , Рогов Е.И., Рубинштейн С.Л., Эльконин Д.Б., Петрушин В.И.. Назайкинский
Е.В., Михайлова М.А.
Исходя из вышеперечисленных фактов, мы
сформулировали тему нашего исследования: «Моделирование текста задачи как
средство развития математического мышления младших школьников»
Объектом нашего исследования является решение
текстовых задач.
Предмет исследования - моделирование текста
задачи как средство развития математического мышления младших школьников.
Цель исследования - выявить методические
особенности моделирования текста задачи как средства развития математического
мышления младших школьников.
Задачи исследования:
Проанализировать литературу по теме
исследования.
Дать характеристику основным понятиям работы.
Выявить и охарактеризовать методические
особенности моделирования текста задачи как средства развития математического
мышления младших школьников.
Провести исследование.
Разработать методические рекомендации для
педагогов с целью уменьшения трудностей при решении задач младшими школьниками.
Гипотеза исследования - мы предполагаем, что
использование метода моделирования при решении задач оказывает положительное
влияние на развитие математического мышления младших школьников.
В процессе исследования были использованы
следующие методы и приемы: анализ теоретических источников по заявленной теме,
анализ программ и методических пособий, анализ учебников, эксперимент.
Структура работы: введение, две главы,
заключение, список использованной литературы.
Глава I. Теоретические основы изучения
моделирования текста задачи как средства развития математического мышления
младших школьников
1.1 Мышление как психический процесс
Познавательная деятельность начинается с
ощущений и восприятий и затем переходит в мышление. Однако любое, даже наиболее
развитое мышление всегда сохраняет связь с чувственным познанием, то есть с
ощущениями, восприятиями и представлениями. Весь свой «материал» мыслительная
деятельность получает только из одного источника - из чувственного познания.
Через ощущения и восприятия мышление непосредственно связано с внешним миром и
является его отражением. Правильность этого отражения непрерывно проверяется в
ходе практического преобразования природы и общества.
В реальной познавательной деятельности каждого
человека чувственное познание и мышление непрерывно переходят одно в другое и
взаимообуславливают друг друга. [31]
Для мыслительной деятельности человека
существенна взаимосвязь не только с чувственным познанием, но и с языком,
речью. В этом проявляется одно из принципиальных различий между человеческой
психикой и психикой животных. С появлением слова становится возможным отвлечь
от познаваемого объекта то или иное свойство и как бы закрепить, зафиксировать
представление или понятий о нем. Мысль обретает в слове необходимую
материальную оболочку, в которой она только и становится непосредственной
действительностью для других людей и для нас самих. Органическая, неразрывная
связь мышления с языком - основным средством общения между людьми, особенно
отчетливо обнаруживает социальную, общественно-историческую сущность
человеческого мышления. Познание неизбежно предполагает преемственность всех
знаний, приобретаемых в ходе человеческой истории. Эта историческая
преемственность знаний возможна лишь в случае их фиксации, закрепления,
сохранения и передачи от одного человека к другому, от поколения к поколению.
Такая фиксация основных результатов познания осуществляется с помощью языка - в
книгах, журналах, чертежах и т. д.
Умственное развитие человека неизбежно
совершается в процессе усвоения знаний, выработанных человечеством в ходе
общественно-исторического развития. Процесс познания мира индивидом обусловлен,
опосредован историческим развитием умственного познания, результаты которого
каждый индивид осваивает в ходе обучения: это как бы общение человека с
человечеством.
В течение всего периода школьного обучения
ребенка перед ним выступает уже как бы готовая, давно сложившаяся система
знаний, понятий, открытых и выработанных человечеством в ходе предшествующей
истории. Но то, что известно человечеству и не является для него новым,
неизбежно оказывается в начале неизвестным и новым для каждого ребенка.
Поэтому усвоение всего исторически накопленного богатства знаний требует от
ребенка больших умственных усилий. Серьезной творческой работы, хотя он
осваивает как бы готовую систему понятий, причем осваивает под руководством
взрослых. Следовательно, тот факт. Что дети усваивают уже известные
человечеству знания и делают это с помощью взрослых, не исключает, а, наоборот,
предполагает необходимость напряженного, самостоятельного мышления у самих детей.
Иначе усвоение знаний будет чисто формальным, поверхностным, бездумным,
механистическим. Таким образом, мыслительная деятельность является необходимой
основой и для усвоения знаний, и для открытия, добывания новых знаний в ходе
исторического развития человечества [8].
Мышление развертывается во времени, включает в
себя некоторые фазы, или планы, есть начало, середина, завершение. Мышление
есть некоторое проявление активности субъекта, то есть оно не только
направленно на отражение внешнего мира мышления, но и является выражением а
определенной активности субъекта [9]. Мышление всегда субъективно, даже в том
случае, когда оно правильно и адекватно отражает внешний мир. Мышление это
всегда искание и открытие существенно нового [31]. По мнению С.Л. Рубинштейна,
в качестве основного предмета психологического исследования мышление выступает
как процесс, как деятельность. Каждый психический процесс имеет свое
результативное выражение в том или ином образовании. Всякое такое образование,
будучи результатом, «продуктом» соответствующего процесса, затем включается в
его дальнейшее протекание. Ни один процесс нельзя охарактеризовать без
относительности к тем образованиям, в которых он, в конечном счете, выражается.
Но образования не могут быть превращены в самостоятельный предмет
психологического исследования. Всякое понятие, будучи результатом мыслительной
деятельности - индивидуальной и вместе с тем, общественной, - является
отражением объективной реальности и ее свойств: это геометрическая,
арифметическая, физическая и т. п. понятий. Через свои продукты мышление
переходит из собственно психологической сферы в сферы других наук - логики,
математики, физики и т. д. Поэтому сделать образование, в частности понятия
исходным в изучении мышления, значит подвергнуть себя опасности утерять предмет
собственно психологического исследования. [34]
Процесс мышления и его результаты, конечно,
взаимосвязаны. Результаты мыслительной деятельности - понятия, знания - сами
включаются в процесс мышления, обогащают его и обуславливают его дальнейший
ход, возникая в результате мышления, понятия сами включаются в него. Мышление
совершается в понятиях. Процесс мышления есть одновременно и движения знания в
нем, именно это составляет содержательную сторону мышления.
Правильное понимание положения о мышлении как
процессе предполагает, что мышление понимается как деятельность субъекта,
взаимодействующего с объективным миром. Мышление потому и является процессом,
что оно есть непрерывное взаимодействие человека с объектом [5]. Положение о мышлении
как процессе приводит к необходимости раскрыть, в чем этот процесс заключается.
Процесс мышления - это прежде всего анализирование, штудирование и обобщение
[34].
Мышление не может быть сведено к
функционированию уже готовых знаний; оно должно быть раскрыто, прежде всего,
как продуктивный процесс, способный приводить к новым знаниям [5].
Основная характеристика наглядно-действенного
мышления отражена в названии: решение задачи осуществляется с помощью реального
преобразования ситуации, с помощью наблюдаемого деятельного акта. Этот вид
мышления широко представлен у людей, занятых реальным производственным трудом,
результатом которого является создание какого- либо конкретного материального
продукта [8].
В психологии выделяется так же, как
самостоятельный вид, наглядно-образное мышление. Функции образного мышления
связаны с представливанием ситуации и изменений в них, которые человек хочет
получить в результате своей деятельности, преобразующей ситуацию, с
конкретизацией общих положений. С помощью образного мышления более полно
воссоздается все многообразие различных фактических характеристик предмета. В
образе может быть зафиксировано одновременное видение предмета с нескольких
точек зрения. Очень важная особенность образного мышления - установление непривычных,
«невероятных» сочетаний предметов и их свойств. В отличие от
наглядно-действенного мышления при наглядно-образном мышлении ситуация
преобразуется лишь в плане образа.
Наглядно-действенное, наглядно-образное,
словесно-логическое мышление образует этапы развития мышления в онтогенезе,
филогенезе. В настоящее время в психологии убедительно показано, что эти три
вида мышления сосуществуют и у взрослого человека и функционируют при решении
различных задач. Описанная классификация не является единственной. В
психологической литературе используется несколько «парных» классификаций.
Различают теоретическое и практическое мышление
по типу решаемых задач и вытекающих отсюда структурных и динамических
особенностей. Теоретическое мышление - это познание законов, правил. Основная
задача практического мышления - подготовка физического преобразования
действительности: постановка цели, создание плана, проекта, схемы [3].
Практическое мышление было глубоко проанализировано советским психологом Б.М.
Тепловым. Разница между теоретическим и практическим видами мышления состоит
лишь в том, что они по разному связаны с практикой. Работа практического
мышления в основном направлена на разрешение частных конкретных задач, тогда
как работа теоретического мышления направлена в основном на нахождения общих
закономерностей [29]. Теоретическое мышление наиболее последовательно изучается
в контексте психологии научного творчества. Его сравнивают с мышлением
эмпирическим. Здесь используются следующий критерий: характер обобщений, с
которыми имеет дело мышление, в одном случае это научные понятия, а в другом -
житейские, ситуативные обобщения. [6].
Проводятся также различия между интуитивным и
аналитическим мышлением. Обычно используются три признака: временный,
структурный, уровень протекания.
Аналитическое мышление развернуто во времени,
имеет четко выраженные этапы, в значительной степени представлено в сознании
самого мыслящего человека. Интуитивное мышление характеризуется быстротой
протекания, отсутствием четко выраженных этапов, является минимально осознанным
[30].
В психологии существует еще одно важное деление:
мышление реалистическое и аутистическое. Первое направлено в основном на
внешний мир, регулируется логическими законами, а второе связно с реализацией
желаний человека. Иногда используется термин «эгоцентрическое мышление», оно
характеризуется, прежде всего, невозможностью принять точку зрения другого
человека [9].
Важным является различение продуктивного и
репродуктивного мышления. Это различие основывается на степени новизны
получаемого в процессе мыслительной деятельности продукта по отношению к
знаниям субъекта. Необходимо также отличать непроизвольные мыслительные
процессы от произвольных: например, непроизвольные трансформации образов
сновидения и целенаправленное решение мыслительных задач. Существуют сложные
отношения между всеми видами мышления. В целом эти соотношения еще не явлены
[4]. Однако ясно главное: термином «мышление» в психологии обозначаются
качественные разнородные процессы [34].
Логическое мышление - это особый вид мышления,
который позволяет устанавливать наиболее общие закономерности, определяющие
развитием природы и общества, самого человека. Мышление возникает на основе
практической деятельности из чувственного познания и далеко выходит за его пределы.
Мышление - это социально-обусловленный. Неразрывно связанный с речью процесс
поисков и открытий существенно нового, процесс опосредованного и обобщенного
отражения действительности в ходе анализа и синтеза существенных связей и
отношений. Мышление - это активная познавательная деятельность субъекта,
необходимая для его полноценной ориентации в окружающем пространстве.
Логическое мышление обнаруживается, прежде
всего, в протекании самого мыслительного процесса. Оно осуществляется только
словесным путем. Человек должен рассуждать, анализировать и устанавливать
нужные связи мышления, отбирать и применять к данной ему конкретной задаче
известные ему подходящие правили, приемы, действия. Он должен сравнивать и
устанавливать искомые связи, группировать разные и различать сходные предметы и
все это выполнять лишь посредством умственных действий. Совершенно естественно,
что, прежде чем ребенок освоит эту сложную форму умственной деятельности, он
допустит ряд ошибок. Они очень типичны для мышления детей. Эти особенности
отчетливо обнаруживаются в детских рассуждениях, в использовании ими понятий в
процессе освоения ребенком отдельных операций логического мышления.
Правильное понимание положения о «мышлении» как
процессе предполагает деятельность субъекта, его взаимодействие с объективным
миром. Мышление потому и является процессом, что оно есть непрерывное
взаимодействие человека с объектом. Процесс мышления - это, прежде всего,
анализирование, синтезирование и обобщение [8].
Под логическим приемом мы понимаем совокупность
действий, направленных на выполнение логической операции или логического
закона. Главным отличительным признаком логического приема является его
ориентировка на логические правила, на требования, исходящие из логики.
Операционным компонентом мышления является
система мыслительных операций: анализа, синтеза, сравнения, обобщения,
классификации.
Каждая операция выполняет определенную функцию и
находится во взаимодействии с другими операциями. Сравнение вскрывает тождество
и различие вещей. Результатом сравнения может стать классификация. Более
глубокое проникновение в суть вещей требует раскрытия их внутренних связей,
закономерностей и существенных свойств. Оно выполняется при помощи анализа и
синтеза. Обобщение выступает как соединение существенного и связывание его с
классом предметов и явлений. Умозаключение - это выделение из одного или
нескольких суждений нового суждения. Исходные суждения называются посылками,
новое суждение - выводом. Для того, чтобы из одного или нескольких суждений был
возможен вывод нового суждения, между ними должна существовать логическая
связь, которую и отражает умозаключение.
В связи с этим встает задача раскрытия состава
мышления, характеристики анализа и синтеза, а так же абстракции и обобщения.
Анализ и синтез - это две стороны, или два
аспекта, единого мыслительного процесса. Они взаимосвязаны и взаимообусловлены.
Анализ по большей части совершается через синтез; анализ какого-нибудь целого
всегда обусловлен тем, по каким признакам в нем объединены его части. Правильный
анализ любого целого всегда является анализом не только частей, элементов,
свойств, но и связи или отношений. Он поэтому ведет не к распаду целого, а к
его преобразованию. Это же преобразование целого, новое соотношение выделенных
анализом компонентов целого и есть синтез. Так же, как анализ осуществляется
через синтез, синтез осуществляется через анализ, охватывающий части, элементы,
свойства в их взаимосвязи.
В плане чувственного познания анализ выражается
в выделении какого-нибудь чувственного свойства объекта, до того должным
образом не выделявшегося. Движение анализа происходит в совершающемся по ходу
познания выделении и акцентировании новых моментов, в результате чего
преобразуется структура подвергающегося анализу целого. Познавательское значение
анализа связано с тем, что он вычленяет и «подчеркивает», выделяет
существенное. Для решения этой задачи анализ расчленяет в чувственном
восприятия непосредственно нерасчлененный, итоговый, суммарный эффект различных
и иногда по существу, разнородных взаимодействий, вычленяет явления в чистом
виде в существенные для него закономерностях, отделяя его от сторонних,
привходящих инородных явлениях, которые маскируют собственную природу
изучаемого явления и закономерности, его определяющие, - существенные в нем. В
этом случае анализ переходит в абстракцию. Таким образом, анализ выступает при
переходе к отвлеченному мышлению [30].
Абстракция - это, по существу, тоже
специфическая форма анализа, форма, которую анализ приобретает при переходе к
абстрактному мышлению в понятиях. Аналитический характер научной абстракции
заключается в том, что она выделяет существенное, отвлекая его от
несущественного: она анализирует и членит то диффузное, еще не
проанализированное целое, в котором существенное и несущественное еще не
расчленены.
Мыслительная деятельность человека представляет
собой решение разнообразных мыслительных задач, направленных на раскрытие
сущности чего-либо. Мыслительная операция - это один из способов мыслительной
деятельности, посредством которого человек решает мыслительные задачи.
Мыслительные операции разнообразны. Это - анализ
и синтез, сравнение, абстрагирование, конкретизация, обобщение, классификация.
Какие из логических операций применит человек, это будет зависеть от задачи и
от характера информации, которую он подвергает мыслительной переработке.
Мыслительная деятельность всегда направлена на
получение какого-либо результата. Человек анализирует предметы, сравнивает их,
абстрагирует отдельные свойства с тем, чтобы выявить общее в них, чтобы раскрыть
закономерности, управляющие их развитием, чтобы овладеть ими.
Обобщение, таким образом, есть выделение в
предметах и явлениях общего, которое выражается в виде понятия, закона,
правила, формулы и т.п.
Мышление дает ответ на такие вопросы, которые
нельзя разрешить путем непосредственного, чувственного отражения. Так,
осматривая место происшествия, следователь находит некоторые следы прошедшего
события. Устанавливая существенные, неизбежно повторяющиеся взаимосвязи между
ними, следователь путем логического мышления реконструирует возможный ход
событий. Эта реконструкция происходит опосредствованно, путем понимания связей
между внешними проявлениями и сущностью того, что происходило в
действительности. Это опосредованное отражение возможно лишь на основе обобщения,
на основе знаний. Благодаря мышлению человек правильно ориентируется в
окружающем мире, используя ранее полученные обобщения в новой, конкретной
обстановке [9].
Деятельность человека разумна благодаря знанию
законов, взаимосвязей объективной действительности.
Мышление опосредованное и обобщенное отражение
существенных, закономерных взаимосвязей действительности. Это обобщенная
ориентация в конкретных ситуациях действительности.
В мышлении устанавливается отношение условий
деятельности к ее цели, осуществляется перенос знаний из одной ситуации в
другую, преобразование данной ситуации в соответствующую обобщенную схему.
Установление всеобщих взаимосвязей, обобщение
свойств однородной группы явлений, понимание сущности конкретного явления как
разновидности определенного класса явлений такова сущность человеческого
мышления. Но мышление, выходя за пределы ощущений и восприятия, всегда остается
неразрывно связанным с чувственным отражением действительности. Обобщения
формируются на основе восприятия единичных объектов, а их истинность
проверяется практикой.
Мышление, являясь идеальным отражением
действительности, имеет материальную форму своего проявления. Механизмом
мышления человека является скрытая, беззвучная, внутренняя речь. Она
характеризуется скрытой, незаметной для человека артикуляцией слов,
микродвижениями органов речи. Последние связаны с возбуждениями в
речедвигательной зоне коры головного мозга. Особенностью внутренней речи
является ее сокращенность, конспективность, свернутость. Но при возникновении
мыслительных затруднений внутренняя речь принимает развернутую форму и нередко
переходит в шепотную или громкую речь. Это позволяет лучше анализировать и
закреплять абстрактный речевой материал: формулировки, условия задач и т.п.
[24]
Мышление социально обусловлено, оно возникает
лишь в общественных условиях существования человека, оно основано на знаниях,
т.е. на общественно-историческом опыте человечества.
Как уже отмечалось, первоначально мышление
человека было непосредственно вплетено в его материальную деятельность, человек
мыслил, действуя практически. Но постепенно из практических действий выделялись
самостоятельные умственные, мыслительные действия, которые подготавливают, ориентируют
практические действия. В процессе исторического развития мыслительные действия
стали подчиняться определенным логическим правилам; постоянно повторяясь и
проверяясь на практике, эти правила закреплялись в сознании человека и
приобрели для него аксиоматический характер [28].
Процесс решения задач несомненно является
моделью, с наибольшей полнотой отражающей структуру интеллектуальной
деятельности, и изучение особенностей этого процесса может дать существенные
материалы для понимания психологии мышления человеком. В процессе мыслительной
деятельности человек познает окружающий мир с помощью особых умственных
операций. Эти операции составляют различные взаимосвязанные, переходящие друг в
друга стороны мышления.
Ученые, занимающиеся исследованиями в области
восприятия и мышления детей приходят к разным выводам относительно процесса
детского мышления. Пиаже полагает, что ребенок начинает с аутистического
мышления, затем переходит к эгоцентрическому мышлению и, наконец, к разумному,
логическому. Аутистическая мысль (Блейлер, Фрейд) не содержит в себе сознания
цели, стремится не к установлению истины, а удовлетворению желания
(органических потребностей и игры), не приспособляется к внешней
действительности, а создает сама себе воображаемую действительность или
действительность сновидения; таким образом, она не социальна, а чисто
индивидуальна, непосредственно не выразима речью. Разумная мысль сознательно
направлена на определенную цель, приспособлена к действительности, заключает
истину или заблуждение; она выразима социализированною речью. Эгоцентрическое
мышление, по Пиаже, занимает промежуточное место: оно направлено не столько на
приспособление к действительности, сколько на удовлетворение желаний, но все же
служит не только органическим потребностям и игре; оно выражается
эгоцентрической речью. До 7 лет, согласно Пиаже, у ребенка преобладает
эгоцентрическая речь, которая свидетельствует об эгоцентризме мысли; она не
соответствует точке зрения собеседника и потому не служит цели социального
общения. Развитие мышления выражается в постепенном расширении содержания
мысли, в последовательном возникновении форм и способов мыслительной
деятельности и изменении их по мере общего формирования личности. Одновременно
у ребёнка усиливаются и побуждения к мыслительной деятельности - познавательные
интересы. Мышление развивается на протяжении всей жизни человека в процессе его
деятельности. На каждом возрастном этапе мышление имеет свои особенности.
Вывод: по мнению С.Л. Рубинштейна, в качестве
основного предмета психологического исследования мышление выступает как
процесс, как деятельность. Результаты мыслительной деятельности - понятия,
знания - сами включаются в процесс мышления, обогащают его и обуславливают его
дальнейший ход, возникая в результате мышления, понятия сами включаются в него.
Мышление совершается в понятиях. Процесс мышления есть одновременно и движения
знания в нем, именно это составляет содержательную сторону мышления.
.2 Особенности математического мышления младших
школьников
Изучение мышления школьников приобрело в
последнее время особую остроту. Но наибольшее внимание практиков и теоретиков
обучения обращено к проблеме развития логического мышления.
Вопросы умственных (вообще интеллектуальных)
возможностей детей школьного возраста никогда ранее не разрабатывались так
интенсивно и широко, как в настоящее время. Непосредственным толчком к
развертыванию исследовательской деятельности в этой области явились задачи
перестройки школьного образования. Несмотря на то, что некоторые из них отчасти
уже выполнены, и в школах обучение ведется по существенно измененным
программам, указанная проблема продолжает оставаться весьма актуальной [22].
Перед психолого-педагогическими науками
поставлена задача: способствовать повышению качества обучения в школе. Это означает,
в частности, что нужно повысить качество знаний, умений и навыков,
приобретаемых детьми в результате усвоения учебного материала. Для этого
требуется осуществить дальнейшее совершенствование содержания обучения и
методов преподавания. Такая работа с необходимостью предполагает учет
особенностей мышления школьников разного возраста, поскольку и содержание
учебного материала будет осваиваться достаточно полноценно, и методы
преподавания будут вполне эффективными лишь в том случае, если, с одной стороны,
они адекватны возрастным возможностям мышления детей и, с другой стороны,
создают условия для расширения и углубления этих возможностей [33].
Для умственного развития младших школьников
нужно использовать три вида мышления. При этом с помощью каждого из них у детей
лучше формируются те или иные качества ума. Так, решение задач с помощью
наглядно - действенного мышления позволяет развивать у учащихся начальных
классов способность управлять своими поисковыми действиями, осуществлять
целенаправленные (а не случайные и хаотичные) попытки решения задач. Такая
особенность этого вида мышления следует из того, что с его помощью решаются
задачи, в которых предметы (между которыми нужно найти отношения) можно брать в
руки, чтобы изменить их состояние и свойства, а также располагать в
пространстве. Поскольку, работая с предметами, ребенку легче наблюдать за
своими действиями по их изменению, то в этом случае и легче управлять
действиями: прекращать практические попытки, если их результат не соответствует
требованиям задачи, или, наоборот, заставлять себя довести попытку до конца, до
получения определенного результата, а не бросать ее выполнение, не узнав
результата.
Итак, с помощью наглядно - действенного мышления
удобнее развивать у детей такое важное качество ума, как способность при
решении задач действовать целенаправленно и продуманно, сознательно управляя и
контролируя свои действия.
Своеобразие наглядно - образного мышления
заключается в том, что, решая задачи с его помощью, человек не имеет
возможности реально изменять образы и представления. Это позволяет
разрабатывать разные планы достижения цели, мысленно сопоставлять эти планы,
чтобы найти наилучший. С помощью наглядно - действенного мышления у детей
формируется умение управлять своими действиями при решении задач, а с помощью
наглядно - образного мышления формируется умение рассматривать разные варианты
плана по достижению поставленной цели в ходе предъявления, какого-нибудь
задания [13].
Своеобразие словесно - логического мышления (в
отличие от наглядно - действенного и наглядно - образного) состоит в том, что
это отвлеченное мышление, в ходе которого человек действует не с вещами и их
образами, а с понятиями о них, оформленными в словах или знаках. При этом
человек действует по определенным правилам, отвлекаясь от наглядных
особенностей вещей и их образов. Поэтому главная цель работы по развитию у
детей словесно -логического, отвлеченного мышления заключается в том, чтобы с
его помощью формировать у них умение рассуждать, делать выводы из тех суждений,
которые предлагаются в качестве исходных, умение ограничиваться содержанием
этих суждений и не привлекать других соображений, связанных с внешними
особенностями тех вещей или образов, которые отражаются и обозначаются в
исходных суждениях.
Конкретные вопросы развития логического мышления
непосредственно связаны с развитием умственной деятельности школьников. В
педагогической психологии многие исследователи пришли к заключению, что основа
этой деятельности - приемы и способы, с помощью которых умственная деятельность
совершается (Н.А. Менчинская, Д.Н. Богоявленский, Е.Н. Кабанова-Меллер, и др.)
[24]. Овладение умственной деятельностью проходит путем смены способов менее
целесообразных и эффективных на более рациональные и совершенные. Задача любого
обучения состоит в сокращении этого пути. Очевидно, что развитие логических
форм мышления должно служить достижению данной цели.
Развитие логического мышления сложно тем, что
требует не только высокой активности умственной деятельности, ее постоянной
динамики, но и обобщенных знаний. Многолетнее изучение мышления на контингенте
младших школьников, проводившееся в русле экспериментального обучения под
руководством В.В. Давыдова, позволило вскрыть значительные интеллектуальные
резервы учащихся начальных классов. Обнаружилось, что дети младшего школьного
возраста, усваивая материал экспериментальных учебных программ, построенных на
теории содержательного обобщения [17], способны овладеть знаниями, умениями и
навыками существенно более высокого содержательного уровня, чем тот, который
обычно считается для них посильным.
Обогащению учащихся прочными и глубокими
знаниями должно сопутствовать решение такой задачи, как достижение высокого
уровня умственного и нравственного развития школьников. Многочисленные
наблюдения педагогов, исследования психологов убедительно показали, что
ребенок, не научившийся учиться, не овладевший приемами мыслительной
деятельности в начальных классах школы, в средних, обычно, переходит в разряд
неуспевающих. Одним из важных направлений в решении этой задачи выступает
создание в начальных классах условий, обеспечивающих полноценное умственное
развитие детей, связанное с формированием устойчивых познавательных интересов,
умений и навыков мыслительной деятельности, качеств ума, творческой инициативы
и самостоятельности в поисках способов решения задач. Однако такие условия
обеспечиваются в начальном обучении пока не в полной мере, поскольку все еще
распространенным приемом в практике преподавания является организация учителем
действий учащихся по образцу: излишне часто учителя предлагают детям упражнения
тренировочного типа, основанные на подражании и не требующие проявления выдумки
и инициативы.
В этих условиях у детей недостаточно развиваются
такие важные качества мышления, как глубина, критичность, гибкость, которые
являются сторонами его самостоятельности. Только развитие самостоятельного
мышления, творческого, поискового, исследовательского есть основная задача
школьного обучения вообще и в начальных классах в частности.
Развитие самостоятельного мышления,
проявляющегося, в частности, в своеобразном видении ребенком проблемной
ситуации, требует индивидуального подхода, который бы учитывал особенности
мыслительной деятельности каждого ученика.
Формирование самостоятельности в мышлении,
активности в поиске путей достижения поставленной цели предполагает решение
детьми нетиповых, нестандартных задач, имеющих иногда несколько способов
решения, хотя и правильных, но в разной степени оптимальных. Для того чтобы
решение таких задач способствовало действительному развитию активного,
поискового мышления, оно должно быть организовано особым образом. В частности,
необходимо провести разбор наиболее распространенных ошибок, которые
встретились при решении, обсуждение разных способов решения, их обоснование и
критику [11].
По мере обучения в школе мышление детей
становится более произвольным, более программируемым, более сознательным, более
планируемым, т.е. оно становится словесно - логическим. Конечно, и другие виды
мышления развиваются дальше в этом возрасте, но основная нагрузка падает на
формирование приемов рассуждения и умозаключения [3].
Успешность учебной деятельности во многом
зависит от особенностей развития мышления. Именно в младшем школьном возрасте,
как показывают специальные исследования, должно достаточно интенсивно
развиваться абстрактно - логическое мышление.
Ребенок, придя в школу, в основном мыслит,
опираясь на конкретные образы. Именно поэтому большинство учителей начальной
школы широко используют наглядность в процессе обучения. Но полное и глубокое
усвоение программного материала предполагает обязательное абстрактно -
логическое мышление. Развитие мышления в младшем школьном возрасте в
значительной степени связано с совершенствованием мыслительных операций:
анализа и синтеза, сравнения, обобщения, систематизации, классификации, с
усвоением различных мыслительных действий [5]. Для создания оптимальных условий
развития мышления необходимо знать эти особенности ребенка.
Умственное развитие, развитие мышления является
важной стороной в развитии личности младших школьников, в частности ее
познавательной сферы. Мышление человека характеризуется активным поиском связей
и отношений между разными событиями, явлениями, вещами, предметами. Именно
направленность на отражение прямо не наблюдаемых связей и отношений (например,
причинно - следственных связей, условных), на выделение в вещах и явлениях
главного и неглавного, существенного и несущественного и отличает мышление как
познавательный процесс от восприятия и ощущения. Младший школьный возраст
содержит в себе значительный потенциал умственного развития детей.
Психолог Л.С. Выготский отмечал интенсивное
развитие интеллекта в младшем школьном возрасте. Развитие мышления приводит, в
свою очередь, к качественной перестройке восприятия и памяти, превращению их в регулируемые,
произвольные процессы. Ребенок 7-8 лет обычно мыслит конкретными категориями.
Затем происходит переход к стадии формальных операций, которая связана с
определенным уровнем развития способности к обобщению и абстрагированию. К
моменту перехода в среднее звено школьники должны научиться самостоятельно
рассуждать, делать выводы, сопоставлять, сравнивать, анализировать, находить
частное и общее, устанавливать простые закономерности [13].
Ребенок, начиная обучаться в школе, должен
обладать достаточно развитым конкретным мышлением. Чтобы сформировать у него
научное понятие, необходимо научить его дифференцировать подходить к признакам
предмета. Надо показать ребенку, что есть существенные признаки, без наличия
которых предмет не может быть подведен под данное понятие. Критерием овладения
тем или иным понятием является умение им оперировать. Если учащиеся 1-2 класса
отмечают, прежде всего, наиболее наглядные внешние признаки, характеризующие
действие объекта или его назначение, то к 3-4 классу школьники уже больше
опираются на знания, представления, сложившиеся в процессе обучения.
Третьеклассники должны уметь устанавливать
иерархию понятий, вычленять более широкие и более узкие понятия, находить связи
между родовыми и видовыми понятиями. Если дошкольник или ученик 1-2 класса
часто подменяют аргументацию и доказательство простым указанием на реальный
факт или опирается на аналогию, далеко не всегда правомерно, то ученик 3-4
класса должен уметь дать обоснованное доказательство, развернуть аргументацию. Аналитическая
деятельность третьеклассника основывается на представлениях и понятиях. Младший
школьник в своем развитии идет от анализа отдельного предмета, отдельного
явления к анализу связей и отношений между предметами и явлениями. Последнее
есть необходимая предпосылка понимания школьником явлений окружающей жизни.
Особые трудности возникают при установлении и понимании причинно - следственных
связей. Младшему школьнику легче устанавливать связь от причины к следствию,
чем от следствия к причине. Это и понятно: при умозаключении от причины к
следствию устанавливаются прямые связи, при умозаключении от факта к вызвавшей
его причине такая связь непосредственно не дана, т.к. указанный факт может быть
следствием самых различных причин, которые надо специально анализировать.
К окончанию третьего класса учащийся должен
научиться и таким элементам анализа, как выявление и других связей между
явлениями и понятиями: рядоположенность, порядок следования, противоположность,
наличие тех или иных функциональных отношений, часть и целое.
За первые три - четыре года учения в школе
прогресс в умственном развитии детей бывает довольно заметным. От доминирования
наглядно - действенного и элементарного образного мышления, от допонятийного
уровня развития и бедного логикой размышления школьник поднимается до словесно
- логического мышления на уровне конкретных понятий. Начало этого возраста
связано, если пользоваться терминологией Ж. Пиаже и Л.С. Выготского, с
доминированием дооперационального мышления, а конец - с преобладанием
операционального мышления в понятиях [13].
Комплексное развитие детского интеллекта в
младшем школьном возрасте идет в несколько различных направлениях: усвоение и
активное использование речи как средства мышления; соединение и
взаимообогащение всех видов мышления: наглядно - действенного, наглядно -
образного и словесно - логического; выделение, обособление и относительно
независимое развитие в интеллектуальном процессе двух фаз: подготовительной и
исполнительной. На подготовительной фазе решения задачи осуществляется анализ
ее условий и вырабатывается план, а на исполнительной фазе этот план
реализуется практически. Полученный результат затем соотносится с условиями и
проблемой. Ко всему сказанному следует добавить умение рассуждать логически и
пользоваться понятиями.
Первое из названных направлений связано с
формированием речи у детей, с активным ее использованием при решении
разнообразных задач. Развитие в этом направление идет успешно, если ребенка
обучают вести рассуждения вслух, словами воспроизводить ход мысли и называть
полученный результат.
Второе направление в развитии успешно
реализуется, если детям даются задачи, требующие для решения одновременно и
развитых практических действий, и умения оперировать образами, и способности
пользоваться понятиями, вести рассуждения на уровне логических абстракций.
Если любой из этих аспектов представлен слабо,
то интеллектуальное развитие ребенка идет как односторонний процесс. При
доминировании практических действий преимущественно развивается наглядно -
действенное мышление, но может отставать образное и словесно - логическое
мышление. Когда преобладает образное мышление, то можно обнаружить задержки в
развитии практического и теоретического интеллекта. При особом внимании только
к умению рассуждать вслух у детей нередко наблюдается отставание в практическом
мышлении и бедность образного мира. Все это, в конечном счете, может сдерживать
общий интеллектуальный прогресс ребенка [11].
Словесно - логическое мышление - завершающая,
высшая стадия развития детского мышления и заключается в оперировании
понятиями. Этот вид мышления возникает в школьном возрасте, когда ведущей
деятельностью для ребенка становится учение, направленное на усвоение систем
понятий по различным учебным предметам.
Логическое мышление в своем развитии проходит
длительный путь.
Словесно - логическое мышление ребенка, которое
начинает формироваться в конце дошкольного возраста, предполагает уже умение
оперировать словами и понимать логику рассуждений. Способность использовать
словесные рассуждения при решении ребенком задач можно обнаружить уже в среднем
дошкольном возрасте, но наиболее ярко оно проявляется в феномене
эгоцентрической речи, описанном Ж. Пиаже. Другое явление, открытое им же и
относящееся к детям данного возраста свидетельствует о том, что даже к концу
дошкольного детства многие дети еще совершенно не владеют логикой [4].
Н.Н. Поддьяков специально изучал, как идет у
детей формирование внутреннего плана действий, характерных для логического
мышления, и выделил шесть этапов развития этого процесса. Эти этапы следующие:
Ребенок еще не в состоянии действовать в уме, но
уже способен с помощью рук, манипулируя вещами, решать задачи в наглядно
-действенном плане, преобразуя соответствующим образом проблемную ситуацию.
В процессе решения задачи ребенком уже включена
речь, но она используется им только для называния предметов, с которыми он
манипулирует в наглядно - действенном плане. В основном же ребенок по -
прежнему решает задачи "руками и глазами", хотя в речевой форме им
уже может быть выражен и сформулирован результат выполненного практического
действия.
Задача решается в образном плане манипулирование
представлениями объектов. Здесь, вероятно осознаются и могут быть словесно
обозначены способы выполнения действий, направленных на преобразование ситуации
с целью найти решение поставленной задачи. Возникает элементарная форма
рассуждения вслух, не отделенного еще от выполнения реального практического
действия, но уже направленного на теоретическое выяснение способа
преобразования ситуации или условий задачи.
Задача решается ребенком по заранее
составленному, продуманному и внутренне представленному плану. В его основе -
память и опыт, накопленные в процессе предыдущих попыток решения подобного рода
задач.
. Задача решается в плане действия в уме
с последующим выполнением той же самой задачи в наглядно - действенном плане с
целью подкрепить найденный в уме ответ и далее сформулировать его словами.
. Решение задачи осуществляется только во
внутреннем плане с выдачей готового словесного решения без последующего
обращения к реальным, практическим действиям с предметами [5].
Важнейший вывод, который сделал Н.Н. Поддьяков
из исследований развития детского мышления, заключается в том, что у детей
пройденные этапы и достижения в совершенствовании мыслительных действий и
операций полностью не исчезают, но преобразуются, заменяются новыми, более
совершенными. При возникновении новой проблемной ситуации, или задачи, все эти
уровни снова могут включаться в поиск процесса ее решения как относительно
самостоятельные и вместе с тем как составляющие звенья логики целостного
процесса поиска ее решения. Иными словами, детский интеллект уже в этом
возрасте функционирует на основе принципа системности. В нем представлены и при
необходимости одновременно включаются в работу все виды и уровни логического
мышления: наглядно-действенное, наглядно-образное и словесно-логическое [5].
В логическом мышлении можно выделить две
основные формы: конкретно - понятийное и абстрактно понятийное мышление (Г.К.
Костюк).
Конкретно - понятийное мышление - начальная
форма развития логического мышления. Все мыслительные операции, которые
формируются в этот период, тесно связаны с опорой на наглядный конкретный
материал. На уровне конкретно - понятийного мышления все рассуждения и умозаключения
детей зависят и определяются конкретным содержанием материала: чем ближе это
содержание опыту ребенка, чем оно конкретнее, тем легче и проще справляется
ребенок с построением умозаключений. На этой стадии развития логического
мышления для получения вывода дети постоянно опираются на конкретные примеры,
действия, образцы как на основу для рассуждения. Представления и конкретные
понятия составляют фундамент конкретно - понятийного мышления. Все мыслительные
операции младших школьников развиваются и формируются на базе использования
этого "строительного" материала.
Вторая форма развития логического мышления -
абстрактно-понятийное мышление - завершающая ступень формирования логического
мышления детей. Она характерна для среднего и старшего школьного возраста,
когда существенно изменяется содержательная сторона мышления: дети начинают
мыслить абстрактными понятиями, общими законами, усваивают систему понятий.
Школьникам становится доступным самостоятельное решение более сложных
познавательных задач, что приводит к преобразованию мыслительных операций: они
обобщаются, формализуются, благодаря чему расширяются возможности их переноса и
применения в новых ситуациях. Появляется такое существенное свойство
мыслительных операций, как их обратимость, возникает система взаимосвязанных,
обобщенных операций. Значительно развиваются способности рассуждать, доказывать
истинность получаемых выводов, осознавать и контролировать процесс рассуждения
(Г.С. Костюк, Т.В. Розанова).
Развитие логического мышления непосредственно связано
с формированием понятий. Развивающиеся понятия у детей делятся на спонтанные,
или житейские, т.е. развивающиеся в стихийном, житейском опыте ребенка, и не
спонтанные, или научные, понятия (Выготский Л.С.). Спонтанные и научные понятия
Л.С. Выготский рассматривал как низшую и высшую ступени развития. При этом он
считал, что с логической точки зрения спонтанные понятия совпадают с
эмпирическими, а не спонтанные понятия - с научными. Чтобы показать предысторию
научных понятий, Л.С. Выготский анализирует процесс развития житейских понятий,
выделяя в нем две ступени: синкреты ("неоформленные, неупорядоченные
множества") и комплексные обобщения [13].
Развитие понятий идет как единая линия, на
основе постоянного взаимодействия: житейские понятия готовят возникновение
научных понятий, а последние, возникнув, изменяют структуру житейских понятий.
Анализ возникновения научных понятий позволил Л.С. Выготскому выдвинуть
предположение о ведущей роли обучения в умственном развитии ребенка [13].
Работы советских психологов (Л.С. Выготский,
Г.С. Костюк, С.Л. Рубинштейн и др.) показали, что логика детского мышления в
своем течении обращается к тем же формам, что и логика взрослого человека. Уже
до школы у детей возникают элементы правильного логического мышления. Однако
умозаключения, дедуктивная форма мышления трудна для младших школьников и
становится доступной им только при определенных условиях. Детские умозаключения
еще очень слабы и тесно связаны с наглядными компонентами. Причем, чем моложе
ребенок, тем эта связь с наглядностью более тесна и необходима [13].
Мышление детей младшего школьного возраста
значительно отличается от мышления дошкольников. Так, если для мышления
дошкольников характерно такое качество, как непроизвольность, малая
управляемость и в постановке мыслительной задачи, и в ее решении, они чаще и
легче задумываются и над тем, что им интересно, что их увлекает; то младшие
школьники в результате обучения в школе, когда необходимо регулярно выполнять
задания в обязательном порядке, научаются управлять своим мышлением, думать
тогда, когда это нужно, а не только тогда, когда интересно, когда нравится то,
о чем нужно думать. Во многом формированию такой произвольности, управляемости
мышления способствуют указания учителя на уроках, побуждающие детей к размышлению,
оценка им результатов мыслительной деятельности школьников и помощь в поисках
правильного решения [27].
При обучении в начальных классах у детей
формируются осознанность, критичность мышления. Это происходит благодаря тому,
что в классе обсуждаются пути решения задач, рассматриваются разные варианты
решения, учитель постоянно требует от учащихся обосновывать, рассказывать,
доказывать правильность своего суждения, т.е. требует от детей, чтобы они
решали задачи сознательно.
Умение планировать свои действия также активно
формируется у младших школьников в процессе школьного обучения. Учитель
побуждает детей сначала продумать план решения задачи, а только потом
приступать к практическому ее решению [3].
На уроках в начальных классах при решении
учебных задач у детей формируются такие приемы логического мышления, как
сравнение, связанное с выделением в предметах общего и различного, анализ,
связанный с выделением и словесным обозначением в предмете разных свойств и
признаков, обобщение, связанное с отвлечением от несущественных особенностей
предметов и объединением их на основе общности существенных особенностей [34].
Вывод: логическое мышление определяет общую
стратегию процесса познавательной деятельности в соответствии с основной
структурой объектов; широкий смысловой контекст, внутри которого осуществляется
наглядно - действенное и наглядно - образное мышление. Его корни лежат в
практике повседневного общения ребенка с взрослыми, в конкретных видах активной
деятельности самого ребенка, его играх, бытовой деятельности. Поэтому развитие
логического мышления - это одна из важных задач начального обучения. Умение
мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять
суждения по определенным правилам - это необходимое условие для успешного
освоения учебного материала.
Глава II. Методология математики
.1 Основные методы и приемы работы с задачей в
начальной школе
Начальный курс математики раскрывается на
системе целесообразно подобранных задач. Значительное место занимает в этой
системе текстовые задачи. Текстовая задача - есть описание некоторой ситуации
на естественном языке с требованием дать количественную характеристику
какого-либо компонента этой ситуации, установить наличие или отсутствие
некоторого отношения между её компонентами или определить вид этого отношения.
Решение задач - это работа несколько необычная, а именно умственная работа. А
чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот
материал, над которым придётся работать, те инструменты, с помощью которых
выполняется эта работа.
Значит, для того чтобы научиться решать задачи,
надо разобраться в том, что собой они представляют, как они устроены, из каких
составных частей они состоят, каковы инструменты, с помощью которых
производится решение задач. Каждая задача - это единство условия и цели. Если
нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду,
чтобы проводить анализ текста задачи с соблюдением такого единства. Это
означает, что анализ условия задачи необходимо соотносить с вопросом задачи и,
наоборот, вопрос задачи анализировать направленно с условием. Их нельзя
разрывать, так как они составляют одно целое [23].
Любая текстовая задача состоит из двух частей:
условия и требования (вопроса). В условии соблюдаются сведения об объектах и
некоторых величинах, характеризующих данные объекта, об известных и неизвестных
значениях этих величин, об отношениях между ними.
Требования задачи - это указание того, что нужно
найти. Оно может быть выражено предложением в повелительной или вопросительной
форме («Найти площадь треугольника.» или «Чему равна площадь прямоугольника?»).
Иногда задачи формируются таким образом, что
часть условия или всё условие включено в одно предложение с требованием задачи.
В реальной жизни довольно часто возникают самые
разнообразные задачные ситуации. Сформулированные на их основе задачи могут
содержать избыточную информацию, то есть такую, которая не нужна для выполнения
требования задачи. На основе возникающих в жизни задачных ситуаций могут быть
сформулированы и задачи, в которых недостаточно информации для выполнения
требований. Так в задаче: «Найти длину и ширину участка прямоугольной формы,
если известно, что длина больше ширины на 3 метра» - недостаточно данных для
ответа на её вопрос. Чтобы выполнить эту задачу, необходимо её дополнить
недостающими данными.
Одна и та же задача может рассматриваться как
задача с достаточным числом данных в зависимости от имеющихся и решающих
значений.
Рассматривая задачу в узком смысле этого
понятия, в ней можно выделить следующие составные элементы:
Словесное изложение сюжета, в котором явно или в
завуалированной форме указана функциональная зависимость между величинами,
числовые значения которых входят в задачу.
Числовые значения величин или числовые данные, о
которых говорится в тексте задачи.
Задание, обычно сформулированное в виде вопроса,
в котором предлагается узнать неизвестные значения одной или нескольких
величин. Эти значения называют искомыми.
Задачи и решение их занимают в обучении
школьников весьма существенное место и по времени, и по их влиянию на
умственное развитие ребенка. Понимая роль задачи и её место в обучении и
воспитании ученика, учитель должен подходить к подбору задачи и выбору способов
решения обоснованно и чётко знать, что должна дать ученику работа при решении
данной им задачи.
Все арифметические задачи по числу действий,
выполняемых для их решения, делятся на простые и составные. Задача, для решения
которой надо выполнить один раз арифметическое действие, называется простой.
Задача, для решения которой надо выполнить несколько действий называется
составной. Простые задачи в системе обучения математике играют чрезвычайно
важную роль. С помощью решения простых задач формируется одно из центральных
понятий начального курса математики - понятие об арифметических действиях и ряд
других понятий [25]. Умение решать простые задачи является подготовительной
ступенью овладения учащимися умением решать составные задачи, так как решение
составной задачи сводится к решению ряда простых задач. При решении простых
задач происходит первое знакомство с задачей и её составными частями.[7]
В связи с решением простых задач дети овладевают
основными приемами работы над задачей.
Нужно, чтобы в сознание детей вошли и укрепились
вторичные сигналы к определенным понятиям, связанным с задачей;
Выработать умение видеть в задаче данные числа и
искомое число;
Научить сознательно выбирать действия и
определять компонен ты этих действий. Разрешение указанных проблем нельзя
расположить в определенной последовательности. В занятиях с детьми довольно
часто приходится добиваться результатов не одного за другим, а идти к
достижению нескольких целей одновременно, постепенно развивая и расширяя
достигнутые успехи в нескольких направлениях.
При знакомстве с задачами и их решением нельзя
избежать специфических терминов, но дети должны их понимать, чтобы осознавать
смысл задачи. Работа с детьми по усвоению ими терминологии начинается с первых
дней занятий в школе и ведётся систематически на протяжении всех лет обучения.
Составная задача включает в себя ряд простых задач, связанных между собой так,
что искомые одних простых задач служат данными других. Решение составной задачи
сводится к расчленению её на ряд простых задач и к последовательному их
решению. Таким образом, для решения составной задачи надо установить систему
связей между данными и искомым, в соответствии с которой выбрать, а затем
выполнить арифметические действия. Рассмотрим в качестве примера задачу: «В
школе дежурили 8 девочек, а мальчиков на 2 больше. Сколько детей дежурило в
школе?» [6]
Эта задача включает две простых:
В школе дежурили 8 девочек, а мальчиков на 2
больше. Сколько мальчиков дежурило в школе?
В школе дежурили 8 девочек и 10 мальчиков.
Сколько всего детей дежурило в школе?
Как видим, число, которое было искомым в первой
задаче, стало данным во второй.
Последовательное решение этих задач является
решением составной задачи: 1)8 + 2=10; 2)8+10=18.
Запись решения составной задачи с помощью
составления по ней выражения позволяет сосредоточить внимание учащихся на
логической стороне работы над задачей, видеть ход решения её в целом. В то же
время дети учатся записывать план решения задачи и экономить время.
Запись решения многих составных задач и
составление по ним выражения связаны с использованием скобок. Скобки -
математический знак, употребляемый для порядка действий. В скобки заключается
то действие, которое нужно выполнить раньше.
В решении составной задачи появилось существенно
новое сравнительно с решением простой задачи: здесь устанавливается не одна
связь, а несколько, в соответствии с которым вырабатываются арифметические
действия. Поэтому проводится специальная работа по ознакомлению детей с
составной задачей, а также по формированию у них умений решать составные задачи
[38].
Общепризнанно, что для выработки у учащихся
умения решать задачи, важна всесторонняя работа над одной задачей, в частности,
и решение её различными способами. Следует отметить, что решение задач
различными способами позволяет убедиться в правильности решения задачи даёт
возможность глубже раскрыть зависимости между величинами, рассмотренными в
задаче. Возможность решения некоторых задач разными способами основана на
различных свойствах действий или вытекающих из них правил. При решении задач
различными способами ученик привлекает дополнительную информацию, поскольку он
непроизвольно выполняет в большем числе выборы суждений, хода мысли из
нескольких возможных; рассматривается один и тот же вопрос с разных точек
зрения. При этом полнее используется активность учащихся, прочнее и
сознательнее запоминается материал. Как правило, различными способами решается
те из задач, где этого требует вопрос, поэтому такая работа носит эпизодический
характер.
В качестве основных в математике различают
арифметический и алгебраический способы решения задач. При арифметическом
способе ответ на вопрос задачи находится в результате выполнения арифметических
действий над числами. Арифметические способы решения задач отличаются друг от
друга одним или несколькими действиями или количеством действий, также
отношениями между данными, данными и искомым, данными и неизвестным,
положенными в основу выбора арифметических действий, или последовательностью
использования этих отношений при выборе действий.
При алгебраическом способе ответ на вопрос
задачи находится в результате составления и решения уравнения.
В зависимости от выбора неизвестного для
обозначения буквой, от хода рассуждений можно составить различные уравнения по
одной и той же задаче. В этом случае можно говорить о различных алгебраических
решениях этой задачи. Но надо отметить, что в начальных классах алгебраический
способ не применяется для решения задач [25].
Опираясь только на чертёж, легко можно дать
ответ на вопрос задачи. Такой способ решения называется графическим. До
настоящего времени вопрос о графическом способе решения арифметических задач не
нашёл должного применения в школьной практике. Графический способ даёт возможность
более тесно установить связь между арифметическим и геометрическим материалами,
развить функциональное мышление детей.
Следует отметить, что благодаря применению
графического способа в начальной школе можно сократить сроки, в течение которых
ученик научится решать различные задачи. В то же время умение графически решать
задачу - это важное политехническое умение.
Графический способ даёт иногда возможность
ответить на вопрос такой задачи, которую дети ещё не могут решить
арифметическим способом и которую можно предлагать во внеклассной работе.
Решение задач различными способами - дело
непростое, требующее глубоких математических знаний, умения отыскивать наиболее
рациональные решения.
В начальных классах ведется работа над группами
задач, решение которых основывается на одних и тех же связях между данными и
искомым, а отличаются они конкретным содержанием и числовыми данными. Группы
таких задач называются задачами одного вида Работа над задачами не должна
сводится к натаскиванию учащихся на решение задач сначала одного вида, а затем
другого и т.д. Главная ее цель - научить детей осознано устанавливать
определенные связи между данными и искомым в разных жизненных ситуациях,
предусматривая постепенное их усложнение. Чтобы добиться этого, учитель должен
предусмотреть в методике обучения решению задач каждого вида такие ступени:
Подготовительную работу к решению задач;
Ознакомление с решением задач;
Закрепление умения решать задачи
а) Подготовительная работа к решению задач
На этой ступени обучения решению задач того или
другого вида должна быть создана у учащихся готовность к выбору арифметических
действий при решении соответствующих задач: они должны усвоить знание тех
связей, на основе которых выбираются арифметические действия, знание объектов и
жизненных ситуаций, о которых говорится в задачах [23].
До решения простых задач ученики усваивают
знание следующих связей:
Связи операций над множествами с арифметическими
действиями, то есть конкретный смысл арифметических действий. Например,
операция объединения непересекающихся множеств связана с действием сложения;
если имеем 4 и 2 флажка, то чтобы узнать, сколько всего флажков, надо к 4
прибавить 2;
Связи отношений «больше» и «меньше» (на сколько
единиц и в несколько раз) с арифметическими действиями, то есть конкретный
смысл выражений «больше на…», «больше в … раз», «меньше на…», «меньше в … раз».
Например, больше на 2, это столько же и еще 2, значит, чтобы получить на 2
больше, чем 5, надо к 5 прибавить 2.
Связи между компонентами и результатами
арифметических действий, то есть правила нахождения одного из компонентов
арифметических действий по известному результату и другому компоненту.
Например, если известна сумма и одно из слагаемых, то другое слагаемое
находится действием вычитания. Из суммы вычитают известное слагаемое.
Связи между данными величинами, находящихся в
прямо или обратно пропорциональной зависимости, и соответствующими
арифметическими действиями. Например, если известна цена и количество, то можно
найти стоимость действием умножения.
Кроме того, при ознакомлении с решением первых
простых задач, ученики должны усвоить понятия и термины, относящиеся к самой
задаче и ее решению (задача, условие задачи, вопрос задачи, решение задачи,
ответ на вопрос задачи).[7] Подготовкой к решению составных задач будет умение
вычленять систему связей, иначе говоря, разбивать составную задачу на ряд
простых, последовательное решение которых и будет решением составной задачи.
При работе над каждым отдельным видом задач требуется своя специальная
подготовительная работа.
б) Ознакомление с решением задач.
На этой второй ступени обучения решению задач
дети учатся устанавливать связи между данными и искомым и на этой основе
выбирать арифметические действия, то есть они учатся переходить от конкретной
ситуации, выраженной в задаче к выбору соответствующего арифметического
действия. В результате такой работы учащиеся знакомятся со способом решения
задач рассматриваемого вида.
В методике работы на этой ступени выделяются
следующие этапы:
этап - ознакомление с содержанием задачи;
этап - поиск решения задачи;
этап - выполнение решения задачи;
этап - проверка решения задачи.
Выделенные этапы органически связанны между
собой, и работа на каждом этапе ведется на этой ступени преимущественно под
руководством учителя.
. Ознакомление с содержанием задачи. Ознакомится
с содержанием задачи - значит прочитать ее, представить жизненную ситуацию,
отраженную в задаче. Читают задачу, как правило, дети. Учитель читает задачу
лишь в тех случаях, когда у детей нет текста задачи или когда они еще не умеют
читать. Очень важно научить детей правильно читать задачу: делать ударение на
числовых данных и на словах, которые определяют выбор действий, таких как
«было», «убрали», «осталось», «стало поровну» и т.п., выделять интонацией
вопрос задачи. Если в тексте задачи встретятся непонятные слова, их надо
пояснить или показать рисунки предметов, о которых говорится в задаче. Задачу
дети читают один - два, а иногда и большее число раз, но постепенно их надо
приучать к запоминанию задачи с одного чтения, так как в этом случае они будут
читать задачу более сосредоточенно [31].
Читая задачу, дети должны представлять ту
жизненную ситуацию, которая отражена в задаче. С этой целью полезно после
чтения предлагать им представить себе то, о чем говорится в задаче, и
рассказать, как они представили.
. Поиск решения задачи. После ознакомления с
содержанием задачи нужно приступить к поиску ее решения: ученики должны
выделить величины, входящие в задачу, данные и искомые числа, установить связи
между данными и искомыми и на этой основе выбрать соответствующие
арифметические действия.
При введении задач нового вида поиском решения
руководит учитель, а затем учащиеся выполняют это самостоятельно.
В том и другом случае используются специальные
приемы, которые помогают детям вычленить величины, данные и искомые числа,
установить связи между ними. К таким приемам относятся иллюстрация задачи,
повторение задачи, разбор и составление плана решения задачи.
Рассмотри каждый из этих приемов.
Иллюстрация задачи - это использование средств
наглядности для вычисления величин, входящих в задачу, данных и искомых чисел,
а также для установления связей между ними. Иллюстрация может быть предметной
или схематичной. Предметная иллюстрация помогает создать яркое представление
той жизненной ситуации, которая описывается в задаче. Ею пользуются только при
ознакомлении с решением задач нового вида и преимущественно в 1 классе. Для
иллюстрации задачи используются либо предметы, либо рисунки предметов, о
которых идет речь в задаче: с их помощью иллюстрируется конкретное содержание
задачи [31].
Наряду с предметной иллюстрацией, начиная с 1
класса, используется и схематическая - это краткая запись задачи.
В краткой записи фиксируются в удобообразной
форме величины, числа - данные и искомые, а также некоторые слова,
показывающие, о чем говорится в задаче: «было», «положили», «стало» и т.п. и
слова, означающие отношения: «больше», «меньше», «одинаково» и т.п.
Краткую запись задачи можно выполнять в таблице
и без нее, а так же в форме чертежа. При табличной форме требуется выделение и
название величины. Расположение числовых данных помогает установлению связей,
между величинами: на одной строке записываются соответствующие значения
различных величин, а значения одной величины записываются одно под другим.
Искомое число обозначается вопросительным знаком. Многие задачи можно
иллюстрировать чертежом. Иллюстрирование в виде чертежа целесообразно
использовать при решении задач, в которых даны отношения значений величин
(«больше», «меньше», «столько же»). Одно из чисел данных в задаче (число детей,
число метров в материи) изображают отрезком, задав определенный масштаб (без
употребления этого слова) и используя данные в задаче соотношения этого числа и
других чисел, изображают эти числа (в 2 раза больше, на 4 кг меньше)
соответствующим отрезком.
Задачи, связанные с движением, также можно
иллюстрировать с помощью чертежа.
Используя иллюстрацию, ученики могут повторить
задачу. При повторении лучше, чтобы дети объясняли, что показывает каждое число
и что требуется узнать в задаче.
При ознакомлении с задачей нового вида, как
правило, используется какая- либо одна иллюстрация, но в отдельных случаях
полезно выполнить предметную и схематичную иллюстрацию.
В процессе выполнения иллюстрации некоторые дети
находят решение задачи, то есть они уже знают, какие действия надо выполнить,
чтобы решить задачу. Однако часть детей может установить связи между данными и
искомыми выбрать соответствующее арифметическое действие только с помощью
учителя. В этом случае учитель проводит специальную беседу, которая называется
разбором задачи [31].
Рассуждение можно строить двумя способами: идти
от вопроса задачи к числовым данным или же от числовых данных идти к вопросу.
Чаще следует использовать первый способ
рассуждения, так как при этом ученик должен иметь в виду не одно выделенное
действие, а все решение в целом. При использовании второго способа разбора
учитель прямо подводит их к выбору каждого действия. Кроме того, такое
рассуждение может привести к выбору «лишних действий».
Разбор составной задачи заканчивается
составлением плана решения - это объяснение того, что узнаем, выполнив то или
иное действие, и указание по порядку арифметических действий.
Решение задачи - это выполнение арифметических
действий, выбранных при составлении плана решения. При этом обязательны
пояснения, что находим, выполняя каждое действие. Надо учить детей правильно и
кратко давать пояснения к выполняемым действиям.
Решение задачи может выполняться устно и
письменно.
В начальных классах могут быть использованы
такие основные формы записи решения:
Составление по задаче выражения и нахождение его
значения;
Запись решения в виде отдельных действий с
пояснением или без них;
С вопросами;
Проверка решения задач. Проверить решение задачи
- значит установить, что оно правильно или ошибочно. [39]
В начальных классах используются следующие
четыре способа проверки:
Составление и решение обратной задачи. В этом
случае детям предлагается составить задачу, обратную по отношению к данной: то
есть преобразовать данную задачу так, чтобы искомое данной задачи стало данным
числом, а одно из данных чисел стало искомым. Если при решении обратной задачи
в результате получится число, которое было известно в данной задаче, то можно
считать, что данная задача решена правильно.
Установление соответствия между числами,
полученными в результате решения задачи, и данными числами. При проверке
решения задачи этим способом выполняют арифметические действия над числами,
которые получаются в ответе на вопрос задачи, если при этом получатся числа,
данные в условии задачи, то можно считать, что задача решена правильно.
Решение задачи другим способом. Если задачу
можно решать различными способами, то получение одинаковых результатов
подтверждает, что задача решена правильно.
Прикидка ответа - то есть до решения задачи
устанавливается больше или меньше какого- то из данных чисел должно быть
искомое число.
в)Закрепление умения решать задачи.
Одним из важных условий для правильного
обобщения младшими школьниками способа решения задач определенного вида
является решение достаточного числа их. Однако, задачи рассматриваемого вида
должны включаться не подряд, а рассредоточено: сначала включаются чаще, а потом
все реже и реже, вместе с другими видами. Это необходимо для того, чтобы
предупредить запоминание способа решения[5].
Выработке умения решать задачи нового вида
помогают упражнения на сравнение решений задач этого вида и ранее рассмотренных
видов, но сходных в каком- то отношении с задачами нового вида и ранее
рассмотренных видов, но сходных в каком- то отношении с задачами нового вида.
Такие упражнения предупреждают смешение способов решения задач этих видов.
Выработке умения решать задачи рассматриваемого
вида помогают так называемые упражнения творческого характера. К ним относятся
решение задач повышенной трудности, решение задач несколькими способами,
решение задач с недостающими и лишними данными, решение задач, имеющих
несколько решений, а так же упражнения в составлении и преобразовании задач.
К задачам повышенной трудности относят такие
задачи, в которых связи между данными и искомым выражены необычно, так же
задачи, вопрос которых сформулирован нестандартно, например: «Хватит ли 50
руб., чтобы купить две книги по 18 руб. и ручку за 8 руб.?»
Решение задач повышенной трудности помогает
выработать у детей привычку вдумчиво относиться к содержанию задачи и
разносторонне осмысливать связи между данными и искомым. Задачи повышенной
трудности следует предлагать в любом классе, имея в виду одно условие: детям
должно быть известно решение обычных задач, к которым сводится решение
предлагаемой задачи повышенной трудности.
Многие задачи могут быть решены различными
способами. Поиск различных способов решения приводит детей к «открытию» новых
связей между данными и искомым [7].
Работа над задачами с недостающими и лишними
данными воспитывает у детей привычку лучше отыскивать связи между данными и
искомым.
Полезно включать и решение задач, имеющих
несколько решений. Решение таких задач будет способствовать формированию
понятия переменной.
Упражнения по составлению и преобразованию задач
являются чрезвычайно эффективными для обобщения способа их решения.
Рассмотрим некоторые виды упражнений по
составлению и преобразованию задач:
Постановка вопроса к данному условию задачи или
изменение данного вопроса. Такие упражнения помогают обобщению знаний о связях
между данными и искомым, так как при этом дети устанавливают, что можно узнать
по определенным данным.
Составление условия задачи по данному вопросу.
При выполнении таких упражнений учащиеся устанавливают, какие данные надо
иметь, чтобы найти искомое, а это так же приводит к обобщению знаний связей
между данными и искомым.
Подбор числовых данных.
Составление задач по аналогии. Аналогичными
называются задачи, имеющие одинаковую математическую структуру. Аналогичные
задачи надо составлять после решения данной готовой задачи, предлагая при этом,
когда возможно, изменять не только сюжет и числа, но и величины.
Составление обратных задач. Упражнения в
составлении и решении обратных задач помогают усвоению связей между данными и
искомым.
Составление задач по их иллюстрациям. Они
помогают детям увидеть задачу в данной конкретной ситуации.
Составление задач по данному решению. Предлагая
составить задачу, надо сначала проанализировать данное решение задачи. В
отдельных случаях целесообразно подсказать детям сюжет или же назвать
величины.[7]
Вывод: Научить детей решать задачи - значит
научить их устанавливать связи между данными и искомым и в соответствии с этим
выбрать, а затем и выполнить арифметические действия. Для того чтобы научиться
решать задачи, надо разобраться в том, что собой они представляют, как они
устроены, из каких составных частей они состоят, каковы инструменты, с помощью
которых производится решение задач.
2.2 Модель текста задачи как основа
наглядно-образного мышления младших школьников
Мышление школьников при изучении математики
строится не только на основе общих психологических механизмов и операций,
адекватных усвоению научного знания, но и включает формирование специфических
механизмов, моделирующих существенные признаки и способы описания познаваемых
объектов, выраженные в использовании символьно-вербальных и символьно-формульных
способов представления информации.
В общей системе обучения задачи играют особую
роль. Через решение задач осуществляется необходимая связь теоретических знаний
с практикой, умение решать задачи определяет степень обученности, общей
подготовленности детей. В них заложены большие возможности для повышения
общего и математического образования школьников: развитие смекалки, начал
исследовательской работы, логического мышления. Раздел обучения решению задач
считается наиболее трудным. И это естественно, т. к. решение задач вообще и
математических в частности процесс творческий, требующий продуктивного
подхода, проникновения в скрытые в каждой задаче связи и зависимости, которые
зачастую могут быть необычными, нестандартными, а иногда уникальными [31].
Школа должна формировать у детей истинное
умение решать задачи, которое заключается в способности решить любую задачу,
доступного для данного возраста уровня трудности, если в ней отсутствуют
незнакомые понятия и если для решения не требуется выполнить незнакомые
операции.
Для начальной школы эти требования означают,
что в тексте задачи каждое слово должно быть детям понятно и решение задач
должно требовать выполнение изученных на данном этапе операций. Текстовые
задачи являются тем богатейшим материалом, на котором будет решаться важнейшая
задача преподавания математики - развитие мышления и творческой активности
учащихся.
В соответствии с теорией поэтапного формирования
умственных действий (П.Я. Гальперин), предлагается с самого начала обучения
решению задач формировать у учащихся общее умение анализировать задачи.
Известно, что решение текстовых задач
представляет большие трудности для учащихся. Известны и то, какой именно этап
решения особенно труден. Это самый первый этап - анализ текста задачи.
По мнению Салминой Н.Г., которая считает, что «…
задача всегда представляет собой некую модель явления или процесса, отражающую
(в математической задаче) количественную сторону этого явления или процесса,
выраженную через систему необходимых компонентов, функциональная зависимость
между которыми и должна быть вскрыта путем анализа.»
Текст задачи - это рассказ о некоторых жизненных
фактах:
У мальчика Димы в трех коробках лежали гвозди,
винты и гайки…
Из листа бумаги вырезали треугольник…
Таня, Коля и папа отправились в поход…
Число яблок в корзине - двузначное…
В тексте важно все: и действующие лица, и их
действия, и числовые характеристики. При работе с математической моделью задачи
(числовым выражением или уравнением) часть этих деталей опускается. Но мы
именно и учим умению абстрагироваться от некоторых свойств и использовать
другие [27].
Умение найти и составить план решения задачи
имеет решающее значение. Это умение вести рассуждение от «начала» и от «конца»
задачи. Способ рассуждений от данных к искомым величинам называется
синтетическим и, наоборот, от искомых (вопроса задачи) к данным (известным)
величинам называется аналитическим. Возможно их
комбинация-аналитико-синтетический способ рассуждений.
Синтетический способ характеризуется тем, что
основным, направляющим вопросом при поиске плана решения задачи является вопрос
о том, что можно найти по двум или нескольким известным в тексте задачи
числовым значениям. По вновь полученным числовым значениям и другим известным в
задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям.
И так до ответа на вопрос задачи. Суть этого способа состоит в вычленение
учащимися простых задач из составной и их решение. Обучение делению составных
задач помогает учащимся овладеть синтетическим способом рассуждений.
Аналитический способ рассуждения характеризуется
тем, что рассуждения начинается от вопроса задачи. Выясняется, что нужно
предварительно узнать, чтобы ответить на вопрос задачи. Выясняется, что для
этого надо найти «что-то». Вновь ставится вопрос: а что нужно знать, чтобы
найти это «что-то»? И т.д. до того, когда ответ на таким образом поставленный
вопрос имеется в условии задачи. После таких рассуждений составляется план
решения задачи [23].
Систематическая и целенаправленная работа по
формированию у учащихся рассмотренных умений будет содействовать развитию их
мышления.
Главная цель задач - развить творческое и
математическое мышление учащихся, заинтересовать их математикой, привести к
«открытию» математических фактов.
Прежде всего отметим, что научить учащихся
решать задачи можно только в том случае, если у учащихся будет желание их
решать, т.е. если задачи будут содержательными и интересными с точки зрения
ученика. Поэтому задача учителя - вызвать у учащихся интерес к решению той или
иной задачи. Одно бесспорно: наибольший интерес у учащихся вызывают задачи,
взятые из окружающей жизни, задачи, связанные со знакомыми вещами, опытом.
Важно показать детям, что от решения математической задачи можно получить такое
же удовольствие, как от разгаданного кроссворда или ребуса. Либо использовать
способы наглядно-образные, картинки, рисунки, графики.
Задачи не должны быть слишком легкими, но и не
слишком трудными, т.к. ученики, не решив задачу или не разобравшись в решении,
предложенном учителем, могут потерять веру в свои силы. В этом случае очень
важно соблюсти меру помощи. Прежде всего учитель не должен знакомить учащихся с
уже готовым решением. Подсказка должна быть минимальной.
Рассмотрим примеры решения таких задач, с тем
чтобы выяснить особенности процесса их решения.
Задача 1 . В трех ящиках 300 яблок. Число яблок
первого ящика составляет половину числа яблок второго ящика и треть числа яблок
третьего ящика. Сколько яблок в каждом ящике?
Решение. Эта задача является практической
(текстовой). Для подобных задач никакого общего правила, определяющего точную
программу их решения не существует. Однако, это не значит, что вообще нет
каких-либо указаний для решения таких задач.
Обозначим количество яблок в первом ящике через
х. Тогда во втором ящике было 2х яблок, в третьем - 3х. Следовательно, сложив
все числа х+2х+3х мы должны получить 300 яблок. Получаем уравнение х+2х+3х=300.
решив уравнение, найдем: х=50 яблок, 2х=100 яблок, 3х=150 яблок. Значит, в
первом ящике было 50 я., во втором -100 я., в третьем -150 я. [25]
Проанализируем процесс приведенного решения
задачи. Сначала мы определили вид задачи «текстовая задача», и, исходя из
этого, возникла идея решения («составить уравнение»). Для этого, пользуясь
весьма общими указаниями и образцами решения подобных задач, полученных на
уроках («надо обозначить одно из неизвестных буквой, например х, и выразить
остальные неизвестные через х, затем составить равенство из полученных
выражений»), мы построили уравнение. Заметим, что эти указания, которыми мы
пользовались, не являются правилами, ибо в них ничего не сказано, какое из
неизвестных обозначить через х, как выразить остальные неизвестные через х, как
получить нужное равенство и т.д. Все это делается каждый раз по-своему, исходя
из условий задачи и приобретенного опыта решения подобных задач.
Полученное уравнение представляет собой уже
стандартную задачу. Решив её, мы тем самым решили и исходную нестандартную
задачу.
Смысл решения данной задачи состоит в том, что с
помощью особого приема (составление уравнения) мы свели её решение к решению
стандартной задачи.
Задача 2. В магазин «Цветы» привезли 30 желтых
тюльпанов и столько же красных. Каждые 3 желтых тюльпана стоили 20 руб., а
каждые 2 красных тюльпана стоили 30 руб. Продавец сложила все эти тюльпаны
вместе и решила сделать букеты по 5 тюльпанов и продавать их по 50 руб.
Правильно ли она рассчитала?
Решение. Найдем стоимость всех тюльпанов, если
бы продавец не складывала тюльпаны вместе (реальную стоимость).
20х30:3+30х30:2=650 руб.
Найдем стоимость тюльпанов в том случае, когда
продавец сложила их по 5 в букеты и стала продавать по 50 руб. (предполагаемая
стоимость).
(30+30):5х50=600 руб.
Сравниваем реальную и предполагаемую стоимость
тюльпанов 650 руб. > 600 руб. Обнаруживаем, что расчет продавца ошибочен,
т.к. при сложении всех тюльпанов и продажи их по 5 шт. в букетах она теряет 50
руб.
Процесс решения этой задачи состоит в следующем:
данную задачу мы разбили на такие подзадачи:
) нахождение реальной стоимости;
) нахождение предполагаемой стоимости;
) сравнение полученных стоимостей и вывод
о расчете продавца.
Решив эти стандартные подзадачи, мы в конечном
итоге решаем и исходную задачу [23].
Методика рассматривает несколько методов решения
задач- алгебраический, арифметический, графический, практический, метод
предположения, метод перебора. Они могут применяться как при решении
стандартных задач, так и нестандартных.
Алгебраический метод решения задач развивает
теоретическое мышление, способность к обобщению, формирует абстрактное мышление
и обладает такими преимуществами, как краткость записи и рассуждений при
составлении уравнений, экономит время. Арифметический метод решения также
требует большого умственного напряжения, что положительно сказывается на
развитии умственных способностей, математической интуиции, на формировании
умения предвидеть реальную жизненную ситуацию. Часто встречаются задачи,
которые можно решить методом перебора. При этом ученик как бы экспериментирует,
наблюдает, сопоставляет факты и на основании частных выводов делает те или иные
общие заключения. В процессе этих наблюдений обогащается его
реально-практический опыт. Именно в этом и состоит практическая ценность задач
на перебор. При этом слово «перебор» используется в смысле разбора всех возможных
случаев, которые удовлетворяют условие задачи, показав, что других решений быть
не может. Встречаются задачи, в которых алгебраический или арифметический метод
недостаточно эффективен. В этом случае при поиске решения используется метод
предположения [31].
Полноценное обучение математике невозможно без
понимания детьми происхождения и значимости математических понятий, роли
математики в жизни общества и в системе наук. Реальные объекты и процессы
бывают столь многогранны и сложны, что лучшим способом их изучения часто
является построение и исследование вспомогательной модели, отражающей лишь
какую-то сторону реальности и потому более простую, чем сама реальность.
Математическая модель - это описание какого либо процесса на математическом
языке. Одной из основных задач школьного курса математики является раскрытие
перед учащимися трех этапов формирования математического знания: построение
математической модели некоторого фрагмента реальной действительности; изучение
математической модели и приложение полученных результатов к реальному миру.
Основное содержание математики начальных классов составляют понятие
натурального числа, действия с числами. С теоретико-множественных позиций
количественное натуральное число является общим свойством класса конечных равномощных
множеств, которые различны по своей сути, но все содержат одинаковое количество
элементов. Каждый класс таких множеств может быть представлен каким то одним
множеством, например, множеством палочек или точек, которые можно рассматривать
как модели числа. В основе сложения чисел лежит операция объединения попарно -
непересекающихся множеств, а в основе вычитания - удаление части множества.
Поэтому при изучении сложения и вычитания чисел полезно выполнение предметных
действий с совокупностями предметов, их интерпретация в виде графических и
символических моделей, а затем запись числовым выражением [31]. При работе с
разрядным числом необходимо использование различных моделей: палочек и пучков
палочек, полосок, квадратов и другого математического счетного материала.
Удобно изображение модели однозначных чисел в виде набора точек, а десятка,
сотни - в виде треугольника (10 точек удобно располагать треугольником),
двузначных чисел - в виде треугольников и точек, то есть числовой фигуры.
Например, число 14 можно представить так:


При сложении и вычитании круглых чисел можно
выполнять предметные действия с треугольниками или изображать их в тетради:
+
=
д + 2 д = 5 д. 30 + 20
= 50
При сложении и вычитании двузначных чисел:
- =
д 3 е - 3 д 2 е = 1 д 1 е 43 - 32 =
11
Анализируя аналогичные примеры, учащиеся сами
сделают выводы: - при сложении единицы складывают с единицами, а десятки с
десятками; при вычитании единицы вычитают из единиц, а десятки из десятков.
Работая с такими моделями, учащиеся могут представить наглядно и «изобрести»
любой вычислительный прием. Аналогично работа проводится и с трехзначными
числами. Сначала внутри треугольника помещаем 10 маленьких треугольников,
символизирующих десятки, затем, моделью сотни служит просто треугольник больших
размеров. Если при выполнении вычислений возникает необходимость дробления
сотни на десятки, то этот треугольник заполняется маленькими треугольниками.
В начальном курсе математики большое внимание
уделяется решению задач. Любую задачу можно рассматривать как словесную модель
некоторой практической ситуации с требованием дать количественную
характеристику какого-либо компонента или установить наличие отношения между
компонентами этой ситуации. Наибольшую трудность для учащихся в решении задачи
представляет перевод текста с естественного языка на математический, т.е. запись
решения. Для облечения поиска решения задачи детей необходимо учить
пользоваться вспомогательными моделями: предметами, схемами, таблицами,
рисунками [39]. Для установления отношений между величинами, данными и искомыми
в задаче, удобно использование в качестве модели линейных схем, которые
являются одновременно краткой записью задачи. Еще до знакомства с задачей
учащихся нужно учить устанавливать соответствие между предметными, текстовыми,
схематическими и символическими моделями, которые они смогут использовать для
интерпретации текста задачи. Тогда процесс решения задачи можно рассматривать
как переход от одной модели к другой: от словесной модели реальной ситуации,
представленной в задаче, к вспомогательной, от нее - к математической. Такие
модели в сочетании с заданиями на сравнение, выбор, преобразование,
конструирование способствуют формированию умения решать задачи. Например,
задания на подбор схемы к тексту задачи, подбор выражения к рисунку,
преобразование условия (вопроса) задачи в соответствии с изменением решения и
наоборот, и т.п. Использование вспомогательных моделей является средством,
которое помогает младшим школьникам усвоить многие математические понятия.
Основная задача школьного учебного предмета
математики состоит в том, чтобы привести учащихся "к возможно более ясному
пониманию концепции действительного числа". Основы этой концепции должны
усваиваться детьми уже в начальной школе. Это значит, что детям с самого начала
должно быть раскрыто общее основание всех видов действительного числа. Таким
основанием является понятие величины [23].
Многообразие чисел, объединенных концепцией
действительного числа, является конкретизацией понятия величины.
Усвоение детьми концепции действительного числа
должно начинаться с овладения ими понятием величины и с изучения её общих
свойств. Тогда все виды действительного числа могут быть усвоены детьми на
основе конкретизации этих свойств. В таком случае, идея действительного числа
будет присутствовать в обучении математике с самого его начала.
Понятие величины связано с отношением
"равно", "больше", "меньше". Множество каких-либо
предметов тогда претворяется в величину, когда устанавливаются критерии,
позволяющие установить, будет ли А равно В, больше В или меньше В. В качестве
примера математической величины В.Ф.Каган рассматривает натуральный ряд чисел,
так как с точки зрения такого критерия, как положение, занимаемое числами в
ряду, этот ряд удовлетворяет определенным постулатам и поэтому представляет
собой величину. Совокупность дробей также претворяется в величину, а правильное
установление критериев сравнения для множества иррациональных чисел (для
претворения его в величину) составляет основу современного построения анализа.
Свойства величин раскрываются при оперировании
человеком реальными длинами, объемами, грузами, промежутками времени и т.д.
(или же при их выражении числами). Возможность организации реальных действий по
преобразованию величин допускает введение соответствующего учебного материала
уже в 1 -м классе.
В основу обучения математике положена концепция
действительного числа. Однако, в отличие от обычной программы, в обучении
предусматривается такой вводный раздел, при усвоении которого дети специально
изучают генетически исходное основание последующего выведения всех видов
действительного числа, а именно изучают понятие величины [27].
Структуру задачи можно представить с помощью
различных моделей. Все модели принято делить на:
предметные (вещественные);
графические;
символические.
К графическим моделям относят рисунок, условный
рисунок, чертеж, схематический чертеж (или схему). В педагогической работе
важное значение имеют предсхематические действия ребенка, результатом которых
являются рисунок и условный рисунок.
Знаковая модель задачи может выполняться как на
естественном языке (т.е. имеет словесную форму), так и на математическом (т.е.
используются символы).
Знаковая модель задачи, выполненная на
естественном языке, -это общеизвестная краткая запись.
Знаковая модель задачи, выполненная на
математическом языке, имеет вид выражения: "3+2".
Психологи и многие математики рассматривают
процесс решения задачи как процесс поиска подходящей модели и её
преобразования. Каждая модель выступает как одна из форм отображения сущности
(структуры) задачи, а преобразование её идет по пути постепенного обобщения,
абстрагирования и, в конечном результате, построения её математической модели.
Таким образом, чтобы решить задачу, надо построить её математическую модель, но
помочь в этом могут другие модели, называемые вспомогательными.
Чтобы самостоятельно решать задачи, ученик
должен освоить различные виды моделей, научиться выбирать модель,
соответствующую предложенной задаче, и переходить от одной модели к другой.
Необходимо отметить, что в данной работе я не
касаюсь краткой записи условия задачи. Этот этап очень важен, однако, я
исходила из того, что он традиционно присутствует в работе учителя. Поэтому
главное внимание я уделяю тем приемам работы над задачей, которые в меньшей
степени используются в традиционной системе, которые помогают мне пробудить у
детей интерес к задаче, к поиску решений этой задачи [31].
При решении простых и составных задач на
сложение и вычитание используется схематический чертеж.
Схематический чертеж прост для восприятия, так
как:
наглядно отражает каждый элемент отношения, что
позволяет ему оставаться и при любых преобразованиях данного отношения;
обеспечивает целостность восприятия задачи;
позволяет увидеть сущность объекта в
"чистом" виде без отвлечения на частные конкретные характеристики
(числовые значения величин, яркие изображения и др.), что трудно сделать,
используя другие графические модели;
обладая свойствами предметной наглядности,
конкретизирует абстрактные отношения, что нельзя увидеть, например, выполнив
краткую запись задачи;
обеспечивает поиск плана решения, что позволяет
постоянно соотносить физическое (или графическое) и математическое действия.
Как было сказано выше, текстовые задачи на
сложение-вычитание в 1-м классе строятся как частные случаи отношения величин,
поэтому моделирование простой задачи у детей не вызывало затруднения, т.к.
величины в задаче находятся в отношении целого и частей.
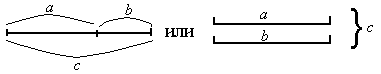
Рис.3 Схематический чертеж.
Если величины связаны отношением
"больше (меньше) на" (Рис. 4.); Сравнение двух величин (Рис. 5.).
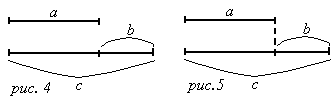
Освоение представлений графической,
знаково-символической модели в 1-м классе.
Со схемами в системе
Д.Б.Эльконина-В.В.Давыдова дети знакомятся с первых уроков, когда находят среди
разных предметов одинаковые по какому-либо признаку: длине, площади, форме,
объему [40].
Учащимся выдается набор полосок
разных по длине, ширине и цвету. Их задача найти равные по какому-либо
признаку. Сразу дети находят одинаковые по цвету, затем, путем наложения,
одинаковые по длине. Перед учащимися ставится следующая задача:
Что нужно сделать, чтобы каждый раз
не измерять полоски, а найти одинаковые сразу и быстро? Дети предлагают свои
варианты: различные значки, но значки должны быть одинаковые, и на одинаковых
полосках ставят значки.
А как записать в тетради, что среди
полосок есть одинаковые?
Ребята обсуждают задание и приходят
к выводу, что нужно зарисовать и поставить значки.
Далее дети выполняют более сложное
задание: сравнивают сосуды по объему и находят равные. Равные сосуды необходимо
запомнить, а лучше как-то отметить. Опять предлагаются значки.
Затем записывают в тетради с помощью
рисунка и значка, что на столе есть одинаковые по объему сосуды.
После этого дети находят сосуды,
одинаковые по другим признакам: материалу и высоте. Записывают в тетради, что
сосуды равны по высоте с помощью вертикальных отрезков.
На последующих уроках дети с помощью
схем учатся находить и определять равные и неравные величины показывать с
помощью схем равенство и неравенство величин (Рис. 6).
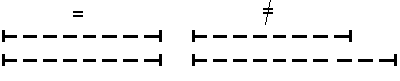
Рис.6
Через несколько уроков вводится
буквенная символика. Все величины обозначаются буквами русского алфавита.
На уроке с помощью весов ученики
устанавливают, что масса банки с водой и мешочка с песком одинакова. Затем дети
записывают равенство масс с помощью отрезков равной величины. Обсуждая схему,
дети приходят к выводу: величины необходимо обозначить, чтобы было понятно и
другим людям. Учитель предлагает обозначить с помощью букв. Буквы подписываются
и на предметах и на схеме (Рис.7).

Рис.7
Делается вывод, что о равенстве
величин можно сказать формулой: А = Б. (Масса "А" равна массе
"Б").
Итак, выполняя предметные действия
(на основе измерения разных величин), отображая эти действия графически,
сначала в виде рисунка, затем модели, учащиеся подходят к знаково-символической
форме: равенству, уравнению.
В задании 60 дети знакомятся с
понятиями "целое" и "части". Свои практические действия они
переносят на бумагу с помощью схем.
В этой теме появляются текстовые
задачи и уравнения, которые решаются с помощью, с опорой на схему. Работа со
схемой в текстовых задачах является продолжением, а не новым материалом, как в
традиционной системе, поэтому проходит легче, вызывая у детей интерес. Очень
важно этот интерес у детей поддержать различными видами работ со схемой,
которые помогли бы ребятам выбрать правильное решение задачи. Поэтому, на мой
взгляд, необходимо, чтобы схему дети составляли сами, без помощи учителя.
Составление схемы
К кормушке прилетело И синиц и К
воробьев. Сколько всего птиц в кормушке?
На доске вычерчиваются все схемы,
которые предлагают ребята. Каждая схема анализируется. После анализа остаются
правильные, из которых выделяется более удобная для выбора решения (Рис.8).
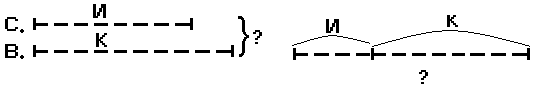
Рис.8
Из группы схем дети выбирают нужную
(Рис.9).
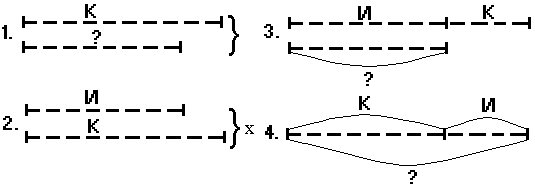
Рис.9
Выбрав схему 4, учащиеся объясняют
решение задачи: все птицы - это целое, которое состоит из двух частей: воробьев
и синиц, поэтому, чтобы найти, сколько всего птиц, нужно сложить К+И.
Анализируя после решения задачи
схему 2, можно перейти к составлению уравнений:
х - И = К х
= К + И
х - К = И х =
И + К.
3. Активно проходит работа по
составлению задач по схеме (Рис.10)
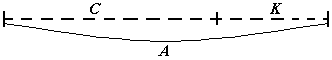
Рис.10
С + К = А, А - С = К
С помощью схемы можно дать понятие обратной
задачи. Дети решили задачу:" В кормушке было А воробьев, прилетели синицы
и стало М птиц. Сколько птиц прилетело?" (см. Рис. 11).
 A + x = M
A + x = M
Затем схема меняется (Рис. 12).
Рис.12
x + B = M
x
= M - B
По схеме дети должны изменить условие задачи и
уравнение к ней.
Во 2 - 4 классах работа над схемой продолжается.
При решении составных задач схема помогает не только найти различные способы
решения, но и выбрать самый рациональный, самый короткий. Например:"На
трех полках стояло 116 книг. Когда с первой полки сняли 8 книг, со второй - 12
книг, а с третьей - 6 книг, на всех полках осталось поровну. Сколько книг
стояло на первой полке первоначально?" [40]
Строится схема (Рис. 13).
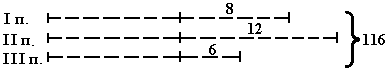
Рис.13
Дети анализируют задачу, а затем
предлагают свой способ решения. Обычно средние и слабые ученики предлагают:
8 + 6 = 14 или 116 -
8 = 108
14 + 12 = 26 108 -
12 = 96
116 - 26 = 90 96 - 6
= 90
90 : 3 = 30 90 : 3
= 30
30 + 8 = 38 30 + 8
= 38
Сильные ученики предлагают свой
вариант решения:
12 + 8 + 6 = 26
116 - 26 = 90
90 : 3 = 30
30 + 8 = 38
Все способы анализируются и
выясняется, что все решили правильно. Выбирается самый рациональный. Те ребята,
которые решили задачу рациональным способом, объясняют, что им помогло выбрать
этот способ. (По схеме видно, что все книги состоят из 2-х частей, тех, что
сняли и тех, которые остались на полках. Все книги, которые сняли - это целое.
Целое состоит из 3-х частей, снимали с трех полок, а целое мы узнаем действием
сложения, складываем все части).
При решении задач на умножение и
деление первоначально использовали чертеж.
"В одной коробке 6 карандашей.
Сколько карандашей в 3 таких коробках?"
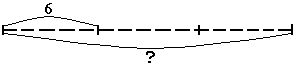
Рис.14
Использовался чертеж и при решении
задач на пропорциональное деление. Например: "Одно число больше другого в
6 раз, а их сумма составляет 350. Найти числа."
Рис.15
При решении задач на движение в
схему были сразу введены условные обозначения: S - сплошная дуга, V - стрелка,
t - пунктирная дуга.
"Навстречу друг другу
одновременно из двух деревень вышли две пешехода. Скорость одного из них 5
км/ч., а другого 4 км/ч. Через 2 час они встретились. Какое расстояние между
деревнями?".
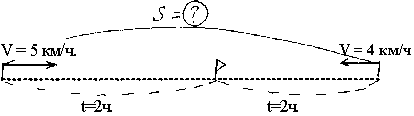
Рис.16
Четкие условные обозначение
позволяют детям строить сложные схемы, видеть в них нужные формулы, отношения
для решения задачи. Иногда мелочь в условных обозначениях, в схеме, позволяет
не запутаться в числовых значениях составной задачи.
Так при решении задач на приведение
к единице обозначение количества пунктирной дугой (на начальном этапе решения
таких задач) позволило более четко представлять условие задачи и не путаться в
числовых данных.

Рис.18
X + A = B
Ученики по чертежу устанавливают, что х - это
часть. Чтобы найти часть, нужно из целого вычесть известную часть А.
И в 3 - 4 классе, когда изучаются свойства
уравнения, схема снова приходит на помощь в проверке уравнений при доказательстве
свойств.
|
Решается
уравнение:
|
5
+ x - a = c x = c + a - 5.
|
Затем с помощью схемы проверяется: (Рис. 19).
Схемы помогают и при решении задач способом
составления уравнения. С помощью схемы составляются уравнения к задачам.
При составлении уравнений к задачам, как и при
решении задач на "приведение к единице", помогает краткая запись в
виде таблицы. По таблице ребята находят равные величины или величины, которые
можно уравнять.
Например: "За несколько пар коньков ценой
5000 руб. Заплатили 20.000рублей, а за столько же пар ботинок 96.000руб.
Сколько стоила пара ботинок?"
|
|
Цена
|
Количество
|
Стоимость
|
|
II
|
5000
|
I
= II
|
20.000
|
|
I
|
?(х)
|
I
= II
|
96.000
|
Одинаковая величина - количество. Эту величину
уравнивают, составляя уравнение:
I = 20.000 : 5.000 II = 96.000 : х
20.000 : 5000 = 96.000 : х
Способ краткой записи: таблицы или схему дети
выбирают сами, если предлагают обе, то обе выносятся на доску, обсуждается, что
больше помогает найти решение задачи или составить уравнение. Такая работа
проводится на начальном этапе, а затем при решении задач ребенок сам для себя
выбирает удобный способ записи условия задачи.
Вывод: Структуру задачи можно представить с
помощью различных моделей. Все модели принято делить на: предметные
(вещественные); графические; символические.
Психологи и многие математики рассматривают
процесс решения задачи как процесс поиска подходящей модели и её
преобразования. Каждая модель выступает как одна из форм отображения сущности
(структуры) задачи, а преобразование её идет по пути постепенного обобщения,
абстрагирования и, в конечном результате, построения её математической модели.
Заключение
Само понятие образного мышления подразумевает
оперирование образами, проведение различных операций (мыслительных) с опорой на
представления. Детям дошкольного возраста (до 5,5 - 6 лет) доступен именно
данный тип мышления. Они еще не способны мыслить абстрактно (символами),
отвлекаясь от реальности, наглядного образа. Поэтому усилия здесь должны быть
сосредоточены на формировании у детей умения создавать в голове различные
образы, т.е. визуализировать. Часть упражнений на развитие способности
визуализации описаны в разделе по тренировке памяти. Мы не стали повторяться и
дополнили их другими.
Примерно в возрасте 6 - 7 лет (с поступлением в
школу) у ребенка начинают формироваться два новых для него вида мышления -
словесно-логическое и абстрактное. Успешность обучения в школе зависит от
уровня развития этих типов мышления.
Недостаточное развитие словесно-логического
мышления приводит к трудностям при совершении любых логических действий
(анализа, обобщения, выделения главного при построении выводов) и операций со
словами. Упражнения по развитие этого вида мышления направлены на формирования
у ребенка умения систематизировать слова по определенному признаку, способности
выделять родовые и видовые понятия, развитие индуктивного речевого мышления,
функции обобщения и способности к абстракции. Надо отметить, что чем выше
уровень обобщения, тем лучше развита у ребенка способность к абстрагированию.
Недостаточное развитие абстрактно-логического
мышления - ребенок плохо владеет абстрактными понятиями, которые невозможно
воспринять при помощи органов чувств (например, уравнение, площадь и т. д.).
Функционирование данного типа мышления происходит с опорой на понятия. Понятия
отражают сущность предметов и выражаются в словах или других знаках.
Обычно этот тип мышления только начинает
развиваться в младшем школьном возрасте, однако в школьную программу уже
включаются задания, требующие решения в абстрактно-логической сфере. Это и
определяет трудности, возникающие у детей в процессе овладения учебным
материалом. Мы предлагаем упражнения, которые не просто развивают
абстрактно-логическое мышление, но и по своему содержанию отвечают основным
характеристикам данного типа мышления.
Методическая система математического развития
ребенка младшего школьного возраста, предоставляющая каждому ребенку условия
для индивидуального продвижения в математическом содержании будет
способствовать практическому созданию единой системы обучения математике и
достижению оптимально возможного для ребенка, соответствующего возрастному
этапу уровня математического развития.
Для решения данной проблемы требуются обширные
исследования. Мы проводили теоретический анализ литературных источников и
педагогический эксперимент. Полученные данные подтвердили актуальность изучения
моделирования текста задачи как средства развития математического мышления
младших школьников.
Обучение моделированию необходимо вести
целенаправленно, соблюдая ряд условий.
Во-первых, все математические понятия,
используемые при решении задач должны изучаться с помощью моделей.
Во-вторых, должна вестись работа по усвоению
знаково-символического языка, на котором строится модель. При этом ученик
осознает значение каждого элемента модели, осуществляя переход от реальности
(предметной ситуации) к модели, и наоборот, от модели к реальности.
В-третьих, необходимый этап обучения - освоение
моделей тех отношений, которые рассматриваются в задачах.
Только освоив модель отношений (т.е. осознав
суть этого отношения), учащийся научится использовать её как средство выделения
сущности любой задачи, содержащей это отношение.
Список использованной литературы
Айдарова
Л.И. Психологические проблемы обучения младших школьников. - М., 1978
Актуальные
проблемы методики обучения математике в начальных классах /Под ред. М.И. Моро,
A.M. Пышкало. - М., 1977.
Амоношвили
Ш.А., Загвязинский В.И. Паритеты, приоритеты в теории и практике
образования//«Педагогика, 2000. - №2. - С.3-7
Аргинская
И.И. Обучаем по системе Л.В. Занкова: Книга для учителя. - М.: Просвещение,
1991.
Баранова
И.В., Борчугова З.Г. Математика, 4 класс. Пробный учебник. М., Просвещение,
1968.
Бархаев
Ю. П. Особенности формирования навыков в учебной деятельности.- Харьков:
"Вестник Харьк. ун-та", 1978. - №171. С. 46-53.
Боданский
Ф.Г. Развитие математического мышления у младших школьников // Развитие психики
школьников в процессе учебной деятельности. Сб. науч. трудов. - М., 1983. - С.
115-125.
Брушлинский
А.В. Психология мышления и проблемное обучение. - М., 1985.
Возрастная
и педагогическая психология //Под ред. М.В. Гамезо. - М.: Просвещение. - 1984.
260 с.
Возрастная
и педагогическая психология. // Под ред. Петровского А.В. - М,1979 г.
Возрастные
возможности усвоения знаний (младшие классы школы) / Под ред. Д.Б. Эльконина,
В.В. Давыдова. - М., 1966.
Возрастные
и индивидуальные возможности образного мышления учащихся / Под ред. И.С.
Якиманской. - М., 1989.
Выготский
Л.В. Педагогическая психология.- М- Педагогика 1991г. с.143-221,137
Галанжина
E.С. Некоторые аспекты развития образного мышления младших школьников. // Искусство
в начальной школе: опыт, проблемы, перспективы. - Курск, 2001.
Гальперин
П.Я. Актуальные проблемы возрастной психологии. - М.: Просвещение, - 1978. -
360 с.
Давыдов
В.В. Основные проблемы развития мышления в процессе обучения //Хрестоматия по
возрастной и педагогической психологии. В 2ч. - М., 1970
Давыдов
В.В. Проблемы развивающего обучения; М.- Просвещение, 1988. -с.230
Дубровина
И.В. Психология: Учебник для студентов средних педагогических учебных
заведений. - М.: Издательский центр «Академия», 1999.
Елесина
Г.Е., Мульдаров В.К. Особенности действий детей 6-7 лет при переходе от
наглядно-действенного и образного мышления к мышлению о понятиях. -
//Психологическая наука и образование. - 1997. - №3. - С. 56-62.
Зак
А.З. Различие в мыслительной деятельности младших школьников. - Воронеж, 2000 .
Занков
Л.В. Обучение и развитие (экспериментально-педагогическое исследование) //
Избранные педагогические труды. - М., 1990.
Зимняя
И.А. Педагогическая психология. - М.: Логос, 2001
Истомина
Н.В. Методика обучения математике в начальных классах. - Ярославль, ЛИНКА -
ПРЕСС, 1997
Кабанова-Меллер
Е.Н. Психология формирования знаний и навыков у школьников. - М.: Изд-во АПН
СССР, 1962
Калмыкова
3.И. Психологический анализ формирования понятия о типе задачи. - Известия АПН
РСФСР, 1947, № 12.
Кожабаев
К.Б. О воспитательной направленности обучения математике в школе: Книга для
учителя. - М.: Просвещение, 1988.
Крутецкий
В.А. Психология математических способностей школьников. - М.: Просвещение,
1968.
Леонтьев
А.Н. Избранные психологические произведения. В 2х тт. - М., 1983
Менчинская
Н.А. Психологические вопросы развивающего обучения и новые программы. -
Советская педагогика. - 1968. - № 6. - С. 56-59.
Немов
Р.С. Психология. Книга 1. Общие основы психологии. М. 1998
Нуралиева
Г.В. Методика обучения математике в начальных классах: Учебное пособие для
учащихся школьных отделений педагогических училищ. 2-е изд., испр. -
Ставрополь: Ставропольсервисшкола, 1999.
Программы
начальной школы. М., Просвещение, 1989.
Пышкало
A.M., Давыдов В.В., Журова Л.Е. Концепция начального o6разования / Начальная
школа. - 1992. - № 7-8. - С. 23-36.
Рубинштейн
С. Л.. Основы общей психологии. СПб., 1998.
Слепкань
З.И. Психолого-педагогические основы обучения математике. - Киев, 1983.
Тихомирова
Л.Ф., Басов А.В. Развитие логического мышления детей. - Ярославль: ТОО
«Гринго», 1995
Фридман
Л.М. Психолого-педагогические основы обучения математике в школе. - М., 1983.
Фройдентпалъ
Г. Математика как педагогическая задача: Ч. 1. Пособие для учителей / Под ред.
Н.Я. Виленкина. - М., 1982.
Фуше
А. Педагогика математики. - М., 1969.
Эльконин
Д.Б. Психологическое развитие в детских возрастах. - М.: Просвещение. - 1995. -
247 с.
1.