Задачі цілочисельного програмування та спеціальні методи знаходження їх оптимальних розв'язків
ЗАДАЧІ ЦІЛОЧИСЕЛЬНОГО ПРОГРАМУВАННЯ
ТА СПЕЦІАЛЬНІ МЕТОДИ ЗНАХОДЖЕННЯ ЇХ ОПТИМАЛЬНИХ РОЗВ’ЯЗКІВ
Зміст
Вступ
Розділ 1. Цілочисельне програмування
1.1 Деякі історичні відомості
1.2 Постановка задачі
1.2 Приклади застосування цілочисельних задач лінійного
програмування у плануванні та управлінні виробництвом
Розділ 2. Методи розв´язання задач
цілочислового програмування
2.1 Геометрична інтерпретація розв’язків цілочислових задач
лінійного програмування на площині
2.2 Методи відтинання. Метод Гоморі
2.3 Комбінаторні методи. Метод гілок та меж
Розділ 3. Розробка математичної моделі складання розкладу занять на
математичному факультеті ВНУ
3.1 Формулювання завдання складання розкладу занять на
математичному факультеті
3.2 Математична модель розкладу у вузі
Висновки
Література
Додаток а. бібліографія
Вступ
Дипломна робота
присвячена задачам цілочисельного програмування та спеціальним методам
знаходження їх оптимальних розв’язків. В ній наведено конкретні приклади
застосування цілочисельних задач лінійного програмування у плануванні та
управлінні виробництвом, а також розроблено математичну модель розкладу занять
на математичному факультеті Волинського національного університету ім. Лесі
Українки.
Робота складається із
вступу, трьох розділів, висновків та списку використаної літератури, додатку в
якому подано відомості про вчених, авторів основних результатів роботи
У першому розділі
наведені деякі історичні відомості, подано загальну постановку задач
цілочисельного програмування та вказано спеціальні методи для знаходження
оптимальних розв’язків таких задач. Наведено конкретні приклади застосування
цілочисельних задач лінійного програмування у плануванні та управлінні
виробництвом.
Другий розділ присвячений
детальному розгляду методів задач цілочислового програмування, таких як
графічний метод, метод Гоморі та методу гілок і меж.
Третій розділ, в якому
містяться основні результати роботи, присвячений розробці математичної моделі
складання розкладу занять на математичному факультеті Волинського національного
університету ім. Лесі Українки.
Актуальність теми в тому, що математичне
програмування зараз проникло у всі інші науки, починаючи з біології і
психології і кінчаючи лінгвістикою. Навряд чи можна вказати сферу практичної і
духовної діяльності людини, де б не застосовувалися методи математичного
дослідження. Якщо раніше математичний апарат переважно використовувався як
інструмент розрахунку, то тепер ставиться завдання вибору найбільш ефективного
розв’язку проблеми, пошук оптимального варіанту.
Постановка завдання лінійного програмування
вперше прозвучала в роботах російського економіста А.Н. Товстого при складанні
плану перевезення вантажу між пунктами так, щоб загальний пробіг транспорту був
найменшим. Математичні основи для вирішення завдань лінійного програмування
були створені в 1939 році академіком Л.В. Канторовичем і його учнями. Методи
лінійного програмування набули широкого поширення при розв’язані економічних
задач, в плануванні виробництва, в сільському господарстві, у військовій
справі. Їх значущість підкреслюється тим, що вони реалізовані в прикладних
комп'ютерних програмах (MS Excel) і можуть використовуватися при необхідності
кожним, хто уміє працювати на ПК.
Розв’язують задачі про дієту, планування прибутку
підприємства або цеху, про розкрій матеріалів для виробництва продукції, про
рентабельність фермерського господарства, про перевезення вантажів або
пасажирів та інші. Це значною мірою може підвищити якість розроблювальних
планів, надійність та ефективність прийнятих рішень. Тому знання системи
лінійного програмування необхідні кожному спеціалісту в області прикладної
математики.
Мета і завдання дослідження:
розглянути методи розв’язання задач
цілочисельного програмування та визначити умови ефективності застосування
кожного з них до розв’язання задачі про складання розкладу занять;
побудувати математичну модель для складання
розкладу занять для студентів математичного факультету.
Об’єктом дослідження є оптимізація навчального
процесу студентів,що забезпечується ефективним розподілом навчальних аудиторій,
та щоденним академічним навантаженням викладачів.
цілочисельне програмування математичний розклад
Предметом дослідження є задача
пошуку оптимального розв’язку, що математично зводиться до задачі знаходження
умовного екстремуму функції багатьох змінних.
Практичне значення одержаних результатів. Результати
роботи можна використати на практичних заняттях при вивченні дисципліни
"Математичні моделі ЕЕС процесів" для студентів 5-го курсу
спеціальності "прикладна математика". Їх також можна запропонувати
для написання магістерської роботи з прикладної математики, ціллю якої було б
автоматизоване складання розкладу занять.
Апробація результатів. Результати
роботи доповідались на IV науково практичній конференції студентів та
аспірантів "Волинь очима науковців: минуле, сучасне, майбутнє" (12-13
травня 2010р., м. Луцьк).
Розділ
1. Цілочисельне програмування
1.1
Деякі історичні відомості
В суто математичному плані деякі оптимізаційні
задачі були відомі ще в стародавній Греції. Однак, сучасне математичне програмування
передусім розглядає властивості та розв’язки математичних моделей економічних
процесів. Тому початком його розвитку як самостійного наукового напрямку слід
вважати перші спроби застосування методів математичного програмування в
прикладних дослідженнях, насамперед в економіці. Початком математичного
програмування вважають праці радянського вченого Л.В. Канторовича. Наприкінці
30-х років у Ленінградському університеті ним уперше були сформульовані та
досліджувались основні задачі, критерії оптимальності, економічна
інтерпретація, методи розв’язання та геометрична інтерпретація результатів
розв’язання задач лінійного програмування (в 1939 році Л.В. Канторович
оприлюднив монографію "Математичні методи організації і планування
виробництва"). Сам термін "лінійне програмування" був введений
дещо пізніше, в 1951 році, у працях американських вчених Дж. Данцига та Г.
Кумпанса. Проте у своїй монографії Дж. Данциг зазначає, що Л.В. Канторовича
слід визнати першим, хто виявив, що широке коло важливих виробничих задач може
бути подане у чіткому математичному формулюванні, що дає можливість здійснити
підхід до таких задач з кількісного боку та розв’язати їх чисельними методами.
В 1947 році Дж. Данциг розробив основний метод
розв’язування задач лінійного програмування - симплексний метод, що стало
початком формування лінійного програмування як самостійного напрямку в
математичному програмуванні. Наступним кроком стали праці Дж. Неймана (1947 р.)
щодо розвитку концепції двоїстості, що сприяло розширенню практичної сфери
застосування методів лінійного програмування.
Періодом найінтенсивнішого розвитку математичного
програмування є п’ятдесяті роки. У цей час з’являються розробки нових
алгоритмів, теоретичні дослідження з різних напрямків математичного
програмування зокрема в 1951 році вийшла праця Г. Куна і А. Таккера, в якій
наведено необхідні та достатні умови оптимальності нелінійних задач; в 1954
році Чарнес і Лемке розглянули наближений метод розв’язання задач з
сепарабельним опуклим функціоналом та лінійними обмеженнями; в 1955 році
опубліковано ряд робіт, присвячених квадратичному програмуванню, крім того в
п’ятдесятих роках сформувався новий напрямок математичного програмування -
динамічне програмування, в розвиток якого значний вклад вніс американський
математик Р. Белман.
У період найбурхливішого розвитку математичного
програмування за кордоном у Радянському Союзі не спостерігалося значних
досягнень через штучні ідеологічні обмеження. Відродження досліджень з
математичного моделювання економіки почалося в 60-80-тих роках і стосувалося
опису "системи оптимального функціонування соціалістичної економіки".
Серед радянських вчених того періоду слід виокремити праці В.С. Немчинова, В.В.
Новожилова, Н.П. Федоренка, С.С. Шаталіна, В.М. Глушкова, В.С. Михалевича, Ю.М.
Єрмольєва та ін.
Першою задачею цілочислового типу яка була
опублікована угорським математиком Б. Егерварі в 1932 році, задача про
призначення персоналу. Систематичні дослідження цілочислового програмування
починаються з 1955р., коли на Другому симпозіумі з лінійного програмування була
розглянута задача про бомбардувальника, відома також як задача про ранець.
На сучасному етапі математичне програмування
включає широке коло задач з відповідними методами розв’язання, що охоплюють
різноманітні проблеми розвитку та функціонування реальних економічних систем.
Розробляються банки економіко-математичних моделей, які в поєднанні з потужною,
швидкодіючою обчислювальною технікою та сучасними програмними продуктами
утворюватимуть системи ефективної підтримки прийняття рішень у різних галузях
економіки.
1.2
Постановка задачі
Існує доволі широкий клас задач математичного
програмування, в економіко - математичних моделях яких одна або кілька змінних
мають набувати цілих значень. Наприклад, коли йдеться про кількість верстатів у
цеху, тобто коли така вимога випливає з особливостей технології виробництва. До
цілочислового програмування належать також задачі оптимізації, в яких змінні
набувають лише двох значень - 0 або 1 (бульові або бінарні змінні). До
цілочислового програмування відносять задачі про призначення, про найкоротший
шлях і т. ін. У реальних задачах часто цілочислових значень набувають не всі, а
одна чи кілька змінних. Такі задачі називають частково цілочисловими.
Задача цілочислового програмування записується
так:
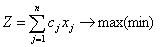 , (1.1)
, (1.1)
за умов
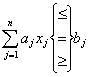 ;
; 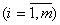 (1.2)
(1.2)
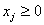
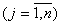 (1.3)
(1.3)
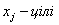
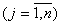 (1.4).
(1.4).
Для знаходження оптимального розв'язку цілочислових задач
застосовують спеціальні методи. Найпростішим методом розв'язування цілочислової
задачі є знаходження її оптимального розв'язку як задачі, що має лише
неперервні змінні, з подальшим округленням останніх. Такий підхід часто є
виправданим.
Для знаходження оптимальних планів задач цілочислової
програмування застосовують дві основні групи методів:
– методи відтинання;
– комбінаторні методи.
Основою методів відтинання є ідея поступового
"звуження" області допустимих розв'язків розглядуваної задачі. Пошук
цілочислового оптимуму починається з розв'язування задачі з так званими
послабленими обмеженнями, тобто без урахування вимог цілочисловості
змінних. Далі вводяться у модель спеціальні додаткові обмеження, що враховують
цілочисловість змінних, многокутник допустимих розв'язків послабленої задачі
поступово зменшуємо доти, доки змінні оптимального розв'язку не набудуть
цілочислових значень. До цієї групи належать:
методи розв'язування повністю цілочислових задач
(дробовий алгоритм Гоморі);
методи розв'язування частково цілочислових задач
(другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).
Комбінаторні методи цілочислової оптимізації
базуються на повному переборі всіх допустимих цілочислових розв'язків, тобто
вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається
лише частина розв'язків (досить невелика), а решта враховується одним зі
спеціальних методів.
Найпоширенішим у цій групі методів є метод віток
і меж. Починаючи з розв'язування послабленої задачі, він передбачає розбиття
початкової задачі на дві підзадачі виключенням областей, що не мають
цілочислових розв'язків, і дослідженням кожної окремої частини многокутника
допустимих розв'язків.
Для розв'язування задач із бульовими змінними
застосовують комбіновані методи, причому оскільки змінні є бульовими, то методи
пошуку оптимуму значно спрощуються.
1.2
Приклади застосування цілочисельних задач лінійного програмування у плануванні
та управлінні виробництвом
Задача про рюкзак. Найпростішою задачею
цілочислового програмування, а саме задачею лише з одним обмеженням, є задача
про рюкзак (або ранець). Така задача має багато прикладів практичного
застосування. Назва "задача про рюкзак" пов’язана з інтерпретацією
задачі вибору найкращого складу предметів, що задовольняють певні умови
гіпотетичної проблеми туриста щодо вибору для походу оптимальної кількості
речей.
Турист може вибирати потрібні речі із списку з n
предметів. Відома вага кожного j-го предмета 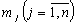 . Визначена також цінність кожного виду
предметів
. Визначена також цінність кожного виду
предметів 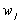 . Максимальна вага всього вантажу в
рюкзаку не може перевищувати зазначеного обсягу М. Необхідно визначити,
скільки предметів кожного виду турист має покласти в рюкзак, щоб загальна
цінність спорядження була максимальною за умови виконання обмеження на вагу
рюкзака.
. Максимальна вага всього вантажу в
рюкзаку не може перевищувати зазначеного обсягу М. Необхідно визначити,
скільки предметів кожного виду турист має покласти в рюкзак, щоб загальна
цінність спорядження була максимальною за умови виконання обмеження на вагу
рюкзака.
Позначимо через 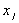 . - кількість предметів j-го виду в рюкзаку. Тоді
математична модель задачі матиме вигляд:
. - кількість предметів j-го виду в рюкзаку. Тоді
математична модель задачі матиме вигляд:
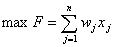 ,
, 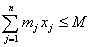 ;
;
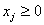 ,
, - цілі числа,
- цілі числа,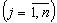
Приклад 1.1:
Фермеру для удобрення земельної ділянки необхідно придбати
107 кг добрив. Він може купити добрива в упаковках по 35 кг вартістю 14 ум. од.
або по 24 кг вартістю 12 ум. од. Метою фермера є закупівля не менше, ніж 107 кг
добрив з мінімальними витратами. Причому потрібно купувати або цілу упаковку,
або не купувати її зовсім, бо частину упаковки придбати неможливо.
Розв’язання. Позначимо кількість упаковок вагою 35 кг
та вагою 24 кг відповідно змінними 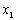 та
та 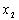 . Маємо модель цієї задачі:
. Маємо модель цієї задачі:
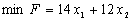
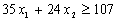 ,
,
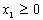 ,
, 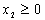 ,
,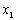 ,
, 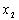 - цілі числа.
- цілі числа.
У результаті розв’язування задачі будь-яким з вищенаведених
методів отримаємо оптимальний план: 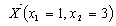 ,
, 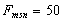 . Отже, за оптимальним планом найменші
витрати, що дорівнюють 50 ум. од., можливі у разі закупівлі однієї упаковки
добрив вагою 35 кг та трьох упаковок вагою по 24 кг.
. Отже, за оптимальним планом найменші
витрати, що дорівнюють 50 ум. од., можливі у разі закупівлі однієї упаковки
добрив вагою 35 кг та трьох упаковок вагою по 24 кг.
Задача оптимального розкрою матеріалів. На підприємстві здійснюється
розкрій m різних партій матеріалів у обсягах 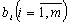 одиниць однакового розміру в кожній
партії. Із матеріалів усіх партій потрібно виготовити максимальну кількість
комплектів Z, у кожен з яких входить p різних видів окремих
частин в кількості
одиниць однакового розміру в кожній
партії. Із матеріалів усіх партій потрібно виготовити максимальну кількість
комплектів Z, у кожен з яких входить p різних видів окремих
частин в кількості 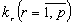 одиниць, враховуючи, що кожну одиницю
матеріалу можна розкроїти на окремі частини n різними способами, причому
у разі розкрою одиниці i-ої партії j-им способом отримуємо
одиниць, враховуючи, що кожну одиницю
матеріалу можна розкроїти на окремі частини n різними способами, причому
у разі розкрою одиниці i-ої партії j-им способом отримуємо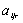 деталей r-го виду.
деталей r-го виду.
Запишемо математичну модель задачі. Позначимо через 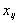 - кількість одиниць матеріалу i-ої
партії, що будуть розкроєні j-им способом. Тоді з i-ої партії за j-го
способу розкрою отримаємо
- кількість одиниць матеріалу i-ої
партії, що будуть розкроєні j-им способом. Тоді з i-ої партії за j-го
способу розкрою отримаємо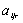
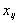 деталей r-го виду. З усієї ж i-ої партії у разі
застосування до неї всіх n способів розкрою отримаємо
деталей r-го виду. З усієї ж i-ої партії у разі
застосування до неї всіх n способів розкрою отримаємо 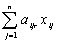 деталей r-го виду, а з усіх m
партій їх буде отримано
деталей r-го виду, а з усіх m
партій їх буде отримано 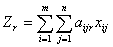 . У кожен комплект має входити
. У кожен комплект має входити 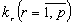 деталей, тому відношення
деталей, тому відношення 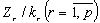 визначає кількість комплектів, які можна виготовити з
деталей r-го виду. Кількість повних комплектів для всіх видів деталей
визначається найменшим з цих відношень.
визначає кількість комплектів, які можна виготовити з
деталей r-го виду. Кількість повних комплектів для всіх видів деталей
визначається найменшим з цих відношень.
У разі повного комплекту має виконуватися рівність
відношень:
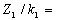

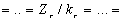
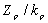 ,
,
звідки p - 1 відношення можна виразити через
будь-яке з них, наприклад, через перше:

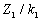 ,
,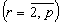 або
або 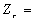
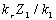 ,
,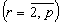 .
.
Замінивши 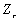 та
та 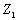 їх значеннями, отримаємо p - 1
обмеження стосовно комплектів:
їх значеннями, отримаємо p - 1
обмеження стосовно комплектів:
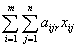 =
=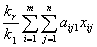 ,
,
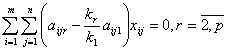
Враховуючи наявну кількість одиниць матеріалу в партіях,
запишемо m обмежень щодо ресурсів:
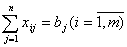 .
.
Зазначимо що, обмеження щодо використання ресурсів можуть
бути рівняннями чи нерівностями залежно від того, повністю чи не повністю
необхідно використати наявний обсяг ресурсів. Крім того, всі 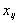 мають задовольняти умову невід’ємності:
мають задовольняти умову невід’ємності: 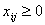
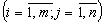 та цілочисловості.
та цілочисловості.
Отже, необхідно знайти найбільше значення функції:
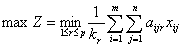
за обмежень:
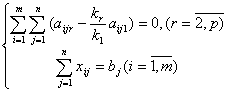
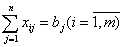
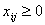
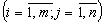 ,
,
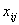 - цілі числа
- цілі числа 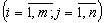 .
.
Розглянемо приклад задачі оптимального розкрою матеріалів.
Приклад 1.2: У цеху розрізують прути завдовжки 6 м на
заготівки довжиною 1,4, 2 і 2,5 м. Цех обслуговує двох замовників, для кожного
з яких окремо необхідно знайти:
1. як розрізати 200 прутів, щоб отримати не
менше як 40, 60 і 50 заготівок завдовжки відповідно 1,4; 2 і 2,5 м. Критерій
оптимізації - мінімум відходів;
2. як розрізати 200 прутів для формування з
отриманих заготівок комплектів, що складаються з двох заготівок довжиною 1,4 м,
та по одній довжиною 2 і 2,5 м. Критерій оптимізації - максимальна кількість
комплектів.
Розв’язання.
1) розв’яжемо задачу за умовами першого замовника. Маємо
партію прутів у кількості 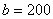 штук. Відома нижня межа кількості заготівок кожного виду.
Введемо такі позначення:
штук. Відома нижня межа кількості заготівок кожного виду.
Введемо такі позначення:
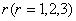 - вид заготівки;
- вид заготівки;
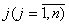 - спосіб розрізання прута;
- спосіб розрізання прута;
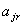 - вихід у разі розрізування прута j-им способом заготівок r-го
виду;
- вихід у разі розрізування прута j-им способом заготівок r-го
виду;
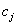 - відходи в разі розрізування прута j-им способом;
- відходи в разі розрізування прута j-им способом;
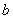 - кількість наявних прутів;
- кількість наявних прутів;
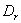 - нижня межа потреби в r-ій заготівці;
- нижня межа потреби в r-ій заготівці;
 - кількість прутів, які розрізані за j-им способом.
- кількість прутів, які розрізані за j-им способом.
Запишемо математичну модель для розв’язування першого
пункту задачі оптимального розкрою.
Критерієм оптимальності є мінімальна кількість відходів: 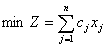 .
.
Кількість отриманих заготівок кожного виду має бути не
меншою від зазначених потреб:
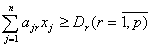
Сумарна кількість прутів, які розрізані різними способами
не може бути більшою від кількості наявних прутів:
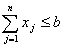 .
.
Змінні задачі  - невід’ємні і цілі числа. Отже, маємо математичну модель:
- невід’ємні і цілі числа. Отже, маємо математичну модель:
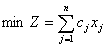 ,
, 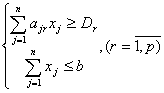
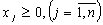 ,
,
 - цілі числа.
- цілі числа. 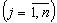
Побудуємо числову економіко-математичну модель розрізування
прутів, розглянувши можливі варіанти їх розрізування:
Таблиця 1.0
|
Довжина
заготівки, м
|
Варіант
розрізування прутів
|
|
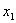 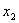 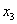 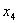 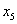 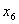 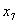
|
|
|
|
|
|
|
|
1,4
|
4
|
-
|
-
|
1
|
1
|
2
|
2
|
|
2
|
-
|
3
|
-
|
1
|
2
|
1
|
-
|
|
2,5
|
-
|
-
|
2
|
1
|
-
|
-
|
1
|
|
Довжина
відходів, м
|
0,4
|
0
|
1
|
0,1
|
0,6
|
1,2
|
0,7
|
Бажано, щоб у множину ввійшли всі можливі
варіанти, навіть такі, які на перший погляд здаються неефективними, наприклад, Х6.
Запишемо числову економіко-математичну модель
розрізування прутів:
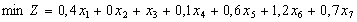
за умов:
а) кількість заготівок завдовжки 1,4 м:
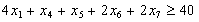 ;
;
б) кількість заготівок завдовжки 2 м:
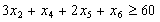 ;
;
в) кількість заготівок завдовжки 2,5 м:
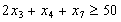 ;
;
г) кількість наявних прутів:
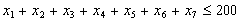 ;
;
д) невід’ємність змінних:
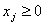
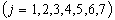 ;
;
є) цілочисловість змінних:
 - цілі числа
- цілі числа 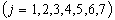 .
.
Отже, загалом маємо математичну модель виду:
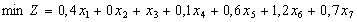
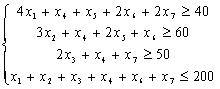
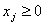
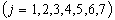
 - цілі числа
- цілі числа  .
.
Розв’язуючи задачу одним із методів цілочислового
програмування, отримуємо набір альтернативних оптимальних планів (загальною
кількістю 146). Наприклад, такий план забезпечує виготовлення всіх видів
заготівок у мінімально можливій кількості за найменшого загального обсягу
відходів, причому для цього використовуються лише 54 прути: 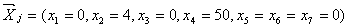 ,
, 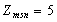 , тобто 4 прути необхідно розрізати другим способом (по три
заготівки довжиною 2 м) та 50 прутів четвертим способом (по одній заготівці
кожного виду). Сумарна довжина залишків дорівнює п’яти метрам. Аналогічне
значення цільової функції (
, тобто 4 прути необхідно розрізати другим способом (по три
заготівки довжиною 2 м) та 50 прутів четвертим способом (по одній заготівці
кожного виду). Сумарна довжина залишків дорівнює п’яти метрам. Аналогічне
значення цільової функції (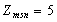 ) дає оптимальний план, за яким виготовляється більша кількість
кінцевої продукції та витрачається весь наявний матеріал:
) дає оптимальний план, за яким виготовляється більша кількість
кінцевої продукції та витрачається весь наявний матеріал:
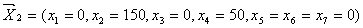 .
.
Отримані оптимальні плани дають набір альтернативних
варіантів для прийняття управлінських рішень за конкретних виробничих умов.
Ускладнимо розглянутий приклад задачі оптимального розкрою
матеріалів, що передбачає тільки один тип матеріалу та відсутність формування
комплектів кінцевої продукції.
) розв’яжемо задачу за умовами другого замовника. Оскільки
в другому пункті задачі відсутні обмеження щодо кількості заготівок, проте
вимагається формування комплектів, необхідно дещо змінити позначення:
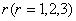 - вид заготівки;
- вид заготівки;
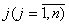 - спосіб розрізування прута;
- спосіб розрізування прута;
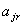 - вихід у разі розрізування прута j-им способом заготівок r-го
виду;
- вихід у разі розрізування прута j-им способом заготівок r-го
виду;
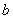 - кількість наявних прутів;
- кількість наявних прутів;
 - кількість прутів, які розрізані за j-им варіантом;
- кількість прутів, які розрізані за j-им варіантом;
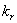 - кількість r-го виду заготівок у комплекті;
- кількість r-го виду заготівок у комплекті;
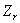 - кількість всіх заготівок r-го виду.
- кількість всіх заготівок r-го виду.
Математична модель у цьому разі суттєво відрізняється від
моделі, що розглянута вище.
З усього матеріалу може бути отримано 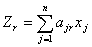 заготівок r-го виду. У кожен
комплект має входити дві заготівки першого типу
заготівок r-го виду. У кожен
комплект має входити дві заготівки першого типу 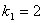 , тому відношення
, тому відношення 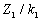 визначає кількість комплектів, які можна скласти з заготівок
першого виду. Аналогічно можна визначити кількість комплектів для інших видів
заготівок
визначає кількість комплектів, які можна скласти з заготівок
першого виду. Аналогічно можна визначити кількість комплектів для інших видів
заготівок  та
та 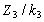 .
.
Кількість можливих повних комплектів визначається найменшим
з цих відношень: 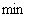 (
(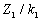 ;
;  ;
; 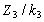 ). До того ж у разі повного комплекту має виконуватися рівність
відношень:
). До того ж у разі повного комплекту має виконуватися рівність
відношень: 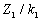 =
= =
=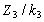 , звідки два з відношень можна виразити,
наприклад, через перше:
, звідки два з відношень можна виразити,
наприклад, через перше:
 =
=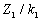 ;
; 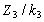 =
=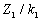 , звідки,.
, звідки,. 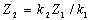 ,
,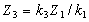
Замінимо 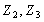 та
та 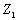 їх значеннями:
їх значеннями:
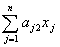 =
=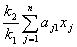 або
або 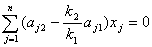 ;
;
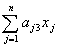 =
=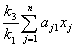 або
або 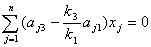 .
.
Враховуючи наявну кількість одиниць матеріалу, запишемо
обмеження щодо використання ресурсів:
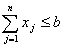 .
.
Всі 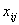 мають задовольняти умову невід’ємності:
мають задовольняти умову невід’ємності: 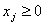 ,
, 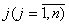 та цілочисловості.
та цілочисловості.
Отже, необхідно знайти найбільше значення функції:
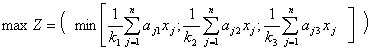
за обмежень:
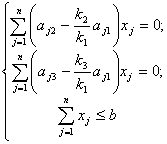
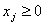 ,
, 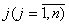 ,
,
 - цілі числа
- цілі числа 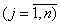 .
.
Запишемо числову математичну модель, скориставшись
попередніми даними розрахунків можливих варіантів розрізування прутів
(табл.6.5).
Із умов формування комплектів маємо: 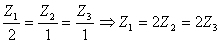 , тобто заготівок першого виду має бути
вдвічі більше, ніж заготівок другого та третього виду.
, тобто заготівок першого виду має бути
вдвічі більше, ніж заготівок другого та третього виду.
Звідси випливає, що за мінімальну кількість комплектів може
бути прийняте одне з двох відношень: 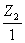 чи
чи 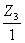 . Виберемо, наприклад,
. Виберемо, наприклад, 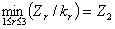 . Використовуючи дані таблиці, запишемо
вираз для цільової функції:
. Використовуючи дані таблиці, запишемо
вираз для цільової функції:
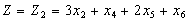 .
.
Обмеження щодо формування комплектів матимуть вигляд: 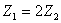 , або
, або
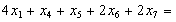
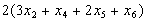 ,
,
Звідси
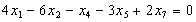 ,
,
аналогічно для 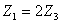 :
:
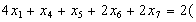
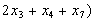 , або
, або
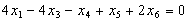 .
.
Обмеження щодо використання наявних прутів:
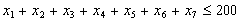 .
.
Обмеження стосовно невід’ємності та цілочисловості змінних:
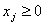
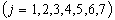 ;
;
 - цілі числа
- цілі числа 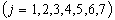 .
.
Отже, загалом маємо таку математичну модель:
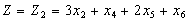
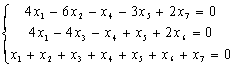
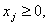
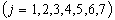
 - цілі числа
- цілі числа 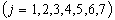 .
.
Розв’язавши задачу будь-яким з вищеописаних методів,
отримаємо оптимальний план:
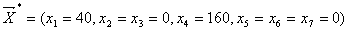 ,
,
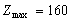 комплектів.
комплектів.
Задача комівояжера. Розглядається n міст  , що пов’язані між собою транспортною
мережею. Відома матриця відстаней від кожного міста до усіх інших:
, що пов’язані між собою транспортною
мережею. Відома матриця відстаней від кожного міста до усіх інших:
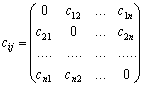
причому в загальному випадку не завжди 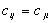 . Комівояжер повинен побувати в кожному
місті тільки один раз і повернутися в те місто, з якого почав рухатися.
Необхідно відшукати такий замкнений маршрут, що проходить через кожне місто
лише один раз і довжина якого мінімальна.
. Комівояжер повинен побувати в кожному
місті тільки один раз і повернутися в те місто, з якого почав рухатися.
Необхідно відшукати такий замкнений маршрут, що проходить через кожне місто
лише один раз і довжина якого мінімальна.
Позначимо:
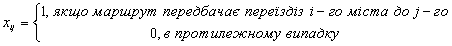
Отже, 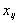 може набувати лише двох значень: одиниці
або нуля. Такі змінні мають назву бульових змінних. Очевидно, що вони є
цілочисловими. Цільовою функцією цієї задачі є мінімізація всього маршруту
комівояжера:
може набувати лише двох значень: одиниці
або нуля. Такі змінні мають назву бульових змінних. Очевидно, що вони є
цілочисловими. Цільовою функцією цієї задачі є мінімізація всього маршруту
комівояжера:
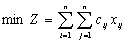 ,
,
де 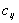 - відстань між містами і та j.
- відстань між містами і та j.
Обмеження щодо одноразового в’їзду в кожне місто:
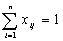
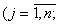
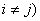 .
.
Обмеження щодо одноразового виїзду з кожного міста:
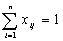
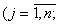
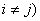 .
.
Зазначені обмеження не повністю описують допустимі маршрути
і не виключають можливості розриву маршруту. Щоб усунути цей недолік, введемо
невід’ємні цілочислові змінні 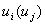
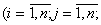
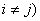 , які в процесі розв’язування задачі набуватимуть значень
порядкових номерів міст за оптимальним маршрутом прямування комівояжера.
Запишемо обмеження, які усувають можливість існування підмаршрутів:
, які в процесі розв’язування задачі набуватимуть значень
порядкових номерів міст за оптимальним маршрутом прямування комівояжера.
Запишемо обмеження, які усувають можливість існування підмаршрутів:
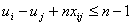
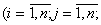
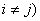 .
.
Доведемо, що для довільного маршруту, який починається в
пункті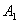 , можна знайти такі
, можна знайти такі 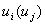 , що задовольняють наведену нерівність.
Нехай комівояжер переїжджає з міста
, що задовольняють наведену нерівність.
Нехай комівояжер переїжджає з міста 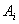 до
міста
до
міста 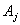 на р-му кроці і допустимо також,
що
на р-му кроці і допустимо також,
що 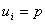 , тоді з міста
, тоді з міста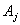 комівояжер вирушить на наступному, (р
+ 1) - му кроці і
комівояжер вирушить на наступному, (р
+ 1) - му кроці і 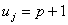 . Звідси випливає, що:
. Звідси випливає, що:
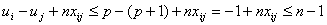 .
.
Така нерівність виконується для будь-яких значень i
та j у разі, коли 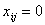 , а при
, а при 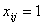 нерівність
виконується як строге рівняння. Отже, якщо вибрано маршрут пересування з i-го
міста до j-го, то згадана нерівність фіксує два підряд порядкових номери
цих міст.
нерівність
виконується як строге рівняння. Отже, якщо вибрано маршрут пересування з i-го
міста до j-го, то згадана нерівність фіксує два підряд порядкових номери
цих міст.
Отже, маємо таку математичну модель:
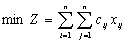
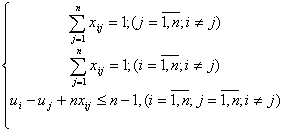
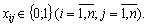
Приклад 1.3:
В економічному регіоні розміщено 6 пунктів (міст).
Комівояжер, який виїжджає з міста 1, має побувати в кожному місті один раз і
повернутися до вихідного пункту. Знайти найкоротший маршрут, якщо відстані між
містами відомі (наведені в км на рис.1.1).
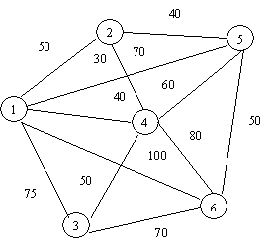
Рис.1.1
Розв’язання. Маємо 6 пунктів, де має побувати
комівояжер.
Позначимо:

Отже, 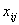 - бульові (цілочислові) змінні. Запишемо
числову економіко-математичну модель задачі комівояжера за даних умов.
- бульові (цілочислові) змінні. Запишемо
числову економіко-математичну модель задачі комівояжера за даних умов.
Виходячи з рис.1.0, бачимо, що всіх можливих маршрутів є
12. З першого міста можна потрапити до кожного з п’яти інших, відповідно за
такими маршрутами 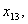 ,
,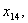
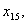
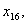 Друге місто пов’язане лише з трьома іншими, а саме, з першим,
четвертим та п’ятим, отже, маємо такі три змінні:
Друге місто пов’язане лише з трьома іншими, а саме, з першим,
четвертим та п’ятим, отже, маємо такі три змінні: 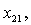
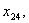
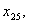 Аналогічно позначаємо змінні, що відповідають можливим маршрутам
пересувань з третього, четвертого, п’ятого та шостого міст:
Аналогічно позначаємо змінні, що відповідають можливим маршрутам
пересувань з третього, четвертого, п’ятого та шостого міст:
з третього - 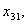
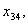
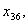
з четвертого - 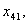 ,
,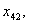
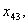
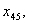
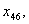
з п’ятого - 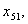
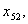
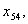
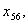
з шостого - 
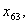
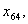
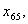
Загалом отримали 24 змінні. Однак деякі змінні, наприклад, 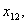 та
та 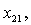
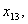 та
та 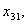 описують один маршрут, довжина якого за умовою задачі не
змінюється залежно від напрямку пересування (у разі переїзду з першого міста до
другого чи з другого до першого необхідно подолати 50 км). Отже, коефіцієнт у
цільовій функції при таких змінних буде однаковим.
описують один маршрут, довжина якого за умовою задачі не
змінюється залежно від напрямку пересування (у разі переїзду з першого міста до
другого чи з другого до першого необхідно подолати 50 км). Отже, коефіцієнт у
цільовій функції при таких змінних буде однаковим.
Критерій оптимальності - мінімізація довжини всього
маршруту комівояжера:
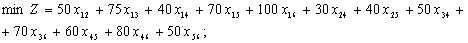
а) обмеження щодо одноразового в’їзду в кожне місто:
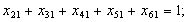
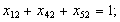
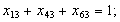
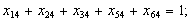
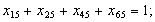
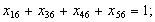
б) обмеження щодо одноразового виїзду з кожного міста:
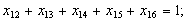
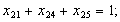
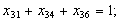
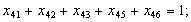
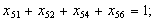
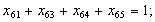
в) обмеження щодо усунення підмаршрутів:
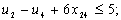 ;
;
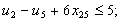
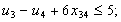
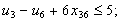
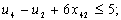
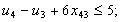
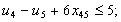
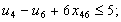
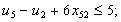
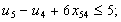
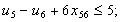
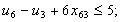
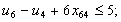
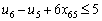 ;
;
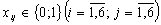
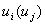 - цілі числа
- цілі числа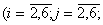
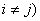 .
.
Такі задачі розв’язуються спеціальними методами.
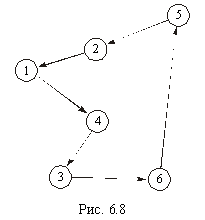
У результаті отримуємо оптимальний варіант пересування
таким маршрутом (рис.1.2).
Тобто з першого міста за оптимальним планом необхідно
переїжджати до четвертого, з четвертого - до третього, з третього - до шостого,
з шостого - до п’ятого, з п’ятого - до другого, а з другого - до першого.
Довжина цього маршруту є мінімальна, дорівнює 300 км.
Зауважимо, що аналогічні задачі нерідко виникають на
практиці, особливо у дрібному бізнесі. Типовим може бути, наприклад, таке
завдання: "Фірма у місті має 25 кіосків, які торгують безалкогольними
напоями. Щоденно з бази автомобілем розвозять до них товар. Як оптимально
організувати розвезення певного обсягу товару?".
Задача з постійними елементами витрат. Відомо, що витрати на
виготовлення будь-якої продукції складаються з двох частин: постійних та
змінних витрат. Нехай розглядається процес виробництва продукції за умов
використання m видів ресурсів.
Відомі обсяги кожного виду ресурсів 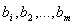 ., а також норми використання i-го
., а також норми використання i-го 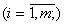 . виду ресурсів на одиницю виготовлення j-го
. виду ресурсів на одиницю виготовлення j-го
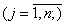 . виду продукції
. виду продукції 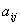 .
.
Умови використання ресурсів на виготовлення продукції можна
записати у вигляді таких обмежень:
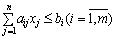 .
.
Витрати на виготовлення продукції поділяють на два види:
постійні витрати - 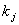 , які не залежать від обсягу виробництва,
і змінні -
, які не залежать від обсягу виробництва,
і змінні - 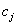 , що розраховуються на одиницю виготовленої
продукції, де j - вид продукції. Необхідно визначити оптимальні обсяги
виробництва продукції
, що розраховуються на одиницю виготовленої
продукції, де j - вид продукції. Необхідно визначити оптимальні обсяги
виробництва продукції 
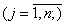 , за яких загальні витрати були б мінімальними.
, за яких загальні витрати були б мінімальними.
Зауважимо, що виготовлення будь-якої кількості продукції 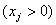 потребує певних фіксованих
потребує певних фіксованих 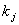 та змінних
та змінних 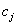
 витрат,
тобто загальна сума витрат на виготовлення продукції обсягом
витрат,
тобто загальна сума витрат на виготовлення продукції обсягом  визначається за формулою:
визначається за формулою: 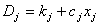 . Однак у разі, якщо
. Однак у разі, якщо 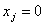 (продукція не випускається), то розрахунок витрат за формулою
(продукція не випускається), то розрахунок витрат за формулою 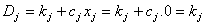 призводить до додатного значення, що
неправильно. Для адекватного відображення функціональної залежності загальних
витрат від обсягу виробленої продукції j-го виду можна скористатися
такою нелінійною функцією:
призводить до додатного значення, що
неправильно. Для адекватного відображення функціональної залежності загальних
витрат від обсягу виробленої продукції j-го виду можна скористатися
такою нелінійною функцією:
 ,
,
де 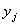 є бульовими змінними виду:
є бульовими змінними виду:
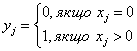
Таку умову можна записати у вигляді лінійної нерівності.
Допустимо, що існує таке досить велике число М, для якого умова 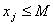 виконуватиметься для всіх допустимих значень
виконуватиметься для всіх допустимих значень  . Тоді обмеження виду:
. Тоді обмеження виду:
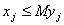
завжди виконується при 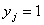 , і, крім того, якщо
, і, крім того, якщо 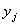 - ціле число, то мінімізація цільової функції забезпечує найменше
значення
- ціле число, то мінімізація цільової функції забезпечує найменше
значення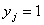 . Якщо
. Якщо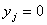 , то нерівність
, то нерівність 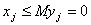 забезпечить
забезпечить 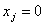 . Отже, маємо таку математичну модель:
цільова функція, що описує мінімальні загальні витрати на виробництво всіх
видів продукції, набуває вигляду:
. Отже, маємо таку математичну модель:
цільова функція, що описує мінімальні загальні витрати на виробництво всіх
видів продукції, набуває вигляду:
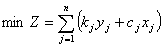
за умов:
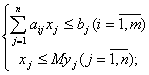
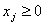
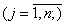 ;
;
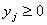
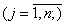 ;
;
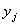 - цілі числа
- цілі числа 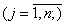 .
.
Приклад 1.4:
Фермер планує виробляти три види продукції: озиму пшеницю,
цукрові буряки та молоко. Загальні витрати складаються з двох частин: постійних
та змінних.
Відповідні дані наведені в табл.1:
Таблиця 1
|
Показник
|
Вид
продукції
|
|
озима
пшениця
|
цукрові
буряки
|
молоко
|
|
Постійні
витрати, тис. грн.
|
40
|
70
|
20
|
|
Змінні
витрати на одиницю продукції, грн/т
|
400
|
150
|
500
|
|
Норма
потреби в ріллі, га/т
|
0,2
|
0,02
|
0,25
|
|
Ціна
одиниці продукції, грн/т
|
800
|
300
|
1000
|
Необхідно визначити оптимальний план виробництва
продукції кожного виду за умови, що фермер має 100 га ріллі.
Розв’язання. Нехай  - обсяг виробництва j-го виду продукції m,
- обсяг виробництва j-го виду продукції m, 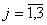 . Функція загальних витрат на виробництво j-го
виду продукції має вигляд:
. Функція загальних витрат на виробництво j-го
виду продукції має вигляд:
 .
.
Цільовою функцією в цьому прикладі може бути максимізація
прибутку:
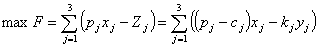 ,
,
де 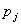 - ціна одиниці j-ї продукції.
- ціна одиниці j-ї продукції.
Обмеження щодо використання ріллі запишемо так:
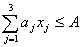
де 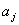 - норма потреби у ріллі на виробництво
одиниці j-ї продукції; А - площа ріллі.
- норма потреби у ріллі на виробництво
одиниці j-ї продукції; А - площа ріллі.
Загалом маємо таку математичну модель:
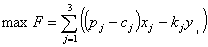
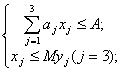
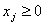
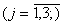 ;
;
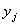 - цілі числа
- цілі числа 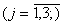 . Запишемо числову економіко-математичну модель цієї задачі.
Очевидно, що максимально можливий обсяг виробництва пшениці становить
. Запишемо числову економіко-математичну модель цієї задачі.
Очевидно, що максимально можливий обсяг виробництва пшениці становить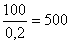 т, цукрових буряків -
т, цукрових буряків - 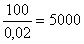 т, молока -
т, молока - 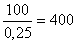 т.
т.
Отже, М може дорівнювати 5000. Звідси маємо:
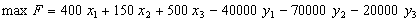
за умов:
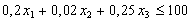 ;
;
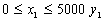 ;
;
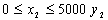 ;
;
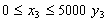 ;
;
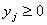 ,
,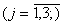 ;
;
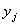 - цілі числа
- цілі числа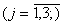 .
.
Розв’язавши задачу, отримаємо оптимальний план:
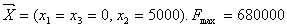 .
.
Можна зробити висновок, що фермеру за цих умов найвигідніше
зайнятися вирощуванням на всій площі ріллі тільки цукрових буряків.
Звичайно, у реальній ситуації існує більший набір можливих
видів продукції, а також більше обмежень щодо використання ресурсів.
Задача планування виробничої лінії. Розглядається процес
функціонування виробничої лінії. Відома схема, яка зображає послідовність робіт
для виготовлення k видів продукції 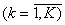 . Відомі також:
. Відомі також: 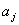 - тривалість виконання j-ї операції
- тривалість виконання j-ї операції 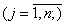 ;
; 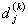 - термін для k-го виробу, до якого необхідно завершити
операцію j;
- термін для k-го виробу, до якого необхідно завершити
операцію j;  - момент початку j-ї операції; t
- тривалість виконання всіх операцій. Передбачається, що в будь-який момент на
верстаті виконується тільки одна операція. Необхідно визначити оптимальні
моменти початку кожної операції.
- момент початку j-ї операції; t
- тривалість виконання всіх операцій. Передбачається, що в будь-який момент на
верстаті виконується тільки одна операція. Необхідно визначити оптимальні
моменти початку кожної операції.
Економіко-математична модель виробничої лінії міститиме
такі групи обмежень:
. Послідовність виконання j-ї операції записується
для всіх пар операцій так: 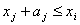
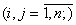 якщо j-та операція передує i-й операції.
якщо j-та операція передує i-й операції.
. Обмеження щодо нерозгалуженості виробничого процесу для
операцій і та j, які не виконуються одночасно (i ≠ j),
має вигляд:
або 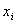 -
- =
=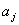 , якщо операція j передує операції і;
, якщо операція j передує операції і;
або  -
- 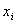 =
= 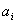 , якщо операція і передує операції j.
, якщо операція і передує операції j.
Зауважимо, що логічні обмеження виду "або-або" не
можуть входити до економіко-математичної моделі задачі лінійного програмування,
оскільки вони породжують неопуклу множину допустимих розв’язків. Тому необхідно
ввести допоміжні змінні, які уможливлюють запис наведених вище логічних умов у
вигляді лінійних обмежень. Це такі бульові змінні:
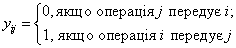
Скориставшись прийомом з попереднього прикладу (введення
досить великого числа М), запишемо обмеження:
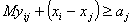
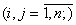 ;
; 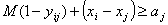
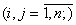 ,
,
де М - досить велике число.
. Обмеження щодо термінів виготовлення кожного виробу:

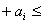
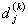
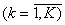 ,
,
де j - остання операція для k-го виробу.
. Усі операції мають бути виконані до моменту t:

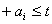 ,
,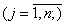
Критерій оптимальності: 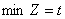 ,
,
тобто ставиться завдання, щоб тривалість виготовлення всіх
видів виробів була мінімальною.
Отже, маємо таку математичну модель:
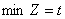
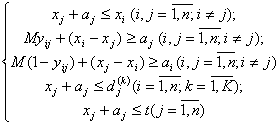
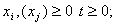
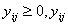 - цілі числа
- цілі числа 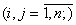 .
.
Приклад 1.5:
Потрібно оптимізувати функціонування виробничої лінії, яка
охоплює 11 операцій з виготовлення двох виробів. Лінію обладнано одним
багатоопераційним верстатом. Послідовність і тривалість (у хвилинах) виконання
операцій відображені на рис.6.9.
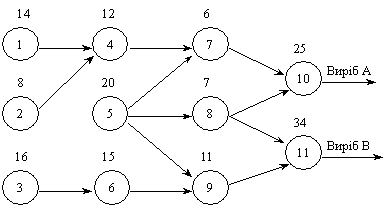
Рис.1.3
Визначені тривалості виготовлення виробів А та В відповідно
дорівнюють 120 і 150 хв. Передбачається, що в кожний момент часу на верстаті
може виконуватися тільки одна операція. Визначити оптимальні моменти початку
кожної операції.
Розв’язання. Позначивши через  момент початку j-ої операції,
запишемо числову економіко-математичну модель функціонування виробничої лінії:
момент початку j-ої операції,
запишемо числову економіко-математичну модель функціонування виробничої лінії: 
за наведених нижче умов.
. Обмеження стосовно послідовності виконання операцій:
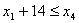 ;
;
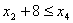 ;
;
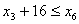 ;
;
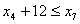 ;
;
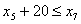 ;
;
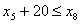 ;
;
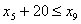 ;
;
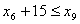 ;
;
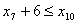 ;
;
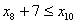 ;
;
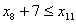 ;
;
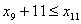 .
.
. Обмеження щодо нерозгалуженості виробничого процесу:
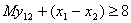 ;
;
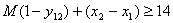 ;
;
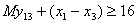 ;
;
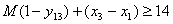 ;
;
...........
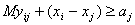 ;
;
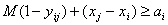 ;
;
...........
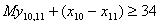 ;
;
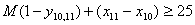 .
.
. Обмеження щодо тривалостей виготовлення виробів:
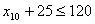 ;
;
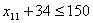 .
.
. Усі операції мають бути виконані до моменту t:
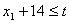 ;
;
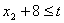 ;
;
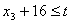 ;
;
.....
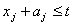 ;
;
.....
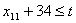 .
.
. Обмеження щодо невід’ємності змінних:
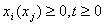 ;
;
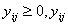 - цілі
- цілі 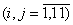 .
.
Отже, маємо частково цілочислову задачу з бульовими
змінними.
Задача про призначення. Ця задача зводиться до
транспортної і може бути розв’язана одним з відомих методів знаходження
оптимального плану транспортної задачі. Проте, такий вид задач належить до
задач цілочислового програмування, оскільки їх змінні є бульовими і оптимальний
план може бути знайденим також методами цілочислового програмування. Не
повертаючись до загальної постановки задачі та побудови її математичної моделі,
наведемо ще один приклад задачі про призначення.
Приклад 1.6:
Необхідно розподілити чотирьох робітників за чотирма видами
устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані
стосовно продуктивності праці кожного робітника на устаткуванні кожному виду
наведено в табл.1.4:
Таблиця 1.4
|
Робітник
|
Продуктивність
праці на устаткуванні, грн/год
|
|
1
|
2
|
3
|
4
|
|
1
|
12
|
9
|
8
|
7
|
|
2
|
10
|
7
|
6
|
5
|
|
3
|
9
|
6
|
4
|
4
|
|
4
|
8
|
5
|
3
|
2
|
Розв’язання. Зазначимо, що дану
задачу можна розглядати як транспортну, в якій робітники ототожнюються з
постачальниками вантажів, а види устаткування - зі споживачами цих вантажів.
Обсяги пропозиції та попиту в кожному разі дорівнюють одиниці. Отже, змінні
будуть бульовими:

Якщо відома продуктивність праці і-го робітника на j-му
устаткуванні, то числова модель про призначення набуває вигляду:
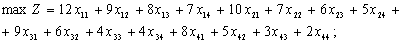
за умов:
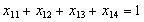 ;
;
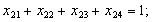 ;
;
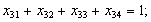 ;
;
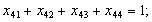 ;
;
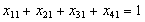 ;
;
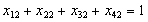 ;
;
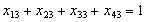 ;
;
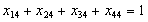 .
.
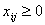
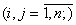 ;
;
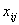 - цілі числа
- цілі числа 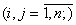 .
.
Зазначимо,що з огляду на особливу структуру цієї задачі,
зокрема на її "транспортний" характер та рівність правих частин
обмежень, для її розв’язування можна застосувати ефективніший алгоритм, ніж для
звичайної задачі цілочислового програмування з бульовими змінними.
Розділ
2. Методи розвґязання задач цілочислового програмування
2.1
Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування
на площині
Для знаходження оптимального розв’язку
цілочислових задач застосовують спеціальні методи. Найпростішим з них є
знаходження оптимального розв’язку задачі як такої, що має лише неперервні
змінні, з дальшим їх округленням. Такий підхід є виправданим тоді, коли змінні
в оптимальному плані набувають досить великих значень у зіставленні їх з
одиницями вимірювання. Нехай, наприклад, у результаті розв’язування задачі про
поєднання галузей у сільськогосподарському підприємстві отримали оптимальне
поголів’я корів - 1235,6. Округливши це значення до 1236, не припустимося
значної похибки. Проте за деяких умов такі спрощення призводять до істотних
неточностей. Скажімо, множина допустимих розв’язків деякої нецілочислової
задачі лінійного програмування має вигляд, зображений на
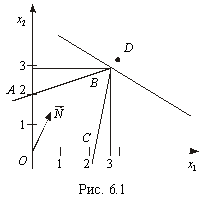
рис.2.1
Максимальне значення функціонала для даної задачі
знаходиться в точці В. Округлення дасть таке значення оптимального плану
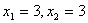 (точка D на рис.2.1). Очевидно, що
точка D не може бути розв’язком задачі, оскільки вона навіть не належить
множині допустимих розв’язків (чотирикутник ОАВС), тобто відповідні
значення змінних не задовольнятимуть систему обмежень задачі.
(точка D на рис.2.1). Очевидно, що
точка D не може бути розв’язком задачі, оскільки вона навіть не належить
множині допустимих розв’язків (чотирикутник ОАВС), тобто відповідні
значення змінних не задовольнятимуть систему обмежень задачі.
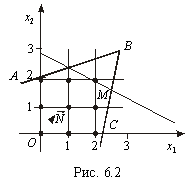
Зауважимо, що геометрично множина допустимих планів
будь-якої лінійної цілочислової задачі являє собою систему точок з
цілочисловими координатами, що знаходяться всередині опуклого багатокутника
допустимих розв’язків відповідної нецілочислової задачі. Отже, для розглянутого
на рис.2.1 випадку множина допустимих планів складається з дев’яти точок
(рис.2.2), які утворені перетинами сім’ї прямих, що паралельні осям 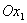 та
та 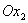 і проходять через точки з цілими координатами 0, 1,2. Для
знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій
функції, пересуваємо у напрямку вектора нормалі
і проходять через точки з цілими координатами 0, 1,2. Для
знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій
функції, пересуваємо у напрямку вектора нормалі 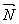 до
перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і
є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний
цілочисловий розв’язок відповідає точці М (
до
перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і
є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний
цілочисловий розв’язок відповідає точці М (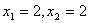 ).
).
Очевидно, особливість геометричної інтерпретації
цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування
полягає лише у визначенні множини допустимих розв’язків. Областю допустимих
розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а
вимога цілочисловості розв’язку приводить до такої множини допустимих
розв’язків, яка є дискретною і утворюється тільки з окремих точок. Якщо у разі
двох змінних розв’язок задачі можна відшукати графічним методом, тобто,
використовуючи цілочислову сітку, можна досить просто знайти оптимальний план,
то в іншому разі необхідно застосовувати спеціальні методи.
Графічний метод
Якщо модель містить тільки дві змінні, задачу можна
розв’язати графічно. У випадку трьох змінних графічний розв’язок стає менш
наочним, а при більшому числі змінних - взагалі неможливим. Незважаючи на це,
розгляд графічного методу дасть змогу зробити висновки, що послужать основою
для розробки загального методу розв’язання задач лінійного програмування.
Перший крок при використанні графічного методу полягає в
поданні області допустимих розв’язків, у якій водночас задовольняються
всі обмеження моделі. Нехай шукана область (простір) розв’язків задачі
показана. Умови невід’ємності змінних обмежують область їх допустимих значень.
Інші межі простору розв’язків потрібно зобразити прямими лініями, побудованими
по рівняннях, що отримані заміною знака "≤" чи "≥"
знаком "=" в обмеженнях. Області, в яких відповідні обмеження
виконуються як нерівності, указуються стрілками, спрямованими вбік допустимих
значень змінних. Отримуємо простір розв’язків задачі. У кожній точці, що
належить внутрішній області або межам, всі обмеження виконуються, тому
розв’язки, що відповідають цим точкам, є допустимими. Серед безкінечного числа
таких точок можна знайти точку оптимального розв’язку, якщо з'ясувати, в якому
напрямку зростає цільова функція. На графік наносять лінію рівня цільової
функції 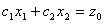 , де
, де 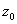 - довільне значення
- довільне значення 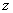 . Будують вектор
. Будують вектор 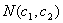 , що є нормаллю до ліній рівня цільової функції й визначає
напрямок оптимізації
, що є нормаллю до ліній рівня цільової функції й визначає
напрямок оптимізації 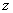 . Лінію рівня зрушують паралельно самій
собі вздовж вектора
. Лінію рівня зрушують паралельно самій
собі вздовж вектора 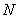 доти, поки вона не вийде за межі області
допустимих розв’язків. Остання точка цієї області й буде точкою оптимуму.
доти, поки вона не вийде за межі області
допустимих розв’язків. Остання точка цієї області й буде точкою оптимуму.
Значення 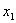 та
та 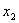 в розв’язуючій точці визначаються шляхом
розв’язання системи рівнянь.
в розв’язуючій точці визначаються шляхом
розв’язання системи рівнянь.
Зазначимо, що у випадку, коли лінії рівня 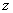 мають такий самий нахил, як пряма
зв’язуючого обмеження (тобто такого, що проходить через оптимальну точку),
матимемо безліч оптимумів на відрізку.
мають такий самий нахил, як пряма
зв’язуючого обмеження (тобто такого, що проходить через оптимальну точку),
матимемо безліч оптимумів на відрізку.
Графічний спосіб
розв'язування ґрунтується на геометричній інтерпретації задачі лінійного
програмування, тому він досить простий для розуміння. Недоліком є те, що
графічним способом можна розв’язати задачу, в якій в обмеженнях є лише дві
змінні, потрібно намагатися малювати лінії з найбільшою точністю, в
протилежному випадку можна отримати велику похибку, а в результаті неправильне
рішення.
2.2 Методи
відтинання. Метод Гоморі
В основу методів цілочислового програмування
покладено ідею Данціга. Допустимо, що необхідно розв’язувати задачу лінійного
програмування, всі або частина змінних якої мають бути цілочисловими. Можливо,
якщо розв’язувати задачу, не враховуючи умову цілочисловості, випадково одразу
буде отримано потрібний розв’язок. Однак така ситуація малоймовірна.
Переважно розв’язок не задовольнятиме умову
цілочисловості. Тоді накладають додаткове обмеження, яке не виконується для
отриманого плану задачі, проте задовольняє будь-який цілочисловий розв’язок.
Таке додаткове обмеження називають правильним
відтинанням. Система лінійних обмежень задачі доповнюється новою умовою і
далі розв’язується отримана задача лінійного програмування. Якщо її розв’язок
знову не задовольняє умови цілочисловості, то будується нове лінійне обмеження,
що відтинає отриманий розв’язок, не зачіпаючи цілочислових планів. Процес
приєднання додаткових обмежень повторюють доти, доки не буде знайдено
цілочислового оптимального плану, або доведено, що його не існує.
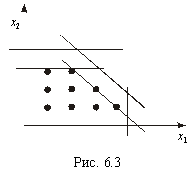
Геометрично введення додаткового лінійного обмеження
означає проведення гіперплощини (прямої), що відтинає від багатогранника
(багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки
з нецілочисловими координатами, однак не торкається жодної цілочислової точки
даної множини.
Отриманий новий багатогранник розв’язків містить всі цілі
точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде
цілочисловим (рис.2.3).
Слід відмітити, що визначення правила для реалізації ідеї
Данціга стосовно формування додаткового обмеження виявилось досить складним
завданням і першим, кому вдалось успішно реалізувати цю ідею, був Гоморі.
Розглянемо алгоритм, запропонований Гоморі, для
розв’язування повністю цілочислової задачі лінійного програмування, що
ґрунтується на використанні симплексного методу і передбачає застосування
досить простого способу побудови правильного відтинання.
Нехай маємо задачу цілочислового програмування:
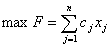 (1.5)
(1.5)
за умов:
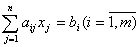 (1.6)
(1.6)
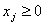
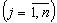 , (1.7)
, (1.7)
 - цілі числа
- цілі числа 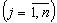 (1.8).
(1.8).
Допустимо, що параметри 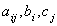
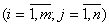 - цілі числа.
- цілі числа.
Не враховуючи умови цілочисловості, знаходимо розв’язок
задачі (1.5) - (1.7) симплексним методом. Нехай розв’язок існує і міститься в
такій симплексній таблиці:
Таблиця 1.5
Змінні 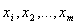 - базисні, а
- базисні, а 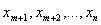 - вільні. Оптимальний план задачі:
- вільні. Оптимальний план задачі: 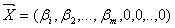 . Якщо
. Якщо 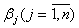 - цілі числа, то отриманий розв’язок є цілочисловим оптимальним
планом задачі (1.5) - (1.8). Інакше існує хоча б одне з чисел, наприклад,
- цілі числа, то отриманий розв’язок є цілочисловим оптимальним
планом задачі (1.5) - (1.8). Інакше існує хоча б одне з чисел, наприклад, 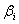 - дробове. Отже, необхідно побудувати
правильне обмеження, що відтинає нецілу частину значення
- дробове. Отже, необхідно побудувати
правильне обмеження, що відтинає нецілу частину значення 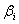 .
.
Розглянемо довільний оптимальний план 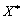 задачі (1.5) - (1.7). Виразимо в цьому плані базисну змінну
задачі (1.5) - (1.7). Виразимо в цьому плані базисну змінну
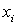 через вільні змінні:
через вільні змінні:
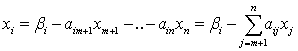 . (1.9)
. (1.9)
Виразимо коефіцієнти при змінних даного рівняння у вигляді
суми їх цілої та дробової частин. Введемо позначення: 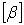 - ціла частина числа b,
- ціла частина числа b, 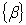 - дробова частина числа b*1. Отримаємо:
- дробова частина числа b*1. Отримаємо:
. Цілою частиною числа а називається найбільше ціле число , що не перевищує а. Дробовою частиною є
число
, що не перевищує а. Дробовою частиною є
число 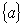 , яке дорівнює різниці між самим числом а
та його цілою частиною, тобто
, яке дорівнює різниці між самим числом а
та його цілою частиною, тобто 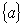 =
=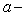
 .
.
Наприклад, для 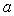 =
=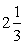
 =2,
=2, 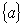 =
=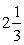
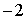 =
=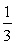 ;
;
для 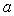 =
=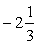
 =
=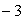 ,
, 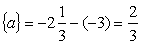

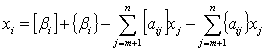 , (1.10)
, (1.10)
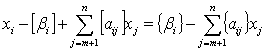 . (1.11)
. (1.11)
Отже, рівняння (1.11) виконується для будь-якого
допустимого плану задачі (1.5) - (1.7). Допустимо тепер, що розглянутий план 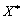 є цілочисловим оптимальним планом задачі.
Тоді ліва частина рівняння (1.11) складається лише з цілих чисел і є
цілочисловим виразом. Отже, права його частина також є цілим числом і
справджується рівність:
є цілочисловим оптимальним планом задачі.
Тоді ліва частина рівняння (1.11) складається лише з цілих чисел і є
цілочисловим виразом. Отже, права його частина також є цілим числом і
справджується рівність:
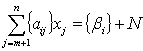 , (1.12)
, (1.12)
де N - деяке ціле число.
Величина N не може бути від’ємною. Якщо б 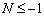 , то з рівняння (1.12) приходимо до
нерівності:
, то з рівняння (1.12) приходимо до
нерівності:
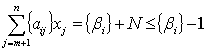 .
.
Звідки 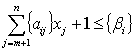 . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина 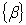 перевищує одиницю, що неможливо. У такий
спосіб доведено, що число N є невід’ємним.
перевищує одиницю, що неможливо. У такий
спосіб доведено, що число N є невід’ємним.
Якщо від лівої частини рівняння (2.12) відняти деяке
невід’ємне число, то приходимо до нерівності:
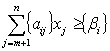 , (1.13)
, (1.13)
яка виконується за допущенням для будь-якого цілочислового
плану задачі (1.5) - (1.7). У такий спосіб виявилося, що нерівність (1.13) є
шуканим правильним відтинанням.
Отже, для розв’язування цілочислових задач лінійного
програмування (1.1) - (1.4) методом Гоморі застосовують такий алгоритм:
. Симплексним методом розв’язується задача без вимог
цілочисловості змінних - (1.1) - (1.3).
Якщо серед елементів умовно-оптимального плану немає
дробових чисел, то цей план є розв’язком задачі цілочислового програмування
(1.1) - (1.4).
Якщо задача (1.1) - (1.3) не має розв’язку (цільова функція
необмежена, або система обмежень несумісна), то задача (1.1) - (1.4) також не
має розв’язку.
. Коли в умовно-оптимальному плані є дробові значення, то
вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної
(елементів відповідного рядка останньої симплексної таблиці, в якому вона
міститься) будується додаткове обмеження Гоморі:
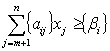 .
.
. Додаткове обмеження після зведення його до канонічного
вигляду і введення базисного елемента приєднується до останньої симплексної
таблиці, яка містить умовно-оптимальний план. Отриману розширену задачу
розв’язують і перевіряють її розв’язок на цілочисловість. Якщо він не
цілочисловий, то процедуру повторюють, повертаючись до п.2. Так діють доти,
доки не буде знайдено цілочислового розв’язку або доведено, що задача не має
допустимих розв’язків на множині цілих чисел.
Доведено, що за певних умов алгоритм Гоморі є скінченним,
але процес розв’язування задач великої розмірності методом Гоморі повільно
збіжний. Слід також мати на увазі, що і кількість ітерацій суттєво залежить від
сформованого правильного відтинання. Наведене правило (1.13) щодо формування
правильного відтинання не єдине. Існують ефективніші відтинання, які
використовуються у другому та третьому алгоритмах Гоморі, однак наявний
практичний досвід ще не дає змоги виділити з них найкращий.
Загалом, алгоритм Гоморі в обчислювальному аспекті є мало
вивченим. Якщо в лінійному програмуванні спостерігається відносно жорстка
залежність між кількістю обмежень задачі та кількістю ітерацій, що необхідна
для її розв’язування, то для цілочислових задач такої залежності не існує.
Кількість змінних також мало впливає на трудомісткість обчислень. Очевидно,
процес розв’язання цілочислової задачі визначається не лише її розмірністю, а
також особливостями багатогранника допустимих розв’язків, що являє собою набір
ізольованих точок.
Як правило, розв’язування задач цілочислового програмування
потребує великого обсягу обчислень. Тому при створенні програм для ЕОМ особливу
увагу слід приділяти засобам, що дають змогу зменшити помилки округлення, які
можуть призвести до того, що отриманий цілочисловий план не буде оптимальним.
Розглянемо приклад розв’язування цілочислової задачі лінійного
програмування методом Гоморі.
Приклад 2.1 Сільськогосподарське підприємство планує
відкрити сушильний цех на виробничій площі 190 м2, маючи для цього 100 тис. грн
і можливість придбати устаткування двох типів: А і В. Техніко-економічну
інформацію стосовно одиниці кожного виду устаткування подано в табл.1.6:
Таблиця 1.6
|
Показник
|
Устаткування
|
Ресурс
|
|
А
|
В
|
|
|
Вартість,
тис. грн
|
25
|
10
|
100
|
|
Необхідна
виробнича площа, м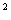 4020190 4020190
|
|
|
|
|
Потужність,
тис. грн/рік
|
350
|
150
|
-
|
Розв’язання. Нехай 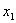 і
і 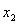 -кількість комплектів устаткування
відповідно типу А і В.
-кількість комплектів устаткування
відповідно типу А і В.
Запишемо економіко-математичну модель задачі:
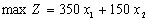 ,
, 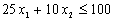 ;
;
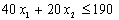 ;
; 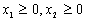 ,
,
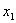 і
і 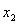 - цілі числа.
- цілі числа.
Розв’язуємо задачу, нехтуючи умовою цілочисловості. Остання
симплексна таблиця набуде вигляду:
Таблиця 6.3
Значення другої змінної є дробовим числом, що не
задовольняє початкові умови задачі. Побудуємо для другого рядка наведеної симплексної
таблиці додаткове обмеження виду 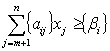 :
:
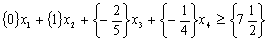 .
.
Оскільки 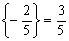 ,
, 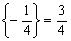 ,
, 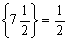 , то додаткове обмеження набуває вигляду:
, то додаткове обмеження набуває вигляду:
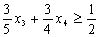 .
.
Зведемо його до канонічної форми та введемо штучну змінну:
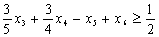 .
.
Приєднавши отримане обмеження до симплексної таблиці (табл.6.3) з
умовно-оптимальним планом, дістанемо:
Таблиця 6.4
|
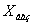 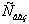 План350150000 - М План350150000 - М
|
|
|
|
|
|
|
|
|
|
|
|
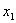 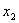 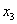 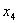 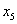 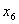
|
|
|
|
|
|
|
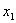 350110 350110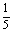 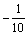 0 0 0 0
|
|
|
|
|
|
|
|
|
|
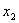 150 150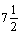 01 01  0 0 0 0
|
|
|
|
|
|
|
|
|
|
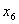 -М -М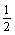 00 00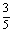 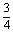 -1 1 -1 1
|
|
|
|
|
|
|
|
|
|
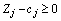
|
1475
|
0
|
0
|
10
|
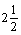
|
0
|
0
|
|
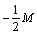
|
0
|
0
|
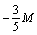
|
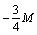
|
М
|
0
|
Розв’язавши наведену задачу, знаходимо
цілочисловий оптимальний план:
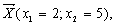
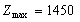 .
.
2.3
Комбінаторні методи. Метод гілок та меж
В основі комбінаторних методів є перебір
можливих варіантів розв’язків поставленої задачі. Кожен з них характеризується
певною послідовністю перебору варіантів та правилами виключення, що дають змогу
ще в процесі розв’язування задачі виявити неоптимальні варіанти без попередньої
їх перевірки. Відносна ефективність різних методів залежить від того, наскільки
кожен з них уможливлює скорочення необхідного процесу перебору варіантів у
результаті застосування правила виключення.
Розглянемо один із комбінаторних методів. Для
розв’язування задач цілочислового програмування ефективнішим за метод Гоморі є метод
гілок і меж. Спочатку, як і в разі методу Гоморі, симплексним методом
розв’язується послаблена (без умов цілочисловості) задача. Потім вводиться
правило перебору.
Нехай потрібно знайти  - цілочислову змінну, значення якої
- цілочислову змінну, значення якої 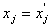 в оптимальному плані послабленої задачі є
дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових
значень, тому відповідний проміжок можна виключити з множини допустимих планів
задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до
в оптимальному плані послабленої задачі є
дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових
значень, тому відповідний проміжок можна виключити з множини допустимих планів
задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до 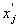 цілочисловими значеннями. Можна стверджувати, що на
інтервалі
цілочисловими значеннями. Можна стверджувати, що на
інтервалі 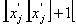 цілих значень немає.
цілих значень немає.
Наприклад, якщо 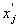 =2,7 дістаємо інтервал
=2,7 дістаємо інтервал 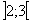 , де, очевидно, немає
, де, очевидно, немає 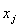 , яке набуває цілого значення і оптимальний розв’язок буде
знаходитися або в інтервалі
, яке набуває цілого значення і оптимальний розв’язок буде
знаходитися або в інтервалі 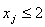 , або
, або 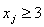 . Виключення проміжку
. Виключення проміжку 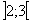 з множини допустимих планів здійснюється
введенням до системи обмежень початкової задачі додаткових нерівностей.
з множини допустимих планів здійснюється
введенням до системи обмежень початкової задачі додаткових нерівностей.
Тобто допустиме ціле значення 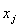 має задовольняти одну з нерівностей виду:
має задовольняти одну з нерівностей виду:
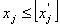 або
або 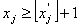 .
.
Дописавши кожну з цих умов до задачі з послабленими
обмеженнями, дістанемо дві, не пов’язані між собою, задачі.
Тобто, початкову задачу цілочислового програмування (1.1) -
(1.4) поділимо на дві задачі з урахуванням умов цілочисловості змінних,
значення яких в оптимальному плані послабленої задачі є дробовими.
Це означає, що симплекс-методом розв’язуватимемо дві такі
задачі:
перша задача:
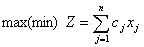 (1.14)
(1.14)
за умов
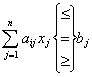 ;
; 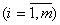 (1.15),
(1.15), 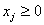
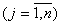 (1.16)
(1.16)
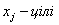
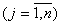 (1.17),
(1.17), 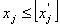 , (1.18)
, (1.18)
друга задача
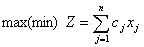 (1.19)
(1.19)
за умов:
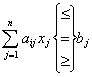 ,
, 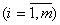 ; (1.20)
; (1.20)
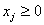
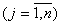 ; (1.21)
; (1.21)
 - цілі числа
- цілі числа 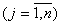 ; (1.22)
; (1.22)
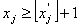 , (1.23)
, (1.23)
де  -дробова компонента розв’язку задачі (1.1)
- (1.4).
-дробова компонента розв’язку задачі (1.1)
- (1.4).
Наведені задачі (1.14) - (1.18) і (1.19) - (1.23) спочатку
послаблюємо, тобто розв’язуємо з відкиданням обмежень (1.17) і (1.22). Якщо
знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є
розв’язками задачі (1.1) - (1.4). Інакше пошук розв’язку задачі триває. Для
дальшого розгалуження вибираємо розв’язок задачі з більшим значенням цільової
функції, якщо йдеться про максимізацію, і навпаки - з меншим значенням цільової
функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не
буде встановлено неможливість поліпшення розв’язку. Здобутий останній план -
оптимальний.
Розв’язування цілочислових задач методом гілок і меж можна
значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі
розв’язування відрізняється від попередньої лише одним обмеженням. Тому за
послідовного розв’язування задач немає сенсу розв’язувати їх симплексним
методом спочатку. Досить буде почергово приєднати нові обмеження виду (1.18) і
(1.23) до останньої симплекс-таблиці попередньої задачі та вилучити (в разі
необхідності) непотрібні "старі" обмеження.
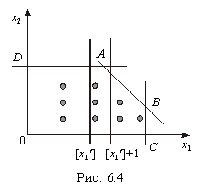
Геометрично введення додаткових лінійних обмежень виду
(1.18) та (1.23) в систему обмежень початкової задачі означає проведення
гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих
планів відповідної задачі лінійного програмування у такий спосіб, що
уможливлюється включення в план найближчої цілої точки цього багатокутника
(рис.6.4). Допустимо, що А - точка максимуму, тоді за методом гілок та
меж багатокутник допустимих планів задачі ABCOD поділяється на дві
частини прямими 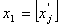 та
та 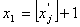 , що виключає з розгляду точку А,
координата якої
, що виключає з розгляду точку А,
координата якої 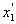 є не цілим числом.
є не цілим числом.
Опишемо алгоритм методу гілок та меж:
Симплексним методом розв’язують задачу (1.1) - (1.3) (без
вимог цілочисловості змінних).
Якщо серед елементів умовно-оптимального плану немає
дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового
програмування (1.1) - (1.4).
Якщо задача (1.1) - (1.3) не має розв’язку (цільова функція
необмежена, або система обмежень несумісна), то задача (1.1) - (1.4) також не
має розв’язку.
Коли в умовно-оптимальному плані є дробові значення, то
вибирають одну з нецілочислових змінних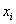 і визначають її цілу частину
і визначають її цілу частину 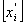 .
.
Записують два обмеження, що відтинають нецілочислові
розв’язки:
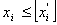
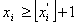 ,
,
Кожну з одержаних нерівностей приєднують до обмежень
початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного
програмування.
У будь-якій послідовності розв’язують обидві задачі. У
разі, коли отримано цілочисловий розв’язок хоча б однієї із задач, значення
цільової функції цієї задачі зіставляють з початковим значенням. Якщо різниця
не більша від заданого числа e, то процес розв’язування може бути
закінчено. У разі, коли цілочисловий розв’язок одержано в обох задачах, то з
розв’язком початкової зіставляється той, який дає краще значення цільової
функції. Якщо ж в обох задачах одержано нецілочислові розв’язки, то для
дальшого гілкування вибирають ту задачу, для якої здобуто краще значення
цільової функції і здійснюють перехід до кроку 2.
Приклад 2.2 Розв’яжемо методом гілок і меж задачу з
прикладу 2.1.
Розв’язання. Відкинувши умову цілочисловості, дістанемо
розв’язок: 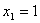 ,
, 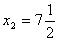 . Отже, допустиме ціле значення
. Отже, допустиме ціле значення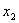 має задовольняти одну з нерівностей
має задовольняти одну з нерівностей 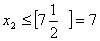 або
або 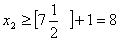 . Приєднуємо до початкової задачі окремо
кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві
утворені задачі:
. Приєднуємо до початкової задачі окремо
кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві
утворені задачі:
Для задачі І (з обмеженням 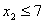 ) оптимальним буде розв’язок
) оптимальним буде розв’язок 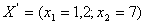 ,
, 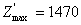 , а для задачі ІІ (з обмеженням
, а для задачі ІІ (з обмеженням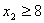 ) - розв’язок
) - розв’язок 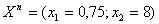 ,
, 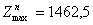 . Оскільки цілочислового плану не знайдено, процес необхідно
продовжити, узявши для дальшого розгалуження першу задачу, оптимальний план
якої дає більше значення функціонала. Розв’язуємо задачу І, окремо приєднуючи
до неї обмеження:
. Оскільки цілочислового плану не знайдено, процес необхідно
продовжити, узявши для дальшого розгалуження першу задачу, оптимальний план
якої дає більше значення функціонала. Розв’язуємо задачу І, окремо приєднуючи
до неї обмеження: 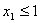 і
і 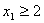 . Отримуємо такі дві задачі:
. Отримуємо такі дві задачі:
Розв’язком задачі ІІІ є план 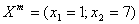 ,
, 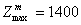 , а задачі IV план
, а задачі IV план 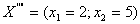 ,
,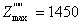 . Обидва розв’язки є цілочисловими, проте
краще значення цільової функції забезпечує розв’язок задачі IV. Тому
оптимальним планом початкової цілочислової задачі буде
. Обидва розв’язки є цілочисловими, проте
краще значення цільової функції забезпечує розв’язок задачі IV. Тому
оптимальним планом початкової цілочислової задачі буде 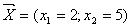 ,
, 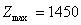 , що збігається з розв’язком, отриманим за методом Гоморі.
, що збігається з розв’язком, отриманим за методом Гоморі.
Схема процесу розв’язування задачі з прикладу 2.1 (рис.2.5)
досить наочно пояснює назву методу гілок та меж. Початкова задача розділяється
(гілкується) на дві простіші, і, якщо серед них не існує задачі з цілочисловим
оптимальним розв’язком, то процес гілкування продовжується. Отже, всі
розглянуті дії можна зобразити у вигляді "дерева":
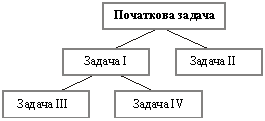
Рис.2.5
Кожен елемент такого "дерева" - це певна задача, що
має відповідний оптимальний план. Після одержання нецілочислового розв’язку
послабленої (тобто без умови цілочисловості) початкової задачі ми перетворили
її на дві інші з додатковими умовами. З них кращим виявився розв’язок задачі І,
однак оскільки він був не цілочисловим, то ми продовжили процес гілкування.
Задачу І введенням додаткових обмежень перетворили в задачу ІІІ та задачу IV.
Оптимальні плани обох цих задач цілочислові, але план задачі IV дає більше
значення функціонала, тому цілочисловим оптимальним планом початкової задачі є
розв’язок задачі IV.
Коротко розглянемо без наведення прикладів ще один цікавий
метод, який можна віднести до типу комбінаторних - метод послідовного аналізу
варіантів. Загальна схема цього методу розроблена українським вченим
В.С. Михалевичем, який працював у київському Інституті
кібернетики. Ідея цього методу полягає в послідовному повторенні таких
процедур:
) розбиття множини варіантів розв’язків задачі на кілька
підмножин, кожна з яких має специфічні властивості;
) використання вищезазначених властивостей для пошуку
логічних суперечностей в опису окремих підмножин;
) виключення із дальшого розгляду тих підмножин варіантів
розв’язків, в описах яких є логічні суперечності.
Отже, методика послідовного аналізу варіантів базується на
відсіві неперспективних варіантів ще до їх побудови. Оскільки у разі відсіву
неперспективних початкових частин варіантів відсівається і вся процедура
продовжень їх розрахунків, то досягається значна економія часу через скорочення
обчислювальних операцій. Відсів неперспективних елементів від
Зрозуміло, що для кожного типу задач цілочислового
програмування формулюються специфічні правила для відсіву варіантів.
Метод послідовного аналізу варіантів успішно застосовувався
для розв’язування різноманітних задач оптимального планування та проектування.
Наприклад, для розрахунку транспортних мереж, розміщення на мережі типу дерева,
проектування розподільних електричних мереж, вибору оптимальних параметрів
магістральних газопроводів тощо.
Розділ
3. Розробка математичної моделі складання розкладу занять на математичному
факультеті ВНУ
3.1
Формулювання завдання складання розкладу занять на математичному факультеті
Ефективність використання науково-педагогічного
потенціалу і якість підготовки фахівців у вузах певною мірою залежать від рівня
організації навчального процесу.
Одна з складових цього процесу, розклад занять,
регламентує трудовий ритм, впливає на творчу віддачу викладачів, тому його
можна розглядати як чинник оптимізації використання обмежених трудових ресурсів
- викладацького складу. Технологію ж розробки розкладу слід сприймати не тільки
як трудомісткий технічний прогрес або об'єкт автоматизації з використанням ЕОМ,
але і як акцію оптимального управління. Таким чином, - проблема розробки
оптимальних розкладів занять у вузах з очевидним економічним ефектом. Оскільки
інтереси учасників учбового процесу багатогранні, то завдання складання
розкладу є багатокритерійною.
Завдання складання розкладу не варто розглядати
тільки як якусь програму, що реалізовує функцію механічного розподілу занять на
початку семестру, на якій її (програми) використання і закінчується. Необхідно,
щоб програма включала засоби для випадку зміни деяких вхідних даних.
Завдання теорії розкладів в загальній її
постановці вважається вельми привабливим, хоча досягнення навіть невеликого
прогресу на шляху до рішення зв'язане, як правило, з величезними труднощами. Не
дивлячись на те, що завданнями теорії розкладів займалися багато кваліфікованих
фахівців, до цих пір нікому не вдалося отримати якихось істотних результатів.
Безуспішні спроби отримання таких результатів, як правило, не публікуються і це
частково обумовлює той факт, що завдання продовжує привертати увагу багатьох
дослідників простотою постановки, що здається.
Розвиток нових інформаційних технологій в області
створення програмних web-додатків дозволив подивитися на проблему складання
розкладу і комунікативної взаємодії в зв'язці: администрация-викладач-студент з
іншої точки зору. Система складання розкладу у вузі обов'язково повинна
реалізовувати ряд основних функцій:
вибір викладачів;
вибір дисциплін;
вибір днів тижня;
закріплення аудиторій;
об'єднання груп в потоки по будь-якій сукупності
дисциплін;
після складання розкладу при необхідності
здійснювати заміну викладачів або змінювати час проведення заняття.
Крім того, існують ще і специфічні для кожного
вузу вимоги щодо функціональних можливостей програмного продукту. У випадку
вузів попит на системи складання розкладів напевно навіть більший, ніж для
шкіл, але справа ускладнюється великою специфікою організації учбового процесу
в кожному окремо взятому вузі. Створити уніфіковане програмне забезпечення не
представляється можливим, а вартість створення спеціалізованого програмного
продукту у сторонніх розробників невиправдано велика.
Метою даної роботи було створення такої
математичної моделі розкладу у вузі, яка дозволяла б ефективно (у задані
терміни та з заданим ступенем оптимальності) вирішувати задачу автоматичного
складання розкладу і володіла б гнучкістю (незначних змін у разі змін вхідній
інформації) для адаптації системи в рамках конкретного практичного завдання.
Для деякого спрощення завдання на початковому
етапі проектування були зроблені такі допущення:
розклад складається з розрахунку не більше двох
пар в день (що цілком підходить для викладачів із півставки навантаження);
всі пари проводяться в одному корпусі;
подальша декомпозиція моделі не проводиться;
всі коефіцієнти моделі і шукані змінні
цілочисельні;
Поставлене завдання повинне вирішуватися одним з
універсальних (не залежних від цілочисельних значень коефіцієнтів) методів
цілочисельного лінійного програмування.
3.2
Математична модель розкладу у вузі
Побудуємо математичну модель розкладу у вузі в
термінах лінійного програмування. Введемо позначення і визначимо змінні та
обмеження.
ГРУПИ
У вузі є N навчальних груп, об'єднаних в R потоків; r -
номер потоку, r = 1., R, 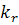
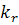 - номер учбової групи в потоці r,
- номер учбової групи в потоці r, 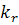
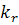 = 1.,
= 1., 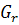
Розбиття на груп на потоки здійснюється виходячи
з принципів:
. Використання двома групами одного і того ж
аудиторного фонду для своїх лекцій автоматично припускає приміщення їх в 1 потік
(передбачається, що всі лекції учбових груп проходять разом).
. Група (або її частина), як одиниця навчального
процесу у вузі, може входити в різні потоки, але тільки поодинці раз в кожний з
них.
. Кількість потоків не лімітується.
ЗАНЯТТЯ
Заняття проводяться в робочі дні і триває 1,5год.
(пара).
Позначимо:
t - номер робочого дня тижня, 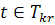
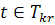 де
де
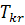
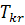 - безліч номерів робочих днів для групи
- безліч номерів робочих днів для групи 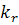
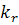 ;- номер пари, j = 1., J;- загальна кількість пар.
;- номер пари, j = 1., J;- загальна кількість пар.
З кожною учбовою групою 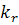
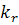 потоку r протягом тижня, згідно учбовому плану, проводиться
потоку r протягом тижня, згідно учбовому плану, проводиться 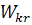
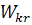 занять, з яких
занять, з яких 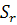
 лекційних і
лекційних і 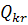
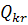 практичних. Позначимо:
практичних. Позначимо:
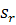
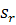 -номер дисципліни в списку лекційних занять для потоку r,
-номер дисципліни в списку лекційних занять для потоку r,
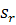
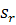 = 1.,;
= 1.,; 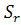
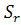
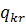
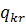 - номер дисципліни в списку практичних занять для групи
- номер дисципліни в списку практичних занять для групи 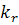
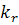 ,
,
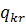
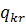 = 1.,
= 1.,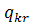
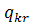 .
.
Передбачається, що лекції проводяться у всіх груп потоку
одночасно і в одній аудиторії. Тоді, якщо по якійсь дисципліні протягом тижня
проводиться більш ніж одне заняття, ця дисципліна згадується в списку лекцій
або практичних занять стільки разів, скільки їх передбачається учбовим планом
для кожного потоку або групи.
ВИКЛАДАЧІ
Хай p - номер (ім'я) викладача, p = 1., P. Введемо в
розгляд булеві значення 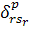
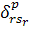 і:
і: 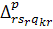
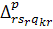
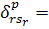
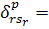 {
{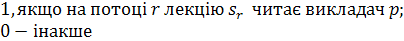
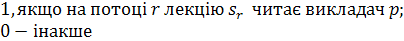
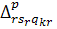
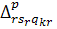 ={
={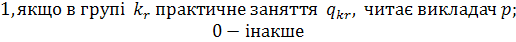
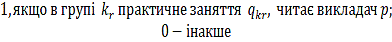
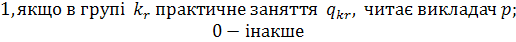
Навчальне навантаження викладачів планується до складання
розкладу занять, унаслідок чого на даному етапі величини 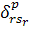
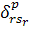 і:
і: 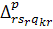
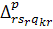 можна вважати заданими. Для кожного викладача p, p = 1.,P, задано
також його аудиторне навантаження -
можна вважати заданими. Для кожного викладача p, p = 1.,P, задано
також його аудиторне навантаження - 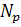
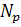 годин в тиждень.
годин в тиждень.
АУДИТОРНИЙ ФОНД
Заняття кожного потоку можуть проводитися тільки в певних
аудиторіях (наприклад, практичні заняття по інформатиці можуть проводиться
тільки в дисплейних класах). Хай:
{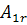
 } - безліч аудиторій для лекцій на потоці r;
} - безліч аудиторій для лекцій на потоці r;
{
 } - безліч аудиторій для практичних занять на потоці r;
} - безліч аудиторій для практичних занять на потоці r;
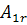 - число елементів множини {
- число елементів множини {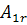
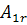 };
};
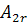
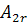 - число елементів множини {
- число елементів множини {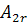
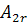 };
};
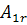
 +
+
 - число аудиторій об'єднання множин {
- число аудиторій об'єднання множин {
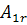 }
}
 {
{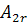
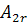 }.
}.
Аудиторний фонд визначається до початку складання розкладу,
тому множини можна вважати заданими.
Завдання складання розкладу полягає у визначенні для кожної
лекції (на потоці) і практичного заняття (у групі) дня тижня і пари цього дня з
урахуванням виконання конструйованих нижче обмежень і мінімізації деякої
цільової функції. Введемо наступні шукані булеві змінні:
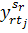
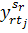 =
=
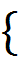
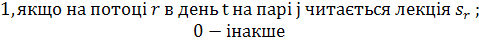
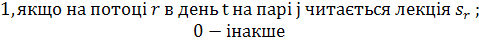 ,
,
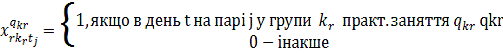
У разі складання розкладу для груп вечірньої
форми навчання J=2.
ОБМЕЖЕННЯ
Для кожної групи 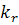
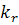 повинні виконуватися всі види аудиторної роботи протягом тижня:
повинні виконуватися всі види аудиторної роботи протягом тижня:
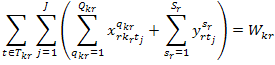
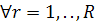 ;
; 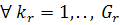
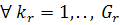 (1)
(1)
У будь-який день t на кожній парі j для кожної групи 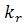
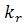 може проводитися не більш за одне заняття:
може проводитися не більш за одне заняття:
 ;
; 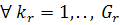
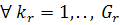 (2)
(2)
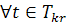
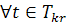
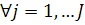
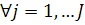
Кожна лекція 
 і практичне заняття
і практичне заняття 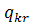
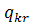 відповідно для всіх потоків r і всіх груп
відповідно для всіх потоків r і всіх груп 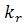
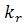 можуть проводитися не більше одного разу в будь-який день t:
можуть проводитися не більше одного разу в будь-який день t:
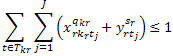
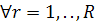
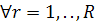 ;
; 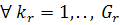
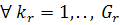 (3)
(3)
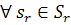
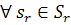
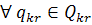
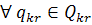
Якщо змінні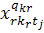
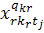 і
і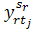
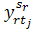 пов'язують всі види занять з часом їх проведення, то
пов'язують всі види занять з часом їх проведення, то 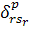
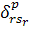 і
і 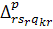
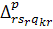 зв'язують час проведення з ім'ям викладача.
зв'язують час проведення з ім'ям викладача.
У кожен день 
 і в кожній парі
і в кожній парі 
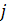 викладач
викладач 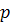
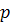 може вести не більш за одне заняття по одній дисципліні на одному
потоці або в одній групі:
може вести не більш за одне заняття по одній дисципліні на одному
потоці або в одній групі:
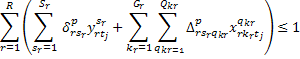
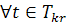
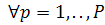
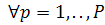 ; (4)
; (4)
Кожен викладач 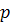
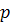 протягом тижня повинен провести аудиторні заняття:
протягом тижня повинен провести аудиторні заняття:
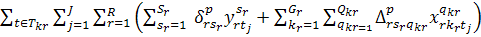
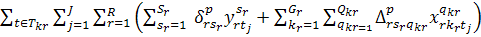 =
=
 (5)
(5)
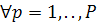
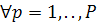
Нарешті, в кожен день на кожній парі число лекцій і
практичних занять не повинне перевищувати наявний на факультеті аудиторний
фонд:
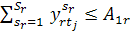
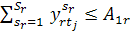 (6)
(6)
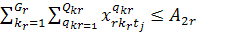
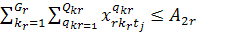 (7)
(7)
Крім того, для всіх сукупностей пересічних множин {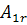
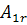 } і {
} і {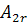
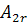 } повинні виконуватися умови:
} повинні виконуватися умови:
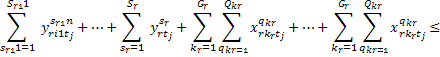 (8)
(8)
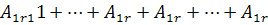
Представленими співвідношеннями вичерпуються
обмеження, яких дотримуються при складанні розкладу. Зрозуміло,що можуть бути і
інші спеціальні умови, але для спрощення моделі вони не розглядалися.
ЦІЛЬВА ФУНКЦІЯ
Щоб повноцінно вести наукову, навчально-методичну
роботу, готуватися до занять, викладач вузу повинен мати вільний час. Це умова
недостатня, але необхідна. Очевидно, що вільним часом він повинен володітити не
в "рваному" режимі, яким, наприклад, є "вікна" між
заняттями із студентами, а по можливості в повністю вільні робочі дні. Цьому
еквівалентна максимізація аудиторного навантаження викладачів в ті дні, коли
вони її мають (формула. (5)). Проте, при цьому претензії на вільний час у
викладачів нерівні, оскільки у них різний творчий потенціал. Тому необхідно
ввести вагові коефіцієнти, за допомогою яких повинні враховуватися відповідний
статус викладача - його вчені ступені і звання, посада, науково-суспільна
активність і т.п. В деяких випадках можна на підставі експертних оцінок
використовувати індивідуальні вагові коефіцієнти, що враховують інші чинники.
Отже, виберемо критерій якості складання розкладу
занять у вигляді максимізації зваженого числа вільних від аудиторної роботи
днів для всіх викладачів, що за умови фіксованої довжини робочого тижня
еквівалентно максимальному сукупному ущільненню аудиторного навантаження.
Розглянемо вираз для величини аудиторного
навантаження в день t викладача p:
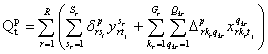 (9)
(9)
Вводяться обмеження вигляду:
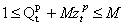
 (10)
(10)
де M - довільне позитивне чимале число; 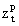 - шукана булева змінна.
- шукана булева змінна.
З (10) випливає, що якщо, 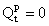 то
то 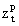 = 1, і якщо,
= 1, і якщо, 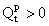 то
то 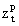 =0
=0
З урахуванням вказаного вище змістовного сенсу критерію
оптимізації в додаткових обмеженнях (10), а також вводячи вагові коефіцієнти
статусу викладача, отримуємо шуканий критерій оптимальності:
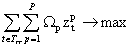 (11)
(11)
Введена цільова функція не є єдино можливою. Введення інших
цільових функцій не змінює обмежень математичної моделі та методів рішення
задачі, але може істотно вплинути на результати обчислень.
МЕТОДИ РОЗВ’ЯЗАННЯ ПОСТАВЛЕНОЇ ЗАДАЧІ
Поставлене в попередньому пункті завдання максимізації
лінійної цільової функції при заданій системі обмежень є завданням лінійного
цілочисельного булева програмування, оскільки всі коефіцієнти обмежень
цілочисельні через дискретність початкових даних завдання; окрім цього шукані
змінні математичної моделі можуть приймати тільки два значення. На даний момент
часу існує декілька можливих методів розв’язання такого роду завдань.
У (3) - (8) описані методи впорядкованої індексації і
модифікованих позначок, засновані на лагранжевій декомпозиції початкової
моделі, що розв’язуються відповідно методами упорядковучої індексації, або
модифікованих позначок. На жаль кількість операцій кожного з методів не
допускає поліноміальної оцінки; крім того, розмірність таблиці наборів
(проміжних значень) методів різко зростає при збільшенні розмірності шуканої
задачі, що недопускається в нашому випадку. Можливо, зміна алгоритму
декомпозиції під конкретну математичну модель дозволить зменшити розмірність
таблиць, але поки такого алгоритму не існує.
У зв'язку з цим в якості методів розв’язання були вибрані
описані в [2] модифікації симплекс-методу для випадку задачі цілочисельного
лінійного програмування. У загальному випадку кількість операцій
симплекс-методу не допускає поліноміальной оцінки (був навіть показаний клас
завдань, для яких кількість операцій складає ), але для випадку нашого завдання середнє число операцій допускає
поліноміальную оцінку:
), але для випадку нашого завдання середнє число операцій допускає
поліноміальную оцінку:  (n - кількість змінних; m - кількість
обмежень).
(n - кількість змінних; m - кількість
обмежень).
ПОВНІСТЮ ЦІЛОЧИСЕЛЬНИЙ АЛГОРИТМ
Цей алгоритм названий повністю цілочисельним, тому що якщо
початкова таблиця складається з цілочисельних елементів, то всі таблиці, що
виходять в процесі роботи алгоритму, містять тільки цілочисельні елементи.
Подібно до двоїстого симплекс-методу, алгоритм починає працювати з двоїсто
допустимої таблиці. Якщо 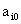 (i = 1., n+m;
(i = 1., n+m; 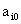 - коефіцієнти цільової функції) -
невідємні,
- коефіцієнти цільової функції) -
невідємні,
цілі, то задача розвв’язана. Якщо для якого-небудь рядка 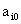 <0, то складається нове рівняння і
записується внизу таблиці. Після цього використовується двоїстий
симплекс-метод. Всі елементи додаткового рядка повинні бути цілими числами, а
ведучий елемент рівний - 1. Введений таким чином ведучий рядок збереже таблицю
цілочисельною.
<0, то складається нове рівняння і
записується внизу таблиці. Після цього використовується двоїстий
симплекс-метод. Всі елементи додаткового рядка повинні бути цілими числами, а
ведучий елемент рівний - 1. Введений таким чином ведучий рядок збереже таблицю
цілочисельною.
Хай дано задача цілочисельного лінійного програмування:
максимізувати
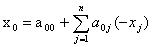
за умов
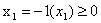
… … …
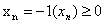 (12)
(12)
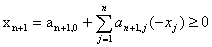 ,
,
… … …
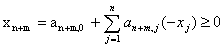
Умови (12) можуть бути записані як
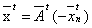 (13)
(13)
Припустимо, що для t=0 (т.е. для початкової таблиці) все 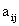 - цілі і стовпці
- цілі і стовпці 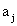 (j = 1., n) - лексикографічно позитивні.
Тоді всі стовпці впродовж обчислень залишаються лексикографічно позитивними.
(j = 1., n) - лексикографічно позитивні.
Тоді всі стовпці впродовж обчислень залишаються лексикографічно позитивними.
Перш ніж викласти спосіб отримання додаткового обмеження з
рядка, що проводить, введемо нове представлення чисел. Нехай [x] позначає
найбільше ціле число, не перевишує x. Для будь-якого числа у (додатнього або
від’ємного) і позитивного можна записати:
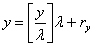 (14)
(14)
де (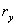 -ненегативний залишок від ділення без
остачі у на
-ненегативний залишок від ділення без
остачі у на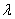 ). Зокрема
). Зокрема 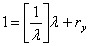 . Тому якщо,
. Тому якщо, 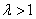 то
то  і r = 1. Якщо,
і r = 1. Якщо, 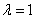
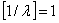 то і r = 0.
то і r = 0.
Додаткова нерівність, що вводиться, повинна виконуватися
при будь-якому цілому рішенні задачі (12). Розглянемо деяке рівняння в t -
таблиці (опускаючи індекс рядка) з  <0:
<0:
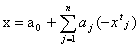 (15)
(15)
де x - відповідна компоненту вектора, 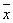 а
а 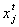 - поточні небазисні змінні. Можна виразити x,
- поточні небазисні змінні. Можна виразити x, 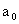 і
і 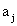 використовуючи введене вище уявлення (14):
використовуючи введене вище уявлення (14):
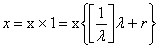 (16)
(16)
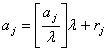 (17)
(17)
Підставивши вирази (16) і (17) в (15) і переставивши члени,
отримаємо:
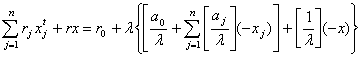 (18)
(18)
Оскільки, 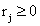 і
і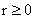 на змінні x і
на змінні x і 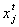 накладена вимога позитивності, ліва
частина рівняння (18) завжди невід’ємна. Розглянемо вираз в правій частині,
поміщений у фігурні дужки. Коефіцієнти в цьому виразі є цілими числами, а
змінні підпорядковані вимозі цілочисельності. Тому весь вираз в дужках повинен
бути цілим. Позначимо його через s.:
накладена вимога позитивності, ліва
частина рівняння (18) завжди невід’ємна. Розглянемо вираз в правій частині,
поміщений у фігурні дужки. Коефіцієнти в цьому виразі є цілими числами, а
змінні підпорядковані вимозі цілочисельності. Тому весь вираз в дужках повинен
бути цілим. Позначимо його через s.:
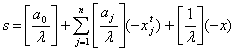 (19).
(19).
Цілочисельна слабка змінна s є невід’ємна. Дійсно, якби s
було від’ємним, тобто приймало б значення - 1, - 2,., то множення на зробило б
всю праву частину рівняння (18), тоді як ліва частина від’ємна.
Розглянемо два випадки 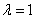 і
і  . Для
. Для
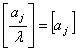 і
і 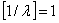 . Підставляючи в рівняння (19) вираз для x
з (15), отримаємо:
. Підставляючи в рівняння (19) вираз для x
з (15), отримаємо:
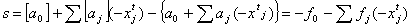 (20)
(20)
Отримане рівняння є не що інше як відсікання Гоморі. Для  маємо
маємо  і рівняння (19) набуває вигляд:
і рівняння (19) набуває вигляд:
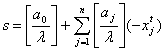 (21)
(21)
Рівняння (21) повинне виконуватися для будь-якого
цілочисельного розв’яз-
ку задачі (12). Відмітимо, що якщо  <0, то
<0, то  в рівнянні (21) Тому рівняння (21) може використовуватися як
ведучий рядок в симплекс-методі. Зокрема, завжди можна вибрати
в рівнянні (21) Тому рівняння (21) може використовуватися як
ведучий рядок в симплекс-методі. Зокрема, завжди можна вибрати 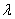 достатньо великим, так щоб провідний
елемент
достатньо великим, так щоб провідний
елемент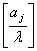 в рядку (21) став рівним - 1, що
дозволить зберегти цілочисельність таблиці. Вибір відповідного
в рядку (21) став рівним - 1, що
дозволить зберегти цілочисельність таблиці. Вибір відповідного 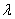 впливатиме на швидкість збіжності
алгоритму. Перш за все опишемо сам алгоритм. Як початковий необхідно узяти
подвійно допустиме рішення, яке можна отримати додаванням обмеження
впливатиме на швидкість збіжності
алгоритму. Перш за все опишемо сам алгоритм. Як початковий необхідно узяти
подвійно допустиме рішення, яке можна отримати додаванням обмеження  , де M - достатнь велика стала, і
проведенням однієї ітерації з доданим рядком і з лексикографічно мінімальним
стовпцем, взятими за ведучих. Алгоритм складається з наступних кроків:
, де M - достатнь велика стала, і
проведенням однієї ітерації з доданим рядком і з лексикографічно мінімальним
стовпцем, взятими за ведучих. Алгоритм складається з наступних кроків:
Крок 0. Почати з подвійно допустимої матриці  в рівнянні (13), елементи якої - цілі
числа (матриця
в рівнянні (13), елементи якої - цілі
числа (матриця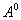 може містити і нецілі елементи,).
може містити і нецілі елементи,).
Крок 1. Серед рядків з 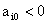 (i=1., n+m) вибрати рядок з найменшим значенням i; цей рядок
стане ведучим. (Якщо
(i=1., n+m) вибрати рядок з найменшим значенням i; цей рядок
стане ведучим. (Якщо 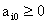 (i=1., n+m), то задача розв’язана.)
(i=1., n+m), то задача розв’язана.)
Крок 2. Вибрати 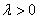 (правило вибору буде описано далі) і написати внизу
таблиці додатковий рядок
(правило вибору буде описано далі) і написати внизу
таблиці додатковий рядок
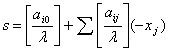
Цей рядок вибирається як ведучій.
Крок 3. Провести крок двоїстого симплекс-метода, викреслити
додатковий рядок і повернутися до кроку 1.
Доведення кінцівки алгоритму.
Правило вибору  формулюється таким чином.
формулюється таким чином.
Крок 0. Хай рядок з номером v є ведучим.
Крок 1. Хай  - лексикографічно мінімальний стовпець серед стовпців з
- лексикографічно мінімальний стовпець серед стовпців з  . Крок 2. Для кожного
. Крок 2. Для кожного 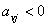 хай
хай 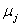 - найбільше ціле, таке, що
- найбільше ціле, таке, що 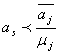 (лексикографічно менше). Крок 3. Хай,
(лексикографічно менше). Крок 3. Хай, 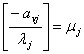 а
а 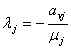 (рядок v - що проводить). Тоді .
(рядок v - що проводить). Тоді . 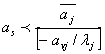 . Крок 4. Покласти
. Крок 4. Покласти 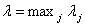 для
для 
Правило вибору 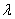 , описане вище, дозволяє зробити ведучий елемент рівним - 1, при
цьому зберігається двоїста допустимість таблиці і в той же час нульовий
стовпець буде максимально лексикографічно зменшуватися.
, описане вище, дозволяє зробити ведучий елемент рівним - 1, при
цьому зберігається двоїста допустимість таблиці і в той же час нульовий
стовпець буде максимально лексикографічно зменшуватися.
ПРЯМИЙ АЛГОРИТМ ЦІЛОЧИСЕЛЬНОГО ПРОГРАМУВАННЯ
Термін "прямий”, застосований до алгоритму
цілочисельного програмування, позначає метод, який приводить до оптимального
розв’язку за допомогою отримання послідовно "покращуючих" розв’язків.
Кожному з цих розв’язків допустимо в тому сенсі, що він задовольняє як лінійним
обмеженням, так і умові цілочисельності. Одним з вірогідних достатків алгоритму
є можливість перервати обчислення, до того як отримано оптимальне рішення, і
використовувати найкраще з отриманих розв’язків як наближене. Крім того, можна
використовувати прямий алгоритм в з'єднанні з двоїстими алгоритмами, щоб
отримувати різні складені алгоритми, які можуть переходити від фази, що дає
подвійно допустимі розв’язки, до фази, що дає прямо допустимі розв’язки.
Природним прецедентом для прямого алгоритму є повністю
цілочисельний алгоритм Гоморі, оскільки в процесі цього алгоритму виходить
послідовність подвійно допустимих цілочисельних розв’язків. Слід нагадати, що
повністю цілочисельний алгоритм Гоморі є модифікацією двоїстого
симплекс-методу. Основна відмінність цього алгоритму полягає в тому, що як
ведучий рядок використовується відсікання Гоморі з провідним елементом, рівним
- 1. Це відсікання виходить з рядка, що проводить, який визначається як один з
можливих провідних рядків в двоїстому симплекс-методі. Використання такого
відсікання як ведучий рядок збереже після ітерації подвійну допустимість і
цілочисельність таблиці.
Виявляється, можна аналогічно модифікувати симплекс-метод так,
щоб отримати алгоритм, який зберігає пряму допустимість і цілочисельність
таблиць. Для опису обчислювальної процедури розглянемо наступне завдання
цілочисельного програмування:
максимізувати
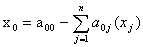 (22)
(22)
за умов
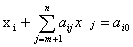
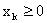 (цілі)
(цілі) 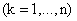
де  і
і  - цілі числа і
- цілі числа і 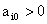 .
.
Припустимо, що стовпець вибраний 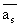 як ведучого і рядок
як ведучого і рядок 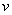 - провідний рядок в ітерації
симплекс-метода
- провідний рядок в ітерації
симплекс-метода 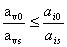 , тобто для всіх рядків
, тобто для всіх рядків 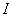 , в яких
, в яких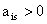 . Перш ніж провести процедуру виключення Гауса в симплекс-методі,
додамо до таблиці відсікання Гоморі, отримане з рядка
. Перш ніж провести процедуру виключення Гауса в симплекс-методі,
додамо до таблиці відсікання Гоморі, отримане з рядка 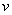 :
:
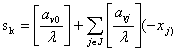
де  - безліч індексів небазисних змінних в
(22), -
- безліч індексів небазисних змінних в
(22), -  нова (базисна) слабка змінна
нова (базисна) слабка змінна  і - невизначена (тимчасово) позитивна
константа.
і - невизначена (тимчасово) позитивна
константа.
Відмітимо, що якщо покласти  =
=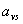 , відсікання (23) володітиме двома
важливими властивостями. По-перше
, відсікання (23) володітиме двома
важливими властивостями. По-перше
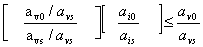
Це означає, що пряма допустимість таблиці збережеться, якщо
використовувати відсікання (23) як ведучий рядок. По-друге , тобто ведучий елемент рівний 1 (якщо
відсікання використовується як провідний рядок). Легко переконатися (шляхом
дослідження формул зміни базисних змінних), що перетворення симплексної таблиці
з одиничним вудучим елементом зберігає цілочисельність елементів симплексної
таблиці.
, тобто ведучий елемент рівний 1 (якщо
відсікання використовується як провідний рядок). Легко переконатися (шляхом
дослідження формул зміни базисних змінних), що перетворення симплексної таблиці
з одиничним вудучим елементом зберігає цілочисельність елементів симплексної
таблиці.
Ці ідеї послужили підставою прямого алгоритму в
цілочисельному програмуванні:
Крок 0. Почати із стовбцевої таблиці, в якій і всіх  елементах
елементах 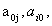 і
і 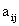 - цілі.
- цілі.
Крок 1. Перевірити виконання умов 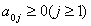 ; якщо вони виконані, то кінець, поточний
базисний розв’язок оптимальний; якщо немає - перейти до кроку 2.
; якщо вони виконані, то кінець, поточний
базисний розв’язок оптимальний; якщо немає - перейти до кроку 2.
Крок 2. Вибрати провідний стовпець 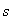 з
з 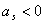 . Вибрати рядок
. Вибрати рядок 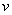 за правилом перевірки відношення
за правилом перевірки відношення 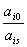 серед рядків з
серед рядків з 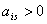 . Цей рядок служить Гоморі, що проводить для відсікання.
. Цей рядок служить Гоморі, що проводить для відсікання.
Крок 3. Отримати відсікання Гоморі з рядка, що проводить, і
дописати її внизу таблиці, тобто додати до обмежень завдання рівняння (23), де 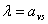 .
.
Крок 4. Провести перетворення таблиці, використовуючи
відсікання (23) як ведучий рядок. Слабка змінна 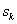 в (23) стане небазисною. Повернутися до кроку 1.
в (23) стане небазисною. Повернутися до кроку 1.
Висновки
Дана дипломна робота складається з трьох розділів,
вступу, деякі історичні відомості, висновки, список використаної літератури, та
додатки.
У першому розділі наведенні деякі історичні
відомості. Цілочисельне програмування є складовою лінійного програмування
основоположником якого вважають радянського вченого Л.В. Канторовича. Сам
термін "лінійне програмування" був введений дещо пізніше, в 1951
році, у працях американських вчених Дж. Данцига та Г. Кумпанса. В 1947 році Дж.
Данциг розробив основний метод розв’язування задач лінійного програмування -
симплексний метод, що стало початком формування лінійного програмування як
самостійного напрямку в математичному програмуванні.
Перша задача цілочислового типу яка була
опублікована угорським математиком Б. Егерварі в 1932 році, задача про
призначення персоналу.
Також в даному розділі наведена загальна
постановка цілочисельної задачі та вказуються спеціальні методи для знаходження
оптимальних розв’язків таких задач. Це методи відтинання та комбінаторні
методи. Основна ідея методів відтинання - поступове "звуження"
області допустимих розв'язків розглядуваної задачі. Пошук цілочислового
оптимуму починається з розв'язування задачі з так званими послабленими
обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі
вводяться у модель спеціальні додаткові обмеження, що враховують цілочисловість
змінних, многокутник допустимих розв'язків послабленої задачі поступово
зменшуємо доти, доки змінні оптимального розв'язку не набудуть цілочислових
значень. До цієї групи належать:
методи розв'язування повністю цілочислових задач
(дробовий алгоритм Гоморі);
методи розв'язування частково цілочислових задач
(другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).
Комбінаторні методи цілочислової оптимізації
базуються на повному переборі всіх допустимих цілочислових розв'язків, тобто
вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається
лише частина розв'язків (досить невелика), а решта враховується одним зі
спеціальних методів.
В цьому розділі також наведенні конкретні приклади
застосування цілочислових задач лінійного програмування у плануванні та
управлінні виробництвом, зокрема задача про ранець, задача оптимального розкрою
матеріалів, задача комівояжера, задача планування виробничої лінії і т. д
Другий розділ присвячений
детальному розгляду методів задач цілочислового програмування. Спочатку було
розглянуто графічний метод. Він є досить простий для розуміння. Недоліком є те,
що графічним способом можна розв’язати задачу, в якій в обмеженнях є лише дві
змінні, потрібно намагатися малювати лінії з найбільшою точністю, в
протилежному випадку можна отримати велику похибку, а в результаті неправильне
рішення.
Також розглянули алгоритм методу Гоморі, який
можна описати за допомогою наступних кроків:
) знаходимо розв'язок задачі без умов
цілочисельності симплекс-методом;
2) якщо оптимальний план цілочисельний, то
вибираємо базисну змінну з найбільшою дробовою частиною і за обмеженням цієї
змінної будуємо нерівність Гоморі;
) до обмежень задачі дописуємо побудову
задачі нерівність Гоморі: розв'язуємо розширену задачу симплекс-методом і
повертаємось до другого кроку. Процес повторюється до тих пір поки оптимальний
розв'язок буде цілочисельним або симплекс-таблиці не покажуть що задача не має
розв'язку.
Наступним кроком було розглянуто схему процесу
розв’язування задачі методом гілок і меж. Вона полягає в тому, що початкова
задача розділяється (гілкується) на дві простіші, і, якщо серед них не існує
задачі з цілочисловим оптимальним розв’язком, то процес гілкування
продовжується.
Третій розділ даної дипломної роботи присвячений
розробці математичної моделі складання графіку занять на математичному
факультеті ВНЗ.
Завдання теорії розкладів в загальній її
постановці вважається дуже привабливим, хоча досягнення навіть невеликого
прогресу на шляху до розв’язання зв'язане, як правило, з величезними
труднощами. Не дивлячись на те, що завданнями теорії розкладів займалися багато
вельми кваліфікованих фахівців, до цих пір нікому не вдалося отримати істотних
результатів. Метою даної роботи було створення такої математичної моделі
розкладу у вузі, яка дозволяла б ефективно (у задані терміни і із заданим
ступенем оптимальності) знаходити задачу автоматичного складання розкладу
занять і володіла б гнучкістю (незначних змін у разі змін вхідній інформації)
для адаптації системи в рамках конкретного практичного завдання.
Література
1. Акулич И.Л. Математическое программирование в примерах и
задачах. - М., 1986. - 320с.
2. Вітлінський В.В., Наконечний С.І., Терещенко Т.О.
Математичне програмування: Навч. - метод. посіб. - К.: Вид-во КНЕУ, 2006-246с.
. Вентцель Е.С., Исследование операцій. - М.: Сов. радіо,
1972. - 552с.
. Жильцов О.Б. Кульян В.Р., Юнькова Е.А. Математичне
програмування з елементами інформаційних технологій: Навч. посіб. \За ред. О.О.
Юнькової. - К.: МАУП, 2006. - 184с.
. Зайченко Ю. П Исследование операцій. - К. ”Вишая школа”,
1980Костевич Л.С., Математическое программирование: Информ. технологии
оптимальных решений: Учеб. пособие. - Минск., 2003. - 424с.
. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б.
Математическое программирование. - М., 1976. - 352с.
. Кутковецький В.Я., Дослідження операцій: Навч. посіб. -
К., 2004. - 350с.
. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б.
Математическое программирование. - М.,”Высшая школа”, 1980.
. Карманов В.Г. Математическое программирование. - М.,
Наука, 1986.
. Романюк Т.П., Терещенко Т.О., Городкова І.М. Математичне
програмування.,-К.,ІЗМН., 1996.
. Суворовський А.А. Математическое программирование. - К.:
ІМКВО, 1992.
. Цегелик Г.Г. Лінійне програмування. - Львів, Світ, 1995.
Додаток
а. бібліографія
Леонід Віталійович Канторович (1912-1986) стояв у витоків
формування сучасної обчислювальної математики. Перші роботи по наближених
методах конформних відображень, варіаційних методах, квадратурних формулах,
чисельним методам вирішення інтегральних рівнянь і рівнянь частинних похідних
були виконані Л.В. Канторовичем на початку 30-х років.
Л.В. Канторович займався науково-організаційною
роботою в Радіанському Союзі. Видатні заслуги Л.В. Канторовича були відмічені
державою. Він нагороджений двома орденами Леніна - найвищими нагородами країни,
трьома орденами Трудового Червоного Прапора, орденами "Знак Шани" і
Вітчизняної війни II ступеня, багатьма медалями. Дослідження Л.В. Канторовича в
області функціонального аналізу, обчислювальної математики, теорії
екстремальних завдань, дескриптивній теорії функцій і теорії множин зробили
вплив на становлення і розвиток вказаних математичних дисциплін, послужили
основою для формування нових наукових напрямів.
Джон фон Нейман (при народженні - Янош
Лайош Нейман 1903-1957р.).
Неймана вніс значний внесок в розвиток багатьох
областей математики, йому належить строге математичне формулювання принципів
квантової механіки, а його праця "Математичні основи квантової
механіки" є класичним навчальним посібником. Учений став одним з творців
теорії ігор, яка лягла в основу математичного підходу до явищ конкурентної
економіки, теорії обчислювальних машин і аксіоматичної теорії автоматів. Він
вніс великий внесок до створення перших ЕОМ і розробки методів їх застосування.
У 1952 році учений розробив перший комп'ютер, що використовує програми,
записані на гнучкому носієві.
Джон фон Нейман був членом Національної Академії
наук США, Американської філософської спілки, а також почесним членом багатьх
зарубіжних академій, наукових установ та об’єднань. Його видатні досягнення
відмічені численними престижними преміями. Більше 150 праць вченого присвячено
проблемам фізики, математики та їх практичним застосуванням, теорії ігор і
комп'ютерної теорії, теорії топологічних груп та метеорології.
Глушков Віктор Михайлович (1923-1982) народився 24
серпня 1923 р. в Ростов-на-Дону в сім'ї гірського інженера. У 1948 р. В.М.
Глушков отримав диплом математичного факультету Ростовського університету. З
1951 р. він працював над докторською дисертацією, присвяченій так званій
"узагальненій п'ятій проблемі Гільберта" і в 1955 р. блискуче
захистив дисертацію. Отримані молодим ученим фундаментальні результати відразу
ж поставили його в перші ряди алгебристів країни. Проте несподівано він
радикально міняє сферу своєї діяльності. За пропозицією директора Інституту
математики АН УРСР Б.В. Гнеденко він в 1956 р. переїжджає до Києва і очолює
лабораторію інституту, якою раніше керував академік С.А. Лебедев. З 1962 р.
очолював Інститут кібернетики (ДІК) АН УРСР, керував науковими семінарами, мав
велику кількість аспірантів і докторів, виступав з доповідями на різних
симпозіумах і конференціях, був редактором створеного ним журналу
"Кібернетика", консультував десятки організацій, читав лекції, вів
велику суспільну роботу.
Круг його наукових інтересів був надзвичайно
широкий: теорія цифрових автоматів, алгебра алгоритмів, мови програмування,
автоматизація проектування ЕОМ, розпізнавання образів, імітаційне моделювання
інтелектуальної діяльності, автоматизовані системи управління технологічними
процесами, підприємствами, галузями, безпаперова інформатика і багато іншого.
Він залишив після себе величезну творчу спадщину,
численних учнів, відому у всьому світі київську школу кібернетиків і добру
пам'ять для нащадків. У 1996 р. міжнародним комп'ютерним співтовариством IEEE
(International Electrical and Electronic Engineers) Computer Society
академікові В.М. Глушкову присвоєно звання "Computer Pioneer" за його
внесок в автоматику та обчислювальну техніку.
Данциг Джордж Бернард (08.11.1914-13.05.2005) американський
математик, професор Каліфорнійського університету. Він розробив симплексний
алгоритм, для розв’язання задач лінійного програмування, за що його називають
"батьком лінійного програмування", (разом з радянським математиком
Л.С. Канторовичем).
У 1936 р. отримав ступінь бакалавра по математиці
і фізиці в Університеті Меріленда, ступінь магістра математики в Університеті
Мічіган і доктора філософії в Університеті Берклі в 1946 р. Став почесним
доктором наук від Університету Меріленд в 1976 р. Йому були присуджені:
Національна наукова медаль США (1975), Приз Джона фон Неймана (1974), Премія
Харві (Ізраїль, 1985). Був членом: Національній Академії Наук, Національної
технічної Академії і американської Академії Мистецтв і Наук.
Шаталін Станіслав Сергійович (24.08.1934 -
03.03.1997). Економіст. Закінчив економічний факультет МГУ (1958). Доктор
економічних наук (1970).
Професор (1972), завідувач кафедри математичних
методів аналізу економіки (1972-1983) економічного факультету Московського
університету.
Директор Інституту народногосподарського
прогнозування (1986), академік РАН (1987). член Президії АН СРСР (1989-1991).
Нагороджений орденами "Знак Пошани"
(1975, 1986), "Дружба народів" (1994). Лауреат Державної премії СРСР
(1968), премії ім. B. C. Немчинова (АН СРСР, 1987).), член Президії АН СРСР
(1989-1991), голова Наукової ради АН СРСР з проблеми "Соціально-культурний
розвиток" (1987-1997), член Президентської ради СРСР (1990-1991), один з
авторів економічної програми "500 днів" (1991), голова оргкомітету і
президент Міжнародного фонду економічних і соціальних реформ
"Реформа" (1992-1994), член Демократичної партії Росії, голова
правління Московського союзу споживачів, член Комісії із зовнішньої політики
при МЗС РФ (1992-1997), член Комісії при Президентові РФ (1992-1997), член
Міжнародного економічного суспільства (1967).
Область наукових інтересів: методологія
народно-господарського планування і прогнозування, комплексні проблеми соціально-культурного
розвитку і підвищення народного добробуту, економіко-математичне моделювання,
методи аналізу і планування міжгалузевих зв'язків і галузевої структури
народного господарства.