Адаптационная оптимизация производственных процессов с технологической обратной связью

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

"САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ"

КАФЕДРА ВЫЧИСЛИТЕЛЬНЫХ МАШИН И КОМПЛЕКСОВ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОМУ ПРОЕКТУ

Адаптационная оптимизация производственных процессов с технологической обратной связью

по дисциплине: Компьютерная обработка экспериментальных данных

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.

Костерев Г. М.

Санкт-Петербург 2012

Содержание

 

Цель работы

Моделирование "черного ящика"

Листинг программы, моделирующей случайную помеху

Определение вида распределения сгенерированной помехи

Построение уравнения регрессии

Получение значений откликов

Листинг программы для получения значений откликов

Аппроксимация уравнения регрессии линейным уравнением

Определение значимости коэффициентов уравнения регрессии

Окончательное уравнение регрессии

Приложение

Список, используемой литературы

Цель работы

1.       Разработать модель "чёрного ящика" по заданным параметрам;

Y = x₁*sin (x₂₎ +x₃-3x₄, где 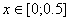 f (ξ) =c*cos (x) (0; π/2)

2.       По выходам "чёрного ящика" определить вид закона распределения случайной величины;

3.       Оценить параметры распределения;

4.       Построить уравнение регрессии, выбрав степень полинома так, чтобы среднеквадратичная ошибка не превышала заданного порога: .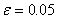

.        Оценить значимость коэффициентов, удалить незначимые.

Моделирование "черного ящика"

f (ξ) =c*cos (x); (0; π/2)

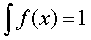
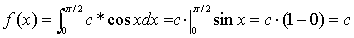
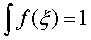=1

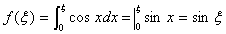
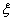= arcsin (x)

Листинг программы, моделирующей случайную помеху

Программа написана и отлажена в среде Visual C++

 

Определение вида распределения сгенерированной помехи

Для этого по полученной выборке построим гистограмму

Границы		Середина	li	попаданий	ni/ (n*li)
0,007111	0,103797	0,0554539	0,096686	10	1,034275
0,103797	0,170849	0,137323	0,067052	10	1,49138
0,170849	0,236928	0, 2038885	0,066079	10	1,51334
0,236928	0,332552	0,28474	0,095624	10	1,045763
0,332552	0,486337	0,4094445	0,153785	10	0,650258
0,486337	0,651913	0,569125	0,165576	10	0,603952
0,651913	0,764266	0,7080895	0,112353	10	0,890052
0,764266	0,877236	0,820751	0,11297	10	0,885191
0,877236	1,10431	0,990773	0,227074	10	0,440385
1,10431	1,53765	1,32098	0,43334	10	0,230766

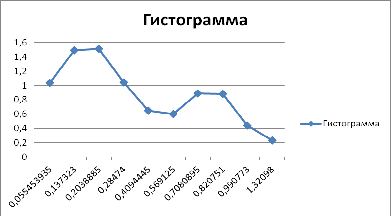
Рис 1. Гистограмма по выборке.

 

По Рис.1 можно выдвинуть гипотезу о синусоидальном характере распределения промоделированной случайной величины.

Проверка гипотезы методом "хи-квадрат":

Диапазон возможных значений элементов выборки разбивается на k интервалов и подсчитываются количества n_i элементов выборки, попавших в каждый i-ый интервал (рис.4.1).

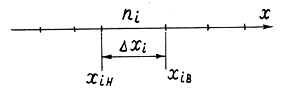
Рис.2.

На основании этого разбиения вычисляется значение статистики

 

_,

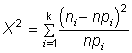где 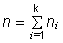- объем выборки, p_i = F (x_{i B}) - F (x_{i H}) - вероятность попадания в i-тый интервал с нижней x_{i H} и верхней x_{i B} границами.

Чтобы обеспечить заданный уровень значимости критерия, в качестве порога, с которым следует сравнивать X², следует брать квантиль хи-квадрат распределения уровня 1-a c²_1-a (k-1). Решающее правило принимает вид: если X² > c²_{1-a (}k-1), то гипотеза отклоняется, в противном случае экспериментальные данные не противоречат гипотезе.

Границы		попадания	p (i)	n*p (i)	x2
0,007111	0, 198428	24	0, 190018	19,00179	1,314727
0, 198428	0,389746	21	0,182824	18,28245	0,403945
0,389746	0,581063	11	0,16896	16,89597	2,057439
0,581063	0,77238	12	0,148929	14,89294	0,56195
0,77238	0,963698	18	0,123465	12,34645	2,588807
0,963698	1,155015	4	0,093494	9,349437	3,06077
1,155015	1,346332	7	0,060113	6,011252	0,162632
1,346332	1,53765	3	0,024537	2,453712	0,121624
		100	0,99234		10,27189

Задавшись уровнем значимости a = 0.05, по таблице квантилей хи-квадрат распределения находим, что для числа степеней свободы k - m - 1 =8 - 1 =7, величина c² = 14,08. Так как экспериментально полученное значение статистики хи-квадрат 10,27 меньше порогового значения то, можно говорить, что экспериментальные данные не противоречат выдвинутой гипотезе о синусоидальном характере распределения случайной величины.

 

Построение уравнения регрессии

Матрица планирования:

Матрица планирования (A) имеет вид:

1	1	1	1	1
1	1	1	-1	-1
1	1	-1	1	-1
1	1	-1	-1	1
1	-1	1	1	-1
1	-1	1	-1	1
1	-1	-1	1	1
1	-1	-1	-1	-1

(At*A) ^ (-1) *At

0,125	0,125	0,125	0,125	0,125	0,125	0,125	0,125
0,125	0,125	0,125	0,125	-0,125	-0,125	-0,125	-0,125
0,125	0,125	-0,125	-0,125	0,125	0,125	-0,125	-0,125
0,125	-0,125	0,125	-0,125	0,125	-0,125	0,125	-0,125
0,125	-0,125	-0,125	0,125	-0,125	0,125	0,125	-0,125

Получение значений откликов

Необходима выборка, полученная с помощью черного ящика. Для этого нам надо поставить несколько опытов с разными значениями x_i. Количество опытов равно 2 в степени количества факторов x, для сокращения количества опытов в 2 раза воспользуемся генератором. Т.е. восемь (2⁴) /2. В каждом опыте выполняем по 6 циклов. Теперь мы получили выборку, представленную в таблице.

-0,885949	-0,545167	0,0595463	0,654982	-0,730886	-0,816489	-0,487277	-1,35567
-0,259396	-0,900356	0,120166	0,769114	-0,552592	-0,987099	-0,736511	-0,785025
-0,467197	-0,413624	1,1685	1,64617	-0,629183	-1,40712	-0,681407	-0,569984
-0,529682	-0,246241	1,05407	0,58574	-0,587344	-1,08421	-0, 208493	-1,14423
-0,894178	-1, 20499	0,440312	0,764431	-0,369641	-0,304032	0,506455	-1,32553
0,0183099	-0,737719	0,427899	0,953205	-0,463721	-1,3228	-0,664128	-1,11012

Листинг программы для получения значений откликов

Программа написана и отлажена в среде Visual C++

программа моделирование обратная связь

Аппроксимация уравнения регрессии линейным уравнением

Неизвестное уравнение регрессии технологического процесса может быть аппроксимировано линейным уравнением:

y =b₀ +b₁x₁ +b₂x₂ +b₃x₃ +b₄x₄

Оценки b_i коэффициентов b_i, i=0,1,.,4, рассчитываются по формулам:

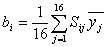, где 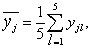S_ij - знак i-го фактора в j-ом опыте ПФЭ.

Результат вычислений оценок коэффициентов:

b0	b1	b2	b3	b4
-0,338314392	0,40406215	-0,341740029	0,115301	0,095083

Уравнение регрессии:

 = - 0,338314392+0,40406215x₁-0,341740029x2+0,115301x₃+0,095083x₄

Отклики, предсказанные уравнением регрессии:

предсказанные отклики
-0,065608817
-0,486375725
0,427705883
0,387269692
-1,063898475
-1,104334667
-0, 190253058
-0,611019967

Для проверки гипотезы адекватности сравним точность, достигнутую моделью, с точностью измерений.

Число степеней свободы:

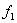=n- (m+1) =8- (4+1) =3

Dад =

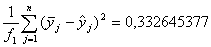
Число степеней свободы:

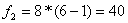
Dвос=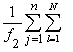

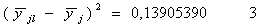
F = Dад/Dвос = 2,392204535

Пороговое значение критерия Фишера F₀ для f₁=3, f₂ =40 и уровня значимости a =0,05 находим по таблице Прил.1 F₀ =2,9.

Так как F<F₀ - линейное уравнение регрессии адекватно.

 

Определение значимости коэффициентов уравнения регрессии

Проверяем значимость отдельных коэффициентов уравнения регрессии с помощью t - статистики Стьюдента.

Для чего по таблице Прил.2 для f= n (N-1) =8 (6-1) =40 и a =0.05 находим пороговое значение t₀= 1.684.

Вычислив для каждого коэффициента регрессии величину

t_i = b_i /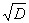, где D = Dвос/Nn = 0,139053903/5*8 = 0,003476

и, сравнив êt_i ê c t₀, приходим к выводу, что коэффициент b₄ незначим.

-5,73797798

6,853092

-5,796078472

1,955558

1,612649

значим

значим

значим

значим

не значим

Окончательное уравнение регрессии

Таким образом, окончательное уравнение регрессии технологического процесса имеет вид

Уравнение регрессии: Y = - 0,338314392+0,40406215x₁-0,341740029x2+0,115301x₃

Приложение

 

Статистический анализ уравнения регрессии:

Уравнение регрессии, найденное с помощью ПФЭ, нуждается в статистическом анализе. Проводятся два вида такого анализа: проверка адекватности модели (т.е. всего уравнения в целом) и проверка значимости отдельных коэффициентов уравнения. Обе эти проверки проводятся в предположении справедливости модели технологического процесса (1). т.е. считается, что значения отклика процесса Yil, (j= 1,.,n; l= 1,.,N) представляют собой независимые нормальные случайные величины с одинаковой дисперсией.

Проверка адекватности модели служит для определения соответствия выбранного вида уравнения регрессии {линейное, неполное квадратное и т.п.) неизвестному точному уравнению регрессии. Эта проверка основывается на сравнении разброса экспериментально полученных значений отклика, относительно найденного уравнения регрессии, с разбросом отклика в каждой точке факторного пространства.

Разброс значений отклика относительно уравнения регрессии характеризуется так называемой дисперсией адекватности, равной

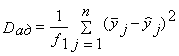, (14)

где n - число опытов в плане; N - число повторений отдельных опытов; 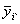 - среднее значение отклика в j-й точке плана; 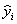 - значение отклика в той же точке плана, предсказываемое найденным уравнением регрессии; f1=n- (m+1) - число степеней свободы дисперсии адекватности; m+1 - число коэффициентов в уравнении регрессии.

Разброс отклика в каждой точке факторного пространства при справедливости модели (1) одинаков и характеризуется уже упоминавшейся дисперсией воспроизводимости, величина которой может быть вычислена по формуле.

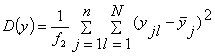 (15)

где yjl - значение отклика в j-й точке плана при l-м повторении опыта;= n (N-1) - число степеней свободы дисперсии воспроизводимости.

Если гипотеза адекватности справедлива, и, следовательно, дисперсии адекватности и воспроизводимости равны, то отношение F=Dад/D{y}, как показано в математической статистике, имеет F - распределение Фишера с f1 и f2 степенями свободы. Если же гипотеза адекватности неверна, то Dад/D{y} будет иметь распределение, отличное от F-распределения Фишера, сдвинутое в сторону больших значений статистики F.

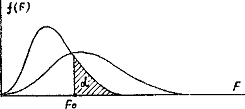
Рис.3.

На основании этого для проверки гипотезы адекватности рассчитанное значение F сравнивается с пороговым значением Fo, которое при справедливости гипотезы адекватности может быть превышено с заданной малой вероятностью α (см. рис.3) Если F ≥ Fo гипотеза адекватности отвергается. Если F < Fo - принимается.

Описанное правило проверки гипотезы адекватности называется тестом или критерием Фишера, а малая вероятность a его уровнем значимости. На практике обычно пользуются значением a, равным 0,05 или 0,01. Таблица пороговых значений F0 для критерия Фишера при этих уровнях значимости приведена в Прил.1.

Если результаты проверки адекватности уравнения регрессии показали, что оно адекватно, то необходимо проверить значимость его коэффициентов. Такая проверка позволяет отбросить незначимые коэффициенты, появление которых вызвано случайными причинами, и тем самым упростить уравнение регрессии. Проверка основывается на том, что при ПФЭ все коэффициенты статистически независимы и имеют одинаковую дисперсию D, для которой известна оценка (13). Для проверки значимости любого коэффициента bi вычисляется

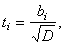
- статистика Стьюдента.

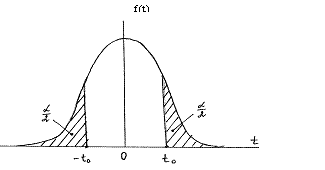
Эта статистика при условии, что истинное значение коэффициента регрессии bi=0 имеет t - распределение Стьюдента с f степенями свободы, где f=n (N-1) - число степеней свободы дисперсии воспроизводимости. Распределение Стьюдента симметрично и имеет математическое ожидание, равное нулю (рис.4). Если же bi ¹0, то распределение статистики t смещается вправо или влево в зависимости от знака bi. На основании этого для проверки значимости коэффициента bi задаются уровнем значимости a таким, что при условии bi=0{ti ³ t0}= a/2, и считают коэффициент  значимым, если ti ³ t0 или ti £ - t0, или что то же самое, если êti ê³ t0 (см. рис.4).

В случае, если имеет место противоположное неравенство êti ê< t0, коэффициент bi считается незначимым и может быть отброшен. Для практических расчетов в Прил.2 приведены значения порога t0 для различных значений уровня значимости a.

F - распределение Фишера - Снедекора:

Значения квантилей F_0.95 (j₁,j₂); j₁ и j₂ - числа степеней свободы числителя и знаменателя.

j2			j1
	1	2	3	4	5	6	12	24	¥
1	164,6	199,5	215,7	224,6	230,2	234	243,9	249,1	254,3
2	18,5	19,2	19,2	19,3	19,3	19,3	19,4	19,4	19,5
3	10,1	9,6	9,3	9,1	9	8,9	8,7	8,6	8,5
4	7,7	6,9	6,6	6,4	6,3	6,2	5,9	5,8	5,6
5	6,6	5,8	5,4	5,2	5,1	5	4,7	4,5	4,4
6	6	5,1	4,3	4,5	4,4	4,3	4	3,8	3,7
7	5,6	4,7	4,4	4,1	4	3,9	3,6	3,4	3,2
8	5,3	4,5	4,1	4,8	3,7	3,6	3,3	3,1	2,9
9	5,1	4,3	3,9	3,6	3,5	3,4	3,1	2,9	2,7
10	5	4,1	3,7	3,5	3,3	3,2	2,9	2,7	2,5
11	4,8	4	3,6	3,4	3,2	3,1	2,8	2,6	2,4
12	4,8	3,9	3,5	3,3	3,1	3	2,7	2,5	2,3
13	4,7	3,8	3,4	3,2	3	2,9	2,6	2,4	2,2
14	4,6	3,7	3,3	3,1	3	2,9	2,5	2,3	2,1
15	4,5	3,7	3,3	3,1	2,9	2,8	2,5	2,3	2,1
16	4,5	3,6	3,2	3	2,9	2,7	2,4	2,2	2
17	4,5	3,6	3,2	3	2,8	2,7	2,4	2,2	2
18	4,4	3,6	3,2	2,9	2,8	2,7	2,3	2,1	1,9
19	4,4	3,5	3,1	2,9	2,7	2,6	2,3	2,1	1,9
20	4,4	3,5	3,1	2,9	2,7	2,6	2,3	2,1	1,9
22	4,3	3,4	3,1	2,8	2,7	2,6	2,2	2	1,8
24	4,3	3,4	3	2,8	2,6	2,5	2,2	2	2,7
26	4,2	3,4	3	2,7	2,6	2,5	2,2	2	1,7
28	4,2	3,3	3	2,7	2,6	2,4	2,1	1,9	1,7
30	4,2	3,3	2,9	2,7	2,5	2,4	2,1	1,9	1,6
40	4,1	3,2	2,9	2,6	2,5	2,3	2	1,8	1,5
60	4	3,2	2,8	2,5	2,4	2,3	1,9	1,7	1,4
120	3,9	3,1	2,7	2,5	2,3	2,2	1,8	1,6	1,3
¥	3,8	3	2,6	2,4	2,2	2,1	1,8	1,5	1

t - распределение Стьюдента:

Значения квантилей t_p (j) (числа в первой строке таблицы нужно умножить на 10)

j			p
	0.750	0.900	0.950	0.975	0.990	0.995	0.999	0.9995
1	0.100	0.307	0.631	1.271	6.366	6.183	63.662
2	0.816	1.886	2.920	4.303	6.965	9.925	22.326	31.593
3	0.765	1.638	2.353	3.182	4.541	5.841	10.213	12.924
4	0.741	1.533	2.132	2.776	3.747	4.604	7.173	8.610
5	0.727	1.476	2.015	2.571	3.365	4.032	5.893	6.869
6	0.718	1.440	1.943	2.447	3.143	3.707	5.208	5.965
7	0.711	1.415	1.895	2.365	2.998	3.499	4.785	5.408
8	0.706	1.397	1.860	2.306	2.896	3.335	4.501	5.041
9	0.703	1.383	1.833	2.262	2.821	3.250	4.297	4.781
10	0.700	1.372	1.812	2.228	2.764	3.169	4.144	4.587
11	0.697	1.363	1.796	2.201	2.718	3.106	4.025	4.437
12	0.695	1.356	1.782	2.179	2.681	3.055	3.930	4.318
13	0.694	1.350	1.771	2.160	2.650	3.012	3.852	4.221
14	0.692	1.345	1.761	2.145	2.624	2.977	3.787	4.140
15	0.691	1.341	1.753	2.131	2.602	2.947	3.733	4.073
16	0.690	1.337	1.746	2.120	2.583	2.921	3.686	4.015
17	0.689	1.333	1.740	2.110	2.567	2.898	3.646	3.965
18	0.688	1.330	1.754	2.101	2.552	2.878	3.610	3.922
19	0.688	1.328	1.729	2.093	2.539	2.861	3.579	3.883
20	0.687	1.325	1.725	2.086	2.528	2.845	3.552	3.850
22	0.686	1.321	1.717	2.074	2.508	2.819	3.505	3.792
24	0.685	1.318	1.711	2.064	2.492	2.797	3.467	3.745
26	0.684	1.315	1.706	2.056	2.479	2.779	3.435	3.707
28	0.683	1.313	1.701	2.048	2.467	2.763	3.408	3.674
30	0.683	1.310	1.697	2.042	2.457	2.750	3.385	3.646
40	0.681	1.303	1.684	2.021	2.423	2.704	3.307	3.551
60	0.679	1.296	1.671	2.000	2.390	2.660	2.232	3.460
120	0.677	1.289	1.658	1.980	2.358	2.617	3.160	3.373
¥	0.674	1.282	1.645	1.960	2.326	2.576	3.090	3.291

Список, используемой литературы

1. Булгаков А, А. Статистические методы обработки информации в АСУ: Учебное пособие /ЛЭТИ.Л., 1981, _ 75 с.

. Булгаков А, А, Идентификация объектов управления в АСУ; Учебное пособие /ЛИАН.Л., 1982. - 97 с.

. Планирование эксперимента в исследовании технологических процессов /Поп ред.Э.К. Лецкого. М.; Мир, 1977. _ 552 с.