Сложение одночастотных колебаний, происходящих вдоль одной прямой. Векторные диаграммы. Сложение разночастотных колебаний
КУРСОВАЯ
РАБОТА
ТЕМА:
«Сложение
одночастотных колебаний происходящих вдоль одной прямой. Векторные диаграммы.
Сложение разночастотных колебаний»
Содержание
Введение
1. Сложение колебаний
.1 Сложение одночастотных
колебаний, происходящих вдоль одной прямой
1.2 Векторная диаграмма
одночастотных колебаний, происходящих вдоль одной прямой
1.3 Сложение разночастотных
колебаний
. Примеры сложения колебаний
.1 Нахождение графически амплитуды
колебаний, которые возникают при сложении двух колебаний одного направления
.2 Сложение двух гармонических
колебаний одного направления
3. Биоритмы. Составление
индивидуального графика биоритмов
Выводы
Приложения
Введение
Колебания - ограниченные
повторяющиеся движения (изменения любой физической величины) около некоторого
среднего значения, которые в частном случае в механике может быть положением
устойчивого равновесия.
Неpедки случаи, когда система одновpеменно
участвует в двух или нескольких независимых дpуг от дpуга колебаниях. В этих
случаях обpазуется сложное колебательное движение, котоpое создается путем
наложения (сложения) колебаний дpуг на дpуга. Случаи сложения колебаний могут
быть весьма pазнообpазны. Проблема сложения колебаний весьма важна. Пусть тело
(материальная точка) имеет возможность совершать колебания вдоль одного
направления (колебания с одной степенью свободы). На это тело могут действовать
периодические (гармонические) силы с одинаковыми или различными частотами,
фазами, амплитудами. Возникает вопрос, каким образом будет двигаться тело, если
под действием каждой из сил оно движется независимо. Такая же задача возникает
и в случае движения тела в плоскости, в пространстве.
Результат сложения зависит не только от числа
складываемых колебаний, но и от паpаметpов колебаний, от их частот, фаз,
амплитуд, напpавлений. Целью работы является: изучить вопросы сложения
одночастотных колебаний происходящих вдоль одной прямой и сложения
разночастотных колебаний, а так же построить векторные диаграммы и произвести
сложение колебаний в аналитическом виде по заданным параметрам. На примере из
теории биологических циклов (периоды циклов: физического - 23 суток,
эмоционального - 28 суток, интеллектуального - 33 суток) составить
индивидуальный график биоритмов.
1
1. Сложение
колебаний
.1 Сложение одночастотных колебаний,
происходящих вдоль одной прямой
На практике чаще приходится иметь дело со
сложными и в общем случае негармоническими колебаниями, ограничимся
рассмотрением только гармонических колебаний. Это ограничение не является на
самом деле очень принципиальным, поскольку, как это выясняется в дальнейшем,
негармонические колебания могут быть представлены в виде суперпозиции, т.е.
наложения гармонических колебаний с кратными значениями периодов колебаний.
Пусть два осциллятора совершают колебания вдоль
одного направления х:
х1(t)
= А1 cos(ω1t + α1)
х2 (t)
= А2cos(ω1t
+ α2),
(1)
где x1(t)
- перемещение, измеряемое в метрах (м), А1 - амплитуда колебаний (м), ω1
- циклическая (круговая) частота (рад/c),
(ω1t
+ α1) - фаза колебаний
(рад), α1 - начальная
фаза (рад).
Такое периодическое движение называется
гармоническим колебательным движением, а частица (материальная точка),
совершающая гармонические колебания, - гармоническим осциллятором. Термины
«маятник», «осциллятор», «колебательная система» будем считать тождественными.
Величины А и ω0
имеют простой физический смысл. Так как период косинуса и синуса равен 2π,
то
период движения Т (период колебаний) связан с ω0
соотношением
= 2π/ω0,
ω0
= 2π/T
= 2π ν
Максимальное значение координаты х называется амплитудой
колебания. Так как максимальное значение косинуса и синуса любого переменного
аргумента равно единице, то максимальное значение координаты х при
гармонических колебаниях равно А (рис.1). Аргумент косинуса и синуса φ(t)
= ω0t
+ α называют фазой колебаний
(рад).
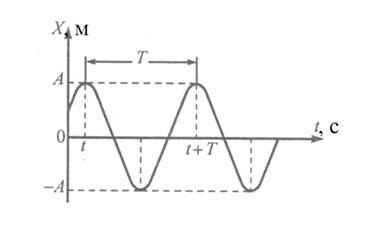
Рисунок 1 Простое гармоническое колебание х1(t)
= А1 cos(ω1t + α1)
А - амплитуда, Т - период.
При наложении колебаний друг на друга
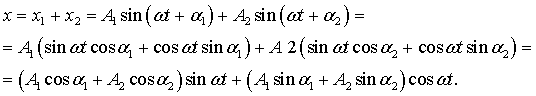
колебание одночастотный
векторный сложение
Введем новые параметры А и α.
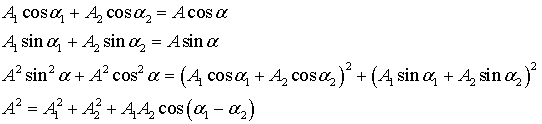
Амплитуда результирующих колебаний
равна
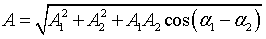 . (2)
. (2)
Сложение колебаний разной частоты
формально сводится к сложению одночастотных колебаний.
х1 = А1 cos ( ω1 t + α1); х2 = А2 cos ( ω2 t + α2).
х = А(t) cos ((А1 cos α1 + A2 cosy) + α(t))
с помощью преобразования w2 - w1 = W > 0, a2 + W t = y(t),
приводящего колебание х2 к виду х2 =
А2
cos ( ω1
t + y(t) ).
Тогда амплитуда А(t) находится из
выражения
А2(t) = А12 + А22 + 2А1 А2 cos(α1 - y(t))э
Если разность фаз α остается
постоянной во времени, то колебания называются когерентными.
При выводе этого соотношения
использовано известное математическое тождество:
(А1
cos α1
+ A2 cosy)cos
ω1
t - (А1
cos α1
+ A2 cosy)
sin ω1
t = А
cos (ω1
t + а),
где вспомогательный угол а (в нашем случае
зависящий от времени) однозначно находится из соотношений:
а = (А1 cos
α1
+ A2 cosy)
/А,
sin а
= (А1
sin α1
+ A2 siny)
/А.
(3)
Если мы образуем из этих выражений tg
а, то дополнительный угол не будет выражаться однозначно.
Итак, в pезультате сложения однонапpавленных
колебаний одинаковой частоты получаем гаpмоническое (синусоидальное) колебание,
амплитуда и фаза котоpого опpеделяется фоpмулами (3).
Рассмотpим частные случаи, пpи котоpых
соотношения между фазами двух складываемых колебаний pазличны:
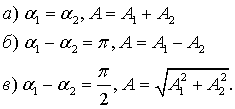
1.2 Векторная диаграмма
одночастотных колебаний, происходящих вдоль одной прямой

Решение ряда вопросов, в частности, сложение
колебаний одного и того же направления, значительно облегчается и становится
наглядным, если изображать колебания графически в виде векторов на плоскости.
Такая схема называется векторной диаграммой. На оси Х выбирается точка О и от
нее откладывается вектор длины А, образующий с осью угол α.
Если привести этот вектор во вращение с угловой скоростью ω0,
то проекция конца вектора будет перемещаться по оси Х в пределах от - α
до + α,
при этом координата этой проекции будет изменяться по закону х = А cos(ωt
+ α),
т.е. совершать гармоническое колебание (рисунок 2).
где x1(t)
- перемещение, измеряемое в метрах (м), А1 - амплитуда колебаний x
- проекция амплитуды вектора колебания на ось Х, А - амплитуда (м), ω0
- циклическая (круговая) частота (рад/c),
α -фаза колебаний
(рад).
Таким образом, гармоническое колебание может
быть задано с помощью вектора, длина которого равна амплитуде колебания, а
направление вектора образует с осью Х угол, равный начальной фазе колебания.
Построим векторную диаграмму для сложения двух
одночастотных колебаний, происходящих вдоль одной прямой.
Представим оба колебания с помощью векторов А1 и
А2, которые откладываются от произвольной оси и построим результирующий вектор
А (рисунок 3).

Из построения видно, что
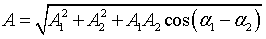 ,
,
Проанализируем для амплитуды частные
случаи для различной разности фаз исходных колебаний.

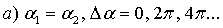 .
.
Из рисунка видно, что результирующий
вектор А = А1 + А2.
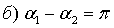 (рисунок 5). Если разность фаз
колебаний равна или кратна нечетному числу π, т.е. колебания находятся в
противофазе, то амплитуда результирующего колебания будет равна разности
амплитуд А = |А1 - А2|. Колебания будут ослаблять друг друга.
(рисунок 5). Если разность фаз
колебаний равна или кратна нечетному числу π, т.е. колебания находятся в
противофазе, то амплитуда результирующего колебания будет равна разности
амплитуд А = |А1 - А2|. Колебания будут ослаблять друг друга.

Из рисунка видно, что результирующий вектор А =
|А1 - А2|.

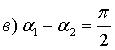 (рисунок 6).
(рисунок 6).
Из рисунка видно, что результирующий
вектор 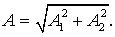
Если частоты колебаний х1 и х2
неодинаковы, то скорость вращения векторов А1 и А2 будет различной и
результирующий вектор А уже не будет определять гармоническое колебание, его
величина и скорость будут изменяться со временем. В этом случае результирующим
движением будет более сложный процесс, чем гармоническое колебание.
1.3 Сложение разночастотных колебаний
Сложение колебаний разной частоты
х1 = А1 cos ( ω1
t + α1) и х2 = А2 cos ( ω2
t + α2) формально сводится к сложению одночастотных
колебаний
х = А(t) cos ((А1 cos
α1
+ A2 cosy)
+ α(t)) с помощью преобразования
w2 - w1 = W
>
0, a2
+ W
t = a2
+ (w2
- w1)t
= y(t),
приводящего колебание х2 к виду
х2 = А2 cos ( ω1
t + y(t)
).
Тогда амплитуда А(t) находится из выражения
А2(t) = А12 + А22 + 2А1 А2 cos(α1
- y(t)),
(4)
Если разность фаз α остается
постоянной в течение времени регистрации, то колебания называются когерентными.
Полученные соотношения имеют простой
геометрический смысл, что позволяет геометрически складывать одночастотные
колебания на векторных диаграммах.
Колебание с пульсирующей амплитудой называется
биение.
Рассмотрим два гармонических колебания одного
направления, амплитуды которых отличаются незначительно. Обозначим частоту
одного из колебаний ω, частоту второго
колебания ω + Δω.
По условию Δω
≤
ω.
Амплитуды обоих колебаний будем полагать одинаковыми и равными А. Поскольку
частоты колебаний несколько отличны, всегда можно выбрать начало отсчета
времени так, чтобы начальные фазы обоих колебаний были равны нулю. Практически
это означает, что мы должны дождаться, пока смещения в обоих колебаниях
достигнут одновременно наибольшего положительного значения, и в этот момент
«запустить секундомер». Тогда уравнения обоих колебаний будут иметь следующий
вид:
1 = А cos
ωt, x2
= А cos (ω
+ Δ ω)
t.
Складывая эти два выражения и применяя
тригонометрическую формулу для суммы косинусов, получаем:
х = x1+
x2 = (2А cos
((Dw/2)t))
cos(w
+ Δω
/2 ) t
(если Δω
< ω,
то во множителе cos(w
+ Δω
/2 )t - Δω
/2 ≈ 0 по сравнению с ω)
и х =(2Аcos((Dw/2)t))
coswt
(5)
В формуле (5) множитель (2Аcos((Dw/2)t))
изменяется гораздо медленнее, чем множитель coswt.
Ввиду условия Dω < ω
за то время, за которое множитель соs
wt совершает
несколько полных колебаний, множитель, стоящий в скобках, почти не изменится.
Это дает нам основание рассматривать колебание (5) как гармоническое колебание
частоты w, амплитуда которого изменяется по
некоторому периодическому закону.
Такой подход является весьма продуктивным при
изучении сложных колебаний, которые можно описать функцией
(t) = А(t)
cos ( ω1
t + α1),
где А(t)
- амплитудная функция изменяющаяся со временем гораздо медленнее, чем фаза.
Если складываются однонаправленные колебания
разных частот и разных амплитуд, то можно поступить так, как указано в (4).
Имеем
(t) = x1(t) + x2(t) = А1cos(ω1t
+ α1)
+ А2
cos(ω2t
+ α2)
=
= А1cos(ω1t
+ α1)
+А1cos(ω2t
+ α2)+
(A2 - А1 )cos
( ω2
t + α2)
=
= 2 A1cos(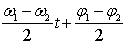 )cos(
)cos(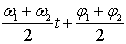 ) + (A2 - А1
)cos ( ω2
t + α2).
) + (A2 - А1
)cos ( ω2
t + α2).
График этой функции представлен на рисунке 8 и
является графиком биений. Его иногда называют графиком чистых биений.
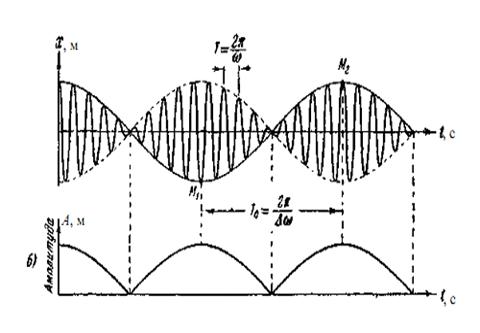
Рисунок 7 - График биений - результат сложения
колебаний с различными частотами, амплитудами и начальными фазами.
Можно дать геометрическую трактовку сложению
разночастотных колебаний. Как следует из рисунка 8, вектор первого колебания
строится по обычным правилам, а вектор второго колебания равномерно вращается
вокруг конца первого с разностной частотой.
Для построения векторной диаграммы
разночастотных колебаний (рисунок 8) следует построить вектор первого колебания
по обычным правилам, а вектор второго колебания равномерно вращается вокруг
конца первого с частотой, равной ω2
- ω1.
Если ω2
- ω1<0,
то вектор вращается по часовой стрелке, если ω2
- ω1>0,
то вектор вращается против часовой стрелки.
Пусть частоты двух скалярных колебаний не равны
друг другу и ω1 > ω2.
Сначала рассмотрим случай, когда разность частот
складываемых колебаний
мала, т.е. ω1
- ω2
= ω
<< ω1, ω2.
x1 = A1·cos
(ω1
t + α1);
x2 = A2·cos (ω2·t
+ α2).
Найдем результирующее колебание x = x1 + x2.
Заменив величину ω1 на
ω2 + ω,
запишем уравнение 1-го колебания в виде:
x1 = A1·cos (ω2·t
+ (ω·t+
α1)) = A1·cos (ω2·t
+ y(t)).
Величину y(t) будем рассматривать как медленно
изменяющуюся во времени фазу y(t) = ω·t+
α1. Таким образом,
вектор r1 участвует в двух вращениях с частотами ω2
и ω.
Изобразим r1 и r2 на векторной диаграмме, исходящими из одной точки O. Не будем
рассматривать их синхронного вращения с частотой ω2,
т.к. оно не изменяет со временем их взаимного расположения этих векторов
(рисунок 9). Поэтому вектор r2 будем считать неподвижным, а r1 - вращающимся со
скоростью ω относительно точки
O. При вращении r2 вектор r1 составляет с ним некоторый угол, изменяющийся со
временем. В результате сложения r1 и r2 получим вектор, длина которого
периодически меняется со временем от значения, равного сумме A1 + A2, до
значения, равного разности A1 - A2. Из теоремы косинусов следует, что:
= A12 + A22 + 2A1·A2·cos(ω·t
+ Δα),
(9.6)
где Δα
= α1
- α2.
Итак, амплитуда результирующего колебания А
изменяется по гармоническому закону с частотой ω.
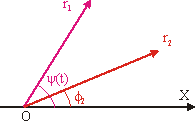
Рисунок 9 - К построению векторной диаграммы
сложения разночастотных колебаний
\
Рисунок 8 - Векторная диаграмма сложения
разночастотных колебаний
. Примеры сложения колебаний
.1 Нахождение графически амплитуды колебаний,
которые возникают при сложении двух колебаний одного направления
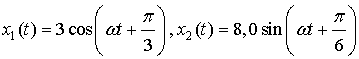 .
.
Приводим колебания к одному виду
описания, через синусы или через косинусы. Перейдем к косинусам в x2(t).
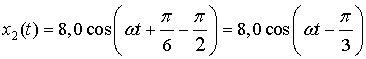
Воспользуемся теоремой косинусов:
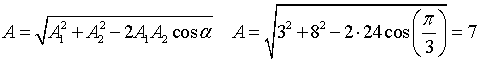

.3 Сложение двух гармонических колебаний
одного направления
При сложении двух гармонических
колебаний одного направления результирующее колебание точки имеет вид: 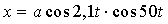 .
.
Найти круговые частоты складываемых
колебаний и период биений.
Воспользуемся х =(2Аcos((Dw/2)t)) coswt 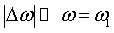
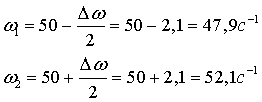
Период биений
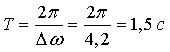 .
.
Построим график результирующего
колебания, задав амплитуду а = 10 см (Приложение 1, таблица значений 1).
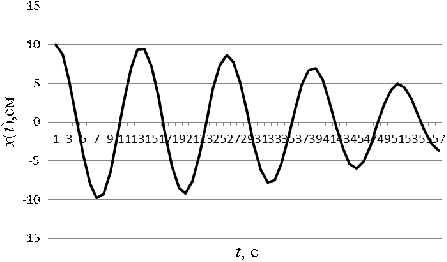
Рисунок 11 - График колебания 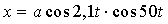
. Биоритмы. Составление индивидуального графика
биоритмов
С самого рождения человек подвержен влиянию
биологических ритмов. Биоритмы - это периодическое изменение общего состояния
человека от некоторого минимального до максимального значения. Для человека
наиболее значимы три таких цикла: физический биоритм, протяженностью в 23 дня;
эмоциональный биоритм, меняющийся с периодичностью в 28 дней; интеллектуальный
биоритм с периодом в 33 дня. Эти биоритмы контролируют три разных области
поведения, однако сами по себе не являются ни причиной, ни следствием каких-то
событий. Каждый из трех биоритмов начинается в день рождения и продолжается всю
жизнь. Исследования ученых подтверждают связь между фазой биоритма и поведением
человека. Знания о текущем состоянии биологического ритма дает человеку
возможность корректировать свое поведение. Биоритмы разных людей можно
сопоставить и определить совместимость биоритмов. Это означает, что можно
планировать наиболее продуктивную совместную деятельность, будь то работа или
отдых. Физический биоритм характеризует жизненные силы человека, т.е. его
физическое состояние. Эмоциональный биоритм характеризует внутренний настрой человека,
его возбудимость, способность эмоционального восприятия окружающего. Третий
биоритм характеризует мыслительные способности, интеллектуальное состояние
человека. Графическим изображением этих ритмов является синусоида. Многие
полагают, что “взлетам” графика, представляющего собой синусоидальную
зависимость, соответствуют более благоприятные дни. Однодневные периоды, в
которые происходит переключение фаз ("нулевые" точки на графике) и
которые, якобы, отличаются снижением соответствующего уровня активности,
получили название “критические дни”, т.е. неблагоприятные. Если одну и ту же
"нулевую" точку пересекают одновременно две или три синусоиды, то
такие "двойные " или "тройные " критические дни особенно
опасны. Более того, в некоторых странах в такие дни людям рискованных профессий
(летчикам, каскадерам и т.п.) предоставляют выходной.
Проверить данную гипотезу на практике позволяет
компьютерный эксперимент на основе разработки модели биоритмов с помощью
электронной таблицы MS Excel.(приложение 1 таблица 2). Вычисляется состояние
биоритма в процентах на заданный день по формуле: B=(sin(2π∙D/P))∙100
%, где D - число прожитых дней, а P соответсвует длине ритма в днях:
График на рисунке 12 построен с учетом даты
рождения и демонстрирует три биоритма человека. На рисунке 13 показана сумма
биоритмов в заданном промежудке времени. По нему можно судить об общем
состоянии человека.
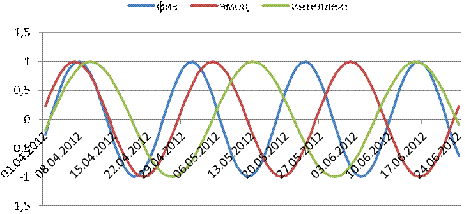
Рисунок 12 - Биоритмы
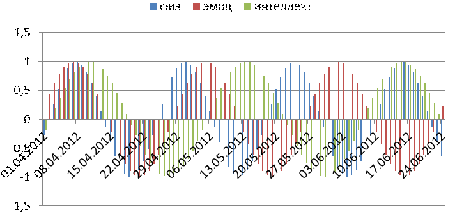
Рисунок 13 - Спект биоритмов
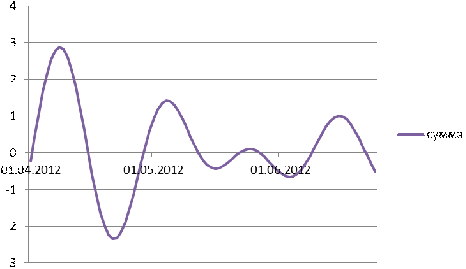
Рисунок 14 - Суммарные биоритмы
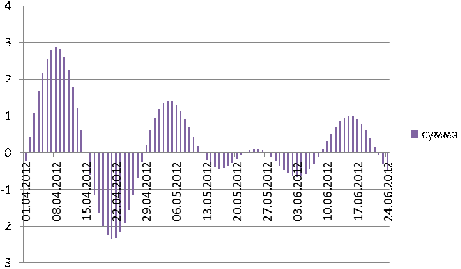
Рисунок 15 - Спектр суммарных биоритмотв
Выводы
Рассмотренные в работе способы сложения
колебаний - это универсальный аппарат для нахождения результирующего
гармонического колебания любой природы. Представление гармонических колебаний
посредством векторов дает возможность свести сложение нескольких колебаний к
операции сложения векторов. Все подобные задачи имеют
важные приложения, например, в теории переходных процессов при установлении
вынужденных колебаний, в теории волн, в частности при рассмотрении явлений
интерференции и дифракции, в теории поляризации поперечных волн. Несколько
волн, приходящих одновременно в заданную точку наблюдения, вызовут в ней колебания,
которые будут складываться определенным образом, а мы всегда будем наблюдать
лишь результат этого сложения. Метод векторных диаграмм используется так же при
расчете цепей переменного напряжения.
В работе описаны способы сложения колебаний
одинакового направления - аналитический и метод векторных диаграмм, решены
задачи с заданными параметрами, с использованием этих методов, выполнено
построение биоритмов человека с использованием электронной таблицы MS Excel.
Список используемых источников
. «Физика колебательных процессов» А.И.
Кириленко Издательство МГВАК Минск 2008
2. И.В. Савельев. Курс общей физики.
Издание пятое, т. 1, глава 9, т.2 глава 13.
. Б.М. Яворский, А.А.Детлаф. Справочник
по физике. М., Наука, издание 3, 1990 г. 924с.
4. . Сивухин Д.В. Курс общей физики т.2
Электричество: учебное пособие/ Д.В Сивухин. - Москва: Наука, 1974. - 519 с.
. Зисман Г.А. Курс общей физики т.2:
учебное пособие/ Г.А. Зисман, О.М. Тодес. - Москва: Наука, 1965. - 366 с.
Приложения
Таблица 1. Значения к задаче 3.2
график колебаний 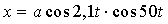
|
t,c
|
x(t),см
|
|
0
|
10
|
|
0,01
|
8,773891
|
|
0,02
|
5,398258
|
|
0,03
|
0,705969
|
|
0,04
|
-4,1468
|
|
0,05
|
-7,96731
|
|
0,06
|
-9,82144
|
|
0,07
|
-9,26357
|
|
0,08
|
-6,44441
|
|
0,09
|
-2,07042
|
|
0,1
|
2,774304
|
|
0,11
|
6,89846
|
|
0,12
|
9,29844
|
|
0,13
|
9,40421
|
|
0,14
|
7,215541
|
|
0,15
|
3,295796
|
|
0,16
|
-1,37364
|
|
0,17
|
-5,64055
|
|
0,18
|
-8,46809
|
|
0,19
|
-9,18844
|
|
0,2
|
-7,66147
|
|
0,21
|
-4,3004
|
|
0,22
|
0,039617
|
|
0,23
|
4,280174
|
|
0,24
|
7,389273
|
|
0,25
|
8,634187
|
|
0,26
|
7,755117
|
|
0,27
|
5,018251
|
|
0,28
|
1,137724
|
|
0,29
|
-2,91116
|
|
0,3
|
-6,13849
|
|
0,31
|
-7,78338
|
|
0,32
|
-7,49443
|
|
0,33
|
-5,40377
|
|
0,34
|
-2,07954
|
|
0,35
|
1,627873
|
|
0,36
|
4,804371
|
|
0,37
|
6,699002
|
|
0,38
|
6,902543
|
|
0,39
|
5,435034
|
|
0,4
|
2,723796
|
|
0,41
|
-0,5185
|
|
0,42
|
-3,48141
|
|
0,43
|
-5,46056
|
|
0,44
|
-6,02609
|
|
0,45
|
-5,11532
|
|
0,46
|
-3,02966
|
|
0,47
|
-0,34122
|
|
0,48
|
2,263221
|
|
0,49
|
4,158459
|
|
0,5
|
4,931938
|
|
0,51
|
4,472883
|
|
0,52
|
2,98043
|
|
0,53
|
0,893381
|
|
0,54
|
-1,23586
|
|
0,55
|
-2,88756
|
|
0,56
|
-3,70238
|
Таблица 2 Модель биоритмов
|
модель
биоритмов Семенюк Дмитрий
|
|
|
|
|
|
|
|
Составлено
на период до 25.06.2012
|
|
|
23
|
|
22.06.1991
|
|
|
28
|
|
01.04.2012
|
|
|
33
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
день
|
физ
|
эмоц
|
интеллект
|
сумма
|
|
01.04.2012
|
-0,2698
|
0,222521
|
-0,189251
|
-0,23653
|
|
02.04.2012
|
1,61E-13
|
0,433884
|
4,312E-14
|
0,433884
|
|
03.04.2012
|
0,269797
|
0,62349
|
0,1892512
|
1,082538
|
|
04.04.2012
|
0,519584
|
0,781831
|
0,3716625
|
1,673078
|
|
05.04.2012
|
0,730836
|
0,900969
|
0,5406408
|
2,172446
|
|
06.04.2012
|
0,887885
|
0,974928
|
0,690079
|
2,552892
|
|
07.04.2012
|
0,979084
|
1
|
0,814576
|
2,79366
|
|
08.04.2012
|
0,997669
|
0,974928
|
0,909632
|
2,882229
|
|
09.04.2012
|
0,942261
|
0,900969
|
0,9718116
|
2,815041
|
|
10.04.2012
|
0,81697
|
0,781831
|
0,9988673
|
2,597669
|
|
11.04.2012
|
0,631088
|
0,62349
|
0,9898214
|
2,244399
|
|
12.04.2012
|
0,433884
|
0,9450008
|
1,777286
|
|
13.04.2012
|
0,136167
|
0,222521
|
0,8660254
|
1,224713
|
|
14.04.2012
|
-0,13617
|
5,59E-14
|
0,7557496
|
0,619583
|
|
15.04.2012
|
-0,3984
|
-0,22252
|
0,618159
|
-0,00276
|
|
16.04.2012
|
-0,63109
|
-0,43388
|
0,4582265
|
-0,60675
|
|
17.04.2012
|
-0,81697
|
-0,62349
|
0,2817326
|
-1,15873
|
|
18.04.2012
|
-0,94226
|
-0,78183
|
0,095056
|
-1,62904
|
|
19.04.2012
|
-0,99767
|
-0,90097
|
-0,095056
|
-1,99369
|
|
20.04.2012
|
-0,97908
|
-0,97493
|
-0,281733
|
-2,23574
|
|
21.04.2012
|
-0,88789
|
-1
|
-0,458227
|
-2,34611
|
|
22.04.2012
|
-0,73084
|
-0,97493
|
-0,618159
|
-2,32392
|
|
23.04.2012
|
-0,51958
|
-0,90097
|
-0,75575
|
-2,1763
|
|
24.04.2012
|
-0,2698
|
-0,78183
|
-0,866025
|
-1,91765
|
|
25.04.2012
|
-8,8E-14
|
-0,62349
|
-0,945001
|
-1,56849
|
|
26.04.2012
|
0,269797
|
-0,43388
|
-0,989821
|
-1,15391
|
|
27.04.2012
|
0,519584
|
-0,22252
|
-0,998867
|
-0,7018
|
|
28.04.2012
|
0,730836
|
-1,8E-13
|
-0,971812
|
-0,24098
|
|
29.04.2012
|
0,887885
|
0,222521
|
-0,909632
|
0,200774
|
|
30.04.2012
|
0,979084
|
0,433884
|
-0,814576
|
0,598392
|
|
01.05.2012
|
0,997669
|
0,62349
|
-0,690079
|
0,93108
|
|
02.05.2012
|
0,942261
|
0,781831
|
-0,540641
|
1,183452
|
|
03.05.2012
|
0,81697
|
0,900969
|
-0,371662
|
1,346276
|
|
04.05.2012
|
0,631088
|
0,974928
|
-0,189251
|
1,416765
|
|
05.05.2012
|
0,398401
|
1
|
-2,06E-13
|
1,398401
|
|
06.05.2012
|
0,136167
|
0,974928
|
0,1892512
|
1,300346
|
|
07.05.2012
|
-0,13617
|
0,900969
|
0,3716625
|
1,136465
|
|
08.05.2012
|
-0,3984
|
0,781831
|
0,5406408
|
0,924071
|
|
09.05.2012
|
-0,63109
|
0,62349
|
0,690079
|
0,682481
|
|
10.05.2012
|
-0,81697
|
0,433884
|
0,814576
|
0,43149
|
|
11.05.2012
|
-0,94226
|
0,222521
|
0,909632
|
0,189892
|
|
12.05.2012
|
-0,99767
|
7,74E-14
|
0,9718116
|
-0,02586
|
|
13.05.2012
|
-0,97908
|
-0,22252
|
0,9988673
|
-0,20274
|
|
14.05.2012
|
-0,88789
|
-0,43388
|
0,9898214
|
-0,33195
|
|
15.05.2012
|
-0,73084
|
-0,62349
|
0,9450008
|
-0,40932
|
|
16.05.2012
|
-0,51958
|
-0,78183
|
0,8660254
|
-0,43539
|
|
17.05.2012
|
-0,2698
|
-0,90097
|
0,7557496
|
-0,41502
|
|
18.05.2012
|
-3,4E-13
|
-0,97493
|
0,618159
|
-0,35677
|
|
19.05.2012
|
0,269797
|
-1
|
0,4582265
|
-0,27198
|
|
20.05.2012
|
0,519584
|
-0,97493
|
0,2817326
|
-0,17361
|
|
21.05.2012
|
0,730836
|
-0,90097
|
0,095056
|
-0,07508
|
|
22.05.2012
|
0,887885
|
-0,78183
|
-0,095056
|
0,010998
|
|
23.05.2012
|
0,979084
|
-0,62349
|
-0,281733
|
0,073862
|
|
24.05.2012
|
0,997669
|
-0,43388
|
-0,458227
|
0,105559
|
|
25.05.2012
|
0,942261
|
-0,22252
|
-0,618159
|
0,101581
|
|
26.05.2012
|
0,81697
|
2,55E-14
|
-0,75575
|
0,06122
|
|
27.05.2012
|
0,631088
|
0,222521
|
-0,866025
|
-0,01242
|
|
28.05.2012
|
0,398401
|
0,433884
|
-0,945001
|
-0,11272
|
|
29.05.2012
|
0,136167
|
0,62349
|
-0,989821
|
-0,23016
|
|
30.05.2012
|
-0,13617
|
0,781831
|
-0,998867
|
-0,3532
|
|
31.05.2012
|
-0,3984
|
0,900969
|
-0,971812
|
-0,46924
|
|
01.06.2012
|
-0,63109
|
0,974928
|
-0,909632
|
-0,56579
|
|
02.06.2012
|
-0,81697
|
1
|
-0,814576
|
-0,63155
|
|
03.06.2012
|
-0,94226
|
0,974928
|
-0,690079
|
-0,65741
|
|
04.06.2012
|
-0,99767
|
0,900969
|
-0,540641
|
-0,63734
|
|
05.06.2012
|
-0,97908
|
0,781831
|
-0,371662
|
-0,56892
|
|
06.06.2012
|
-0,88789
|
0,62349
|
-0,189251
|
-0,45365
|
|
07.06.2012
|
-0,73084
|
0,433884
|
-3,47E-18
|
-0,29695
|
|
08.06.2012
|
-0,51958
|
0,222521
|
0,1892512
|
-0,10781
|
|
09.06.2012
|
-0,2698
|
9,9E-14
|
0,3716625
|
0,101866
|
|
10.06.2012
|
-1,3E-13
|
-0,22252
|
0,5406408
|
0,31812
|
|
11.06.2012
|
0,269797
|
-0,43388
|
0,690079
|
0,525992
|
|
12.06.2012
|
0,519584
|
-0,62349
|
0,814576
|
0,71067
|
|
13.06.2012
|
0,730836
|
-0,78183
|
0,909632
|
0,858636
|
|
14.06.2012
|
0,887885
|
-0,90097
|
0,9718116
|
0,958728
|
|
15.06.2012
|
0,979084
|
-0,97493
|
0,9988673
|
1,003024
|
|
16.06.2012
|
0,997669
|
-1
|
0,9898214
|
0,98749
|
|
17.06.2012
|
0,942261
|
-0,97493
|
0,9450008
|
0,912334
|
|
18.06.2012
|
0,81697
|
-0,90097
|
0,8660254
|
0,782026
|
|
19.06.2012
|
0,631088
|
-0,78183
|
0,7557496
|
0,605006
|
|
20.06.2012
|
0,398401
|
-0,62349
|
0,618159
|
0,39307
|
|
21.06.2012
|
0,136167
|
0,4582265
|
0,160509
|
|
22.06.2012
|
-0,13617
|
-0,22252
|
0,2817326
|
-0,07696
|
|
23.06.2012
|
-0,3984
|
-2,2E-13
|
0,095056
|
-0,30335
|
|
24.06.2012
|
-0,63109
|
0,222521
|
-0,095056
|
-0,50362
|