Использование законов и свойств арифметических действий при формировании вычислительных навыков

Использование законов и свойств арифметических действий при формировании вычислительных навыков

Министерство образования и науки РФ

Комитет по образованию Администрации Волгоградской области

ГОУ СПО «Михайловкой профессионально-педагогический колледж»

Специальность «Преподавание в начальных классах»

ИСПОЛЬЗОВАНИЕ ЗАКОНОВ И СВОЙСТВ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ ПРИ ФОРМИРОВАНИИ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ

Выпускная квалификационная работа

Выполнила:

Студентка группы 42 н

Горбунова Е.С.

Руководитель:

Макарова Л.М.

г.Михайловка, 2011

Оглавление

Введение

Глава 1. Теоретический аспект изучения законов и свойств арифметических действий в начальной школе

.1 Проблема формирования вычислительных навыков младших школьников в современных условиях

.2 Теоретические основы законов и свойств арифметических действий

.3 Методика изучения законов и свойств арифметических действий в традиционной и вариативных программах обучения начальной школы

Выводы по 1 главе

Глава 2. Опытно-экспериментальная работа по формированию вычислительных навыков при изучении законов и свойств арифметических действий в начальной школе

.1 Диагностика уровня сформированности вычислительных навыков младших школьников при изучении законов и свойств арифметических действий

.2 Методические приемы, направленные на изучение законов и свойств арифметических действий

Выводы по 2 главе

Заключение

Список литературы

Приложение

Введение

вычислительный навык арифметический школьник

Одной из целей федерального компонента государственного стандарта начального образования является «освоение системы знаний, умений и навыков, опыта осуществления разнообразных видов деятельности».

Содержание, система и основные методические направления работы, связанной с изучением арифметических действий в начальных классах, определены программой. Из требований программы вытекают следующие задачи:

·             Довести до сознания детей смысл рассматриваемых действий, научить их правильно выбирать нужное арифметическое действие при решении различных простых задач.

·        На доступном для младших школьников уровне и в доступной для них форме познакомить их с теми свойствами рассматриваемых действий, которые являются теоретической основой изучаемых приёмов устных и письменных вычислений. Научить применять изученные свойства в разнообразных условиях, используя соответствующие знания в целях рационализации вычислений, а также в целях отыскания наиболее рационального способа решения задач.

·        Обеспечить сознательное и прочное усвоение детьми основных приёмов устных и письменных вычислений, умение сознательно выбирать такие из известных приёмов вычислений, которые более всего отвечают особенностям каждого конкретного примера.

·        Сформировать у детей сознательные и прочные навыки быстрых и правильных вычислений.

Для успешного решения каждой из этих конкретных задач курса необходимо не только определить содержание и систему соответствующих упражнений, но целесообразно использовать различные методы обучения.

Приём вычисления над числами складывается из ряда последовательных операций, выполнение которых приводит к нахождению результата требуемого арифметического действия над этими числами; причём выбор операций в каждом приёме определяется теми теоретическими положениями, которые используются в качестве теоретической основы.

Приобрести вычислительный навык - значит, для каждого случая знать какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро. В качестве сформированности полноценного вычислительного навыка можно выделить следующие критерии: правильность, осознанность, рациональность, обобщённость, автоматизм и прочность. Вместе с тем, учитывая, что ученик при выполнении вычислительного приёма должен отдавать отчёт в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом - системой операций, относится к основным критериям и степень овладения умением контролировать себя при выполнении вычислительного приёма.

Проблема формирования у учащихся вычислительных умений и навыков всегда привлекала особое внимание психологов, дидактов, методистов, учителей. В методике математики известны исследования Е.С. Дубинчук, А.А. Столяра, С.С. Минаевой, Н.Л. Стефановой, Я.Ф. Чекмарева, М.А. Бантовой, М.И. Моро, Н.Б. Истоминой, С.Е. Царевой и др.

Формирование у младших школьников вычислительных навыков остаётся одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы при изучении арифметических действий.

Действующие на сегодняшний день программы по математике обеспечивают достаточный уровень формирования вычислительных навыков школьников. Изучение вычислительного приема происходит после того, как школьники усвоят его теоретическую основу (определения арифметических действий, свойства действий и следствия, вытекающие из них).

В большинстве случаев уже в начальных классах школы для нахождения результата арифметического действия можно использовать в качестве теоретической основы различные теоретические положения, что приводит к разным приёмам вычислений.

Осознание смысла действий, существующих между ними связей, зависимости между компонентами и результатами действий может быть обеспечено только в том случае, если рассмотрение этих теоретических вопросов будет вестись на прочной базе собственного опыта детей. При этом следует учитывать, что речь здесь должна идти не только о жизненном опыте, приобретаемом детьми в ходе разнообразных практических действий с предметами, но и об опыте, накапливаемом при изучении математики в школе.

В связи с этим актуальной является тема выпускной квалификационной работы «Использование законов и свойств арифметических действий при формировании вычислительных навыков».

Объект исследования - учебно-воспитательный процесс в начальной школе.

Предмет исследования - изучение законов и свойств арифметических действий при формировании вычислительных навыков на уроках математики.

Цель исследования - разработать эффективные приемы формирования вычислительных навыков при изучении законов и свойств арифметических действий.

Задачи исследования:

1.       Рассмотреть проблемы формирования вычислительных навыков в современных условиях.

2.       Проанализировать методику изучения законов и свойств арифметических действий.

.        Отобрать содержание и методические приёмы, используемые при изучении законов и свойств арифметических действий.

.        Провести диагностику сформированности вычислительных навыков у младших школьников.

.        Показать практическую применимость рассматриваемых положений на школьных уроках математики в начальной школе.

Гипотеза - если при изучении законов и свойств арифметических действий использовать дидактический материал, упражнения развивающего характера, то уровень сформированности вычислительных навыков младших школьников повысится.

Методы исследования:

·          теоретический (анализ методической литературы, моделирование);

·        эмпирический (диагностирующие, формирующие эксперименты, изучение письменных работ учащихся, наблюдение; беседа).

·        математическая обработка результатов.

База исследования: МОУ Стеженская СОШ Алексеевского района Волгоградской области, 2 класс.

Структура работы состоит из введения, двух глав, заключения, списка литературы, приложения.

Общий объем работы. Работа состоит из 78 страниц.

Глава 1. Теоретический аспект изучения законов и свойств арифметических действий в начальной школе

.1 Проблема формирования вычислительных навыков младших школьников в современных условиях

Концепция модернизации российского образования на период до 2010 года определяет цели общего образования на современном этапе. Она подчеркивает необходимость «ориентации образования не только на усвоение обучающимся определенной суммы знаний, но и на развитие его личности, его познавательных и созидательных способностей». Одной из основных задач обучения математике в школе является формирование у школьников сознательных и прочных вычислительных навыков, которые являются основополагающим элементом вычислительной культуры человека.

Сегодня всё меньше и меньше внимания в новых экспериментальных и вариативных учебниках по математике уделяется формированию у учащихся вычислительных навыков, как устных, так и письменных. Постепенно снижается подготовленность детей в данном направлении: возрастает число ошибок в определении порядка действий в выражениях, снижается уровень сформированности умения решать текстовые задачи (в частности за счёт ухудшения техники чтения, вычислительных умений). В связи с этим, одной из основных задач обучения школьников математике является повышение вычислительной культуры учащихся на всех ступенях обучения в образовательном учреждении и в первую очередь в начальной школе [Бантова 1995: 39].

О.А. Ивашова под вычислительной культурой школьников понимает учебную вычислительную деятельность, ориентированную на развитие личности ученика в процессе осмысленного овладения ее содержанием (знаниями и умениями математического и общекультурного характера), организованную с учетом социальных условий и характеристик необходимой обществу культуры.

Формирование вычислительной культуры младшего школьника влияет на повышение его общей культуры. Поэтому очень важно на начальных этапах обучения развивать речь ребенка, научить методам и приемам устных и письменных вычислений, намечать план решения задач и самостоятельно выполнять этот план, контролируя и оценивая свою деятельность. Но решение данных задач возможно лишь в специальных условиях, способствующих развитию мышления учащихся в процессе обучения математике и формированию вычислительной культуры учащихся.

Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин.

Формирование у школьников 1-4 классов вычислительных навыков остается одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы как в практической жизни человека, так и в учении.

Эти навыки должны формироваться осознанно и прочно, так как на их базе строиться весь начальный курс обучения математике предусматривает, формирование вычислительных навыков на основе сознательн6ого использования приемов вычислений. Последнее становится возможным благодаря тому, что в программу включено знакомство с некоторыми важнейшими свойствами арифметический действий и вытекающими из них следствиями.

Из исследований прошлых лет наибольшим авторитетом пользуются работы М.А. Бантовой. Обратимся к ее статье «Система формирования вычислительных навыков», опубликованной дважды в журнале «Начальная школа» (№10, 1975 и №11, 1993).

М.А. Бантова определила вычислительный навык как высокую степень овладения вычислительными приемами. «Приобрести вычислительные навыки - значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро». [Бантова, с.39]

О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции, приводящие к решению.

М.А. Бантова выделяет следующие характеристики полноценного вычислительного навыка: правильность, осознанность, рациональность, обобщенность, автоматизм и прочность. [Бантова, 1995: 39]

Правильность - ученик правильно находит результат арифметического действия, то есть правильно выбирает и выполняет операции, составляющие приём.

Осознанность - ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения, в любой момент может объяснить как он решал и почему так можно решать.

Рациональность - ученик выбирает для данного случая более рациональный приём, то есть выбирает те из возможных операций, выполнения которых легче других и быстрее приводит к результату.

Обобщенность - ученик может применить приём вычисления к большому числу случаев, то есть способен перенести приём вычисления на новые случаи.

Автоматизм - ученик выполняет и выделяет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операций.

Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.

Прочность - ученик сохраняет сформированные вычислительные навыки на длительное время.

Традиционная методика не ориентирует на обобщение и выделение способа действия вне ситуации конкретного примера, то есть не даются схемы ориентировочной основы формируемого действия. Предлагаемые М.А. Бантовой и другими методистами этапы формирования вычислительного приёма по содержанию не соответствуют основным этапам теории П.Я. Гальперина.

Учитывая это, мы, сохраняя в основном название этих этапов, предлагаем изменить содержание, методы и средства так, чтобы включить в эти четыре этапа описанную П.Я. Гальпериным систему поэтапного формирования умственных действий.

Первый этап - актуализация опорных знаний. Его цель - обеспечение необходимых условий для усвоения вычислительного приёма. Такими условиями следует считать знания, необходимые для выполнения вычислительного приёма.

Первая учебная ситуация - выявление условий, необходимых для выполнения арифметических действий. Цель - диагностика освоенности тех опорных знаний, из которых будет строиться вычислительный приём. Если результаты диагностики покажут, что уровень осознанности этих знаний недостаточно высок, то в процессе обучения следует включить вторую учебную ситуацию.

Вторая учебная ситуация - подготовка к усвоению вычислительного приёма. Цель - помочь учащимся усвоить те теоретические положения, на которых основывается вычислительный приём. Для этого необходимо проанализировать приём и установить, какими знаниями должен овладеть ученик и какие вычислительные навыки должны быть сформированы на данный момент.

Второй этап - введение вычислительного приёма. Цель данного этапа состоит в том, чтобы помочь детям построить полную развёрнутую ориентировочную основу вычислительного приёма.

Третья учебная ситуация - введение ориентировочной основы. Цель - усвоение детьми сути приёма, то есть того, какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия. Ведущая роль на данном этапе принадлежит учителю. Он организует поиск способа, помогает детям анализировать, сравнивать разные возможные способы действия, направляет детей на анализ операционного состава действия, то есть выделяет отдельные шаги в процессе получения конечного результата.

Третий этап - усвоение вычислительного приёма. Цель - формирование умения применять схему ориентировочной основы действия в различных условиях, обеспечивая постепенное свёртывание операций. Учащиеся должны твёрдо усвоить систему операций, составляющих приём, и предельно быстро выполнять эти операции, то есть овладеть вычислительным приёмом.

Четвёртая учебная ситуация. Цель - научить учащихся самостоятельно выполнять все операции, составляющие приём, комментируя выполнение каждой из них вслух.

При этом учитель использует такую форму работы, как совместное выполнение действия в паре. Необходимость в такой работе обусловлена тем, что ребёнок должен осмыслить каждую операцию как отдельную от другой. Кроме того, для формирования полноценного действия необходимо осуществлять контроль за ходом его выполнения.

Внутри данной учебной ситуации для достижения поставленной цели необходимо придерживаться такой последовательности:

заполнение готовой схемы-опоры (проговаривается каждая операция);

выполнение приёма с опорой на ООД (проговаривание вслух каждой операции);

проверочная работа, цель - выявить освоение учениками ООД.

Если результат такой проверки положительный, то следует перейти к следующей учебной ситуации, т. к. не следует задерживаться на данном этапе, чтобы избежать привыкания детей к развёрнутой записи.

Пятая учебная ситуация - частичное свёртывание выполнения операций. Цель - научить детей выделять основные операции в каждом вычислительном приёме. Результатом является проговаривание детьми вслух лишь промежуточных результатов.

Шестая учебная ситуация.     Цель - научить детей полному свёртыванию схемы, выполнению операций « в уме».

Дети самостоятельно выполняют задания, обмениваются тетрадями, и проверяют работу друг у друга.

Четвёртый этап - формирование прочных навыков. Цель - создание условия для применения приёма в разнообразных ситуациях и доведение до автоматизма навыка выполнения действия.

Основным средством процесса формирования навыков становятся проверочные, самостоятельные и контрольные работы различного направления [Зайцев, 2005: 48].

Седьмая учебная ситуация. Детям предлагается выполнить серию работ, цель которых - формирование адекватной оценки своего умения применять приём и коррекция работы. Отметки здесь не ставятся, а вводятся знаки «+» и «минус».

Самостоятельная работа проводится после нескольких проверочных работ. Цель самостоятельной работы - промежуточный контроль за окончательным результатом освоения приёма. Задания подбираются разного уровня сложности. Детям предлагается выбрать тот уровень, на котором они хотят и могут работать. По результатам обсуждения итогов такой работы учитель распределяет детей на группы в соответствии с их трудностями в освоении приёма.

-я группа - дети, не освоившие схему-опору.

-я группа состоит из детей, которые не могут работать по свёрнутой схеме.

-я группа - дети, которые не могут выполнять творческие задания, перенос знаний в нестандартных условиях затруднён.

-я группа детей освоила вычислительный приём.

Восьмая учебная ситуация. Задания дифференцируются по группам:

-я группа - дети работают в парах, воспроизводится повторно учебная ситуация второго этапа (третья).

-я группа - повторяются учебные ситуации третьего этапа (четвёртая и пятая).

-я группа - происходит возвращение на третий и четвёртый этапы (шестая, а затем седьмая учебные ситуации).

-я группа - выполняются задания творческого характера, применяя приём в разных ситуациях. Детей можно использовать и как помощников учителя.

Таким образом, процесс формирования вычислительных навыков влияет на процесс развития умственной деятельности ребёнка.

Итак, при формировании вычислительных навыков в традиционной системе рассматривается позиция: делай то, что тебе предлагают, чтобы научиться делать это быстро и правильно. Этот путь предполагает сообщение учащимся образца, алгоритма выполнения операций, на основании которого учащиеся многократно её выполняют. В результате такой репродуктивной деятельности достигается запоминание предложенного алгоритма и вырабатывается запланированный навык, при этом дети часто не осознают, на основе каких знаний выбраны операции и установлен порядок их выполнения.

В развивающей системе действует следующая позиция: делай для того, чтобы продвинуться в решении стоящей перед тобой математической проблемы или чтобы обнаружить такую проблему. Таким образом, используется косвенный путь формирования навыков, который предполагает включение учеников в продуктивную творческую деятельность, в самостоятельное установление алгоритма операции. В результате такого подхода к формированию вычислительных навыков дети приобретают прочные и осознанные навыки выполнения математических действий. Когда такая цель достигнута, необходимо перейти к наращиванию скорости выполнения вычислений.

Наиболее разработанной в плане управления процессом обучения является система обучения, основанная на теории поэтапного формирования умственных действий П.Я. Гальперина. Применение этой теории при изучении арифметических действий в начальной школе способствует формированию осознанных и прочных вычислительных навыков.

.2 Теоретические основы законов и свойств арифметических действий

Подход к сложению целых неотрицательных чисел позволяет обосновать известные законы сложения: переместительный и сочетательный.

Докажем сначала переместительный закон, т. е. докажем что для любых целых неотрицательных чисел а и b выполняется равенство a + b= b + а.

Пусть а - число элементов в множестве А, Ь - число элементов в множестве В и А В=0. Тогда по определению суммы целых неотрицательных чисел а + b есть число элементов объединения множеств А и В: а + Ь = п (А//В). Но множество А В равно множеству В A согласно переместительному свойству объединения множеств, и, Значит, п(АU В) = п(В U А). По определению суммы п(ВиА) = Ь + а, поэтому a+b=b+a для любых целых неотрицательных чисел а и Ь.

Докажем теперь сочетательный закон, т. е. докажем что для любых целых неотрицательных чисел а, Ь, с выполняется равенство (a + b)+c = a + (b + c).

Пусть а = п(А), Ь = п(В), с = п(С), причем АUВ=0, ВUС=0 Тогда по определению суммы двух чисел можно записать (а+ Ь)+ с = п(А//)В) + п(С) = п((АUВUС).

Так как объединение множеств подчиняется сочетательному закону, то n((AUB)U C) = n(A U(BUC)). Откуда по определению суммы двух чисел имеем п (А \J(BUC))=n (А) + п (BU C) = a + (b + с). Следовательно, (а+ Ь)+ с - a+(b + с) для любых целых неотрицательных чисел a, b и с.

Каково назначение сочетательного закона сложения? Он объясняет, как можно находить сумму трех слагаемых: для этого достаточно сложить первое слагаемое со вторым и к полученному числу прибавить третье слагаемое или прибавить первое слагаемое к сумме второго и третьего. Заметим, что сочетательный закон не предполагает перестановки слагаемых.

И переместительный и сочетательный законы сложения могут быть обобщены на любое число слагаемых. При этом переместительный закон будет означать, что сумма не изменяется при любой перестановке слагаемых, а сочетательный - что сумма не изменяется при любой группировке слагаемых (без изменения их порядка).

Из переместительного и сочетательного законов сложения вытекает, что сумма нескольких слагаемых не изменится, если их переставить любым способом и если любую их группу заключить в скобки.

Вычислим, используя законы сложения, значение выражения 109 + 36+ 191 +64 + 27.

На основании переместительного закона переставим слагаемые 36 и 191. Тогда 109 + 36+191+64 + 27= 109+191+36 + 64 + 27.

Воспользуемся сочетательным законом, сгруппировав слагаемые, а затем найдем суммы в скобках: 109+ 191 +36 + 64 + 27 ==(109 + 191) + (36 + 64) + 27 = 300 + 100 + 27.

Применим еще раз сочетательный закон, заключив в скобки сумму чисел 300 и 100: 300+ 100 + 27 =(300+ 100) + 27.

Произведем вычисления: (300+ 100)+ 27 = 400+ 27 = 427.

С переместительным свойством сложения учащиеся начальных классов знакомятся при изучении чисел первого десятка. Сначала оно используется при составлении таблицы сложения однозначных чисел, а затем для рационализации различных вычислений.

Сочетательный закон сложения в начальном курсе математики в явном виде не изучается, но постоянно используется. Так, он является основой приема прибавления числа по частим: 3 + 2 = 3 + (1 + 1) = (3+ 1)+ 1 =4+ 1 =5. Кроме того, в тех случаях, когда надо прибавить число к сумме, сумму к числу, сумму к сумме, сочетательный закон используется в сочетании с переместительным. Например, прибавлять сумму 2+1 к числу 4 предлагается следующими способами:

)        4 + (2+1) = 4 + 3 = 7;

+2+ 1 = 6+1 =7;

+ (2+1) = 5 + 2 = 7.

Проанализируем эти способы. В случае 1 вычисления выполнены в соответствии с указанным порядком действий. В случае 2 применено сочетательное свойство сложения. Вычисления же в последнем случае опираются па переместительный и сочетательный законы сложения, причем промежуточные преобразования опущены. Они таковы. Сначала на основании переместительного закона переставили местами слагаемые 1 и 2: 4+(2-1) = 4 + (1+2). Затем воспользовались сочетательным законом: 4 + (1 +2) =(4+ 1) + 2. И, наконец, произвели вычисления согласно порядку действий (4 +1)+ 2 = 5 + 2 = 7.

Правила вычитания числа из суммы и суммы из числа

Обоснуем известные правила вычитания числа из суммы и суммы из числа.

Правило вычитания числа из суммы. Чтобы вычесть число из суммы, достаточно вычесть это число из одного из слагаемых суммы и к полученному результату прибавить другое слагаемое.

Запишем это правило, используя символы: Если а, Ь, с - целые неотрицательные числа, то:

а)       при а>с имеем, что (а+Ь) - с = (а - с)+Ь;

б)      при Ь>с имеем, что (a+b) - c==a + (b - с);

в)      при а>с и Ь>с можно использовать любую из данных
формул.

Пусть а >с, тогда разность а -с существует. Обозначим ее через р: а - с =р. Отсюда а = р+с. Подставим сумму р+-с вместо а в выражение (а+Ь) - с и преобразуем его: (а + 6) -с = (р + c+b) - c = p+b+-c - c = p+b

Но буквой р обозначена разность а -с, значит, имеем (а+Ь) - - с = (а - с)+Ь, что и требовалось доказать.

Аналогично проводятся рассуждения и для других случаев. Приведем теперь иллюстрацию данного правила (случай «а») при помощи кругов Эйлера. Возьмем три конечных множества А, В и С, такие, что п(А) = а, п(В) = Ь, п(С) = с и AUB=0, СUА. Тогда {a+b) - с есть число элементов множества (AUB)\C, а число (а - с)+Ь есть число элементов множества {А\С)UВ. На кругах Эйлера множество (АUВ)\С изображается заштрихованной областью, представленной на рисунке .

Легко убедиться в том, что множество (А\С)UВ изобразится точно такой же областью. Значит, (AUB)\C = (A\C)UB для данных

множеств А, В и С. Следовательно, п((АUВ)\С) = п((А\С)UВ)и (а + Ь)- с - (а - с)+Ь.

Аналогично можно проиллюстрировать и случай «б».

Правило вычитания из числа суммы. Чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т. е. если а, Ъ, с - целые неотрицательные числа, то при а>Ь+с имеем а-(Ь+с) = (а - Ь)-с.

Обоснование этого правила и его теоретико-множественная иллюстрация выполняются так же, как и для правила вычитания числа из суммы.

Приведенные правила рассматриваются в начальной школе на конкретных примерах, для обоснования привлекаются наглядные изображения. Эти правила позволяют рационально выполнять вычисления. Например, правило вычитания из числа суммы лежит в основе приема вычитания числа по частям:

-2 = 5-(1 + 1) = (5-1)-1=4-1=3.

Смысл приведенных правил хорошо раскрывается при решении арифметических задач различными способами. Например, задача «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок. 6 лодок вернулись. Сколько лодок с рыбаками должно еще вернуться?» может быть решена тремя способами:

/ способ. 1. 20 + 8 = 28 2. 28 - 6 = 22

// способ. 1. 20 - 6=14 2. 14 + 8 = 22

III способ. 1. 8 - 6 = 2 2. 20 + 2 = 22

Законы умножения

Докажем законы умножения, исходя из определения произведения через декартово произведение множеств.

.Переместительный закон: для любых целых неотрицательных чисел а и Ъ справедливо равенство a•b = b•a.

Пусть а = п(А), Ь = п(В). Тогда по определению произведения а•Ь = п{А•В). Но множества А•В н В•А равномощны: каждой паре (а, Ь) из множества АХВ можно поставить в соответствие единственную пару (Ь, а) из множества ВхА, и наоборот. Значит, п(АХВ) = п(ВхА), и поэтому a-b = n {AXB) = n (BXA) = b-а.

.        Сочетательный закон: для любых целых неотрица
тельных чисел а, Ь, с справедливо равенство (а• Ь) •с = а• (Ь•с).

Пусть а = п(А), b = п (В), с = п (С). Тогда по определению произведения {a-b)-c = n((AXB)XQ, a a-(b -c) = n (AX(BXQ). Множества (АхВ)ХС и А X {ВХ Q различны: первое состоит из пар вида ((а, Ь), с), а второе - из пар вида (а, (Ь, с)), где а£А, Ь£В, с£С. Но множества (АХВ)ХС и АХ(ВХС) равномощны, так как существует взаимно однозначное отображение одного множества на другое. Поэтому п{(АХВ) •С) = п {А•(В•С)), и, значит, (а•Ь) •с = а• (Ь•с).

.        Распределительный закон умножения относительно сложения: для любых целых неотрицательных чисел а, Ь, с справедливо равенство (a +b) x c = ac+ be.

Пусть а - п (А), Ь = п (В), с = п(С)и АUВ= 0. Тогда по определению произведения имеем (a+b) x c = n ((AUB) • C. Откуда на основании равенства (*) получаем п ((А UВ) • С) = п((А • С)U(В• С)), и далее по определению суммы и произведения п ((А • С)U(В• С)) - = п(А•С) + п(В•С) = ас + Ьс.

.        Распределительный закон умножения относительно вычитания: для любых целых неотрицательных чисел a, b и с и a^b справедливо равенство (а - Ь)с = = ас - Ьс.

Этот закон выводится из равенства (А\В) •С = (А •С)\(В•С) и доказывается аналогично предыдущему.

Переместительный и сочетательный законы умножения можно распространить на любое число множителей. Как и при сложении, эти законы часто используются совместно, т. е. произведение нескольких множителей не изменится, если их переставить любым способом и если любую их группу заключить в скобки.

Распределительные законы устанавливают связь умножения со сложением и вычитанием. На основе этих законов происходит раскрытие скобок в выражениях типа (а+Ь)с и (а - Ь) с, а также вынесение множителя за скобки, если выражение имеет вид ас -be или

ас + Ьс.

В начальном курсе математики изучается переместительное свойство умножения, оно формулируется так: «От перестановки множителей произведение не изменится» - и широко используется при составлении таблицы умножения однозначных чисел. Сочетательный закон в начальной школе в явном виде не рассматривается, но используется вместе с переместительный при умножении числа на произведение. Происходит это следующим образом: учащимся предлагается рассмотреть различные способы нахождения значения выражения 3• (5•2) и сравнить полученные результаты.

Приводятся случаи:

)        3• (5•2) = 3•10 = 30;

)        3• (5•2) = (3•5) •2 = 15•2 = 30;

)        3• (5•2) = (3•2) •5 = 6•5 = 30.

Первый из них основан на правиле порядка действий, второй - на сочетательном законе умножения, третий - на переместительном и сочетательном законах умножения.

Распределительный закон умножения относительно сложения рассматривается в школе на конкретных примерах и носит название правил умножения числа на сумму и суммы на число. Рассмотрение этих двух правил диктуется методическими соображениями.

Правила деления суммы на число и числа на произведение

Познакомимся с некоторыми свойствами деления натуральных чисел. Выбор этих правил определен содержанием начального курса математики.

Правило деления суммы на число. Если числа а и Ь делятся на число с, то и их сумма а + Ь делится на с; частное, получаемое при делении суммы а+Ь на число с, равно сумме частных, получаемых при делении а на с и Ъ на с, т. е.

(а + Ь): с = а: с + b: с.

Доказательство. Так как а делится на с, то существует такое натуральное число т = а:с, что а = с-т. Аналогично существует такое натуральное число п - Ь:с, что Ь = с-п. Тогда а+Ь = = c-m + c-/2 = c-(m + n). Отсюда следует, что а+Ь делится на с и частное, получаемое при делении а+Ь на число с, равно т+п, т. е. а:с+Ь:с.

Доказанное правило можно истолковать с теоретико-множественных позиций.

Пусть а = п{А), Ь = п(В), причем АГ\В=0. Если каждое из множеств А и В можно разбить на с равномощных подмножеств, то и объединение этих множеств допускает такое же разбиение.

При этом если в каждом подмножестве разбиения множества А содержится а:с элементов, а в каждом подмножестве множества В содержится Ь:с элементов, то в каждом подмножестве множества А[)В содержится а:с+Ь:с элементов. Это и значит, что (а + Ь): с = а: с + Ь: с.

Правило деления числа на произведение. Если натуральное число а делится на натуральные числа Ъ и с, то, чтобы разделить а на произведение чисел Ъ и с, достаточно разделить число а на b (с) и полученное частное разделить на с (Ь): а:(Ь • с) -(а: Ь): с = (а:с): Ь Доказательство. Положим (а:Ь):с = х. Тогда по определению частного а:Ь = с-х, отсюда аналогично а - Ь-(сх). На основании сочетательного закона умножения а = (Ьс)-х. Полученное равенство означает, что а:(Ьс) = х. Таким образом, a:(bc) = (a:b):c.

Правило умножения числа на частное двух чисел. Чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на делитель, т. е.

a-(b:c) = (a-b):c.

Применение сформулированных правил позволяет упростить вычисления.

Например, чтобы найти значение выражения (720+ 600): 24, достаточно разделить на 24 слагаемые 720 и 600 и полученные частные сложить:

(720+ 600): 24 = 720:24 + 600:24 = 30 + 25 = 55. Значение выражения 1440:(12• 15) можно найти, разделив сначала 1440 на 12, а затем полученное частное разделить на 15:

: (12 • 15) = (1440:12): 15 = 120:15 = 8.

Указанные правила рассматриваются в начальном курсе математики на конкретных примерах. При первом знакомстве с правилом деления суммы 6 + 4 на число 2 привлекаются иллюстративный материал. В дальнейшем это правило используется для рационализации вычислений. Правило деления числа на произведение широко применяется при делении чисел, оканчивающихся нулями.

.3 Методика изучения законов и свойств арифметических действий в традиционной и вариативных программах обучения начальной школы

Одним из возможных методических подходов к реализации новой программы по математике является обучение сложению в пределах 100 на основе иного подхода к использованию сочетательного, а затем и переместительного свойства сложения.

В учебнике математики для IV класса (Н. Я. Виленкин и др.) сказано: «В выражении а + Ь + с действия выполняют по порядку слева направо. Если же воспользоваться сочетательным законом, то можно сначала сложить второе и третье слагаемые, а затем к первому слагаемому прибавить полученную сумму» (стр. 71).

Использование сочетательного закона дает возможность обосновать вычислительные приемы для многих случаев сложения, например, 26+3=20+6+3=20+9=29, 18+7=10+8+7=10+15= = 10+10+5 = 20+5=25 и др.

Вычитание по частям является приемом обратным прибавлению по частям, который основан на использовании сочетательного свойства сложения.

Вычитание из части уменьшаемого связано с сочетательным свойством сложения, согласно которому можно рядом стоящие слагаемые объединить в любые группы, а следовательно, если из суммы вычесть одно из слагаемых, то останутся другие слагаемые.

Изложенные соображения о значении сочетательного закона сложения для обоснования приемов сложения могут быть положены в основу методики обучения первоклассников вычислительным приемам.

Опыт ознакомления учащихся с сочетательным свойством сложения и его использованием при вычислениях был проведен по следующему плану:

1.  Подготовка к изучению сочетательного свойства сложения.

2.  Ознакомление детей с сочетательным свойством сложения.

3.  Обоснование приемов сложения и вычитания на основе сочетательного свойства сложения.

4.  Сложение и вычитание рассматриваются в таком порядке.

В 1 классе сначала изучается сложение и вычитание разрядных чисел ( 70+20, 60-40). Затем рассматривается свойство прибавления числа к сумме, пользуясь которым и ранее усвоенными знаниями вводятся приемы для случаев: 46+20, 46+2. Здесь же, используя прием перестановки слагаемых, рассматривают случай 2+46. Далее изучается свойство вычитания числа из суммы и приемы для случаев: 48-30, 48-3 и 40-3. Следующим рассматривается свойство прибавления суммы к числу, на основе которого раскрываются табличные случаи сложения с переходом через десяток ( 9+3 ). Вслед за этим изучается свойство вычитания суммы из числа и табличные случаи вычитания ( 12•5 ). Наконец, рассматриваются парами приемы сложения и вычитания, основанные на двух последних свойствах: 47+9 и 47-9; 30+12 и 30-12; 65+14 и 65-14; 36+19 и 36-19. Во 2 классе изучаются свойства прибавления суммы к сумме и вычитания суммы из суммы, на основе которых вводятся приемы поразрядного сложения и вычитания.

Рассмотрим подробнее методику изучения свойств и вычислительных приемов.

Сложение и вычитание двузначных разрядных чисел сводится к сложению и вычитанию однозначных чисел, которые выражают число десятков. Например, чтобы к 50 прибавить 30, достаточно к 5 десяткам прибавить три десятка, получится 8 десятков, или 80, а чтобы из 5 десятков вычесть три десятка, получится 2 десятка, или 20. Объяснение решения двух-трех примеров сопровождается иллюстрацией и такой записью

70+20 60-40

дес.+2дес.=9дес. 6дес.-4дес.=2дес.

+20=90 60-40=20

Рассматриваемый прием вычислений настолько прост, что обычно не вызывает затруднений у детей. Однако при возникновении затруднений у отдельных учащихся необходимо вернуться к соответствующим устным пояснениям, а если понадобится, то и к иллюстрации. Работа над рассматриваемыми случаями сложения и вычитания служит делу закрепления знания нумерации в пределах 100, табличного сложения и вычитания в пределах 10. Поэтому упражнения такого вида полезно включать и в дальнейшем. На последующих двух-трех уроках, ученики проговаривают объяснение вслух, а затем про себя. Это тем более важно, что для успешного усвоения следующих приемов вычислений соответствующие навыки должны быть уже достаточно отработанными.

Следующий шаг в работе над темой - ознакомление с различными способами прибавления числа к сумме. Остановимся подробнее на методике соответствующей работы, поскольку то, что относится к рассмотрению этого свойства, в полной мере может быть отнесено и ко всем другим.

Введению свойства прибавления числа к сумме должна предшествовать специальная подготовительная работа, в результате которой учащиеся знакомятся с математическими выражениями «сумма чисел…» и «разность чисел…», учатся читать и записывать выражение со скобками, заменять двузначные неразрядные числа суммой их разрядных слагаемых. Эти вопросы рассматриваются при изучении сложения и вычитания чисел в пределах 10 и нумерации чисел в пределах 100.

Изучение каждого свойства строится примерно по одному плану: сначала, используя наглядные пособия, надо раскрыть суть самого свойства, затем научить детей применять его при выполнении различных упражнений учебного характера, и, наконец, научить, пользуясь знанием свойства, находить рациональные приемы вычислений с учетом особенностей каждого конкретного случая.

Рассмотрим, как можно провести ознакомление детей со свойством прибавления числа к сумме.

Раскрывая суть свойства, надо показать детям, что число к сумме можно прибавить различными способами: можно вычислить сумму и к полученному результату прибавить число, можно прибавить число ко второму слагаемому и полученный результат сложить с первым слагаемым.

Покажем, как это можно сделать.

Учитель пишет на доске выражение (5+3)+2.

Прочитайте пример. (К сумме чисел 5 и 3 прибавить 2).

Назовите сумму. (5+3.) Назовите первое слагаемое этой суммы. (5.)

Назовите второе слагаемое. (3.) Назовите число, которое надо прибавить к этой сумме. (2.) Как найти результат? (Вычислю сумму, получится 8; прибавлю 2, получится 10.)

На доске запись: (5+3)+2=8+2=10.

Учащиеся неоднократно уже встречались с заданиями такого вида. Поэтому сама задача - вычислить значение выражения вида: (5+3)+2 - для детей не нова. Рассмотрение различных способов решения психологически не может быть оправдано в данном случае и какой-либо выгодой в отношении большей легкости одного из этих способов, так как после усвоения таблицы сложения все эти способы одинаково просты для детей. Постановку задачи рассмотрения различных способов прибавления числа к сумме можно, конечно, объяснить просто указанием на то, что знание этих способов пригодится в дальнейшем.

Учитель вывешивает на доске рисунки двух гаражей и предлагает двум ученикам приготовить прямоугольники голубого, зелёного и красного цветов, вырезанные из бумаги.

Это гаражи. Число машин в первом гараже будет изображать первое слагаемое. Сколько машин надо поставить в первый гараж? (5.)

Учитель вставляет в прорези 5 машин голубого цвета, вырезанные из картона, а учащиеся раскладывают на партах 5 голубых прямоугольников.

Число машин во втором гараже будет изображать второе слагаемое. Сколько машин поставим во второй гараж? (3.)

Учитель «ставит» во второй гараж 3 зелёные машины, а дети раскладывают на партах 3 зелёных прямоугольника.

Приехали ещё 2 машины (прикрепляют к доске 2 красные машины, а учащиеся кладут на парту 2 красных прямоугольника).

На доске располагаются рисунки.

Красные машины надо поставить в гараж. В какой гараж их можно поставить? (В первый или во второй). Поставим их в первый гараж. (Учитель «ставит» машины в первый гараж, а дети придвигают красные прямоугольники к голубым.) Как теперь узнаем, сколько всего машин? (К 5 прибавить 2, получится 7, ещё прибавить 3, получится 10.) Да, число 2 мы прибавим к 5, первому слагаемому, потом к полученному результату, к 7, прибавили второе слагаемое 3. Сравните ответы. (Получилось тоже 10.) Если получилось столько же, сколько при решении первым способом, значит, можно прибавлять число к сумме и таким способом. Кто расскажет, как мы сейчас прибавляли число к сумме? (Ученик рассказывает.)

Аналогичным образом с использованием тех же пособий раскрывается ещё один способ: можно прибавить число ко второму слагаемому - к 3 и полученный результат сложить с первым слагаемым - с 5.

Сколько способов прибавления числа к сумме мы рассмотрели? (Три.) Да, три способа: можно решить пример так, как и раньше это делали - вычислить сумму чисел 5 и 3 и к результату, к 8, прибавить число 2; можно прибавить число 2 к первому слагаемому, к 5, и к полученному результату, к 7, прибавить второе слагаемое 3; а можно прибавить число 2 ко второму слагаемому, к 3, и полученный результат, 5, сложить с первым слагаемым - с 5.

Далее так же рассматривается решение тремя способами ещё одного примера на прибавление числа к сумме. При этом используется то же наглядное пособие.

При раскрытии свойства можно использовать и другие пособия, например: в вёдра вливать воду литрами, в конверты вкладывать открытки, в тарелки раскладывать фрукты и т. д.

После коллективного рассмотрения с демонстрацией и подробным анализом хода решения одного примера или задачи можно обратиться к учебнику и, рассматривая предложенные в нём иллюстрации различных способов вычислений, провести аналогичную работу по этим иллюстрациям и подписям, которые к ним даны.

После описанной работы дети, как правило, оказывается уже в состоянии самостоятельно (или с комментированием) выполнить следующее задание учебника, связанное с вычислением тремя способами значений аналогичных выражений.

На следующем уроке, рассматривая три способа прибавления числа к сумме, одновременно с использованием наглядных пособий выполняют развёрнутую запись. Эту запись учитель выполняет на доске или на плакате, а учащиеся в тетрадях. Например, решение тремя способами примера (4+2)+3 следует записать следующим образом:

.(4+2)+3=6+3=9

.(4+2)+3=(4+3)+2=7+2=9

.(4+2)+3=4+(2+3)=4+5=9

Выполнение каждой записи учащиеся сопровождают объяснением сначала под руководством учителя, а потом самостоятельно. На этом этапе не следует требовать от детей обобщённой формулировки правила прибавления числа к сумме, достаточно, чтобы они умели объяснить решение различными способами данных конкретных примеров.

В таком же плане проходит работа и над другими свойствами. Однако по мере рассмотрения новых свойств увеличивается доля самостоятельного участия детей в «открытии» различных способов нахождения результатов.

Например, усвоению свойства прибавления числа к сумме будут способствовать такие упражнения:

. Прочитайте пример и вычислите результат разными способами: (6+1)+2

а) Вычислю сумму, получится 7; прибавлю к ней число 2, получится 9: (6+1)+2=7+2=9

б) Прибавлю число 2 к 6, к первому слагаемому, получится 8; к этому результату прибавлю второе слагаемое 1, получится тоже 9:

(6+1)+2=(6+2)+1=8+1=9

в) Прибавлю число 2 к 1, ко второму слагаемому, получится 3; этот результат прибавлю к первому слагаемому - к 6, получится тоже

(6+1)+2=6+(1+2)=6+3=9

Рассмотрение таких примеров - важнейший момент в деле подготовки к использованию рассмотренных свойств действий в более сложных случаях сложения в пределах 100. Именно на этих примерах до сознания детей должно быть доведено, что тот или иной способ вычислений выбирается с учётом особенностей предложенного примера. Именно здесь должно быть показано, какие преимущества даёт знание рассмотренных возможных способов прибавления числа к сумме.

. Найдите результат удобным способом:

(8+6)+4 (30+7)+20 (60+5)+4

Выполняя такие упражнения, ученики мысленно воспроизводят все три способа нахождения результата и выбирают наиболее рациональный. Первое время учителю надо подводить детей к выбору такого способа. Например, находя значение первого выражения, учитель говорит, что легче (лучше) прибавить 4 к тому числу, при сложении с которым получится 10, так как к 10 легче прибавлять; находя значения двух других выражений, учитель указывает, что удобнее десятки прибавлять к десяткам, а единицы к единицам:

. Закончите запись.

(8+7)+2=(8+2)… (40+3)+5=40+(…)

Ученик даёт примерно такое объяснение: слева записано, что надо к сумме чисел 8 и 7 прибавить 2, а справа записано, что число 2 прибавили к 8, к первому слагаемому; чтобы справа получилось столько же, сколько слева, надо к полученной сумме прибавить второе слагаемое 6.

Усвоению свойств помогает также решение некоторых задач разными способами и сравнение решений.

Как только будет усвоено свойство, можно переходить к изучению вычислительных приёмов, основанных на соответствующем свойстве.

Для подготовки учащихся к приёму вычитания, основанному на знании таблицы сложения, надо включать специальные упражнения, направленные на усвоение состава чисел второго десятка. Так, пользуясь составленной таблицей, учащиеся называют, суммой каких двух однозначных чисел является, например, число 11 (12, 13, …., 18), и записывают 11=9+2; 11=8+3 и т. д.

После изучения свойства вычитания суммы из числа по той же методике, как и другие свойства, рассматривают вычитание вида 12-5.

Для этого случая вычитания целесообразно рассмотреть три приёма: первый основывается на использовании свойства вычитания суммы из числа, второй - на использовании свойства вычитания числа из суммы, а третий - на знании состава чисел второго десятка и связи между суммой и слагаемым.

Подготовкой к введению первого приёма будет решение удобным способом примеров вида 13-(3+2). При ознакомлении с приёмом используется то же наборное полотно, которое применялось при раскрытии приёма сложения вида 9+5.

Предлагается решить пример 12-5. Каждый ученик у себя на парте, а один из них на доске, откладывает на наборном полотне 12 кружков. Учитель спрашивает, как удобнее вычесть 5 из 12. Ученики предложат вычесть сначала 2 (вынимают 2 кружка), а потом ещё 3 (вынимают 3 кружка). Выясняется, что число 5 заменили суммой удобных слагаемых 2 и 3, вычли сначала одно слагаемое, а потом из полученного результата другое.

Запись: 12-5=12-(2+3)=(12-2)-3=7

При этом ученик ведёт объяснение, руководствуясь ранее данным планом: « Заменю число 5 суммой удобных слагаемых 2 и 3; получился пример: из 12 вычесть сумму чисел 2 и 3; удобнее сначала вычесть 2, первое слагаемое, а из полученного результата, из 10, вычесть 3, второе слагаемое, получится 7».

Не исключено, что сами дети предложат приём замены уменьшаемого суммой разрядных слагаемых:

-5=(10+2)-5=(10-5)+2=7

Однако при этом неоднократно появляется типичная ошибка: отняв всё вычитаемое от десяти, ребёнок оставляет без внимания свободные единицы уменьшаемого и получает неправильный ответ (например, в данном случае число 5 вместо числа 7). Трудность для первоклассника состоит ещё и в том, что нужно преодолеть инерцию действия: приходится после вычитания применять сложение. Лучше поэтому сначала придерживаться вычитания суммы из числа, а затем раскрыть на одном и том же примере оба приёма в порядке сопоставления. Заметим, что преодоление посильных трудностей имеет определённое воспитательное значение.

Во 2 классе после изучения свойств прибавления суммы к сумме и вычитания суммы из суммы вводятся приёмы поразрядного сложения и вычитания двузначных чисел.

К этому времени учащиеся настолько овладевают общим приёмом использования свойств для обоснования вычислительных приёмов, что способны самостоятельно найти новые приёмы. Затем, решая примеры, они так записывают решение:

+14=(60+5)+(10+4)=(60+10)+(5+4)=79.

-14=(60+5)-(10+4)=(60-10)+(5-4)=51.

Одновременно дают объяснение: заменим каждое число суммой разрядных слагаемых, получится пример: к сумме чисел 60 и 5 прибавить сумму чисел 10 и 4; удобнее сложить первые слагаемые ( 60 и 10 ), затем вторые слагаемые ( 5 и 4 ), сложить результаты, получится 79.

На этапе закрепления знания приёма и формирования вычислительного навыка в отношении всех рассмотренных случаев вычислений ученики должны выполнять краткое объяснение сначала вслух, а затем про себя: называть только, какие действия и над какими числами они выполняют и какие получили результаты. Например, для случая 30-12 краткое объяснение будет таким: из 30 вычту 10, получится 20; из 20 вычту 2, получится 18. При этом запись тоже надо выполнять кратко: записывать пример и результат (30-12=18).

Необходимо систематически накапливать факты для установления связи между действием деления и умножения. После первоначального ознакомления с действиями умножения и деления можно приступить к углублению этих понятий через изучение их свойств.

В различных методиках и пособиях переместительное свойство поясняется наглядно на рисунках путем сравнения результатов умножения (произведений) при разном порядке сомножителей (подсчет треугольников, кружочков, клеток и т. д. ведется по строкам, а потом по столбцам).

Например, подсчитаем число клеток в прямоугольнике:

а)       по столбцам - 3 • 5 = 15,

б)по строкам - 5 • 3 = 15.

Число клеток в этом прямоугольнике

всегда 15, значит, можно говорить о

равенстве выражений (произведений)

3 • 5 и 5 .3,

т. е. 3 • 5 = 5 • 3.

Подмечая это свойство на ряде примеров, дети сами делают вывод. Неправильно было бы считать, что этим свойство и доказано. Очень важно распространить вывод на произведение любых чисел, а для этого недостаточно лишь утверждения учителя, что так будет всегда, необходимо показать, что подобные рассуждения можно повторить для любых чисел, т. е. показать выполнение свойства для произведения любых чисел.

Можно сравнивать и результаты при вычислении:

•4 = 6 + 6 + 6 + 6 = 24,  6-4 = 4-6.

• 6 = 4 + 4 +4+ 4 + 4 + 4 = 24.

Решая поставленные задачи (исследуя факты), учащиеся могут самостоятельно сделать вывод, что от перемены порядка сомножителей произведение не изменяется (от перемены мест сомножителей произведение не изменится). На этом законе и основан прием вычисления произведения и составления таблиц умножения, когда второй сомножитель больше первого. Преимущество этого вычислительного приема можно показать на примере:

•9 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2= 18,

•2 = 9 + 9=18.

Позднее необходимо рассмотреть с учащимися доказательство переместительного закона и его запись в общем виде (буквенную).

Важно еще познакомить детей с распределительным свойством умножения относительно сложения (умножение числа на сумму и суммы на число), которое частично практически используется уже при составлении таблиц умножения и необходимо при изучении приемов внетабличного умножения. Использование этого свойства позволит не только повысить культуру математического мышления, но и вооружит учащихся обобщенными приемами устного умножения, подготовит базу для выработки алгоритма письменного умножения. В период подготовки к изучению распределительного свойства дети упражняются:

а) в чтении и записи выражений

+ 5 .. 4; 4 . 7 + 54; 4 • 7 + 6 • 9; 5 • (6 + 3). «Сумма числа 16 и произведения чисел 5 и 4», «произведение числа 5 на сумму чисел 6 и 3»;

б) в наборе нужного числа двоек, троек, разными группами (сначала на кружочках разного цвета).

Можно распределительное свойство объяснить на основе сравнения результатов решения одной и той же задачи двумя способами. Например, надо вычислить число кружочков на рисунке.

I        способ. В одном столбике кружков - 3

Всего столбиков на рисунке - (4 + 2)

Всего кружков будет - 3 . (4 + 2) Итак, 3 • (4 + 2) = 3 • 6 = 18.

II       способ. На рисунке белых кружков- 3-4, черных кружков -3-2.

Всего кружков - 3 • 4 + 3 • 2

3 • 4 + 3 • 2 = 12 + 6 = 18.

Сравнить значения выражений 3 • (4 + 2) и

-4 + 3-2 и записать, что 3 • (4 + 2) = 3 . 4 + 3 • 2.

В беседе с детьми надо отметить, что для умножения числа на сумму умножают число на каждое слагаемое и эти произведения складывают.

Более трудными являются для учащихся рассуждения, основанные на сочетательном законе сложения, хотя они доступны учащимся этого возраста и помогают осознать прием набора равными группами, который используется при составлении таблиц. 3 • (4 + 2) = 3 • 6 = 3 + 3 + 3 + 3 + 3 +3= 3•4 + 3•2 =78 и окончательно 3 • (4 + 2) = 3 • 4 + 3 •2.

Кроме общепринятой формы записи (в строчку) при умножении числа на сумму, интересная форма записи (в столбик) приводится в эстонских учебниках.

• 6 = 2 • (2 + 4) = = 2• 2 + 2 • 4 = = 4 + 8 = 12

Для усвоения распределительного свойства полезны упражнения:

.        В сравнении и вычислении значения выражений

9 • (4 + 3) =          9 • 7 =

7• (5 + 4) = 7 • 9 =

8• (6 + 2) = 8 • 8 =

Из этой работы надо сделать практический вывод, что всегда можно более трудные случаи табличного умножения свести к более легким (второй сомножитель заменить суммой двух чисел и вычислить по правилу умножения числа на сумму): 8-9 = 8- (5 + 4) = 8 • 5 + 8 • 4 = 40 + 32 = 72.

.        В умении свернуть запись

• 7 + 3 • 2 = 3 • (7 + 2), 8 • 4 + 8 • 3 = 8 • (4 + 3).

.        В вычислении произведения разными способами (выбрать
более удобный)

• (5 + 4), 8 • (2 + 1), 7 • (6 + 4).

Объяснение свойства умножения суммы на число можно аналогично начинать с решения задач. В методике предлагаются и другие пути изложения этого вопроса:

а) на основе использования переместительного свойства умножения и свойства умножения числа на сумму

(3 + 4)-2 = 2-(3 + 4) = 2-3 + 2-4 = 3-2 + 4-2.

Окончательно имеем:

(3 + 4) • 2 = 3 • 2 + 4 • 2;

б)      на основе определения умножения, переместительного и сочетательного свойств сложения

(3 + 4) • 2 = (3 + 4) + (3+ 4) = (3 + 3) + (4 + 4) -= 3-24-4-2;

в)      на основе непосредственного знакомства с правилом:

«Умножить сумму на число можно разными способами, получая одинаковые результаты:

.        Можно вычислить сумму и умножить полученный результат на число: (5 + 4) • 3 = 9 • 3 = 27.

,        Можно умножить на число каждое из слагаемых суммы и
полученные произведения сложить (5 + 4) • 3 = 5 • 3 4 4 • З.

Лучше рассмотреть с детьми свойство на конкретных примерах («открыть» его), а позднее познакомить их с доказательством (как приведено в случае «б») и записью в общей форме (а + Ь) . с = а .с 4- b • с. Теперь надо подчеркнуть, что для удобства (облегчения) вычислений можно представить в виде суммы любой сомножитель. На основе этого вывода позднее будем формировать приемы внетабличного умножения.

Третье свойство умножения - сочетательное - не находит широкого применения при вычислениях в пределах сотни, так как считается малодоступным детям этого возраста. Очень важно помочь детям увидеть и осознать, что произведение может быть больше любого сомножителя, равняться одному из сомножителей и быть равным нулю. Вывод дети в состоянии сделать, сравнивая результаты вычислений (на основе определения произведения), для примеров вида:

-5=15 3-5 = 3 + 3 + 3 + 3 + 3=15

-5 = 5 -1.8-1 + 1 + 1+1 + 1-5

-5 = 0 0-5 = 0 + 0 + 0 + 0 + 0 = 0

Эта работа явится пропедевтикой к рассмотрению умножения на 1 и 0, которые особо выделяются в программе (особые случаи). Их вводят с помощью правил, так как они не вытекают из определения умножения. При определении множителя как оператора действия умножение на 1 не требует особого определения (3 • 1 = 3, «три посчитать 1 раз, получим 3»).

Обобщая случаи 1 • 3 = 3 и 3 • 1 = 3, можно сделать вывод, что произведение любого числа и единицы равно этому числу.

Иначе, умножить число на единицу - значит оставить его без изменения.

Надо познакомить учащихся с записью в общем виде: а • 1 = а, 1 •а = а.

Более отвлеченными и потому более трудными являются для учащихся случаи умножения на нуль. Кроме определения, которое дается для этого случая, в различных методиках рекомендуются некоторые пояснения.

Например, на основе выявления закономерности изменения произведения при уменьшении множителя на одну единицу.

• 4 = 20 (произведение уменьшается

-3-15 каждый раз на 5 единиц)

• 2 = 10

-1-5   и, наконец,

-0 = 0.

Сравнивая случаи 0-5 - 0и5-0=»0 и обобщая 0 • а => 0, а . 0 = 0, можно сделать вывод:

При умножении любого числа на нуль произведение равно нулю.

Необходимо сообщить учащимся о невозможности делить на нуль.

После формирования первоначальных понятий о новых действиях (умножения и деления), изучив ряд свойств, можно установить непосредственную связь действия деления с умножением. Теперь результаты деления дети должны получить не с помощью операций над предметными множествами, а получать из соответствующих случаев умножения. Работу лучше всего проводить путем решения практических задач, создавая игровые ситуации.

Итак, в программе Моро М.И. уделяется значительное внимание формированию у учащихся осознанных и прочных, во многих случаях доведенных до автоматизма навыков вычислений, программа предполагает вместе с тем и доступное детям обобщение учебного материала, понимание общих принципов и законов, осознание тех связей, которые существуют между рассматриваемыми явлениями.

В основе построения программы Н.Б. Истоминой лежит методическая концепция, выражающая необходимость целенаправленной и систематической работы по формированию у младших школьников приемов умственной деятельности: анализа и синтеза, сравнения, классификации, аналогии и обобщения - в процессе усвоения математического содержания.

Направленность процесса обучения математике в начальных классах на формирование основных мыслительных операций позволяет включить интеллектуальную деятельность младшего школьника в различные соотношения с другими сторонами его личности, прежде всего с мотивацией и интересами, оказывая тем самым положительное влияние на развитие внимания, памяти (двигательной, образной, вербальной, эмоциональной, смысловой), эмоции и речи ребенка.

Практическая реализация концепции находит выражение:

в логике построения содержания курса, в основе, которой лежит система математических понятий и общих способов действий;

в методическом подходе к формированию понятий и общих способов действий, в основе которого лежит установление соответствия между предметными - вербальными - схематическими и символическими моделями;

в системе учебных заданий, которая адекватна концепции курса, логике построения его содержания и нацелена на осознание школьниками учебных задач, на овладение способами их решения и на формирование у них умения контролировать и оценивать свои действия.

В связи с этим процесс выполнения учебных заданий носит продуктивный характер, который исходя из психологических особенностей младших школьников определяется соблюдением баланса между логикой и интуицией, словом и наглядным образом, осознанным и подсознательным, догадкой и рассуждением.

Итак, основу отбора и структуирования содержания, процессуальную характеристику изучения вопросов этой линии курса математики составляют следующие приоритетные концептуальные положения:

элементы теории множества представляют теоретические основы арифметических действий и связанных с ними математических понятий и способов действий, хотя их применяют в неявной форме;

раскрытие смысла арифметических действий связано с определением число элементов множества (в объединении попарно непересекающихся множеств; в дополнении подмножеств; в объединении равномощных множеств), число элементов равномощных подмножеств и число равномощных подмножеств полученных при разбиении множества;

сложение-вычитание, умножение-деление взаимно обратные арифметические действия;

законы и свойства арифметических действий вводятся в явном виде и применяются на практике, которые позволяют реализовать соотношения теоретических и практических вопросов и проиллюстрировать обусловлен- ность математических закономерностей, правил, выводов из нужд и потребностей жизни;

последовательность введения арифметических действий и способов вычислений определяются расширением области рассматриваемых чисел по концентрам, которые исключают излишние дублирование и повторение, а обеспечивает преемственное развитие и реализует оптимальное соотношение устных и письменных приемов вычислении;

введение каждого нового приема вычисления обоснуется его необходимостью, а тем приемам вычислений, которые рассматриваются неоднократно в связи с расширением области изучаемых чисел, следует обучать только один раз, когда их вводят впервые, после чего как известный прием используется для новых чисел;

осуществление укрупнения знаний на основе связи между арифметическими действиями, одновременно рассматривая сложение и вычитание, а также умножение и деления как взаимно обратные действия, предусматривая параллельное обучение выполнению действие и его проверки с помощью использования обратного ему действия.

Выводы по 1 главе

Изучение и усвоение арифметических действий является неотъемлемой частью обучения математике. Знания арифметических действий, их компоненты в терминологии является одним из основных требований программы математики начальной школы. На их знание и их свойств фактически основывается вся остальная математика, основные ее понятия и программный материал.

Каждое из четырех арифметических действий должно прочно связаться в сознании детей с теми конкретными задачами, которые требуют его применения. Смысл действий и раскрывается главным образом на основе практических действий с множествами предметов и на системе соответствующих текстовых задач. На их основе доводится до сознания детей связь между компонентами и результатами действий, связь между действиями, рассматриваемые свойства действий и изучаемые математические отношения.

Сложение и умножение чисел обладают свойствами коммутативности, ассоциативности, умножение дистрибутивно относительно сложения.

Учителя начальных классов должны целенаправленно вести работу по формированию свойств арифметических действий. Также учитель сам должен хорошо уметь анализировать и решать задачи, знать с какой целью, где какая задача должна быть использована для формирования и усвоения теоретических вопросов. Широко использовать наглядный материал, который помогает лучшему усвоению темы урока.

Глава 2. Опытно-экспериментальная работа по формированию вычислительных навыков при изучении законов и свойств арифметических действий в начальной школе

.1 Диагностика уровня сформированности вычислительных навыков младших школьников при изучении законов и свойств арифметических действий

Мы проводили эксперимент на базе 2 класса МОУ Стеженская СОШ Алексеевского района Волгоградской области (программа «Школа России»).

Суть эксперимента заключалась в том, чтобы практически проверить выдвинутую нами гипотезу, а именно, если при изучении законов и свойств арифметических действий использовать дидактический материал, упражнения развивающего характера, то уровень сформированности вычислительных навыков младших школьников повысится.

В эксперименте приняли участие 7 учащихся.

Для того, чтобы исследовать, насколько дети владеют навыками использования законов и свойств арифметических действий в концентре 100, мы провели диагностику.

Цель: выявить уровень сформированности знаний учащихся по изучению арифметических действий сложения и вычитания в концентре «Сотня» (Приложение 1).

Учащимся предлагалось решить 20 выражений с арифметическими действиями сложения и вычитания, используя законы и свойства, выбрать удобный способ решения примеров, в концентре «Сотня»

Анализ результатов:

Высокий уровень - «5» (20 правильных ответов).

Уровень выше среднего - «4» (18-19 правильных ответов).

Средний уровень - «4» (15-17 правильных ответов)

Уровень ниже среднего - «3» (11-14 правильных ответа)

Низкий уровень - «2» (0- 10 правильных ответа.)

Таблица №1

Уровень сформированности знаний учащихся по изучению законов и свойств арифметических действий до эксперимента

Покажем результаты всего класса в процентном отношении:

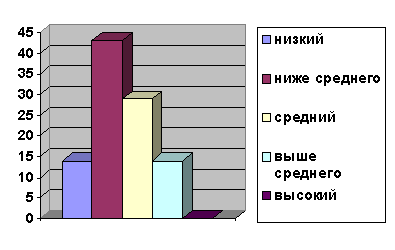
Низкий уровень - 1 учащийся (14 %)

Уровень ниже среднего - 3 учащихся (43%)

Средний уровень-2 учащихся (29 %)

Уровень выше среднего - 1 учащихся (14%)

Покажем на диаграмме 1:

Диаграмма 1

Уровень сформированности знаний учащихся по изучению законов и свойств арифметических действий до эксперимента

Рассматривая результаты контрольной работы № 1, можно сделать вывод о том, что в целом ученики класса в достаточно устойчивой степени владеют навыками сложения и вычитания, используют переместительный и сочетательный законы, свойства арифметических действий сложения и вычитания. Они старались, как можно точнее выполнять заданные примеры, и делали это осознанно.

Исходя из анализа проведённых ряда контрольных работ по данной теме, можно логично сделать вывод, что при сложении и вычитании двузначных чисел около 50% детей допускают ошибки в вычислениях, не видят удобный способ выполнения действий, делают ошибки в прибавлениях числа к разности, вычитания числа из суммы, разности.

Не лучше обстоит дело с вычитанием чисел с переходом через десяток, смешивают вычислительные приёмы, переносят вновь изученных правил на ранее усвоенные и другие ошибки допускают второклассники.

Поэтому при подготовке к уроку, учитывая особенности учащихся, необходимо не только выявить целесообразность распределения в учебнике упражнений, предназначенных для закрепления, с точки зрения их связи с основным материалом, изучаемом на данном уроке, но и продумать формы работы.

Что мы и учитывали при проведении формирующего эксперимента, в ходе которого мы значительное место уделяли отработке навыка по выполнению арифметических действий сложения и вычитания, решению примеров разных вида, а также использовали дидактические игры, наглядный материал, занимательные и познавательные задания.

После формирующего эксперимента мы провели итоговую контрольную работу №2, цель которой заключалась в проверке сформированности приемов использования законов и свойств арифметических действий в концентре «Сотня» (Приложение 2).

Был получен следующий результат:

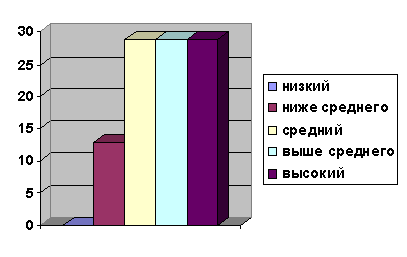
Уровень ниже среднего -1 учащийся (13%)

Средний уровень-2 учащихся (29%)

Уровень выше среднего - 2 учащийся (29%)

Высокий уровень-2 учащихся (29%).

Таблица №2

Уровень сформированности знаний учащихся по изучению законов и свойств арифметических действий после эксперимента

Покажем результат на диаграмме 2:

Диаграмма 2

Уровень сформированности знаний учащихся по изучению законов и свойств арифметических действий после эксперимента

Рассматривая результаты контрольной работы № 2, можно сделать вывод о том, что в целом ученики 2 класса в достаточно устойчивой степени владеют навыками сложения и вычитания в пределах сотни, используют переместительный, сочетательный закон относительно сложения.

Сравним результаты:

Диаграмма 3

Уровень сформированности знаний учащихся по изучению законов и свойств арифметических действий до и после эксперимента

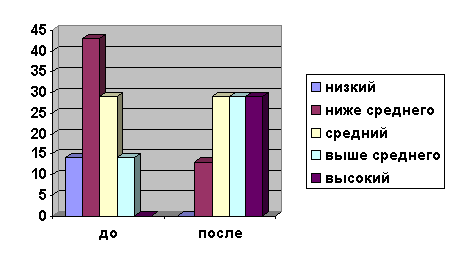
Мы видим, что уровень сформированности знаний учащихся по использования законов и свойств арифметических действий сложения и вычитания в концентре «Сотня» повысился, что говорит об эффективности предложенной методики изучения арифметических действий сложения и вычитания в концентре «Сотня», основанной на отработке навыка по выполнению арифметических действий сложения и вычитания, решении примеров разных вида, а также использовании дидактических игр, наглядного материала, занимательных и познавательных заданий.

.2 Методические приемы, направленные на изучение законов и свойств арифметических действий

Изучение законов и свойств арифметических действий мы рассматривали при изучении действий сложения и вычитания в концентре «Сотня».

Рассмотрим, как происходило знакомство с законами и свойствами арифметических действий .

Цель:

воспроизведение ЗУН по порядку действий в числовом выражении, умение применить переместительное свойство сложения;

создать затруднение в индивидуальной деятельности.

Учитель: Прочитайте выражения на доске и найдите их значения устно.

(11+7)-(3+6)

(635+198)+2

+16+19+25+31+34+37

-(5+2) +4

(178+597)+3

Уч-ся на индивидуальных досках пишут значения выражений.

Учитель: Прочитайте первое выражение? Назовите результат.

Уч-ся: Из суммы 11 и 7 вычитается сумма 3и6. Разность равна 9»

Учитель: Прочитайте второе выражение? Назовите результат.

Уч-ся: Из 12 вычитаем сумму 5 и 2 и к разности прибавляем 4, сумма равна 9.

Учитель: Прочитайте третье выражение? Назовите результат.

Уч-ся: Сумма выражения 13+16+19+25+31+34+37 равна 175.

Учитель: Как вы нашли сумму? Чем пользовались? Какой прием использовали?

Уч-ся: От перестановки слагаемых сумма не меняется.

Лена и Алеша показывают свою работу: (13+37)+ (16+34) + (19+31) +25+175! Замечательно.

Учитель: Прочитайте следующие выражения? Назовите результат.

Уч-ся: В выражении «к сумме чисел 635 и198 прибавляется 2.

Учитель: (подводящий диалог) Что вам показалось трудным? (нахождение суммы в скобках )

Как выполнила решения Катя:35+98=133 133+2=135 и 35+ (98+2)=135

Какое решение вам больше понравилось? Почему? Как в математике называют такие действия -рационально, проще. Итак, у нас две гипотезы

-я: можно вычислить выражение по порядку действий и получить результат.

-я: можно изменить порядок действий и получить тот же результат.

Какая из них верная и предстоит нам сегодня решить.

Учитель: Сегодня мы будем говорить о рациональном способе сложения чисел.

Постановка проблемы

Цель: постановка проблемы, самоопределение учащихся.

Учитель: А что мы с вами взяли девизом нашего урока? Будем пробовать! Искать! Давайте искать решение!

Достаточно ли нам его в нашем выражении? Нужен другой закон, позволяющий нам быстро вычислять 35+(98+2)=35+100=135.

Учитель: Чем отличаются наши выражения?

+(98+2)=35+100=135

(35+98)+2=135

Уч-ся: Пользовались переместительным свойством сложения и поставили скобки.

Учитель: А для чего вы их использовали?

Уч-ся: Так быстрее вычислять.

Учитель: Молодцы! ВЫ думали, вы пробовали, вы объединили удобные слагаемые для нахождения суммы. (открывается тема урока - «Свойства сложения»)

Табличка: a+b=b+a (переместительное свойство сложения)

Итак, в числовом выражении у нас все получилось. А как быть с буквенными выражениями?

Посмотрите на эти выражения: (а+в)+с и а+(в+с), сравните их, используя схемы.

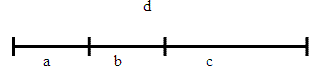
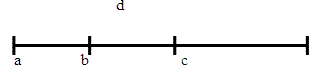
Учитель: Сейчас вы будете работать в парах, помогите друг другу сравнить эти выражения, выясните, что общего в этих выражениях и почему целое обозначено одной буквой. А сумма частей найдена по-разному.

(учащиеся на индивидуальных карточках составляют выражения, по графическим моделям)

(a+b)+c =d a+(b+c)=d

(a+b)+c ?=? a+(b +c)

Учитель: Давайте прочитаем полученные выражения: если к сумме двух чисел «a и b» прибавить число c то результат равен числу « d ». Если к числу а прибавить сумму чисел «b и c», то результат будет равен этому же числу « d»

Учащиеся составили опорный конспект сочетательного свойства сложения.

Итак, при рассмотрении буквенного выражения мы подошли к одному результату. Учитель снимает знак вопроса над записью

(a+b)+c=a+(b+c)

Открытие нового знания

На доске появляются две таблицы :a+b=b+a (a+b)+c=a+(b+c)

в обоих случаях выражение равно «d».

Учитель: Какое свойство вы знали? (о перестановке слагаемых)

Какое свойство вы открыли сегодня? Что оно позволяет нам делать? Проверим наши выражения числовые(35+98)+2=135 и 35+(98+2)=135. Изменилось значение суммы? Нет. Сочетательное свойство сложения позволяет упрощать вычисления!

Объединять удобные слагаемые и тем самым упрощать вычисления.

В математике это свойство получило название -сочетательного свойства сложения. Расскажите его друг другу, как вы сформулируете его своими словами?

Олег и Марина- Дима и Лена - Илья и Саша.

Чтобы к сумме двух чисел, прибавить третье число, можно к первому числу прибавить сумму второго и третьего.

Чтобы к числу прибавить сумму двух чисел, можно сначала прибавить к нему первое слагаемое, а потом второе слагаемое.

Значение суммы чисел не зависит от выбора порядка действий.

Распространяется это свойство на любое число слагаемых. Если в выражении содержится только знак “+”, то переставлять и группировать слагаемые можно так, как удобно для вычислений.

(78+97)+3=78+ (97+3)= 78+ 100=178

(27+94 )+ (6 +73 )= (27+73) +(94 +6 )= 200

Учащиеся проговаривают в парах буквенные выражения друг другу. А чтобы вам лучше запомнить, как объяснять сочетательное свойство сложения, давайте заглянем в учебник страница 41.

Пользуясь свойствами сложения выполните задания учебника №2.

Первичное закрепление

Цель<: вербальное фиксирование сочетательного свойства сложения, запись выражений по новому правилу.

Вот теперь мы на практике убедимся в применении свойств сложения.

Учитель: Прочитайте задание №2 ,внимательно изучите программу действий.

Уч-ся: Максим, Саша, Дима и Никита.

. Прочитаем выражение.

. Сравним, в каком выражении проще находить значении.

. Вычислим значение выражения.

Учитель: Сравните левую и правую части выражений, что вы заметили?

Уч-ся: В выражениях изменен порядок слагаемых и порядок действий. Легко заметить, что слагаемые в правом столбике сгруппированы так, что значение выражений без труда вычисляется устно.

Учитель: Назовите друг другу правило по которому вы вычисляли.

Проходит работа в парах.

Вывод: Значение суммы не зависит от порядка слагаемых и порядка действий.

Повторение

Цель: включение знания в систему

задание: стр. 42 № 6 (3) на индивидуальных карточках.

Учитель:

Назовите многоугольники.

Найдите прямые углы в многоугольниках

У каких четырехугольниках все углы прямые? (TEFK)

На индивидуальных карточках выполните задание по нахождению периметра.

Уч-ся выполняют измерение сторон, составляют выражение по нахождению суммы 8+6+12+14=(8+12)=(6+14)

Учитель: Какие свойства сложения вы применили, что позволило вам быстро выполнить сложение?

Следующий урок был посвящен сочетательному свойству сложения.

Тема. «Сочетательное свойство сложения. Скобки».

Цели. Познакомить с сочетательным свойством сложения, с новым математическим знаком - скобками; совершенствовать устные и письменные вычислительные навыки табличного сложения и вычитания однозначных чисел в пределах 20 с переходом через разряд.

Актуализация знаний

У. Пойдем по лесной тропинке так, чтобы не беспокоить обитателей леса, - только со стороны будем наблюдать за ними.

Игра «Распутай клубок»

На доске записаны равенства, в которых часть чисел закрыта геометрическими фигурами:

По команде учителя дети записывают на индивидуальных экранах пропущенное число и дают объяснение своим действиям.

У. Откуда начнем распутывать клубок? Почему?

Дети. Начнем с выражения 15 - 8, так как известны два числа.

У. Внимание! Напишите на своих экранах значение разности чисел 15 и 8.

Дети написали 7 и одновременно все подняли свои экраны.

А теперь на какое равенство обратим внимание?

Д. На первое. Там кроме числа 12 изображен такой же треугольник, а значит, должно быть число 7.

У. Верно. Уменьшите 12 на 7.

На экранах дети написали число 5.

Как нам дальше распутать клубок?

Д. Посмотрим на четвертое равенство, так как там кроме числа 9 изображен такой же квадрат, что и в первом равенстве. Значит, на нем должно быть написано число 5.

У. Верно. Найдите значение суммы чисел 5 и 9.

На экранах дети написали число 14.

Д. Возьмем второе равенство, так как там кроме числа 8 есть такой же круг, что и в четвертом равенстве. Значит, на нем должно быть написано число 14.

У. Верно. Найдите значение разности 14 и 8.

На экранах дети написали число 6.

Д. Возьмем пятое равенство, так как там кроме числа 40 есть такой же прямоугольник, что и во втором равенстве. Значит, на нем должно быть написано число 6.

У. Верно. Найдите значение разности чисел 40 и 6.

На экранах дети написали число 34.. Знакомство с новым материалом

У. Лесная тропинка привела нас на полянку. Осмотримся. Около деревьев - ковер из разноцветных листьев. У каждого из вас на столе кленовые листочки с заданием. Двое учеников будут работать по заданиям с обратной стороны доски.

Догадайтесь, по какому правилу записаны равенства слева и справа, и вставьте числа в «окошки».

Учащиеся выполняют задание самостоятельно.

9 + 1 + 6 = 10 + 6

+ 3 + 2 = 10 + 2

+ 2 + 5 = ... + ...

+ 1 + 7 = ... + ...

+ 1 + 6 = 9 + 7

+ 3 + 2 = 7 + 5

+ 2 + 5 = ... + ...

+ 1 + 7 = ... + ...

- Посмотрим, как выполнили задание ребята, работавшие у доски. Что вы можете сказать о содержании заданий?

Д. У всех задания одинаковые.

У. А как они их выполнили?

Д. По-разному.

У. Почему так получилось?

Д. Не все разгадали правило: один знает больше, а другой меньше. Такое задание мы выполняем в первый раз.. Формулировка темы урока

У. Проанализируем равенства и выясним, кто выполнил задание правильно. Сравним левые части равенств первого и второго столбиков.

Д. Они одинаковые. Складываем три числа.

У. Сравним правые части равенств первого и второго столбиков.

Д. В первом столбике сначала сложили первые два числа, а потом прибавили третье.

Во втором столбике сначала сложили второе и третье числа и результат прибавили к первому числу.

У. Какие числа вставим в «окошки»?

Д. 8 + 2 + 5 = 10 + 5

+ 1 + 7 = 10 + 7

+ 2 + 5 = 8 + 7

+ 1 + 7 = 9 + 8

У. Кто догадался и сможет сформулировать тему урока?

Д. Будем складывать три числа разными способами.

У. Мы познакомимся еще с одним свойством сложения. Повторите, как складывали три числа?

Д. В первом столбике сначала сложили первые два числа, а потом прибавили третье.

Во втором столбике сначала сложили второе и третье числа, и результат прибавили к первому числу.

У. Как все это можно записать? Наверное, должен быть какой-то знак?

Д. Это скобки.

У. Что показывают скобки?

Д. Какое действие нужно выполнять первым.

На доске открывается запись.

(9 + 1) + 6 =

(7 + 3) + 2 =

(8 + 2) + 5 =

(9 + 1) + 7 =

+ (1 + 6)

+ (3 + 2)

+ (2 + 5)

+ (1 + 7)

У. Что вы еще заметили?

Д. Три числа складывали по-разному, а значение суммы одинаково. Оно не зависит от порядка выполнения действий.

У. Проверим, правы ли вы. Откройте учебник на с. 47, прочитайте правило. Вы открыли сейчас для себя сочетательное свойство сложения.. Первичное закрепление материала

У. Прочитайте задание

Д. «Покажи с помощью скобок, какие два слагаемых ты заменишь значением суммы, и найди значение каждого выражения».

У. Объясните, почему в одних выражениях находили сначала сумму первого и второго чисел и прибавляли третье, а в других к первому числу прибавляли сумму второго и третьего чисел. Поднимите руку те, кто хотел это задание выполнить самостоятельно. Вы будете работать по вариантам. Первый столбик - для учеников 1-го варианта, второй столбик - для 2-го варианта, а третий столбик - дополнительный для тех, кто быстро выполнит задание.

Двое учащихся пишут на доске. Дети выполняют задание. Проверяются все примеры.

Прочитайте выражение, значение которого - «круглое число».

Д. 30 + (4 + 6) = 40

+ (24 + 6) = 90

+ (37 + 3) = 80

У. Прочитайте выражение, значение которого на 7 меньше, чем наибольшее двузначное число.

Д. (20 + 70) + 2 = 92

У. Прочитайте выражение, значение которого - число, состоящее из одинакового количества десятков и единиц.

Д. (30 + 40) + 7 = 77

У. Прочитайте выражение, значение которого - число, идущее перед 50.

Д. 40 + (6 + 3) = 49

У. Самые внимательные, назовут выражения, значения которых мы еще не проверили. Объясните, почему в одних выражениях мы находили сначала сумму первого и второго чисел и прибавляли третье, а в других к первому числу прибавляли сумму второго и третьего чисел.

Д. Нам удобнее складывать числа, при сложении которых получается «круглое» число, - так быстрее производить вычисления.

У. Чтобы запомнить новое свойство сложения и быстро его вспомнить, если забыли, необходимо выбрать схему, состоящую из букв или знаков. Эти схемы находятся на стенах класса. Посмотрите на них, выберите одну и объясните свой выбор.

(* + *) + * = * + (* + *)

(а + b) + с = а + (b + с)

(0 + 0) + 0 = 0 + (0 + 0)

Д. Все схемы подходят. В математике используют латинские буквы, поэтому выберем схему (а + в) + с = а + (в + с).

Самостоятельная работа в группах

Учащиеся распределяются на группы, получают задания на полосках разного цвета. Необходимо найти и записать значения данных выражений, используя сочетательное свойство сложения, затем прикрепить полоску с выражением на магнитной доске под соответствующей формулой:

(а + b) + с

а + (b + с)

Задания для групп могут выглядеть аналогично данным:

+ 3 + 6 =

+ 2 + 8 =

+ 9 + 1 =

+ 4 + 2 =     20 + 3 + 7 =

+ 40 + 8 =

+ 36 + 4 =

+ 30 + 3 =

У. Все молодцы! Идем по лесной тропинке дальше. Отгадайте загадку о лесном зверьке:

Не птица, а с дерева на дерево летает.

Д. Это белка.

У. Верно. Помогите белке разместить запасы на зиму по трем дуплам. Работаем в тетрадях на печатной основе «Учимся решать комбинаторные задачи». Выполняем задание 20 на с. 20 самостоятельно.

Проверка:

Прочитайте задание 21 на с. 20.

У. Выполните это задание самостоятельно.

Дети группируют буквы.

Что у вас получилось?

Д. Получилось шесть вариантов.

У. Обведите варианты, где получились слова, имеющие смысл.

Д. Это сон и нос.

У. Назовите животных, которые на зиму ложатся в спячку.

Д. Медведь, еж, уж.

У. Какую зимующую птицу называют «лесным доктором»?

Д. Дятла. Своим клювом он достает насекомых из-под коры деревьев, тем самым спасая их от вредителей.. Итог урока

У. Наше путешествие по осеннему лесу подошло к концу. Какое открытие вы сделали сегодня на уроке?

Д. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел. Это сочетательное свойство сложения.

Работали мы и над правилом вычитания суммы из числа.

Цели:

ввести правило вычитания суммы из числа, использовать его для рационализации вычислений;

отрабатывать вычислительные навыки;

развивать умение решать задачи, составлять выражения к задачам;

способствовать развитию мыслительных операций, математических способностей, речи учащихся.

Актуализация знаний

. Числовые ряды

Живёт на свете маленький зайчик. Больше всего он любит прятаться в разные математические задания.

Какое число спряталось за зайчонком?

Какая прослеживается закономерность в каждом ряду?

… 56 54 52 (58)

… 130 160 190 220 (100)

22 32 … 52 (42)

. Составление равенств

Я предлагаю вам игру.

И три числа я вам даю.

А вы на числа посмотрите,

Что с ними делать предложите.

(58, 42, 100)

Чем являются числа 42 и 58? Число 100?

Как найти целое?

Как найти часть?

Как называются числа при сложении?

Как называются числа при вычитании?

. Нахождение значений выражений.

Зайчонок приготовил для вас следующее задание. Прочитайте и найдите значение выражения. (Один ученик выбирает выражение, читает его, ученики решают, ответ показывают с помощью веера цифр).

+ (57 +18) = 98

+ (12 + 65) = 82

(28 + 36) + 4 = 68

Какие свойства сложения позволили упростить вычисления? (Переместительное, сочетательное свойства сложения).

- (24 + 4) = 50

(96 - 46) + 13 = 63

(54 - 34) - 6 = 14

- (7 + 15) = 65

Постановка учебной задачи

Как удобнее вычесть из 87 сумму чисел 7 и 15?

Из 87 удобно сначала вычесть 7, получится 80, а затем вычесть 15, получится 65:

- 7 - 15 = 65

Ответы получились одинаковые. Значит выражения 87 - (7 + 15) и 87 - 7 - 15 тоже должны быть равны, но это нужно доказать.

Заменим числовые выражения буквенными.

а - (в + с) а - в - с

Выясним, равны ли эти выражения.

. «Открытие» нового знания

Сравним выражения, используя схемы.

а - (в + с)

Что нужно выполнить первым действием? (Найти сумму в и с).

Чему равно значение первого выражения? (d)

Чему равно значение второго выражения? (d)

Какой можно сделать вывод?

а - (в + с) = а - в - с

Как можно вычесть сумму из числа?

Чтобы вычесть сумму из числа, можно сначала вычесть одно слагаемое, а потом другое.

Составление выражений и нахождение их значений.

а) 914 - 58 - 42 = 814

б) 914 - (58 + 42) = 814

Как удобнее считать? (Удобнее из числа вычесть сумму).

. Решение задачи.

№3, с. 44

Отгадайте, о чём идёт речь?

Сперва назови ты за городом дом,

В котором лишь летом семьёю живём.

Две буквы к названью приставь заодно,

Получится то, что решать суждено.

Прочитайте задачу.

Что известно в задаче?

Что надо найти?

Заполним схему. (Схема в учебнике и на доске).

Что надо найти часть или целое?

Как найти часть?

Составим выражение.

- 15 - 13 = 17 (м.)

- (15 + 13) = 17 (м.)

Какой из способов удобнее?

Нахождение значений выражений удобным способом с комментированием.

Приведём образцы некоторых упражнений, которые мы использовали в ходе эксперимента, а так же рассмотрим приёмы работы с упражнениями.

ситуация:

Цель: помочь детям усвоить порядок выполнения операций и построить полную развёрнутую ориентировочную основу. Происходит введение вычислительного приёма. Для лучшего усвоения вычислительного приёма мы использовали наглядное пособие в виде полотна бумаги с прорезанными кармашками, куда вставляются карточки с числами. Эта ситуация рассчитана на три урока. Приведём фрагменты уроков.

Фрагмент урока №1.

Учитель. Вот два числа - 25 и 31. Назовите разрядные единицы.

Дети. В числе 25 - два десятка и пять единиц, в числе 31 - три десятка и одна единица.

Учитель. Ребята, если нам нужно сложить эти два числа, как мы будем складывать?

Дети. Мы сначала сложим десятки, а потом единицы.

Учитель. Сегодня я покажу вам, как удобнее складывать два двузначных числа. Посмотрите на доску. В эти кармашки наборного полотна я вставлю числа.

Посмотрите, как расположены разрядные единицы?

Дети. Единицы располагаются под единицами, десятки - под десятками.

Учитель. Теперь складываем единицы с единицами, десятки с десятками. Какой ответ?

Дети. Ответ - 56.

При введении ориентировочной основы ставится проблемная ситуация, как при помощи новых для детей приёмов сложения чисел решать примеры, где необходим переход одних разрядных единиц в другие разрядные единицы.

Фрагмент урока №2.

Учитель. Мы научились решать примеры в столбик. Давайте проверим чему мы научились.

На доске примеры: +12 + 43 +15 +18

16 52 67

( Дети решают.)

Учитель. Я вижу, вам трудно решить последний пример. Почему?

Дети. Единиц получается больше десяти.

Учитель. Значит, здесь можно выделить новую единицу - десяток. А куда эту единицу нужно записать?

Дети. Наверное, в соседний разряд, в десятки?

Учитель. Давайте попробуем рассуждать вместе. Какое число 8 или 7 удобнее дополнить до десятка?

Дети. 8.

Учитель. Где же взять эти единицы?

Дети. У числа 7.

Учитель. А сколько нужно взять?

Дети. 2 единицы.

Учитель. Сколько единиц останется от числа 7?

Дети. 5 единиц.

Учитель. Давайте покажем, что мы сделали с числами.

Появляется запись:

+18

85

На этом уроке делается запись на доске, а ученики смотрели и слушали, затем делали вывод: «Чтобы сложить два числа, нужно одно число разложить на удобные слагаемые так, чтобы в сумме с другим получился десяток».

На следующем уроке дети работали самостоятельно на наборном полотне, контролировали, оценивали работу товарищей.

Фрагмент урока №3.

Дети работали с наборным полотном.

+27

16

43

Учитель. Ребята, вы хорошо научились работать с карточками, а теперь давайте запишем этот пример в тетради: 27+16.

Пишем каждую цифру в отдельной клеточке, не забывайте о том, что разрядные единицы пишутся под разрядными единицами. Какое число мы должны разложить?

Дети. Число 6 раскладываем на 3 и 3. Складываем 7 и 3, получается десяток.

Учитель. Покажем стрелочками наши действия:

+27

16

А теперь оставшиеся единицы подпишем под единицами, посчитаем десятки.

Фрагмент урока №4.

Детям предлагается решить примеры, записанные на доске:

+77 +36                         +29

14 35                          37

71                               66

Учитель. Ребята, посмотрите на эти примеры внимательно. Давайте составим общую схему этих примеров с помощью окошек.

Дети выделяют общее и составляют схему-опору:

+

---------------

Идёт работа со схемой. Решаются примеры, в которых нужно заполнить все окошки.

+ +

--------------- --------------

На этом процессе введения ориентировочной основы заканчивается.

ситуация:

Цель: научить детей самостоятельно выполнять все операции, составляющие приём. Здесь была использована такая форма работы, как работа в паре.

) Дети получили задание. Выполнив его, они проверяли выполнение этого задания друг у друга.

) Дети сами давали друг другу задание решить примеры и проверяли их.

) Каждый ученик выступал в роли учителя, объясняя приём другому ученику.

На уроках использовали и разнообразные задания логического характера:

1.       Разгадай правило, по которому составлены выражения, и запиши верные равенства

70 - 50 90 - 60 80 - 60

- 20 90 - 30 -

+ 20 60 + 30 +

2. Вставь пропущенные числа:

77, 78, 79, , 81, , .

, 47, 57, , , 87, .

, 84, 74, , , , .

, 87, 85, , , 79.

. Разгадай правило, по которому составлен первый столбик выражений, и запиши верные равенства:

93 - 3          54-2           89-7            78-5

93 - 30

- 3

- 30

. Составь с числами 10 7 19 17 16 6 9 верные числовые равенства

. Можно ли утверждать, что значения выражений в каждой паре одинаковы?

+ 8    84 + 6        49 + 1; 68 + 2     86 + 4        41 + 9

. Сравни выражения и поставь знак >, <, =, чтобы неравенства были верными.

- 3…38 - 2                     90 - 50…43 - 2

- 3…25 + 30                  74 + 20…98 - 3

. 30 см - 3 см…2 дм 6см

см + 6 см…2дм

дм 6см… 3дм

. У Коли 12 марок, а у Саши на 3 марки больше. Обозначь отрезками марки Коли и Саши. Построй отрезок, который будет показывать, сколько марок у Коли и Саши вместе.

На одной полке 35 книг, на другой - 15 книг. Построй отрезки и покажи, на сколько больше книг на первой полке.

Покажем еще приемы работы над свойствами арифметических действий.

Тема: Сложение и вычитание без перехода через десяток

На этих уроках мы продолжали знакомить детей с устными и письменными приемами сложения и вычитания двузначных чисел без перехода через десяток: 60 + 24, 56 - 20, 56 - 2, 23 + 15, 69 - 24.

Важно, чтобы учащиеся хорошо усвоили, что при выполнении сложения и вычитания в столбик десятки пишут под десятками, а единицы - под единицами. С этой целью мы использовали задания на моделирование рассматриваемых алгоритмов действий с помощью разнообразного счетного материала, в которых требуется объяснить по рисунку, как выполнили действия.

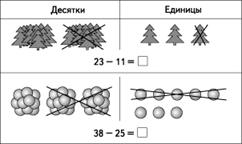
Такие задания способствуют лучшему усвоению изучаемых приемов вычислений, овладению умениями обосновывать действия и интерпретировать их с помощью наглядного материала.

На столах у детей пучки палочек (по 10 палочек) и палочки россыпью.
 - Отложим на счетных палочках число 35. (Дети откладывают 3 десятка и 5 единиц.)

А сейчас прибавьте к 35 число 2. (Дети прибавляют 2 палочки.)

Куда вы положили 2 палочки - к пучку или палочкам россыпью? (К палочкам россыпью.)

Пучки палочек - это ...? (Десятки.)

Палочки россыпью - это ...? (Единицы.)

Число 2 - это ...? (Единицы.)

Что вы сделали, если говорить на языке терминов? (К единицам прибавили единицы.)

Сколько получилось всего палочек? (37.)

Запишем решение этого примера на доске:

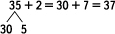
Какой можно сделать вывод? (Единицы складывают с единицами.)

Откройте учебник на с. 24 и объясните по рисунку, как выполнено сложение. Почему ответы получились одинаковыми? (Дети объясняют.)

Письменные способы решения примеров 35 + 2 и 2 + 35 учитель показывает на доске, объясняет, как записывать числа при сложении столбиком. Учащиеся записывают примеры в тетрадях

Фрагмент 5

Тема: Сложение и вычитание с переходом через десяток

У меня в руках красивые яблоки. (Учитель показывает картинки, на которых изображены яблоки. На обороте каждой картинки записан пример.) Мы можем подарить их белочке, если правильно вычислим ответы. (Учитель поочередно переворачивает каждое яблоко, а учащиеся решают примеры и записывают их в строчку в тетрадях.)

Прочитайте ответы, которые у вас получились. (23, 65, 32, 79, 80, 34.) Какое число лишнее? Почему? (80 - круглое число, а все остальные числа не круглые.)

Запишите эти числа в порядке убывания. (Дети записывают на следующей строчке ряд чисел: 80, 79, 65, 34, 32, 23.)

У меня есть еще одно яблоко. (Учитель показывает картинку.)

Чем оно отличается от других яблок? (Оно отличается цветом и формой. Это яблоко красное и круглое, а остальные яблоки желтые и продолговатые.)

Прочитайте пример, записанный на красном яблоке. (Учитель переворачивает картинку, и учащиеся читают пример.)

Красный цвет обозначает «Внимание!». Как вы думаете, почему этот пример выделен красным цветом? (Мы такие еще не решали.)

А чем интересен этот пример? (Если сложить отдельные единицы, то получится 10.)

Сколько всего десятков в числе 32? (3 десятка.) Сколько отдельных единиц в этом числе? (2 единицы.)

С помощью палочек отложите на парте число 32. (Дети откладывают 3 десятка и 2 единицы.)

А сейчас прибавьте к 32 число 8. (Дети прибавляют 8 палочек.)

Куда вы положили 8 палочек - к пучкам по 10 палочек или к палочкам россыпью? (К палочкам россыпью.)

Что вы сделали, если говорить на языке терминов? (К единицам прибавили единицы.)

Сколько получилось палочек россыпью? (10.)

Свяжем 10 палочек в пучок. Получим еще один десяток палочек.

Сколько всего десятков палочек у нас получилось? (4 десятка палочек.) Сколько всего палочек? (40.)

Запишем решение этого примера на доске:

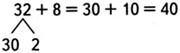
Какой можно сделать вывод? (Если сумма единиц равна 10, то один десяток прибавляем к десяткам.)

Откройте учебник на с. 38 и объясните по рисунку, как выполнено сложение. (Дети объясняют.)

Письменные способы решения примеров 26 + 4 и 3 + 47 учитель показывает на доске, объясняет, как записывать числа при сложении столбиком. Учащиеся записывают примеры в тетрадях.

Также мы применяли и игры.

Игра «Математическое лото»

Учитель прикрепляет на доску рисунок бочонка с цифрой 1. Дети садятся парами.

У. Итак, пришло время начинать игру. Удачи всем игрокам! Какое задание скрывается за первым бочонком?

Д. Решение круговых примеров.

Каждая пара достает из конвертов карточки с заданиями и решает круговые примеры.

56 + 3

- 20

+ 3

+ 8

- 2

+ 30

+ 5

- 50

+ 7

- 23

+ 9

+ 30

У. Молодцы! Подумайте и скажите, по какому признаку можно разделить данные числовые выражения на две группы?

Д. В один столбик все суммы, а в другой все разности.

В один столбик выражения, в которых все компоненты - двузначные числа, а в другой остальные.

У. Вы блестяще справились с этим заданием. Надеюсь, вы сможете так же удачно справиться со всеми последующими и выиграть главный приз нашей игры! Выполняя каждое последующее задание, вам необходимо будет фиксировать полученные результаты в игровом билете.

Учитель прикрепляет на доску бочонок с цифрой 2.

Второй бочонок и следующее задание. Вам необходимо взять такую карточку с примерами, на которой цвет круга совпадает с цветом квадратов на вашем игровом билете.

-я группа (желтые круги)

20 -13 =            52 + 2 =

10    3               50             2

20 - 2 =             50 + 22 =

10    10              20             2

43 + 2 =            82 + 6 =

40    3               80             2

2-я группа (зеленые круги)

- 83 = _____

- 22 = _____

+ 7 = _____

+ 32 = _____

+ 30 = _____

+ 8 = _____

У учащихся во всех группах после решения примеров получаются одинаковые ответы: 7, 18, 45, 54, 72, 88.

У. Надеюсь, все успели отметить (зачеркнуть или подчеркнуть) полученные результаты в игровом билете. Мы продолжаем игру и открываем третий бочонок.

Учитель прикрепляет на доску бочонок с цифрой 3.

Что необходимо сделать, чтобы узнать следующие числа, которые нужно будет зачеркнуть в игровом билете?

Д. Сравнить числа или выражения.

У. Это задание мы будем выполнять в тетради.

Два ученика выполняют задание у доски под диктовку учителя.

Сравните два выражения. Первое - сумма чисел 18 и 6. Второе - разность чисел 70 и 34.

Следующая пара выражений: первое - разность 100 и 17; второе - сумма 40 и 43.

На доске:

+ 6 ... 70 - 34

- 17 ... 40 + 43

Чему равны значения выражений?

Д. 24, 36, 83.

У. Зачеркните в билете числа, полученные в ходе вычислений. Продолжаем. Совсем немного осталось времени до того момента, когда будут известны обладатели главного приза игры. Последний бочонок в игре!

Учитель прикрепляет на доску бочонок с цифрой 4.

За четвертым бочонком скрывается задача. Ее текст вы найдете на обратной стороне билета.

Задача. В игровом мешке было 90 бочонков. В первом туре из мешка достали 7 бочонков, во втором - 20. Сколько бочонков осталось в игровом мешке? (У доски рассматриваются варианты решений задачи).

На доске:

Было - 90 б.

Достали - 7 б. и 20 б.

Ост. - ? б.способ

) 7 + 20 = 27 (б.)

) 90 - 27 = 63 (б.)способ

) 90 - 7 = 83 (б.)

) 83 - 20 = 63 (б.)

Полученный ответ - это последнее число, необходимое нам для того, чтобы определить ключевое слово, - результат нашей игры.

Образец карточки после выполнения детьми заданий.

Если вы правильно выполнили все задания, то без труда сможете прочитать слово, пользуясь ключом.

Учитель прикрепляет на доску карточку-ключ.

Д. Победитель.

У. Игра закончена. Прошу поднять руку тех, кто смог прочитать слово. Главный приз - пять баллов - получили обладатели __ билетов. Призовой фонд не разыгран в полном объеме, поэтому переносится на следующий тираж.

Конспекты уроков в приложении 4.

Выводы по 2 главе

Мы организовали исследование на базе 2 класса МОУ Стеженская СОШ Алексеевского района Волгоградской области.

В исследовании приняло участие 7 учащихся.

В начале исследования мы провели контрольную работу с целью выяснить уровень сформированности вычислительных навыков.

Определив уровень сформированности вычислительных навыков, мы приступили к эксперименту. Мы подобрали ряд методических приемов, направленных на усвоение законов и свойств арифметических действий в концентре сотни, который применили в экспериментальном классе.

Затем мы повторно провели контрольную работу. Сравнив результат с результатом, полученным перед экспериментом, мы пришли к выводу, что уровень вычислительных навыков повысился у учащихся экспериментального класса.

Таким образом, мы использовали при изучении законов и свойств арифметических действий дидактический материал, упражнения развивающего характера, тем самым повышали уровень сформированности вычислительных навыков младших школьников.

Заключение

В ходе решения первой задачи мы рассмотрели проблемы формирования вычислительных навыков в современных условиях и определили, что особое внимание в начальной школе уделяется изучению основных свойств арифметических действий, а именно, переместительного, сочетательного и распределительного (относительно сложения и вычитания).

Вычислительное умение - это развернутое осуществление действия, в котором каждая операция осознается и контролируется. Вычислительное умение предполагает усвоение вычислительного приема. Любой вычислительный прием можно представить в виде последовательности операций, выполнение каждой из которых связано с определенным математическим понятием или свойством.

Умение осознанно контролировать выполняемые операции, позволяет формировать вычислительный навык более высокого уровня, чем без наличия этого умения. Это значит, что все ранее раскрытые нами качественные характеристики, проявляются при формировании вычислительного навыка на более высоком уровне. Как видим, умение контролировать себя в процессе формирования вычислительного навыка требует от ученика полноценного, осознанного, обобщённого и самостоятельного владения всеми операциями, определяющими процесс выполнения вычислительного приёма.

Опираясь на конкретный смысл арифметических действий, их свойства, связи и зависимости между результатами и компонентами действий, а также десятичный состав чисел, раскрываются приемы устных и письменных вычислений. Такой подход к изучению приемов вычислений обеспечивает, с одной стороны, формирование осознанных умений и навыков, т.к. учащиеся смогут обосновать любой вычислительный прием, а с другой стороны, при такой системе лучше усваиваются свойства действий, их законы и т.д.

Затем проанализировали методику изучения законов и свойств арифметических действий.

Свойства арифметических действий (переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения) не являются специальным предметом изучения в начальной школе, а рассматриваются в связи с формированием устных приёмов вычислений. Это означает, что в процессе обучения на конкретных простых числовых примерах рассматриваются различные способы прибавления числа к сумме, суммы к числу; вычитания числа из суммы, суммы из числа; умножения суммы на число и др. с целью формирования умения осознанно выбирать те способы, которые позволяют рационально осуществлять процесс вычислений.

При решении третьей задачи мы отобрали содержание и методические приёмы, используемые при изучении законов и свойств арифметических действий.

Закрепление знания свойств, которые дети формулируют в виде правил (и называют правилами), происходит в результате их применения при выполнении специальных упражнений. Это нахождение значений данных выражений разными способами и наиболее удобным способом, преобразование выражений, решение задач различными способами и др.

Из курса математики известно, что для сложения целых неотрицательных чисел выполняются коммутативное и ассоциативное свойства. В начальном курсе математики учащиеся знакомятся с коммутативным свойством сложения, называя его «переместительное свойство сложения» или «перестановка слагаемых». Для его разъяснения могут быть использованы действия с предметными множествами, сравнение числовых равенств, в которых переставлены слагаемые, сравнение суммы длин одинаковых отрезков (полосок).

Исследования этих свойств опирается прежде всего на предметные действия ребенка, фиксирующиеся с помощью графических и знаковых моделей. В связи с этим рассматривается порядок действий и его изменение, определяемый только с опорой на графическую модель, а не на правила, предполагающие подразделение действий над числами на действия двух ступеней (действие первой ступени - сложение и вычитание, второй - умножение и деление).

В ходе решения четвертой задачи мы провели диагностику сформированности вычислительных навыков у 7 учащихся 2 класса МОУ Стеженская СОШ Алексеевского района Волгоградской области с помощью контрольной работы.

Наконец, при решении последней задачи мы показали практическую применимость рассматриваемых положений на школьных уроках математики в начальной школе, используя дидактические игры, упражнения развивающего характера, наглядность. Мы подобрали ряд методических приемов, направленных на усвоение законов и свойств арифметических действий в концентре сотни, который применили в экспериментальном классе.

В конце эксперимента мы повторно провели диагностику знаний учащихся, которая показала, что уровень вычислительных навыков у учащихся вырос.

Тем самым доказали выдвинутую гипотезу, что процесс изучения законов и свойств арифметических действий будет осуществляться более эффективно, если на уроках использовать дидактический материал, упражнения развивающего характера.

Список литературы

1.       Актуальные проблемы методики обучения математики в начальных классах». М.: Педагогика, 1977.

2.       Александрова Э. И. Методика обучения математике в начальной школе. 1 класс (Система Д.Б.Эльконина - В.В.Давыдова): Пособие для учителя четырехлетней начальной школы. М.: Вита - Пресс, 2002.

3.       Антоненко Т.Е. // Начальная школа / Приемы занимательности. - 2009, №5.

4.       Аргинская И.И. // Начальная школа / Особенности обучения младших школьников математике. Методические основы личностно ориентированной системы обучения, направленной на общее развитие школьника. - 2005, №18.

.        Аргинская И.И. // Начальная школа / Особенности обучения младших школьников математике. Особенности программы и учебных пособий по математике для начальной школы. - 2005, №19.

.        Аргинская И.И. // Начальная школа / Особенности обучения младших школьников математике. Методические особенности изучения чисел и действий с ними в системе Л.В. Занкова. - 2005, №21.

7.       Аргинская, И.И. Обучаем по системе Л.В. Занкова: 1-й год обучения: Кн. для учителя / И.И. Аргинская, Н.Я. Дмитриева, А.В. Полякова, З.И. Романовская. - М.: Просвещение, 1991.

8.       Аргинская, И.И. Обучаем по системе Л.В. Занкова: 2-й год обучения: Кн. для учителя / И.И. Аргинская, Н.Я. Дмитриева, А.В. Полякова, З.И. Романовская. - М.: Просвещение, 1993.

.        Аргинская, И.И. Обучаем по системе Л.В. Занкова: 3-й год обучения: Кн. для учителя / И.И. Аргинская, Н.Я. Дмитриева, А.В. Полякова, З.И. Романовская. - М.: Просвещение, 1994.

.        Аргинская, И.И. Математика: методическое пособие к учебнику 2-го класса четырёхлетней начальной школы // И.И.Аргинская.-М., Центр общего развития, 2000.

.        Аргинская, И.И. Математика: Учебник для 3 класса четырехлетней начальной школы / И.И.Аргинская, Е.А.Ивановская. - Самара, 2000.

12.     Аргинская, И.И. Математика. Методическое пособие к учебнику 1-го класса четырехлетней начальной школы / И.И,Аргинской. - М., ЦОР 1, 2003.

13.     Аргинская, И. И. Математика / И.И,Аргинская, Е.П.Бененсон, Л.С.Итина. - Самара: Учебная литература. 2002. - 196 с.

14.     Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах: Учебное пособие для учащихся школьного отделения пед. училищ. (спец. № 2001)/ Под ред. М.А. Бантовой -3-е изд. испр. - М: Просвещение, 1984.

15.     Бантова М.А. Система формирования вычислительных навыков // Начальная школа. - 1995. - № 11.

.        Грудёнов Я.Н. «Психолого-дидактические основы методики обучения математики» - М.: Педагогика, 1987.

17.     Гальперин, П.Я.. К вопросу о формировании начальных математических понятий. Сообщения I - V. , П.Я.Гальперин, Л.С.Георгиес // Доклады АПН РСФСР, 1960, № 1, 3, 4-6.

18.     Гонин, Е.Г. Теоретическая арифметика / Е.Г.Гогин. - М.: Учпедгиз, 1961. - 171 с.

.        Давыдов, В.В. Математика, 3 класс: Учебник для 4-летней начальной школы / В.В.Давыдов. - М., 1998.

20.     Давыдов, В.В. Проблемы развивающего обучения / В.В.Давыдов. И., 1986. - 184 с.

21.     Давыдов, В. В. Логико - психологические проблемы начальной математики как учебного предмета / В.В.Давыдов. - М.: Просвещение, 1966. - 206 с.

22.     Демидова, Т.Е. Содержательная линия «Занимательные и нестандартные задачи» в учебниках «Моя математика» / Т.Е.Демидова, С.А.Козлова, А.Г.Рубин //Начальная школа плюс До и После. - 2005. - № 9.- с.15.

23.     Доронина, И.М. Использование методики УДЕ на уроках математики в III классе / И.М.Доронина // Начальная школа. - 1999. - № 11.

24.     Зайцев, В.В. Математика для младших школьников: Методическое пособие для учителей и родителей / В.В,Зайцев. - Владос, 2001. - 128 с.

25.     Зайцев, В.В. Развивающее обучение математике младших школьников в условиях вариативных методических системах: Учебное пособие / В.В,Зайцев, Е.П.Гладышев. - Волгоград: Перемена, 2001. - 109 с.Из опыта работы в трёхлетней начальной школе: Русский язык и математика. / Под ред. М.С. Васильевой, В.А. Кустарёвой, А.М. Пышкало - М.: Педагогика, 1973.

27.     Игнатьева Т.В. / Программы общеобразовательных учреждений. Начальные классы (1-4): Сборник программ / Т.В. Игнатьева, Л.А. Вохмянина, - М.: Просвещение, 2000.

28.     Истомина Н.Б. / Методика обучения математике в начальных классах: Учебное пособие для студентов сред. и высш. пед. учеб. заведений. - М.: Издательский центр "Академия", 2002. - 288с.

29.     Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах: Пособие для учителя - М.: Просвещение, 1985.

. Математика 1 класс: Поурочные планы (по учебнику Л.Г. Петерсон для четырехлетней начальной школы) / Авт. сост. Т.В. Бут. Волгоград, 2003.

31.     Микулина Г.Г. Роль предметных действий при изучении последовательности чисел. // Начальная школа. - 1997. - №9.

32.     Методика начального обучения математике.: Учебное пособие/ Под ред. Л.Н. Скаткина - М.: Просвещение, 1972.

33.     Методика начального обучения математике./ Под ред. А.А. Столяра, ВВ.А. Дрозда- Минск.: Высшейшая школа, 1988.

.        Моро М.И. и др. Математика во 2 классе: Пособие для учителя трехлетней начальной школы / М.И. Моро, М.А. Бантова, Г.В.Бельтюкова. - М.: Просвещение , 1989.

.        Моро М.И., Пышкало А.М. Методика обучения математике в 1-3 классах.: Пособие для учителя. - М.: Просвещение, 1975.

.        Моро М.И., Пышкало А.М. Методика обучения математике в 1-3 классах: Пособие для учителя - 2-е изд., перераб. и доп. - М.: Просвещение, 1978.

.        Основы методики начального обучения математике: Пособие для учителей./ Под ред. А.С. Пчелко - М.: Просвещение, 1965.

38.     Петерсон, Л.Г. Программа по математике для трехлетней и четырехлетней начальной школы/ Л.Г.Петерсон // Начальная школа. - 1996 - №11. - с.39.

39.   Петерсон, Л.Г. Математика. 1 класс. Методические рекомендации для учителей / Л.Г.Петерсон. - М., 2002. - 95 с.

40.     Петерсон, Л.Г. Математика. 2 класс. Методические рекомендации для учителей / Л.Г.Петерсон. - М., 2002. - 86 с.

41.     Программы образовательных учреждений. Начальные классы. В 2 ч. Ч. 1. Математика / М. И. Моро, Ю. М. Колягин, М. А. Бантова, Г. В. Бельтюкова и др. - М.: Просвещение, 2000.

42.     Программы общеобразовательных учреждений. Начальные классы (1-4). По системе Л.В.Занкова. М., 2000.

.        Программы для четырехлетней начальной школы: Образовательная система Д.Б.Эльконина - В.В.Давыдова. М.: Издатель Рассказов, 2000.

44.     Пчелко, А.С. Основы методики начального обучения математике. Пособие для учителей. Под ред. А.С. Пчелко. М.: Просвещение, 1965.

45.     Рудницкая, В.Н. Тематические и итоговые контрольные работы по математике в начальной школе: Методическое пособие / В,Н.Рудницкая. - М.: Дрофа, 1995.

.        Рудницкая, В.Н. Математика: 1 класс: Методика обучения / В.Н.Рудницкая, Т.В. Юдачева. - М.,: Вентана - Граф, 2003.

.        Рудницкая, В.Н. Математика: 3 класс: Методика обучения / В.Н.Рудницкая, Т.В. Юдачева. - М.,: Вентана - Граф, 2004.

48.   Стойлова, А.П., Пышкало А.М. Основы начального курса математики: Учебное пособие для учащихся пед. уч-щ по спец. № 2001 “Преподавание в начальных классах общеобр. шк.”. - М.: Просвещение, 2004. - 326 с.

49.     Тикунова, Л.И. Проверочные работы по русскому языку и математике: Пособие для учителя начальной школы/ Л.И. Тикунова., В.Г. Горецкий., В.П. Канакина и др. - М.: Просвещение, 1998.

50.     Уткина, И.Г. Изучение трудных тем по математике в 1-3 классах: Из опыта работы учителей г. Москвы./ сост. И.Г. Уткина - М.: Просвещение, 1992.

51.   Уткин, Н.Г. Сборник упражнений и проверочных работ по математике 1-3 классы: Пособие для учителя/ Н.Г.Уткина, А.М,Пышкало. -М.: Просвещение, 1980. - 132 с.

52.     Чилингирова, Л. Играя, учимся математике / Л.Чилингирова, Б.Спиридонова. - М.: Просвещение, 1993. - 285 с.

53.   Чуприкова, Н.И. Умственное развитие и обучение. Психологические основы развивающего обучения / Н.И.Чуприкова. - М.: Альматея, 1995. - 252 с.

54.     Шадрина И.В. Содержание подготовительной работы к изучению чисел. // Начальная школа. - 1991. - №8.

. Эрдниев П.М. Обучение математике в начальных классах: Книга для учителя - М.: Столетие, 1995.

56.     Эрдниев П.М. Преподавание математике в школе. (Из опыта обучения методом укрупнённых упражнений )- М.: Просвещение, 1978.

57.     Эрдниев П.М., Эрдниев Б.П. Теория и методика обучения математике в начальной школе. М.: Педагогика, 1988.

Приложение 1

Самостоятельная работа №1

Вычисли удобным способом

(14+67)+3=

+(99+452)=

+14+16+18=

(90+ 53)+(47+10)=

Реши:

Приложение 2

Самостоятельная работа №2

Задание 1.

Найди выражение, значение которого равно 70.

а) 95 - (35 + 10)

б) 95 - (35 - 10)

в) 95 - 35 - 10

Задание 2.

Выбери запись, соответствующую выражению 30 - (15 + 3)

а) К разности чисел 30 и 15 прибавить 3

б) Число 30 уменьшили на разность чисел 15 и 3

в) Из 30 вычесть сумму чисел 15 и 3

Задание 3.

В каком выражении верно указан порядок действий?

1 3 2 4

а) (a + b) - (c + d) + m

3 1 4

б) (a + b) - (c + d) + m

1 2 3 4

в) (a + b) - (c + d) + m

Задание 4.

Выбери верное равенство

а) a - (b + c) = a - b + c

б) a - (b + c) = a - b - c

в) a - (b + c) = a - c - b

Приложение 3

Конспект урока по математике

Тема: «Прибавление суммы к числу».

Цели: - познакомить детей с правилами прибавления суммы к числу;

решать примеры на сложение и вычитание;

развивать у учащихся умение выделить главное в изучаемом материале, воспитывать самостоятельность;

Тип урока: изучение нового материала.

ХОД УРОКА

1. Математический диктант ( повторение).

) 80 уменьшить на 20.

) 46 увеличить на 4.

) Уменьшаемое 80, вычитаемое 6. Найдите разность.

) Первое слагаемое 30, второе 18. Найдите сумму.

) Сумма равна 40, первое слагаемое 8. Найдите второе слагаемое.

) Первое слагаемое 50, второе 4. Найдите на сколько первое слагаемое больше второго.

Проверка. Учитель предлагает ответы, а дети проверяют свои результаты при помощи светофора.

Примечание. На уроке труда дети изготавливают два квадрата. Один красного цвета, а другой - зелёного. Склеивают обратной стороной и получается квадрат (светофор), у которого одна сторона красная, а другая зелёная. Если ученик согласен с ответом, он показывает зелёную сторону, если не согласен - показывает красную.

.Самостоятельная работа.

) Замените число суммой разрядных слагаемых: 27, 18, 63, 90.

) Представьте число в виде суммы двух слагаемых: 8, 7, 9.

Проверка. Фронтальный опрос.

. Объяснение нового материала.

) Подготовительная работа:

(30+3)+7 (40+6)+10

(80+10)-6 (80+10)-7

Прочитайте примеры, в которых к сумме надо прибавить число. Назовите разные способы прибавления числа к сумме. Назовите самый удобный способ. Прочитайте примеры, в которых из суммы надо вычесть число. Вычислите самым удобным способом.

) Работа с иллюстрацией учебника (стр.116).

Дети читают выражение: 4+(2+1). Выясняется, как изображено первое слагаемое (4 птички сидят на ветке), второе слагаемое - сумма (летят 2 птички и ещё одна птичка). Дети находят, сколько всего птичек летит (2+1=3), а всего птичек: 4 сидят да 3 летят, получается 7. Учитель предлагает посмотреть картинки второго ряда и сказать, как можно узнать по-другому, сколько всего птичек. Дети рассуждают: «Сидели 4 птички, к ним прилетели ещё 2 птички, и стало их 6, а потом ещё прилетела птичка, и стало их 7». Выясняется, что здесь к числу 4 прибавили сначала первое слагаемое, а к полученной сумме прибавили второе слагаемое. Так же рассматривается третий способ прибавления к числу суммы.

Вывод: сумму к числу можно прибавить тремя способами.

) Объяснить три способа решения примеров № 232 (фронтальная работа с классом).

) Решите удобным способом (решение комментируется):

+(8+4)

+(3+5)

+(6+8)

. Решение задач.

. Решение задачи № 234 под руководством учителя.

На доске краткая запись:

Н. - 40 шт.

Л. - ?

В. - 60 шт.

- Прочитайте задачу и повторите её, пользуясь краткой записью. Можно ли сразу ответить на вопрос задачи? Какое выполните действие? Почему? Запишите решение.

Учитель вносит изменение в краткую запись, а учащимся предлагает составить новую задачу:

Н. - 40 шт.

100 шт.

В. - ?

Скажите условие задачи. Какой вопрос? Чем является число 100? (Суммой.) Чем является число 40? (Слагаемым.) Если известны сумма и одно слагаемое, как найти второе? Составьте уравнение:

[ ]+x =[ ]

Один ученик составляет уравнение на доске. Решите задачу.

. Самостоятельная работа № 233.

Примечание. В помощь некоторым учащимся можно предложить карточку с краткой записью задачи, например:

) Прочитайте задачу. Повторите её, пользуясь краткой записью:

Было - 20 кар. и 10 кар.

Отдали - 6 кар.

Осталось - ?

) Запишите решение, заполнив пропуски:

([ ]+[ ])-[ ]=[ ]

Проверка индивидуальный опрос учащихся.

. Итог.

. Домашнее задание.