Уравнение плоскости и прямой. Метод Крамера и Гауса
Задание 1
Написать уравнение плоскости, проходящей через
точку 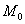 и
перпендикулярной прямой L:
и
перпендикулярной прямой L: 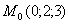 ,
, 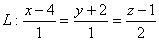 .
.
Решение
Сделаем рисунок.
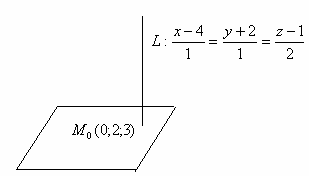
Рис. 1
Уравнение плоскости ищем в виде: 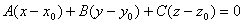 ,
где
,
где 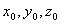 -
точка, через которую проходит плоскость, а
-
точка, через которую проходит плоскость, а 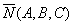 -
нормальный вектор плоскости. Направляющий вектор прямой
-
нормальный вектор плоскости. Направляющий вектор прямой 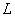 :
:
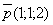 ,
он будет нормальным для искомой площади.
,
он будет нормальным для искомой площади.
Следовательно, уравнение плоскости примет вид:
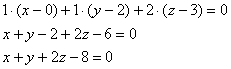
Ответ: 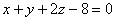 .
.
Задание 2
Написать уравнение прямой, проходящей через
точки 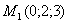 и
и
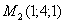 .
.
Решение
Уравнение прямой имеет вид: 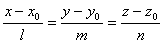 ,
где
,
где 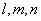 -
координаты любого ненулевого вектора
-
координаты любого ненулевого вектора 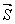 ,
параллельного прямой (направляющего вектора прямой), а
,
параллельного прямой (направляющего вектора прямой), а 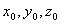 -
координаты любой точки, лежащей на прямой.
-
координаты любой точки, лежащей на прямой.
Возьмём в качестве точки, лежащей на прямой,
точку 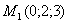 ,
а за направляющий вектор
,
а за направляющий вектор 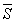 примем вектор
примем вектор 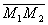 ,
лежащей на прямой.
,
лежащей на прямой.
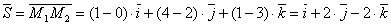 .
.
Тогда уравнение прямой, проходящей через точки А
и В, имеет вид:
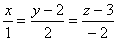 .
.
Ответ: 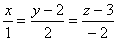 .
.
Задание 3
Для матрицы А, В и С. Найти, если возможно, 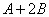 ,
,
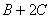 ,
,
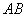 ,
,
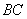 .
.
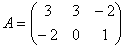 ,
, 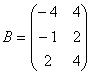 ,
,
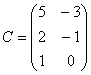 .
.
Решение
Сумма матриц определена только для матриц,
имеющих равное число строк и столбцов, следовательно, А+2В - не определена.
Вычислим:
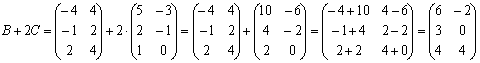 .
.
Произведение матриц определено только, если в
первом сомножителе столько столбцов, сколько во втором строк. Следовательно,
произведение АВ - определено, а ВС - нет.
Вычислим:
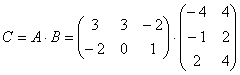 =[элемент матрицы
произведения, стоящий в
=[элемент матрицы
произведения, стоящий в 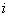 -ой строке и
-ой строке и 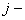 ом
столбце равен
ом
столбце равен 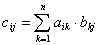 ]=
]=
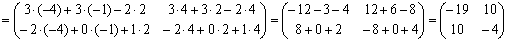 .
.
Задание 4
Решить систему линейных алгебраических уравнений
по формулам Крамера.
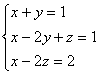
Решение
Составим и вычислим главный определитель
системы, т.е. определитель, составленный из коэффициентов при неизвестных:
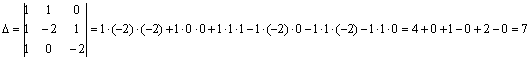
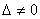 , следовательно,
система уравнений имеет единственное решение, которое можно найти по формулам:
, следовательно,
система уравнений имеет единственное решение, которое можно найти по формулам:
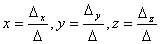 , где
, где 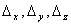 получаются,
если в определителе
получаются,
если в определителе  заменить столбец
коэффициентов при соответствующем неизвестном на столбец свободных членов.
заменить столбец
коэффициентов при соответствующем неизвестном на столбец свободных членов.
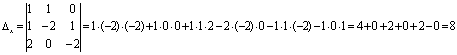
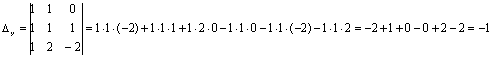
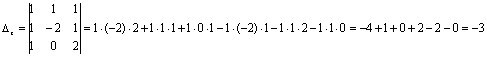
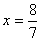 ,
, 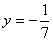 ,
,
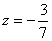 .
.
Проверка.
Подставим 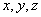 в
уравнения системы.
в
уравнения системы.
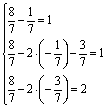
Ответ: 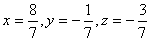 .
.
Задание 5
Исследовать и решить систему линейных алгебраических
уравнений методом Гаусса.
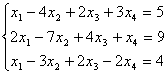
Решение
Запишем расширенную матрицу системы
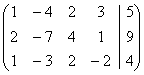
Преобразуем матрицу к треугольному виду, для
этого строку 1 умножим на (-2) и сложим со второй строкой, результат запишем во
вторую строку. Умножим строку 1 на (-1) и сложим с третьей строкой, результат
запишем в третью строку.

Третью строку убираем
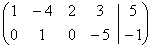
Следовательно, ранг матрицы системы равен рангу
расширенной матрицы системы и равен двум. Значит, базисных переменных две и
свободных две. Система имеет бесконечное множество решений. Найдём их.
Из строки 2 получившейся матрицы найдём 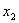 :
:
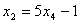 .
.
Из строки 1 найдём 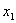 :
:
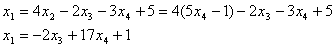
Ответ:
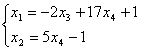 ,
, 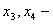 свободные
переменные.
свободные
переменные.
Задание 6
Изобразите на комплексной плоскости точки,
соответствующие числам 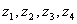 :
:
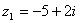 ,
, 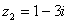 ,
,
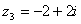 ,
,
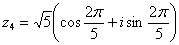 .
.
Решение
Для изображения точек на плоскости выделим
необходимые значения, которые соответствуют комплексной плоскости.
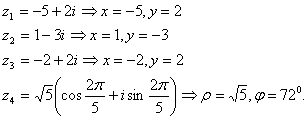
Покажем это на комплексной плоскости.
Рис. 2
Задание 7
Найдите в алгебраической форме 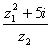 .
.
Решение
Согласно условия: 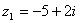 и
и
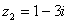 .
.
Найдём 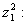
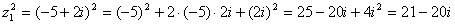 .
.
Найдём 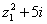 :
:
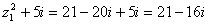 .
.
Найдём 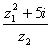 :
:
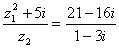 , умножим числитель
и знаменатель на сопряжённый знаменателю множитель
, умножим числитель
и знаменатель на сопряжённый знаменателю множитель 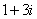 ,
тогда
,
тогда
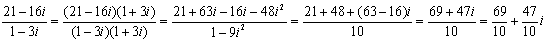 .
.
Ответ: 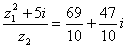 .
.
Задание 8
Переведите число 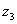 в
тригонометрическую форму и найдите
в
тригонометрическую форму и найдите 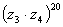 .
Ответ дать в тригонометрической и показательной форме.
.
Ответ дать в тригонометрической и показательной форме.
Решение
Согласно условия: 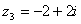 и
и
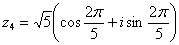 .
.
Запишем 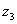 в
тригонометрической форме, применив формулу:
в
тригонометрической форме, применив формулу: 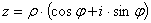 .
Каждое комплексное число определяется модулем и аргументом:
.
Каждое комплексное число определяется модулем и аргументом:
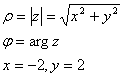
Тогда, 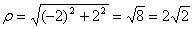 .
Проанализируем аргумент. Так как
.
Проанализируем аргумент. Так как 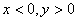 ,
то
,
то 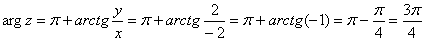 .
.
Откуда, 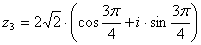 .
.
Так как комплексные числа, заданные в тригонометрической
форме, то, для их произведения применим формулу:
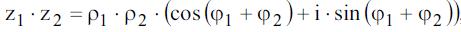
Тогда,
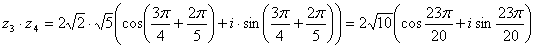 .
.

Тогда, запишем результат в тригонометрической
форме:
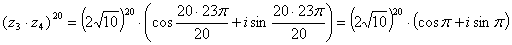 .
.
Запишем результат в показательной форме,
применив формулу:
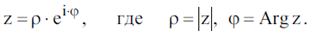
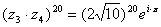 .
.
Ответ: 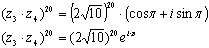
Задание 9
Решите квадратные уравнения: 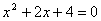 ,
,
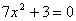 .
.
Решение
) 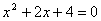
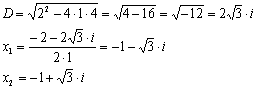
Ответ: 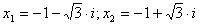 .
.
) 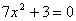 ,
,
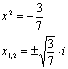
Ответ: 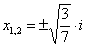 .
.
Задание 10
Вычислить предел: 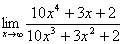 .
.
Решение
Неопределённость вида 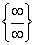 ,
для её раскрытия разделим числитель и знаменатель на переменную в старшей
степени, т.е. на
,
для её раскрытия разделим числитель и знаменатель на переменную в старшей
степени, т.е. на 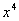 . Тогда можем
записать:
. Тогда можем
записать:
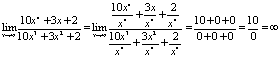
Задание 11
Вычислить предел: 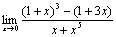 .
.
Решение
Неопределённость вида 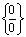 .
Применим кубическую формулу:
.
Применим кубическую формулу:
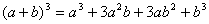 , а затем сократим
на критический множитель
, а затем сократим
на критический множитель 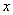 :
:
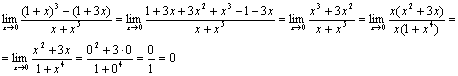
Задание 12
Вычислить предел: 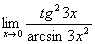 .
.
Решение
Неопределённость вида 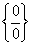 .
Применим таблицу бесконечных эквивалентных малых величин.
.
Применим таблицу бесконечных эквивалентных малых величин.
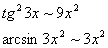
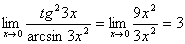 .
.
Задание 13
Вычислите производную: 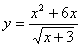 .
.
Решение
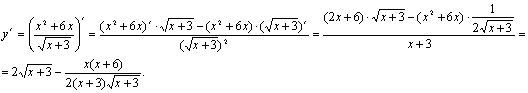
Задание 14
Вычислите производную: 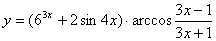 .
.
Решение
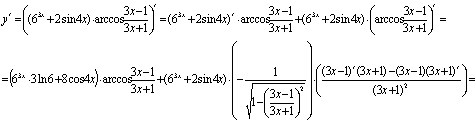
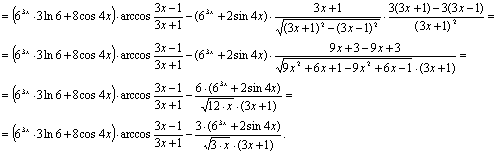
Задание 15
Исследуйте функцию и постройте её график: 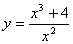 .
.
Решение
.Функция не является периодической.
Проверим чётность и нечётность функции
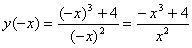 ,
, 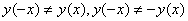 .
Следовательно, функция
.
Следовательно, функция 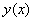 - общего вида.
- общего вида.
.Функция непрерывная во всех точках оси, кроме
точки 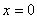 .
.
.Выясним, будет ли прямая 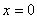 вертикальной
асимптотой графика функции. Для этого вычислим односторонние пределы
вертикальной
асимптотой графика функции. Для этого вычислим односторонние пределы
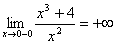 ,
,
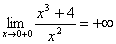 .
.
Итак, график функции имеет вертикальную
асимптоту 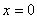 . Найдём асимптоты
графика функции при
. Найдём асимптоты
графика функции при 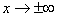 .
.
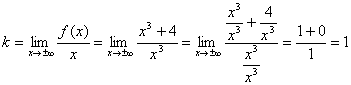 .
.
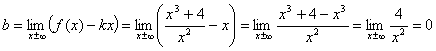 .
.
Таким образом, прямая 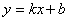 ,
т.е.
,
т.е. 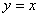 ,
является наклонной асимптотой одновременно для правой и левой ветвей графика
функции.
,
является наклонной асимптотой одновременно для правой и левой ветвей графика
функции.
. Исследуем функцию на возрастание и убывание и
найдём точки её экстремумов.
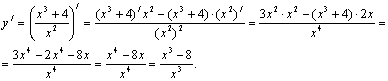
Производная 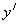 существует
и конечна везде в области определения функции.
существует
и конечна везде в области определения функции.
Найдём экстремальные точки: 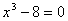 ,
,
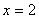 .
.
Найдём промежутки монотонности функции, для
этого строим таблицу.
Таблица 1
|
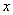
|
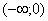
|
0
|
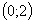
|
2
|
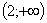
|
|
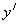
|
+
|
Не
существует
|
-
|
0
|
+
|
|
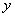
|
|
|
 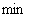
|
|
|
Таким образом, функция убывает на промежутке 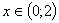 и
возрастает на промежутках
и
возрастает на промежутках 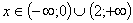 .
.
Найдём ординату в экстремальной точке:
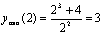 .
.
. Найдём интервалы выпуклости и вогнутости
графика функции. Найдём вторую производную функции:
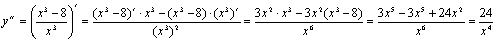
Вторая производная в ноль не обращается,
следовательно, точек перегиба нет.
Для исследования направленности выпуклости
графика функции строим таблицу 2.
Таблица 2
Заметим, что в таблицу необходимо включать и
точки разрыва графика функции.
Итак, график функции будет вогнут вверх на всей
числовой оси области определения
. Используя результаты исследования, строим
график функции.
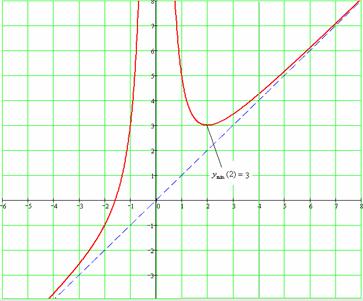
Рис. 3
Задание 16
Вычислить определённый интеграл: 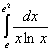 .
.
Решение
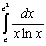 .
.
Применим метод замены переменной, для этого
положим 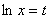 ,
дифференцируя, можем записать:
,
дифференцируя, можем записать: 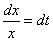 , а также найдём
новые пределы интегрирования:
, а также найдём
новые пределы интегрирования: 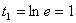 ,
, 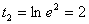 .
Подставляя замену переменной и переходя к новым пределам интегрирования, можем
записать:
.
Подставляя замену переменной и переходя к новым пределам интегрирования, можем
записать:
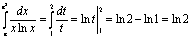 .
.
Задание 17
Вычислить определённый интеграл: 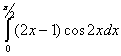 .
.
Решение
Применим метод интегрирования по частям по
следующей формуле: 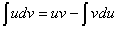 .
.
Положим
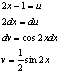
Тогда,
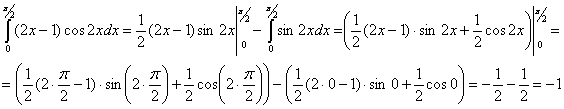
Задание 18
Решение
Положим 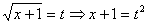 ,
дифференцируя, запишем
,
дифференцируя, запишем 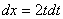 . Перейдём к новым
пределам интегрирования:
. Перейдём к новым
пределам интегрирования: 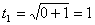 ,
,  .
Подставляя замену в исходный интеграл, а, также перейдя к новым пределам
интегрирования, получим
.
Подставляя замену в исходный интеграл, а, также перейдя к новым пределам
интегрирования, получим
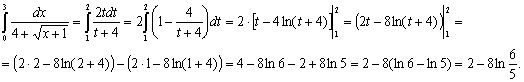
Задание 19
Вычислить площадь фигуры, ограниченной заданными
линиями: 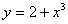 ,
,
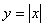 ,
,
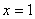 .
.
Решение
Сделаем рисунок.
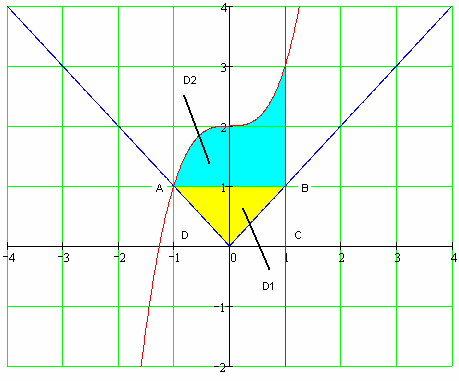
Рис. 4
Площадь фигуры состоит из двух областей: D1 и
D2.
Найдём площадь фигуры D1:
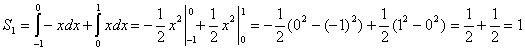
Найдём площадь фигуры D2 из которой не забудем
вычесть площадь прямоугольника ABCD, которая равна: 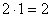 .
.
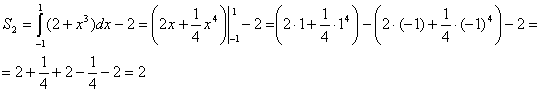
Тогда, 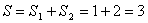 кв.ед.
кв.ед.
Задание 20
уравнение дуга число кривая
Вычислите длину дуги кривой: 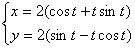 ,
,
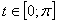 .
.
Решение
Длина дуги кривой, заданная в параметрическом
виде вычисляется по формуле:
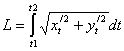 .
.
Найдём производные:
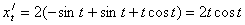 ,
,
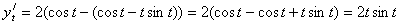 .
.
Тогда,
 .
.