Применение численных методов для решения математических задач
Содержание
Введение
. Общая теоретическая часть
.1 Действия с приближенными
величинами
.2 Основные численные методы
.2.1 Решение алгебраических и
трансцендентных уравнений
.2.2 Интерполяция функций
.2.3 Метод наименьших квадратов и
его применение
.2.4 Численное интегрирование
.2.5 Другие задачи, решаемые
численными методами
. Применение метода наименьших
квадратов к построению эмпирических функциональных зависимостей
. Расчетная часть
Заключение
Список использованной литературы
Введение
Численные методы в настоящее время относятся к
основным методам решения задач математики и различных ее приложений. Они
характеризуются тем, что сводят процесс решения математической задачи к
некоторой конечной последовательности операций над числами и приводят к результатам,
представленным в виде чисел, числовых векторов и матриц, числовых таблиц и т.
п. Их значение возрастает параллельно с развитием вычислительной техники. В то
же время полученные численными методами результаты обычно содержат погрешности,
являясь лишь приближениями к искомым ответам. Вызвано это рядом объективных
причин, среди которых есть не связанные непосредственно с методами вычислений.
Чтобы разобраться в них, проанализируем основные
этапы математического решения прикладных задач, а именно:
. Построение математической модели задачи.
. Определение исходных данных.
. Решение полученной математической задачи.
Погрешности появляются уже на первом этапе, ибо
математическая модель задачи - это приближенное, идеализированное описание
задачи на языке математики. При моделировании объекты и процессы
задачи-оригинала, взаимосвязи между ее параметрами заменяются на математические
понятия и соотношения.
Ради того чтобы получаемая в итоге
математическая задача оказалась доступной для дальнейших исследований, учитывают
лишь наиболее важные параметры, условия и особенности исходной задачи. Понятно,
что чем меньше факторов отбрасывается, тем точнее получается модель.
Несмотря на приближенность результатов
математического моделирования, без него в приложениях математики не обойтись.
Оно представляет собой обязательную ступень при переходе от нематематической
задачи к математической. Более того, удовлетворительное исследование многих
явлений реального мира оказывается возможным лишь тогда, когда удается
построить их математические модели.
Следующей причиной появления погрешностей
является то, что установить точные значения исходных параметров во многих
случаях невозможно. Серьезные проблемы с этим возникают не только при
исследовании, например, космических объектов или земной атмосферы, когда для
определения исходных данных приходится прибегать к различным прикидкам и
сложным измерительным процедурам, но и при решении достаточно простых бытовых
задач.
Целью курсового проекта является изучение теории
основных численных методов математики и их практическое освоение через
выполнение заданий расчетной части.
1. Общая теоретическая часть
.1 Действия с приближенными
величинами
Измерить или вычислить какую-либо величину
абсолютно точно не всегда возможно. Поэтому в вычислительной практике
преимущественно имеют дело не с точными значениями величин, а с их
приближенными значениями.
Под приближенным значением величины понимают
значение, незначительно отличающееся от точного значения и заменяющее последнее
в вычислениях. При решении практических задач приходится не только приближенно
находить значения величин, входящих в данную формулу и производить над ними
указанные в формуле действия, но и оценивать возможные погрешности, допущенные
как при определении числовых значений отдельных величин, так и при подсчете
окончательного результата.
При работе с приближёнными величинами приходится
решать следующие задачи:
давать математические характеристики точности
приближённых величин;
оценивать точность результата, когда известна
точность исходных данных;
находить точность исходных данных,
обеспечивающую заданную точность результата;
согласовывать точность исходных данных с тем,
чтобы не затрачивать излишней работы при отыскании или вычислении одних данных,
если другие данные слишком грубы;
Определение: абсолютная погрешность
- это абсолютная величина разности между точным значением величины 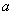 и её
приближённым значением
и её
приближённым значением 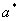 :
:
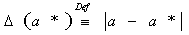 (1.1)
(1.1)
Здесь следует различать два случая:
точное значение числа 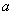 нам
известно, что на практике очень редко, тогда пользуемся формулой (1.1).
нам
известно, что на практике очень редко, тогда пользуемся формулой (1.1).
точное значение числа 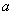 неизвестно,
тогда вводят понятие предельной абсолютной погрешности.
неизвестно,
тогда вводят понятие предельной абсолютной погрешности.
Определение: предельной абсолютной
погрешностью приближённого числа называют всякое число, не меньшее абсолютной
погрешности этого числа.
Таким образом, если 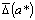 -
предельная абсолютная погрешность приближённого числа
-
предельная абсолютная погрешность приближённого числа 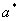 , то
, то
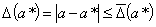 (1.2)
(1.2)
отсюда следует, что
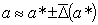 (1.3)
(1.3)
Значение предельной абсолютной
погрешности, обычно, подбирается интуитивно по смыслу задачи.
Понятия абсолютной погрешности и
предельной абсолютной погрешности, хотя и дают представление о точности
вычислений, однако не всегда достаточны.
Определение: относительной
погрешностью 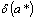 приближённого
числа
приближённого
числа 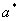 называется
отношение абсолютной погрешности
называется
отношение абсолютной погрешности 
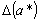 этого числа к модулю
соответствующего точного числа
этого числа к модулю
соответствующего точного числа 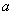
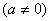 :
:
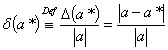 (1.4)
(1.4)
Поскольку точное значение величины 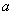 нам часто
не известно, то рассмотрим понятие предельной относительной погрешности
нам часто
не известно, то рассмотрим понятие предельной относительной погрешности 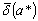 .
.
Определение: предельной
относительной погрешностью 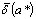 данного приближённого числа
данного приближённого числа 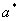 называется
всякое число, не меньшее относительной погрешности этого числа:
называется
всякое число, не меньшее относительной погрешности этого числа:
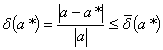 (1.5)
(1.5)
Отсюда следует, что
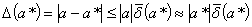 (1.6)
(1.6)
т.е. 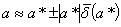 (1.7)
(1.7)
но, как известно:
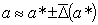 (1.8)
(1.8)
Сопоставление формул (1.7) и (1.8)
даёт соотношение между предельной абсолютной 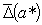 погрешностью и предельной
относительной погрешностью
погрешностью и предельной
относительной погрешностью 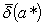 :
:
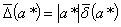 (1.9)
(1.9)
Из этой формулы иногда выражают 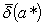 и пишут:
и пишут:
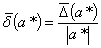 (1.10)
(1.10)
Вышеизложенная теория погрешностей
основана на допущении, что 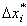 -погрешности настолько малы, что их
квадратами можем уже пренебрегать (на этом основано «обрезание» формулы Тейлора).
-погрешности настолько малы, что их
квадратами можем уже пренебрегать (на этом основано «обрезание» формулы Тейлора).
Поэтому все введённые формулы теряют
силу, если эти условия нарушены. В таких случаях нужно использовать и
квадратичные члены, чтобы получить более точную теорию.
Но надо учитывать, что в этом случае
формулы значительно усложняются.
.2 Основные численные методы
.2.1 Решение алгебраических и
трансцендентных уравнений
Пусть задана непрерывная функция f(х) и
требуется найти все или некоторые корни уравнения
f(x)=0.
(1.11)
Эта задача распадается на несколько задач.
Во-первых, надо исследовать количество, характер и расположение корней.
Во-вторых, найти приближенные значения корней. В-третьих, выбрать из них
интересующие нас корни и вычислить их с требуемой точностью.
Первая и вторая задачи решаются аналитическими и
графическими методами. Когда ищутся только действительные корни уравнения, то
полезно составить таблицу значений f(x).
Если в двух соседних узлах таблицы функция имеет разные знаки, то между этими
узлами лежит нечетное число корней уравнения (по меньшей мере, один). Если эти
узлы близки, то, скорее всего, корень между ними только один. Но выявить по
таблице корни чётной кратности сложно. По таблице можно построить график
функции у=f(х) и графически
найти точки его пересечения с осью абсцисс. Этот способ более нагляден и дает
неплохие приближенные значения корней. Во многих задачах техники такая точность
уже достаточна. В технике еще популярны графические методы решения уравнений
(номография). Построение графика позволяет выявить даже корни чётной кратности.
Иногда удается заменить уравнение (1.11)
эквивалентным ему уравнением j(х)=y(х),
в котором функции y1=j(х)
и y2=y(х) имеют несложные графики.
Например, уравнение хsinх-1=0
удобно преобразовать к виду sinx=l/x.
Абсциссы точек пересечения этих графиков будут корнями исходного уравнения.
Приближенные значения корней уточняют различными
итерационными методами.
.2.2 Интерполяция функций
Итак, как было сказано выше, задачей
интерполяции является поиск такого многочлена, график которого проходит через
заданные точки.
Пусть функция y=f(x)
задана с помощью таблицы (табл. 1).
Таблица 1
|
x
|
x0
|
x1
|
x2
|
xn
|
|
y
|
y0
|
y1
|
y2
|
yn
|

Необходимо получить многочлен Pn(x)
такой, чтобы выполнялось условие: Pn(xi)=yi.
Для этого зададимся конкретным видом многочлена.
Пусть Pn(x)
имеет следующий вид:
Pn(xi)=a0+a1x+a2x2+…+anxn.
Для того, чтобы определить коэффициенты a0,
a1,…
необходимо решить систему из n
уравнений с n неизвестными:
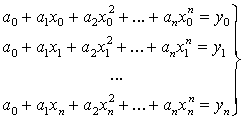
Полином с коэффициентами, полученными путём
решения системы называют интерполяционным полиномом Лагранжа и обозначают Ln(x).
Решение системы весьма трудоёмко, поэтому интерполяционный полином Лагранжа
представляют в виде линейной комбинации многочленов степени n:

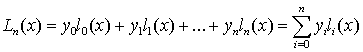 .
.
Необходимо, чтобы каждый многочлен li(x)
обращался в нуль во всех узлах интерполяции, за исключением i-го,
в котором он равен 1 (Рис. 2). Если li(x)
удовлетворяет таким условиям, то в i-ом
узле интерполяции многочлен Ln(x)
примет значение yi,
что удовлетворяет условию поставленной задачи. Таким условиям удовлетворяет
многочлен вида:
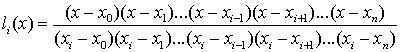 (1.12)
(1.12)
Таким образом, интерполяционный
многочлен Лагранжа можно представить следующей общей формулой:
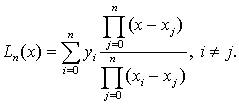 (1.13)
(1.13)
1.2.3 Метод наименьших квадратов и
его применение
В задачу аппроксимации входит нахождение такой
функции y=f(x),
что расстояния между заданными точками yi
и значениями f(xi)
были минимальными (Рис. 3). Обозначим отклонение:
εi=yi-f(xi)

В качестве оценки общего отклонения кривой f(x)
от табличных данных (Табл. 1) можно было бы взять сумму отклонений εi,
но отклонения могут быть разными по знаку и, не смотря на большие εi
их сумма может быть близка к нулю. Очевидно, что необходимо брать сумму
абсолютных значений отклонений, но на практике неудобно пользоваться этой
функцией, поэтому в качестве критерия оценки отклонения кривой берут сумму
квадратов отклонений:
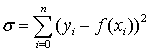 .
.
Для определения функции f(x)
необходимо, во-первых, задать её общий вид, например, f(x)=ax+b,
во-вторых, подставив f(x)
в и минимизировав σ, найти
коэффициенты (a и b).
Такой метод определения коэффициентов для функции f(x)
называется методом наименьших квадратов. Наиболее часто встречающиеся виды
функции f(x)
для метода наименьших квадратов приведены в таблице 2. Формула y=f(x)
называется эмпирической формулой или уравнением регрессии y
на x.
Таблица 2
|
Общий
вид функции
|
Аналитическая
формула
|
Вид
регрессии
|
|
y=f(x,a,b)
|
y=ax+b
|
линейная
|
|
y=f(x,a,m)
|
y=axm
|
степенная
|
|
y=f(x,a,m)
|
y=aemx
|
показательная
|
|
y=f(x,a,b)
|
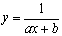
|
дробно-линейная
|
|
y=f(x,a,b)
|
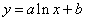
|
логарифмическая
|
|
y=f(x,a,b)
|
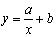
|
гиперболическая
|
|
y=f(x,a,b)
|
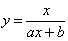
|
дробно-рациональная
|
1.2.4 Численное интегрирование
Основная идея большинства методов численного
интегрирования состоит в замене подынтегральной функции на более простую,
интеграл от которой легко вычисляется аналитически. При замене подынтегральной
функции на полином нулевой, первой и второй степени получаются соответственно
методы прямоугольников, трапеций и парабол (Симпсона)[3, C.161].
Методы численного интегрирования
основываются на геометрическом смысле интеграла. Как известно интеграл 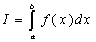 есть
площадь криволинейной трапеции ограниченной подынтегральной функцией f(x) на отрезке
[a,b]. Для
вычисления интеграла I отрезок [a,b] разбивают
на n отрезков
длиной h. На каждом
отрезке криволинейную трапецию приближают прямоугольником, так как его площадь
можно легко вычислить. Затем суммируют все полученные площади, получая тем
самым приближённое значение интеграла.
есть
площадь криволинейной трапеции ограниченной подынтегральной функцией f(x) на отрезке
[a,b]. Для
вычисления интеграла I отрезок [a,b] разбивают
на n отрезков
длиной h. На каждом
отрезке криволинейную трапецию приближают прямоугольником, так как его площадь
можно легко вычислить. Затем суммируют все полученные площади, получая тем
самым приближённое значение интеграла.
Метод левых прямоугольников
На рис. 4 проиллюстрирован, так называемый,
метод левых прямоугольников. Его название объясняется тем, что высота
прямоугольника f(x)
вычисляется в левой границе отрезка h.
Выведем формулу для приближённого вычисления интеграла I.

Как видно из рисунка площадь первого слева
прямоугольника S0=f(x0)h.
Площадь следующего S1=f(x1)h.
Легко заметить, что площадь i-го
прямоугольника Si=f(xi)h.
Всего таких прямоугольников n,
нумерация их ведётся от 0 до n-1.
Таким образом, приближённое значение интеграла, полученное этим методом,
вычисляется по формуле:
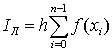 . (1.14)
. (1.14)
Оценим погрешность формулы (1.14) на
отрезке [xi,xi+h]. Для этого
разложим функцию f(x) по формуле
Тейлора, выбирая xi за центр разложения и предполагая
наличие у функции требуемых по ходу рассуждений непрерывных производных.
f(x)=f(xi)+(x-xi)f’(xi)+…
(1.15)
В формуле (1.15) для определённости
отбросим члены, содержащие производные высших порядков, т.е. 2-ю и выше. Тогда
получим:
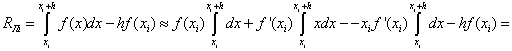
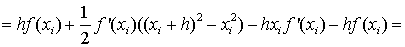
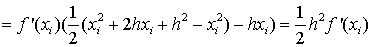 , т.е.
, т.е.
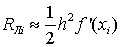 (1.16)
(1.16)
Чтобы получить общую погрешность
метода на отрезке [a,b]
просуммируем все RЛi:
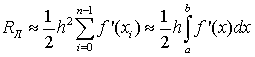 (1.17)
(1.17)
Поскольку в (1.15) были отброшены
члены, содержащие более высокие степени длины интервала, то выражение
остаточного члена (1.17) является асимптотическим, т.е. выполняющимся при h→0 с
точностью до членов более высокого порядка малости. Но для справедливости этой
оценки необходимо существование непрерывной f’(x); если f’(x)
кусочно-непрерывна, то удаётся сделать лишь мажорантную оценку
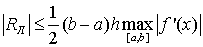 (1.18)
(1.18)
Эту формулу можно записать иначе
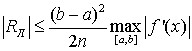 , (1.19)
, (1.19)
где n -
количество отрезков, на которые разбит отрезок [a,b].
Перед началом вычислений по данному
методу необходимо определиться с h или, что, по сути, то же самое, с n. Пусть
известны границы отрезка [a,b], задана
подынтегральная функция f(x) и точность
ε,
с
которой должен быть вычислен интеграл. Чтобы определить h и n
воспользуемся простым и очевидным неравенством:
|RЛ|≤ε, (1.20)
откуда получаем для непрерывной f’(x):
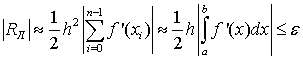
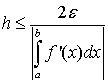 (1.21)
(1.21)
либо если учесть, что 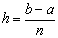 получим
получим
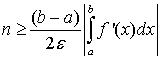 . (1.22)
. (1.22)
Для кусочно-непрерывной f’(x) с учётом
(1.20) и (1.21) справедливо следующее
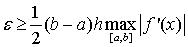
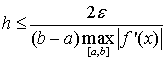 (1.23)
(1.23)
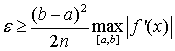
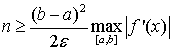 (1.24)
(1.24)
Метод правых прямоугольников

Этот метод похож на предыдущий. Отличие в том,
что высота прямоугольников вычисляется по правой границе (Рис. 5).
Выводы формул для данного метода аналогичны
предыдущему. Основные отличия заключаются в нумерации. Формула метода правых
прямоугольников выглядит следующим образом:
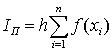 . (1.25)
. (1.25)
Рассуждения и конечные формулы,
связанные с определением погрешности метода и выбором ширины основания
прямоугольников аналогичны тому, что получено в предыдущем методе.
Метод средних прямоугольников
Чтобы уменьшить погрешность методов левых и
правых прямоугольников был предложен метод средних, т.е. метод в котором высота
прямоугольника вычисляется в середине отрезка h
(Рис. 6). Обращаясь к рисунку легко увидеть, что площади прямоугольников
вычисляются по следующим формулам[3, C.
158]:
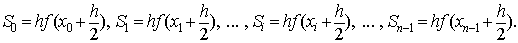 (1.26)
(1.26)

Оценим погрешность формулы (1.26) на
отрезке [xi,xi+h]. Прежде
всего, получим разложение по формуле Тейлора для данного метода. Центр
разложения в данном случае будет точка 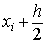 . Тогда получим:
. Тогда получим:
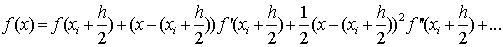 (1.27)
(1.27)
В формуле (1.27) отбросим члены,
содержащие 3-ю и выше производные. Получим:
Ii-IСр.i=RСр.i
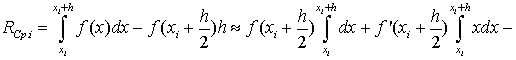
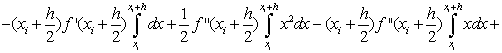
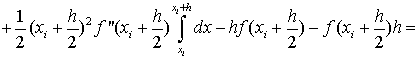
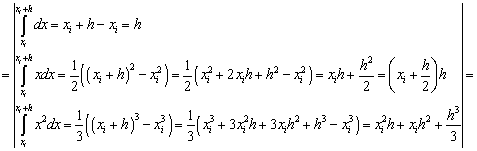
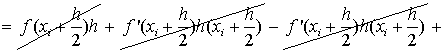
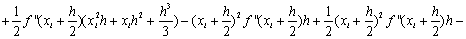
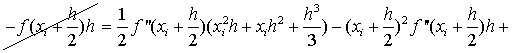
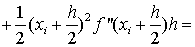
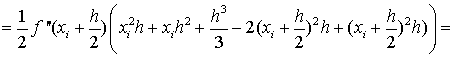
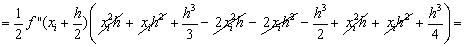
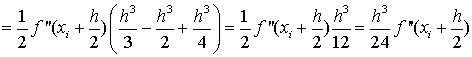 , т.е.
, т.е.
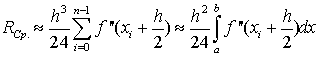 . (1.28)
. (1.28)
Аналогично тому, как были получены
формулы (1.18), (1.19), (1.20), (1.21), (1.22) можно получить формулы, по
которым оцениваются n и h, для
данного метода. Запишем окончательные формулы для непрерывной f’’(x).
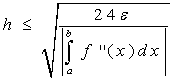 (1.29)
(1.29)
 (1.30)
(1.30)
Для кусочно-непрерывной f’’(x) получаем
мажорантные оценки:
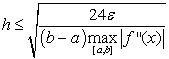 (1.31)
(1.31)
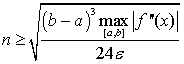 (1.32)
(1.32)
Сравнивая формулы (1.17) и (1.28)
погрешностей методов приходим к выводу, что погрешность метода средних во много
раз ниже погрешности метода левых или правых прямоугольников, т.е. метод
средних во много раз точнее.
Метод трапеций
Метод трапеций основан на том, что криволинейная
трапеция приближается прямолинейной (Рис. 7). Т.е. площади вычисляются по
следующей формуле:
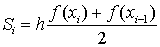

Метод Симпсона

Этот метод основан на том, что функция f(x)
приближается на отрезке [xi-h,
xi+h]
параболой (причём xi
отстоит от xi+1
на расстоянии 2h) (Рис.8).
То есть через заданные точки проводится парабола. Но известно, что уравнение
параболы имеет вид ρ(x)=ax2+bx+c,
т.е. чтобы определить коэффициенты a,
b, c
необходимо решить систему из трёх уравнений, а для этого необходимо знать
координаты как минимум трёх точек, через которые проходит парабола ρ(x).
В связи с этим, в отличие от предыдущих методов, для вычисления площади
отдельной криволинейной трапеции понадобиться не две, а три точки.
Общая формула Симпсона:
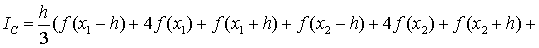
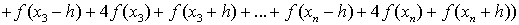
Для упрощения этой формулы учтём,
что
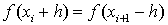 ,
,  ,
, 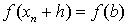 ,
,
где a и b - границы
отрезка интегрирования [a, b]. С учётом
этого получим:
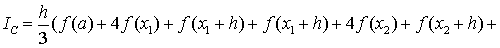
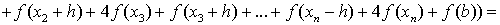
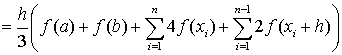 ,
,
где n -
количество отрезков длиною 2h. То есть количество отрезков h, на которые
разбит отрезок [a, b] должно
быть обязательно чётным. Длина отрезка [a, b] равна 2nh.
Метод Симпсона является наиболее
точным из всех описанных методов численного интегрирования.
1.2.5 Другие задачи, решаемые
численными методами
Область применения численных методов в
математике огромна. Они применяются и при решении различных уравнений, и при
вычислении определенных интегралов, и в приближении функции.
Рассмотрим различные способы решения уравнений.
Метод половинного деления
(дихотомия)
Пусть мы нашли такие точки a и b что f(a)f(b)£0,
т. е. на отрезке [a,b]
лежит не менее одного корня уравнения. Найдем середину отрезка xc=(a+b)/2
и вычислим f(xc).
Из двух половин отрезка выберем ту, для которой f(xc)f(a
или b)£0,
т.е. отрезок на котором функция меняет знак. Затем новый отрезок опять делим
пополам и выберем ту половину, на концах которой функция имеет разные знаки, и
т. д. (рис. 9).

Если требуется найти корень с точностью e,
то продолжаем деление пополам до тех пор, пока длина отрезка не станет меньше 2e.
Тогда середина последнего отрезка даст значение корня с требуемой точностью.
Дихотомия проста и очень надежна: к простому корню она сходится для любых
непрерывных функций f(x),
в том числе недифференцируемых; при этом она устойчива к ошибкам округления.
Скорость сходимости невелика: за одну итерацию точность увеличивается примерно
вдвое, т. е. уточнение трех цифр требует 10 итераций (т.к. длина отрезка, на
котором лежит корень, после 10 итераций равна 1/210=1/1024»10-3).
Зато точность ответа гарантируется.
Перечислим недостатки метода.
. Для начала расчета надо найти отрезок,
на котором функция меняет знак.
. Если в этом отрезке несколько корней,
то заранее неизвестно, к какому из них сойдется процесс (хотя к одному из них
сойдется).
. Метод неприменим к корням четной
кратности.
. Для корней высокой нечетной кратности
он сходится, но менее точен и хуже устойчив к ошибкам округления, возникающим
при вычислении f(x).
. На системы уравнений дихотомия не
обобщается.
Утверждение 1. С помощью данного метода
невозможно найти корни чётной кратности.
Доказательство.
Чётно кратный корень это корень уравнения вида
(x+a)2n=0,
где n
- целое, nÎ[0,¥].
Решением этого уравнения будет корень x=-a
кратности 2n. В общем виде
уравнение может иметь как чётно, так и нечётно кратные корни. Можно записать
общий вид уравнения имеющего (k+m)
только действительных корней так:
(x+x1)2n1(x+x2)2n2…(x+xk)2nk(x+xk+1)2n(k+1)+1(x+xk+2)2n(k+2)+1…
….(x+xk+m)2n(k+m)+1=0,
где n1,…,n(k+m)
Î[0,¥]
- целые числа; x1¹
x2¹…¹
xk+m.
В уравнении k
чётно кратных и m нечётно
кратных корней. Оно раскладывается на (k+m)
уравнений, из которых легко получаются корни. Если задать начальный отрезок [-x1-r,-x1+r],
где r - мало, и
проверить условие смены знака функции на его границах, то обнаружим, что знак
не меняется в силу чётности степени. А если аналогично проверить нечётно
кратные корни, то получим обратную ситуацию.
Следствие 1.
Если корень имеет чётную кратность, то на границах
бесконечно малого отрезка с центром в этом корне функция имеет одинаковые
знаки.
Следствие 2.
Если корень имеет нечётную кратность, то на
границах бесконечно малого отрезка с центром в этом корне функция имеет разные
знаки.
Пусть на заданном отрезке [a,b]
лежит 1 корень чётной кратности, тогда в силу следствия 1 на границах отрезка
знак меняться не будет, что означает остановку выполнения итераций и
недостижение необходимой точности. Если же на отрезке [a,b]
лежит 1 чётно кратный корень и 1 нечётно кратный корень, то чётно кратный
корень будет просто игнорирован методом, т.к. условие смены знака являющееся
также основным условием, с помощью которого определяется корень на текущем
полуотрезке, в силу следствия 1 не выполнится. Следовательно, чётно кратный
корень не может быть найден с помощью данного метода.
Утверждение 2. Если на концах начального отрезка
значения функции имеют один знак, то метод может не сойтись, то есть, возможно,
ни один из корней не будет найден с заданной точностью.
Утверждение 3. Если на концах начального отрезка
значения функции имеют разные знаки, то будет найден с заданной точностью один
из корней лежащих на нём.
Метод секущих
В данном методе, в отличие от метода Ньютона,
проводятся не касательные, а секущие (Рис. 10). Из рисунка легко получить
итерационную формулу:
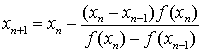 .
.

В качестве начального приближения необходимо
задать не только x0,
но и x1.
Метод секущих имеет одно преимущество перед методом Ньютона - здесь не нужно
вычислять производную. Но этот метод имеет также существенные недостатки.
Сходимость итераций может быть немонотонной не только вдали от корня, но и в
малой окрестности корня [7, C.39].
В знаменателе формулы стоит разность значений
функции. Вдали от корня это не существенно; но вблизи корня, особенно корня
высокой кратности, значения функции малы и очень близки. Возникает потеря
значащих цифр, приводящая к «разболтке» счёта. Это ограничивает точность, с
которой можно найти корень; для простых корней это ограничение не велико, а для
кратных может быть существенным.
От «разболтки» страхуются так называемым приёмом
Гаврика. Выбирают не очень малое ε, ведут
итерации до выполнения условия |xn+1-xn|<ε
и
затем продолжают расчёты до тех пор, пока |xn+1-xn|
убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчёт
прекращают и последнюю итерацию не используют. Все ограничения по сходимости
итераций для данного метода такие же, как и в методах простых итераций и
Ньютона. А вот определение достижения заданной точности, как видно из описания
метода, затруднительно, и, даже, возможна ситуация, когда из-за «разболтки»
счёта заданная точность не будет достигнута никогда. При использовании метода
секущих в явном виде определить точность трудно, поэтому используют косвенный
метод. Считают, что вблизи корня |xn+1-xn|~|xт-xn+1|.
Конечно эта оценка весьма примерна, но при больших n
(в идеале при n→∞) это
так и есть.
2. Применение метода наименьших
квадратов к построению эмпирических функциональных зависимостей
уравнение интерполяция численный
интегрирование
Данный метод относится к классу
аппроксимационных методов. Идея метода состоит в том, чтобы по данным
эксперимента построить приближенно функцию, отображающую зависимость ее от 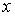 , в виде
многочлена с тем расчетом, чтобы сумма квадратов отклонений построенной функции
от экспериментальной в узловых точках была минимальна. Будем строить функцию в
виде многочлена
, в виде
многочлена с тем расчетом, чтобы сумма квадратов отклонений построенной функции
от экспериментальной в узловых точках была минимальна. Будем строить функцию в
виде многочлена
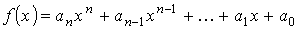 .
.
Используем для построения результаты
эксперимента, заключенные в таблице
Построить многочлен, значит,
определить его коэффициенты 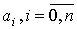 . Для этого введем функцию
. Для этого введем функцию
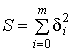
и потребуем, чтобы
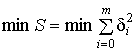 ,
,
где 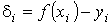 - отклонение функции от
экспериментальной в узлах
- отклонение функции от
экспериментальной в узлах 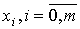 .
.
Используя вид 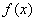 , получим:
, получим:
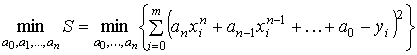 .
.
Необходимыми условиями экстремума
функции 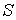 является
равенство нулю ее первой производной по всем переменным
является
равенство нулю ее первой производной по всем переменным 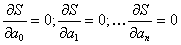 . Расписав
эти условия, получим СЛАУ вида:
. Расписав
эти условия, получим СЛАУ вида:
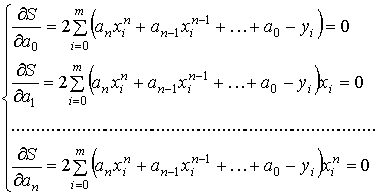
Запишем систему для определения 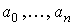 в
нормальной форме:
в
нормальной форме:
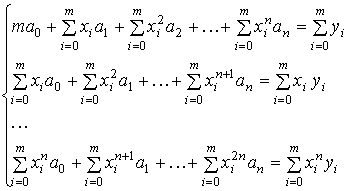
Решаем систему одним из известных
методов и находим 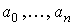 , которые
затем подставляем в искомый многочлен.
, которые
затем подставляем в искомый многочлен.
Запишем алгоритм метода наименьших
квадратов.
Вводим таблицу чисел 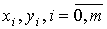 .
.
Вычисляем 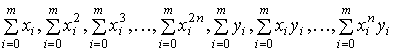 .
.
Решая любым известным методом
полученную систему линейных алгебраических уравнений, находим 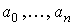 -
коэффициенты искомого многочлена.
-
коэффициенты искомого многочлена.
Для таблицы узловых точек, построим
аппроксимационный многочлен второго порядка методом наименьших квадратов вида:
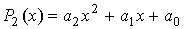 .
.
Для этого необходимо вычислить следующие суммы
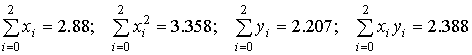
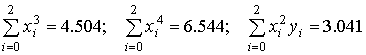
и решить СЛАУ относительно
неизвестных коэффициентов 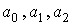 вида:
вида:
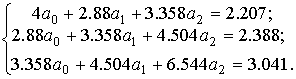
Значения неизвестных коэффициентов
равны:
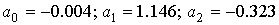 .
.
Тогда искомый многочлен второго
порядка будет иметь вид:
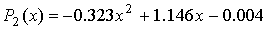 .
.
Нетрудно заметить, что в узловых
точках значения многочлена и табличной функции не совпадают. Погрешность
вычислений по данной формуле в контрольной точке, по сравнению с истинным
значением, составляет
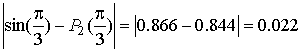 .
.
3. Расчетная часть
Задача 1. Найти
действительные корни уравнения 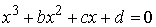 методами простых итераций и
касательных (Ньютона) с точностью до 0,00001.
методами простых итераций и
касательных (Ньютона) с точностью до 0,00001.
Нахождение приближенных значений
действительных корней включает в себя:
а) определение их числа;
б) отделение корней, т.е отыскание
достаточно малых промежутков в каждом из которых заключен один и только один
корень уравнения;
с) вычисление корней с заданной
точностью.
f(x) = х3
-4х2 +6х -3
Определим число корней уравнения
графическим способом. Для этого преобразуем исходное уравнение к следующему
эквивалентному виду:
х3 = 4х2-6х +3
Построив графики функций f1(x) = х3
f2(x) = 4х2
-6х +3, определяем, что у решаемого уравнения имеется только один корень,
который находится в интервале 0,9 < х < 1,2
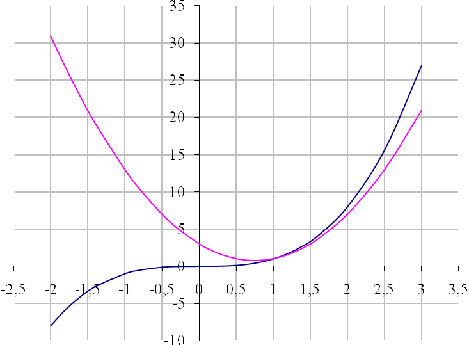
Метод Ньютона. Определим
поведение первой и второй производной функции f(x) на интервале
уточнения корня.
Для функции f(x) = х3
-4х2 +6х -3 имеем:
f `(x) = 3х2
-8х +6; f `(0,9) =
1,23; f `(1,2) =
0,72;
f ``(x) = 6x - 8; f ``(0,9) =
-2,6; f ``(1,2) =
-0,8.
В качестве начального приближения
выберем левую границу интервала, х(0) = 0,9.
Дальнейшие вычисления производим по
формуле:
f(x(k)) = х3(k)-4х2(k) +6х(k) -3, f `(x(k)) = 3х2(k) -8х(k) +6.
Итерации завершаются при выполнении
условия | х(к+1) - х(к) | < ε.
Результаты вычислений занесем в
таблицу:
|
k
|
х(k)
|
f(x(k))
|
f `(x(k))
|
-f(x(k))/f `(x(k))
|
|
0
|
0,9
|
-0,111
|
1,23
|
0,0902439
|
|
1
|
0,95
|
-0,052625
|
1,1075
|
0,0475169
|
|
2
|
0,98
|
-0,020408
|
1,0412
|
0,01960046
|
|
3
|
0,985555
|
-0,01466
|
0,987424
|
-0,01484
|
|
4
|
0,995555
|
-0,00446
|
0,995733
|
-0,00448
|
|
5
|
0,99999
|
-0,000001
|
0,99999
|
0,000001
|
|
6
|
1
|
0
|
1
|
х= 1
Метод простой итерации.
Уравнение f(x)
= х3 -4х2 +6х -3 можно записать в виде
х = 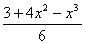 .
.
За основной интервал возьмем
(0,9;1,2), положим
φ (х) = 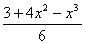 .
.
1) φ (х) 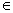 [0,9; 1,2]
при
[0,9; 1,2]
при 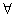 х
х 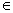 [0,9; 1,2]
[0,9; 1,2]
2) φ` (х) = 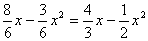 .
.
В качестве начального приближения
положим х(0) = (0,9+1,2) / 2=1,05
Вычисляем последовательные
приближения х(k) с одним
запасным знаком.
|
k
|
х(k)
|
φ
(x(k))
|
|
0.
|
1,05
|
1,042063
|
|
1.
|
1,04
|
1,033589
|
|
2.
|
1,03
|
1,025146
|
|
3.
|
1,02
|
1,016732
|
|
4.
|
1,01
|
1,00835
|
|
5.
|
1,0001
|
1,000083
|
|
6.
|
1
|
1
|
х=1
Задача 2. Вычислить
приближенное значение интеграла 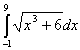
По формуле: а) трапеции (n=10); б)
Симпсона (n=10); в)
Гаусса (n=5);
а) трапеции (n=10)
|
Xi
|
Yi
|
|
-1
|
2,236068
|
|
0
|
2,44949
|
|
1
|
2,645751
|
|
2
|
3,741657
|
|
3
|
5,744563
|
|
4
|
8,3666
|
|
5
|
11,44552
|
|
6
|
14,89966
|
|
7
|
18,68154
|
|
8
|
22,75961
|
|
9
|
27,11088
|
Формула трапеций:
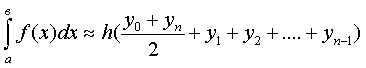
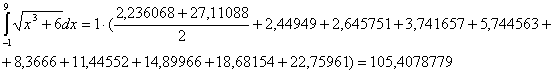
б) Симпсона (n=10)
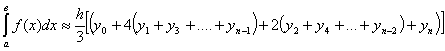 - формула Симпсона или формула
парабол.
- формула Симпсона или формула
парабол.

в) Гаусса (n=5);
I = 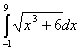
Абсциссы t1 и
коэффициенты Ai
квадратурных формул Гаусса при n=5,
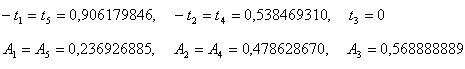
При вычислении интеграла 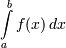 следует
сделать замену переменной
следует
сделать замену переменной
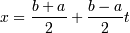 .
.
тогда формула Гаусса будет иметь вид
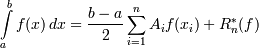
где 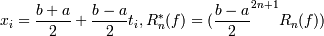 .
.
Решение.
Сделаем замену переменной
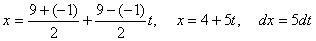
Находим новые пределы интегрирования
|
х
|
-1
|
9
|
|
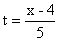 -11 -11
|
|
|
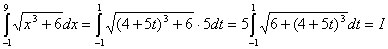
По формуле Гаусса при n=5 находим
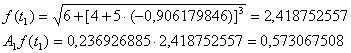

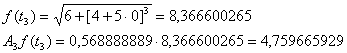


Затем по формуле Гаусса при n=5 находим
I 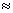 5[ A1f(t1)
+ A2f(t2) + A3f(t3) + A4f(t4)
+ A5f(t5) ] = 5(0,573067508+ 1,373591893+
4,759665929+8,368935366+5,931916724)= 105,035887
5[ A1f(t1)
+ A2f(t2) + A3f(t3) + A4f(t4)
+ A5f(t5) ] = 5(0,573067508+ 1,373591893+
4,759665929+8,368935366+5,931916724)= 105,035887
Задача 3. Построить
интерполяционные многочлены Лагранжа и Ньютона для таблично заданной функции:
|
х
|
1,6
|
3,1
|
5,0
|
8,4
|
|
f (x)
|
3,05
|
4,74
|
6,25
|
5,71
|
Интерполяционный многочлен Лагранжа
L4 (x) = 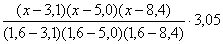 +
+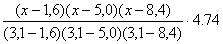 +
+
+ +
+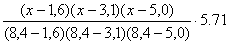 =
=
= -0,0879х3+1,45х2
-7,34х +11,44 + 0,314х3 - 4,71х2 + 19,9х - 21,1 -
0,285х3 + 3,73х2
-11,25х + 10,46 + 0,047х3 - 0,46х2 + 1,34х -1,17 =
= - 0,012х3 - 0,01х2
+ 2,65х -0,37
L4(x)=
- 0,012х3 - 0,01х2 + 2,65х -0,37
Интерполяционный многочлен Ньютона
у10 = 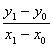 =
= 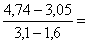 1,13, у21
=
1,13, у21
=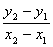 =
= 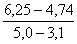 = 0,79,
= 0,79,
у32 =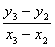 =
=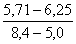 = -0,16,
= -0,16,
у210 =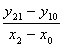 =
=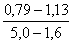 = -0,1, у321
=
= -0,1, у321
=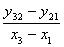 =
= 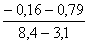 =-0,18,
=-0,18,
у3210 =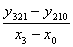 =
= 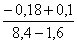 = -0,011.
= -0,011.
У= 3,05 + 1,13(х - 1,6) + 0,011(х -
1,6)(х - 3,1)(х - 5) =
= 0,011x3-0,11x2+1,443x+0,9692
Задача 4.
Нахождение оценок параметров линейной y=a0+a1x
и квадратичной y=a0+a1x+a2x2
моделей функциональной зависимости величин у и х по результатам наблюдений (xi;yi),
i= 1,2,…,5, заданной
таблицей:
|
x
|
-
2
|
0
|
1
|
2
|
3
|
|
y
|
0,45
|
0,45
|
0,55
|
0,65
|
0,65
|
Будем считать, что min
эмпирической формулы выбран, и ее можно представить в виде
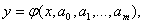 (3.1)
(3.1)
где φ - известная
функция, а0, а1,…., аm -
неизвестные постоянные параметры. Задача состоит в том, чтобы определить такие
значения параметров, при которых эмпирическая формула дает хорошее приближение
данной функции, значения которой в точках xi равны
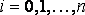
Рассмотрим способ определения
параметров эмпирической формулы - метод средних. Он состоит в том, что
параметры а0, а1,…., аm зависимости
(3.1) определяются с использованием условия равенства нулю суммы отклонений
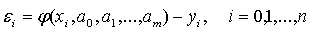
во всех точках хi:
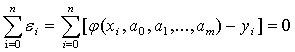 (3.2)
(3.2)
Путем группировки отклонений εi,разбивается
на систему, состоящую из m+1 уравнений. Например,
ε0+ ε1 + ε2 =0,
ε3 + ε4 + ε5 + ε6 =0
εn-1 + εn =0
Решая эту систему уравнений, можно
найти неизвестные параметры.
у=а0+а1х
Воспользуемся методом средних:
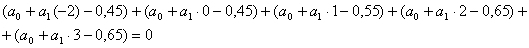
Запишем вместо этого уравнения
систему двух уравнений путем его расщепления:
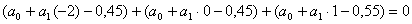
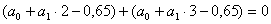
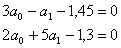
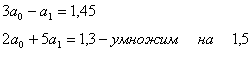
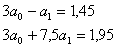
Вычитаем из второго уравнения
первое, получаем
,5а1=0,5
а1=0,059; а0=0,5
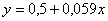 -эмпирическая формула,
-эмпирическая формула,
Проверим: х=3 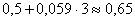
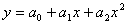 (3.3)
(3.3)
Воспользуемся методом средних и
запишем уравнение (3.2) для всех точек:
ε1 + ε2 +ε3 + ε4 + ε5 =0,
запишем вместо этого систему трех
уравнений:
ε1 + ε2+ ε3=0,
ε4 + ε5 =0
ε1 + ε2=0
Используя выражение (3.3) и
табличные данные, получаем
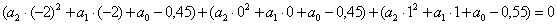
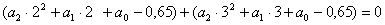
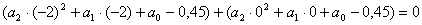
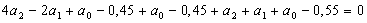
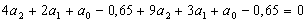
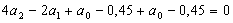
Или окончательно:
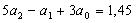
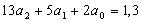
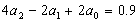
Решим эту систему трех уравнений
первой степени с тремя неизвестными.
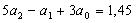
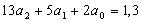
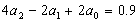
а2=0,004; а1=0,052;
а0=0,494
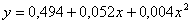 -эмпирическая формула
-эмпирическая формула
Проверим:
х=1; 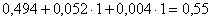
Заключение
В данной работе нахождении действительных корней
уравнения методом простых итераций и касательных (Ньютона) с точностью до 0,
00001 были получены следующие результаты:
Метод Ньютона. Для функции f(x)
= х3 -4х2 +6х -3 имеем х=1.
Метод простой итерации х =1.
В обоих случаях получены приближенные значения
корня уравнения.
При вычислении приближенного
значения интеграла 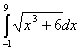
По формуле трапеции (n=10)
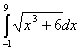 = 105,4078779
= 105,4078779
По формуле Симпсона (n=10)
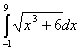 = 105,0832546
= 105,0832546
По формуле Гаусса
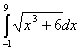 =105,035887
=105,035887
Интерполяционный многочлен Лагранжа
L4(x)=
- 0,012х3 - 0,01х2 + 2,65х -0,37
Интерполяционный многочлен Ньютона
У= 3,05 + 1,13(х - 1,6) + 0,011(х - 1,6)(х -
3,1)(х - 5) =
= 0,011x3-0,11x2+1,443x+0,9692
Параметры линейной y=a0+a1x функции: 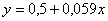 ,
,
квадратичной y=a0+a1x+a2x2 функции: 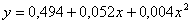
Список использованной литературы
1. Бахвалов, Н.С. Численные методы. - М.:
Наука, 1973.
2. Вержбицкий, В.М. Численные методы.
Линейная алгебра и нелинейные уравнения. - М. : Высшая школа, 2000.
. Вержбицкий, В.М. Численные методы.
Математический анализ и обыкновенные дифференциальные уравнения. - М.: Высшая
школа, 2001-382c.
. Волков, Е.А. Численные методы. - М. :
Наука, 1987.
5. Калиткин
Н.Н. Численные методы. - М.: Наука, 1978. - 512с.
6. Киреев В.И., Пантелеев А.В. Численные
методы в примерах и задачах. - М.: Изд-во МАИ, 2000.
7. Пирумов, У.Г. Численные методы : учеб.
пособие для студ. втузов. - М. : Дрофа, 2003 - 188с.
8. Самарский
А.А. Введение в численные методы. - М.: Наука, 1982. - 272с.
9. Фильчаков
П.В. Справочник по высшей математике. - Киев: Наукова думка, 1975. - 500с.
. Хемминг
Р.В. Численные методы/ Пер. с англ. М.: Наука, 1998. - 400с.
. Численные
методы анализа Б. П. Демидович, И. А. Марон и Э. З. Шувалова. - М.: Наука,
1998. - 368с.