Определение объема и площади геометрических фигур. Системы линейных неравенств
Задание 1
57. даны вершины треугольника АВС. Найти
) длину стороны АВ;
) уравнения сторон АВ и АС и их угловые
коэффициенты;
) внутренний угол А;
) уравнение медианы проведенной ихз вершины В;
) уравнение высоты СD
и ее длину;
)уравнение окружности для которой высота СD
есть диаметр и точки пересечения этой окружности со стороной АС;
) уравнение биссектрисы внутреннего угла А;
) площадь треугольника АВС;
) систему линейных неравенств, определяющих
треугольник АВС.
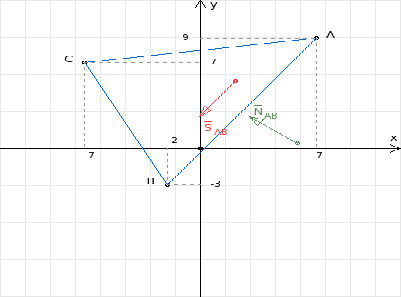
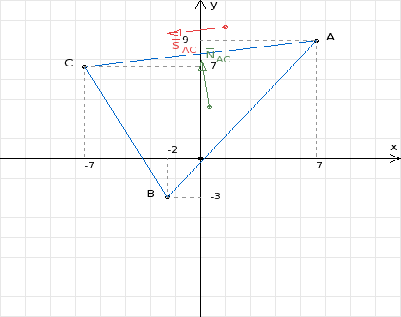
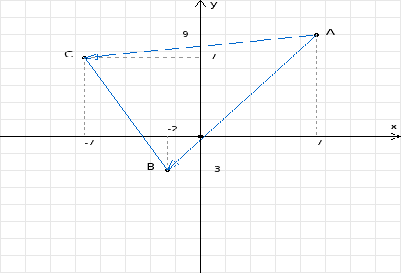
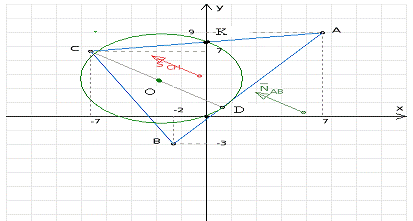
Сделать чертеж.
Дано:
А(7, 9); В(-2, -3); С(-7, 7)
Решение:
1) Найдем длину вектора 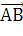
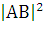 = (хb
- xa)2 + (yb - ya)2 =
((-2)-7)2 + (-3 - 9)2 = 92 + 122 =
225
= (хb
- xa)2 + (yb - ya)2 =
((-2)-7)2 + (-3 - 9)2 = 92 + 122 =
225
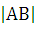 =
= 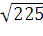 =
15 - длина
стороны АВ
=
15 - длина
стороны АВ
2) Найдем уравнение стороны АВ
Уравнение прямой, проходящей через точки
А(ха; ув) и В(ха;
ув) в общем виде
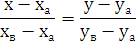
Подставим координаты точек А и В в это уравнение
прямой
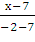 =
= 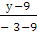
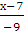 =
= 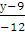
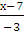 =
= 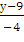
SAB
= (- 3, - 4) называется направляющим вектором прямой АВ. Этот вектор параллелен
прямой АВ.
4(х - 7) = - 3(у - 9)
4х + 28 = - 3у + 27
4х + 3у + 1 = 0 - уравнение прямой АВ
Если уравнение записать в виде: у = 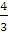 х
-
х
- 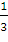 то
можно выделить его угловой коэффициент: k1
=4/3
то
можно выделить его угловой коэффициент: k1
=4/3
Вектор NAB
= (-4, 3) называется нормальным вектором прямой AB.
Вектор N AB = (-4, 3) перпендикулярен
прямой AB.
Аналогично найдем уравнение стороны АС
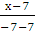 =
= 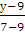
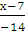 =
= 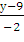
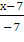 =
= 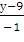
SAС
= (- 7, - 1) - направляющий вектор стороны АС
(х - 7) = - 7(у - 9)
х + 7 = - 7у + 63
х + 7у - 56 = 0 - уравнение стороны АС
у = 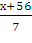 =
=
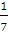 х
+ 8 откуда угловой коэффициент k2
= 1/7
х
+ 8 откуда угловой коэффициент k2
= 1/7
Вектор N AC = (- 1, 7) - нормальный
вектор прямой AC.
Вектор N AC = (- 1, 7)
перпендикулярен прямой AC.
3) Найдем угол А
Запишем формулу скалярного произведения векторов
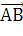 и
и
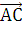
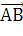 *
* 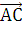 =
=
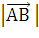 *
*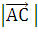 cos ∟A
cos ∟A
Для нахождения угла А достаточно найти косинус
данного угла. Из предыдущей формулы запишем выражение для косинуса угла А
cos ∟A = 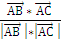
Находим скалярное произведение векторов 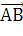 и
и
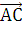
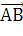 = (хв -
ха; ув - уа) = (- 2 - 7; - 3 - 9) = (-9, -12)
= (хв -
ха; ув - уа) = (- 2 - 7; - 3 - 9) = (-9, -12)
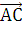 = (хс -
ха; ус - уа) = (- 7 - 7; 7 - 9 ) = (-14; -2)
= (хс -
ха; ус - уа) = (- 7 - 7; 7 - 9 ) = (-14; -2)
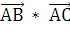 = -9*(-14) +
(-12)*(-2) = 150
= -9*(-14) +
(-12)*(-2) = 150
Длина вектора 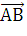 =
15 (нашли ранее)
=
15 (нашли ранее)
Найдем длину вектора 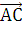
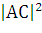 = (хС -
xа)2
+ (yс -
ya)2 =
(-14)2 + (-2)2 = 200
= (хС -
xа)2
+ (yс -
ya)2 =
(-14)2 + (-2)2 = 200
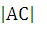 =
= 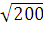 =
14,14 - длина стороны АС
=
14,14 - длина стороны АС
Тогда cos
∟A
= 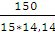 =
0,7072
=
0,7072
∟A
= 450
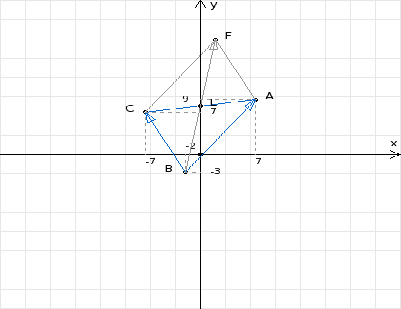
4) Найдем уравнение медианы ВЕ,
проведенной из точки В на сторону АС
Уравнение медианы в общем виде 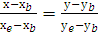
Теперь необходимо найти направляющий вектор
прямой ВЕ.
Достроим треугольник АВС до параллелограмма АВСD,
таким образом, чтобы сторона АС являлась его диагональю. Диагонали в
параллелограмме делятся пополам, т. е. АЕ = ЕС. Следовательно, точка E лежит на
прямой BF.
В качестве направляющего вектора прямой BE можно
принять вектор 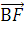 , который и найдем
.
, который и найдем
.
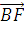 =
= 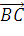 +
+
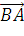
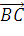 = (хc
- хb;
уc
- уb)
= (- 7- (-2); 7 - (-3)) = (-5. 10)
= (хc
- хb;
уc
- уb)
= (- 7- (-2); 7 - (-3)) = (-5. 10)
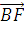 =
= 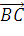 +
+
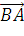 =
(-5 + 9; 10 + 12) = (4; 22)
=
(-5 + 9; 10 + 12) = (4; 22)
Подставим в уравнение
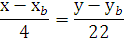
Подставим координаты точки С (-7; 7)
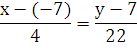
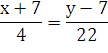
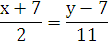
(х + 7) = 2(у - 7)
х + 77 = 2у - 14
х - 2у + 91 = 0 - уравнение медианы ВЕ
Так как точка Е - середина стороны АС, то ее
координаты
хе = (ха + хс)/2
= (7 - 7 )/2 = 0
уе = (уа + ус)/2
= (9 + 7)/2 = 8
Координаты точки Е (0; 8)
5) Найдем уравнение высоты CD
и ее длину
Уравнение в общем виде
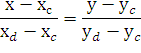
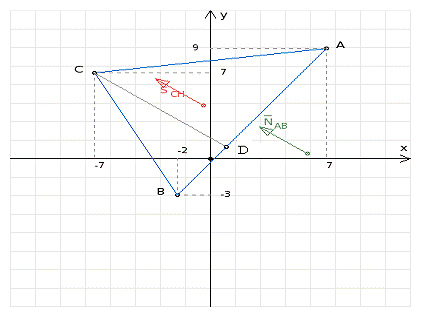
Необходимо найти направляющий вектор прямой СD
Прямая СD
перпендикулярна прямой АВ, следовательно, направляющий вектор прямой СD
параллелен нормальному вектору прямой АВ
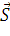 CD
‖
CD
‖
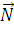 AB
AB
То есть в качестве направляющего вектора прямой CD
можно принять нормальный вектор прямой АВ
Вектор 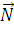 AB
найден ранее:
AB
найден ранее: 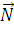 AB
(-4, 3)
AB
(-4, 3)
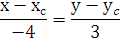
Подставим координаты точки С, (- 7; 7)
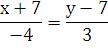
(х + 7) = - 4(у - 7)
х + 21 = - 4у + 28
х + 4у - 7 = 0 - уравнение высоты С D
Координаты точки D:
Точка D
принадлежит прямой АВ, следовательно, координаты точки D(xd.
yd) должны
удовлетворять уравнению прямой АВ, найденному ранее
Точка D
принадлежит прямой CD,
следовательно, координаты точки D(xd.
yd) должны
удовлетворять уравнению прямой CD,
Составим систему уравнений на основе этого
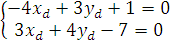
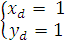
Координаты D(1;
1)
Найдем длину прямой CD
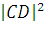 = (хd
- xc)2 + (yd - yc)2 = (1
+ 7)2 + (1 - 7)2 = 64 +36 = 100
= (хd
- xc)2 + (yd - yc)2 = (1
+ 7)2 + (1 - 7)2 = 64 +36 = 100
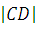 =
=  =
10
- длина
прямой СD
=
10
- длина
прямой СD
6) Найдем уравнение окружности
диаметром СD
Очевидно, что прямая СD
проходит через начало координат так как ее уравнение -3х - 4у = 0,
следовательно, уравнение окружности можно записать в виде
(х - а )2 + (у - b)2
= R2
- уравнение окружности с центром в точке (а; b)
Здесь R
= СD/2 = 10 /2 = 5
(х - а )2 + (у - b
)2 = 25
Центр окружности О (а; b)
лежит на середине отрезка СD.
Найдем его координаты:
х0 = a
= 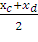 =
=
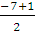 =
- 3;
=
- 3;
y0
= b = 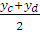 =
=
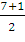 =
4
=
4
Уравнение окружности:
(х + 3)2 + (у - 4)2 = 25
Найдем пересечение этой окружности со стороной
АС:
точка К принадлежит одновременно окружности и
прямой АС
х + 7у - 56 = 0 - уравнение прямой АС, найденной
ранее.
Составим систему
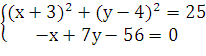
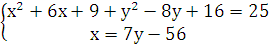
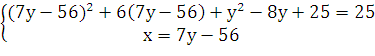
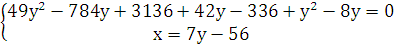
Таким образом, получили квадратное уравнение
у2 - 750у +2800 = 0
у2 - 15у + 56 = 0
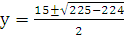 =
= 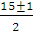
у1 = 8
у2 = 7 - точка, соответствующая точке
С
следовательно координаты точки Н:
х = 7*8 - 56 = 0
Н (0; 8)
7) Найдем уравнение биссектрисы
внутреннего угла А
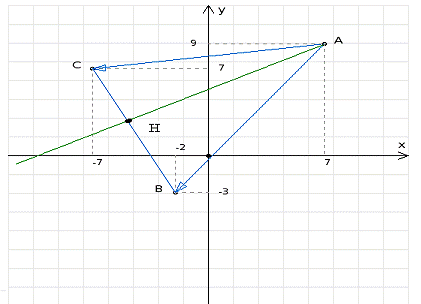
Воспользуемся свойством биссектрисы
треугольника:
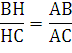
Если точка Н(xh
yh) лежит на прямой,
проходящей через две точки В(х1, у1) = (-2, -3) и С(х2,
у2) = (-7, 7) И дано отношение γ , в
котором точка Н делит отрезок ВС, то координаты точки Н определяются как
х = 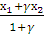 у
=
у
= 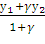
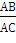 =
= 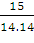 =
1.06066
=
1.06066
тогда xh
= 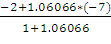 =
-4,574
=
-4,574
yh
= 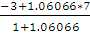 =
2,147
=
2,147
Зная две точки Н(- 4,574; 2,147) и А(7, 9)
найдем уравнение прямой
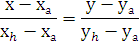
Подставим координаты точек А и H
в это уравнение прямой
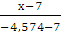 =
= 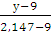
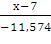 =
= 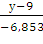
6,853(х - 7) = - 11,574(у - 9)
6,853х + 47,971 = -11,574у +104,166
,85х + 11,574у - 56,195 = 0 - уравнение биссектрисы
АН
8) Площадь треугольника
Площадь ориентированного треугольника в
декартовой системе координат:
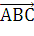 =
= 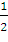
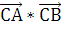
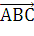 =
= 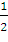
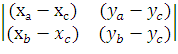 =
=
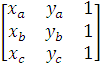
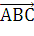 =
= 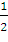
 =
=
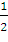
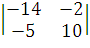 =
=
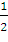 (-10*14
- (-5)*(-2))=
(-10*14
- (-5)*(-2))= 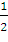 (-140 - 10) =
-150/2 = -75
(-140 - 10) =
-150/2 = -75
Окончательно: S
= 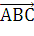 =
75
=
75
9) Составим систему линейных
неравенств
Запишем уравнения сторон треугольника АВС
4х + 3у + 1 = 0 - уравнение прямой АВ
х + 7у - 56 = 0 - уравнение стороны АС
уравнение стороны ВС:
С(хс; ус) и В(ха;
ув) в общем виде
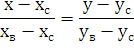
Подставим координаты точек С(-7, 7) и В(-2, -3)
в это уравнение прямой
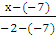 =
= 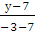
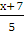 =
= 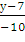
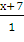 =
= 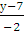
2(х + 7) = 1(у - 7)
х - 14 = у - 7
х - у - 7 = 0 - уравнение прямой СВ
Рассмотрим точку О (0, 0), лежащую внутри
треугольника,
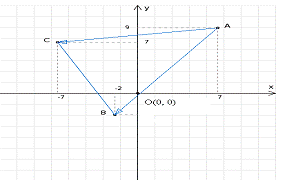
очевидно, что в итоге система неравенств примет
вид
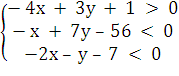
Замечание: проверим принадлежность, найденной
ранее точки пересечения биссектрисы с о стороной ВС, подставив координаты точки
Н в уравнение для прямой ВС:
*(-4,574) - 2,147 - 7 = 0
,147 - 2,147 - 9 = 0 - точка найдена верно!
Задание 2
Даны силы 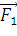 и
и
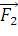 и
координаты точки М. найти:
и
координаты точки М. найти:
) равнодействующую силу 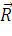 сил
сил
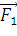 и
и
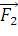 ,
ее величину и направляющие косинусы;
,
ее величину и направляющие косинусы;
) работу силы 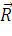 при
перемещении ее точки приложения из начало координат в точку М;
при
перемещении ее точки приложения из начало координат в точку М;
) момент силы 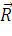 ,
приложенной к началу координат, относительно точки М. Сделать чертеж.
,
приложенной к началу координат, относительно точки М. Сделать чертеж.
Дано:
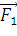 = - 7
= - 7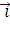 -
-  +
+
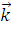
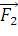 = 4
= 4 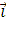 +
+
 +
3
+
3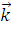
M (-2, -1, - 1)
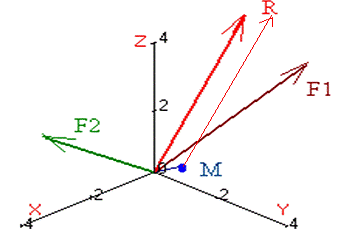
) Равнодействующая сила 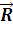 есть
векторная сумма
есть
векторная сумма 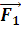 и
и 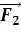
Модули заданных сил:
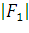 =
= 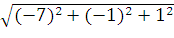 =
=
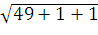 =
=
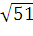
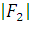 =
= 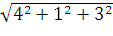 =
=
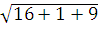 =
=
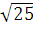 =
5
=
5
Найдем сумму векторов 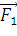 и
и
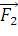 -
равнодействующую силу
-
равнодействующую силу
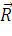 =
{(x1
+ x2);
(y1
+ y2);
(z1
+ z2)}
= {(-7 + 4); (-1 + 1); (1 + 3)} = {- 3; 0; 4}
=
{(x1
+ x2);
(y1
+ y2);
(z1
+ z2)}
= {(-7 + 4); (-1 + 1); (1 + 3)} = {- 3; 0; 4}
Ее величина: 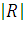 =
=
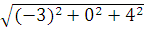 =
=
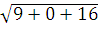 =
=
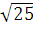 =
5
=
5
Направляющие косинусы:
Cos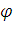 1
=
1
= 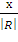 =
=
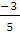 =
- 0.6
=
- 0.6
Cos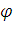 2
=
2
= 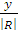 =
=
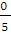 =
0
=
0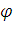 3
=
3
= 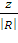 =
=
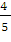 =
0.8
=
0.8
) Найдем
вектор
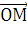 =
=
={(xМ
- x0 ); (yМ
- y0); (zМ
- z0)} = {(-2 + 0); (-1 - 0); (-1 - 0
)} = {- 2;
-1;
-1}
Тогда работа по перемещению точки приложения
силы 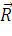 :
:
А = 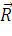 *
*
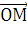 =
{- 3; 0; 4}*
=
{- 3; 0; 4}*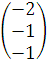 = 6 - 0 - 4 = 2
= 6 - 0 - 4 = 2
) Вычислим момент силы 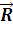 ,
приложенной к началу координат, относительно точки М
,
приложенной к началу координат, относительно точки М
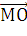 = (2, 1, 1), тогда
искомый момент будет равен векторному произведению векторов
= (2, 1, 1), тогда
искомый момент будет равен векторному произведению векторов 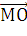 и
и
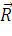 :
:
Т = 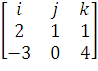 =
i (1*4 - 0*1) - j(2*4
- 1*(-3)) + k(2*0 - (-3)*1) = 4i
- 11j +3k
=
i (1*4 - 0*1) - j(2*4
- 1*(-3)) + k(2*0 - (-3)*1) = 4i
- 11j +3k
Задание 3
треугольник тетраэдр геометрический неравенство
) длину ребра А1А2;
) угол между А1А2 и А1А3;
) угол между ребром А1А4 и
гранью А1А2А3;
) площадь грани А1А2А3;
) объем пирамиды;
) уравнение прямой А1А2;
) уравнение плоскости А1А2А3;
) уравнение высоты, опущенной из вершины А4
на грань А1А2А3 и ее длину;
) координаты центра тяжести пирамиды, считая
плотность постоянной.
Построить чертеж.
Дано:
А1 (-7, -1, 2)
А2 (3, 9, 7)
А3 (-3, -3, -2)
А4(-13, -1, -4).
Решение начнем с построения чертежа (рис 1)
1) Найдем длину ребра А1А2
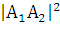 = (х2 -
x1)2
+ (y2-
y1)2
+ (z2
- z1)2
= (3 - (-7))2 + (9 - (-1))2 +(7 - 2)2 = =102
+ 102 + 52 = 225
= (х2 -
x1)2
+ (y2-
y1)2
+ (z2
- z1)2
= (3 - (-7))2 + (9 - (-1))2 +(7 - 2)2 = =102
+ 102 + 52 = 225
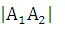 =
= 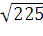 =
15 - длина стороны
=
15 - длина стороны 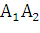
2) угол между А1А2
и А1А3
Найдем координаты векторов:
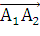 = ((х2
- x1)
+ (y2-
y1)
+ (z2
- z1))
= (10; 10; 5), его длина
= ((х2
- x1)
+ (y2-
y1)
+ (z2
- z1))
= (10; 10; 5), его длина 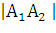 = 15
= 15
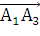 = ((х3
- x1)
+ (y3-
y1)
+ (z3
- z1))
= (-3 - (-7); -3 - (-1); -2 - 2 ) = (4; - 2; - 4), его длина
= ((х3
- x1)
+ (y3-
y1)
+ (z3
- z1))
= (-3 - (-7); -3 - (-1); -2 - 2 ) = (4; - 2; - 4), его длина 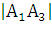 =
=
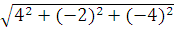 =
=
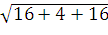 =
=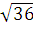 = 6
= 6
запишем выражение для косинуса угла φ
cos φ = 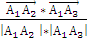
φ
= 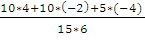 =
=
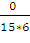 =
0, т. е. угол φ = 900
- прямой
=
0, т. е. угол φ = 900
- прямой
следовательно, треугольник - основание пирамиды А1А2А3
- прямоугольный треугольник
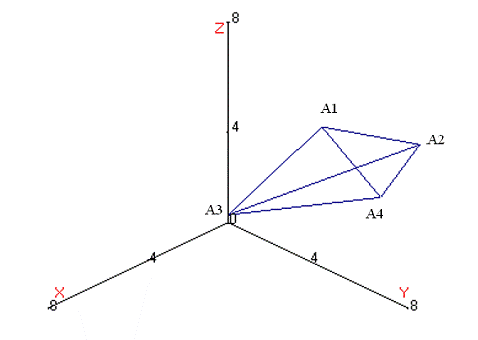
Рис.1. Исходная пирамида
3) Угол между ребром А1А4
и плоскостью А1А2А3 есть угол β
= ∟КА1А4 между ребром
А1А4 и ортогональной проекцией А1К на
плоскость А1А2А3
Направляющий вектор
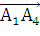 = ((х4
- x1)
+ (y4-
y1)
+ (z4
- z1))
=
= ((х4
- x1)
+ (y4-
y1)
+ (z4
- z1))
=
= {(-13) - (-7); -1 - (-1); (-4 - 2)} = (-6; 0;
-6) = (х14; у14; z14)
Пусть 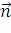 =
(xn; yn;
zn) - нормальный
вектор к плоскости А1А2А3, тогда φ
= угол
между А1А4 и
=
(xn; yn;
zn) - нормальный
вектор к плоскости А1А2А3, тогда φ
= угол
между А1А4 и 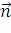 и
искомый угол
и
искомый угол
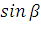 =
= 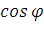 =
=
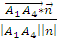 =
=
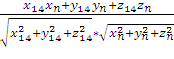
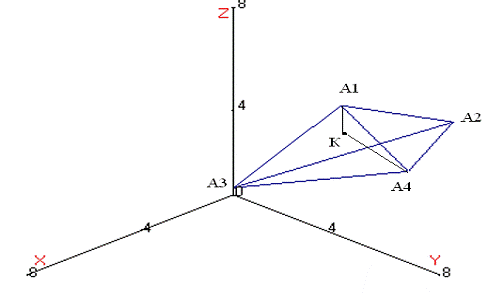
Рис. 2.
Находим нормальный вектор 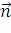
xn = 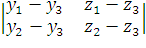 =
=
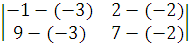 =
=
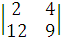 =
18 - 48 = -30n =
=
18 - 48 = -30n = 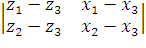 =
= 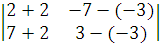 =
=
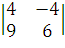 =
24 + 36 = 60n = -
=
24 + 36 = 60n = - 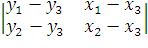 =
= 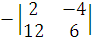 =
-(12 + 48) = - 60
=
-(12 + 48) = - 60
вектор 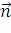 =
(-30; 60; -60) = (-1; 2; -2)
=
(-30; 60; -60) = (-1; 2; -2)
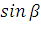 =
= 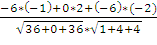 =
=
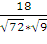 =
=
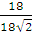 =
=
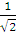 =
=
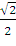
β = 450
4) Площадь грани А1А2А3
Найдем векторное произведение 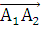 *
*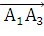
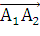 = (10, 10, 5)
= (10, 10, 5)
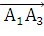 = (4, -2, -4)
= (4, -2, -4)
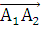 *
*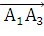 =
= 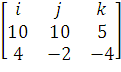 =
i
=
i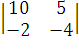 - j
- j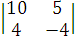 + k
+ k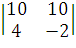 =
=
 (-40+10) - j(-40
- 20) + k(-20 - 40 ) = -30i
+60j - 60k
= {-30; 60; -60}
(-40+10) - j(-40
- 20) + k(-20 - 40 ) = -30i
+60j - 60k
= {-30; 60; -60}
тогда площадь грани А1А2А3
S
А1А2А3
= 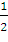
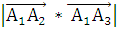 =
=
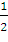
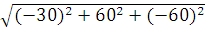 =
=
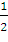
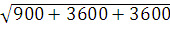 =
=
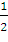
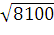 =
90/2 = 45
=
90/2 = 45
5) Объем пирамиды
Найдем координаты векторов 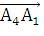 ;
;
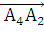 и
и
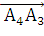 :
:
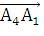 = (-7-(-13), -1 -
(-1), 2 - (-4)) = (6, 0, 6)
= (-7-(-13), -1 -
(-1), 2 - (-4)) = (6, 0, 6)
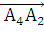 = (3 - (-13), 9 -
(-1), 7- (-4)) = (16, 10, 11)
= (3 - (-13), 9 -
(-1), 7- (-4)) = (16, 10, 11)
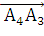 = (-3- (-13), -3 -
(-1), -2 - (-4)) = (10, -2, 2)
= (-3- (-13), -3 -
(-1), -2 - (-4)) = (10, -2, 2)
Находим смешанное произведение векторов ( 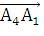 х
х
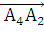 )*
)*
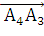 :
:
( 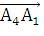 х
х
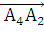 )*
)*
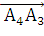 =
=
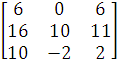 =
6*(10*2 - (-2)*11) - 0 + 6(16*(-2) - 10*10) = 6*42 + 6*(-32 - 100) = 6*42 +
6*(-132) = - 6*90 = - 540
=
6*(10*2 - (-2)*11) - 0 + 6(16*(-2) - 10*10) = 6*42 + 6*(-32 - 100) = 6*42 +
6*(-132) = - 6*90 = - 540
Найдем объем пирамиды:
V= 1/6*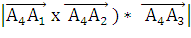 = 1/6*540 = 90
= 1/6*540 = 90
6) Уравнение прямой А1А2
Воспользуемся формулой
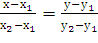 =
= 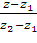
Подставим в формулу координаты точек
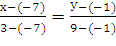 =
= 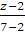
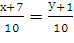 =
= 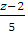
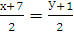 =
= 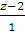
7) Уравнение плоскости А1А2А3
Возьмем произвольную точку А (х, у, z),
принадлежащую плоскости уравнение которой необходимо найти.
Находим координаты следующих векторов:
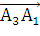 = (-7- (-3), -1 -
(-3), 2 - (-2)) = (-4, 2, 4)
= (-7- (-3), -1 -
(-3), 2 - (-2)) = (-4, 2, 4)
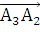 = (3 - (-3), 9 -
(-3), 7 - (-2)) = (6, 12, 9)
= (3 - (-3), 9 -
(-3), 7 - (-2)) = (6, 12, 9)
Данные векторы имеют своё начало в точке А3
Очевидно, что если все четыре точки лежат в
одной плоскости, то объем треугольной пирамиды, ребрами которой являются
найденные векторы, равен нулю.
Равенство нулю объема рассматриваемой пирамиды
записывается следующим образом:
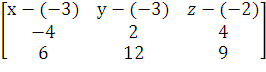 = 0
= 0
Представим данный определитель в виде разности
двух определителей
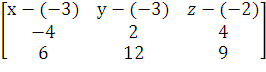 =
= 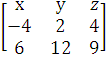 -
-
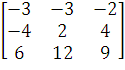 =
0
=
0
х(18 - 48) - у (-36-24) + z(-48
-12) - {-3*(18 - 48) + 3*(-36 - 24) - 2*(-48 - 12)} = -30х +60у -60z
- (90 - 180 + 120) = -30х +60у - 60z
-30 = 0
окончательно:
х +60у - 60z
-30 = 0
х +2у -2z
- 1 = 0
8) Tак
как высота А4К (рис. 2) перпендикулярна плоскости А1А2А3
в качестве ее направляющего вектора можно выбрать вектор нормали
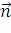 = (-30; 60; -60) =
(-1; 2; -2)
= (-30; 60; -60) =
(-1; 2; -2)
Так как прямая проходит через точку А4
ее каноническое уравнение принимает вид:
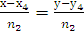 =
= 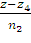
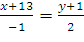 =
= 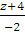
Длина высоты - это расстояние от вершины А4(-13,
-1, -4) до плоскости А1А2А3 -х +2у -2z
- 1 = 0
А4К = 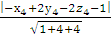 =
=
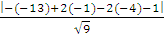 =
=
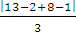 =
6
=
6
9) Найдем координаты центра
масс G
тетраэдра:
Хц.м = 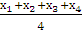 =
=
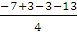 =
-5
=
-5
Yц.м
= 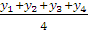 =
=
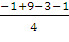 =
1
=
1
Zц.м
= 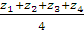 =
=
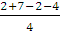 =
0.75
=
0.75
(Хц.м., Yц.м,
Zц.м)
= (- 5; 1; 0.75)
Задание 4
Составить уравнение геометрического места точек,
для каждой из которых отношение расстояния до данной точки А (х1, у1)
к расстоянию до данной прямой у = b
равно числу k . полученное
уравнение привести к каноническому виду и построить кривую.
Дано:
А(7, -4)
у = 2,
k = 1.
Решение:
Обозначим искомое геометрическое место точек
через М (х, у), тогда
· расстояние между точками
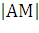 =
= 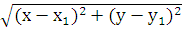 =
=
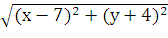
· расстояние от точки M (х, у) до
прямой Ax + By + C = 0
d = 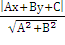 =
=
 =
=
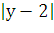
по условию 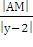 =
1
=
1
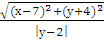 = 1
= 1
Произведем последовательные преобразования:
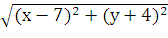 =
= 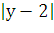
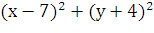 =
= 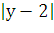 2
2
(х - 7)2 + у2 +8у + 16 - у2
+4у - 4 = 0
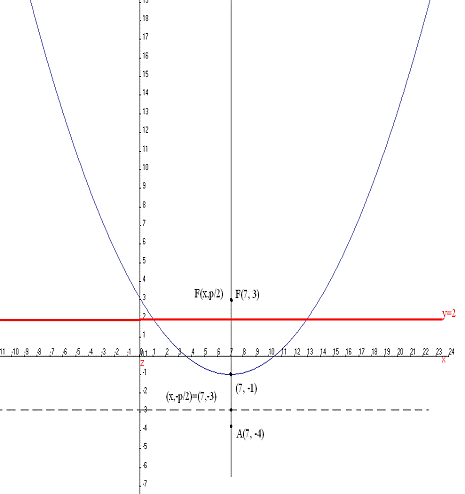
(х - 7)2 = 12у + 12
(х - 7)2 = - 2*(-6)(у + 1)
А это уравнение параболы относительно х
х2 = -2ру - каноническое уравнение
параболы
6 - фокальный параметр
у = - 3 - директриса
координаты вершины параболы: (7; -1)
координаты фокуса: (7; 3)
Задание 5
Линия задана уравнением в полярной системе
координат. Требуется:
) построить по точкам, от φ
= 0
до φ
= 2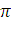 ;
;
) найти уравнение данной линии в прямоугольной
системе координат, у которой начало совпадает с полюсом, а положительная
полуось абсцисс - с полярной осью;
) по полученному уравнению определить какая это
линия
Дано: r
= 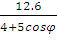
Решение:
1) сделаем построения по точкам
|
φ
|
0
|
π/6
|
π/4
|
π/3
|
π/2
|
2π/3
|
3π/4
|
5π/6
|
π
|
|
r
|
1,512
|
1,672
|
1,938
|
3,15
|
8,4
|
27,128
|
-38,167
|
-12,6
|
|
φ
|
7π/6
|
5π/4
|
4π/3
|
3π/2
|
5π/3
|
7π/4
|
11π/6
|
2π
|
|
|
r
|
-38,167
|
27,128
|
8,4
|
3.15
|
1,938
|
1,672
|
1,512
|
1,4
|
|
Выделенные элементы смысла не имеют.
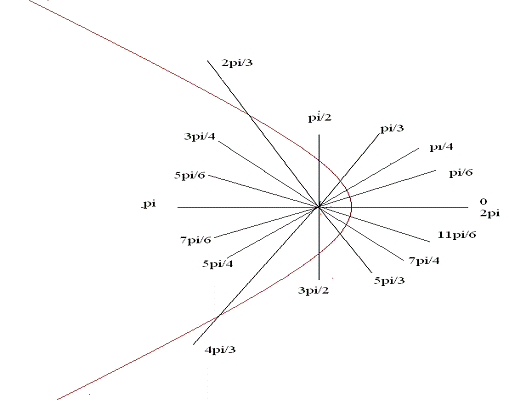
2) перейдем к декартовой
системе координат
r = 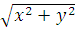
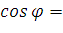

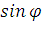 =
= 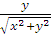 =
=
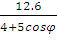 =
=
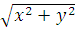 =
=
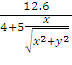
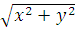 =
= 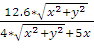
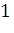 =
= 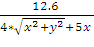
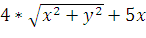 = 12.6
= 12.6
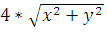 = 12.6 - 5x
= 12.6 - 5x
(x2 + y2) =
158.76 - 126x + 25x2
9x2
- 16y2
- 126x + 158.76
(x2
- 14x + 49) - 16y2
- 282.24 = 0
(x
- 7)2 - 16y2
= 282.24
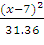 -
- 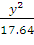 =
1 - уравнение гиперболы
=
1 - уравнение гиперболы
Центр смещен по оси Х в точку (+7, 0)
a = 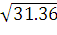 =
5.6 b =
=
5.6 b = 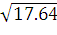 =
4.2
=
4.2
координаты вершин гиперболы:
А1 (7 - 5,6; 0) = (1,4; 0)
А2 (7 + 5,6; 0) = (13,6; 0)
Асимптоты:
у1 = bx/a
= 0.75(x - 7)
y2
= -bx/a
= -0.75(x - 7)
эксцентриситет гиперболы: е = 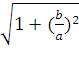 =
=
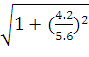 =
1.25
=
1.25
c = a*e
= 5.6*1.25 = 7
следовательно, фокусы гиперболы
F1
= (7 - 7; 0) = (0; 0)
F2
= (7 + 7; 0) = (14; 0)