Субмикронные полевые транзисторы с барьером Шоттки
Міністерство освіти і науки
молоді та спорту України
Харківський Національний
Університет імені В.Н. Каразіна
Радіофізичний факультет
Кафедра фізичної і
біомедичної електроніки та комплексних інформаційних технологій
Звіт з переддипломної
практики
СУБМІКРОННІ ПОЛЬОВІ
ТРАНЗИСТОРИ З БАР’ЄРОМ ШОТТКІ
Науковий керівник
к.ф.-м. н., с.н.с.
О. В. Боцула
Автор
студент групи РР-43
Я.О. Кадничанський
Харків 2012
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
. ЭЛЕКТРОННЫЙ ТРАНСПОРТ В ПОЛУПРОВОДНИКАХ
.1 Всплеск во времени дрейфовой скорости насыщения при
воздействии электрического поля
.2 Всплеск дрейфовой скорости в коротких структурах
.3 Баллистический транспорт в полупроводниках и субмикронных
приборах
.4 Методы математического моделирования кинетических
процессов
.5 Полевой транзистор с барьером Шоттки
. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИКИ СУБМИКРОННЫХ СТРУКТУР
.1 Общая процедура моделирования
.1.1 Модель зоны проводимости и механизмы рассеяния
.1.2 Задание начальных условий
.1.3 Движение частицы во внешнем поле и определение времени
свободного пробега
.1.4 Законы сохранения и правила отбора при рассеянии
.1.5 Определение состояния частицы после рассеяния
.1.6 Определение вероятности рассеяния и конечного состояния
.2 Вычисление распределения потенциала и электрического поля
.3 Электронный транспорт в субмикронном транзисторе с
барьером Шоттки
ВЫВОДЫ
СПИСОК ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Характерные размеры современных полупроводниковых
приборов могут быть значительно меньше 1 мкм. В таких условиях длина прибора
может стать сравнимой со средней длиной свободного пробега носителей в
полупроводнике, а время пролета может оказаться примерно равным или меньше
среднего времени релаксации. Как отмечалось в работе, в таких условиях не
успевает установиться равновесное распределение, и средняя дрейфовая скорость
электронов в активной области прибора может существенно превосходить значения
насыщенной или даже максимальной скорости в длинных образцах. Это увеличение
скорости за счет нестационарных эффектов получило название «эффекта всплеска
скорости». В предельном случае, когда можно полностью пренебречь столкновениями
электронов с решеточными фононами и примесями, перенос электронов был назван
«баллистическим». Благодаря возможному улучшению характеристик приборов за счет
высоких скоростей электронов в приборах малого размера эта область привлекла
особое внимание исследователей.
Электронный перенос в коротких приборных структурах
весьма сложен.
В настоящей работе он исследуется в субмикронных полевых транзисторах с
барьером Шоттки (ПТШ). Наиболее широкое применение на СВЧ находят ПТШ на
арсениде галлия, который имеет высокую подвижность электронов. Лучшие образцы
полевых транзисторов из арсенида галлия характеризуются коэффициентом шума, 0,5
- 1,4дБ на частотах 0,5 - 18ГГц и 5-6 дБ на частотах миллиметрового диапазона и
выше.
1. ЭЛЕКТРОННЫЙ ТРАНСПОРТ В ПОЛУПРОВОДНИКАХ
.1 Всплеск во времени дрейфовой скорости насыщения при
воздействии электрического поля
Будем
прикладывать к полупроводнику электрическое поле в виде импульса с крутым
передним фронтом. Задача заключается в том, чтобы отрезок времени, на котором
действует поле, был короче времени между столкновениями 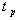 . Следовательно, на протяжении этого отрезка времени
электрон будет разгоняться без столкновений до величины дрейфовой скорости,
определяемой обычной формулой для
. Следовательно, на протяжении этого отрезка времени
электрон будет разгоняться без столкновений до величины дрейфовой скорости,
определяемой обычной формулой для  (1.1.6),
где только время релаксации
(1.1.6),
где только время релаксации 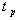 будет
заменено на отрезок времени
будет
заменено на отрезок времени 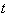 -
длительность импульса приложенного напряжения:
-
длительность импульса приложенного напряжения:
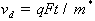 ,
, 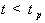 (1.1.1)
(1.1.1)
Исходя
из этих простых рассуждений можно ожидать, что в достаточно сильных
электрических полях скорость  достигнет
величин, значительно больших, чем в случае воздействия более протяженного во
времени стационарного электрического поля, когда включаются механизмы
рассеяния, уменьшающие скорость.
достигнет
величин, значительно больших, чем в случае воздействия более протяженного во
времени стационарного электрического поля, когда включаются механизмы
рассеяния, уменьшающие скорость.
Для
определения оптимальной протяженности во времени прикладываемого к образцу
(каналу транзистора) импульса поля проводят исследования, используя ступеньки
напряжения с идеально резким фронтом.
На
рис. 1.1 приведены рассчитанные по методу Монте-Карло зависимости дрейфовой
скорости в Si для температуры 293 и 77 К; на вставке изображена зависимость
напряженности электрического поля (Е = 10 кВ/см) от времени. Кроме того,
показано изменение средней энергии электронов. Видно, что изменение дрейфовой
скорости во времени для таких условий характеризуется начальным всплеском (overshoot),
который достигает максимума, а затем быстро спадает до стационарного значения.
Весь процесс разгона и затухания, как видно, происходит за время 0,5...1,0 пс.

Рис.
1.1. Воздействие на энергию и скорость электронов импульса электрического поля
длительностью 6 пс и напряженностью:
1-5 кВ/см, 2-10 кВ/см; а
-  - дрейфовая
скорость всех электронов,
- дрейфовая
скорость всех электронов,  - в Г-долине; б -энергия электронов в
Г-долине (штриховые кривые) и относительное число электронов в боковых долинах
(сплошные кривые) [7]
- в Г-долине; б -энергия электронов в
Г-долине (штриховые кривые) и относительное число электронов в боковых долинах
(сплошные кривые) [7]
Электроны
сначала разгоняются до скорости 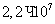 см/с, а
затем (через
см/с, а
затем (через 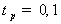 пс при 77 К), достигнув энергии оптических фононов,
начинают активно рассеиваться на них и теряют накопленный добавок к стационарной
скорости. За время, примерно равное 0,1 пс, дрейфовая скорость
пс при 77 К), достигнув энергии оптических фононов,
начинают активно рассеиваться на них и теряют накопленный добавок к стационарной
скорости. За время, примерно равное 0,1 пс, дрейфовая скорость  спадает до стационарного значения, т. е. в сумме
всего за 0,2...0,4 пс она достигает стационарного значения, характерного для
сильного электрического поля
спадает до стационарного значения, т. е. в сумме
всего за 0,2...0,4 пс она достигает стационарного значения, характерного для
сильного электрического поля 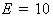 кВ/см (
кВ/см (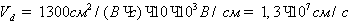 ). Из рисунка также видно, что средняя энергия
электрона при этом плавно растет во времени, насыщаясь практически в момент
достижения стационарного значения
). Из рисунка также видно, что средняя энергия
электрона при этом плавно растет во времени, насыщаясь практически в момент
достижения стационарного значения  .
.
На
рис. можно проследить этот процесс в динамике.
Видно,
что энергия электронов в Г-долине после выключения электрического поля довольно
долго сохраняет величину выше стационарной, а скорость электронов резко падает.
Это происходит вследствие того, что электроны в Г-долине из-за столкновений
быстро теряют возможность бесстолкновительного движения (хотя энергия велика),
а большое количество электронов в боковых долинах, хотя и обладает энергией
выше стационарной, имеет гораздо более низкую скорость (подвижность). Также
хорошо видно, что повышение электрического поля с 5 до 10 кВ/см, увеличивает
максимальную скорость, но сам эффект всплеска (так как 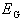 становится больше
становится больше 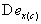 ) длится
гораздо меньше из-за междолинного переброса.
) длится
гораздо меньше из-за междолинного переброса.
После
выключения электрического поля некоторое время электроны двигаются по инерции
или, как еще говорят, «баллистически». Затем многочисленные столкновения быстро
прекращают этот инерционный полет электронов. Причем такой спад идет намного
быстрее, чем процесс остывания и возвращения электронов к равновесному
распределению между долинами.
Именно
задержка последних двух процессов при резком уменьшении внешнего поля даже на
небольшую величину приводит к сильному уменьшению дрейфовой скорости. Этот
эффект называется «обратным всплеском скорости» - в англоязычной литературе -
«undershoot» или эффект Риса [9] по имени ученого, впервые объяснившего таким
образом это явление.
Подводя
итоги, можно сказать, что эффект всплеска скорости во времени позволяет
получить максимальные дрейфовые скорости, в несколько раз превышающие их
стационарные значения. Величины времен релаксации, получаемые при этом (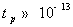 с,
с, 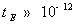 с),
позволяют предполагать, что возможности использования исследуемых
полупроводниковых материалов сохраняются до 100...500 ГГц.
с),
позволяют предполагать, что возможности использования исследуемых
полупроводниковых материалов сохраняются до 100...500 ГГц.
1.2
Всплеск дрейфовой скорости в коротких структурах
На
коротких отрезках времени можно получить значительное (в разы!) увеличение
дрейфовой скорости. Если приложить к каналу транзистора соответствующее
электрическое поле так, чтобы электроны пролетали активную область за очень
короткий промежуток времени, то средняя дрейфовая скорость в этой области
окажется значительно выше стационарной.
Если
скорость электрона будет на уровне 107 см/с, то он пролетит область
10-5 см (0.1 мкм) за 10-12 с. Это означает, что ожидаемый
всплеск дрейфовой скорости во времени будет достаточно длительным, т. е. будет
существовать во все время пролета. Иными словами, этот всплеск скорости во
времени приведет к всплеску скорости в субмикронных структурах по
пространственной координате на всю толщину структуры.
Рассуждения
о всплеске скорости во времени основывались на изменении параметров полупроводников
в условиях воздействия «теоретического импульса» со сверхрезким фронтом
(субпикосекундным!), что почти нереально. В то же время осуществление всплеска
скорости в пространстве - явление, реализуемое в полупроводниковых структурах и
носит стационарный характер.
Необходимый
скачок (резкое увеличение электрического поля) реализуется за счет заранее
заданной неоднородности полупроводниковой структуры по координате. Когда
электроны попадают в область резкого изменения электрического поля, они испытывают
резкое изменение скорости или эффект всплеска. Такой неоднородной структурой
может служить хорошо известная и легко осуществимая  - структура, которая была получена в [10] с помощью
двусторонней имплантации Si в пластину GaAs.
- структура, которая была получена в [10] с помощью
двусторонней имплантации Si в пластину GaAs.
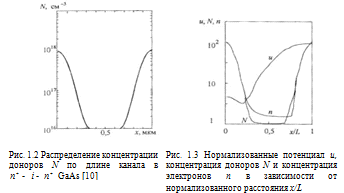
В
результате последующего отжига дефектов и неизбежной в таких случаях
диффузионной разгонки получена структура с распределением концентраций доноров,
показанным на рис. 1.2.
На
рис. 1.3 приведены рассчитанные с использованием рис. 1.2 зависимости
концентрации доноров, носителей заряда и потенциала (в относительных единицах)
от нормализованного расстояния X/L, где L - длина канала, которая в результате
расчета составила 0,75 мкм. К этой структуре прикладывался импульс напряжения
(300 пс), длинный по сравнению с временами релаксации, которые, как отмечалось
выше, порядка 1 пс (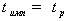 ). Исходя из этого соотношения такую большую
длительность импульса можно трактовать просто как подключение «постоянного»
напряжения к структуре. Амплитуда импульса изменялась от 0,2 до 10 В. Расчеты
проводились для комнатной температуры.
). Исходя из этого соотношения такую большую
длительность импульса можно трактовать просто как подключение «постоянного»
напряжения к структуре. Амплитуда импульса изменялась от 0,2 до 10 В. Расчеты
проводились для комнатной температуры.
Ясно,
дрейфовая скорость сначала должна расти, пока энергия, полученная электроном от
поля, не достигнет энергии переброса, а затем упадет до стационарных значений
из-за междолинных перебросов и рассеяния на оптических фононах. Но эти эффекты
начинают сказываться только при значительно больших полях, что и приводит к
насыщению роста тока. До такого насыщения рост тока обусловлен наличием
пространственного всплеска дрейфовой скорости (пространственный «overshoot»).
Измерив
ВАХ описанных выше структур, можно определить подвижность, а затем и скорость
электронов в зависимости от электрического поля и расстояния.
На
рис. 1.4 представлена полученная в результате таких расчетов зависимость
дрейфовой скорости от электрического поля, а на рис. 1.5 показано изменение
дрейфовой скорости в реальном пространстве структуры. Видно, что дрейфовая
скорость во всем объеме структуры, за исключением районов 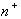 - контактов, порядка 3·107 см/с.
- контактов, порядка 3·107 см/с.
Проанализируем
теперь физическую картину происходящего в короткой структуре. Наиболее удачно
такой анализ проведен в [6].
Если
принять, что после скачкообразного включения электрического поля в течение
всего времени пролета электронов через структуру напряженность электрического
поля остается постоянной, то расстояние, которое проходит электрон до
достижения энергии, равной энергии междолинного перехода (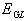 ), можно рассчитать по формуле
), можно рассчитать по формуле
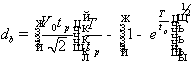 , (1.2.1)
, (1.2.1)
где
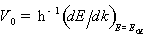 -максимальная скорость, которую может достичь
электрон, прежде чем испытает междолинное рассеяние; Т - время, за которое
электроны приобретают энергию, чуть меньшую
-максимальная скорость, которую может достичь
электрон, прежде чем испытает междолинное рассеяние; Т - время, за которое
электроны приобретают энергию, чуть меньшую 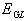 . Если
. Если  - толщина активной части прибора, то понятно, что
необходимо так подбирать T (т. е. значение поля
- толщина активной части прибора, то понятно, что
необходимо так подбирать T (т. е. значение поля 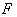 ), чтобы
), чтобы 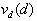 было максимальным.
было максимальным.
Результаты
таких расчетов из [6] представлены на рис. 1.6. Видно, что на довольно больших
расстояниях (доли микрон) дрейфовая скорость превышает стационарную скорость.
Рис.
1.6 Зависимость максимального значения дрейфовой скорости от расстояния
в GaAs для двух концентраций примеси:
кривая
1-n = 0, кривая 2-п = см-3, T =293 К
см-3, T =293 К
Эта
ясная и простая картина, конечно, в реальном случае изменяется из-за таких
причин, как неоднородности концентраций, объемного заряда и средней энергии
носителей заряда по толщине структуры. Наличие этих факторов приводит к
диффузии носителей и изменению конфигурации поля.
1.3
Баллистический транспорт в полупроводниках и субмикронных приборах
Электрон
при взаимодействии с электрическим полем переходит в возбужденное состояние,
затем он возвращается к равновесию в результате взаимодействия (столкновений) с
различными дефектами. Чаще всего для этого достаточно одного-двух столкновений.
Отсюда можно заключить, что время релаксации (за которое возбуждение электрона
уменьшается в  раз) порядка времени, необходимого для прохождения
длины свободного пробега электрона,
раз) порядка времени, необходимого для прохождения
длины свободного пробега электрона,
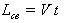 . (1.3.1)
. (1.3.1)
Известно,
что в общем случае время релаксации есть функция энергии. Напомним, что
существуют два времени релаксации: 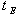 - время
релаксации по энергии и
- время
релаксации по энергии и 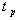 - время релаксации по импульсу, причем, так как
- время релаксации по импульсу, причем, так как 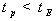 ,
,
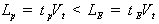 . (1.3.2)
. (1.3.2)
Это
означает, что размеры активной области нужно сравнить с этими длинами
релаксации. Кроме того, отметим, что в процесс включился эффект увеличения
дрейфовой скорости за времена менее 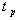 , что
привело к увеличению
, что
привело к увеличению 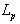 и, следовательно, возникновению явления, которое мы
назвали пространственный overshoot. Другими словами, ни контакты, ни дефекты
кристалла не успевают нарушить обычного движения электрона, что похоже на
свободное движение тела в классической физике.
и, следовательно, возникновению явления, которое мы
назвали пространственный overshoot. Другими словами, ни контакты, ни дефекты
кристалла не успевают нарушить обычного движения электрона, что похоже на
свободное движение тела в классической физике.
Рассмотрим
зависимость 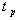 и
и  от
энергии электрона. На рис. 1.14, а приведена зависимость интегральной частоты
(темпа) рассеяния от энергии электрона, на рис. 1.14, б - скорость, которую
может достичь электрон в центральной долине. Штриховая линия соответствует
параболической долине, откуда и взято значение эффективной массы, необходимой
для расчета. Точка 1 - энергия оптического фонона, точка 2 - энергия
междолинного перехода. Понятно, что высокую скорость могут получить электроны,
обладающие энергией ниже энергии оптических фононов и междолинного перехода. Из
рисунка хорошо видно, что в первом случае мы получим скорость не выше
от
энергии электрона. На рис. 1.14, а приведена зависимость интегральной частоты
(темпа) рассеяния от энергии электрона, на рис. 1.14, б - скорость, которую
может достичь электрон в центральной долине. Штриховая линия соответствует
параболической долине, откуда и взято значение эффективной массы, необходимой
для расчета. Точка 1 - энергия оптического фонона, точка 2 - энергия
междолинного перехода. Понятно, что высокую скорость могут получить электроны,
обладающие энергией ниже энергии оптических фононов и междолинного перехода. Из
рисунка хорошо видно, что в первом случае мы получим скорость не выше 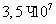 см/с и порядка 108 см/с во втором.
Последний случай, конечно, более интересен для практики.
см/с и порядка 108 см/с во втором.
Последний случай, конечно, более интересен для практики.
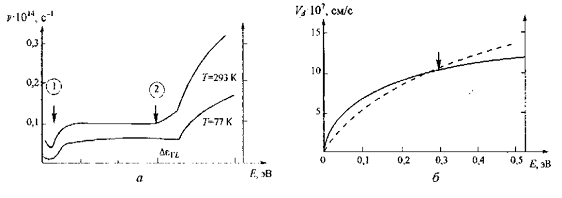
Рис.
1.7 Зависимости интегральной частоты столкновений в Г-долине (а) и
скорости электронов (б) от энергии электронов [6]
Теперь
нам нужно отыскать наилучший путь достижения такого состояния электронной
системы, когда энергия электронов была бы чуть меньше энергии междолинных
переходов, а скорость и энергия изменялись вначале как можно более резко. Для
этого имеет смысл рассмотреть возможность влияния электрических полей различной
конфигурации на энергию и скорость электрона.
Предположим,
что время релаксации по импульсу и эффективная масса остаются постоянными для
энергий, меньших энергии междолинных переходов. Кроме того, как обычно,
считаем, что 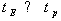 . С этими предположениями для нахождения связи между
. С этими предположениями для нахождения связи между  и Т можно снова использовать классические
релаксационные выражения или уравнения баланса усредненных импульса и энергии
(1.1.2) и (1.1.3).
и Т можно снова использовать классические
релаксационные выражения или уравнения баланса усредненных импульса и энергии
(1.1.2) и (1.1.3).
Если
электрическое поле во время движения носителя заряда (случай overshoot)
остается постоянным, расстояние, пройденное ими за время Т, записывается, как
мы уже зафиксировали, в виде
 . (1.3.3)
. (1.3.3)
В
случае же баллистического движения (предполагая включение очень короткого
импульса электрического поля в самом начале движения) пройденное расстояние
будет равно
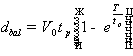 . (1.3.4)
. (1.3.4)
В
рамках принятых нами допущений для точки 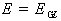 зависимости
зависимости
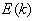 начальная скорость равна
начальная скорость равна
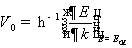 . (1.3.5)
. (1.3.5)
Эта
величина есть также максимальная скорость для 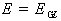
В
предположении постоянства эффективной массы по всей Г-долине до перехода в
верхнюю долину 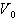 можно найти и из выражения
можно найти и из выражения
 .
.
Тогда
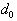 будет являться характеристическим расстоянием
(постоянной), зависящим только от природы полупроводника,
будет являться характеристическим расстоянием
(постоянной), зависящим только от природы полупроводника,
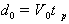 . (1.3.6)
. (1.3.6)
Из
сравнения уравнений, определяющих  для
overshoot и ballistic, при
для
overshoot и ballistic, при  получаем
получаем
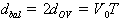 . (1.3.7)
. (1.3.7)
Это
означает, что, используя баллистическое движение, для одного и того же
полупроводника и на одном расстоянии можно достичь скорости в два раза выше,
чем для случая overshoot. Однако это преимущество, естественно, может быть
реализовано только при прохождении носителем очень коротких расстояний.
На
рис. 1.8 показаны кривые, рассчитанные по приближенным формулам (1.3.3) и
(1.3.4) (сплошные линии) и методом Монте-Карло (значки) при 77 К, которые могут
быть использованы для оценок условий осуществления режимов overshoot и ballistic
для любых полупроводников. По этим «универсальным», по утверждению авторов,
кривым можно определить максимальную среднюю скорость 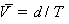 , которую приобретает носитель, проходя расстояние
, которую приобретает носитель, проходя расстояние  в поле 10 кВ/см. Эта величина (значение скорости)
построена в зависимости от расстояния в относительных единицах
в поле 10 кВ/см. Эта величина (значение скорости)
построена в зависимости от расстояния в относительных единицах 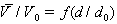 . Из рис. 1.8 следует, что при равных условиях для
одних и тех же расстояний баллистическая скорость действительно приблизительно
вдвое превышает скорость носителей в режиме overshoot. Все это, конечно,
справедливо для расстояний меньше
. Из рис. 1.8 следует, что при равных условиях для
одних и тех же расстояний баллистическая скорость действительно приблизительно
вдвое превышает скорость носителей в режиме overshoot. Все это, конечно,
справедливо для расстояний меньше 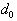 . Дня
расстояний, превышающих этот предел (
. Дня
расстояний, превышающих этот предел (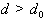 ), чисто
баллистическое движение невыгодно, но режим overshoot тем не менее продолжает
обеспечивать повышенную среднюю скорость. В последнем случае инерционным
движением можно пренебречь и средняя скорость будет рассчитываться по формуле
), чисто
баллистическое движение невыгодно, но режим overshoot тем не менее продолжает
обеспечивать повышенную среднюю скорость. В последнем случае инерционным
движением можно пренебречь и средняя скорость будет рассчитываться по формуле
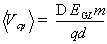 , (1.3.8)
, (1.3.8)
где
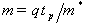 . Крайняя кривая справа соответствует
. Крайняя кривая справа соответствует 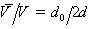 .
.
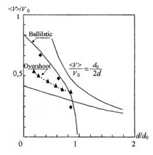
Рис.
1.8 Максимальная среднепролетная скорость электронов, проходящих
расстояние  , в функции
координаты [5,6]
, в функции
координаты [5,6]
Необходимо
отметить, что в большинстве расчетов ballistic effect предполагалось
взаимодействие электрического поля различной конфигурации во времени с объемом
полупроводника, который всегда считался пространственно строго однородным.
Такую ситуацию довольно трудно осуществить на практике, но это наиболее простой
путь при проведении грубых оценок характера взаимодействия электрического поля
с носителями заряда, когда они проходят активную часть субмикронного прибора.
.4
Методы математического моделирования кинетических процессов
Исходными
посылками при моделировании электронных процессов в полупроводнике является
представление о электронах как частицах с заданным соотношением между энергией 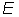 и волновым вектором
и волновым вектором 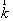 .
.
В
фазовом пространстве 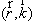 движение каждой частицы в электрическом поле может
быть представлено движущейся точкой и описывается уравнениями:
движение каждой частицы в электрическом поле может
быть представлено движущейся точкой и описывается уравнениями:
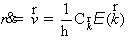 , (1.4.1)
, (1.4.1)
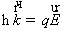 , (1.4.2)
, (1.4.2)
где
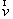 скорость,
скорость, 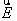 напряженность
электрического поля,
напряженность
электрического поля, 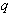 - заряд
электрона.
- заряд
электрона.
Распределение
электронов в фазовом пространстве описывается функцией распределение 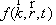 . Эволюция функции распределения в результате
рассеяния, наличия потока электронов в пространстве, определяется путем решения
кинетического уравнения Больцмана:
. Эволюция функции распределения в результате
рассеяния, наличия потока электронов в пространстве, определяется путем решения
кинетического уравнения Больцмана:
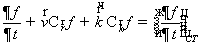 . (1.4.3)
. (1.4.3)
Зная
функцию распределения можно определить все основные параметры: плотность
электронов проводимости, плотность тока, плотность и поток кинетической
энергии. Среди методов решения кинетического уравнения Больцмана наибольшее
распространения получил метод Монте-Карло.
Метод
Монте-Карло состоит в непосредственном моделировании на ЭВМ движения электронов
в ускоряющем электрическом поле и их рассеяния на фононах и дефектах
кристаллической решетки. При этом рассчитываются и усредняются траектории
движения большого числа электронов. В зависимости от требуемой точности для
расчета по функции распределения средних значений (концентраций, энергий,
скоростей) необходимо от нескольких тысяч до десятков тысяч статистических
испытаний, что предполагает значительные затраты счетного времени.
Среди
методов решения кинетического уравнения известен также итерационный метод Риса,
основанный на определении статических функций распределения поля при заданной
величине электрического поля путем решения интегрального уравнения,
эквивалентного интегро-дифференциальному кинетическому уравнению. Однако
сложность метода Риса и отсутствие той физической наглядности, которая присуща
методу Монте-Карло, привели к тому, что метод Риса мало используется сейчас.
Метод
Монте-Карло, как и метод Риса, имеет смысл применять при уменьшении размеров
приборов до субмикронных величин, при снижении рабочих температур до азотных и
более, при работе на предельных частотах, в условиях существенной
неравновесности полупроводниковой плазмы.
В случае, если электроны обмениваются энергией путем электрон-электронных
столкновений быстрее, чем теряют ее за счет электрон-фононного рассеяния,
симметричная часть функции распределения становится максвелловской с
эффективной электронной температурой Те:
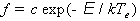 . (1.4.4)
. (1.4.4)
При еще более высокой концентрации электронов межэлектронные столкновения
перераспределяют и энергии, и импульсы, приводя к так называемой смещенной
максвелловской функции распределения:
 , (1.4.5)
, (1.4.5)
где
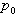 импульс дрейфа. При использовании этой функции можно
получить феноменологические уравнения переноса для каждой из долин путем
усреднения кинетического уравнения по концентрации, импульсу и энергии.
импульс дрейфа. При использовании этой функции можно
получить феноменологические уравнения переноса для каждой из долин путем
усреднения кинетического уравнения по концентрации, импульсу и энергии.
Поскольку
усредняемые величины, как правило, слабо зависят от энергии, то форма функции
распределения при неизменности положения ее максимума мало сказываемся на
значении усредненных величин.
Температурные
модели предполагают, что температура носителей в верхних и нижней долинах
различна и оправданы физически. Успех применения температурных моделей
объясняется прежде всего тем, что экспериментально измеряемые параметры образца
определяются не самой функцией распределения, а макроскопическими величинами
(средними величинами концентрации носителей, дрейфовой скорости и энергии
носителей). Температурные модели могут использоваться для инженерных расчетов
приборов, работающих в миллиметровом диапазоне (они умеренно трудоемки и достаточно
точны), однако, чтобы это приближение можно было применить, среднее время между
электрон-электронными столкновениями должно быть гораздо меньше, чем время
релаксации по импульсу. Если число электронов в зоне проводимости определяется
концентрацией ионизованных доноров, такая ситуация реализоваться не может и,
следовательно, смещенная функция распределения Максвелла может рассматриваться
лишь в качестве грубого приближения. Кроме того, экспериментальные данные и
теоретические расчеты указывают на неприменимость концепции эффективной
электронной температуры для коротких образцов.
Метод
моделирования Монте-Карло стал важным методом моделирования полупроводниковых
приборов. Этот метод эквивалентен точному решению уравнения Больцмана.
Для
описания электронного переноса весьма полезными оказываются менее точные, но
более простые аналитические модели, которые могут помочь лучше понять физику
приборов. Среди таких моделей можно выделить локально - полевую модель, в
которой все основные величины локально зависят от электрического поля.
Плотность дрейфового и электронного токов в этой модели равны:
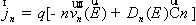 , (1.4.6)
, (1.4.6)
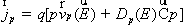 , (1.4.7)
, (1.4.7)
где
 ,
,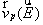 ,
, 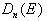 ,
,  - дрейфовые скорости и коэффициенты диффузий
соответственно электронов и дырок.
- дрейфовые скорости и коэффициенты диффузий
соответственно электронов и дырок.
Уравнения
в этой модели не выводятся из уравнения Больцмана. На высоких частотах,
сравнимых с обратным временем энергетической релаксации (которое для электронов
в центральном минимуме зоны проводимости арсенида галлия по порядку величины
близко к 2 пс), скорость и диффузия не следуют мгновенно за изменениями
электрического поля. Поэтому эффективная дифференциальная подвижность,
например, оказывается частотно-зависимой, и уравнения (1.16) и (1.17)
неприменимы.
.5 Полевой транзистор с барьером Шоттки
ПТШ - полупроводниковый прибор планарно-эпитаксиального типа с затвором
на барьере Шоттки, имеющий контакты на внешней поверхности кристалла
полупроводника n-типа. История рождения и жизни полевого транзистора -
поучительный пример открытия, намного опередившего время.
Изобретенный в 1930 году он пережил второе рождение в 70 - 80-х годах.
Благодаря поразительным успехам физики твердого тела и полупроводниковой
технологии был создан новый тип полевых транзисторов СВЧ - ПТШ, способных
усиливать и генерировать электромагнитные колебания практически во всём СВЧ
диапазоне вплоть до миллиметровых волн и обладающих при этом малыми
собственными шумами.
Полевые транзисторы (ПТ) были разработаны позже биполярных транзисторов.
Конструктивно-технологические отличия ПТ, вытекающие из их принципа действия,
позволяют повысить частотную границу СВЧ транзисторных устройств по сравнению с
устройствами на биполярных транзисторах.
Отметим некоторые преимущества ПТШ по сравнению с биполярными
транзисторами. Благодаря более простой и совершенной технологии изготовления
ПТШ имеет меньший разброс электрических параметров. Ток в них течёт не через
р-n-переходы, а между омическими контактами однородной среде канала. Благодаря
этому ПТШ обладают более высокой линейностью передаточной характеристики, у них
нет шумов токораспределения, а плотность тока может быть большой,
следовательно, уровень их шумов меньше, отдаваемые мощности больше. Подвижность
электронов в слабом поле арсенида галлия (GaAs), из которого изготавливают ПТШ,
примерно в 2 раза выше, чем в кремнии (Sі), а вместо ёмкостей эмиттерного и
коллекторного переходов у ПТШ имеется сравнительно малая ёмкость обратно
смещенного затвора на барьере Шоттки, поэтому они могут работать на более
высоких частотах до 90-120ГГц. Внутренняя обратная связь через паразитные
ёмкости в ПТШ незначительна, усилители работают на них более устойчиво в широком
диапазоне частот. Несмотря на то, что теплопроводность GaAs в 3 раза меньше,
чем у Sі, биполярные транзисторы уступают ПТШ по коэффициенту шума уже на
частотах выше 1 -1,5 ГГц.
В 90-х годах происходит интенсивное освоение миллиметрового диапазона волн.
Создание приборов для верхней части сантиметрового и миллиметрового диапазонов
волн стимулировало переход к субмикронным длинам затвора и новым
технологическим решениям, что потребовало углубления физических представлений о
процессах, происходящих в таких транзисторах, и вызвало многочисленные
исследования в этой области.
Разработка и проектирование полупроводниковых и гибридных интегральных
микросхем СВЧ диапазона с применением ПТШ на основе арсенида галлия
определились как самостоятельное направление развития СВЧ техники. Важнейшими
качествами таких микросхем по сравнению с микросхемами на биполярных
транзисторах являются более высокое быстродействие и лучшие шумовые
характеристики. Именно эти параметры и определили основные области их
применения. Они широко используются в радиоприёмной, радиопередающей и
измерительной аппаратуре СВЧ диапазона.
Полевые транзисторы СВЧ являются тонкоплёночными приборами. Их
изготавливают, как правило, из арсенида галлия с электронной проводимостью.
Наибольшее распространение получили приборы с затвором Шоттки. Структура
полевого транзистора с барьером Шоттки изображена на рисунке 1.
Эпитаксиальная плёнка 1 в этих приборах наращивается на поверхность
полупроводниковой подложки 2 c низкой концентрацией примесей (удельное сопротивление
высокоомной подложки более 10 Ом). Толщина плёнки составляет несколько десятых
долей микрометра. В верхний слой плёнки вплавляют два омических контакта -
исток 3, сток 5, а между ними третий электрод - затвор 4, образующий барьер
Шоттки на границе металл- полупроводник.
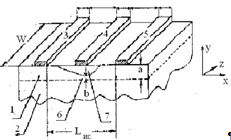
Под действием напряжения, приложенного к промежутку сток-исток, в
эпитаксиальном слое 1 транзистора возникает канал 6, поле в котором ускоряет
носители при их движении от истока к стоку. Управление потоком носителей
осуществляется посредством модуляции ширины канала b в поперечном направлении,
возникающей при изменении толщины слоя объёмного заряда в области затвора
(переход металл-полупроводник) под действием напряжения сток-затвор. Поскольку
переход в полевом транзисторе смещен в обратном направлении, управление потоком
носителей достигается в нём в первом приближении без протекания постоянного
тока через этот переход.
Носителями зарядов в полевом транзисторе являются заряды одного знака -
электроны. В этом смысле полевые транзисторы (в отличие от биполярных) являются
униполярными. Соответственно механизм проводимости в них управляется силами
электрического происхождения (дрейфом), а не диффузией. В качестве затвора в рассматриваемых
полевых транзисторах применяется, как уже упоминалось, контакт
металл-полупроводник.
Затвор 4 используется для управления током транзистора с помощью внешнего
сигнала. При протекании тока через канал возникает падение напряжения на
распределённом сопротивлении канала вдоль его длины. Поэтому часть барьера
Шоттки, расположенная ближе к стоку, оказывается сильнее смещённой в обратном
направлении, чем остальная часть транзистора. Это приводит к несимметричному
расширению слоя обеднённого заряда 7 под затвором. Область обеднённого слоя
может расширяться до высокоомной подложки 2 и перекрывать проводящий канал b.
При этом ток в цепи исток-сток практически перестает зависеть от напряжения
стока; наступает рёжим насыщения тока исток - сток на рабочем участке
характеристики транзистора.
Повышение обратного смещения на электроде затвора вызывает увеличение
ширины обеднённой области и, тем самым, сужение n-канала. При этом возрастает
сопротивление n-канала и уменьшается ток стока. Таким образом, осуществляется
модуляция электронного потока в n-канале с помощью в управляющего напряжения.
Слой под затвором, обеднённый электронами, уменьшает высоту канала. Если
помимо постоянного напряжения Uсм к затвору приложить переменное
напряжение Uиз(t), то в соответствии с изменением этого напряжения
изменяется эффективная высота канала hэфф, а следовательно, и ток
стока:
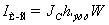
где Jси - плотность тока стока; W- ширина канала.
Из
самых общих физических представлений известно, что время пролёта 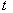 носителей через промежуток, в котором они
взаимодействуют с электрическим полем в транзисторе, т.е. область под затвором
длиной Ь, не должно превышать половины периода СВЧ колебаний τ < Т/2, а угол пролета ωL/ν<π. Здесь ω- круговая
частота, ν-средняя скорость дрейфа носителей. Поскольку шумовая
температура Тш
~ ωL, в малошумящих транзисторах
стремятся по возможности уменьшить величину угла пролёта. На частотах до 5ГГц в
малошумящих транзисторах соотношение ωL/V<0 удовлетворяется при L~1мкм, а уменьшение L сверх этого
предела в большинстве случаев технически и экономически неоправданно. Это
объясняется рядом причин и в том числе большей стоимостью, меньшей надежностью,
устойчивостью и динамическим диапазоном транзисторов с субмикронными длинами
затворов.
носителей через промежуток, в котором они
взаимодействуют с электрическим полем в транзисторе, т.е. область под затвором
длиной Ь, не должно превышать половины периода СВЧ колебаний τ < Т/2, а угол пролета ωL/ν<π. Здесь ω- круговая
частота, ν-средняя скорость дрейфа носителей. Поскольку шумовая
температура Тш
~ ωL, в малошумящих транзисторах
стремятся по возможности уменьшить величину угла пролёта. На частотах до 5ГГц в
малошумящих транзисторах соотношение ωL/V<0 удовлетворяется при L~1мкм, а уменьшение L сверх этого
предела в большинстве случаев технически и экономически неоправданно. Это
объясняется рядом причин и в том числе большей стоимостью, меньшей надежностью,
устойчивостью и динамическим диапазоном транзисторов с субмикронными длинами
затворов.
При
длине затвора L>1мкм пролётное время τ>10-11с, что
на порядок превышает время релаксации энергии и импульса электрона. Поэтому
нестационарные явления при таких длинах затвора не оказывают существенного
влияния на поведение транзистора. Транзисторы с L>1мкм условно относятся к
классу “больших”. Отметим, что характерной величиной здесь является длина
затвора, а не полная длина канала от истока до стока, поскольку модуляция
толщины канала происходит в основном в области канала, прилежащей к затвору.
Области канала вне затвора оказывают меньшее, но, тем не менее, существенное
влияние. Эти области вносят паразитные сопротивления, ухудшающие характеристики
полевого транзистора, что находит отражение в эквивалентной схеме транзистора.
Транзисторы
с 0,2<L<1мкм относятся к классу “умеренно малых”, для них пролётные
времена сопоставимы со временами релаксации энергии и импульса электрона.
Заметим, что транзисторы с длиной затвора 0,1 мкм и менее в рамках такой
классификации можно было бы отнести к разряду “малых”. В настоящее время
созданы транзисторы с длиной затвора L=0,065мкм.
Типичные
характеристики маломощного ПТШ представлены на рисунке 1.10.

Рис.
1.10 Выходные ВАХ ПТШ
На
выходных характеристиках можно выделить три области:
1. Линейная
область существует при малых значениях напряжения, когда прибор еще не
достигает насыщения. Данный режим является важным в случае применения
транзисторов в смесителях и других нелинейных устройствах. Линейная область
характеризуется линейной зависимостью между током и напряжением (т.е. закона
Ома). Когда Uси достигает Uси нас, канал у конца затвора
со стороны стока сужается, т. е. практически полностью смыкается, так что
дальнейшее увеличение тока не происходит (идеальный случай).
- Когда канал
смыкается, транзистор переходит в область насыщения, где ток стока практически
не зависит от Uзи. В приборах с коротким каналом, таких как
арсенид-галлиевый ПТШ, возникает иной механизм насыщения тока стока из- за появления
в канале больших напряженностей электрического поля, приводящих к насыщению
скорости дрейфа. Этот режим насыщения возникает при Е > 3кВ/см, что для
арсенид-галлиевых ПТШ соответствует UСИ = 1 - 2В. С увеличением UС
растёт напряженность поля Е в канале и падает подвижность электронов  µn=ν/Е. В этой области ток стока практически не зависит от
Uс, но является функцией Uз. Рост Iс с
уменьшением модуля из объясняется значением Uэфф, что
вытекает из выражения (1).
µn=ν/Е. В этой области ток стока практически не зависит от
Uс, но является функцией Uз. Рост Iс с
уменьшением модуля из объясняется значением Uэфф, что
вытекает из выражения (1).
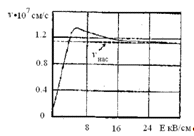
Рис. 1.11 Насыщение скорости
Мгновенное напряжение на стоке Uс(t) может изменяться от нуля
до напряжения пробоя Uпр. При отрицательном напряжении на затворе
ток затвора мал (десятки - сотни микроампер). Большинство транзисторов в
усилителях (особенно в линейных малосигнальных) работают в области насыщения
(подвижные носители заряда в канале двигаются со скоростью насыщения), которая
располагается между линейной областью и областью пробоя.
2. Область
пробоя или область высоких электрических полей при больших значениях Uси
(обычно 10 - 20В) зависит от тока стока и технологии изготовления транзистора.
Обычно предпринимаются существенные усилия для увеличения пробивных напряжений,
что особенно важно для повышения выходной мощности и надёжности
транзистора. В случае применения транзистора в линейных и малошумящих
усилителях эта область не является важной, так как оптимальный режим работы
транзистора не соответствует возникновению в канале больших полей.
Из переходной характеристики Iс = f(Uзи) (рисунок
7) видно, что рабочим диапазоном изменения напряжения на затворе является
участок отрицательных напряжений Uз от напряжения отсечки Uзи
до напряжения открывания барьера Шоттки.

Рис. 1.12 Переходная характеристика ПТШ
Для маломощного GaAs ПТШ важными являются следующие параметры на
постоянном токе.с нач - начальный ток стока равный Iс нас
при Uзи=0;с нас - максимальный ток стока,
соответствующий области насыщения. Типичными значениями напряжений на выводах
транзистора для этого тока считаются: Uзи=0В, Uси=5В для
мощных и Uси=1,5-2В - для малошумящих ПТШ.- отношение ∆Iс/∆Uзи
(крутизна характеристики), которое в области насыщения является приблизительно
постоянным;зи отс - напряжение отсечки, соответствующее
отрицательному значению напряжения на затворе, при котором ток стока
уменьшается до нуля (Iс = 10мкА). Эти параметры связаны между собой
приближенным соотношением Iснас =SUзи
Крутизна характеристики S и проводимость gm совпадают по
физическому смыслу.
2. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИКИ СУБМИКРОННЫХ СТРУКТУР
.1 Общая процедура моделирования
2.1.1
Модель зоны проводимости и механизмы рассеяния
Для
проведения расчетов выбираем трехдолинную модель 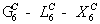 зоны
проводимости и закон дисперсии, который учитывает непараболичность, но не
учитывает анизотропию.
зоны
проводимости и закон дисперсии, который учитывает непараболичность, но не
учитывает анизотропию.
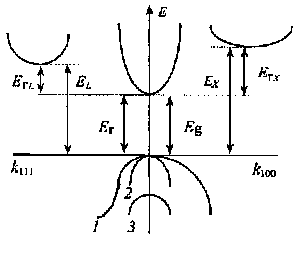
Рис. 2.1 Энергетическая диаграмма для GaAs
Реализуется многочастичный метод Монте-Карло. В качестве возможных
механизмов рассеяния учитываем:
)рассеяние на деформационном потенциале акустических фононов;
)рассеяние на деформационном потенциале оптических фононов (L - долина);
) междолинное рассеяние между неэквивалентными долинами;
) междолинное рассеяние между эквивалентными долинами;
) полярное оптическое рассеяние;
) рассеяние на ионизированных примесях.
2.1.2 Задание начальных условий
На
первом этапе определяются начальные значения энергии, импульса и координаты
частиц. Для этого используем центральную предельную теорему, согласно которой
сумма  независимых случайных величин, распределенных
равномерно в интервале
независимых случайных величин, распределенных
равномерно в интервале 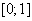
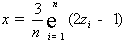 (2.1)
(2.1)
при
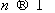 и имеет нормальное (максвеловское) распределение
и имеет нормальное (максвеловское) распределение
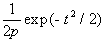 (2.2)
(2.2)
При
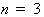 отклонение от максвеловского закона не превышает 10%,
что является приемлемой точностью, поэтому импульс частицы представляется в
виде:
отклонение от максвеловского закона не превышает 10%,
что является приемлемой точностью, поэтому импульс частицы представляется в
виде:
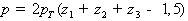 , (2.3)
, (2.3)
где
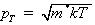 (2.4)
(2.4)
Направление
импульса в пространстве задается двумя углами: азимутальным 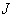 (
(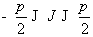 ) и
полярным
) и
полярным  (
(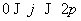 ) и определяется с помощью генерации двух случайных
чисел
) и определяется с помощью генерации двух случайных
чисел 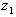 и
и 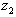 :
:
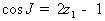 ;
; 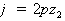 (2.5)
(2.5)
Составляющие
импульса вычисляются по формулам:
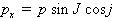 ;
; ;
; 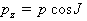 (2.6)
(2.6)
.1.3
Движение частицы во внешнем поле и определение времени свободного пробега
Поведение
электрона в полупроводнике представляет собой отрезки свободного движения во
внешних полях, разделенных мгновенными рассеяниями. Величина отрезка свободного
движения определяется вероятностью 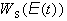 рассеяться
частицей имеющей энергию
рассеяться
частицей имеющей энергию 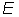 в единицу времени.
в единицу времени. 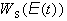 -
квантово-механическая вероятность, определяемая всеми существующими механизмами
рассеяния.
-
квантово-механическая вероятность, определяемая всеми существующими механизмами
рассеяния.
Если
частица начала двигаться в момент времени 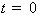 , то
вероятность рассеяться к моменту времени
, то
вероятность рассеяться к моменту времени 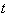
 (2.7)
(2.7)
Учитывая,
что распределение  на интервале
на интервале 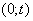 равномерно
и вычисляя интеграл с (2.7), получим:
равномерно
и вычисляя интеграл с (2.7), получим:
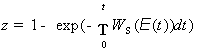 (2.8)
(2.8)
или
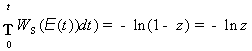 (2.9)
(2.9)
Для
того, чтобы иметь возможность анализировать быстропротекающие процессы
прибегаем к численному решению уравнения (2.9). Для этой цели после каждого
акта рассеяния генерируется случайное число 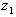 . Затем
на последующих временных шагах согласно уравнениям (1.1) и (1.2) происходит
изменение состояния частицы и одновременно вычисляется интеграл в (2.9). Момент
времени
. Затем
на последующих временных шагах согласно уравнениям (1.1) и (1.2) происходит
изменение состояния частицы и одновременно вычисляется интеграл в (2.9). Момент
времени 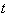 , в который происходит рассеяние определяется
условием:
, в который происходит рассеяние определяется
условием:
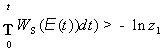 (2.10)
(2.10)
Пока
неравенство (2.10) не выполняется частица меняет свое положение в пространстве
согласно уравнениям:
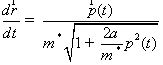 (2.11)
(2.11)
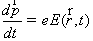 (2.12)
(2.12)
В
постоянном электрическом поле: 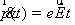
Если
поле направлено вдоль оси 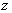 , то решение уравнения (2.12):
, то решение уравнения (2.12):
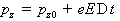 ,
,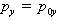 ,
, 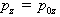 , (2.13)
, (2.13)
где
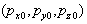 - координаты вектора
- координаты вектора 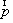 в момент
в момент
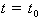 ,
, 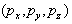 -
координаты вектора
-
координаты вектора 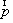 в момент времени
в момент времени 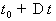
полупроводник субмикронный полевой
транзистор
2.1.4 Законы сохранения и правила
отбора при рассеянии
Правила отбора определяют возможные переходы частицы
из одного состоянии в другое. Так как будут анализироваться только электронные
полупроводники, то рассмотрим только правила касающиеся переходов внутри зоны
проводимости.
Закон
сохранения энергии является первым правилом отбора т. е. возможны только такие
переходы, при которых энергия системы в конечном состоянии равна ее энергии в
начальном состоянии. Другие переходы запрещены. Для упругого рассеяния на
примесях, дефектах и др. при переходе из состояния 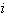 в состояние
в состояние 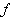
 (2.14)
(2.14)
 , (2.15)
, (2.15)
где
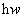 - энергия квазичастицы, знак + относится к
поглощению, а знак “-” - к излучению.
- энергия квазичастицы, знак + относится к
поглощению, а знак “-” - к излучению.
Закон
сохранения импульса является вторым правилом отбора и при рассеянии на фононах
при переходе из состояния 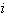 в состояние
в состояние 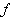 имеет
вид:
имеет
вид:
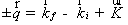 , (2.16)
, (2.16)
где
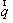 -импульс фонона,
-импульс фонона, 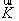 - вектор
обратной решетки. При рассеянии на дефектах обычно
- вектор
обратной решетки. При рассеянии на дефектах обычно 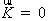 .
.
Дополнительным
ограничением является то, что при двухчастичном взаимодействии число
квазичастиц изменяется на одну.
Если
не рассматривать процессы с перебросом (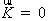 ), то из
(2.16) получаем:
), то из
(2.16) получаем:
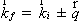 (2.17)
(2.17)
Используя
(2.15) и (2.17), с учетом (1.44) получаем:
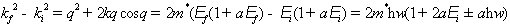 , (2.18)
, (2.18)
где
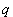 - угол между
- угол между 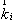 и
и 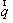 . Из (2.18) находим:
. Из (2.18) находим:
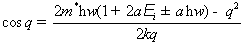 (2.19)
(2.19)
Из
условия  следует ограничение на величину передаваемого
импульса:
следует ограничение на величину передаваемого
импульса:
 (2.20)
(2.20)
.1.5 Определение состояния частицы после рассеяния
Для
моделирования кинетических процессов необходимо выбрать механизмы, которые
являются актуальными в условиях численного эксперимента. Для каждого механизма
нужно определить 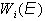 - вероятность ухода частицы с энергией
- вероятность ухода частицы с энергией 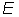 из состояния
из состояния 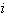 в
состояние
в
состояние 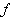 под действием данного механизма и при его реализации
найти энергию и импульс частицы в состоянии
под действием данного механизма и при его реализации
найти энергию и импульс частицы в состоянии 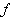 .
.
Для
розыгрыша механизма рассеяния используем метод Неймана. Для этого сравниваем
равномерно распределенное в интервале (0…1) число 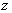 с величинами сумм:
с величинами сумм:
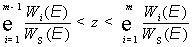 , (2.21)
, (2.21)
где
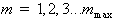 ,
, -число
учитываемых механизмов рассеяния. При выполнении неравенства (2.21) для
рассеяния выбирается механизм с номером
-число
учитываемых механизмов рассеяния. При выполнении неравенства (2.21) для
рассеяния выбирается механизм с номером 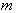 . Далее
для выбранного механизма рассеяния по известным значениям энергии и импульса до
рассеяния находим значения энергии и импульса после рассеяния.
. Далее
для выбранного механизма рассеяния по известным значениям энергии и импульса до
рассеяния находим значения энергии и импульса после рассеяния.
.1.6 Определение вероятности рассеяния и конечного состояния
Рассеяние при взаимодействии с деформационным потенциалом акустических
фононов.
Для
длинноволновых акустических фононов при 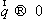 закон
дисперсии имеет вид
закон
дисперсии имеет вид
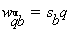 (2.22)
(2.22)
Вероятность рассеяния:
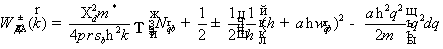 (2.23)
(2.23)
Пределы
интегрирования определяем выражением:
 , (2.24)
, (2.24)
где
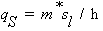
Из
(2.24) получаем величины передаваемых импульсов :
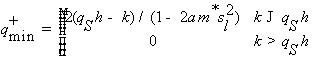 ; (2.25)
; (2.25)
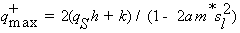 (2.26)
(2.26)
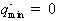 ;
; 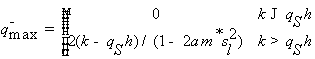 (2.27)
(2.27)
Таким
образом, электрон с импульсом 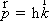 при
рассеянии на акустическом фононе может поглотить или испустить фонон с волновым
вектором
при
рассеянии на акустическом фононе может поглотить или испустить фонон с волновым
вектором 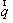 , изменяющимся в пределах
, изменяющимся в пределах
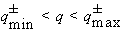 ,
,
где
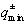 и
и 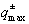 определены
в (2.25) - (2.27). Вероятность передачи импульса
определены
в (2.25) - (2.27). Вероятность передачи импульса 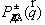 есть
подынтегральная функция в (2.23). Для определения волнового вектора фонона,
участвующего в рассеянии, воспользуемся методом Неймана.
есть
подынтегральная функция в (2.23). Для определения волнового вектора фонона,
участвующего в рассеянии, воспользуемся методом Неймана.
Рассеяние при взаимодействии с деформационным потенциалом
оптических фононов.
Характерным
свойством таких колебаний является независимость частоты колебаний от волнового
вектора 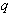 в широком интервале его значений вблизи
в широком интервале его значений вблизи 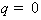 :
:
 (2.28)
(2.28)
Соответствующий
таким колебаниям вероятность рассеяния:
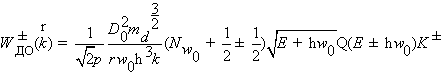 , (2.29)
, (2.29)
где
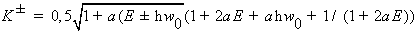 (2.30)
(2.30)
Величины передаваемых импульсов :
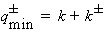 ;
; 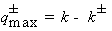 (2.31)
(2.31)
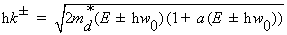 (2.32)
(2.32)
Полярное оптическое рассеяние.
В
полярных материалах типа А3В5, А2 В6
колебания противоположно заряженных атомов, кроме потенциалов деформации,
приводят к появлению дальнодействующих макроскопических электрических полей и
вызывают полярное оптическое (ПО) рассеяние. Это рассеяние доминирует в
центральной долине зоны Бриллюэна в диапазоне энергий 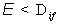 .
.
Вероятность
рассеяния
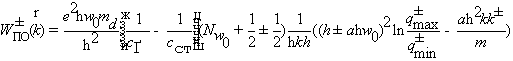 (2.33)
(2.33)
где
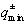 и
и 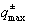 определены
в (2.31), а
определены
в (2.31), а 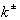 определяется выражением (2.32)
определяется выражением (2.32)
Междолинное рассеяние.
Для
вероятности медолинного рассеяния можно использовать формулу аналогичную (2.29)
- (2.32)
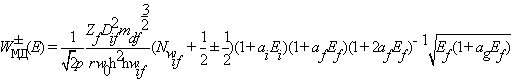 ,(2.34)
,(2.34)
где
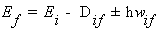 ,
, 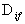 -
разность энергий минимумов долин
-
разность энергий минимумов долин 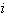 и
и 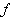 . Множитель
. Множитель 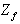 , равный
числу однотипных долин без исходной
, равный
числу однотипных долин без исходной
.2
Вычисление распределения потенциала и электрического поля
При реализации метода крупных частиц в неоднородной полупроводниковой
структуре возникает необходимость иметь эффективный алгоритм решения уравнения
Пуассона.
Расчетная область разбивается на сетку и на каждом временном шаге DT при
моделировании полупроводниковой структуры необходимо знать распределение
потенциалов в узлах расчетной сетки.
В данной работе рассматривается случай, когда расчетная область
выбирается в виде прямоугольника (рис 2.2).
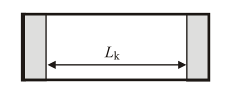
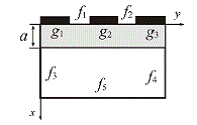
а) б)
Рис. 2.2 Расчетная область прямоугольного диода (а) и транзистора (б)
Выделив геометрическую область для моделирования, мы должны теперь задать
граничные условия. Электроны текут из источника к стоку под воздействием их
собственного пространственного заряда и внешнего напряжения, приложенного к
электродам.
Для
области а) оператор Лапласа обладает свойством симметрии (по крайней мере по
одной из переменных), а на границах по переменной заданы 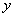 условия Неймана (на границах по другой переменной
заданы условия Дирихле).
условия Неймана (на границах по другой переменной
заданы условия Дирихле).
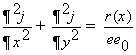
 (2.35)
(2.35)
 (2.36)
(2.36)
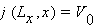 (2.37)
(2.37)
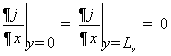 (2.38)
(2.38)
В этом случае наиболее подходящим методом решения уравнения Пуассона
(2.35) является алгоритм, основанный на методе разделения переменных и
использующий по одной координате преобразование Фурье (метод Хокни) [30].
Что касается области б), моделирующий полевой транзистор с барьером
Шоттки, ясно, что на границе, примыкающей к электродам, потенциал должен
принимать заданные значения.
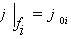 , (2.39)
, (2.39)
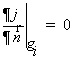 (2.40)
(2.40)
Иначе
говоря, нормальная компонента градиента потенциала равна нулю.
Для
области б) оператор Лапласа уже не обладает свойством симметрии так как границы
при  и
и  существенно
различны.
существенно
различны.
Для
расчета потенциала а области б) была выл выбран один из разновидностей метод
релаксации - многосеточный метод.
Оправданием
нулевых условий для границы, не содержащей электродов является естественная
тенденция свободного заряда компенсировать любое изменение поля в масштабе
дебаевской длины от любого заданного изменения (например, край электрода).
На
верхней поверхности нулевые условия для поля являются хорошей аппроксимацией
из-за больших изменений диэлектрической постоянной от эпитаксиального слоя (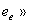 12) до окружающего воздуха (
12) до окружающего воздуха (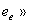 1). На таком разрыве нормальное значение
электрического смещения
1). На таком разрыве нормальное значение
электрического смещения 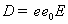 непрерывно. Следовательно,
непрерывно. Следовательно,
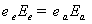 (2.41)
(2.41)
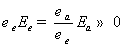 (2.42)
(2.42)
где
индексы е и а относятся соответственно к эпитаксиальной области и
воздуху. Поскольку 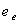
 и Еа
имеет конечное значение, электрическое поле внутри эпитаксиального слоя должно
быть малым. В действительности более тонкий расчет включил бы вычисление
электрического поля в воздушной области. Однако ясно, что это является
уточнением, которое нет нужды рассматривать в первую очередь
и Еа
имеет конечное значение, электрическое поле внутри эпитаксиального слоя должно
быть малым. В действительности более тонкий расчет включил бы вычисление
электрического поля в воздушной области. Однако ясно, что это является
уточнением, которое нет нужды рассматривать в первую очередь
Рассмотрим
теперь условия, которые необходимо наложить на движение электронов у границ.
Требование отсутствия тока через границы, за исключением электродов, лучше
всего удовлетворяется отражением любых электронов, которые попадают на границу.
Иными словами, нормальную к границе компоненту скорости электрона обращают. На
электродах источника и стока омический контакт, как предполагается, поглощает
все попадающие на электрод электроны и инжектирует на каждом временном шаге
достаточное количество электронов для поддержания необходимой плотности в
строке ячеек сетки потенциала, примыкающих к электродам. Инжекция происходит с
полумаксвелловским распределением по скоростям. На электроде затвора контакт с
барьером Шоттки представляется с помощью напряжения, равного разности
приложенного потенциала и высоты барьера. Здесь имеется поглощение частиц, а
инжекция отсутствует. Эти последние условия на затворе на практике неважны,
поскольку при обычных условиях смещения очень мало электронов будет достигать
затвора.
2.3 Электронный транспорт в субмикронном транзисторе с
барьером Шоттки
Особенность
процессов, протекающих в приборах на основе GaAs при уменьшении длины можно
понять, рассматривая короткие структуры  , где
, где 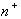 - области, являются областями с повышенным
содержанием донорной примеси (
- области, являются областями с повышенным
содержанием донорной примеси (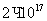 см-3)
с размером 0,2 мкм.
см-3)
с размером 0,2 мкм.  - область (канал диода с длиной
- область (канал диода с длиной 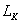 ) легирована до концентрации
) легирована до концентрации 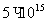 см-3 с размером 0,4 мкм при подаче
постоянного напряжения.
см-3 с размером 0,4 мкм при подаче
постоянного напряжения.
На рис. 2.3 показано распределение величины дрейфовой скорости в диоде
общей длиной 0,4 мкм из которого видно, что в диоде вблизи катодного контакта
существует область, где величина скорости заметно выше чем в остальной части
диода.
Размер этой области около 0,2 мкм. Это и есть область так называемого
пространственного overshoot. Следовательно если уменьшать длину канала до
величин сравнимых с 0,2 мкм влияние неоднородного распределения скорости будет
увеличиваться.
Рассматривались
полевые транзисторы с барьером Шоттки с общей длиной 1 мкм и 0.6 мкм. Канал
транзистора имел легирование 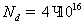 см-3.
Длина истока и стока для транзистора с длиной 1 мкм была взята 0,25 мкм, для
транзистора с длиной 0,6 мкм она составила 0,15 мкм. Размеры затвора меньше
0,125 мкм и 0,075 мкм соответственно для обоих размеров.
см-3.
Длина истока и стока для транзистора с длиной 1 мкм была взята 0,25 мкм, для
транзистора с длиной 0,6 мкм она составила 0,15 мкм. Размеры затвора меньше
0,125 мкм и 0,075 мкм соответственно для обоих размеров.
Результаты
расчета распределения потенциала в диоде показаны на рис. 2.3 и 2.4
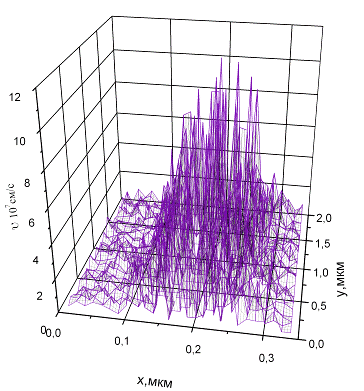

Рис. 2.3 Распределение величины дрейфовой скорости в диоде
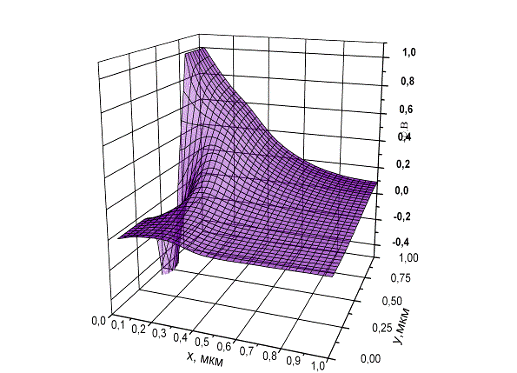

Рис. 2.4 Распределение величины потенциала по расчетной области
транзистора
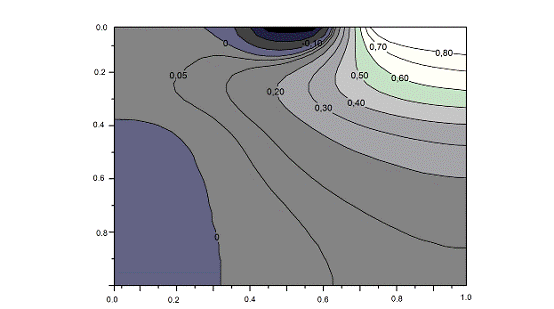
Рис. 2.5 Расположение эквипотенциальных линий внутри транзистора
Как видно, из приведенных зависимостей вблизи отрицательно заряженного
затвора формируется область с отрицательным потенциалом, вытесняющим электроны
из канала.
Действие потенциала затвора на распределение электронов в канале и
эффективную толщину канала иллюстрировано на рис 2.6 для трех значений
напряжения на затворе: -0,2 В, -0, 5 В и -0, 8 В.
Видно уменьшении эффективного размера канала приблизительно в 2 раза при
изменении напряжения от -0,2 В, -0, 5 В и -0, 8 В
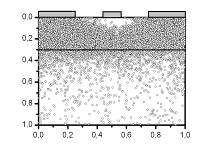
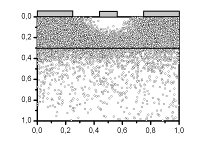
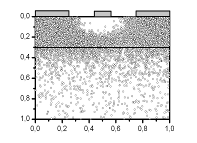
а) б)
в)
Рис. 2.6 Распределение электронов в транзисторе при трех напряжениях на
затворе
Результирующие выходные и переходные характеристики транзисторов с длиной
1 мкм и 0,6 мкм показаны на рис. 2.7-2.10
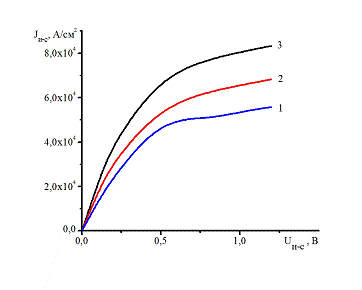
1
- 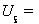 -0,2 В; 1 -
-0,2 В; 1 - 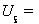 0,1 В; 1
-
0,1 В; 1
- 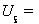 0,4 В;
0,4 В;
Рис.
2.7 Выходные характеристики транзистора с длиной 1 мкм.

-
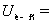 0,1 В ; 2-
0,1 В ; 2- 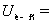 0,2 В ;
3-
0,2 В ;
3- 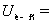 0,5 В ; 4-
0,5 В ; 4- 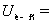 0,8 В ;
0,8 В ;
-
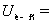 1,0 В ; 6-
1,0 В ; 6- 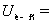 1,2 В ;
1,2 В ;
Рис.
2.8 Переходные характеристики транзистора с длиной 1 мкм
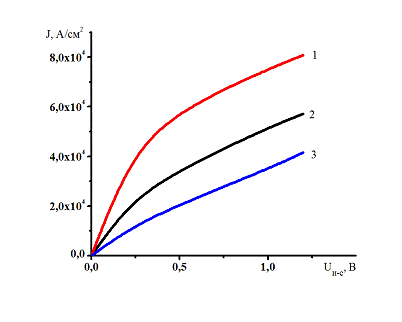
-
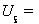 -0,2 В; 1 -
-0,2 В; 1 - 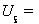 0,1 В; 1
-
0,1 В; 1
- 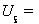 0,4 В;
0,4 В;
Рис.
2.9 Выходные характеристики транзистора с длиной 0,6 мкм
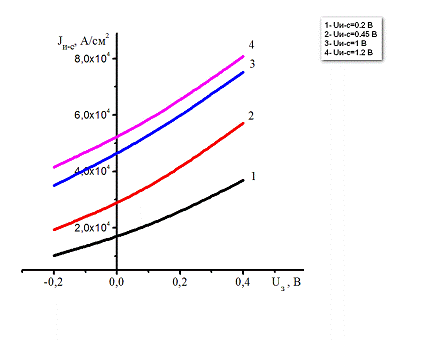
-
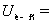 0,2 В ; 2-
0,2 В ; 2- 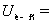 0,45 В ;
3-
0,45 В ;
3- 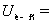 1,0 В ; 4-
1,0 В ; 4- 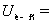 1,2 В.
1,2 В.
Рис.
2.10 Переходные характеристики транзистора с длиной 0,6 мкм
По
полученным характеристикам видно, что в целом они соответствуют характеристикам
полевых транзисторов с барьером Шоттки. Отличием есть отсутствие выраженного
участка насыщения.
Это
объясняется тем, что процессы переноса носителей заряда в этих приборах связаны
с дрейфом носителей и вид выходной характеристики соответствует зависимости от
напряжения средней скорости носителей в канале. Уменьшение длины приводит к
снижению интенсивности рассеяния и соответственно с невозможностью рассеивания
на фононах. Движение носителей приобретает баллистический характер, что
отчетливо демонстрируют характеристики прибора с 0,6 мкм. Начальные участки
практически линейные - рассеяния нет, пролет бесстолкновительный.
ВЫВОДЫ
Таким
образом в результате выполнения работы получены следующие результаты:
Была
реализована численная модель расчета субмикронного полевого транзистора с
барьером Шоттки.
Получены
пространственные распределения основных электрофизических параметров
(потенциала, поля, скорости, концентрации).
Получены
электрические характеристики транзистора, которые находятся в согласии с
теорией рассматриваемых транзисторов.
Реализованная
модель открывает перспективы исследования более сложных транзисторных структур,
сходных по физическим принципам работы с рассмотренными.
СПИСОК
ЛИТЕРАТУРЫ
1. Шур М.
Современные приборы на основе арсенида галлия: Пер. с англ.-М.: Мир, 1991
-632 c.
. Хокни
Р., Иствуд Дж. Численное моделирование методом частиц.- М.: Мир 1987.- 640 с.
3. G.
Klimeck, S.S. Ahmed, Atomistic simulation of realistically sized nanodevices
using NEMO 3- D- Part I. Models and Benchmarks//Electron devices. - 54, 9.-
2007. -C. 2072.
. K.
R. Mok etc. Predictive of advanced Nano - CMOS Device Based on kMC process
simulation//Electron devices. - 54, 9.- 2007. -C. 2155.
5. Иващенко
В. М., Митин В. В. Моделирование кинетических явлений в полупроводниках. Метод
Монте-Карло. - К.: Наукова думка, 1990.- 192 с.