Методы оптимизации
1. Метод
покоординатного спуска
Существуют методы оптимизации, которые для своей реализации требуют
вычисления первых или вторых производных минимизируемой функции. Однако в
практических задачах нередко встречаются случаи, когда минимизируемая функция
либо не обладает нужной гладкостью, либо является гладкой, но вычисление ее
производных с нужной точностью требует слишком большого объема работ, много
машинного времени. В таких случаях желательно иметь методы минимизации, которые
требуют лишь вычисления значения функции. Одним из таких методов является метод
покоординатного спуска (метод Гаусса-Зейделя).
Сначала опишем этот метод для задачи:
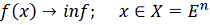
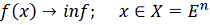 . (1)
. (1)
Обозначим
 -
единичный координатный вектор, у которого i-я координата
равна 1, остальные равны нулю, i = 1,…,n. Пусть
-
единичный координатный вектор, у которого i-я координата
равна 1, остальные равны нулю, i = 1,…,n. Пусть 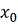
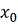 -
некоторое начальное приближение, а
-
некоторое начальное приближение, а 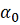
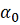 -
некоторое положительное число, являющееся параметром метода. Допустим, что нам
уже известны точка
-
некоторое положительное число, являющееся параметром метода. Допустим, что нам
уже известны точка 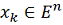
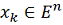 и число
и число 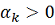
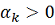 при
каком-либо
при
каком-либо 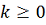
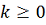 .
Положим:
.
Положим:
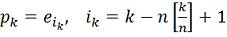
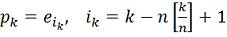 , (2)
, (2)
где
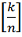
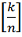 означает
целую часть числа
означает
целую часть числа 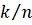
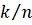 . Условие
(2) обеспечивает циклический перебор координатных векторов
. Условие
(2) обеспечивает циклический перебор координатных векторов 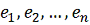
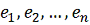 , т. е.
, т. е.
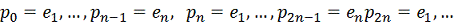
Вычислим
значение функции 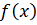
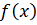 в точке
в точке 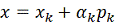
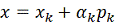 и
проверим неравенство
и
проверим неравенство
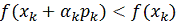
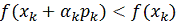 . (3)
. (3)
Если
(3) выполняется, то примем:
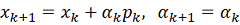
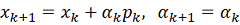 . (4)
. (4)
В
том случае, если (3) не выполняется, вычисляем значение функции 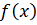
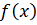 в точке
в точке 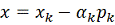
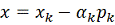 и
проверяем неравенство:
и
проверяем неравенство:
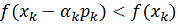
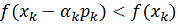 . (5)
. (5)
В
случае выполнения неравенства (5) положим:
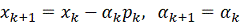
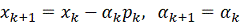 . (6)
. (6)
Назовем
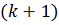
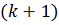 -ю
итерацию удачной, если справедливо хотя бы одно из неравенств (3) или (5). Если
-ю
итерацию удачной, если справедливо хотя бы одно из неравенств (3) или (5). Если
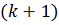
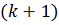 -я
итерация неудачная, т. е. не выполняются оба неравенства (3) и (5), то полагаем:
-я
итерация неудачная, т. е. не выполняются оба неравенства (3) и (5), то полагаем:
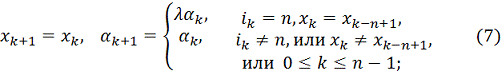
Здесь
λ,
0<λ<1 - фиксированное число,
являющееся параметром метода. Условия (7) означают, что если за один цикл из n
итераций при переборе направлений всех координатных осей 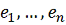
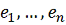 с шагом
с шагом 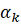
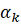 реализовалась
хотя бы одна удачная итерация, то длина шага
реализовалась
хотя бы одна удачная итерация, то длина шага 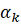
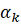 не
дробится и сохраняется на протяжении по крайней мере следующего цикла из n
итераций. Если же среди последних n итераций не оказалось ни одной
удачной итерации, то шаг
не
дробится и сохраняется на протяжении по крайней мере следующего цикла из n
итераций. Если же среди последних n итераций не оказалось ни одной
удачной итерации, то шаг 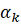
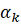 дробится.
Таким образом, если на итерации с номером
дробится.
Таким образом, если на итерации с номером 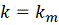
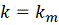 произошло
дробление
произошло
дробление 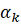
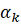 , то
, то
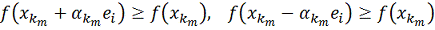
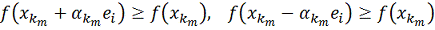 (8)
(8)
при
всех i=1,…,n. Метод покоординатного спуска для задачи (1) описан.
Заметим,
что хотя метод (2) - (7) для своей реализации не требует знания градиента
минимизируемой функции. Оказывается, если функция 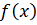
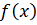 не
является гладкой, то метод покоординатного спуска может не сходиться ко
множеству решений задачи (1).
не
является гладкой, то метод покоординатного спуска может не сходиться ко
множеству решений задачи (1).
Описанный
выше метод покоординатного спуска нетрудно модифицировать применительно к
задаче минимизации функции на параллелепипеде:
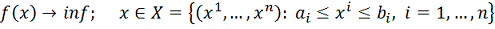
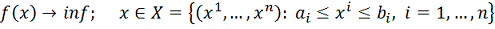 ,
,
где
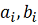
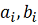 -
заданные числа,
-
заданные числа, 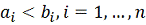
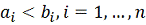 . А
именно, пусть k-е приближение
. А
именно, пусть k-е приближение 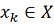
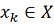 и число
и число 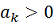
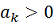 при
некотором
при
некотором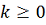
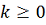 уже
найдены. Выберем вектор
уже
найдены. Выберем вектор 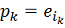
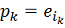 согласно
формуле (2), составим точку
согласно
формуле (2), составим точку 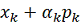
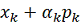 и
проверим условия:
и
проверим условия:
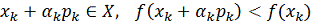
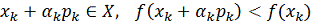 . (10)
. (10)
Если
оба условия (10) выполняются, то следующее приближение 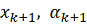
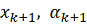 определяем
по формулам (4). Если же хотя бы одно условие (10) не выполняется, то
составляем точку
определяем
по формулам (4). Если же хотя бы одно условие (10) не выполняется, то
составляем точку 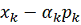
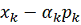 и
проверяем условия:
и
проверяем условия:
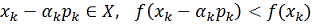
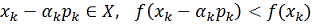 . (11)
. (11)
В
случае выполнения обоих условий (11) следующее приближение определяем по
формулам (6), а если хотя бы одно из условий (11) не выполняется, то следующее
приближение находится по формулам (7).
Существуют
и другие варианты метода покоординатного спуска. Можно, например, строить
последовательность 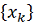
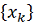 по
правилу:
по
правилу:
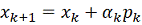
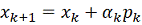 , (12)
, (12)
где

 определяется
согласно (2), а
определяется
согласно (2), а 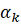
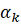 -
условиями:
-
условиями:
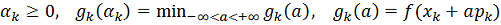
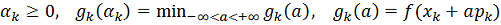 . (13)
. (13)
Метод
(12), (13) имеет смысл применять в том случае, когда величина 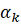
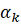 из (13)
находится в явном виде. Так будет, если функция
из (13)
находится в явном виде. Так будет, если функция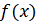
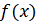 квадратичная,
т е.
квадратичная,
т е.
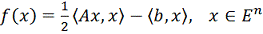
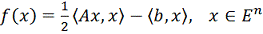 , (14)
, (14)
где
A- симметричная положительно определенная матрица, 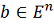
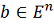 .
Нетрудно убедиться, что для функции (14) метод (12), (13) приводит к хорошо
известному методу Зейделя из линейной алгебры.
.
Нетрудно убедиться, что для функции (14) метод (12), (13) приводит к хорошо
известному методу Зейделя из линейной алгебры.
Хотя
скорость сходимости метода покоординатного спуска, вообще говоря, невысокая,
благодаря простоте каждой итерации, скромным требованиям к гладкости
минимизируемой функции этот метод довольно широко применяется на практике.
Существуют
и другие методы минимизации, использующие лишь значения функции и не требующие
для своей реализации вычисления производных. Например, используя вместо
производных их разностные аппроксимации, можно построить модификации, требующие
вычисления лишь значений функции в подходящим образом выбранных точках.
Другой
подход для минимизации негладких функций, основанный лишь на вычислении
значений функции, дает метод случайного поиска. Метод поиска глобального
минимума также относится к методам, не требующим вычисления производных
минимизируемой функции.
Рассмотрим
еще один вариант описания метода Гаусса-Зейделя.
Пусть
требуется найти наименьшее значение целевой функции 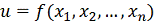
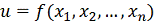 . В
качестве начального приближения выберем в п-мерном пространстве некоторую точку
M0 с координатами
. В
качестве начального приближения выберем в п-мерном пространстве некоторую точку
M0 с координатами 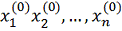
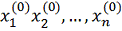 .
Зафиксируем все координаты функции и, кроме первой. Тогда
.
Зафиксируем все координаты функции и, кроме первой. Тогда 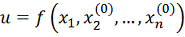
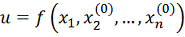 -
функция одной переменной x1. Решая одномерную задачу оптимизации для этой
функции, мы от точки M0 перейдем к точке
-
функция одной переменной x1. Решая одномерную задачу оптимизации для этой
функции, мы от точки M0 перейдем к точке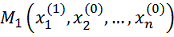
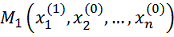 , в
которой функция и принимает наименьшее значение по координате x1 при
фиксированных остальных координатах. В этом состоит первый шаг процесса
оптимизации, состоящий в спуске по координате x1.
, в
которой функция и принимает наименьшее значение по координате x1 при
фиксированных остальных координатах. В этом состоит первый шаг процесса
оптимизации, состоящий в спуске по координате x1.
Зафиксируем
теперь все координаты, кроме x2, и рассмотрим функцию этой переменной 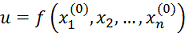
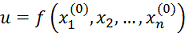 . Снова
решая одномерную задачу оптимизации, находим ее наименьшее значение при
. Снова
решая одномерную задачу оптимизации, находим ее наименьшее значение при 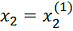
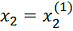 , т.е. в
точке
, т.е. в
точке 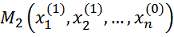
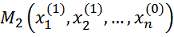 .
Аналогично проводится спуск по координатам
.
Аналогично проводится спуск по координатам 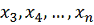
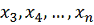 , а затем
процедура снова повторяется от x1 до xn и т.д. В результате этого процесса
получается последовательность точек M0,M1,…, в которых значения целевой функции
составляют монотонно убывающую последовательность
, а затем
процедура снова повторяется от x1 до xn и т.д. В результате этого процесса
получается последовательность точек M0,M1,…, в которых значения целевой функции
составляют монотонно убывающую последовательность 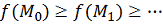
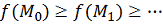 На любом
k-м шаге этот процесс можно прервать, и значение
На любом
k-м шаге этот процесс можно прервать, и значение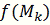
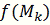 принимается
в качестве наименьшего значения целевой функции в рассматриваемой области.
принимается
в качестве наименьшего значения целевой функции в рассматриваемой области.
Таким
образом, метод покоординатного спуска сводит задачу о нахождении наименьшего
значения функции многих переменных к многократному решению одномерных задач
оптимизации по каждому проектному параметру.
Данный
метод легко проиллюстрировать геометрически для случая функции двух переменных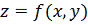
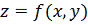 ,
описывающей некоторую поверхность в трехмерном пространстве. На рисунке 1
нанесены линии уровня этой поверхности. Процесс оптимизации в этом случае
проходит следующим образом. Точка
,
описывающей некоторую поверхность в трехмерном пространстве. На рисунке 1
нанесены линии уровня этой поверхности. Процесс оптимизации в этом случае
проходит следующим образом. Точка 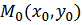
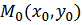 описывает
начальное приближение. Проводя спуск по координате х, попадем в точку
описывает
начальное приближение. Проводя спуск по координате х, попадем в точку 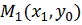
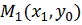 . Далее,
двигаясь параллельно оси ординат, придем в точку
. Далее,
двигаясь параллельно оси ординат, придем в точку 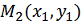
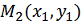 и т.д.
и т.д.
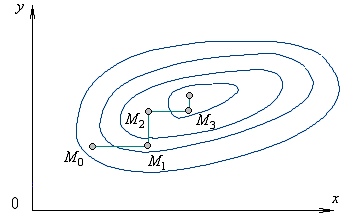
Рисунок
1 - Геометрическая интерпретация метода покоординатного спуска для целевой
функции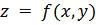
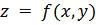 .
.
Важным
здесь является вопрос о сходимости рассматриваемого процесса оптимизации.
Другими словами, будет ли последовательность значений целевой функции 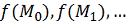
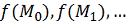 сходиться
к наименьшему ее значению в данной области? Это зависит от вида самой функции и
выбора начального приближения.
сходиться
к наименьшему ее значению в данной области? Это зависит от вида самой функции и
выбора начального приближения.
Для
функции двух переменных очевидно, что метод неприменим в случае наличия изломов
в линиях уровня. Это соответствует так называемому оврагу на поверхности. Здесь
возможен случай, когда спуск по одной координате приводит на “дно” оврага.
Тогда любое движение вдоль любой координаты ведет к возрастанию функции,
соответствующему подъему на “берег” оврага. Поскольку поверхности типа “оврага”
встречаются в инженерной практике, то при использовании метода покоординатного
спуска следует убедиться, что решаемая задача не имеет этого недостатка.
Для
гладких функций при удачно выбранном начальном приближении (в некоторой
окрестности минимума) процесс сходится к минимуму. К достоинствам метода
покоординатного спуска следует также отнести возможность использования простых
алгоритмов одномерной оптимизации.
Пример.
Составить программу для расчета минимума целевой функции 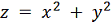
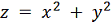 методом
покоординатного спуска.
методом
покоординатного спуска.
Алгоритм
программы представлен на рисунке 2.
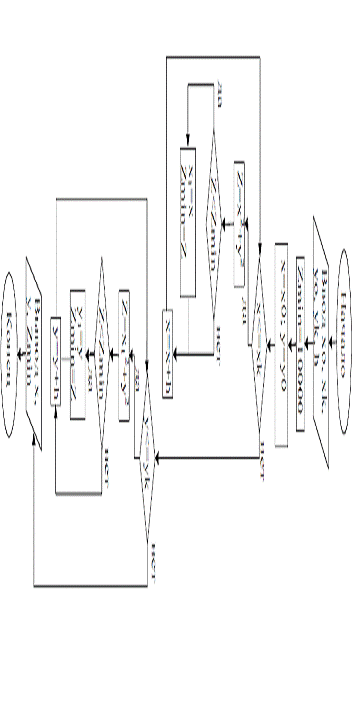
Рисунок
2 - Алгоритм программы для расчета минимума целевой функции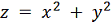
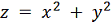 методомпокоординатного спуска.
методомпокоординатного спуска.
Текст
программы приведен ниже.
ProgramKoordinatny_spusk;
usescrt;a,z,x,x0,x1,xk,y,y0,y1,yk,zmin,h:real;,n:integer;;(‘Ввод
X0:’);(x0);(‘ВводXk:’);(xk);(‘ВводY0:’);(y0);(‘ВводYk:’);(yk);(‘ВводH:’);(h);:=100000;:=x0;
y:=y0;(x<=xk) do:=sqr(x)+sqr(y);(z<zmin) then
begin:=x;:=z;;:=x+h;(y<=yk) do:=sqr(x1)+sqr(y);(z<zmin) then
begin:=y;:=z;;:=y+h;;(‘Pri X=’,x1:4:2,’ Y=’,y1:4:2,’Zmin=’,zmin:4:2);
readkey.
2. Метод
Хука-Дживса
Метод Хука-Дживса был разработан в 1961 году, но до сих пор является
весьма эффективным и оригинальным. Поиск состоит из последовательности шагов
исследующего поиска вокруг базисной точки, за которой в случае успеха следует
поиск по образцу.
Описание этой процедуры представлено ниже:
А.
Выбрать начальную базисную точку 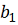
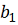 и шаг
длиной
и шаг
длиной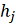
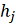 для
каждой переменной
для
каждой переменной 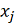
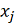 , j= 1,
2, …,n. В приведенной ниже программе для каждой переменной
используется шаг h, однако указанная выше модификация тоже может
оказаться полезной.
, j= 1,
2, …,n. В приведенной ниже программе для каждой переменной
используется шаг h, однако указанная выше модификация тоже может
оказаться полезной.
Б.
вычислить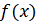
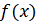 в
базисной точке
в
базисной точке 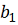
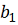 с целью
получения сведений о локальном поведении функции
с целью
получения сведений о локальном поведении функции 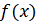
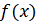 . Эти
сведения будут использоваться для нахождения подходящего направления поиска по
образцу, с помощью которого можно надеяться достичь большего убывания значения
функции. Функция
. Эти
сведения будут использоваться для нахождения подходящего направления поиска по
образцу, с помощью которого можно надеяться достичь большего убывания значения
функции. Функция 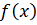
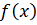 в
базисной точке
в
базисной точке 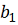
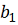 находится
следующим образом:
находится
следующим образом:
. Вычисляется
значение функции 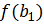
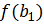 в
базисной точке
в
базисной точке 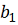
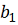 .
.
2. Каждая
переменная по очереди изменяется прибавлением длины шага. Таким образом, мы
вычисляем значение функции 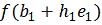
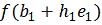 , где
, где 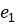
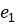 -
единичный вектор в направлении оси
-
единичный вектор в направлении оси 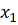
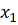 . Если
это приводит к уменьшению значения функции, то
. Если
это приводит к уменьшению значения функции, то 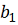
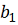 заменяется
на
заменяется
на 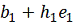
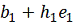 . В
противном случае вычисляется значение функции
. В
противном случае вычисляется значение функции 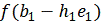
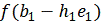 , и если
ее значение уменьшилось, то
, и если
ее значение уменьшилось, то 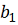
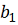 заменяется
на
заменяется
на 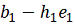
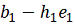 . Если ни
один из проделанных шагов не приводит к уменьшению значения функции, то точка
. Если ни
один из проделанных шагов не приводит к уменьшению значения функции, то точка 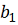
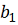 остается
неизменной и рассматриваются изменения в направлении оси
остается
неизменной и рассматриваются изменения в направлении оси 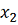
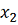 , т. е.
находится значение функции
, т. е.
находится значение функции 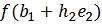
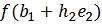 и т. д.
Когда будут рассмотрены все nпеременные, мы будем иметь новую базисную точку
и т. д.
Когда будут рассмотрены все nпеременные, мы будем иметь новую базисную точку 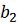
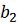 .
.
3. Если
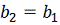
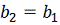 , т. е.
уменьшение функции не было достигнуто, то исследование повторяется вокруг той
же базисной точки
, т. е.
уменьшение функции не было достигнуто, то исследование повторяется вокруг той
же базисной точки 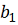
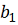 , но с
уменьшенной длиной шага. На практике удовлетворительным является уменьшение
шага (шагов) в десять раз от начальной длины.
, но с
уменьшенной длиной шага. На практике удовлетворительным является уменьшение
шага (шагов) в десять раз от начальной длины.
. Если
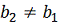
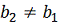 , то
производится поиск по образцу.
, то
производится поиск по образцу.
В. При поиске по образцу используется информация, полученная в процессе
исследования, и минимизация функции завершается поиском в направлении, заданном
образцом. Эта процедура производится следующим образом:
1. Разумно
двигаться из базисной точки 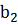
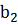 в
направлении
в
направлении 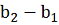
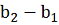 ,
поскольку поиск в этом направлении уже привел к уменьшению значения функции.
Поэтому вычислим функцию в точке образца:
,
поскольку поиск в этом направлении уже привел к уменьшению значения функции.
Поэтому вычислим функцию в точке образца:
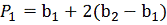
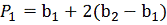 (1)
(1)
В
общем случае:
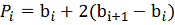
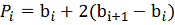 (2)
(2)
2. Затем
исследование следует продолжать вокруг точки 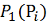
 .
.
Г. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена
заданного малого значения.
Ниже приведена блок-схема данного метода.
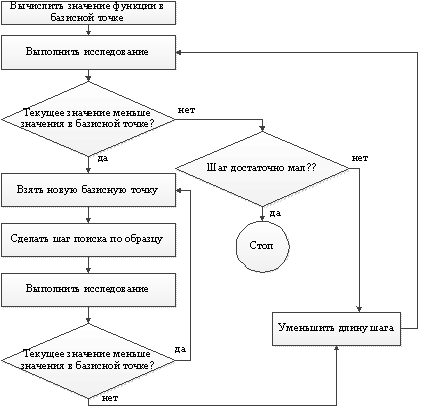
Рисунок
- Блок-схема для метода Хука-Дживса
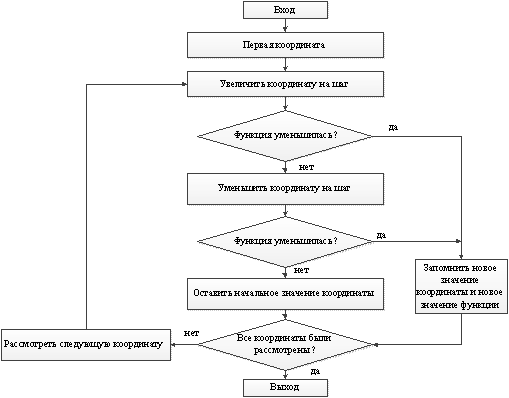
Рисунок
- Блок-схема алгоритма для написания программы
PRINT
“МЕТОД ХУКА-ДЖИВСА”
REM ФУНКЦИЯ
ВЫЧИСЛЯЕТСЯ В ВИДЕ Z=F(X1,X2,…,XN) В СТРОКЕ 2000
PRINT “ВВЕДИТЕ
ЧИСЛО ПЕРЕМЕННЫХ”:INPUTN
DIM X(N),B(N),Y(N),P(N)
PRINT “ВВЕДИТЕ
НАЧАЛЬНУЮ ТОЧКУ X1,X2,…,XN”
60 FOR I=1 TO N:INPUT X(I):NEXT I
PRINT “ВВЕДИТЕ ДЛИНУ ШАГА”:INPUTH
K=H:F E=0
FOR I=1 TO N
Y(I)=X(I):P(I)=X(I):B(I)=X(I):NEXT I
110GOSUB
2000:FI=Z
PRINT “НАЧАЛЬНОЕ
ЗНАЧЕНИЕ ФУНКЦИИ” Z
130 FOR I=1 TO N:PRINT X(I);“ “;:NEXT I:PRINT””
140PS=0:BS=1
REM ИССЛЕДОВАНИЕ
ВОКРУГ БАЗИСНОЙ ТОЧКИ
180 J=1:FB=FI
X(J)=Y(J)+K
GOSUB 2000
IF Z<FI THEN GOTO 280
X(J)=Y(J)-K
GOSUB 2000
IF Z<FI THEN GOTO 280
X(J)=Y(J)
GOTO 290
Y(J)=X(J)
290GOSUB
2000
FI=Z
PRINT
“ИССЛЕДУЮЩИЙ ПОИСК” Z
320 FOR I=1 TO N:PRINT X(I);“ “;:NEXT I:PRINT””
IF J=N THEN GOTO 360
J=J+1
GOTO 200
IF FI<FB-1E-08 THEN GOTO 540
370REM
ПОСЛЕ ОПЕРАТОРА 360, ЕСЛИ ФУНКЦИЯ УМЕНЬШИЛАСЬ, ПРОИЗВЕСТИ ПОИСК ПО ОБРАЗЦУ
380 IF PS=1 AND BS=0 THEN GOTO 420
390REM
НО ЕСЛИ ИССЛЕДОВАНИЕ ПРОВОДИЛОСЬ ВОКРУГ ТОЧКИ ШАБЛОНА РТ, И УМЕНЬШЕНИЕ ФУНКЦИИ
НЕ БЫЛО ДОСТИГНУТО, ТО ИЗМЕНИТЬ БАЗИСНУЮ ТОЧКУ В ОПЕРАТОРЕ 420
REM В ПРОТИВНОМ
СЛУЧАЕ УМЕНЬШИТЬ ДЛИНУ ШАГА В ОПЕРАТОРЕ 490
410 GOTO 490
FOR I=1 TO N:P(I)=B(I):Y(I)=B(I):X(I)=B(I):NEXT I
GOSUB 2000:BS=1:PS=0
FI=Z:FB=Z
PRINT “ЗАМЕНА БАЗИСНОЙ ТОЧКИ” Z
FOR I=1 TO N:PRINT X(I);“ “;:NEXT I:PRINT””
470REM
(СЛЕДУЕТ ЗА КОММЕНТАРИЕМ В СТРОКЕ 395) И ПРОВЕСТИ ИССЛЕДОВАНИЕ ВОКРУГ НОВОЙ
БАЗИСНОЙ ТОЧКИ
J=1:GOTO
200
K=K/10
PRINT “УМЕНЬШИТЬ
ДЛИНУ ШАГА”
IF |<< 1E-08 THENGOTO
700
REM ИССЛЕДОВАНИЕ
ВОКРУГ НОВОЙ БАЗИСНОЙ ТОЧКИ
J=1:GOTO
200
REM ПОИСК ПО
ОБРАЗЦУ
540 FOR I=1 TO N:P(I)=2*Y(I)-B(I)
B(I)=Y(I):X(I)=P(I):Y(I)=X(I)
NEXT I
GOSUB 2000:FB=FI:PS=1:BS=O:FI=Z
PRINT “ПОИСК ПО ОБРАЗЦУ” Z
FOR I=1 TO N:PRINT X(I);“ “;:NEXT I:PRINT””
600
REM ПОСЛЕ ЭТОГО ПРОИЗВЕСТИ ИССЛЕДОВАНИЕ ВОКРУГ ПОСЛЕДНЕЙ
ТОЧКИ ОБРАЗЦА
610 J=1:GOTO 200
PRINT “МИНИМУМ НАЙДЕН”
FOR I=1 TO N:PRINT “X”I“-”P(I):NEXT I:PRINT
750
PRINT “МИНИМУМ ФУНКЦИИ РАВЕН” FB
PRINT
“КОЛИЧЕСТВО ВЫЧИСЛЕНИЙ ФУНКЦИИ РАВНО” FE
790 END
FE=FE+1
2020
REM СЧЕСЧИК КОЛИЧЕСТВА ВЫЧИСЛЕНИЙ ФУНКЦИИ
RETURN
Приведенная
выше программа реализует описанную процедуру. Одной или двух точек бывает
недостаточно для определения начальной точки. Первая точка всегда должна
выбираться осмотрительно. ЭВМ работает только с ограниченной точностью, и
ошибки могут накапливаться в процессе сложных вычислений, особенно если шаг
имеет «неудобную» длину. (Обычно избегают «неудобной» длины, но программа
должна быть работоспособна и в таких ситуациях). Поэтому в строке 36, где
выясняется вопрос об изменении базисной точки, мы избегаем уменьшения длины
шага из-за накапливания ошибки введением длины шага, равной 10-8. Мы отслеживаем,
где производится исследование - в базисной точке (BS = 1, PS =
0)или в точке образца (BS = 0, PS = 1). Как можно убедиться на практике, если не
принимаются такие меры предосторожности,даже программа с удовлетворительной
логикой будет неработоспособна.
В
приведенной программе минимальная длина шага равна 10-8, но она может быть
изменена (например, в строке 51). Для контроля за выполнением процедуры в
программу введена печать промежуточных результатов. Для увеличения скорости
счета могут быть удалены строки с номерами 12, 13, 31, 32, 45, 46, 50, 58, 59.
Программа,
начинающаяся со строки 20, выполняет значение минимизируемой функции:
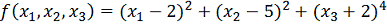
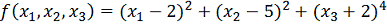 .
.
Минимум,
очевидно, находится в точке (2; 5; -2). Для начальной точки (4; -2; 3) и
начального шага длиной 1 приведены некоторые промежуточные результаты. По ним
можно легко проследить за изменениями в ходе исследований и поиска по образцу.
Заметим, что значение 97,0000001 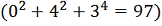
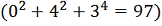 является
значением функции в точке, полученной ранее. Количество выполненных вычислений
функции запоминается в счетчике. Это часто используется как средство сравнения
эффективности различных методов поиска. Чем лучше метол, тем меньше в общем
случае требуется вычисления значений функции
является
значением функции в точке, полученной ранее. Количество выполненных вычислений
функции запоминается в счетчике. Это часто используется как средство сравнения
эффективности различных методов поиска. Чем лучше метол, тем меньше в общем
случае требуется вычисления значений функции
Метод
Хука-Дживса
введите
число переменных 3
введите
начальную точку х1,х2,…,xN 4 -2 3
введите
длину шага 1
начальное
значение функции 678
-2
3
исследующий
поиск 675
-2
3
исследующий
поиск 662
-1
3
исследующий
поиск 293
-1
2
Поиск
по образцу 106
0
1
исследующий
поиск 106
0
1
исследующий
поиск 97
1
1
исследующий
поиск 32
1
0
поиск
по образцу 5
3
-2
исследующий
поиск 4
3
-2
исследующий
поиск 1
4
-2
исследующий
поиск 1
4
-2
поиск
по образцу 20
7
-4
исследующий
поиск 20
7
-4
исследующий
поиск 17
6
-4
исследующий
поиск 2
6
-3
Замена
базисной точки 1
4
-2
исследующий
поиск 1
4
-2
исследующий
поиск 0
5
-2
Поиск
по образцу 1
6
-2
исследующий
поиск 1
6
-2
исследующий
поиск 0
5
-2
исследующий
поиск 0
5
-2
замена
базисной точки 0
5
-2
исследующий
поиск 0
5
-2
исследующий
поиск 0
5
-2
исследующий
поиск 0
5
-2
уменьшение
длины шага
исследующий
поиск 0
исследующий
поиск 0
5
-2
5
-2
исследующий
поиск 0
5
-2
Уменьшение
длины шага
минимум
найден
х1=2
х2=5
х3=-2
минимум
функции равен 0
количество
вычислений функции равно 127
Список
использованных источников
метод оптимизация
алгоритм
1 Васильев Ф. П. Методы оптимизации: научное издание. /Ф.
П. Васильев - М.: Изд-во Факториал Пресс, 2002. - 824 с.
2 Аоки М. Введение в методы оптимизации: учебн. /М.
Аоки. перевод с англ., Главная редакция физико-математической литературы М.:
изд-во Наука, 1977. - 344 с.
Аттетков А. В., Галкин С. В., Зарубин В. С. Методы
оптимизации: учеб.для вузов / под ред. В. С. Зарубина, А. П. Крищенко. - 2-е
изд., стереотип. - М.: изд-во МГТУ им. Н. Э. Баумана, 2003. - 440 с.
Банди Б. Методы оптимизации. Вводный курс: пер. с
англ. - М.: Радио и связь, 1988. - 128 с.
Корнеенко В. П. Методы оптимизации: Учеб. / В. П.
Корнеенко. - М.: Высш. шк., 2007. - 664 с.
Пантелеев А. В. Методы оптимизации в примерах и
задачах: Учеб.пособие / А. В. Пантелеев, Т. А. Летова. - М.: Высш. шк., 2005. -
544 с.
РеклейтисГ.Оптимизация в технике: в 2 кн. / Г.
Реклейтис, А. Рейвиндран. - М.: Мир, 1986. - 320 с.
Батищев Д. И. Оптимизация в САПР: Учебник/ Д.И.
Батищев, Я. Е.Львович, В.Н.Фролов. - Воронеж: Изд-во ВГУ, 1997. - 238 с.
Сухарев А..Г., Тимохов А..В., Федоров В.В. Курс
методов оптимизации. М.: Наука. 1985. - 254 с