Реконструкция генных сетей на основе данных микрочиповых экспериментов: отбор генов мишеней и сравнение различных моделей регуляции
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. Генная
экспрессия, основные определения
2. Микрочиповые
эксперименты
. Выявление
генов изменивших уровень экспрессии
. Гипергеометрический
метод
. Анализ
данных по раку молочной железы
. Моделирование
генной экспрессии
. Линейная
модель
. Методы
сглаживания
. Стохастическая
модель
. Сравнение
моделей
. Программная
реализация в системе biouml
ЗАКЛЮЧЕНИЕ
СПИСОК
ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ
1
ПРИЛОЖЕНИЕ
2
ВВЕДЕНИЕ
Хорошо известно, что биологические системы
обладают свойствами саморегуляции, то есть способностью перестраиваться в
зависимости от внешних воздействий так, чтобы сохранился оптимальный уровень их
функционирования.
Существуют различные способы регуляции
жизнедеятельности клетки, которые можно условно отнести к генетическому, биохимическому
и физиологическому уровням регуляции. В пределах каждого из них действуют
механизмы, в основе которых лежит последовательность конкретных метаболических
процессов. Понять динамические свойства этих регуляторных механизмов можно лишь
на основе общесистемного подхода, рассматривающего поведение каждого из
элементов сложной системы как результат его взаимодействия с остальными
элементами.
Одним из наиболее развитых подходов для решения
этой проблемы в современной биохимии является математическое моделирование.
Данная работа выполнена в рамках более
глобального проекта, имеющего своей целью наиболее полное формальное описание,
реконструкция и моделирование регуляции клеточного цикла в норме и патологии
(канцерогенез), а также связанных с ним процессов апоптоза и дифференцировки
клеток высших эукариот. Информация о генах и белковых комплексах, участвующих в
регуляции клеточного цикла будет интегрирована из многих баз данных, а также
путем аннотирования статей, содержащих экспериментальные данные.
Целью данной работы являются:
Реконструкция работы клетки на
уровне регуляции экспрессии генов и построение генных сетей на основе анализа
данных микрочиповых экспериментов.
Задачи, решаемые в работе:
· Рассмотрение и сравнение различных
математических методов анализа данных микрочиповых экспериментов, предложение
своих методов.
· Построение и сравнение различных
математических моделей генной регуляции.
· Написание программного продукта,
реализующего рассмотренные методы.
1. Генная экспрессия, основные определения
ДНК
(Дезоксирибонуклеиновая кислота) и РНК (Рибонуклеиновая кислота) -
органические соединения, обеспечивающее хранение, передачу из поколения в
поколение и реализацию генетической программы развития и функционирования живых
организмов.
Ген
- это участок ДНК, кодирующий одну полипептидную цепь (белок) или одну молекулу
тРНК, мРНК или рРНК. Это - смысловая единица генетического кода.
мРНК
- матричная РНК, служит для переноса информации с ДНК в цитоплазму для
последующей трансляции белка. Рибосмоные и транспортные РНК (рРНК и тРНК)
обеспечивают процесс трансляции белка с мРНК.
Генная экспрессия
- это процесс, в результате которого по информации, закодированной в гене,
синтезируется конечный продукт - белок. Уровнем экспрессии называется
количество нарабатываемого белка. В этом процессе можно выделить несколько
этапов. Два основных из них - это транскрипция и трансляция.
Транскрипция -
это процесс синтеза всех видов РНК по матрице ДНК, осуществляемый при помощи
специального фермента РНК-полимеразы. После транскрипции происходит обработка
получившейся молекулы мРНК (вырезание не кодирующих частей, обеспечение защиты
от нуклеаз, разрушающих РНК), после чего начинается второй этап - трансляция
белка с помощью рРНК и тРНК
Практически важнейшим процессом в функционировании
любого живого организма является регуляция генной экспрессии, контролирующая
производство того или иного белка, в зависимости от нужд организма. В
частности, этот процесс определяет рост и формирование живого организма и его
составных частей. Неправильная регуляция часто является причиной болезней или
неправильного формирования организма. Экспрессия генов может регулироваться на
всех стадиях процесса: и во время транскрипции, и во время трансляции, и на
стадии пост-трансляционных модификаций белков. Главную роль в системе регуляции
генной экспрессии являются специальные белки - транскрипционные факторы.
Транскрипционные факторы
- это белки, контролирующие процесс транскрипции (переноса информации с
молекулы ДНК в мРНК) путем связывания со специфичными участками ДНК
(промоторами, служащими стартовыми площадками для начала транскрипции). Так как
сама ДНК остается неизменной, то процесс транскрипции генов напрямую связан с
концентрацией соответствующих транскрипционных факторов.
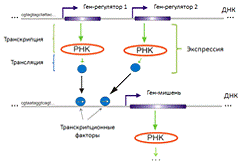
Рисунок 1. Процессы генной
экспрессии и регуляции
Транскрипционные факторы выполняют свою функцию
самостоятельно либо в комплексе с другими белками. Они обеспечивают снижение
(репрессоры) или повышение (активаторы) константы связывания РНК-полимеразы с
регуляторными последовательностями регулируемого гена, что соответственно
приводит к увеличению или уменьшению нарабатываемой с данного гена РНК.
Транскрипционные факторы различны у разных
генов, кроме того сами транскрипционные фактора, также кодируются с помощью
специальных генов. Таким образом, обеспечивается влияние одних генов на другие.
Схематически процессы экспрессии и регуляции генов изображены на рисунке 1. Мы
будем говорить, что некоторый ген X
активирует (подавляет) другой ген Y,
если увеличение уровня экспрессии X
влечет увеличение (уменьшение) уровня экспрессии Y.
Известны ситуации, когда ген активирует или подавляет сам себя либо когда ген X
активирует ген Y в то время
как Y подавляет X.
Таким образом, поддерживается нужный уровень различных белков в организме. В
случае, когда клетка сталкивается с новыми условиями (инфекция, стресс и т.д.)
она реагирует путем изменения экспрессионной программы. Во многих случаях в
начале активируется несколько транскрипционных факторов, которые в свою очередь
активируют многие другие гены для адекватного ответа на новые условия. Из
вышесказанного ясно, что гены могут образовывать очень сложные структуры -
генные сети.
Генная сеть
- это совокупность совместно экспрессирующихся, влияющих друг на друга генов,
выполняющих в организме некоторую специфическую функцию. Примером может служить
процесс апоптоза, т.е. программируемой клеточной смерти. Апоптоз нужен для
уничтожения старых или неправильно функционирующих (с повреждениями ДНК)
клеток. Значительное усиление этого процесса ведет к массовой гибели клеток, в
частности, вирус СПИДа провоцирует апоптоз клеток иммунной системы в то время
как ослабление, как правило к раку. Генную сеть апоптоза составляют, как
гены-инициаторы апоптоза, так и гены, блокирующие его. Решение о гибели клеток
происходит по совокупности их работы.
Важной задачей является изучение процессов
межгенных взаимодействий и моделирование работы генной сети. Будучи
построенным, такие модели могут дать информацию о реакции организма на различные
условия, на точные причины многих генетически обусловленных болезней, таких как
раковые опухоли, что крайне важно при создании новых лекарств, которые будут
направлены на регулирование работы конкретных генов с минимумом возможных
побочных действий.
Исходными данными для решения этой задачи служит
информация, получаемая об уровне генной экспрессии в результате микрочипового
эксперимента.
. Микрочиповый эксперимент, исходные данные
Технология ДНК-микрочипов появилась сравнительно
недавно, около 20 лет назад. Однако, широкие перспективы ее применения в
биологии и медицине привели к ее бурному развитию в последнее десятилетие.
Сейчас уже можно говорить, что именно эта технология служит основным
поставщиком информации для анализа изменения экспрессии генов.
ДНК-микрочип
- это миниатюризированные матрицы, в которых на подложке в определенном порядке
распределены и прикреплены фрагменты ДНК, соответствующие отдельным генам или
их частям. Такие организованные матрицы позволяют проводить эксперименты по одновременному
анализу структуры и экспрессии тысяч генов.
С помощью микрочипов можно изучать:
- экспрессию
генов в различных тканях.
- изменение
экспрессии генов в ходе клеточного цикла и в ходе развития.
- -
экспрессию генов в норме и при патологии (в нормальных и раковых клетках).
- изменение
экспрессии генов с течением времени как результат внешнего воздействия
(взаимодействие клетки с патогеном, лекарством).
- наличие
чужеродной ДНК/РНК вирусов для диагностики различных заболеваний (например,
ЗППП)
- анализ
мутаций и полиморфизмов.
Основываясь на характере числовых данных в чипе,
можно построить две независимые классификации микрочипов:
- статические
(данные замерены единовременно).
- динамические
(данные распределены во времени).
А также
- с
конкурентной гибридизацией (тестовый образец против контроля).
- без
конкурентной гибридизации (только тестовый образец).
Здесь возможны любые комбинации. В статических
экспериментах проводятся единовременные замеры экспрессии генов в различных
образцах (пробах), в то время как в динамических, экспрессия каждой пробы
замеряется многократно в некоторые последовательно идущие моменты времени.
Данные, полученные в результате статического эксперимента (например, замеры
экспрессии генов в раковых клетках взятых у различных пациентов),
предполагаются независимыми и одинаково распределенными, в то время как данные,
полученные из динамического эксперимента зачастую проявляют сильную
автокорреляцию между последовательно расположенными точками.
В случае конкурентной гибридизации сравнивается
экспрессия в исследуемых образцах (например, опухолевых тканях) и в норме.
Данные представляют собой числовое отношение 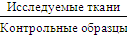 .
Гены в двух образцах конкурируют за место на подложке. Также существуют
микрочипы, в которых исследуется экспрессия генов только в исследуемых тканях
без контроля.
.
Гены в двух образцах конкурируют за место на подложке. Также существуют
микрочипы, в которых исследуется экспрессия генов только в исследуемых тканях
без контроля.
Хотя, за прошедшее десятилетие данная технология
сильно эволюционировала, стала достаточно надежной, все же очень часто
разнообразные технические сбои и неточности в планировании эксперимента
приводят к различным артефактам в результатах, что может сильно осложнять их
последующий анализ.
В дальнейшем рассмотрим различные виды анализа
данных микрочиповых экспериментов.
3. Выявление генов изменивших уровень экспрессии
Задача выявления генов изменивших свою
экспрессию вследствие некоего воздействия либо в течение клеточного цикла очень
важна, т.к. позволяет выявить например последствия приема того или иного
лекарства или отобрать гены с отличающимся поведением для последующего анализа.
Перед тем как начинать строить зависимости между генами необходимо отобрать те
из них, которые нас интересуют, а именно гены, изменившие свою экспрессию. Т.к.
работать с целым списком (обычно порядка 40000 клонов) слишком трудоемко и к
тому же бессмысленно. Опишем те методы, которые были реализованы в плагине и
использовались для анализа.
Напомним, что исходными данными являются матрицы
значений экспрессии генов:
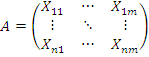
Строка соответствует отдельной пробе (гену, либо
его участку).
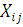 - экспрессия i-той
пробы в условиях эксперимента j.
Основными типами данных являются повременные замеры экспрессии (
- экспрессия i-той
пробы в условиях эксперимента j.
Основными типами данных являются повременные замеры экспрессии (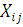 - экспрессия в момент времени
- экспрессия в момент времени 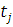 ) и замеры у разных
пациентов (
) и замеры у разных
пациентов (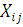 - экспрессия у
j-того пациента).
- экспрессия у
j-того пациента).
Задача ставится следующим образом: необходимо
выделить из общей группы те пробы, которые значимо изменили свою экспрессию
либо с течением клеточного цикла, либо в результате воздействия на пациентов.
Часто данные представляют собой отношение экспрессии объекта у пациента к
экспрессии данного объекта в норме.
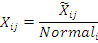
В этом случае задача сводится к выявлению того,
насколько значимо 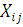 отклоняется от
единицы в ту или иную сторону.
отклоняется от
единицы в ту или иную сторону.
В противном случае приходится сравнивать
экспрессию пробы в исследуемой ткани с экспрессией у некоторой контрольной
группы, например в качестве этой группы может браться экспрессия той же пробы,
но в нулевой момент времени. В этом случае необходимо сравнить насколько
значимо различаются данные нам значения 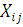 и
и
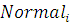 .
.
Решать эту задачу будем с точки зрения статистического
подхода. При этом проба рассматривается как случайная величина.
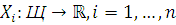
Замер экспрессии у j-того
пациента, соответственно - реализация случайной величины.
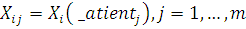
В случае повременных замеров имеем случайный
процесс:
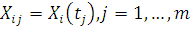
Таким образом, мы имеем в качестве исходных
данных выборки для некоторых случайных величин с неизвестным распределением.
Требуется либо сравнить значения в выборке с некоторым фиксированным значением
(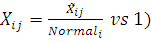
либо сравнить экспрессию в норме и патологии,
при этом нужно иметь несколько реализаций объекта в норме для успешного
статистического анализа. Т.е. здесь сравниваются две выборки, и оценивается
различие между ними. Рассмотрим некоторые стандартные методы, которые могут
применяться к этой задаче.
Замечание.
Во всех случаях мы будем получать так называемый скор (score).
Величину, которая будет давать нам информацию о том, насколько значимо
изменилась экспрессия и, соответственно, какова вероятность того, что
экспрессия изменилась исключительно по случайным причинам.
. Статистика Стьюдента
Этот критерий предназначен для проверки гипотезы
однородности средних значений 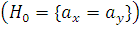 в двух выборках,
извлеченных из нормальных генеральных совокупностей:
в двух выборках,
извлеченных из нормальных генеральных совокупностей:
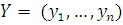 - первая выборка
значений экспрессии для гена,
- первая выборка
значений экспрессии для гена,
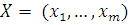 - вторая выборка
значений экспрессии для гена,
- вторая выборка
значений экспрессии для гена,
имеющих одинаковую (хотя и неизвестную)
дисперсию 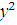 . В качестве
критической статистики в данном критерии используется величина:
. В качестве
критической статистики в данном критерии используется величина:
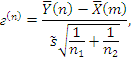
где
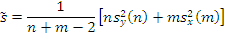
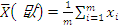 ,
, 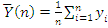
- соответствующие выборочные средние,
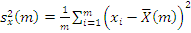 ,
,
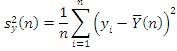
соответствующие выборочные дисперсии,
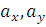 - математические
ожидания распределений, описывающих вероятностный закон, которому подчиняются
наблюдения соответствующей выборки.
- математические
ожидания распределений, описывающих вероятностный закон, которому подчиняются
наблюдения соответствующей выборки.
При справедливости гипотезы однородности средних
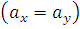 ,
для выборок с указанными свойствами, статистика
,
для выборок с указанными свойствами, статистика 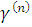 должна
подчиняться распределению Стьюдента с
должна
подчиняться распределению Стьюдента с 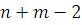 степенями
свободы.
степенями
свободы.
Таким образом, используя двухсторонний критерий,
P-значение вычисляем
по формуле:
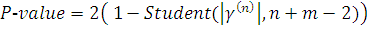
В случае, когда проверяемая и контрольная группы
представляют собой связанные данные (например, после воздействия некоторого и
до него) применяется критерии Стьюдента для связанных выборок [3]:
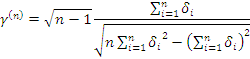
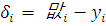
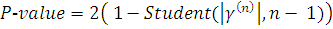
Окончательно, получаем:
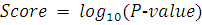
Минусами этого метода являются: предположения
нормальности данных и равенства дисперсий. Коме того, сам характер метода
подразумевает сравнение средних, что не всегда правомерно для решения исходной
задачи.
Плюсами метода является низкая вычислительная
сложность и простота алгоритма. Кроме того для проведения теста достаточно
иметь по три элемента в каждой выборке, что важно поскольку данные о замерах в
одних и тех же условиях (в один момент времени, например), часто содержат малое
количество значений.
. Критерий ранговых сумм Вилкоксона
Свободный от распределения критерий суммы рангов
для гипотезы об отсутствии эффекта обработки.
Имеем 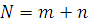 наблюдений
наблюдений
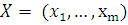 и
и
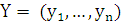 .
.
Положим:
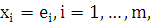
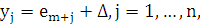
где 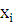 и
и
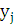 -
наблюдаемые, а
-
наблюдаемые, а 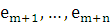 - ненаблюдаемые
случайные величины; интересующий нас параметр
- ненаблюдаемые
случайные величины; интересующий нас параметр 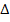 -
это неизвестный сдвиг в положении, обусловленный “обработкой”.
-
это неизвестный сдвиг в положении, обусловленный “обработкой”.
Все 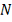
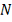 случайных величин
случайных величин 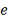
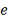 взаимно независимы.
взаимно независимы.
Все 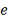
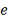 извлечены из одной генеральной
совокупности.
извлечены из одной генеральной
совокупности.
Проверяем гипотезу 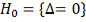
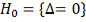 , для этого:
, для этого:
Объединим выборочные значения обоих
выборок и расположим их в порядке возрастания, т.е. образуем общий вариационный
ряд, и каждой величине из этого ряда сопоставим ее ранг 
 , равный порядковому номеру величины
в общем вариационном ряду. Заметим, что если нулевая гипотеза имеет место, то
любое распределение рангов по этим двум выборкам равновероятно.
, равный порядковому номеру величины
в общем вариационном ряду. Заметим, что если нулевая гипотеза имеет место, то
любое распределение рангов по этим двум выборкам равновероятно.
В качестве статистики критерия
берется сумма рангов 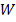
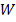 одной (например, первой выборки):
одной (например, первой выборки):
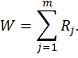
Предположим, что проверяем гипотезу 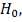
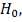 против альтернативы
против альтернативы 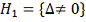
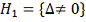 . Для этого подсчитываем все
различные способы группирования рангов, при которых статистика
. Для этого подсчитываем все
различные способы группирования рангов, при которых статистика 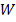
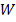 принимает значения, равные или
меньше наблюдаемого
принимает значения, равные или
меньше наблюдаемого 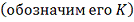
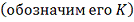 , после чего вычисляем отношение
этого числа к общему числу возможных распределений рангов по двум выборкам,
которое равно
, после чего вычисляем отношение
этого числа к общему числу возможных распределений рангов по двум выборкам,
которое равно 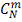
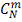 .
.
Отсюда промежуточное P-значение
вычисляем по формуле:
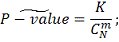
Далее, если 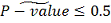
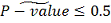 , то в качестве итогового P-значения
мы берем:
, то в качестве итогового P-значения
мы берем:
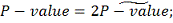
Если же наше 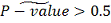
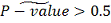 , тогда подсчитываем все различные
способы группирования рангов, при которых статистика
, тогда подсчитываем все различные
способы группирования рангов, при которых статистика 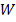
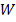 принимает значения, равные или
больше наблюдаемого
принимает значения, равные или
больше наблюдаемого 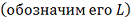
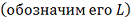 , аналогично с предыдущим
подсчитываем итоговое P значение:
, аналогично с предыдущим
подсчитываем итоговое P значение:
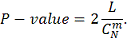
. Тест Колмогорова
Свободный от распределения критерий для проверки
однородности двух выборок .
Имеем 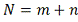
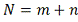 наблюдений
наблюдений 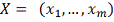
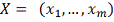 и
и 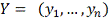
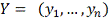 .
.
Предположим, что:
Все 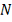
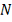 наблюдений
наблюдений 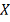
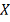 и
и 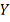
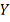 взаимно независимы.
взаимно независимы.
Все эти 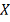
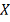 извлечены из одной непрерывной
совокупности
извлечены из одной непрерывной
совокупности 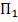
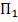 .
.
Все 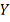
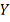 извлечены из одной непрерывной
совокупности
извлечены из одной непрерывной
совокупности 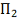
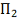 .
.
Рассматриваем гипотезу о том, что
совокупности 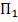
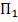 и
и 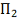
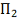 идентичны, т.е. о том, что обе
выборки извлечены из одной и той же совокупности. Её можно переписать так:
идентичны, т.е. о том, что обе
выборки извлечены из одной и той же совокупности. Её можно переписать так:
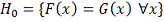
Будем тестировать эту гипотезу против альтернативы
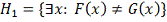
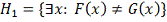 .
.
Для проверки 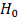
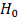 делаем:
делаем:
Будем считать, что наши выборки
упорядочены по возрастанию:
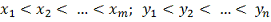
(если это не так просто
упорядочиваем их).
Статистика критерия
Колмогорова-Смирнова измеряет различия между эмпирическими функциями
распределения, построенными по выборке:
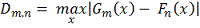
Однако на практике значение данной статистики
удобнее вычислять при помощи формул:
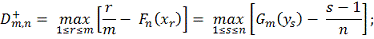

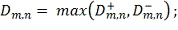
Если гипотеза 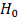
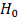 справедлива, то при неограниченном
увеличении объемов выборок:
справедлива, то при неограниченном
увеличении объемов выборок:
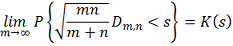
Т.е. статистика 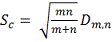
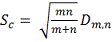 в пределе подчиняется распределению
Колмогорова
в пределе подчиняется распределению
Колмогорова 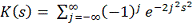
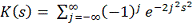 . Однако условное распределение
. Однако условное распределение 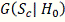
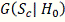 статистики
статистики 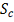
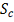 сходится к
сходится к 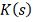
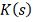 медленно и существенно отличается
от него при не очень больших
медленно и существенно отличается
от него при не очень больших 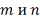
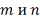 . Гладкость распределения статистики
очень сильно зависит от величины
. Гладкость распределения статистики
очень сильно зависит от величины 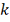
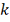 - наименьшего общего кратного
- наименьшего общего кратного 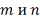
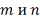 . Поэтому предпочтительнее применять
критерий, когда объемы выборок
. Поэтому предпочтительнее применять
критерий, когда объемы выборок 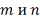
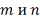 не равны и представляют собой
взаимно простые числа. В таких случаях наименьшее общее кратное
не равны и представляют собой
взаимно простые числа. В таких случаях наименьшее общее кратное 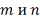
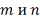 максимально, а распределение
статистики намного больше напоминает непрерывную функцию распределения. Но и
тогда при небольших значениях
максимально, а распределение
статистики намного больше напоминает непрерывную функцию распределения. Но и
тогда при небольших значениях 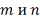
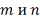 проявляется значительное отклонение
проявляется значительное отклонение
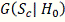
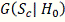 от предельного
от предельного 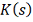
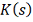 -
- 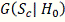
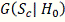 заметно сдвинуто влево от
заметно сдвинуто влево от 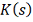
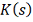 и с ростом
и с ростом 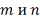
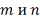 приближается к нему слева.
приближается к нему слева.
В этой связи можно предложит простую
модификацию статистики 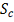
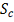 :
:
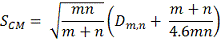
у которой практически отсутствует последний
недостаток.
Таким образом, вычислив статистику 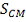
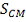 , P-значение
вычисляем по формуле:
, P-значение
вычисляем по формуле:
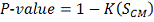
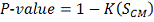 .
.
4. Критерий однородности Лемана-Розенблатта
Свободный от распределения критерий
однородности Лемана-Розенблатта представляет собой критерий типа 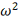
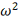 .
.
Имеем 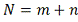
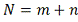 наблюдений
наблюдений 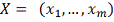
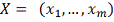 и
и 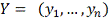
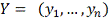 .
.
Предположим (точно так же как и в
критерии Колмогорова-Смирнова), что:
Все 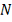
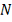 наблюдений
наблюдений 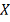
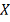 и
и 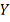
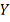 взаимно независимы.
взаимно независимы.
Все эти 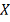
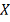 извлечены из одной непрерывной
совокупности
извлечены из одной непрерывной
совокупности 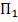
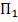 , распределенной согласно закону
, распределенной согласно закону 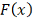
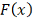 .
.
Все 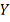
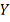 извлечены из одной непрерывной
совокупности
извлечены из одной непрерывной
совокупности 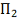
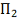 , распределенной согласно закону
, распределенной согласно закону 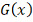
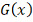 .
.
Рассматриваем гипотезу о том, что
совокупности 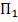
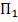 и
и 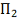
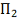 идентичны, т.е. о том, что обе
выборки извлечены из одной и той же совокупности. Её можно переписать так:
идентичны, т.е. о том, что обе
выборки извлечены из одной и той же совокупности. Её можно переписать так:
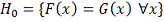
Будем тестировать эту гипотезу против
альтернативы
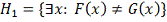
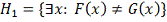 .
.
Для проверки 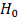
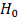 делаем:
делаем:
Будем считать, что наши выборки
упорядочены по возрастанию:
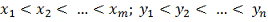
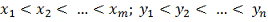
(если это не так просто
упорядочиваем их).
Статистика критерия имеет вид:
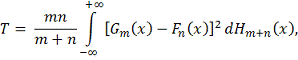
Где
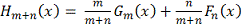
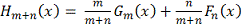
эмпирическая функция распределения,
построенная по объединенному вариационному ряду двух выборок. Статистика 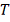
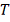 используется в форме:
используется в форме:

где 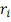
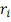 - порядковый номер (ранг)
- порядковый номер (ранг) 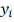
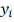 ,
, 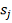
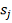 - порядковый номер (ранг)
- порядковый номер (ранг) 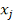
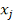 в объединенном вариационном ряду.
в объединенном вариационном ряду.
Статистика 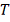
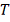 в пределе распределена как
в пределе распределена как 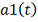
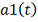 :
:
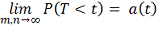
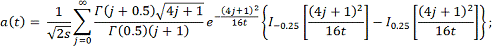
где 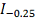
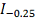 и
и 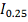
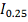 - модифицированные функции Бесселя:
- модифицированные функции Бесселя:
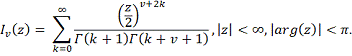
В отличие от статистики
Колмогорова-Смирнова распределение статистики 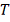
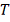 быстро сходится к предельному.
быстро сходится к предельному.
Таким образом, вычислив статистику 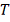
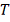 , P значение
вычисляем по формуле:
, P значение
вычисляем по формуле:
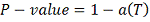
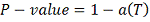 .
.
5. Статистическая регрессия
Метод построения статистической регрессии
используется в случае, когда данные представляют собой замеры по времени и
требуется исследовать поведение экспрессии объекта после начала некоторого
воздействия, либо просто во время клеточного цикла. Часто бывает целесообразно
исследовать не только сам факт изменения экспрессии объекта, но и характер
этого изменения.
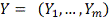
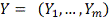 - выборка значений экспрессии для
гена.
- выборка значений экспрессии для
гена.
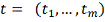
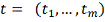 - временные точки, в которых
замерена экспрессия
- временные точки, в которых
замерена экспрессия
Т.е. значение 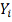
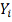 замерено в момент времени
замерено в момент времени 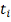
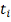
Строим полиномиальную регрессию:
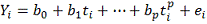
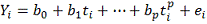
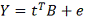
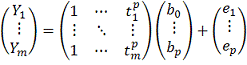
Где 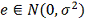
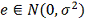
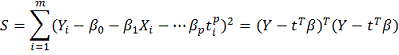
- сумма квадратов отклонений
Из требования 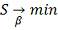
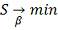 , получаем систему для нахождения
МНК оценок для b:
, получаем систему для нахождения
МНК оценок для b:
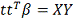
Также нам потребуется оценка для дисперсии
коэффициентов:
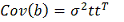
Оценка для 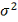
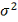 :
:
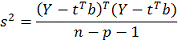
Проверяя гипотезу 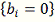
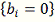 будем использовать статистику
будем использовать статистику
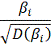
в случае справедливости нулевой
гипотезы, она имеет распределение Стьюдента с 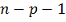
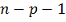 степенями свободы. Отсюда, формула
для P-значения i-того
коэффициента:
степенями свободы. Отсюда, формула
для P-значения i-того
коэффициента:

Где 
 находится из (2), а
находится из (2), а 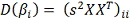
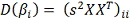
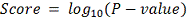
Чаще всего здесь приходится исследовать
существование линейной зависимости экспрессии от времени и квадратичной при
условии того что пик приходится на исследуемый промежуток времени.
. Гипергеометрический тест
Отдельно рассмотрим метод, специально
разработанный для решения исходной задачи - обнаружения объектов (клонов и
генов) с повышенным и пониженным уровнем экспрессии. Здесь в отличие от предыдущих
методов анализ отдельных объектов проводится при учете всей совокупности данных
в таблице.
Пусть: 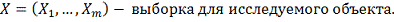
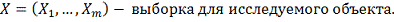
Исследуется нулевая гипотеза: 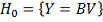
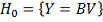 означающая, что любые отклонения
значений выборки от фиксированного значения происходят исключительно по
случайным причинам. В качестве альтернативы выдвинем гипотезу
означающая, что любые отклонения
значений выборки от фиксированного значения происходят исключительно по
случайным причинам. В качестве альтернативы выдвинем гипотезу 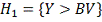
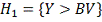 .
.
При этом мы предполагаем, что для
подавляющего количества генов в таблице нулевая гипотеза верна.
Параметр метода BV (Boundary Value) -
предназначен для разграничения между повышенной и пониженной экспрессией.
Эвристически эту гипотезу можно
принять или отклонить, например, оценивая количество элементов в выборке,
превышающих пороговое значение достаточно сильно. Т.е. задать решающее правило
следующим образом:
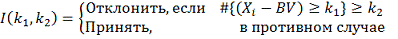
Но тогда необходимо оценить с какой
вероятностью мы ошибемся, если будем применять это правило при разных 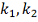
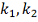 .
.
Для удобства, построим вариационный
ряд:
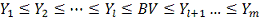
Ясно, что в качестве 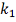
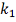 не уменьшая общности можно
рассматривать только значения из ряда
не уменьшая общности можно
рассматривать только значения из ряда 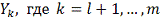
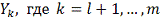 .
.
Допустим, мы фиксировали 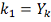
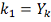 , введем обозначение:
, введем обозначение:
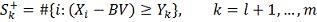
В случае верности нулевой гипотезы,
отклонения от 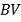
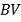 произошли по случайным причинам и в
этом случае
произошли по случайным причинам и в
этом случае 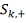
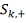 имеет гипергеометрическое
распределение с параметрами
имеет гипергеометрическое
распределение с параметрами 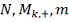
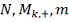 , где:
, где:
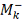
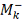 - количество значений в таблице
больше либо равных
- количество значений в таблице
больше либо равных 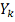
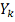 .
.
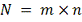
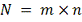 - общее количество данных в
таблице.
- общее количество данных в
таблице.
Замечание. Случайная
величина, имеющая гипергеометрическое распределение 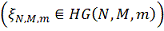
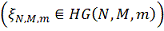 представляет собой (может быть
интерпретирована как) количество обладающих заданным свойством элементов среди
представляет собой (может быть
интерпретирована как) количество обладающих заданным свойством элементов среди 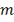
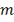 элементов, случайно извлеченных
(без возвращения) из совокупности N элементов, среди которых
элементов, случайно извлеченных
(без возвращения) из совокупности N элементов, среди которых 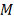
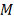 обладают данным свойством.
обладают данным свойством. 

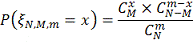
Таким образом, вероятность ошибиться
при отвержении гипотезы 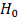
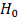 c помощью
критерия
c помощью
критерия 
 может быть вычислена по формуле:
может быть вычислена по формуле:
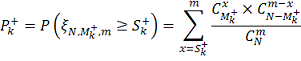
Таким образом, мы получили серию
критериев с критическими статистиками 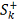
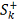 где k пробегает
все значения, для которых
где k пробегает
все значения, для которых 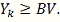
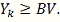 Логично из этих критериев выбрать
критерий с наименьшей ошибкой первого рода:
Логично из этих критериев выбрать
критерий с наименьшей ошибкой первого рода:
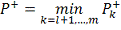
Аналогичным образом вводим
альтернативную гипотезу 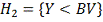
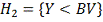 и обозначения:
и обозначения:
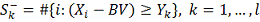
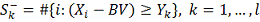 - набор критических статистик.
- набор критических статистик.
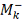
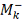 - количество значений в таблице
меньше либо равных
- количество значений в таблице
меньше либо равных 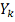
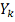 .
.
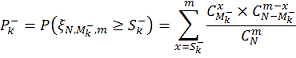
Это вероятности ошибиться, отвергнув нулевую
гипотезу из-за слишком маленьких значений в выборке. Аналогично выбираем тот
критерий, который имеет наименьшую вероятность ошибки первого рода.
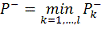
И, окончательно

Причем, если 
 то, отвергнув нулевую гипотезу,
целесообразно объявить исследуемый объект повысившим свою регуляцию. Если же
то, отвергнув нулевую гипотезу,
целесообразно объявить исследуемый объект повысившим свою регуляцию. Если же 
 , то ген объявляется понизившим
регуляцию.
, то ген объявляется понизившим
регуляцию.
Введем обозначения:
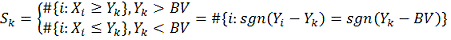
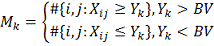
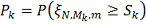
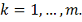
Тогда алгоритм можно описать следующим образом:
Упорядочиваем значения

Идем по массиву значений и находим
величины 

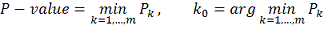
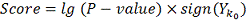
Итоговый ответ для каждого объекта -
это скор, знак которого указывает на то, вероятность чего больше: того, что ген
повысил или понизил экспрессию, а абсолютное значение, на то какова вероятность
ошибиться при отвержении нулевой гипотезы. Скор близкий к нулю означает, что
нулевая гипотеза, скорее всего, верна. Десятичный логарифм здесь взят для
удобства. Т.е. например скор, равный 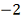
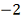 указывает нам, что если мы
отвергнем гипотезу о том, что объект не изменил свою экспрессию и примем
альтернативу
указывает нам, что если мы
отвергнем гипотезу о том, что объект не изменил свою экспрессию и примем
альтернативу 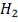
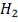 то мы ошибемся с вероятностью 0,01.
Вероятность ошибки при принятии альтернативы
то мы ошибемся с вероятностью 0,01.
Вероятность ошибки при принятии альтернативы 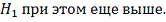
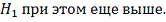
Важным моментом является то, что мы
предполагаем (а обычно так и есть), что большая часть генов действительно не
изменила своей экспрессии и отклоняется от некоторого среднего уровня только
случайно или из-за погрешностей в измерении и поэтому правомерно использовать
значения как некоторую “кучу” из которой можно брать случайные значения,
характерные для экспрессии генов в данном эксперименте. Хотя количество данных
в строке может быть каким угодно, но чем больше значений, тем достовернее
результаты теста. При анализе данных, в которых для каждого объекта есть всего
одно измерении экспрессии, тест вырождается в простое ранжирование объектов и
выборе в качестве изменивших свою экспрессию объектов с большими значениями
экспрессии.
В качестве BV можно
выбирать, например 1 (когда данные уже представляют собой отношение паталогии к
норме), уровень экспрессии в норме (для каждого объекта выбирается своё BV),
усредненная экспрессия контрольной группы или средняя экспрессия самого гена
(тогда исследуется отклонения гена от его среднего сзначения).
Минусом метода является относительно
большая вычислительная сложность: 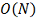
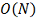 . Плюсами - робастность, гибкость,
возможность анализировать таблицы с разным числом значений для разных проб, в том
числе и равных 1 (это важно т.к. часто микрочиповые таблицы содержат
пропущенные значения) а также возможность проведения мета-анализа. Кроме того,
в отличие от статистики Стьюдента, гипергеометрический тест использует
информацию не только о средних значениях. Робастность метода заключается в
устойчивости к случайным выбросам в данных, гипергеометрический метод учитывает
все данные при обработке каждого отдельного гена. В этих данных неизбежно
присутствует некоторое количество выбросов связанных с допущенными ошибками в
эксперименте. В связи с этим вероятность того что в наугад выбранной строке
будет, например, один выброс довольно высока.
. Плюсами - робастность, гибкость,
возможность анализировать таблицы с разным числом значений для разных проб, в том
числе и равных 1 (это важно т.к. часто микрочиповые таблицы содержат
пропущенные значения) а также возможность проведения мета-анализа. Кроме того,
в отличие от статистики Стьюдента, гипергеометрический тест использует
информацию не только о средних значениях. Робастность метода заключается в
устойчивости к случайным выбросам в данных, гипергеометрический метод учитывает
все данные при обработке каждого отдельного гена. В этих данных неизбежно
присутствует некоторое количество выбросов связанных с допущенными ошибками в
эксперименте. В связи с этим вероятность того что в наугад выбранной строке
будет, например, один выброс довольно высока.
Мета-анализ
Часто бывает нужно проанализировать
сразу несколько разнотипных микрочиповых таблицы, например, для больных разными
типами рака или для экспериментов, проведенных в разных лабораториях. С целью
выявления некоторых общих тенденций и наиболее устойчивых факторов. Результаты
такого анализа являются более общими, содержат меньше информации, но в то же
время более обобщенные и надежные. Кроме того, объектами в микрочиповых
таблицах часто являются не сами гены, а их участки и, таким образом несколько
объектов могут соответствовать одному и тому же гену. В таком случае после
анализа мы получаем несколько скоров для одного гена, а нам необходимо принять
одно решение для гена - либо он повысил свою экспрессию, либо понизил, либо не
изменил. Для этих целей, в частности и был разработан гипергеометрический тест,
т.к. он позволяет проводить мета-анализ.
В качестве входных данных мы имеем
несколько микрочиповых таблиц 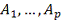
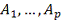 . Ключами в которых являются
объекты, а значениями - замеры экспрессии для них.
. Ключами в которых являются
объекты, а значениями - замеры экспрессии для них.
Проводится гипергеометрический
анализ каждой таблицы отдельно.
На выходе для каждой имеем таблицу 
 .
.
Для каждого исследованного объекта с
помощью баз данных находим соответствующий ему ген. И объединяем все полученные
таблицы в одну. Ключами в ней служат уже гены, а значениями - скоры полученные
в разных таблицах либо в одной и той же таблице для разных участков данного
гена.
Проводим гипергеометрический анализ
получившейся таблицы с параметром 
 . Получаем унифицированный ответ для
каждого гена.
. Получаем унифицированный ответ для
каждого гена.
Действительно, пусть мы получили для
некоторого гена набор скоров
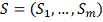
Очевидно, что некоторые из этих скоров могли
быть получены по ошибочным данным или по случайным выбросам. Проводя еще раз
гипергеометрический анализ мы проверяем насколько отклонения от нуля в этом
наборе могут быть объяснены случайными причинам.
. Анализ данных по раку молочной железы
Был проведен анализ данных микрочипового эксперимента,
призванного выявить реакцию организма больного раком пациента на потенциальные
лекарства. Данные представляют собой замеры уровня экспрессии генов пациентов
больных раком молочной железы, после введения препаратов. В качестве
потенциальных лекарств тестировались вещества RITA
в объеме 0,1μM и 1μM,
Nutlin в объеме 10μM.
Замеры
проводились в следующих временных точках (единицы измерения в часах):

Количество исследованных объектов - 22276.
Одной из задач анализа была оценка того, как
изменится экспрессия генов в первые часы после приема препаратов. В частности
очень важно проанализировать поведение генов, которые влияют на процесс
апоптоза - программируемой клеточной смерти, которая наступает при нарушении
правильного функционирования клетки (например, в результате мутации ДНК). В
клетках раковых опухолей процесс апоптоза подавлен, что позволяет раковым
клеткам продолжать делиться. Одним из самых важных противораковых генов
является ген tp53 (tumor
protein 53), который
активируется при повреждениях генетического аппарата, а также при стимулах,
которые могут привести к подобным повреждениям, или являются сигналом о
неблагоприятном состоянии клетки (стрессовом состоянии). Его функция состоит в
удалении из пула реплицирующихся клеток тех клеток, которые являются
потенциально онкогенными (отсюда образное название белка р53 - хранитель
генома). Сам процесс апоптоза, конечно, регулируется не одним геном, а целой
генной сетью, однако решающим фактором является именно tp53, тогда как
остальные гены заменяемы (существует несколько сигнальных путей, ведущих к
tp53). Числовые значения в таблице варьировались от 0.1 до 70390. Перед началом
анализа, данные подвергнулись следующей обработке: все значения экспрессии
меньшие заданного порога, равного 200 были приравнены к этому порогу. Это было
сделано ввиду стохастической природы данных: все значения меньше 200
представляют собой в основном случайный шум.
На первом этапе анализа данные были
разбиты на три таблицы в соответствии с исследовавшимся препаратом: RITA_0.01, RITA_1 и Nutlin, далее
каждая из этих таблиц анализировалась отдельно. В каждой временной точке кроме
контроля (0ч.) было проведено только одно измерение экспрессии для каждого
препарата, поэтому временные точки были сгруппированы следующим образом: 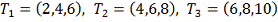
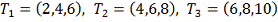 и каждая из этих групп сравнивалась
с контрольной группой в качестве которой выступали 3 замера уровня экспрессии в
0ч.
и каждая из этих групп сравнивалась
с контрольной группой в качестве которой выступали 3 замера уровня экспрессии в
0ч.
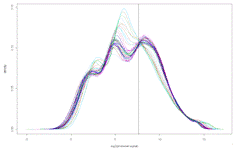
Рисунок 2. Эмпирические плотности
распределения экспрессий генов в разные моменты времени. Вертикальной линией
обозначен порог по которому отсекались несущественные значения
Статистический анализ проводился с
помощью статистик Стьюдента, Вилкоксона и гипергеометрического теста. Граничным
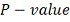
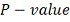 было выбрано значение 0,01. Т.е.
отбирались только те гены, скор которых превышал 2, что является довольно
сильным ограничением. Стоит отметить, что корреляции между скорами, полученными
по одним и тем же данным различными методами во всех 27 случаях был выше 0,95,
что позволяет говорить о надежности результата. Количество генов, отобранных
различными методами для препаратов RITA и Nutlin приведены в
таблицах 1 и 2 соответственно.
было выбрано значение 0,01. Т.е.
отбирались только те гены, скор которых превышал 2, что является довольно
сильным ограничением. Стоит отметить, что корреляции между скорами, полученными
по одним и тем же данным различными методами во всех 27 случаях был выше 0,95,
что позволяет говорить о надежности результата. Количество генов, отобранных
различными методами для препаратов RITA и Nutlin приведены в
таблицах 1 и 2 соответственно.
Таблица
1
Количество объектов изменивших свою экспрессию
под воздействием препарата RITA
в объеме 1uM
|
2-4-6
часов
|
4-6-8
часов
|
6-8-10
часов
|
|
Статистика
Стьюдента
|
2684
|
4297
|
4625
|
|
Статистика
Вилкоксона
|
5340
|
6137
|
6293
|
|
Гипергеометрический
тест
|
6933
|
7240
|
7220
|
|
Пересечение
|
2684
|
4296
|
4625
|
Таблица
2
Количество объектов изменивших свою экспрессию
под воздействием препарата Nutlin
в объеме 10uM
|
2-4-6
часов
|
4-6-8
часов
|
6-8-10
часов
|
|
Статистика
Стьюдента
|
981
|
2180
|
3040
|
|
Статистика
Вилкоксона
|
3109
|
4450
|
5356
|
|
Гипергеометрический
тест
|
5581
|
6355
|
7030
|
|
Пересечение
|
981
|
2180
|
3040
|
По этим таблицам видно, что хотя корреляции
между результатами большие, но сами методы дают различные результаты. Это
связано с тем, что методы Вилкоксона и гипергеометрический имеют дискретный
характер, в отличие от метода Стьюдента. В то же время видно, что все гены
отобранные методом Стьюдента также отобраны и другими методами. Однако, помимо
пересечения с результатами анализа методом Стьюдента необходимо исследовать
также результаты других анализов. Так, например, играющий важную роль в
процессе апоптоза, онкоген JUN
при гипергеометрическом анализе показал довольно большое значение скора:
5,033741591, в то время как при анализе методом Стьюдента скор не превысил
порога в 2.
Итого было получено 27 таблиц скоров (для
каждого из трех препаратов было проведено по три сравнения каждое тремя
методами). Окончательно отбирались только те гены, скор которых превысил
пороговое значение для всех методов анализа.
На втором этапе, после импорта
полученных списков в базу данных Explain
(<#"580806.files/image176.gif">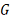 . Для простоты будем называть его
ген-мишень. Обозначим результат измерения уровня экспрессии гена-мишени в
момент времени t через
. Для простоты будем называть его
ген-мишень. Обозначим результат измерения уровня экспрессии гена-мишени в
момент времени t через 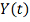
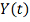 .
.
Обозначим набор генов, прямо или
косвенно влияющих на ген-мишень: 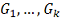
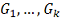 . Это - гены-регуляторы. Обозначим
через
. Это - гены-регуляторы. Обозначим
через 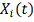
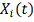 - результат измерения уровня экспрессии
i-того регулятора в момент времени t.
- результат измерения уровня экспрессии
i-того регулятора в момент времени t.
Как именно связан уровень экспрессии
гена-мишени с уровнями экспрессии генов-регуляторов? В самом общем виде можно
представить зависимость следующим образом:
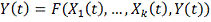
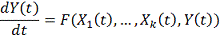
На данный момент не существует каких-либо
общепризнанных моделей. Ниже приведены примеры достаточно простых и в то же
время имеющих свои характерные особенности моделей:
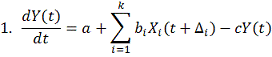
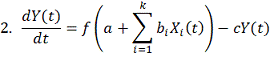
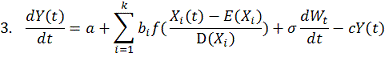
здесь:
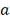
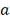 - фоновый уровень экспрессии,
независящий от регуляторов.
- фоновый уровень экспрессии,
независящий от регуляторов.
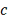
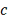 - коэффициент деградации.
- коэффициент деградации.
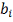
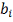 - уровень влияния i-того
регулятора на ген-мишень.
- уровень влияния i-того
регулятора на ген-мишень.
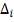
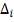 - временная задержка нужная для
завершения процесса трансляции транскрипционных факторов.
- временная задержка нужная для
завершения процесса трансляции транскрипционных факторов.
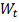
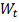 - стандартный винеровский процесс,
представляющий собой ошибку измерения.
- стандартный винеровский процесс,
представляющий собой ошибку измерения.
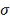
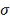 - квадратный корень из дисперсии
ошибки.
- квадратный корень из дисперсии
ошибки.
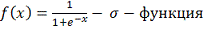
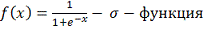
Моделирует процесс “насыщения” гена мишени.
Начиная с некоторого предела, наработка новых транскрипционных факторов уже
практически не влияет на процесс транскрипции гена-мишени.
Задача построения модели регуляции гена-мишени
состоит из нескольких этапов:
1. Найти набор генов
регуляторов 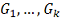
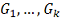 .
.
. Выбрать вид модели,
описывающей регуляцию гена-мишени.
. Вычислить коэффициенты
модели.
Первичной задачей здесь является
нахождение генов-регуляторов, а не точных параметров модели. Ясно, что какую бы
целевую функцию в качестве критерия оптимальности построенной модели мы не
выбрали, единственности решения у данной задачи не будет. В связи с этим
необходимо на первом этапе работы отбирать потенциальные гены-регуляторы исходя
из биологических и иных соображений (например, отбирать только сильно
экспрессирующиеся гены). Кроме того, при сравнении двух близких решений 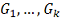
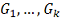 и
и 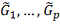
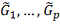 по очевидным причинам можно
исходить только из биологических соображений.
по очевидным причинам можно
исходить только из биологических соображений.
. Линейная модель
Рассмотрим линейную дифференциальную модель
регуляции гена-мишени одним геном-регулятором со сдвигом по времени.
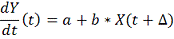
Известными данными являются замеренные
экспрессии гена-мишени и гена-регулятора в фиксированные моменты времени.
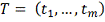
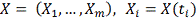
Необходимо найти параметры 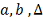
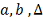 и оценить насколько выбранный
регулятор объясняет поведение гена-мишени. Рассмотрим далее только первую
модель, для второй все действия аналогичны. Исходя из биологических
соображений, параметр
и оценить насколько выбранный
регулятор объясняет поведение гена-мишени. Рассмотрим далее только первую
модель, для второй все действия аналогичны. Исходя из биологических
соображений, параметр 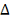
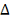 должен принадлежать определенному
заранее интервалу
должен принадлежать определенному
заранее интервалу 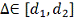
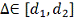 . В частности может быть
. В частности может быть 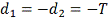
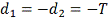 , где T - период
клеточного цикла. Выберем достаточно большое
, где T - период
клеточного цикла. Выберем достаточно большое 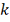
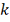 и разделим этот интервал на равные
части. Обозначим:
и разделим этот интервал на равные
части. Обозначим:
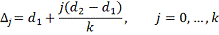
Необходимо интерполировать значения X, заданные
в сетке. Для этого могут применяться различные методы. В следующей главе
рассматриваются несколько самых распространенных методов применительно к данной
задаче, а также сравнивается их работа:
. Интерполирующий сплайн.
2. Сглаживающий “коридорный”
сплайн.
. Сглаживающий сплайн с постоянным
параметром.
. Ядерное сглаживание с помощью ядра
Епанечникова.
. Сглаживание методом наименьших
квадратов.
Методы сглаживания нужны в первую очередь для
численного дифференцирования профиля генной экспрессии. Сглаживая профили
экспрессии мы получаем значения численной производной экспрессии гена-мишени и
значения экспрессии гена-регулятора в сдвинутых точках, по которым строится
статистическая регрессия:
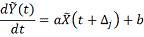
Таким образом, мы получаемнабор
параметров 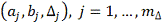
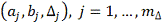 . Качество регрессии для каждого
. Качество регрессии для каждого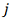
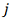 оцениваем по формуле:
оцениваем по формуле:
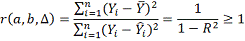
Где 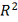
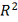 - коэффициент детерминации. Чем
больше
- коэффициент детерминации. Чем
больше 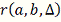
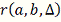 тем лучше модель аппроксимирует
тем лучше модель аппроксимирует 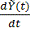
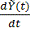 , значения близкие к 1 говорят об
отсутствии связи между X и Y. Таким
образом, выбирается модель с максимальной величиной
, значения близкие к 1 говорят об
отсутствии связи между X и Y. Таким
образом, выбирается модель с максимальной величиной 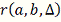
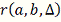 .
.
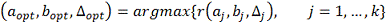
Альтернативным способом является минимизация
среднеквадратичного отклонения:
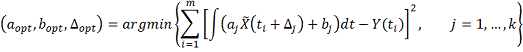
Однако здесь возможно накопление ошибки,
связанное с численным дифференцированием и последующим численным же
интегрированием. Расчеты показали, однако, что в случае равномерной сетки как
сглаживающий сплайн, так и ядро Епанечникова дают хороший результат при
восстановлении профиля после численного дифференцирования. В качестве метода
интегрирования использовался алгоритм Дорманда-Принца. В случае неравномерной
сетки, ядерное сглаживание дает большую погрешность, тогда как сплайн
по-прежнему показывает хорошие результаты.
Алгоритм
1. Фиксируется ген-мишень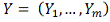
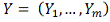 .
.
. Выбирается потенциальный
ген-регулятор 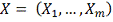
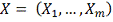 .
.
. Полученные профили
экспрессии сглаживаются одним из методов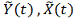
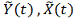 .
.
. Выбирается величина сдвига 
 Строится линейная регрессия:
Строится линейная регрессия:
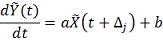
Находятся параметры 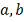
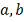 , коэффициент детерминации.
, коэффициент детерминации.
. Проделываем шаги 4-5 для 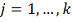
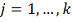 . Находим оптимальную задержку
. Находим оптимальную задержку 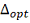
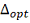 .
.
. Повторяем шаги 2-5 для
каждого потенциального гена-регулятора.
. Выбираем ген-регулятор с
наилучшим коэффициентом детерминации.
Данный метод достаточно прост в реализации и
имеет малую вычислительную сложность. Наибольшую сложность здесь имеет
численное интегрирование. Сама модель носит базовый характер в силу своей
простоты, представляется, что ее можно использовать в качестве некоторого
первого приближения, т.к. ни один из существующих на данный момент методов не
может однозначно правильно и точно решить исходную задачу.
Возможны модификации метода
1. С биологической точки зрения целесообразно
добавить коэффициент деградации
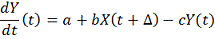
В этом случае считается множественная регрессия.
. Можно рассматривать модель с несколькими
регуляторами:
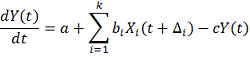
. Методы сглаживания
Часто в работе с микрочиповыми таблицами имеет
смысл преобразовывать дискретные данные в непрерывные. Это может быть связано с
необходимостью вычислить значение в промежуточной точке, вычислить численную
производную профиля экспрессии или в связи с тем, что некоторые значения уровня
экспрессии могут быть пропущены из-за погрешности эксперимента. К сожалению
данные полученные с помощью микрочипового эксперимента неизбежно несут
некоторую иногда довольно значительную погрешность, так что точная интерполяция
смысла практически не имеет. Рассмотрим несколько методов сглаживания данных,
предложенных в литературе [7-10]. Всюду ниже, аналогично предыдущему, будем
обозначать:
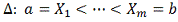
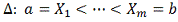
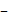
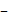 сетка.
сетка.
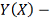
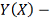 дискретно заданная функция, которую
требуется сгладить.
дискретно заданная функция, которую
требуется сгладить.
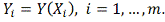
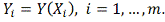
. Сглаживающий “коридорный” сплайн
Если погрешность исходных данных относительно
велика, то это может крайне неблагоприятно влиять на поведение
интерполяционного сплайна и особенно его производных. В частности, график
сплайна обычно имеет ярко выраженные осцилляции. Поэтому возникает вопрос,
нельзя ли построить сплайн, проходящий вблизи заданных значений, но более
«гладкий», чем интерполяционный. Такие сплайны называются сглаживающими, а
процедура их построения сглаживанием.
Сглаживающие сплайны возникают при решении
задачи о минимизации функционала:
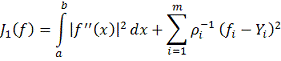
Где 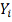
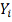 и
и 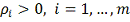
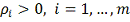 - заданные величины. Видно, что чем
меньше коэффициенты
- заданные величины. Видно, что чем
меньше коэффициенты 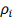
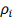 , тем ближе проходит функция
минимизирующая функционал
, тем ближе проходит функция
минимизирующая функционал 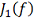
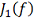 к заданным значениям
к заданным значениям 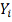
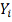 . Доказано, что среди всех функций
. Доказано, что среди всех функций 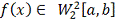
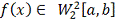 , кубический сплайн
, кубический сплайн 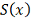
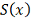 , удовлетворяющий условиям
, удовлетворяющий условиям 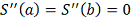
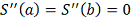 , минимизирует функционал
, минимизирует функционал 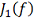
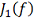 . [7] Исходя из этого требования сам
сплайн строится итерационным способом.
. [7] Исходя из этого требования сам
сплайн строится итерационным способом.
Данный сплайн очень хорош в задачах
инженерной геометрии и в других видах задач, где крайне важно, чтобы кривая
сглаженного профиля не отдалялся от заданных данных более чем на некоторую
заданную величину (т.е. лежал в коридоре). “Коридорный” сплайн имеет тенденцию
с увеличением количества проделываемых итераций, вытаскивать значения во всех
узлах сетки на границы коридора, т.е. максимально возможно, при заданной ошибке
в узле 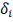
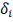 , выглаживать кривую.
, выглаживать кривую.
2. Сглаживающий сплайн с постоянным весовым
параметром
Данные, полученные в результате микрочипового
эксперимента, зачастую имеют крайне разнородный характер: профили некоторых
проб могут значительно изменяться при переходе в каждую следующую временную
точку, другие же наоборот, практически не изменяют значение. Очень часто
наблюдается картина, когда в целом пологий профиль имеет несколько сильных
всплесков (которые, вероятно, были вызваны некоторыми проблемами при измерении
и, скорее всего, не несут содержательной информации). В этих случаях не
целесообразно загонять значения сглаженного профиля на границы выбранного
коридора, тем более, что и рациональный выбор самого коридора не редко является
нетривиальной задачей.
Для рассматриваемой задачи
сглаживания микрочиповых данных более адекватным выглядит другой способ
построения сглаживающего сплайна. Рассмотрим, как и ранее, функционал 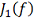
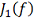 , только теперь положим
, только теперь положим 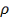
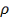 равным некоторой константе, тогда
равным некоторой константе, тогда 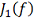
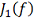 можно переписать в виде:
можно переписать в виде:
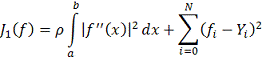
Основным вопросом при построении
такого сплайна является выбор параметра 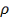
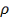 . Можно попытаться выбирать значение
. Можно попытаться выбирать значение
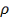
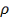 , минимизируя некоторую оценку
величины
, минимизируя некоторую оценку
величины 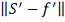
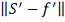 . В [9] показано, что в случае
равномерной сетки с шагом
. В [9] показано, что в случае
равномерной сетки с шагом 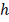
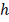 значение
значение 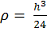
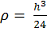 дает минимум оценке величины
дает минимум оценке величины 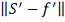
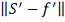 . Однако, обратим внимание, что при
таком значении
. Однако, обратим внимание, что при
таком значении 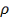
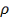 достигается лишь минимум некоторой
оценки этой величины, поэтому в конкретных случаях минимум погрешности
приближения может достигаться при других значениях
достигается лишь минимум некоторой
оценки этой величины, поэтому в конкретных случаях минимум погрешности
приближения может достигаться при других значениях 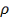
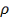 . Значение
. Значение 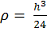
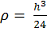 , может служить лишь некоторым
ориентиром при выборе параметра сглаживания.
, может служить лишь некоторым
ориентиром при выборе параметра сглаживания.
Для построения такого сплайна
требуется меньшее количество арифметических операций, чем для “коридорного”, к
тому же при сглаживании таким сплайном наиболее острые (резкие) пики сглаживаются
сильнее, чем пологие участки, что кажется более адекватным по отношению к
микрочиповым данным.
3. Метод наименьших квадратов
Введем непрерывную функцию 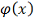
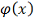 для аппроксимации дискретной
зависимости
для аппроксимации дискретной
зависимости 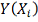
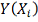 . Обозначим отклонения в узлах
. Обозначим отклонения в узлах 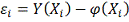
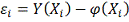 и
и 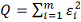
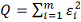 . Метод построения аппроксимирующей
функции
. Метод построения аппроксимирующей
функции 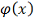
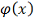 из условия минимума величины Q
называется методом наименьших квадратов (МНК).
из условия минимума величины Q
называется методом наименьших квадратов (МНК).
Широко распространен выбор базисных
функций 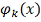
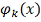 в виде степеней
в виде степеней 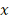
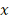 :
:
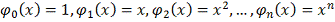
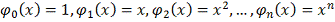 .
.
Однако такой выбор базисных функций не является
оптимальным с точки зрения решения системы нормальных уравнений с наименьшими
погрешностями. При выборе такого базиса построение аппроксимирующего полинома
выше 7 степени приводит к значительным погрешностям при решении системы
нормальных уравнений.
Намного лучшие результаты может дать применение
ортогональных полиномов (Чебышева, Лежандра, Лаггера, Якоби). Выбор таких
полиномов в качестве базисных функций обеспечивает лучшую обусловленность
системы нормальных уравнений и позволяет строить качественные аппроксимации
больших степеней.
Метод наименьших квадратов является классическим
инструментом для сглаживания экспериментальных данных. Естественность
постановки и простота реализации являются основными преимуществами этого
подхода. Во многих работах по данной тематике исследователями применялся именно
этот метод. Увеличением степени полинома можно добиться любой необходимой
точности приближения исходных данных, однако при обработке микрочиповых
экспериментов очень большая точность даже вредна. С другой стороны подбор
оптимальной степени в каждом конкретном случае затрудняет автоматизацию. Кроме
того, для этого метода характерны сильные колебания численной производной,
которая, обычно, имеет правильный тренд (т.е. сохраняет нужные промежутки
возрастания и убывания), однако, по абсолютному значению может существенно отличаться
от реальных.
. Ядерное сглаживание
Опишем (согласно [10]) еще один
подход сглаживанию данных, основанный на задании последовательности весов 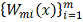
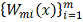 . В дальнейшем фиксируем
. В дальнейшем фиксируем 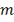
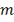 и для простоты будем обозначать эту
последовательность
и для простоты будем обозначать эту
последовательность 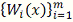
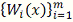 . Вычисление приближенного значения
сглаживаемой функции в произвольной точке
. Вычисление приближенного значения
сглаживаемой функции в произвольной точке 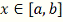
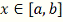 вычисляется по формуле:
вычисляется по формуле:

Соответственно для производной (в случае
дифференцируемости весовых функций):
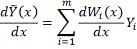
Ядерный подход состоит в том, что
весовая функция 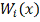
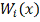 задается посредством функции
плотности
задается посредством функции
плотности 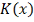
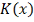 , которая регулирует размер и форму
весов вблизи точки
, которая регулирует размер и форму
весов вблизи точки 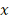
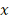 . Эту функцию принято называть
ядром. Ядро - это непрерывная ограниченная симметричная функция
. Эту функцию принято называть
ядром. Ядро - это непрерывная ограниченная симметричная функция 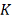
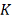 с единичным интегралом:
с единичным интегралом:

Вид весовых функций, использующий ядро был
предложен в работах (Nadaraya,
1964) и (Watson, 1964):
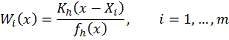
где
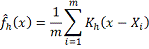
- Ядерная
оценка Розенблатта-Парзена для маргинальной плотности переменной x.
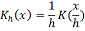
Параметр 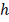
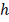 задающий размер весов называется
шириной окна, оно определяет сколько соседних узлов будут браться во внимание
при вычислении оценки в заданной точке.
задающий размер весов называется
шириной окна, оно определяет сколько соседних узлов будут браться во внимание
при вычислении оценки в заданной точке.
Согласно эти формулам окончательная
оценка значения сглаживаемой функции и ее первой производной:
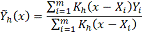
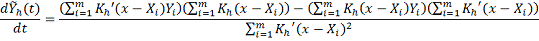
Вообще говоря, можно брать различные ядерные
функции, но как практика, так и теория ограничивают выбор. Так, например,
ядерные функции, принимающие очень малые значения могут приводить к машинному
нулю компьютера, поэтому разумно рассматривать такие ядерные функции, которые
равны нулю вне некоторого фиксированного интервала (финитные).
Чаще всего из-за некоторых оптимальных свойств
используется ядро Епанечникова:
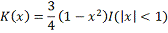
где 
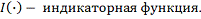
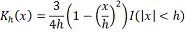
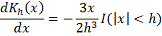
Основным вопросом при построении
ядерного сглаживания является выбор параметра ширины окна. Большое h означает
меньшую дисперсию, но большее отклонение. При сужении окна 
 данные
данные 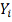
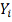 воспроизводятся точно, однако, это
может негативно сказываться при вычислении производной от сглаживания. Слишком
сильное увеличение окна приводит к чрезмерному сглаживанию кривой. Более точно:
воспроизводятся точно, однако, это
может негативно сказываться при вычислении производной от сглаживания. Слишком
сильное увеличение окна приводит к чрезмерному сглаживанию кривой. Более точно:
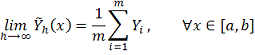
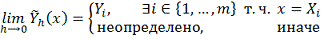
Для корректного вычисления значений
первой производной сглаженной функции во всех точках интервала [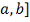
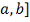 должно выполняться:
должно выполняться:
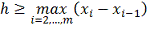
Идейно простой подход и хорошее быстродействие,
безусловно, являются преимуществами ядерного сглаживания. Тонким местом в этом
методе является выбор параметра ширины окна. При сглаживании данных на
равномерной сетке выбрать ширину окна, исходя из специфики дынных, достаточно
просто, в этом случае метод дает неплохие результаты. В случае же неравномерной
сетки, достаточно часто встречающейся на практике, выбор окна является
непростой задачей, осложняющей автоматизацию процесса. При выборе какого-то
фиксированного параметра ширины окна результаты зачастую получаются
неудовлетворительными, особенно явно это сказывается на производной сглаженного
профиля. Порекомендовать этот метод можно только для работы с равномерной
сеткой, однако в этом случае он показал себя немногим хуже сглаживающих
сплайнов, при существенно меньшем времени работы
Выводы
Сглаживание данных является очень важным этапом
обработки информации, полученной в результате микочипового эксперимента. Выбор
метода сглаживания может достаточно сильно повлиять на итоговые результаты
работы модели и, соответственно, на заключительные выводы, касающиеся
биологической стороны проблемы. По результатом многочисленных тестирований и
сравнений работы различных методов сглаживания в разнообразных условиях, можно
сделать вывод, что наиболее адекватным (из рассмотренных выше), учитывающим
специфику анализируемых в данной работе данных является сглаживание кубическим
сплайном с постоянным весовым параметром. Еще более актуальным выглядит
применение данного метода сглаживания при анализе больших объемов данных, так
как в отличие от всех остальных, рассмотренных методов, данный не требует никакого
предварительного задания параметров (выбор которых зачастую приходится
осуществлять эвристически, просматривая достаточно большие объемы информации
вручную), что способствует наиболее простой автоматизации данного метода. Кроме
того сглаживающий сплайн с постоянным весовым параметром обладает очень
неплохим быстродействием.
Далее приведены результаты работы методов
сглаживания на данных по генной экспрессии дрожжей [15]. Данные представляют
собой замеры по времени с разницей в 7 минут. Тест проходил следующим образом:
сначала данные сглаживались, затем считалась производная от сглаженного
профиля, после чего производная интегрировалась методом Дорманда-Принца. На
рисунках 2 и 3 приведены графики, получившиеся после сглаживания ядром
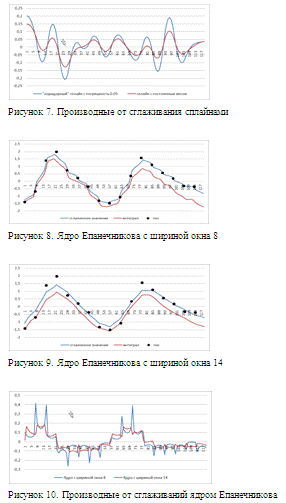
Епанченикова с шириной окна 8 и 14 соответственно. На рисунке 4 -
соответствующие производные. Из-за характера сглаживающего ядра производные
получаются разрывные, однако видно, что в случае ширины окна 8 (на 1 больше чем
шаг сетки) восстановленные интегрированием профиль гена в целом повторяет
динамику наблюдаемых данных, однако погрешность достаточно большая. Ядро с
шириной окна 14, показывает неприемлемые результаты сглаживания самого профиля,
однако при сглаживании производной, сглаженный профиль получается более гладким,
чем при ширине окна 8. Это важно, т.к. в случае сглаживания с шириной окна 8,
даже небольшой сдвиг по времени может сильно изменить параметры модели. На
рисунках 5 и 6. Приведены результаты сглаживания сплайнами. Видно, что оба
сплайна практически точно восстанавливают значения после интегрирования за счет
своей гладкости, однако сплайн с постоянным весом сильнее сглаживает профиль.
На рис. 8-10 приведен пример сглаживания ядром профиля другого ген. Здесь сам
профиль имеет более простую структуру, так что использования ядерного
сглаживания оправдано. В целом может показаться, что ядерное сглаживание
однозначно хуже сплайнов, однако в решаемой нами задаче точность играет
второстепенную роль, т.к. сами данные заданы с погрешность и не требуется точно
подогнать один профиль к другому.
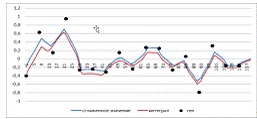
Рисунок 2. Ядро Епанечникова с шириной окна 8
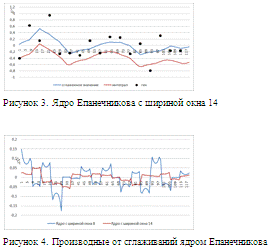
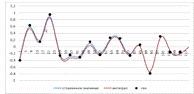
Рисунок 5. "Коридорный"
сплайн
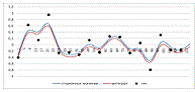
Рисунок 6. Сплайн с постоянным весом
. Стохастическая модель
Опишем стохастическую модель
регуляции, предложенную в статьях [12] и [13]. Как и прежде, имеем: 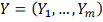
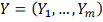
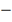
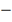 профиль экспрессии регулируемого
гена, где
профиль экспрессии регулируемого
гена, где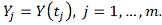
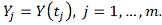
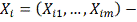
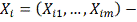 профиль j-того ген-регулятора
профиль j-того ген-регулятора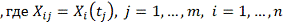
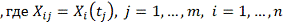
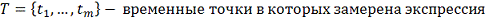
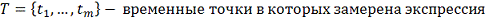 .
.
Для удобства будем далее обозначать 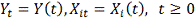
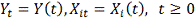 .
.
Регуляция гена-мишени описывается
следующим уравнением:
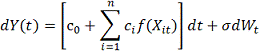
где:
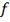
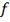 - регуляторная функция.
- регуляторная функция.
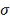
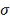 - дисперсия случайной ошибки.
- дисперсия случайной ошибки.
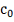
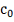 - константа, включающая в себя
уровень деградации и фоновую экспрессию.
- константа, включающая в себя
уровень деградации и фоновую экспрессию.
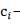
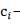 вклад i-того
регулятора.
вклад i-того
регулятора.
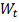
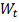 - винеровский процесс. Т.е:
- винеровский процесс. Т.е:
1. 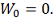
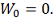
2. 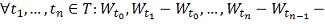
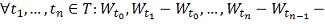 независимы в совокупности.
независимы в совокупности.
. 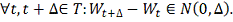
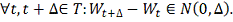
Такой процесс описывает броуновское
движение, или в данном случае - случайную ошибку эксперимента. 

В качестве регуляторной функции
предлагается выбрать сигма-функцию.
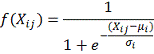
где:

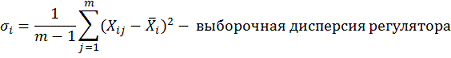
Пусть набор регуляторов и целевой
ген фиксированы, и их профили экспрессий известны. Требуется по этой информации
найти вектор 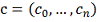
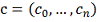 и
и 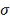
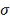 . Для достаточно малых
. Для достаточно малых 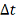
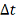 имеем аппроксимацию:
имеем аппроксимацию:

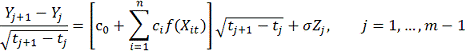
Где 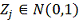
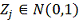
Обозначив
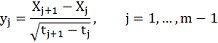

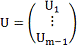
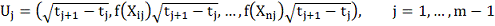
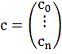
Имеем в матричной записи:
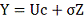
Здесь нам известны 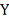
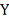 и
и 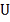
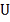 , причем
, причем 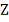
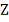 - стандартный гауссовский вектор.
- стандартный гауссовский вектор.
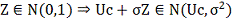
Поэтому 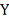
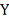 - также гауссовский вектор и для
него можно построить функцию максимального правдоподобия:
- также гауссовский вектор и для
него можно построить функцию максимального правдоподобия:
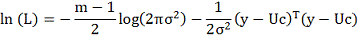
Дифференцируя ее по 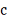
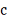 и
и 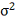
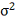 , и приравнивая производные к нулю,
находим оценки методом максимального правдоподобия:
, и приравнивая производные к нулю,
находим оценки методом максимального правдоподобия:
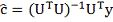
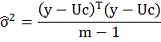
Таким образом:
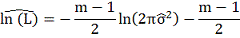
Для оценки качества приближения
теоретических данных используется критерий AIC:
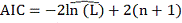
Лучшей является та модель, величина 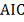
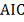 которой меньше. Окончательно, метод
можно описать следующим образом:
которой меньше. Окончательно, метод
можно описать следующим образом:
Алгоритм
1. Фиксируем ген-мишень.
2. Добавляем в модель один случайный
ген-регулятор.
3. Составляем матрицу 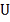
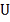 , вектор
, вектор 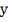
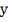 и находим оценки
и находим оценки 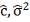
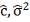 , далее находим
, далее находим 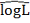
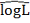 и
и 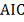
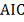 .
.
. Повторяем шаг 3 для всех
потенциальных регуляторов, выбираем оптимальный, т.е. регулятор для которого
полученное значение 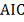
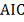 наименьшее.
наименьшее.
. Фиксируем выбранный
оптимальный регулятор.
. Повторяем шаги 3-4,
добавляя в модель с фиксированным регулятором дополнительный регулятор и
находим регулятор который в паре с фиксированным представляет оптимальную
модель.
. Продолжаем добавлять новые
регуляторы, пока не случится одно из двух
a. AIC начнет возрастать.
b. Количество регуляторов достигнет
некоторого ограничения.
Алгоритм отличается высокой скоростью работы.
. Сравнение моделей
Модели тестировались на данных по
генной экспрессии дрожжей [14], доступных по адресу
<#"580806.files/image317.gif">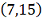 и
и 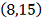
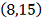 , сплайн с постоянным весом.
, сплайн с постоянным весом.
Целевая функция: коэффициент
детерминации регрессии и среднеквадратичное отклонение интеграла правой части
от исходных данных.
Метод интегрирования: алгоритм
Дорманда-Принца.
Кроме того, строилась стохастическая
модель для 1 регулятора.
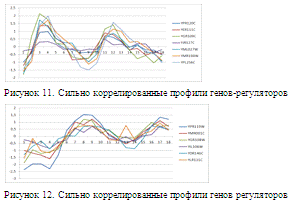
Следует отметить, что, в отобранных
потенциальных генах-регуляторах достаточно много генов регуляторов с сильно
коррелирующими профилями экспрессии. На рисунках 11,12 приведены наиболее
сильно коррелированные профили потенциальных генов-регуляторов. Это сильно
осложнило анализ, так как уже при небольших изменениях параметров, модель
выбирала другой регулятор в качестве лучшего. В таблице 5 приведено количество
одинаковых отобранных регуляторов при различных вариантах реализации линейной
модели (из общего числа - 5943).
Таблица
5
Количество совпавших регуляторов при разных
методах сглаживания
|
Ядро
(7,15)
|
Ядро
(8,15)
|
Сплайн
0.01
|
Сплайн
0.05
|
Сплайн
с постоянным весом
|
|
Ядро
(7,15)
|
-
|
4861
|
143
|
128
|
268
|
|
Ядро
(8,15)
|
-
|
-
|
158
|
146
|
288
|
|
Сплайн
0.01
|
-
|
-
|
-
|
2271
|
2642
|
|
Сплайн
0.05
|
-
|
-
|
-
|
-
|
1821
|
Из таблицы 6 видно, что лучшие результаты по
приближению производной (погрешность и качество регрессии) демонстрирует
ядерное сглаживание с параметрами 8,15. Однако, завышенные скоры здесь могут
свидетельствовать о сильном сглаживании производной. Лучшее приближение
интеграла получается при сглаживании сплайном с постоянным весом. “Коридорный”
сплайн занимает промежуточное положение. Также из таблицы 6 видно, что
стохастическая модель в среднем приближает профиль экспрессии даже хуже чем
линейная модель с ядерным сглаживанием и параметрами (7,15). В последней графе
таблицы приведено среднее время в секундах, за которое строится приближение для
одного гена с помощью одного регулятора (т.е. множество потенциальных
регуляторов состояло из 1 элемента). Видно, что здесь бесспорным лидером
является стохастическая модель, работающая в среднем в 10 раз быстрее линейной,
это в первую очередь связано с необходимостью численно интегрировать правую
часть в линейной модели.
Таблица 6
Сравнение
линейных моделей с разными методами сглаживания
|
Вид
модели
|
SSE приближения
производной
|
SSE приближения
профиля
|
Средний
скор
|
Среднее
время работы (с.)
|
|
Ядро
(7,15)
|
0,00102
|
1,2074
|
6,1596
|
0,0137
|
|
Ядро
(8,15)
|
0,000994
|
1,1859
|
6,3475
|
0,01355
|
|
Сплайн
0.01
|
0,005909
|
1,1417
|
3,2208
|
0,01218
|
|
Сплайн
0.05
|
0,007406
|
1,3962
|
3.0
|
|
|
Сплайн
с постоянным весом
|
0,002
|
0,5
|
4.3
|
0,0116
|
|
Стохастическая
|
-
|
1,22097
|
-
|
0.001
|
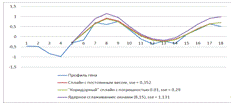
Рисунок 13. Лучший результат для трех моделей
SSE (Sum
of Squared
Error) - суммарное
квадратичное отклонение
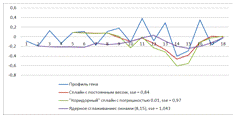
Рисунок 14. Худший результат для трех моделей
SSE (Sum
of Squared
Error) - суммарное
квадратичное отклонение
Далее будем изучать работу ядра с параметрами
8,15, “коридорного” сплайна с погрешность 0.01 и сплайна с постоянным весом.
Ясно, что имеет смысл сравнивать модели только на тех генах-мишенях, выбор
регуляторов для которых совпал у различных моделей.
Стохастическая модель несет в себе больше
биологического смысла за счет моделирования процесса транскрипции с помощью
сигма-функции, учитывающей процесс насыщения (т.е. с начиная с какого-то
момента увеличение уровня экспрессии регулятора больше не влияет на уровень
экспрессии гена-мишени) и добавленной случайной погрешности, которая в
эксперименте неизбежна. Кроме того, стохастическая модель требует значительно
меньше времени на построение. Однако серьезным недостатком является
значительная потеря точности при дискретизации модели, как видно из таблиц 6 и
7, точность стохастической модели хуже, чем у линейной при сглаживании ядром. В
таблице 7 приведены результаты для 6 лучших приближений с помощью линейной
модели (среди всех случаев, когда 3 варианта реализации выбирали один и тот же
регулятор) В приложении 2 на рисунках П2.1-П2.6 приведены соответствующие
графики. Видно, что в некоторых случаях стохастическая модель выбирает тот же
регулятор, что и линейная, однако чаще они различны и слабо коррелированны.
Таблица
7
Суммарные квадратичные ошибки и AIC
для линейных и стохастических моделей регуляции генов
|
Ген-мишень
|
Ядро
(8,15)
|
“Коридорный”
сплайн
|
Сплайн
с постоянным весом
|
Стохастическая
модель
|
AIC
|
|
YDR225W
|
2,257
|
1,782
|
1,3844
|
2,312
|
-18,3794
|
|
YML034W
|
1,13188
|
0,29515
|
0,35275
|
3,3949
|
-34,5137
|
|
YGL192W
|
5,7415
|
0,5534
|
0,25269
|
0,6442
|
-41,301
|
|
YPL141C
|
0,7017
|
0,597962
|
0,46421
|
4,16162
|
-22,2028
|
|
YMR232W
|
14,2411
|
3,89097
|
2,2747309
|
2,52127
|
-10,5695
|
|
YDR150W
|
1,8640
|
0,36604
|
0,375060
|
0,46466
|
-44,0042
|
Также видно, что стохастическая модель хоть и
приближает хуже, но чаще всего дает вполне приемлемый результат. Кроме того,
ясно, что с биологической точки зрения, модель с одним регулятором и не должны
давать стопроцентной точности, так как в реальности каждый ген может
потенциально регулироваться несколькими регуляторами, которые могут, как
мешать, так и помогать друг другу. С другой стороны, очевидно, что путем
добавления регуляторов можно приблизить любой профиль экспрессии с какой угодно
точностью. Стохастический алгоритм позволяет довольно быстро строить модели для
большого числа регуляторов, так например, на рисунке 14 на примере гена,
показавшего худшие результаты при моделировании экспрессии с помощью одного
регулятора, показано как растет точность при увеличении количества регуляторов.
При этом на каждом следующем шаге добавлялся два новых регулятора, а все старые
сохраняются в модели. Таким образом, необходимо соблюдать некий баланс,
ограничивая число регуляторов сверху исходя из биологических соображений.

Рисунок 15. Работа стохастической модели при
разном количестве регуляторов. SSE
(Sum of
Squared Error)
- суммарное квадратичное отклонение
Рассмотренные выше модели достаточно просты и
могут служить только некоторым первым шагом в моделировании регуляции генной
экспрессии. Разумным подходом на сегодняшний момент представляется агрегация
разнообразных моделей в некоторый комплекс, позволяющий строить различные
модели и в каждом конкретном случае выбирать лучшую. При этом необходимо
руководствоваться биологическими соображениями, т.к. простая подгонка профилей
экспрессии зачастую не несет никакого биологического смысла.
. Программная реализация
В ходе работы на языке
программирования Java был написан плагин к бесплатно распространяющейся
системе формального описания и симуляции сложных биологических систем BioUML
(<#"580806.files/image323.gif">
ПРИЛОЖЕНИЕ 2
Ниже приведены графики для построенных линейной
и стохастической моделей. Отобраны 6 лучших приближений профиля экспрессии
среди всех построенных с помощью линейной модели, для этих случаев построены
приближения стохастическим алгоритмом.
Везде ниже на графиках, если не указано иное:
экспериментально полученные значения экспрессии
гена.
результат построения линейной модели с помощью
сглаживания ядром с параметрами (8,15).
результат построения линейной модели с помощью
“коридорного” сплайна с погрешностью 0,01.
результат построения линейной модели с помощью
сплайна с постоянным весом.
результат построения стохастической модели
Значения среднеквадратичных ошибок для всех
построенных моделей приводятся в таблице 7.
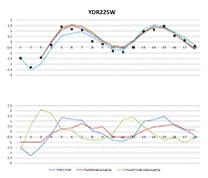
Рисунок 1. Вверху - результаты построения
линейной и стохастической моделей. Внизу - выбранные разными моделями
регуляторы
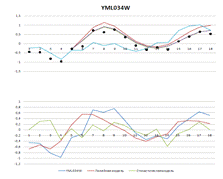
Рисунок 2. Вверху - результаты построения
линейной и стохастической моделей. Внизу - выбранные разными моделями
регуляторы
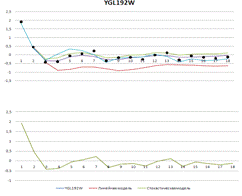
Рисунок 3. Вверху - результаты построения
линейной и стохастической моделей. Внизу - выбранные разными моделями
регуляторы
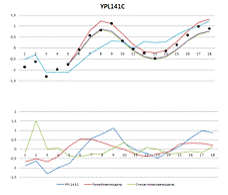
Рисунок 4. Вверху - результаты построения
линейной и стохастической моделей. Внизу - выбранные разными моделями
регуляторы
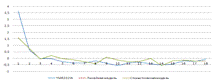
Рисунок 5. Вверху - результаты построения
линейной и стохастической моделей. Внизу - выбранные разными моделями
регуляторы.
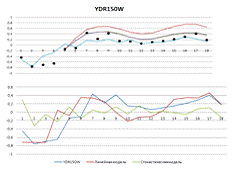
Рисунок 3. Вверху - результаты
построения линейной и стохастической моделей. Внизу - выбранные разными
моделями регуляторы