Разработка арифметико-логического устройства для выполнения операций по заданным логическим функциям
разработка
арифметико-логического устройства для выполнения операций по заданным
логическим функциям
Содержание
Введение
.
Формы записи булевых функций
1.1
Методика составление логических функций
.2
Методика минимизации логических функций
2.
Методика синтеза комбинационного устройства на логических элементах и
мультиплексоре
2.1
Логическая функция в виде СДНФ
.2
Методика минимизация логической функции
.3
Методика преобразование функции в минимальный базис ИЛИ-НЕ
.
Методика проектирование устройства с памятью
Список
литературы
Введение
логическое устройство функция
Научно-технический прогресс, развитие
современной научной мысли, развитие практически всех отраслей народного
хозяйства тесно связаны с использованием электронных вычислительных машин (ЭВМ)
и вычислительных систем (ВС). Можно утверждать, что успешное разрешение
современных научных и технических проблем в значительной степени зависит от
уровня развития электронной вычислительной техники. В связи с этим во всём мире
уделяется большое внимание развитию и совершенствованию средств электронной
вычислительной техники и программному обеспечению.
На пути развития электронной вычислительной
техники можно выделить шесть поколений электронных вычислительных машин,
отличающиеся элементной базой, конструктивно-технологическим обеспечением,
техническими характеристиками, степенью доступа к ЭВМ, со стороны
пользователей.
Смене поколений сопутствовало изменение основных
технико-экономических показателей электронных вычислительных машин и в первую
очередь таких, как быстродействие, надежность и стоимость.
Возможности улучшения технико-экономических
показателей электронной вычислительной машины в значительной степени зависят от
элементов, используемых для построения их электронных схем. Поэтому при рассмотрении
этапов развития электронных цифровых вычислительных машин каждое поколение
обычно в первую очередь характеризуется элементной базой.
В курсовом проекте разрабатывается
арифметико-логическое устройство для выполнения операций по заданным логическим
функциям.
1. Формы записи булевых функций
Цифровые устройства, значения выходного сигнала
которых зависят только от значений сигналов на его входах в данный момент
времени, называются комбинационными. Эти устройства являются основой построения
различных цифровых устройств.
Состояние комбинационных устройств может быть
описано несколькими способами: булевой функцией, таблицей истинности, в
совершенной дизъюнктивной нормальной форме (СДНФ) или в совершенной
конъюнктивной нормальной форме (СКНФ).
Покажем запись состояния схемы в виде булевой
функции: F=AB+CD.
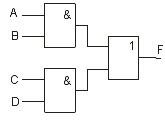
Рисунок 1
Таблица истинности булевой функции
складывается на основе условия работы приспособления. Такая таблица содержит
n+1 столбцов аргумента и 2n рядов, где n - число аргументов булевой
функции. Например, если приспособление реализует функцию трех переменных 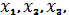
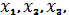 таблица булевой функции
таблица булевой функции 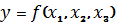
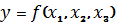 будет содержать 4 столбика
будет содержать 4 столбика 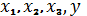
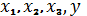 и 8 рядов.
и 8 рядов.
Столбики значений аргументов
заполняются по стандартной форме записи. В первом столбике чередуются 0 и 1, во
втором - чередуются по 2 нуля и по 2 единицы и т.д. В построении таким способом
таблицы каждый ряд значений аргументов 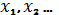
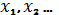
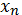
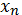 представляет собой двоичное число
предыдущего ряда, к которому в младшем разряде прибавлена 1. Таким способом,
ряды значений аргументов создают натуральный ряд чисел, записанных в двоичной
системе счисления, начиная с нуля.
представляет собой двоичное число
предыдущего ряда, к которому в младшем разряде прибавлена 1. Таким способом,
ряды значений аргументов создают натуральный ряд чисел, записанных в двоичной
системе счисления, начиная с нуля.
Последний столбец таблицы является
столбцом значений функции. Он заполняется для каждого ряда на основе условия
работы приспособления, которое разрабатывается. Пусть, например, комбинационное
устройство имеет три входа 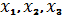
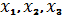 и один выход
и один выход 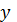
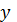 . Известно, что на выходе появится
единицы (
. Известно, что на выходе появится
единицы (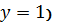
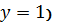 тогда, когда только на один вход
тогда, когда только на один вход 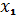
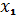 или
или 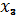
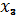 подается единица, или единица
поступит на все входы. В этом случае таблица истинности содержит четыре столбца
и восемь рядов. Столбцы значений
подается единица, или единица
поступит на все входы. В этом случае таблица истинности содержит четыре столбца
и восемь рядов. Столбцы значений 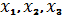
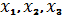 заполняются по стандартной форме
записи. Затем находят ряды, в которых только
заполняются по стандартной форме
записи. Затем находят ряды, в которых только 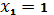
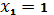 или
или 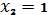
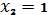 и в этих рядах записывают
и в этих рядах записывают 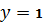
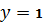 . В итоге получается таблица
значений функции.
. В итоге получается таблица
значений функции.
Таблица 1 - - таблица истинности
|
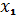
|
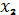
|
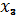
|
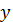
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
СДНФ
Если узел обеспечивает перемещение
сигнала от одного из информационных входов 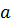
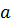 или
или 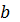
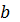 к выходу
к выходу 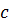
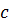 , называется логическим узлом. Его
работу отображает таблица, на основе которой записывается булево выражение
СДНФ:
, называется логическим узлом. Его
работу отображает таблица, на основе которой записывается булево выражение
СДНФ:
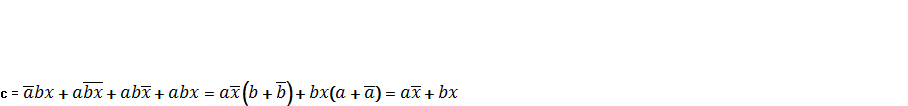
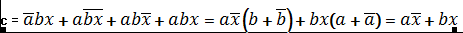
Таблица 2 - таблица истинности
|
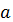
|
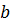
|
x
|
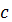
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1
|
Схема логического узла, который реализует булеву
функцию
 представлена на рисунке 2.
представлена на рисунке 2.
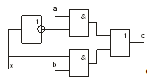
Рисунок 2
.1 Методика составление логических
функций
Простую логическую функцию иногда
можно записать в аналитической форме непосредственно из словесного определения.
В общем случае для получения аналитической формы используют таблицы истинности.
Пусть логическая функция задана таблицей (3). Чтобы на наборах 1, 2, 3, 6 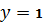
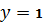 , единице должна быть равна каждая
из конъюнкций
, единице должна быть равна каждая
из конъюнкций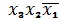
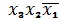 или
или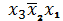
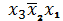 , или
, или 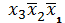
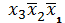 , или
, или 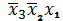
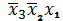 , где
, где 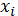
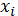 записывают в инверсной форме, если
он в этом наборе равен нулю (иначе конъюнкция не будет равна единице).
записывают в инверсной форме, если
он в этом наборе равен нулю (иначе конъюнкция не будет равна единице).
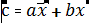
Таблица 3 - - таблица истинности
|
Номер
набора
|
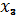
|
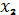
|
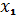
|
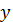
|
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
1
|
0
|
1
|
|
2
|
1
|
0
|
1
|
1
|
|
3
|
1
|
0
|
0
|
1
|
|
4
|
0
|
1
|
1
|
0
|
|
5
|
0
|
1
|
0
|
0
|
|
6
|
0
|
0
|
1
|
1
|
|
7
|
0
|
0
|
0
|
0
|
Таким образом функцию, представляемую таблицей
(3) запишем в виде
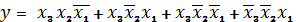
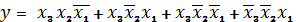 (1)
(1)
Такая форма логической функции
называется совершенной дизъюнктивной нормальной формой (СДНФ). Она
представляется логической суммой простых конъюнкций, каждая из которых содержит
все переменный в прямом или инверсном виде не более одного раза; в такие
конъюнкции не входят суммы переменных, а также отрицания произведений двух или
более переменных. Входящие в СДНФ конъюнкции называются минтернами или
конституентами единиц.
Логическая сумма конъюнкций,
отличается от (1) тем, что все конъюнкции или некоторые из них не содержат всех
переменных (в прямом или инверсном виде), представляет собой дизъюнктивную
нормальную форму (ДНФ) функции.
Логическая функция может быть
составлена не только по единичным, но и по нулевым значениям. Из таблицы
следует, что на наборах 0, 4, 5, 7 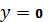
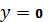 . Что бы на каждом указанном наборе
имело место
. Что бы на каждом указанном наборе
имело место 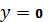
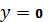 , нулю должна равняться дизъюнкция
переменных из этого набора, т.е. каждое слагаемое дизъюнкции; если в данном
наборе переменная равна единице, то в дизъюнкцию должна входить инверсия. На
всех указанных наборах функция из таблицы будет равна нулю, если осуществить
конъюнкцию составленных дизъюнкций:
, нулю должна равняться дизъюнкция
переменных из этого набора, т.е. каждое слагаемое дизъюнкции; если в данном
наборе переменная равна единице, то в дизъюнкцию должна входить инверсия. На
всех указанных наборах функция из таблицы будет равна нулю, если осуществить
конъюнкцию составленных дизъюнкций:
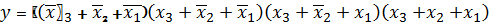
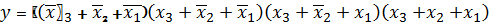 (2)
(2)
Здесь 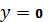
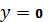 обеспечивают: первый сомножитель
при
обеспечивают: первый сомножитель
при 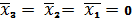
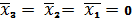 (при
(при 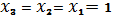
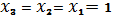 , т.е. на наборе № 0), второй
сомножитель при
, т.е. на наборе № 0), второй
сомножитель при 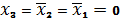
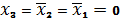 (при
(при 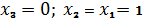
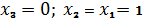 , т.е. на наборе № 4), третий
сомножитель при
, т.е. на наборе № 4), третий
сомножитель при 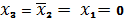
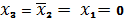 (при
(при 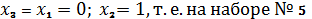
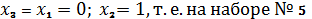 ), четвертый сомножитель при
), четвертый сомножитель при 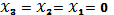
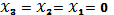 , т.е. на наборе № 7.
, т.е. на наборе № 7.
Форма, в которой выражена функция
(2), называется совершенной конъюнктивной нормальной формой (СКНФ). Она
представляется логическим произведением дизъюнкций, каждая из которых содержит
все переменные в прямом или инверсном виде не более одного раза. Входящие в
произведение сомножители - дизъюнкции - называются макстермами или
конституентами нулей.
Логическое произведение дизъюнкций,
отличающееся от (2) тем, что все дизъюнкции или некоторые из них не содержат
всех переменных (в прямом или инверсном виде), представляет собой конъюнктивную
нормальную форму (КНФ) функции.
Так одна и та же одна логическая
функция, выраженная определенной таблицей истинности, записывается в виде СДНФ
и СКНФ, то каждую из этих форм можно преобразовать в другую. Логическая функция
имеет единственные СДНФ и СКНФ, что непосредственно следует из методики их
получения.
1.2 Методика минимизации логических функций
Минимизацией называют процедуру
упрощения логической функции, с тем чтобы она содержала минимальное количество
членов при минимальном числе переменных.
В некоторых простых случаях
минимизацию можно осуществить, непосредственно используя основные законы
булевой алгебры. В качестве примера упростим выражение (1), используя закон
склеивания:
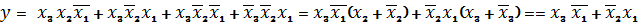
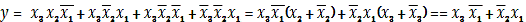
Полученное выражение равносильно
исходному, но значительно проще его.
Пусть имеется логическая функция:
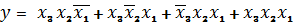
Добавим дважды к ее правой части уже
имеющийся член 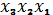
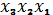 (отчего функция не изменится);
тогда
(отчего функция не изменится);
тогда
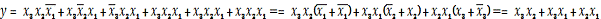
И это выражение проще исходного.
Следует отметить, что такие
элементарные приемы минимизации удается использовать нечасто - при малом
количестве членов функции и небольшом числе переменных. В других случаях
применяются специальные методы минимизации, облегчающие поиск склеивающихся
членов. К ним относится метод минимизации с помощью карт Карно.
Карта Карно построена так, что в ее
соседние клетки попадают смежные члены функции - члены, отличающиеся значение
одной переменной: в один член эта переменная входит в прямой форме, а в другой
- в инверсной. Благодаря этому возникает наглядное представление о различных вариантах
склеивания смежных членов.
Карта Карно имеет столько клеток, сколько
комбинаций (наборов) можно составить из прямых и инверсных значений n
переменных по n членом в каждой. Т.к. при n=2 карта содержит четыре клетки
рисунок 1, а при n=3 - восемь клеток рисунок 2, при n = 4 - шестнадцать клеток
рисунок 3.
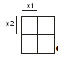
Рисунок 3
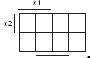
Рисунок 4
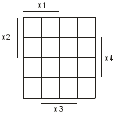
Рисунок 5
Каждая клетка соответствует
определенной комбинации переменных. Так, например, левая верхняя клетка карты
рисунок 1 соответствует комбинации 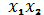
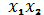 : над столбцом левых клеток указан
: над столбцом левых клеток указан 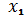
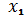 в прямой форме, возле верхней
строки записан в прямой форме
в прямой форме, возле верхней
строки записан в прямой форме 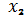
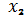 . Левая нижняя клетка той же карты
соответствует комбинации
. Левая нижняя клетка той же карты
соответствует комбинации 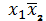
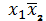 , так как на нижнюю строку клеток не
распространяется «действие»
, так как на нижнюю строку клеток не
распространяется «действие» 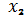
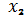 - клетки этой строки отвечают
комбинациям, где присутствует
- клетки этой строки отвечают
комбинациям, где присутствует 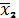
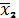 . Клетке нижней строки третьего
слева столбца рисунок 2 соответствует комбинация
. Клетке нижней строки третьего
слева столбца рисунок 2 соответствует комбинация 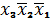
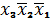 , клетке второго слева столбца
третьей сверху строки рисунок 3 соответствует комбинация
, клетке второго слева столбца
третьей сверху строки рисунок 3 соответствует комбинация 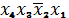
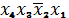 и т.д.
и т.д.
Наборы переменных, на которых 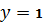
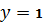 , т. е. минтермы функции, отмечаются
в соответствующих клетках карты единицами, В остальные клетки записываются нули
или их оставляют пустыми. Две стоящие в соседних клетках единицы -
свидетельство того, что в составе СДНФ имеются члены, отличающиеся значением
одной переменной. Такие члены, как известно, склеиваются. Склеивание каждой
пары минтермов уменьшает число входящих в них переменных на единицу.
, т. е. минтермы функции, отмечаются
в соответствующих клетках карты единицами, В остальные клетки записываются нули
или их оставляют пустыми. Две стоящие в соседних клетках единицы -
свидетельство того, что в составе СДНФ имеются члены, отличающиеся значением
одной переменной. Такие члены, как известно, склеиваются. Склеивание каждой
пары минтермов уменьшает число входящих в них переменных на единицу.
Общие правила склеивания членов,
занесенных в карту Карно, следующие:
) склеиваться могут 2, 4. 8 и т. д.
членов; при этом соответствующие единицы в клетках для наглядности охватывают
контурами; каждый должен быть прямоугольником;
) одним контуром следует объединять
максимальное количество клеток;
) одна и та же единица может
охватываться разными контурами, т.е. один и тот же минтерм может склеиваться с
несколькими смежными; последнее объясняется тем, что значение функции не
меняется при прибавлении уже имеющихся членов;
) крайние строки, а также крайние
столбцы карты считаются смежными; их можно таковыми представить, если мысленно
свернуть карту в горизонтальный или вертикальный цилиндр.
Функция, минимизированная с помощью карты Карно,
состоит из суммы простых конъюнкций. Каждая из них получается в результате
склеивания членов, которым соответствует охваченные контуром единицы. В такую
конъюнкцию войдут только те переменные, значения которых в пределах контура не
меняются.
Пусть логическая функция задана таблицей
истинности - таблица 4.
Таблица 4 - таблица истинности
|
Номер
набора
|
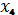
|
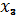
|
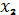
|
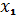
|
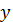
|
|
0
|
1
|
1
|
1
|
1
|
1
|
|
1
|
1
|
1
|
1
|
0
|
1
|
|
2
|
1
|
1
|
0
|
1
|
1
|
|
3
|
1
|
1
|
0
|
0
|
1
|
|
4
|
1
|
0
|
1
|
1
|
0
|
|
5
|
1
|
0
|
1
|
0
|
0
|
|
6
|
1
|
0
|
0
|
1
|
1
|
|
7
|
1
|
0
|
0
|
0
|
1
|
|
8
|
0
|
1
|
1
|
1
|
0
|
|
9
|
0
|
1
|
1
|
0
|
0
|
|
10
|
0
|
1
|
0
|
1
|
0
|
|
11
|
0
|
1
|
0
|
0
|
0
|
|
12
|
0
|
0
|
1
|
1
|
1
|
|
13
|
0
|
0
|
1
|
0
|
1
|
|
14
|
0
|
0
|
0
|
1
|
1
|
|
15
|
0
|
0
|
0
|
0
|
1
|
Из нее по указанной методике легко составляется
СДНФ функции:
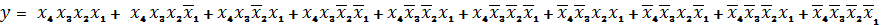
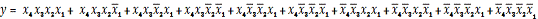 (3)
(3)
Непосредственно из таблицы 4 в карту
Карно (рисунок 5) занесены значения всех выписанных минтермов.
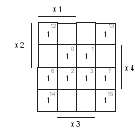
Рисунок 5
Для удобства проверки в правом
верхнем углу клетки указав номер минтерма по его месту в табл. 4. Контурами
охвачены единицы, соответствующие склеиваемым минтермам. Ниже приведены
номера минтермов и результаты их склеивания: 0, 1, 2, 3: 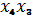
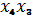 ; 6, 2, 3, 7:
; 6, 2, 3, 7: 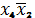
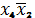 ; 12, 13, 14, 15:
; 12, 13, 14, 15: 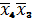
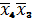 .
.
В результате функция (3)
представляется в виде:
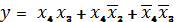
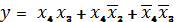
Полученная форма функции проще
первоначальной. Интересно отметить, что она не содержит переменной 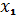
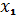 .
.
В карту Карно (рисунок 6) внесены
значения минтермов функции
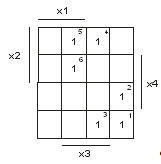
Рисунок 6
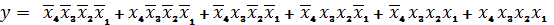
Склеивание минтермов 5, 6; 5, 4; 1,
2; 1, 3 дает следующую минимизированную функцию:
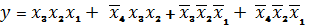
Склеивание минтермов 5, 6; 4, 3; 1,
2; приводит к другой форме:
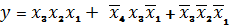
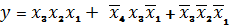 ,
,
что проще полученной первоначально.
Из приведенного примера следует, что
минимизация с помощью карт Карно не приводит к однозначной форме для получения
наиболее простой формы необходимо рассматривать всевозможные варианты
склеивания.
При числе аргументов, большем
четырех, используют обычно другие методы минимизации - применение карт Карно
становится трудоемким.
Встречается необходимость
минимизировать функцию, значения которой на некоторых наборах переменных не
определены. Такой случай может иметь место, если значение функции на этих
наборах безразлично или если определенные наборы переменных невозможны по
условиям задачи. На таких избыточных (запрещенных, факультативных) наборах можно
прядать функции любое значение - 0 или 1. Рациональное доопределение функции
может оказаться весьма эффективным для ее минимизации.
Такое доопределение функции
произведем в ходе решения задачи о температурах в точках объема.
Превышение допустимого уровня температуры
в точках 4, 3, 2, 1 обозначим соответственно


а тот факт, что в указанных точках
температура ниже допустимого уровня, обозначим как

 .
.
Все возможные комбинации четырех
двоичных переменных


приведены в переключательной таблице
5
Таблица 5 - переключательная таблица
|
n
|
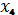
|
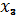
|
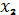
|
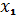
|
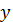
|
|
0
|
1
|
1
|
1
|
1
|
1
|
|
1
|
1
|
1
|
1
|
0
|
0
|
|
2
|
1
|
1
|
1
|
-
|
|
3
|
1
|
1
|
0
|
0
|
1
|
|
4
|
1
|
0
|
1
|
1
|
-
|
|
5
|
1
|
0
|
1
|
0
|
-
|
|
6
|
1
|
0
|
0
|
1
|
-
|
|
7
|
1
|
0
|
0
|
0
|
-
|
|
8
|
0
|
1
|
1
|
1
|
1
|
|
9
|
0
|
1
|
1
|
0
|
-
|
|
10
|
0
|
1
|
0
|
1
|
-
|
|
11
|
0
|
1
|
0
|
0
|
-
|
|
12
|
0
|
0
|
1
|
1
|
0
|
|
13
|
0
|
0
|
1
|
0
|
1
|
|
14
|
0
|
0
|
0
|
1
|
-
|
|
15
|
0
|
0
|
0
|
0
|
-
|
По условиям задачи опасным являются
одновременные перемешивания температуры в точках 4, 3, 2, 1; 3, 2, 1; 2.
Поэтому против комбинаций







 0
0
в графе 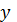
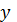 проставлены единицы.
проставлены единицы.
Комбинации
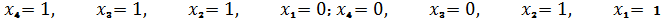
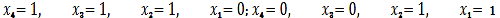
не являются опасными (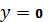
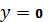 ). Прочерки в графе
). Прочерки в графе 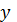
 сделаны против тех комбинаций,
которые по условию задачи не являются реальными, т.е. по существу запрещены:
сделаны против тех комбинаций,
которые по условию задачи не являются реальными, т.е. по существу запрещены:





 ;
;

 ;
;



 ;
;

 ;
;

 ;
;



 ;
;
После перенесения данных из таблицы 5
в карту Карно рисунок 5 заметим, что с целью минимизации выгодно доопределить
функцию, положив ее равной 1 на наборах 5, 7, 15, 6, 2, 10 и равной 0 на
наборах 4, 14, 11, 9 рисунке 6. При этом минимизированное значение функции
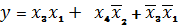
Такую функцию должно реализовать
устройство, включающее сигнал тревоги.
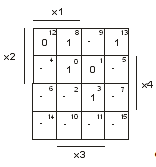
Рисунок 7
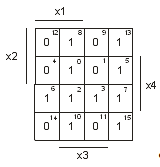
Рисунок 8
2. Методика синтеза комбинационного устройства
на логических элементах и мультиплексоре
.1 Логическая функция в виде СДНФ
Для записи логической функции в виде СДНФ
необходимо сначала составить таблицу истинности работы комбинационного
устройства. Составим таблицу истинности работы устройства (таблица 1).
Таблица 6 - таблица истинности
|
№
|
X4
|
X3
|
X2
|
X1
|
X0
|
Y0
|
Y1
|
Y2
|
Y3
|
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
2
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
|
3
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
|
|
4
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
|
|
5
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
6
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
|
|
7
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
8
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
|
|
9
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
10
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
|
11
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
12
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
|
|
13
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
14
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
|
|
15
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
|
|
16
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
|
17
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
18
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
|
19
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
|
|
20
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
21
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
22
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
|
23
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
|
25
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
26
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
27
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
28
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
29
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
30
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
|
31
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
32
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из полученной таблицы истинности записываем
логические функции в виде СДНФ для элементов Y0, Y1, Y2,
Y3.
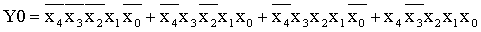

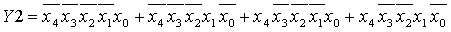
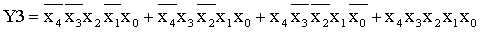
Для полученных функций строим схемы на элементах
И, ИЛИ, ИЛИ-НЕ.
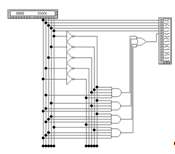
Рисунок 9 - Структурная схема для Y0 на
элементах И,ИЛИ,ИЛИ-НЕ.
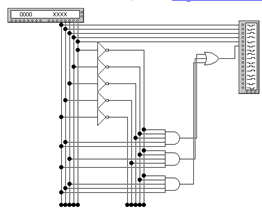
Рисунок 10 - Структурная схема для Y1 на
элементах И,ИЛИ,ИЛИ-НЕ.
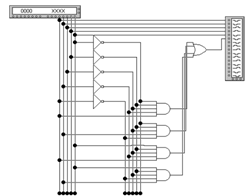
Рисунок 11 - Структурная схема для Y2 на
элементах И, ИЛИ, ИЛИ-НЕ.
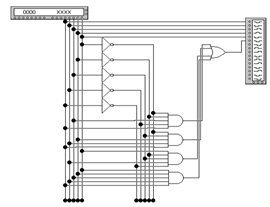
Рисунок 12 - Структурная схема для Y3 на
элементах И,ИЛИ,ИЛИ-НЕ.
2.2 Методика минимизации логической функции
Для минимизации функции используем карты Карно,
из-за их простоты и наглядности. Построим для каждой функции свою карту. Склеив
функцию получим минтерму.
Таблица 7 - Карта Карно для функции Y0
|
х4х3х2
х1х0 .
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
01
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
11
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
10
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
Склеиваем полученные минтермы:
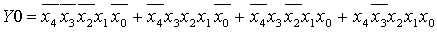
Таблица 8 - Карта Карно для функции
y1
|
х4х3х2
х1х0 .
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
01
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
11
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
|
10
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Склеиваем полученные минтермы:

Таблица 9 - Карта Карно для функции
y2
|
х4х3х2
х1х0 .
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
01
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
11
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
10
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
Склеиваем полученные минтермы:
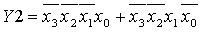
Таблица 10 - Карта Карно для функции
y3
|
х4х3х2
х1х0 .
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
01
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
11
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
|
10
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
Склеиваем полученные минтермы:
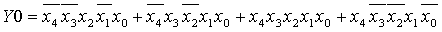
.3 Методика преобразование функции в
минимальный базис ИЛИ-НЕ
Переводим все функции в базис
ИЛИ-НЕ:
Реализуем в базисе ИЛИ-НЕ функцию y0.
Для этого применив закон де Моргана, получим:
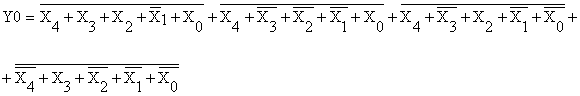
Схемная реализация функции y0
в базисе ИЛИ-НЕ представлена на рисунке 13, а график работы на рисунке 14.
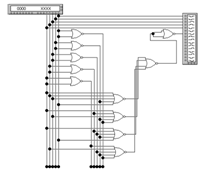
Рисунок 13 - Структурная схема на
элементах ИЛИ-НЕ для функции y0
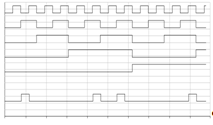
Рисунок 14 - График работы
устройства для выходной функции y0
Реализуем в базисе ИЛИ-НЕ функцию y1.
Для этого применив закон де Моргана, получим:
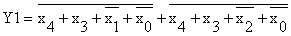
Схемная реализация функции y1
в базисе ИЛИ-НЕ представлена на рисунке 15, а график работы на рисунке 16.
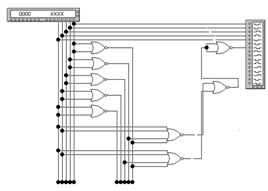
Рисунок 15 - Структурная схема на
элементах ИЛИ-НЕ для функции y1
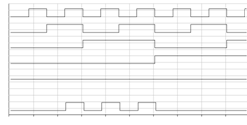
Рисунок 16 - График работы
устройства для выходной функции y1
Реализуем в базисе ИЛИ-НЕ функцию y2.
Для этого применив закон де Моргана, получим:
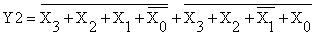
Схемная реализация функции y2
в базисе ИЛИ-НЕ представлена на рисунке 17, а график работы на рисунке 18.
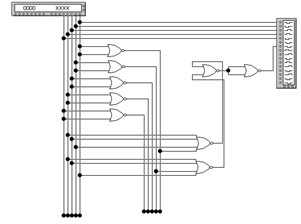
Рисунок 17 - Структурная схема на
элементах ИЛИ-НЕ для функции y2
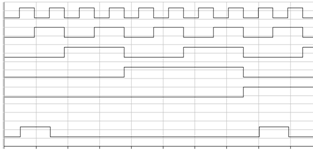
Рисунок 18 - График работы
устройства для выходной функции y2
Реализуем в базисе ИЛИ-НЕ функцию y3.
Для этого применив закон де Моргана, получим:
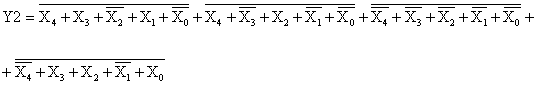
Схемная реализация функции y3
в базисе ИЛИ-НЕ представлена на рисунке 19, а график работы на рисунке 20.
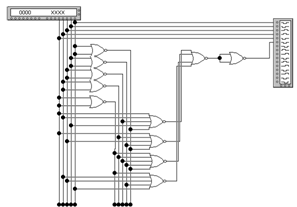
Рисунок 19 - Структурная схема на
элементах ИЛИ-НЕ для функции y3
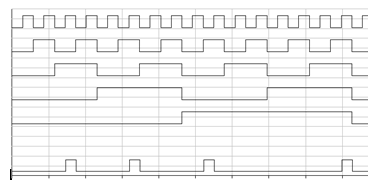
Рисунок 20 - График работы
устройства для выходной функции y3
3. Методика проектирование
устройства с памятью
Составим таблицу истинности
счетчика, используя таблицу переходов D-триггера - таблица 11.
Таблица 11 - таблица переходов
D-триггера
|
№
|
Q05
|
Q04
|
Q03
|
Q02
|
Q01
|
Q5
|
Q4
|
Q3
|
Q2
|
Q1
|
D5
|
D4
|
D3
|
D2
|
D1
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
|
2
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
|
3
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
|
4
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
|
5
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
|
6
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
|
7
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
8
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
|
9
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
|
10
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
|
11
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
|
12
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
|
13
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
|
14
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
15
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
16
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
|
№
|
Q05
|
Q04
|
Q03
|
Q02
|
Q01
|
Q5
|
Q4
|
Q3
|
Q2
|
Q1
|
D5
|
D4
|
D3
|
D2
|
D1
|
|
17
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
|
18
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
|
19
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
|
20
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Составим карты Карно для каждого входа триггера:
Карта Карно для D5 представлена в
таблице 12.
Таблица 12 - Карта Карно для D5
|
Q3Q2Q1
Q5Q4
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
01
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
|
11
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
|
10
|
1
|
1
|
1
|
1
|
~
|
~
|
0
|
1
|
Карта Карно для D4 представлена в
таблице 13.
Таблица 13 - Карта Карно для D4
|
Q3Q2Q1
Q5Q4
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
|
01
|
1
|
1
|
1
|
1
|
1
|
|
1
|
1
|
|
11
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
|
10
|
0
|
0
|
0
|
0
|
~
|
~
|
0
|
0
|
Карта Карно для D3 представлена в
таблице 14.
Таблица 14 - Карта Карно для D3
|
Q3Q2Q1
Q5Q4
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
|
01
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
|
11
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
|
10
|
0
|
0
|
1
|
0
|
~
|
~
|
0
|
1
|
Карта Карно для D2 представлена в
таблице 15.
Таблица 15 - Карта Карно для D2
|
Q3Q2Q1
Q5Q4
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
|
01
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
|
11
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
|
10
|
0
|
1
|
0
|
1
|
~
|
~
|
0
|
0
|
Карта Карно для D1 представлена в
таблице 16.
Таблица 16 - Карта Карно для D1
|
Q3Q2Q1
Q5Q4
|
000
|
001
|
011
|
010
|
110
|
111
|
101
|
100
|
|
00
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
|
01
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
|
11
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
~
|
|
10
|
1
|
|
|
1
|
~
|
~
|
0
|
1
|
Склеиваем полученные минтерны:
5
= Q4Q3Q2Q1 + Q5Q2 +
Q5Q3
D4 = Q4Q3Q2Q1
+ Q4Q2 + Q4Q3 + Q4Q2Q1
D3 = Q3Q2Q1
+ Q5Q3Q2Q1 + Q3Q2
D2 = Q2Q1 + Q5Q2Q1
+ Q3Q2Q1 2 = Q2Q1
+ Q3Q2Q1 + Q5Q2Q1
Структурная схема получившегося счетчика
представлена на рисунке 21, а график работы счетчика на рисунке 22.
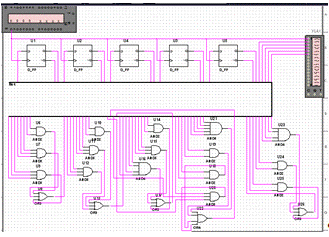
Рисунок 21 - Структурная схема счетчика
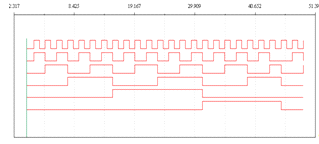
Рисунок 22 - График работы счетчика
Список литературы
логическое устройство функция
1.
А.К. Мурышкин, А.И. Петрачков, П.Н. Кунинин. «Основы микропроцессорной техники:
Учебное пособие.» - Новокузнецк, издание СибГГМА, 1996. - 86с.
.
А.Г. Алексеенко, И.И. Шагурин. «Микросхемотехника.» - М.: Радио и связь, 1990.
- 496с.
.
В.Л. Шило. «Популярные цифровые микросхемы.» - М.: Радио и связь, 1987. - 352с.
.
В.Л Горбунов, Д.И. Панфилов, Д.Л. Переснухин. - М.: Высшая школа, 1988. - 272с.
.
«Аналоговые и цифровые интегральные микросхемы. Справочное пособие.» Под ред.
С.В. Якубовского. - - М.: Радио и связь, 1985. - 432с.
.
К.К. Александров, Е.Г. Кузьминина. «Электротехнические чертежи и схемы.» - М.:
Энергоатомиздат, 1990. - 288с.
.
Фрике К. - «Вводный курс цифровой электроники.» - Москва, Техносфера, 2003 г.
.
Угрюмов Е.П. «Цифровая схемотехника.» - Санкт-Петербург, БХВ-Петербург, 2002 г.
.
Пухальский Г.И., Новосельцева Т.Я. «Проектирование дискретных устройств на
интегральных микросхемах: Справочник.» - Москва, Радио и связь, 1990 г.
.
Зельдин Е.А. «Цифровые интегральные микросхемы в информационно-измерительной
аппаратуре.» - Ленинград, Энергоатомиздат, 1986 г.