Исследование в экономике теории магистралей
ВВЕДЕНИЕ
В экономической теории на первоначальном этапе
ее развития редко использовались математические формулировки. Тем не менее,
многие классические доктрины экономики в словесной, завуалированной форме по
существу содержали определенные математические утверждения; это иногда
оставалось скрытым и от самих приверженцев таких доктрин. По мере развития
экономической науки внутренне присущие ей математические черты постепенно
проявлялись все сильнее. На более поздней стадии ее истории некоторые
экономисты стали предлагать даже полную математизацию экономической теории.
По-видимому, самым выдающимся представителем зарождавшегося математического
направления в экономической теории был французский экономист Леон Вальрас.
Именно он в конце XIX столетия заложил основы теории общего экономического
равновесия. Эта теория основана на том, что между соответствующими величинами в
экономике существует не односторонняя причинно-следственная связь, а
многосторонняя взаимозависимость, которую математически можно представить
некоторой системой соотношений между этими величинами.
Одной из теорий в экономике является теория
магистрали.
Целью данной курсовой работы заключается в
изучении использования в экономике теорий магистрали.
Поставленная цель решается посредством следующих
задач:
изучить историю развития теорий в экономике;
исследовать экономику и математику;
рассмотреть понятие магистрали;
оценить магистральные траектории в линейных
моделях экономики;
охарактеризовать модель Неймана;
применить методы вычисления теории магистралей;
вычислить с помощью методов теории магистралей.
Объектом исследования в данной курсовой работе
являются теории магистрали.
Предметом исследования является использование в
экономике теорий магистрали.
В данной курсовой работе были использованы следующие
методы: аналитический, монографический, аналитический,
экономико-математические, статистические методы.
Работа состоит из введения, трех глав,
заключения и списка использованных источников.
В первой главе нами были использованы источники:
Максимова В.Ф., Региональная экономика России: учебник / М., 2002.; Вечканова
Г.Р, Микроэкономика: учебник / СПб,2010.; Курс экономики: учебник, М., 2010;
Экономическая теория. Конспект лекций., М., 2009., Экономическая теория,
учебник, М., 2008.; Россия в цифрах, М., 2011.
Во второй главе нами были использованы
источники: Максимова В.Ф., Региональная экономика России: учебник / М., 2002.;
Экономическая теория, учебник, М., 2008, Курс экономики, учебник, М., 2010.,
Макконнелл К.Р., Экономикс: принципы, проблемы и политика, учебник, М., 2007.
В третьей главе нами были использованы
источники: Ершов М.К., Экономический рост: новые проблемы и новые риски,
электронный источник, №12,2008
. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕОРИЙ МАГИСТРАЛИ
1.1 Эволюция экономической
мысли теории магистрали
Истоки применения математики в экономике
теряются во тьме веков: ведь экономика никогда не могла существовать без
измерения и счета. В XV в. итальянский математик Лука Пачоли разработал методы
бухгалтерского учета на принципе двойной записи каждой операции, действующие до
сих пор. В XVIII в. французские экономисты пришли к выводу, что в экономике,
как и в природе (физике), действуют законы, которые нужно выявлять. Этих
экономистов назвали физиократами. Глава физиократов лейб-медик Людовика XV Франсуа
Кенэ опубликовал в 1758 г. «экономическую таблицу», где анализировал
кругооборот денег в экономике по аналогии с кругооборотом крови в человеческом
организме. Эту идею в XIX в. развил Карл Маркс, разработав свои схемы
общественного воспроизводства. А уже в XX в. развитие этих идей завершил
американский экономист, эмигрант из России В.В.Леонтьев, который создал метод
межотраслевого баланса (МОБ, «затраты-выпуск»), за что получил Нобелевскую
премию по экономике [9, с. 217].
В 1838 г. французский инженер Анри Курно
опубликовал работу «Исследование математических принципов теории богатства». В
1870 г. Леон Вальрас создал математическую модель общего экономического
равновесия. Она произвела столь сильное впечатление, что некоторые экономисты
высказали мнение, будто на этом развитие экономической теории заканчивается. Но
в XX в. появилось множество других моделей экономического равновесия. В 1874 г.
Л. Вальрас написал: «Чистая теория экономики есть наука, напоминающая во всем
физико-математические науки».
Одновременно с А. Курно немецкий экономист
Госсен издал книгу по анализу потребительского спроса. В ней он изложил два
закона, которые теперь называются первым и вторым законами Госсена. Книгу эту
не покупали, и автор сжег ее тираж, - к счастью, не весь. Австрийская школа
экономистов во главе с К. Менгером разрабатывала теорию предельной полезности.
Независимо от этих ученых в этом направлении работали итальянец В.Парето,
англичанин Эджуорт, американец Д.Б. Кларк. Появился маржинализм, что
зафиксировано в книге А. Маршалла «Принципы экономики», изданной в 1890 г.
Развитие идей маржинализма продолжили в XX в. русский математик Е.Е. Слуцкий и
англичанин Д. Хикс.
Американский математик, выходец из Венгрии, Джон
фон Нейман в первой половине XX в. разработал теорию магистралей. В 1929 г.
американцы К.И. Кобб и П.Х. Дуглас описали производственную функцию для
американской обрабатывающей промышленности за период с 1899 г. по 1922 г. В
1953 г. появилась книга американского математика Н.Винера «Кибернетика или
управление и связь в животном и машине». Позже Винер добавил к биологическим и
техническим системам общественные, а значит и экономику. В 50-х гг. XX в.
американский математик Р. Беллман создал метод динамического программирования,
а американский экономист Р. Солоу - модель экономического роста. Под
руководством российского математика Л.С. Понтрягина был разработан метод под
названием «принцип максимума».
В 1939 г. российский математик Л.В. Канторович
(1912-1986) опубликовал первую в мире работу по линейному программированию.
Аналогичную работу независимо от него выполнил американский математик Д.
Данциг, но опубликовал ее только в 1945 г. Общепризнанно, что приоритет
создания линейного программирования принадлежит Л. Канторовичу. За эту работу
он в 1965 г. получил Ленинскую, а в 1975 г.- Нобелевскую премии по экономике.
Л.Канторович - единственный экономист из социалистических стран, ставший
лауреатом Нобелевской премии [3, с. 70].
В СССР, а затем в России,
экономико-математическое направление интенсивно разрабатывалось в Центральном
экономико-математическом институте, Институте экономики и организации
промышленного производства (Новосибирский Академгородок) и других научных
учреждениях.
Центральная идея структурных моделей связана с
понятием сбалансированной траектории, игравшим важную роль в формировании
экономики развития как новой научной дисциплины. Модели показывают, что
траектория является сбалансированной и обладает относительно высоким темпом
роста лишь, если соблюдаются определенные пропорции между компонентами системы,
на достижение которых и должна быть направлена экономическая политика. К
структурном можно отнести модели Харрода (Harrod,
1939) и Домара (Domar,
1946), модель фон Неймана (von
Neumann, 1937) и ее
обобщения (Гейл, 1959), динамические варианты модели Леонтьева (Leontief,
1961, 1966). Статья Солоу (Solow,
1956), которую считают началом современной теории экономического роста, была
написана как ответ на работы Харродда и Домара. В модели Солоу также основную
роль играет наличие определенной структуры (постоянной нормы накопления). Фелпс
(Phelps, 1961) в рамках
модели Солоу предложил принцип формирования оптимальной структуры - золотое
правило. Структурные модели послужили основой для первых моделей эндогенного
роста, которые ставили целью дать детальное экономическое объяснение механизма
формирования темпа роста (Uzawa,
1961, Arrow, 1962), и
моделей с овеществленным научно-техническим прогрессом (vintage
models) (Канторович,
Горьков, 1959, Johansen,
1959, Solow 1960).
Основной критерий оптимальности структурных моделей - максимизация темпа роста
на сбалансированной траектории - использовался позднее и в ряде моделей новой
теории эндогенного роста [7, c.
176]
1.2 Понятие и сущность магистрали
Магистраль - понятие, играющее важную роль в
теории экономической динамики. Обычно это луч в пространстве продуктов
многопродуктовых и многосекторных моделей, на котором расположены элементы
траектории максимального постоянного пропорционального роста производственных
выпусков (Приложение А, А-1). Оптимальная траектория многопродуктовой и
многосекторной модели с продолжительным временным горизонтом при весьма
скромных предпосылках выходит из исторически обусловленного начального вектора
и приближаются к магистрали (часто в смысле углового расстояния), затем располагаются
вдоль магистрали, мало отличаясь от траектории максимального постоянного
пропорционального роста, расположенной на магистрали, и в конце временного
промежутка модели оптимальная траектория, подчиняясь целевой функции, может
отойти от магистрали. Таким образом, оптимальная траектория состоит из трех
вышеописанных участков. Продолжительность первого и третьего участков не
зависят от временного горизонта оптимизационной модели. С ростом временного
горизонта модели удлиняется второй участок оптимальной траектории, который
является ее основным участком и целиком определяется технологическим множеством
оптимизационной модели. Характер поведения первого участка оптимальной
траектории в основном регламентируется начальным вектором, а последний участок
в существенном зависит от территориальной целевой функции оптимизационной
модели, т.е. такой целевой функции, которая явно зависит лишь от последнего
периода временного промежутка модели.
Магистраль - это особая траектория развития,
которая обладает следующими важными свойствами:
с течением времени оптимальная траектория,
исходящая из любого начального состояния становится близкой к магистрали;
по исходной модели можно построить некоторый
специальный функционал - критерий (максимальная производительность, потенциал
экономической системы), максимальное значение которого достигается лишь при
условии совпадения траектории развития с магистралью. С помощью этого критерия
представляется возможным оценить, насколько далеки те или иные состояния или
решения от оптимальных. При решении чисто практических задач такой критерий
оптимальности позволяет обосновать и рассчитать нормативы экономической
эффективности использования природных ресурсов и других факторов общественного
производства;
магистраль вычисляется значительно легче с точки
зрения трудоемкости и размерности задачи, чем оптимальная траектория, выходящая
из произвольного начального состояния.
Вместо луча исследователи были вынуждены для
описания характера поведения оптимальных траекторий с продолжительным временным
горизонтом использовать множества большей размерности называемые гранями
равновесия, а также косые магистрали, индуцируемые переменными во времени
технологическими множествами многопродуктовых и многосекторных динамических
моделей [15, с. 136].
В большинстве магистральных теорем, известных в
литературе, максимизируемая функция представляет собой сумму полезностей во
времени, где полезность в каждый момент зависит только от текущего потребления.
Неудовлетворительность таких функций при объяснении некоторых эмпирических
фактов еще в довоенные годы была отмечена П. Самуэльсоном. Между тем, в
фундаментальном обзоре по магистральной теории, вошедшем в "Handbook of
Mathematical Economics" (1986), Л. Маккензи приводит лишь две работы П.
Самуэльсона и К. Иваи, в которых были предприняты попытки ослабить требование
об аддитивности в однопродуктовых стационарных моделях. В основе метода
доказательства П. Самуэльсона лежит спектральный анализ, поэтому он не применим
к нестационарным моделям. Метод К. Иваи опирается на идеи динамического
программирования и также существенно использует стационарность модели.
Отметим, что магистральным свойством могут
обладать не только оптимальные траектории производственных выпусков, но и
оптимальные траектории цен, двойственных моделей. В случае сильноагрегированных
моделей экономического роста в форме задач оптимального управления роль
магистрали играет траектория максимального роста, соответствующая максимальной
норме потребления. Здесь оптимальная траектория также состоит из трех участков,
главным из которых является второй, который совпадает с магистралью, а первый и
второй участки соответствуют более низким нормам потребления. Начиная с 60-х
годов 20 в., в ряде стран (СССР, союзные республики, Япония) было выполнено
большое число работ, посвященных расчетам магистралей и оптимальных траекторий
на базе реальных и экспертных данных. [14, c.
98]
.3 Теоремы о магистрали
Поскольку горизонт T
и целевой функционал выбираются, вообще говоря, произвольно, важны результаты о
независимости от них поведения оптимальных траекторий. В 1958 г. Дорфман,
Самуэльсон и Солоу (Dorfman
et al.,
1958) высказали гипотезу о наличии в моделях экономической динамики магистралей
- особых множеств состояний, на которых (или вблизи которых) проводит большую
часть времени T-шаговая
оптимальная траектория, если горизонт T
достаточно велик. Эти авторы предложили удачную аналогию: водители автомашин
при длительных поездках выезжают на скоростную дорогу, движутся по ней, а затем
в какой-то момент покидают. Наличие магистралей позволяло сделать выводы об
общих «магистральных путях» развития групп стран (клубов) и о существовании
определенных оптимальных пропорций, на которые следует ориентироваться в
экономической политике. Подтверждению гипотезы послужили теоремы о магистрали,
доказанные в 1961 г. Раднером и Моришимой для модели фон Неймана и в 1964 г.
Никайдо для модели фон Неймана-Гейла. В дальнейшей литературе видное место
занимает монография Макарова и Рубинова (1973). В обзорах McKenzie,
1976, 1986, 1998, Рубинов, 1982 выделено три типа теорем о магистрали: о
средней магистрали (близость достаточно длинных оптимальных траекторий к
магистрали за исключением конечного числа периодов), о ранней магистрали
(близость достаточно длинных конечных оптимальных траекторий на начальном
участке к некоторой бесконечной траектории) и о поздней магистрали (сходимость
бесконечных оптимальных траекторий к магистрали). Очевидной лакуной было
отсутствие результатов о поведении оптимальных траекторий на финальном участке.
«Финальные магистрали» наглядно видны на фазовых диаграммах, распространенных в
макроэкономической литературе, однако их природа не получила объяснения, до
того, как теоремы о финальной магистрали были получены для модели фон Неймана -
Гейла независимо Беленьким (1990) и Матвеенко (1988, 1989), а затем для модели
с конечным числом состояний (Матвеенко, 1990, 1998) и для однопродуктовой
модели рамсеевского типа (Матвеенко, 1999). При определенных предположениях,
для рассматриваемых классов моделей выявлена «трехчастная» структура»: при
достаточно большом горизонте, T-шаговая
оптимальная траектория с фиксированными концами состоит из трех участков:
первый участок близок или совпадает с соответствующим участком бесконечной
оптимальной траектории (ранней магистрали), которая зависит лишь от начального
состояния (не зависит от конечного состояния и от горизонта); на втором участке
траектория проходит по средней магистрали или вблизи нее; на третьем участке
траектория, рассматриваемая в обратном времени, проходит по финальной магистрали
или вблизи нее, причем финальная магистраль определяется только конечным
состоянием. Начальный участок может быть построен пошагово с помощью
функции-значения (или эффективного функционала), а финальный участок (в
обратном времени) - с помощью второй функции-значения (или второго эффективного
функционала). [11, c. 56]
Виды теорем магистрали:
магистраль
v1
траектория
u1
Рисунок 1 - Слабая теорема теории магистрали
магистраль
v1
траектория
u1
Рисунок 2 - Сильная теорема теории магистрали
магистраль
v1
траектория
u1
Рисунок 3 - Сильнейшая теорема теории магистрали
В различных предположениях утверждения о
существование магистрали (теоремы о магистрали) доказаны в трех формах: слабой,
сильной и сильнейшей. В слабых теоремах отмечено, что оптимальные траектории
могут отклоняться от магистрали. Теоремы о магистрали в сильной форме утверждают,
что отклонение от магистрали может приходиться только на начальном и конечном
участках оптимальной траектории. Теоремы о магистрали в сильнейшей форме
говорят, что большую часть времени оптимальные траектории находятся на
магистрали.
В данной главе мы рассматривали
эволюционно-исторические развития теории магистрали, понятие и сущность
магистрали, их виды и обоснование каждого из них.
2. МЕТОДИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЕ В
ЭКОНОМИКЕ ТЕОРИЙ МАГИСТРАЛИ
.1 Магистральные траектории в линейных моделях
экономики
В математической экономике магистралью
называется траектория экономического роста, на которой пропорции
производственных показателей (такие как темп роста производства, темп снижения
цен) неизменны, а сами показатели (такие как интенсивность производства,
валовой выпуск) растут с постоянным максимально возможным темпом. Таким
образом, магистраль - это траектория или луч максимального сбалансированного
роста. Ее часто сравнивают со скоростной автострадой. Так, например, для того
чтобы добраться из Кемерово в Киселевск как можно быстрее, наиболее
целесообразно сначала проехать по автостраде Кемерово-Новокузнецк, а затем уже
съехать на ответвляющуюся от нее дорогу в районе Киселевска. Так мы потеряем на
дорогу меньше времени и доедем до конечного пункта с большим комфортом, чем
если бы мы ехали по обычному шоссе через Ленинск-Кузнецкий и Белово [9, c.
83].
Поскольку «оптимальное» или «эффективное»
развитие экономики в любом смысле так или иначе связано и должно сопровождаться
экономическим ростом, то для достижения любой конечной цели следует поступать
аналогичным образом: сначала вывести производство на магистральный путь, т.е.
на траекторию (или луч) Неймана, характеризующуюся максимальным темпом роста и
минимальной нормой процента, а по истечении определенного срока времени вывести
ее к задуманной цели. Такими целями могут быть максимизация прибыли,
минимизация затрат, максимизация полезности от потребления товаров, достижение
конкурентного равновесия при наиболее благоприятных условиях, т.е. на более
высоком уровне благосостояния населения, и т.д. [12, c.
84].
Итак, с одной стороны мы имеем магистральные
модели, а с другой - оптимизационные или еще шире - нормативные модели
экономики. Изучение этих двух моделей во взаимосвязи, т.е. изучение связи между
магистральными и оптимальными (в том или ином смысле) траекториями и является
предметом магистральной теории. Можно говорить, что магистральная теория
является одним из средств качественного анализа оптимальных траекторий.
Основной целью этой теории является исследование условий так называемых
«слабой» и «сильной» теорем о магистралях. Слабая теорема утверждает, что за
исключением некоторого малого периода (или некоторого числа дискретных моментов
из), не зависящего от продолжительности T планового периода, все оптимальные
траектории сосредотачиваются в относительной близости к магистральной
траектории. Сильная теорема говорит о том, что те небольшие промежутки времени,
на которых оптимальные траектории удалены от магистральной, если они существуют,
то разве лишь в начале периода, т.е., или в конце периода, т.е.; а в середине
периода оптимальные траектории расположены в относительной близости к
магистральной [14, с. 69].
В общем случае в моделях экономической динамики
даже при неизменности технологических возможностей утверждения теорем о
магистрали не выполняются. Для их выполнения приходится вводить различные
дополнительные предположения о свойствах исходной модели экономики. Другой путь
состоит в изучении реальных отраслевых пропорций и сравнении их с
магистральными. Благодаря техническому прогрессу и изменчивости во времени
общественных предпочтений различных благ, реальное состояние экономики при
детальном (дезагрегированном) ее описании всегда значительно отличается от
магистрального. В то же время, как показывают полученные в этом направлении
результаты исследований, при высоком уровне агрегирования экономические
пропорции близки к магистральным.
Теоремы о магистралях доказываются для ряда
оптимизационных моделей расширяющейся экономики. Наиболее общей из них является
известная теорема Раднера для нелинейных моделей расширения.
Приведем подобную теорему линейной модели
Неймана в следующем пункте.
.2 Модель Неймана
Классическая (исходная) модель Неймана строится
при следующих предпосылках:
экономика, характеризуемая линейной технологией,
состоит из отраслей, каждая из которых обладает конечным числом
производственных процессов, т.е. выпускается несколько видов товаров, причем
допускается совместная деятельность отраслей;
производственные процессы разворачиваются во
времени, причем осуществление затрат и выпуск готовой продукции разделены
временным лагом;
для производства в данный период можно тратить
только те продукты, которые были произведены в предыдущем периоде времени,
первичные факторы не участвуют;
спрос населения на товары и, соответственно,
конечное потребление в явном виде не выделяются;
Перейдем к описанию модели Неймана. На
дискретном временном интервале 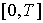 с точками
с точками 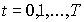 рассматривается
производство, в котором n видов затрат с помощью m технологических процессов
превращаются в n видов продукции. Мы не будем указывать число отраслей, так как
в дальнейшем не понадобится подчеркивать принадлежность товаров или технологий
к конкретным отраслям. В модели Леонтьева технологические коэффициенты были
отнесены к единице продукта. В модели Неймана, принимая в качестве
производственных единиц не отрасли, а технологические процессы, удобно отнести
эти коэффициенты к интенсивности производственных процессов.
рассматривается
производство, в котором n видов затрат с помощью m технологических процессов
превращаются в n видов продукции. Мы не будем указывать число отраслей, так как
в дальнейшем не понадобится подчеркивать принадлежность товаров или технологий
к конкретным отраслям. В модели Леонтьева технологические коэффициенты были
отнесены к единице продукта. В модели Неймана, принимая в качестве
производственных единиц не отрасли, а технологические процессы, удобно отнести
эти коэффициенты к интенсивности производственных процессов.
Интенсивностью производственного процесса j
называется объем продуктов, выпускаемых этим процессом за единицу времени.
Уровень интенсивности j-го процесса в момент времени t обозначим через 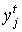 (
(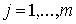 ).
Заметим, что
).
Заметим, что 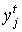 является вектором,
число компонент которого соответствует числу выпускаемых j-ым процессом видов
товаров и
является вектором,
число компонент которого соответствует числу выпускаемых j-ым процессом видов
товаров и 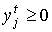 .
.
Предположим, что функционирование j-го процесса
(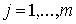 )
с единичной интенсивностью требует затрат продуктов в количестве
)
с единичной интенсивностью требует затрат продуктов в количестве 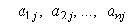 и
дает выпуск товаров в количестве
и
дает выпуск товаров в количестве 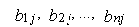
Введем обозначения 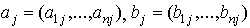 .
Пара
.
Пара 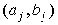 характеризует
технологический потенциал, заложенный в j-ом процессе (его функционирование с
единичной интенсивностью). Поэтому пару
характеризует
технологический потенциал, заложенный в j-ом процессе (его функционирование с
единичной интенсивностью). Поэтому пару 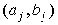 можно
назвать базисом j-го производственного процесса, имея в виду, что для любой
интенсивности
можно
назвать базисом j-го производственного процесса, имея в виду, что для любой
интенсивности 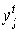 соответствующую
пару затраты-выпуск можно выразить как
соответствующую
пару затраты-выпуск можно выразить как 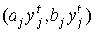 .
Поэтому последовательность пар
.
Поэтому последовательность пар  (1) представляющих
собой затраты и выпуски всех производственных процессов в условиях их
функционирования с единичными интенсивностями, будем называть базисными
процессами.
(1) представляющих
собой затраты и выпуски всех производственных процессов в условиях их
функционирования с единичными интенсивностями, будем называть базисными
процессами.
Все m базисных процессов описываются двумя
матрицами
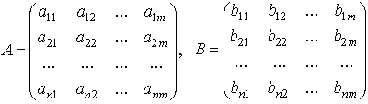 , (2)
, (2)
где A- матрица затрат, B- матрица выпуска.
Вектор 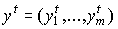 называется
вектором интенсивностей. Соответствующие этому вектору затраты и выпуски по всем
m процессам можно получить как линейную комбинацию базисных процессов с
коэффициентами
называется
вектором интенсивностей. Соответствующие этому вектору затраты и выпуски по всем
m процессам можно получить как линейную комбинацию базисных процессов с
коэффициентами 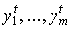 :
:
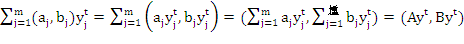 ,
(3)
,
(3)
Говорят, что в производственном процессе 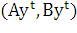 базисные
процессы участвуют с интенсивностями
базисные
процессы участвуют с интенсивностями 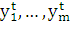 .
Как видно из, неймановская технология, описываемая двумя матрицами A и B
единичных уровней затрат и выпуска, является линейной в начале параграфа).
Рассматривая все допустимые «смеси» базисных процессов, получаем расширенное
множество производственных процессов
.
Как видно из, неймановская технология, описываемая двумя матрицами A и B
единичных уровней затрат и выпуска, является линейной в начале параграфа).
Рассматривая все допустимые «смеси» базисных процессов, получаем расширенное
множество производственных процессов
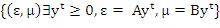 (4)
(4)
которое и отражает допустимость совместной
деятельности отраслей. Возможность совместного производства нескольких
продуктов в одном процессе следует из того, что в каждом процессе j может быть
отличной от нуля более чем одна из величин 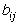 .
Множество представляет собой неймановскую технологию в статике (в момент t).
Если в матрице A положить n=m, матрицу B отождествить с единичной матрицей, а
.
Множество представляет собой неймановскую технологию в статике (в момент t).
Если в матрице A положить n=m, матрицу B отождествить с единичной матрицей, а 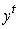 интерпретировать
как вектор валового выпуска, то превращается в леонтьевскую технологию.
интерпретировать
как вектор валового выпуска, то превращается в леонтьевскую технологию.
Продолжим описание модели Неймана. Согласно
предпосылок, затраты 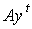 в момент t не могут
превышать выпуска
в момент t не могут
превышать выпуска 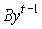 , соответствующего
предыдущему моменту t-1 (Приложение В, таблица В-1).
, соответствующего
предыдущему моменту t-1 (Приложение В, таблица В-1).
Поэтому должны выполняться условия:
 , (5)
, (5)
где  -
вектор запаса товаров к началу планируемого периода.
-
вектор запаса товаров к началу планируемого периода.
Обозначим через 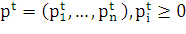 ,
вектор цен товаров. Неравенство (5) можно трактовать как непревышение спроса
над предложением в момент t. Поэтому в стоимостном выражении (в ценах момента
t) должно быть:
,
вектор цен товаров. Неравенство (5) можно трактовать как непревышение спроса
над предложением в момент t. Поэтому в стоимостном выражении (в ценах момента
t) должно быть:
 (6)
(6)
По предложению 5 прибыль базисного процесса 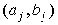 на
отрезке [t-1,T] равна величине
на
отрезке [t-1,T] равна величине 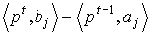 , т.е. затраты
осуществляются по цене начала периода, а готовая продукция - по цене момента ее
реализации. Таким образом, издержки по всем базисным процессам можно записать
как
, т.е. затраты
осуществляются по цене начала периода, а готовая продукция - по цене момента ее
реализации. Таким образом, издержки по всем базисным процессам можно записать
как 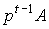 ,
а выручку - как
,
а выручку - как 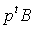 (Приложение В,
таблица В-2).
(Приложение В,
таблица В-2).
Будем говорить, что базисные процессы
неубыточны, если 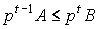 неприбыльны - если
неприбыльны - если
 (7)
(7)
В модели Неймана предполагается неприбыльность
базисных процессов. Это объясняется тем, что издержки и выручки разведены во
времени, т.е. относятся к разным моментам времени, и в условиях расширяющейся
экономики «характерен случай падения цен (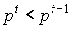 ),
т.е. покупательская способность денег в момент t будет выше, чем в момент t-1.
С таким обоснованием можно согласиться или не согласиться. Главная же причина
неприбыльности базисных процессов заложена в определении экономического
равновесия. Поясним это чуть подробнее.
),
т.е. покупательская способность денег в момент t будет выше, чем в момент t-1.
С таким обоснованием можно согласиться или не согласиться. Главная же причина
неприбыльности базисных процессов заложена в определении экономического
равновесия. Поясним это чуть подробнее.
Основной предмет исследования Джона фон Неймана
- это возможность существования равновесия в рассматриваемой им динамической
модели экономики при заданных в каждый момент ценах. Как следует, при
равновесии в условиях совершенной конкуренции имеет место стоимостной баланс.
Таким образом, в условиях равновесия не создается никакой прибыли, и
неравенство является отражением этого факта. Поэтому, если в (7) для некоторого
базисного процесса j имеет место строгое неравенство, т.е. предложение
превышает спрос:
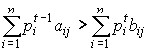 , (8)
, (8)
то должно быть 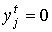 .
Иначе говоря, отсутствие «отрицательной прибыли» обеспечивается нулевой
интенсивностью. Отсюда получаем
.
Иначе говоря, отсутствие «отрицательной прибыли» обеспечивается нулевой
интенсивностью. Отсюда получаем
 , (9)
, (9)
Описание модели Неймана завершено. Совокупность
неравенств и уравнений (6) - (9):
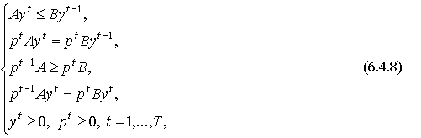 (10)
(10)
где 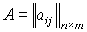 и
и
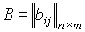 -
матрицы затрат и выпуска соответственно, называется (динамической) моделью
Неймана.
-
матрицы затрат и выпуска соответственно, называется (динамической) моделью
Неймана.
Говорят, что в экономике наблюдается
сбалансированный рост производства, если существует такое постоянное число  ,
что для всех m производственных процессов
,
что для всех m производственных процессов
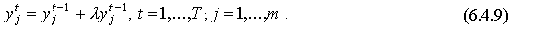 , (11)
, (11)
Постоянное число 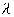 называется
темпом сбалансированного роста производства.
называется
темпом сбалансированного роста производства.
Содержательно (11) означает, что все уровни
интенсивности возрастают одинаковыми темпами
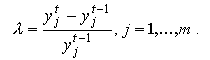
Раскрывая рекуррентно правую часть(11), получаем
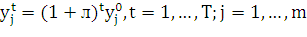 (12)
(12)
где 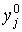 -
интенсивность процесса j, установившаяся к началу планового периода. Заметим,
что t в правой части (12) является показателем степени, а в левой - индексом.
-
интенсивность процесса j, установившаяся к началу планового периода. Заметим,
что t в правой части (12) является показателем степени, а в левой - индексом.
В случае сбалансированного роста производства, с
учетом постоянства темпа роста, последовательность 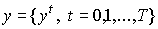 называется
стационарной траекторией производства.
называется
стационарной траекторией производства.
Говорят, что в экономике наблюдается
сбалансированное снижение цен, если существует такое постоянное число 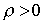 ,
что для всех n товаров
,
что для всех n товаров
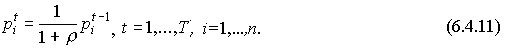 (13)
(13)
Постоянное число 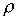 называется
нормой процента.
называется
нормой процента.
Содержательно (13) означает, что цены на все
товары снижаются одинаковыми темпами
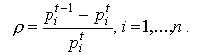
Название «норма процента» для темпа снижения 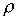 принято
по ассоциации с показателем нормы процента (нормы доходности) в формуле
сложного процента
принято
по ассоциации с показателем нормы процента (нормы доходности) в формуле
сложного процента 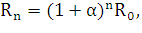 где
где 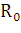 -
сумма начального вложения,
-
сумма начального вложения, 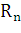 - получаемая через
n периодов конечная сумма, α-
норма процента. Так как речь идет о снижении, то «норма процента» в (13) входит
с отрицательным знаком
- получаемая через
n периодов конечная сумма, α-
норма процента. Так как речь идет о снижении, то «норма процента» в (13) входит
с отрицательным знаком
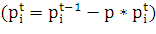 .
.
Из равенства (12) получаем
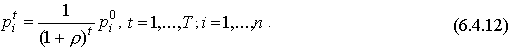 , (14)
, (14)
где 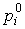 -
цены, установившиеся к началу планового периода.
-
цены, установившиеся к началу планового периода.
В случае сбалансированного снижения цен
последовательность 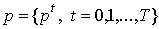 называется
стационарной траекторией цен.
называется
стационарной траекторией цен.
Подставляя (12) и (14) в модель Неймана (10),
получаем ее «стационарную» форму:
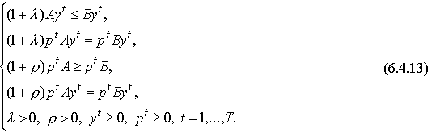 (15)
(15)
Эта система соотношений показывает, что по
стационарным траекториям y и p экономика развивается согласно неизменному динамическому
закону. Поэтому такую ситуацию естественно назвать равновесной.
Четверка 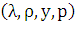 ,
где y - стационарная траектория производства, p- стационарная траектория цен, а
λ
и
ρ-
соответствующие им темп сбалансированного роста производства и норма процента
(темп сбалансированного снижения цен), называется состоянием (динамического)
равновесия в модели Неймана (10).
,
где y - стационарная траектория производства, p- стационарная траектория цен, а
λ
и
ρ-
соответствующие им темп сбалансированного роста производства и норма процента
(темп сбалансированного снижения цен), называется состоянием (динамического)
равновесия в модели Неймана (10).
Сделаем следующие предположения:
а) 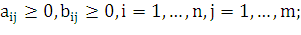
б) для каждого j существует хотя бы одно i,
такое что 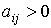 ;
;
в) для каждого i существует хотя бы одно j,
такое что 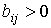 ;
;
г) для каждого t 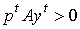 .
.
Теорема. Если выполнены условия а-б то в модели
Неймана (10) существует состояние равновесия.
Условия б-в говорят о наличии в каждом столбце
матрицы A и каждой строке матрицы B по крайней мере одного положительного элемента.
Содержательно это означает, что среди всех производственных процессов нет
таких, которые ничего не тратят, и каждый из n видов продуктов действительно
производится. Условие имеет чисто техническое предназначение.
Число 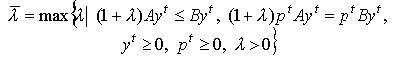
называется максимальным темпом сбалансированного
роста, а число
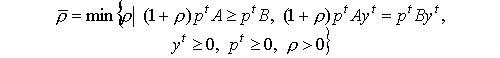
называется минимальной нормой процента.
Оказывается, что в состоянии равновесия числа 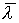 и
и
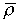 существуют
и равны между собой:
существуют
и равны между собой:
 , (16)
, (16)
если только начальные точки y0 и p0 также
удовлетворяют этому равенству.
Траектория производства 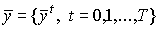 ,
удовлетворяющая условиям (15) при
,
удовлетворяющая условиям (15) при 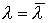 и
и
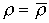 и
соответствующая максимальному сбалансированному росту, т.е.
и
соответствующая максимальному сбалансированному росту, т.е. 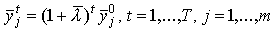 ,
называется траекторией равновесного роста (или траекторией Неймана, или
магистралью). Поскольку эту траекторию можно представить в виде
,
называется траекторией равновесного роста (или траекторией Неймана, или
магистралью). Поскольку эту траекторию можно представить в виде 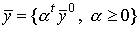 ,
где
,
где 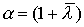 ,
то ее еще называют лучом Неймана а цены (14), соответствующие минимальной норме
процента
,
то ее еще называют лучом Неймана а цены (14), соответствующие минимальной норме
процента 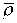 ,
называют неймановскими ценами.
,
называют неймановскими ценами.
магистральный траектория
экономический макросистема
2.3 Методы вычисления теорий магистралей
На основе модели Неймана могут
быть построены различные оптимизационные задачи. Одна из возможных постановок
выглядит так:
при ограничениях
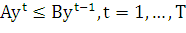 (18)
(18)
В этой задаче требуется найти такую траекторию 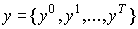 ,
чтобы доход от продажи всего выпуска к концу планового периода был максимальным
при условии, что затраты каждого периода не превышают выпусков предыдущего
периода.
,
чтобы доход от продажи всего выпуска к концу планового периода был максимальным
при условии, что затраты каждого периода не превышают выпусков предыдущего
периода.
Всякую траекторию,
удовлетворяющую условиям и доставляющую максимальное значение целевой функции,
будем называть оптимальной траекторией и обозначать через 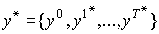 (здесь
(здесь
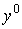 -
установившаяся к началу планового периода интенсивность выпуска). В общем
случае в данной задаче может существовать не одна оптимальная траектория
(Приложение А, А-2).
-
установившаяся к началу планового периода интенсивность выпуска). В общем
случае в данной задаче может существовать не одна оптимальная траектория
(Приложение А, А-2).
Предположим, что в модели
Неймана существует единственная стационарная траектория 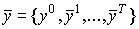 производства,
соответствующая максимальному темпу сбалансированного роста
производства,
соответствующая максимальному темпу сбалансированного роста 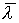 ,
т.е.
,
т.е. 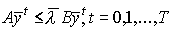
Поскольку 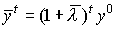 ,
где в любой момент t
,
где в любой момент t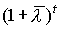 есть скаляр, то
вместо предыдущего неравенства можно писать
есть скаляр, то
вместо предыдущего неравенства можно писать 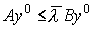 .
Далее, имея в виду представление
.
Далее, имея в виду представление 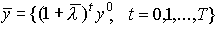 ,
мы условно можем написать
,
мы условно можем написать 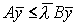 .
.
В дальнейшем нам понадобится
понятие "расстояния" между векторами интенсивностей в пространстве 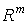 .
Под расстоянием между двумя векторами интенсивностей
.
Под расстоянием между двумя векторами интенсивностей 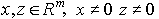 ,
будем понимать число
,
будем понимать число
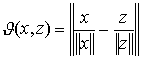 (19)
(19)
где 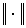 -
норма вектора, т.е. число, равное длине данного вектора. Объясним наглядно
смысл такого расстояния. Для удобства обозначим
-
норма вектора, т.е. число, равное длине данного вектора. Объясним наглядно
смысл такого расстояния. Для удобства обозначим 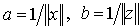 .
Тогда
.
Тогда
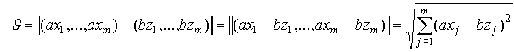 (20)
(20)
Далее, для любого вектора x длина вектора 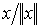 равна
единице. Действительно, так как норма числа есть само число, то
равна
единице. Действительно, так как норма числа есть само число, то
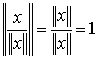
Например, для 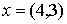 имеем:
имеем:
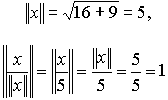 (Приложение Б,
рисунок Б-4)
(Приложение Б,
рисунок Б-4)
Поэтому 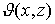 равно
длине отрезка между точками
равно
длине отрезка между точками 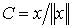 ,
, 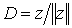 ,
лежащими на единичной окружности. Из этого рисунка видно: 1) если возможно
представление
,
лежащими на единичной окружности. Из этого рисунка видно: 1) если возможно
представление  , где
, где 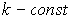 (т.е.
x и z коллинеарные вектора), то
(т.е.
x и z коллинеарные вектора), то 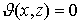 ;
;
) для 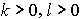 ,
,
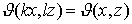 .
.
Нетрудно видеть, что 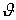 есть
непрерывная по обоим аргументам функция.
есть
непрерывная по обоим аргументам функция.
С помощью введенного понятия
расстояния дадим строгое определение понятия магистрали.
Определение. Луч Неймана 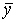 называется
сильной магистралью в задаче (1-2), если для каждого
называется
сильной магистралью в задаче (1-2), если для каждого 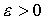 существуют
такие зависящие от
существуют
такие зависящие от 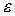 (но не зависящие
от T) числа
(но не зависящие
от T) числа  и
и 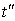 ,
что для всякой оптимальной траектории
,
что для всякой оптимальной траектории 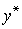 этой
задачи и для всех
этой
задачи и для всех 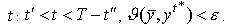 (Приложение А,
А-3).
(Приложение А,
А-3).
Заметим, что ввиду второго
свойства расстояния 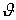 для всех
для всех
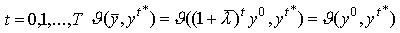
Из определения следует, что
постоянный луч 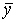 как бы
аппроксимирует оптимальные траектории: всякая оптимальная траектория
как бы
аппроксимирует оптимальные траектории: всякая оптимальная траектория 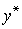 почти
все время идет вдоль луча
почти
все время идет вдоль луча 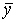 , т.е. она
сохраняет высокий (почти максимальный) темп интенсивностей производственных
процессов, если только величина T горизонта планирования много больше, чем
, т.е. она
сохраняет высокий (почти максимальный) темп интенсивностей производственных
процессов, если только величина T горизонта планирования много больше, чем  и
и
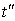 .
.
Приведем для полноты и понятие
слабой магистрали.
Определение. Луч Неймана 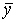 называется
слабой магистралью в задаче (17-18),если для любого
называется
слабой магистралью в задаче (17-18),если для любого 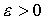 существует
такое (зависящее от
существует
такое (зависящее от 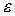 ) число r, что для
любой оптимальной траектории
) число r, что для
любой оптимальной траектории 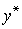 этой задачи
неравенство
этой задачи
неравенство 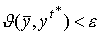 нарушается не более
чем для r моментов t,
нарушается не более
чем для r моментов t, 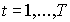 , причем число r не
зависит от длины T планового периода (Приложение А, А-4).
, причем число r не
зависит от длины T планового периода (Приложение А, А-4).
Очевидно, сильная магистраль
является одновременно и слабой магистралью (достаточно положить 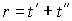 ).
).
Прежде чем сформулировать
теорему о магистрали для задачи (17-18), рассмотрим более простой и частный
случай этой модели - динамический аналог оптимизационной задачи Леонтьева: 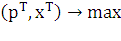 (21)
при ограничениях
(21)
при ограничениях 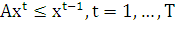 (22)
(22)
где A-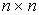 -технологическая матрица,
-технологическая матрица, 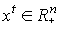 - вектор валового
выпуска в момент t,
- вектор валового
выпуска в момент t, 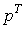 - вектор цен в
момент T.
- вектор цен в
момент T.
В модели Леонтьева равенство 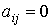 означает,
что отрасль i не нуждается в товарах отрасли j. Вообще говоря, может
существовать целая группа отраслей
означает,
что отрасль i не нуждается в товарах отрасли j. Вообще говоря, может
существовать целая группа отраслей 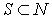 (
(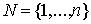 - множество всех отраслей), которые не нуждаются в товарах отраслей из
множества
- множество всех отраслей), которые не нуждаются в товарах отраслей из
множества 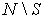 , а для своего
производства обходятся только товарами из группы S. В этом случае говорят, что
множество отраслей S изолировано от остальных в том смысле, что эта группа
отраслей может функционировать отдельно от остальных.
, а для своего
производства обходятся только товарами из группы S. В этом случае говорят, что
множество отраслей S изолировано от остальных в том смысле, что эта группа
отраслей может функционировать отдельно от остальных.
Матрица A называется
неразложимой, если во множестве всех отраслей N нет изолированных подмножеств.
Неразложимость матрицы A означает, что каждая отрасль использует продукцию всех
отраслей (Приложение А, А-5).
Неразложимая матрица A
называется примитивной, если множество N нельзя разбить на непересекающиеся
подмножества 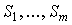 , такие, что если
, такие, что если 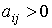 для
для
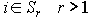 ,
то
,
то 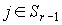 ,
а при
,
а при 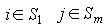 (Приложение
А, А-6).
(Приложение
А, А-6).
Приведем еще несколько
необходимых определений. Собственным вектором матрицы A называется такой
ненулевой вектор 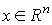 , что
, что 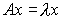 где
где
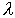 -
некоторый скаляр, называемый собственным числом матрицы A, соответствующим
собственному вектору x. Неотрицательный собственный вектор неотрицательной
неразложимой матрицы A называется вектором Фробениуса матрицы A, а
соответствующее ему собственное число - числом Фробениуса матрицы A (Приложение
А, А-7).
-
некоторый скаляр, называемый собственным числом матрицы A, соответствующим
собственному вектору x. Неотрицательный собственный вектор неотрицательной
неразложимой матрицы A называется вектором Фробениуса матрицы A, а
соответствующее ему собственное число - числом Фробениуса матрицы A (Приложение
А, А-7).
Неразложимая матрица A
называется устойчивой, если для любого x последовательность 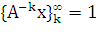 сходится,
где
сходится,
где 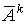 -
k-ая степень матрицы
-
k-ая степень матрицы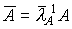 ,
, 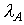 -
число Фробениуса для матрицы A. Предельной точкой этой последовательности при
-
число Фробениуса для матрицы A. Предельной точкой этой последовательности при 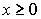 и
и
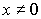 является
вектор
является
вектор 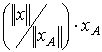 ,
где
,
где 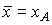 -
вектор Фробениуса для матрицы A (Приложение А, А-8).
-
вектор Фробениуса для матрицы A (Приложение А, А-8).
Примитивная матрица всегда
устойчива.
Относительно задачи (3-4)
сделаем следующие предположения:
1. 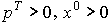 ;
;
2. матрица A
неотрицательна, неразложима и примитивна.
Теорема. Если выполнены условия
1), 2), то сильной магистралью в задаче (21-22) является вектор Фробениуса 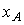 матрицы
A, т.е.
матрицы
A, т.е. 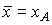 ,
где
,
где 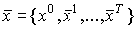 -
стационарная траектория динамической модели Леонтьева (4) (
-
стационарная траектория динамической модели Леонтьева (4) (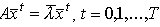 ).
).
Целевая функция в задаче
(21-22) относится к конечному моменту планового периода и называется
терминальной. В динамической оптимизационной задаче Леонтьева с нетерминальной
целевой функцией возникает так называемая проблема горизонта планирования. Дело
в том, что по оптимальной траектории выпуск к моменту T может оказаться
недостаточным для обеспечения нормального функционирования экономики за
горизонтом планирования. Поэтому требуется наложить специальные ограничения
снизу на вектор 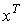 , что приводит к
дополнительным сложностям при исследовании магистральных свойств оптимальных
траекторий.
, что приводит к
дополнительным сложностям при исследовании магистральных свойств оптимальных
траекторий.
Вернемся теперь к задаче
Неймана (17-18) и предположим выполненными следующие условия:
а) существует такое число 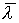 ,
что соотношения
,
что соотношения 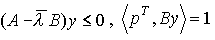 определяют
единственный вектор
определяют
единственный вектор 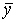 ; б)
; б) 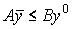 в)
существует стационарная траектория цен
в)
существует стационарная траектория цен 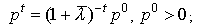 ;
г) матрица A неотрицательна, неразложима и примитивна; д) для любого достаточно
малого числа
;
г) матрица A неотрицательна, неразложима и примитивна; д) для любого достаточно
малого числа  существуют такие
(зависящие от
существуют такие
(зависящие от 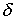 ) числа
) числа 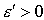 и
и
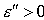 ,
что для оптимальной траектории
,
что для оптимальной траектории 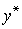 из неравенства
из неравенства 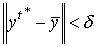 вытекают
неравенства
вытекают
неравенства 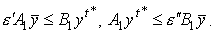
В последнем условии A1
и B1 - это такие подматрицы матриц A и B
(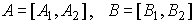 ),
что
),
что 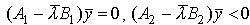 .
.
В отличие от условий а-г,
допускающих соответствующие экономические интерпретации, условие е) носит чисто
технический характер и нужно сугубо для доказательства следующей теоремы.
Теорема. При выполнении условий
а-д для любого 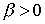 существует такое
число
существует такое
число 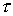 ,
не зависящее от T, что для любой оптимальной траектории
,
не зависящее от T, что для любой оптимальной траектории 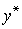 задачи
(17-18) выполняется условие
задачи
(17-18) выполняется условие 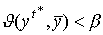 для всех
для всех 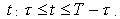
Эта теорема утверждает, что
почти все время все оптимальные траектории 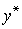 близки
к сильной магистрали
близки
к сильной магистрали 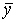 .
.
Важная роль магистральных
траекторий состоит в том, что в случае отсутствия возможности вычисления
оптимальных траекторий при планировании производства можно ориентироваться на
движение по лучу Неймана, т.е. планировать функционирование отраслей с
интенсивностями, близкими к тем, которые задаются стационарной траекторией  .
.
В данной главе нами рассмотрены магистральные
траектории в линейных моделях экономики, ознакомлены с моделью Неймана и
изучены методы использования теории магистрали.
3. ОЦЕНКА ЭКОНОМИЧЕСКОГО РАЗВИТИЯ РЕГИОНА С
ПОЗИЦИИ ТЕОРИИ МАГИСТРАЛЕЙ (НА ПРИМЕРЕ КУРСКОЙ ОБЛАСТИ)
3.1 Формирование магистральной
траектории для региона
Экономика Курской области формировалась и
развивалась под воздействием исторических, геополитических, природно-ресурсных,
инновационных, агроклиматических факторов. С начала образования регион выполнял
политические, административные функции, являлся центром размещения передовой
для своего времени промышленности. Экономика области активно формировалась в XX
веке.
В настоящее время Курская область представляет
собой развитый промышленно-аграрный регион, имеющий макрорегиональное влияние.
В структуре годового выпуска валовой продукции отраслей материального
производства доминируют черная металлургия и электроэнергетика - полюса роста мезоэкономики.
Ведущими отраслями, обеспечивающими основной
объем ВРП Курской области и ВРП Белгородской области, являются: промышленность,
сельское хозяйство, торговля и коммерческая деятельность по реализации товаров
и услуг, строительство, транспорт и связь.
Проанализируем показатели ВРП Курской и
Белгородской областей и сравним, найдем разницу с помощью теории магистрали.
На первом этапе анализируем ВРП по Курской
области за 2006-2010 гг. (Приложение В, Таблица В-3).
На основе данных таблицы В-3 составим график
показателей ВРП по годам.
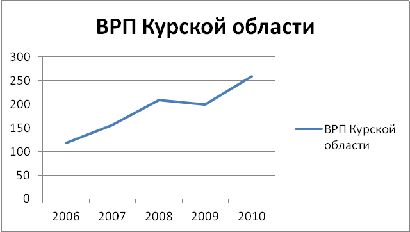
Рисунок 5- График показателей ВРП
Ось Х-ось периода (г.), ось У- ось показателей
ВРП (млрд.руб.). Составим уравнение по данным показателей, добавив линию тренда
(рис.6):
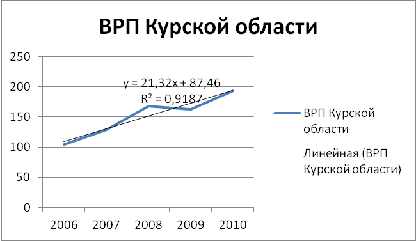
Рисунок 6- График показателей ВРП (с
составленным уравнением)
Показатель множественной корреляции R
в квадрате равен 0,9187,то это означает наличие сильной связи.
На втором этапе анализируем ВРП по Белгородской
области за 2006-2010 гг.(Приложение В, таблица В-4).
На основе данных таблицы В-4 составим график
показателей ВРП по годам.
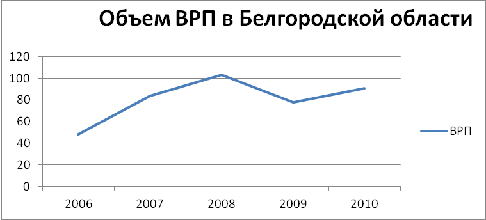
Рисунок 7 - Объем ВРП в Белгородской области
Ось Х-ось периода (г.), ось У - ось показателей
ВРП (млрд. руб.). Составим уравнение по данным показателей, добавив линию
тренда (рис. 9):
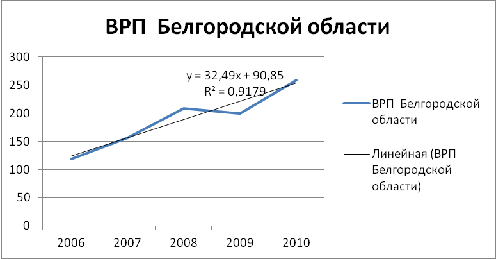
Рисунок 8 - Объем ВРП в Белгородской области (с
составленным уравнением)
Показатель множественной корреляции R
в квадрате равен 0,9179,то это означает наличие сильной связи.
Построим на основе проведенных данных магистраль
развития
Год
P(магистраль)
2010
2 1
ВРП Курской области
2007 ВРП Белгородской области
2006
Млрд.
руб.
0
20
40
60
80
100
120
140 160 180
200
Рисунок 11: P-
магистраль; 1- ВРП Белгородской области; 2- ВРП Курской области
.2 Исследование экономического развития с
использованием векторного метода в теории экономического анализа
В практике анализа финансово-хозяйственной
деятельности организаций используются такие понятия, как «вектор экономического
развития», «вектор инвестиций», «вектор инноваций» и др. При этом конечной
целью анализа является определение направления движения этих векторов,
прогнозирование развития процессов. Но, как правило, в результате анализа
даются лишь качественные характеристики направлений вектора. Например: вектор
экономического развития (ВЭР) направлен в сторону повышения фонда оплаты труда;
роста реальных инвестиций; ВЭР имеет направление в сторону роста инвестиций и
инноваций и т.д.
При таких выводах не предусматривается
количественной оценки того или иного вектора развития в его полном
представлении [5, c. 39].
Существуют задачи и модели, в которых
прогнозирование развития процесса не представляет трудностей. Например, когда
можно применить горизонтальный и вертикальный анализ системы показателей,
полностью определенной по показателям в виде элементарной суперпозиции. К.
анализу такой системы можно отнести, например, анализ бухгалтерского баланса, в
котором арифметическая сумма значений строк составляет полный итоговый
результат. В этом случае с позиции векторного анализа модель системы полностью
определена в одномерном пространстве. Задача определения влияния факторов на
результат и наиболее вероятных направлений развития организации, отображаемых в
виде составляющих итога баланса, не считается сложной [5, c.
40].
Пример 1. Выполним анализ вектора
магистрали по данным ВРП Курской области и ВРП Белгородской области. В качестве
основного математического аппарата исследований используем элементы теории
векторной алгебры, где для описания любого вектора 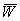 в
многомерном евклидовом векторном пространстве n параметров
используются следующие количественные характеристики и параметры: длина вектора
L, его
проекции Пi на оси координат хi и углы
направлений αi между
вектором
в
многомерном евклидовом векторном пространстве n параметров
используются следующие количественные характеристики и параметры: длина вектора
L, его
проекции Пi на оси координат хi и углы
направлений αi между
вектором 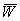 и его
проекциями на соответствующие оси ортогональной (взаимно перпендикулярной)
системы координат.
и его
проекциями на соответствующие оси ортогональной (взаимно перпендикулярной)
системы координат.
Параметры модели для количественной
оценки параметров любого вектора, в том числе и экономического развития, можно
представить в следующем виде.
Длина L вектора (на
основании теоремы Пифагора в евклидовом пространстве):
L = [(П1)2
+ (П2)2+...+ (Пn)2]1/2
(23)
Значения косинусов углов αi между
проекциями Пi на оси координат вектора 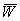 можно
представить в виде:
можно
представить в виде:
cos αi = Пi /L, (24)
отсюда
αi
=arcos Пi
/L, (25)
α0 = 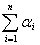 (26)
(26)
где а0 - результирующий
угол, сумма углов направлений αi [5,c.41].
Соотношения (23) - (26) необходимы
для выявления определенного эталонного значения вектора, относительно которого
можно оценивать изменение вектора развития в дальнейшем.
Рассмотрим ситуацию, когда все
значения параметров Пi равны между
собой. Тогда L = 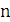
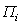 α1 = α2 =...= αi =… αn - все углы
равны («золотая середина», биссектрисные углы).
α1 = α2 =...= αi =… αn - все углы
равны («золотая середина», биссектрисные углы).
В этом случае направление вектора 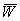 формируется
в равной степени всеми его составляющими, а длина вектора - минимальная.
Например, длина вектора в прямоугольной (ортогональной) системе координат,
когда вектор
формируется
в равной степени всеми его составляющими, а длина вектора - минимальная.
Например, длина вектора в прямоугольной (ортогональной) системе координат,
когда вектор 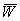 направлен
под углом 45о к осям координат (под углом биссектрисы). Тогда
направлен
под углом 45о к осям координат (под углом биссектрисы). Тогда
L = 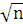 Пi =
Пi = 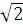 Пi [5,c.41].
Пi [5,c.41].
Значения биссектрисных углов αi в случае
равнонаправленности угловых составляющих вектора 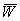 по отношению к осям координат и,
соответственно, равенства параметров Пi
определяются с учетом формулы (25):
по отношению к осям координат и,
соответственно, равенства параметров Пi
определяются с учетом формулы (25):
αi
=arcos 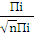 = arcos
= arcos 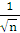 . (26)
. (26)
угол главной биссектрисы (сумма биссектрисных
углов):
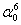 =
= 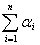 = n αi
=
n arcos
= n αi
=
n arcos 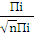 = n arcos
= n arcos 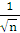 .
.
В случае, когда α1 = α2 =...= αi =… αn вектор 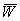 будет
направлен по главному биссектрисному углу.
будет
направлен по главному биссектрисному углу.
Из формул (23) - (25) следует, что
изменение величины любой составляющей проекции вектора на ось координат -
приводит к изменению как длины L самого вектора 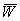 , так и его
направления в многомерном пространстве координат-параметров. При этом величины
остальных проекций на оси координат также изменяются.
, так и его
направления в многомерном пространстве координат-параметров. При этом величины
остальных проекций на оси координат также изменяются.
В задачах анализа направления
развития экономических процессов приходится учитывать определенные особенности.
Во-первых, факторы (параметры), определяющие направление развития
экономического процесса, могут быть взаимосвязаны. Во-вторых, иногда невозможно
разделить влияние действующих факторов, которые не поддаются объединению в
одной модели. Поэтому при анализе изменения направления вектора экономического
развития необходимо выбирать соответствующий инструмент измерения для оценки
степени влияния факторов на формирование направления вектора с использованием
его угловых и координатных параметров.
С помощью рисунка 11 найдем вектор Р
этап- Опустим перпендикуляры от ВРП Курской и
ВРП Белгородской областях.. Чтобы ВРП Курской области достигла ВРП Белгородской
области нужно изменить угол наклона;
этап - С помощью теоремы Пифагора найдем прямые
ВРП Курской области и ВРП Белгородской области.
Год
2этап P(магистраль)
2010 2 1этап 1
2009 ВРП Курской области
ВРП Белгородской области
2006
Млрд.руб.
0
20
40
60
80
100
120
140
16
0
180
200
Рисунок 12: P-
магистраль; 1- ВРП Белгородской области; 2- ВРП Курской области.
Прямая ВРП Белгородской области (1) равна194,04
млрд.руб.; прямая ВРП Курской области (2) равна 269,03 млрд.руб. Для того,
чтобы выйти на магистраль развития Курской области, необходимо увеличит ВРП
Курской области на 74,99 млрд.руб.. Для увеличения ВРП Курской области,
необходимо увеличить инвестиции Курской области.
Таблица
5
Инвестиции Белгородской области
|
Х-Года
|
2006
|
2007
|
2008
|
2009
|
2010
|
|
У
- млрд. руб.
|
48,4
|
83,4
|
103,3
|
78
|
90,9
|
Таблица
6
Инвестиции в Курской области
|
Годы
|
2006
|
2007
|
2008
|
2009
|
2010
|
39,11
|
56,47
|
78,99
|
84,28
|
86,7
|
Таким образом, теоремы о магистрали описывают
свойства инвариантности оптимальных траекторий экстремальных динамических задач
по отношению к назначению целевого функционала с и к выбору самой оптимальной
траектории.
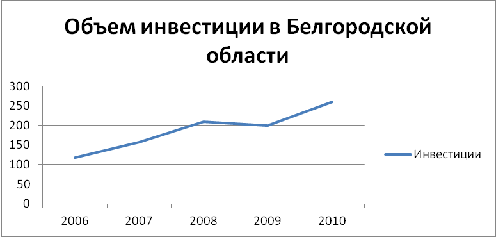
Рисунок 9-Объем инвестиций в Белгородской
области
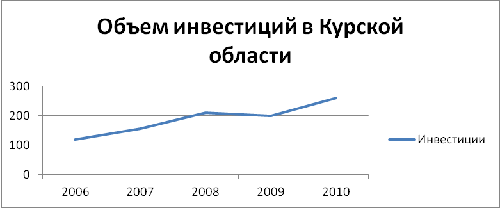
Рисунок 10- Объем инвестиций в Курской области
.3 Определение перспективных направлений
развития региона экономических макросистем на магистральный путь развития
Впервые П. Самуэлсон предложил именовать
магистралью всякую сбалансированную траекторию с максимальным темпом роста. В
связи с этим возникла бытовая трактовка достижения экономических целей
оптимальным образом. А именно: для того, чтобы оптимальным путем «добраться» из
начального пункта X0 в конечный пункт Xk следует быстрее выбраться на
магистраль (улучшенную дорогу для скоростного движения), «двигаться» по ней
возможно дольше и лишь в конце свернуть в пункт назначения.
Естественно, что перевод экономической системы
на магистральные темпы развития так же, как и переход к заданной цели, требует
внешних усилий в виде инвестиционных вложений, причем возможно не разовых, а
распределенных во времени. Для сложных многосекторных экономических систем от
инвестора требуется еще и знание, в каких пропорциях инвестиции должны быть
распределены в подсистемах или отраслях. Ответы на такие вопросы можно
получить, рассматривая управление экономическими системами с позиций, развитых
в теории оптимального управления и вариационного исчисления, теории систем и
системного анализа.
Любое управление предполагает наличие объекта
управления (управляемой системы), субъекта управления (управляющей системы) и
внешней среды. Основное назначение управляющей системы - поддерживать
установленный и по каким-либо свойствам признанный нормальным режим работы
объекта управления, а также обеспечивать нормальное функционирование отдельных
элементов объекта управления в условиях воздействия внешней среды. Объект
управления во взаимодействии с управляющей системой образует замкнутую систему
управления. Связь, с помощью которой управляющая система воздействует на объект
управления, называется обратной связью. В теории автоматического регулирования
функцию управления называют программой управления.
В экономических задачах программа управления
соответствует принятию решения на перспективу. Синтез оптимальных управлений в
случае отклонения состояния системы от планового значения дает оптимальное
решение и при новом ее состоянии. Изложенная ниже методика синтеза оптимальных
управлений позволяет выводить динамические макросистемы на магистральные темпы
функционирования.
Имеем две динамические макросистемы, одну из
которых будим называть развивающейся,
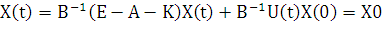 (27)
(27)
а вторую эталонной системой следующего вида:
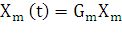 (t),
(t), 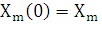 0
(28)
0
(28)
здесь X(t) и Xm(t) - уровень валового
внутреннего продукта развивающейся и магистральной системы; А - матрица прямых
материальных затрат; В - матрица приростных фондоемкостей; К - матрица
конечного потребления; Е - единичная матрица U(t) - внешнее инвестиционное
воздействие; Gm -матрица замкнутой магистральной системы.
Системы дифференциальных уравнений (27) и (28)
записаны в нормальной форме Коши и представляют собой балансовые модели
макроэкономических систем В.В. Леонтьева. Моделирование и анализ динамических
свойств таких систем, основанный на контроле за расположением собственных чисел
на комплексной плоскости, был проведен Е.Л. Торопцевым.
Особенности развития макроэкономики России
отражаются в системе национальных счетов (СНС). Неотъемлемой частью СНС
являются таблицы «Затраты-выпуск», которые содержат подробные характеристики
производства и использования товаров и услуг, а также доходов, формирующихся в
процессе производства. Симметричная таблица «Затраты-выпуск», более известная
среди российских пользователей статической информации как межотраслевой баланс
производства и распределения товаров и услуг, устанавливает производственные
связи типа «отрасль-отрасль». В таблицах собрана информация по 22-м отраслям.
К сожалению, экономические параметры,
предоставляемые ежегодным статистическим сборником, можно использовать только в
статических моделях; данная работа посвящена изучению динамических моделей. В
качестве примера будут рассмотрены малоразмерные трехотраслевые модели
макросистем, которые получены путем агрегирования. В качестве статических
параметров для этих систем (матрицы A
и K) использовались
данные симметричной таблицы «Затраты-выпуск». Параметры системы, отвечающие за
динамические характеристики модели (матрица В), а также начальные условия (X0
и Xm0), подобраны на
основе проведения множественных имитационных вычислений таким образом, чтобы
была возможность наглядной демонстрации переходных процессов, возникающих в
макросистемах с инвестиционнымвоздействием. Экономические параметры моделей
представлены в таблице.
На таб.7 представлены результаты интегрирования
систем (27) и (28). Магистральное развитие эталонной системы (28) отражено на
графике тонкими линиями. В этой системе на всем временном интервале соблюдаются
оптимальные пропорции развития, что приводит к постоянному росту валового
внутреннего продукта (ВВП). Для развивающейся системы (27) внешнее
инвестиционное воздействие U(t)=0,
следствием чего является не оптимальный и не сбалансированный план формирования
валовых выпусков, приводящий к угасанию одной из отраслей с течением времени.
Таблица
7
Экономические параметры динамической модели
развивающейся системы
|
Прямые
затраты (A)
|
Конечное
потребление
(K)
|
Приростные
фондоемкости
(B)
|
Матрица
замкнутой эталонной системы (Gm)
|
|
0,
08
|
0.03
|
0.06
|
00.21
|
0
|
0
|
0.31
|
00.4
|
0.67
|
-2.48
|
10.18
|
1.52
|
|
00.12
|
0.23
|
0.01
|
0
|
0.18
|
0
|
0.5
|
00.32
|
0.54
|
10.7
|
-1.81
|
1.3
|
|
00.02
|
0
|
0.09
|
0
|
0
|
0.16
|
0.48
|
00.6
|
0.2
|
10.22
|
10.04
|
-2.33
|
Развивающаяся система не в состоянии
самостоятельно перераспределить пропорции ВВП оптимальным образом, поэтому в
модели предусмотрена внешняя инвестиционная составляющая U(t), пока неизвестная,
но благодаря которой должен получиться результат совмещения ВВП развивающейся и
эталонной системы. Из этого следует, что разность
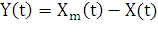 (29)
(29)
стремиться к нулю при t=f, т. е. Y(f)=0. Для
практических целей необходимо синтезировать такое внешнее управление U(t),
которое бы за конечное время 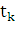 приводило разность
Y(
приводило разность
Y(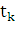 )
к нулю. При этом, начиная со времени
)
к нулю. При этом, начиная со времени 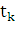 ,
уровень ВВП развивающейся системы должен совпадать с уровнем эталонной системы.
,
уровень ВВП развивающейся системы должен совпадать с уровнем эталонной системы.
В данной главе мы изучили формирование
магистральной траектории для региона, исследовали экономическое развитие с
использованием векторного метода в теории экономического анализа, определили
перспективные направления развития региона экономических макросистем на
магистральном пути развития.
Таким образом, в первой главе нами были изучены
исторические факты о зарождении теории магистрали, по которым можно сделать
вывод, что главным основоположником теории магистрали является Джон фон Нейман,
американский математик, выходец из Венгрии, который разработал он в первой
половине XX в.. Магистраль - основное понятие математической теории
равномерного пропорционального роста экономики, основы которой были заложены
американским математиком Дж. Фон Нейманом. Это траектория (путь) развития, при
которой теоретически за длительное время достигается максимальная скорость
роста экономики (другие названия - неймановская траектория, траектория
максимального сбалансированного роста, стационарная оптимальная траектория).
Также можем отметить, что магистральным свойством могут обладать не только
оптимальные траектории производственных выпусков, но и оптимальные траектории
цен, двойственных моделей. Существуют несколько видов теории в магистрали:
слабая, сильная и сильнейшая теоремы теории магистрали. Нами были сделаны
выводы, что в слабых теоремах отмечено, что оптимальные траектории могут
отклоняться от магистрали. Теоремы о магистрали в сильной форме утверждают, что
отклонение от магистрали может приходиться только на начальном и конечном
участках оптимальной траектории. Теоремы о магистрали в сильнейшей форме
говорят, что большую часть времени оптимальные траектории находятся на
магистрали.
Во второй главе нами были приведены методы
использования и вычисления в экономике теории магистрали и модель Неймана. Из
метод вычисления теории магистрали можно сделать вывод, что магистраль - это
траектория или луч максимального сбалансированного роста. Ее часто сравнивают
со скоростной автострадой. Так, например, для того чтобы добраться из Кемерово
в Киселевск как можно быстрее, наиболее целесообразно сначала проехать по
автостраде Кемерово-Новокузнецк, а затем уже съехать на ответвляющуюся от нее
дорогу в районе Киселевска. Так мы потеряем на дорогу меньше времени и доедем
до конечного пункта с большим комфортом, чем, если бы мы ехали по обычному
шоссе через Ленинск-Кузнецкий и Белово. С помощью методов, нами был получен
результат, что для достижения любой конечной цели следует поступать таким
образом: сначала вывести производство на магистральный путь, т.е. на траекторию
(или луч) Неймана, характеризующуюся максимальным темпом роста и минимальной
нормой процента, а по истечении определенного срока времени вывести ее к
задуманной цели. Такими целями могут быть максимизация прибыли, минимизация
затрат, максимизация полезности от потребления товаров, достижение
конкурентного равновесия при наиболее благоприятных условиях, т.е. на более
высоком уровне благосостояния населения, и т.д.
В третьей главе нами был произведен расчет по
векторному методу. Нами была поставлена цель, каким образом должен ВРП Курской
области достичь такого же уровня, как ВРП в Белгородской области. В итоге нами
был получен результат, для того, чтобы достичь ВРП Курской области ВРП
Белгородской области необходимо увеличить производство, а для увеличения
производства нужны дополнительные инвестиции.
Подводя итог данной курсовой работе необходимо
отметить значение экономики и математики. Экономика еще со средних веков
пользуется разнообразными количественными характеристиками и потому вобрала в
себя большое число математических методов. Сегодня в экономической науке на
первый план выступает экономические модели как инструмент исследования и прогноза
экономических явлений. Модели развивают наши представления о закономерностях
экономических процессов и способствуют формированию образа мышления и анализа
на новом, более высоком уровне. В последнее время для обозначения специфичности
моделей, применяемых в экономике, употребляют термин «экономико-математическое
моделирование». И это не случайно, поскольку экономическая теория давно уже
использует элементы математики в своих выводах. Более того, настоятельность
решения актуальных экономических проблем часто инициирует и развитие
математического аппарата.
Использование математических методов и моделей
актуально как на уровне деятельности фирмы в условиях рынка, так и в
макроэкономике - на уровне планирования и анализа аспектов экономической
деятельности региона и страны. Сегодня, в условиях глобализации мировой
экономики и становления общества нового типа - информационного общества -
математические модели становятся мощным инструментом прогнозов эволюции
цивилизации на нашей планете, что позволяет определять оптимальные магистрали
развития экономики.
В математической экономике магистралью
называется траектория экономического роста, на которой пропорции
производственных показателей (такие как темп роста производства, темп снижения
цен) неизменны, а сами показатели (такие как интенсивность производства,
валовой выпуск) растут с постоянным максимально возможным темпом. Таким
образом, магистраль - это траектория или луч максимального сбалансированного
роста.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Агапова,
Т.А. Макроэкономика [Текст]: учебник.4-е изд./ Серегина, С.Ф. под общ. Ред.
А.В. Сидоровича. М.: МГУ, Издательство «Дело и сервис», 2007. - 447 с.
2. Байнев,
В.Ф. Экономика региона [Текст]: учеб. пособие для вузов / В.Ф. Байнев, С.А.
Пелих; под общ. ред. С.А. Пелиха. Мн.: ИВЦ Минфина, 2011. 269 с.
. Вечканова,
Г.Р., Микроэкономика. [Текст] 8-е изд./ Вечканов Г.С. - СПб.: Питер, 2010. -
208 с.
. Гавриленков
Е. Российская экономика [Текст]: перспектива макроэкономической политики //
Вопросы экономики. - 2004. - №4. - С.21-35.
. Ершов,
М.К. «Экономический рост: новые проблемы и новые риски» [ Электронный ресурс]
// Ершов М.К.,Вопросы экономики.- 2008. - №12. - С. 32-40.
. Зубкова,
А.Г. Стратегическое планирование: концепции, методы [Текст]: Учебное пособие. -
М.: Изд-во МЭИ, 2005. - 238 с.
. Курс
экономики: Учебник / Под редакцией Б.А. Райзберга.- М.: Высшая школа, 2010. -
С. 226.
. Макконнелл,
К.Р. Экономикс: принципы, проблемы и политика [Текст]: учебник для эк. вузов. В
2 т.; под общ. ред. К.Р. Макконнелл, С.Л. Брю. пер. с англ. - М.: ИНФРА-М,
2007. - 387 с.
. Максимова
В.Ф. Микроэкономика. М. [Текст]: ЕАОИ, 2009. - 204 с.Региональная экономика
России: Учебник / Под ред. Т.Г. Морозовой. - М.: ЮНИТИ-ДАНА, 2002. - 472 с.
. Российский
статистический ежегодник: 2010: Стат. сб. / Росстат. М., 2011. 434с.
. Россия
в цифрах: 2011: Крат. стат. сб. / Росстат. М., 2011. 300 с.
. Фетисов,
Г.Г., Региональная экономика и управление [Текст]: учебное пособие / Орешкин
В.П.- М.: ИНФРА-М, 2008. - 416 с.
. Шумпетер,А.О.
Теория экономического развития. М. [Текст]: Норма, 2006. - 397 с.
. Экономическая
теория. [Текст]: учебное пособие / Под ред. Николаевой И.П. 2-е изд., перераб.
и доп. - М.: Юнити-Дана, 2008. - 527 с.
. Экономическая
теория. Конспект лекций. Васильева Е.В., Макеева Т.В. М.: Юрайт, 2009. - 192 с.
. Экономический
обзор. Развитие российской экономики в 2009 г. [Текст] // ЭКО. - 2010. - №2. -
С. 30-36.
. Яковец
Ю.В. Стратегия научно-технологического прорыва. [Текст]:
Норма,M. 2007. - 410
с.
18. Словарь
по экономике и финансам. Режим доступа:
<http://slovari.yandex.ru/dict/glossary>
. Федеральная
служба государственной статистики. Режим доступа: http://www.gks.ru/