Постановка задачі оптимізації
Вступ
оптимізація класичний
максимум
Оптимізація в широкому розумінні
застосовується в науці, техніці і в будь-якій іншій галузі людської діяльності.
Оптимізація -це цілеспрямована діяльність, що полягає в здобутті найкращих
результатів за відповідних умов. Пошуки оптимальних рішень привели до створення
спеціальних математичних методів і вже у XVIII столітті були закладені
математичні основи оптимізації (варіаційне числення, чисельні методи та
ін.).Проте до другої половини XX століття методи оптимізації в багатьох галузях
науки і техніки застосовувалися рідко, оскільки практичне використання
математичних методів оптимізації вимагало величезної обчислювальної роботи, яку
без ЕОМ реалізувати було важко, а у ряді випадків - неможливо. Особливо великі
труднощі виникали при вирішенні завдань оптимізації процесів в хімічній
технології із-за великого числа параметрів і їх складного взаємозв'язку між
собою[1].
На сьогоднішній день за наявності
ЕОМ це завдання помітно спрощується. Сучасні хімічні підприємства використовують
різноманітні методи оптимізації для пошуку оптимальних значень параметрів. Це є
одним з важливих завдань, що вирішуються при створенні нових технічних систем,
управлінні виробництвом або технологічними процесами [2].
Постановка задачі
оптимізації
Оптимізація - це цілеспрямована
діяльність, що полягає в здобутті найкращих результатів за відповідних умов[3].
Постановка задачі оптимізації
передбачає:
.Наявність об'єкту та мети
оптимізації. Формулювання кожної задачі оптимізації повинне вимагати екстремального
значення лише однієї величини, тобто одночасно системі не повинно приписуватися
два і більше критерії оптимізації, оскільки практично завжди екстремум одного
критерію не відповідає екстремуму іншого.
Типовим прикладом неправильної
постановки задачі оптимізації є отримання максимальної продуктивності при
мінімальній собівартості. Помилка полягає в тому, що ставиться завдання пошуку
оптимуму двох величин, що по суті перечать одна одній.
Правильна постановка задачі
наступна:
а) отримати максимальну
продуктивність при заданій собівартості;
б) отримати мінімальну собівартість
при заданій продуктивності.
У першому випадку критерій
оптимізації - продуктивність, а в другому - собівартість.
. Наявність ресурсів оптимізації,
під якими розуміють можливість вибору значень деяких параметрів об'єкту, що
оптимізується. Об'єкт повинен володіти певними мірами свободи - діями, що
управляють.
. Можливість кількісної оцінки
величини, що оптимізується, оскільки лише в цьому випадку можна порівнювати
ефекти від вибору тих або інших дій, що управляють.
. Облік обмежень.
Величина, що зазвичай оптимізується,
пов'язана з економічністю роботи даного об'єкту (апарат, цех, завод ). Варіант
роботи об'єкту, що оптимізується, повинен оцінюватися кількісною мірою -
критерієм оптимальності.
Критерієм оптимальності називається
кількісна оцінка якості об'єкту, що оптимізується. На підставі вибраного
критерію оптимальності складається цільова функція, що є залежністю критерію
оптимальності від параметрів, що впливають на її значення. Вигляд критерію
оптимальності або цільової функції визначається конкретним завданням
оптимізації.
Таким чином, завдання оптимізації
зводиться до знаходження екстремуму цільової функції. Найбільш загальною
постановкою оптимального завдання є вираження критерію оптимальності у вигляді
економічної оцінки (продуктивність, собівартість продукції, прибуток,
рентабельність). Проте в окремих випадках, коли об'єкт є частиною
технологічного процесу, не завжди вдається виділяти прямий економічний
показник, який би повністю характеризував ефективність роботи даного об'єкту. У
таких випадках критерієм оптимальності може служити технологічна
характеристика, що побічно оцінює економічність роботи агрегату (час контакту,
вихід продукту, міра перетворення, температура). Наприклад,встановлюється
оптимальний температурний профіль, тривалість циклу - «реакція - регенерація».
Але у будь-якому випадку критерій оптимальності має економічну природу,
кількісну оцінку і відображає найбільш істотні сторони процесу.
У тому випадку, коли випадкові
обурення невеликі і їх дію на об'єкт можна не враховувати, критерій
оптимальності може бути представлений як функція вхідних, вихідних параметрів і
таких, що управляють.
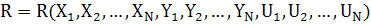 (1.1)
(1.1)
Оскільки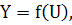 то
при фіксованих
то
при фіксованих 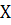 можна записати:
можна записати:
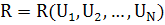 (1.2)
(1.2)
При цьому зміна значень параметрів,
що управляють, двояко позначається на величині :
:
прямо, оскільки параметри, що
управляють безпосередньо входять у вираження критерію оптимізації;
побічно - через зміну вихідних
параметрів процесу, які залежаться від керівників.
Як правило, для конкретних завдань
оптимізації хімічних виробництв критерій оптимальності не може бути записаний у
вигляді аналітичного вираження. Для оптимізації замість математичної моделі
можна використовувати і сам об'єкт, проте оптимізація дослідним шляхом має ряд
істотних недоліків:
а) необхідний реальний об'єкт;
б) необхідно змінювати технологічний
режим в значних межах, що не завжди можливо;
в) тривалість випробувань і
складність обробки даних. Наявність математичної моделі (за умови, що вона
досить надійно описує процес) дозволяє значно простіше вирішити завдання
оптимізації аналітичним або обчислювальним методами[1].
Характеристика методів вирішення
завдань оптимізації
При вирішенні конкретної задачі
оптимізації дослідник перш за все повинен вибрати математичний метод, який
приводив би до кінцевих результатів з найменшими витратами на обчислення або ж
давав можливість отримати найбільший об'єм інформації про майбутнє рішення.
Вибір того або іншого методу в значній мірі визначається постановкою
оптимальної задачі, а також математичною моделлю, яка використовується для
оптимізації об'єкту.
В даний час для вирішення
оптимальних завдань застосовують в основному наступні методи: 1) методи
дослідження функцій класичного аналізу; 2) методи, засновані на використанні невизначених
множників Лагранжа; 3) варіаційне числення; 4) динамічне програмування; 5)
принцип максимуму; 6) лінійне програмування; 7) нелінійне програмування.
Як правило, не можна рекомендувати
який-небудь один метод, який можна використовувати для вирішення всіх без
виключення задач, що виникають на практиці. Одні методи в цьому відношенні є
загальнішими, інші - менш загальними. Цілу групу методів (методи дослідження
функцій класичного аналізу. метод множників Лагранжа, нелінійне програмування)
на певних етапах рішення оптимальної задачі можна застосовувати у поєднанні з
іншими методами, наприклад динамічним програмуванням і принципом максимуму.
Деякі методи спеціально розроблені
або найкраще підходять для вирішення оптимальних завдань з математичними моделями
певного вигляду. Так, математичний апарат лінійного програмування спеціально
створений для вирішення завдань з лінійними критеріями оптимальності і
лінійними обмеженнями на змінні і дозволяє вирішувати більшість завдань,
сформульованих в такій постановці.
Динамічне програмування ідеально
пристосоване для вирішення завдань оптимізації багатостадійних процесів,
особливо завдань, в яких на кожній стадії є невелике число змінних.
Методи дослідження функцій
класичного аналізу
Методи дослідження функцій класичного
аналізує найбільш відомими методами вирішення нескладних оптимальних завдань
які відомі з курсу математичного аналізу. Звичайною областю використання даних
методів є завдання з відомим аналітичним вираженням критерію оптимальності, що
дозволяє знайти не дуже складне, також аналітичне вираження для похідних.
Отримані прирівнюванням до нуля похідні рівняння, що визначають екстремальні
рішення оптимальної задачі, украй рідко удається вирішити аналітичним шляхом,
тому, як, правило, застосовують обчислювальні машини. При цьому треба вирішити
систему кінцевих рівнянь, найчастіше нелінійних, для чого доводиться
використовувати чисельні методи, аналогічні методам нелінійного програмування.
Додаткові труднощі при рішенні
оптимальної задачі методами дослідження функцій класичного аналізу виникають
унаслідок того, що система рівнянь, що отримується в результаті їх
використання, забезпечує лише необхідні умови оптимальності. Тому всі рішення
даної системи (а їх може бути і декілька) мають бути перевірені на достатність.
В результаті такої перевірки спочатку відкидають рішення, які не визначають
екстремальні значення критерію оптимальності, а потім серед екстремальних
рішень, що залишаються, вибирають рішення, що задовольняє умову оптимального
завдання, тобто найбільшому або найменшому значенню критерію оптимальності
залежно від постановки задачі.
Методи дослідження за наявності
обмежень на область зміни незалежних змінних можна використовувати лише для
пошуку екстремальних значень усередині вказаної області. Особливо це
відноситься до задач з великим числом незалежних змінних (практично більше
двох), в яких аналіз значень критерію оптимальності на границі допустимої
області зміни змінних стає досить складним.
Метод множників Лагранжа
Метод множників Лагранжа застосовують
для вирішення задач такого ж класу складності, як і при використанні звичайних
методів дослідження функцій, але за наявності обмежень типу рівності на
незалежні змінні.
В основному при використанні методу
множників Лагранжа доводиться вирішувати ті ж задачі, що і без обмежень. Деяке
ускладнення в даному випадку виникає лише від введення додаткових невизначених
множників, внаслідок чого порядок системи рівнянь, що вирішується для
знаходження екстремумів критерію оптимальності, відповідно підвищується на
число обмежень. В останньому, процедура пошуку рішень і перевірки їх на
оптимальність відповідає процедурі вирішення завдань без обмежень.
Множники Лагранжа можна
застосовувати для вирішення задач оптимізації об'єктів на основі рівнянь з
частковими похідними і завдань динамічної оптимізації. При цьому замість
вирішення системи кінцевих рівнянь для відшукання оптимуму необхідно
інтегрувати систему диференціальних рівнянь.
Також множники Лагранжа
використовують як допоміжний засіб і при вирішенні спеціальними методами задач
інших класів з обмеженнями типу рівності, наприклад, у варіаційному численні і
динамічному програмуванні. Особливо ефективне вживання множників Лагранжа в
методі динамічного програмування, де з їх допомогою інколи удається понизити розмірність
вирішуваної задачі.
Методи варіаційного числення
Даний метод зазвичай використовують
для вирішення задач, в яких критерії оптимальності представляються у вигляді
функціоналів і вирішеннями яких служать невідомі функції. Такі завдання
виникають зазвичай при статичній оптимізації процесів з розподіленими
параметрами або в завданнях динамічної оптимізації.
Варіаційні методи дозволяють в цьому
випадку звести рішення оптимальної задачі до інтеграції системи диференціальних
рівнянь Ейлера, кожне з яких є нелінійним диференціальним рівнянням другого
порядку з граничними умовами, заданими на обох кінцях інтервалу інтеграції.
Число рівнянь вказаної системи при цьому дорівнює числу невідомих функцій, які
визначаються при рішенні оптимальної задачі. Кожну функцію знаходять в
результаті інтеграції отримуваної системи.
Рівняння Ейлера виводяться як
необхідні умови екстремуму функціонала. Тому отримані інтеграцією системи
диференціальних рівнянь функції мають бути перевірені на екстремум функціонала.
За наявності обмежень типу рівності,
що має вигляд функціоналів, застосовують множники Лагранжа, що дає можливість
перейти від умовної задачі до безумовної. Найбільш значні труднощі при
використанні варіаційних методів виникають в разі вирішення задач з обмеженнями
типу нерівностей.
Динамічне програмування
Динамічне програмування служить
ефективним методом вирішення задач оптимізації дискретних багатостадійних
процесів, для яких критерій оптимальності задається як адитивна функція
критеріїв оптимальності окремих стадій. Вказаний метод можна розповсюдити і на
випадок, коли критерій оптимальності заданий в іншій формі, проте при цьому
зазвичай збільшується розмірність окремих стадій.
По суті методом динамічного
програмування є алгоритм визначення оптимальної стратегії управління на всіх
стадіях процесу. При цьому закон управління на кожній стадії знаходять шляхом
вирішення окремих завдань оптимізації послідовно для всіх стадій процесу за
допомогою методів дослідження функцій класичного аналізу або методів
нелінійного програмування. Результати рішення зазвичай не можуть бути виражені
в аналітичній формі, а виходять у вигляді таблиць.
Обмеження на змінні задач не надають
впливу на загальний алгоритм рішення, а враховуються при вирішенні окремих
завдань оптимізації на кожній стадії процесу. За наявності обмежень типу
рівності інколи навіть вдається понизити розмірність цих завдань за рахунок
використання множників Лагранжа. Використання методу динамічного програмування
для оптимізації процесів з розподіленими параметрами або в задачах динамічної
оптимізації приводить до вирішення диференціальних рівнянь в часткових
похідних. Замість вирішення таких рівнянь значно простіше представити
безперервний процес як дискретний з чималим числом стадій. Подібний прийом
виправданий особливо в тих випадках, коли є обмеження на змінні задачі і пряме
вирішення диференціальних рівнянь ускладнюється необхідністю обліку вказаних
обмежень.
При вирішенні задач методом
динамічного програмування, як правило, використовують обчислювальні машини, що володіють
достатнім об'ємом пам'яті для зберігання проміжних результатів рішення, які
зазвичай виходять в табличній формі.
Принцип максимуму
Даний принцип застосовують для
вирішення задач оптимізації процесів, які описуються системами диференційних
рівнянь. Перевагою математичного апарату принципу максимуму є те, що рішення
може визначатися у вигляді розривних функцій; це властиво багатьом задача
оптимізації, наприклад задачам оптимального управління об'єктами, які
описуються лінійними диференційними рівняннями.
Знаходження оптимального рішення при
використанні принципу максимуму зводиться до задачі інтеграції системи
диференційних рівнянь процесу і зв'язаної системи для допоміжних функцій за
граничних умов, заданих на обох кінцях інтервалу інтеграції, тобто до рішення
краєвої задачі. На область зміни змінних можуть бути накладені обмеження.
Систему диференційних рівнянь інтегрують, застосовуючи звичайні програми на
цифрових обчислювальних машинах.
Принцип максимуму для процесів, що
описуються диференційними рівняннями, при деяких припущеннях є достатньою
умовою оптимальності. Тому додаткової перевірки на оптимум отримуваних рішень
зазвичай не вимагається.
Для дискретних процесів принцип
максимуму в тому ж формулюванні, що і для безперервних - несправедливий. Проте
умови оптимальності, що отримуються при його вживанні для багатостадійних
процесів, дозволяють знайти досить зручні алгоритми оптимізації.
Лінійне програмування
Лінійним програмуванням є
математичний апарат, розроблений для вирішення оптимальних задач з лінійними
виразами для критерію оптимальності і лінійними обмеженнями на область зміни
змінних. Такі задачі зазвичай зустрічаються при вирішенні питань оптимального
планування виробництва з обмеженою кількістю ресурсів, при визначенні
оптимального плану перевезень (транспортні завдання) і т.д.
Для вирішення великого кола задач
лінійного програмування є практично універсальний алгоритм - симплексний метод,
що дозволяє за кінцеве число ітерацій знаходити оптимальне вирішення переважної
більшості задач. Тип використовуваних обмежень (рівність або нерівності) не
позначається на можливості вживання вказаного алгоритму. Додаткової перевірки
на оптимальність для отримуваних рішень не вимагається. Як правило, практичні
задачі лінійного програмування відрізняються значним числом незалежних змінних.
Тому для їх вирішення зазвичай використовують обчислювальні машини, необхідна
потужність яких визначається розмірністю вирішуваної задачі.
Методи нелінійного програмування
Дані методи застосовують для
вирішення оптимальних задач з нелінійними функціями мети. На незалежні змінні
можуть бути накладені обмеження також у вигляді нелінійних співвідношень, що
мають вигляд рівності або нерівностей. По суті методи нелінійного програмування
використовують, якщо жоден з перерахованих вище методів не дозволяє як-небудь
просунутися в рішенні оптимальної задачі. Тому вказані методи інколи називають
також прямими методами вирішення оптимальних задач.
Для здобуття чисельних результатів
важливе місце відводиться нелінійному програмуванню. У вирішенні оптимальних
завдань таким методам, як динамічне програмування та принцип максимуму на
певних етапах їх використання.
Назвою «Методи нелінійного
програмування» об'єднується велика група чисельних методів, багато з яких
пристосовані для вирішення оптимальних задач відповідного класу. Вибір того або
іншого методу обумовлений складністю обчислення критерію оптимальності і
складністю обмежуючих умов, необхідною точністю рішення, потужністю наявної
обчислювальної машини і т.д. Ряд методів нелінійного програмування практично
постійно використовується у поєднанні з іншими методами оптимізації, як,
наприклад, метод сканування в динамічному програмуванні. Крім того, ці методи
служать основою побудови систем автоматичної оптимізації - оптимізаторів, що
безпосередньо застосовуються для управління виробничими процесами [3].
Оптимізація методом крутого
сходження по поверхні відгуку
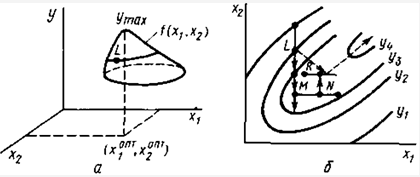
Рисунок 3.1 - Рух по поверхні
відгуку (а) до екстремуму в однофакторному експерименті і в методі крутого
сходження (б)
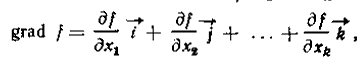 (1.3)
(1.3)
де 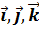 -орти
координатних осей.
-орти
координатних осей.
Передбачається, що функція 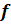 безперервна,
диференційна, однозначна і не має особливих точок. Бокс та Уілсон запропонували
кроковий метод руху по поверхні відгуку. В області точки
безперервна,
диференційна, однозначна і не має особливих точок. Бокс та Уілсон запропонували
кроковий метод руху по поверхні відгуку. В області точки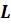 ставиться
експеримент для локального опису поверхні відгуку лінійним рівнянням регресії:
ставиться
експеримент для локального опису поверхні відгуку лінійним рівнянням регресії:
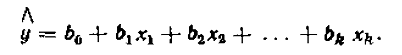 (1.4)
(1.4)
Далі рухаються по поверхні відгуку у
напрямі градієнта лінійного наближення:
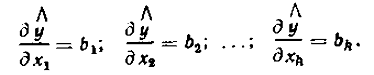 (1.5)
(1.5)
При постановці дослідів величина
кроку має бути пропорційна значенню коефіцієнта 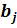 ;
на інтервал варіювання
;
на інтервал варіювання 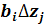 . Якщо одного
лінійного наближення недостатньо, то ставиться нова серія дослідів з центром у
точці, яка відповідає найбільшому значенню
. Якщо одного
лінійного наближення недостатньо, то ставиться нова серія дослідів з центром у
точці, яка відповідає найбільшому значенню 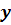 ,
і знаходиться новий напрям для руху по поверхні відгуку. Такий кроковий процес
триває до досягнення області, близької до екстремуму, або «майже стаціонарної
області».
,
і знаходиться новий напрям для руху по поверхні відгуку. Такий кроковий процес
триває до досягнення області, близької до екстремуму, або «майже стаціонарної
області».
Напрям градієнта залежить від
вибраного інтервалу варіювання незалежних факторів. При зміні в 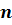 разів
інтервалу варіювання для деякого
разів
інтервалу варіювання для деякого 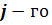 фактора
змінюється в
фактора
змінюється в 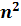 разів величина
кроку для цього фактора, оскільки в
разів величина
кроку для цього фактора, оскільки в 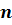 разів
змінюється коефіцієнт регресії
разів
змінюється коефіцієнт регресії 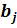 і також в
і також в 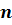 разів
-інтервал варіювання. Інваріантними до зміни інтервалу залишаються лише знаки
складових градієнта.
разів
-інтервал варіювання. Інваріантними до зміни інтервалу залишаються лише знаки
складових градієнта.
Вдалий вибір інтервалу варіювання
багато в чому пов'язаний з наявністю апріорної інформації про параметричну
чутливість процесу. Інтервал варіювання має бути досить великий, щоб діапазон
зміни вихідної величини був у декілька разів (не менше 3-4 разів) більше
помилки відтворюваності. В той же час для більшості процесів лінійне наближення
поверхні відгуку адекватне експерименту лише при невеликих інтервалах
варіювання. Якщо на інтервали варіювання не накладено жодних обмежень, їх
прагнуть вибрати так, щоб отримати рівняння регресії, симетричне відносно
коефіцієнтів при лінійних членах. Обробка результатів експерименту, пов'язаного
з крутим сходженням, повинна супроводжуватися ретельним статистичним аналіз
отриманих результатів.
Приклад визначення оптимального
складу фотохромного скла
Визначався оптимальний склад
фотохромного скла в системі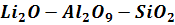 . Як параметри
оптимізації (
. Як параметри
оптимізації (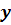 ) розглядалася
оптична густина в опроміненому стані. Необхідно було визначити склад скла і
умови його варіння, що забезпечують максимальну оптичну густину.
) розглядалася
оптична густина в опроміненому стані. Необхідно було визначити склад скла і
умови його варіння, що забезпечують максимальну оптичну густину.
В якості незалежних факторів були
вибрані: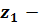 вихідна концентрація хлору,г-атом на 100 г скла;
вихідна концентрація хлору,г-атом на 100 г скла;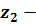 вихідна концентрація брому,г-атом на 100 г скла;
вихідна концентрація брому,г-атом на 100 г скла;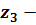 співвідношення
співвідношення
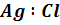 ;
;
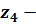 температура
варіння
температура
варіння 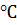 ;
;
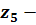 час
витримки, год;
час
витримки, год; 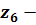 вміст
вміст 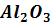 ,
мол. долі;
,
мол. долі; 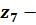 співвідношення
співвідношення 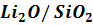
Умови експерименту наведені в
таблиці 1.
Таблиця 1 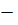 Умови
експерименту
Умови
експерименту
|
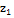
|
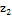
|
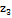
|
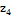
|
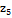
|
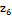
|
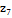
|
|
Основний рівень 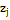 Інтервал
варіювання Інтервал
варіювання 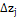 +1 -1 +1 -1
|
0,0425 0,0205 0,063 0,022
|
0,0187 0,0093 0,028 0,0094
|
0,0675 0,0325 0,1 0,035
|
0,325 25 0,350 0,300
|
1,75 0,25 2 1,5
|
0,1395 0,0125 0,157 0,124
|
0,4165 0,0835 0,5 0,333
|
Розв’язок. Для визначення
коефіцієнтів лінійного рівняння регресії
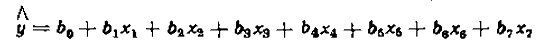
використана 1/16 від ПФЕ 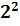 з
генеруючими співвідношеннями
з
генеруючими співвідношеннями
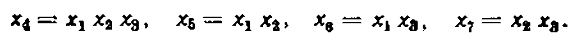
Кожен дослід в матриці планування
повторений два рази.
Середні значення оптичної густини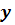 отримані
по двох вимірах. Перевіримо однорідність дисперсій
отримані
по двох вимірах. Перевіримо однорідність дисперсій 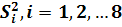 по
критерію Кохрена.
по
критерію Кохрена.
Сума дисперсій
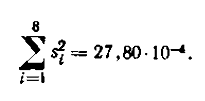
Критерій Кохрена
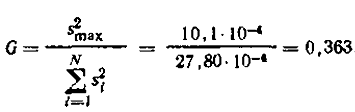
Табличне значення критерію Кохрена
для рівня знаачимості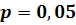 і чисел ступенів
свободи
і чисел ступенів
свободи 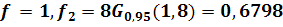 .
.
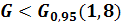 ,
отже дисперсії однорідні. У зв'язку з цим дисперсія однорідності
визначається як середнє арифметичне:
,
отже дисперсії однорідні. У зв'язку з цим дисперсія однорідності
визначається як середнє арифметичне:
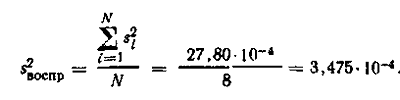
Число ступенів свободи дисперсії
дорівнює
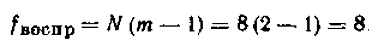
Коефіцієнти рівняння регресії
визначаємо за формулою (1.6):
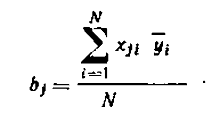 (1.6)
(1.6)
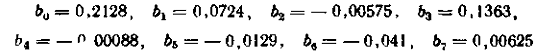
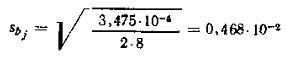
Оцінимо значущість коефіцієнтів за
критерієм Стьюдента. Для цього визначимо помилку коефіцієнтів
і складемо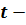 відношення для всіх коефіцієнтів рівняння регресії:
відношення для всіх коефіцієнтів рівняння регресії:
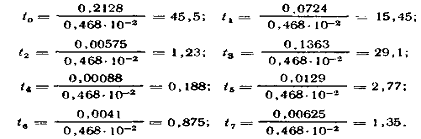
Табличне значення критерію Стьюдента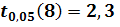 .
Коефіцієнти
.
Коефіцієнти 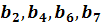 незначиміоскількискладені
для них
незначиміоскількискладені
для них 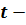 відношення
менше табличного.
Післявиключеннянезначимихкоефіцієнтіврівняннярегресіїприймевигляд
відношення
менше табличного.
Післявиключеннянезначимихкоефіцієнтіврівняннярегресіїприймевигляд
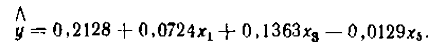
Дисперсія адекватності
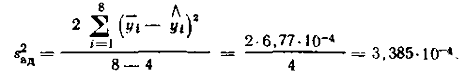
Таблиця 2 - Матриця планування
|
№
|
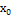
|
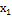
|
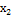
|
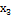
|
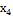
|
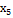
|
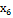
|
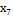
|
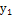
|
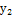
|
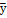
|
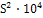
|
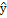
|
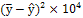
|
+ + + + + + + +
|
- + - + - + - +
|
++- -++- -
|
- - - - + + + +
|
+ - -+ - + + -
|
- + + - - + + -
|
+ - + - - + - +
|
- - + + + + - -
|
0 0,108 0 0,194 0,298 0,400 0,255 0,453
|
0 0,15 0 0,16 0,292 0,408 0,278 0,408
|
0 0,129 0 0,177 0,295 0,404 0,266 0,431
|
0 8,82 0 5,78 0,18 0,32 2,6 10,1
|
0,017 0,136 -0,0089 0,1618 0,2896 0,4086
0,2638 0,4344
|
2,9 0,49 0,77 2,3 0,29 0,21 0,073 0,1156
|
Тоді 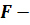 відношення
дорівнює
відношення
дорівнює
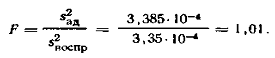
Табличне значення критерію Фішера
для 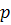 =
0,05,
=
0,05, 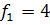 і
і
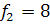 ,
,
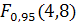 =3,8.
=3,8.
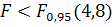 і
рівняння регресії адекватне досліду. Використовуємо отримане рівняння для
крутого сходження по поверхні відгуку для збільшення оптичної густини скла. При
крутому сходженні незначущі параметри були зафіксовані на нульовому рівні, час
витримки на нижньому рівні 1,5 год. Таким чином, змінювалися лише вихідна
концентрація хлору (
і
рівняння регресії адекватне досліду. Використовуємо отримане рівняння для
крутого сходження по поверхні відгуку для збільшення оптичної густини скла. При
крутому сходженні незначущі параметри були зафіксовані на нульовому рівні, час
витримки на нижньому рівні 1,5 год. Таким чином, змінювалися лише вихідна
концентрація хлору (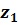 ) і співвідношення
) і співвідношення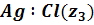 .
Перші три досліди при крутому сходженні (9, 10, 11) були «уявними» (таблиця 3).
.
Перші три досліди при крутому сходженні (9, 10, 11) були «уявними» (таблиця 3).
Таблиця 3 - Перші три досліди при
крутому сходженні
|
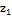
|
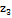
|
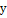
|
Номер досліду
|
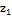
|
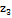
|
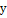
|
|
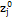 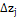 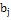 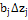 Крок Крок
|
0,0045 0,0205 0,0724 0,00148 0,0048
|
0,0675 0,099 0,1363 0,00443 0,0111
|
|
9 10 11 12 13 14 15 16
|
0,0462 0,0498 0,0536 0,0573 0,0610 0,0647
0,0683 0,0719
|
0,0787 0,0897 0,1008 0,1119 0,1230 0,1341
0,1452 0,1563
|
- - - 0,552 0,500 0,476 0,436 0,426
|
За кроки взяті величини, в 2,5 рази
більші, ніж 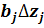 . Кращий результат
отриманий в 12-ому досліді. Подальше збільшення концентрації хлору і
співвідношення
. Кращий результат
отриманий в 12-ому досліді. Подальше збільшення концентрації хлору і
співвідношення 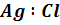 погіршує
фотохромні властивості скла. У зв'язку з цим були реалізовані пропущені досліди
10 і 11. Отримані наступні значення оптичної густини скла:
погіршує
фотохромні властивості скла. У зв'язку з цим були реалізовані пропущені досліди
10 і 11. Отримані наступні значення оптичної густини скла:
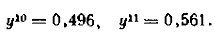
Таким чином, в якості оптимального
рекомендується склад скла, отриманий в11-ому досліді[4].
Висновки
На сьогоднішній день в хімії і
хімічній технології потрібний перехід
від
лабораторних
досліджень
до промислової реалізації.
Методи кібернетики дозволяють не лише скоротити цей шлях, але і різко зменшити
число необхідних дослідів, швидко виявити оптимальний варіант здійснення
процесу. Використання методів кібернетики і обчислювальної техніки змінює старі
традиційні методи проведення експерименту від ручного управління, контролю,
збору і обробки інформації до діалогової системи : експериментатор - електронна
машина[4].
При вирішенні конкретної задачі
оптимізації дослідник перш за все повинен вибрати математичний метод, який
приводив би до кінцевих результатів з найменшими витратами на обчислення або ж
давав можливість отримати найбільший об'єм інформації про майбутнє рішення [3].
Література
1.
Понятие об оптимизациихимико-технологическихпроцессов и систем. Постановка задачиоптимизации[Електронний
ресурс]: стаття. - режим доступу до
статті:http://mm.lti-gti.ru/works_lectures/5.htm. (дата звернення 05.12.12 р.)
2.
Планирование эксперимента [Електронний ресурс]: стаття. - режим доступу до
статті:http://opds.sut.ru/old/electronic_manuals/pe/f031.htm. (дата звернення
05.12.12 р.)
3.
Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии / под
ред. В.В. Кафарова. - М.: Химия, 1969. - 563 с.
.
Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической
технологии: учеб.пособие для студентов химико-технологических специальностей
высших учебных заведений/ С.Л. Ахназарова, В.В. Кафаров. - М.:Высшая школа,
1985. -329 с.