Разработка технологического процесса и определение технико-экономичес-
ких показателей производства...
Содержание
Введение
1. Расчет основных параметров проектируемой цифровой системы
передачи информации
2. Расчет спектра АИМ сигнала
3. Дискретизация сообщений по времени
4. Квантование отсчетов по уровню и их кодирование
5. Расчёт погрешностей квантования
6. Формирование линейного сигнала
7. Расчет спектра линейного сигнала
8. Разработка структурной схемы многоканальной системы передачи с
ИКМ
Заключение
Литература
Введение
Цифровые системы передачи (ЦСП) обладают рядом преимуществ по
сравнению с аналоговыми системами передачи, которые передают сообщение в виде
непрерывных функций времени.
Системы передачи с частотным разделением каналов (ЧРК)
характеризуются применением аналоговых методов модуляции, при которых
модулирующий параметр может принимать любые значения в некоторых допустимых
пределах. Помехоустойчивость в таких системах сравнительно невелика. Помехи
вызывают паразитную модуляцию основных параметров сигналов-переносчиков и после
модуляции попадают на выход канала. Помехоустойчивые методы модуляции (ЧМ и ФМ)
улучшают соотношение сигнал-помеха (S/N) на выходе канала. Однако, поскольку при аналоговых методах
модуляции все значения модулируемых параметров являются разрешенными, при
приеме невозможно отличить паразитную модуляцию от полезной, а, следовательно,
невозможно отделить полезный сигнал от помехи.
Основные преимущества систем передачи с ИКМ заключаются в
следующем:
. Высокая помехоустойчивость за счет передачи сообщения
двоичными сигналами.
. Цифровые методы передачи позволяют значительно повысить
помехоустойчивость и уменьшить накопление помех вдоль тракта передачи путем
восстановления (регенерации) сигнала.
. Удобство настройки и эксплуатации цифровых систем, меньшая
чувствительность к искажениям, что обеспечивает более высокие технико-экономические
показатели цифровых систем передачи по сравнению с аналоговыми (системы с
разделением каналов по частоте).
цифровая система передача информация
4. Возможность использования сравнительно простых методов
запоминания и хранения сообщений путем записи их в различного рода цифровых
регистрах и запоминающих устройствах.
. Принцип временного разделения каналов, применяемый в
системах с ИКМ, используется в электронных автоматических телефонных станциях,
что позволяет одновременное использование систем передачи и систем коммутации.
Недостатком цифровых систем связи является расширение полосы
частот, требуемой для передачи сообщений с помощью ИКМ. Но этот недостаток не
является определяющим по сравнению с теми преимуществами, которыми обладают
цифровые системы передачи.
В основном многоканальные системы передачи применяются для
передачи речевых сигналов, которые относятся к непрерывным. Речь представляет
собой широкополосный процесс, частотный спектр которого простирается от 50-100
до 8000-10000 Гц. Установлено, однако, что качество речи получается вполне
удовлетворительным при ограничении спектра частотами 300-3400 Гц. При указанной
полосе частот разборчивость фраз составляет более 99%, при этом сохраняется
удовлетворительная натуральность звучания.
Для передачи непрерывного сообщения с помощью ИКМ необходимо
выполнять следующие операции:
1. дискретизацию сообщений по времени;
2. квантование полученных импульсов по амплитуде;
. кодирование квантованных сигналов.
1.
Расчет основных параметров проектируемой цифровой системы передачи информации
1. Количество всех каналов 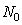 с
учетом телефонных, синхронизации и управления:
с
учетом телефонных, синхронизации и управления:
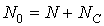 ,
,
где 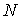 - заданное количество каналов;
- заданное количество каналов; 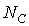 - количество каналов синхронизации:
- количество каналов синхронизации:
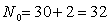
. Длительность цикла передачи (период дискретизации):
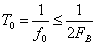 ,
,
где 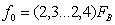 ; выбираем
; выбираем 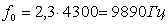 ,
тогда
,
тогда
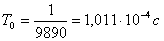
3. Длительность канального интервала:
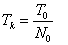
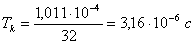
. Длительность тактового интервала между кодовыми импульсами в
канальном интервале:
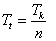
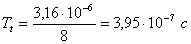
5. Длительность кодового импульса:
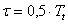
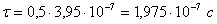
. Тактовая частота линейного сигнала:
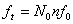 ,
,
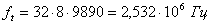
. Длительность управляющих канальных импульсов:
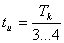
выбираем коэффициент 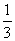 , тогда
, тогда
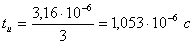
. Требуемая полоса пропускания линейного тракта ИКМ-системы передачи:
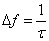
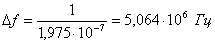
2.
Расчет спектра АИМ сигнала
Преобразование аналогового сигнала в дискретный называется
дискретизацией. В результате дискретизации получается амплитудно-импульсный
сигнал (АИМ). Различают амплитудно-импульсную модуляцию первого (АИМ-1) и
второго (АИМ-2) рода.
При АИМ-1 амплитуда импульса следует за изменениями
модулирующего сигнала в течение всего времени существования этого импульса. Модулированная
последовательность в этом случае определяется выражением
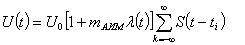
где 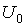 - амплитуда немодулированных прямоугольных импульсов;
- амплитуда немодулированных прямоугольных импульсов;
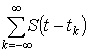 -
последовательность немодулированных импульсов с периодом следования
-
последовательность немодулированных импульсов с периодом следования 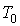 ;
;
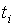 -
момент появления i-го импульса, где
-
момент появления i-го импульса, где 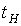 - время начала действия первого импульса;
- время начала действия первого импульса;
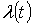 -
непрерывное сообщение;
-
непрерывное сообщение;
Произведем расчет спектра АИМ-1 сигнала для аналогового сообщения
с частотами 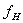 и
и 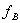 .
.
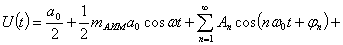
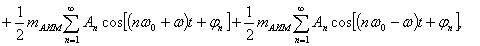
где 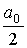 - постоянная составляющая;
- постоянная составляющая;
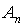 -
амплитуда
-
амплитуда 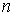 -й гармоники;
-й гармоники;
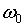 -
круговая частота основной (первой) гармоники;
-
круговая частота основной (первой) гармоники;
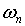 -
начальная фаза
-
начальная фаза 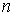 -й гармоники.
-й гармоники.
Если модулирующий (дискретизируемый) сигнал 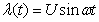 , то сигнал на выходе балансного модулятора при АИМ-2
определяется соотношением:
, то сигнал на выходе балансного модулятора при АИМ-2
определяется соотношением:
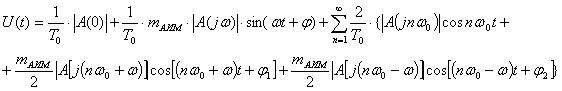
где, 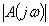 - модуль спектральной плотности немодулированных
импульсов.
- модуль спектральной плотности немодулированных
импульсов.
Для прямоугольного импульса модуль спектральной плотности:
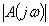 =
=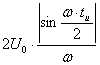 ;
;
где tи - длительность импульса
Определим нулевую, верхнюю и нижнюю частоты:
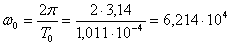 рад/c
рад/c
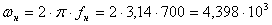 рад/c
рад/c
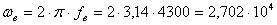 рад/c
рад/c
Постоянная составляющая спектра (при 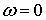 ):
):
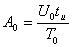
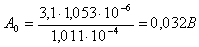
Спектр модулирующего сигнала определяется из выражения:
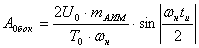
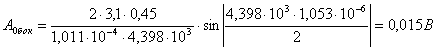
Гармоники частоты дискретизации 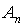 :
:
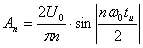 .
.
Расчет для первой гармоники:
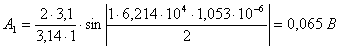
Боковые полосы для значений 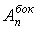 :
:
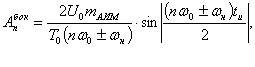
где 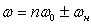
Расчет для 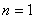 :
:
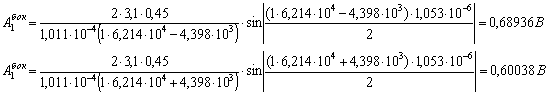
Результаты всех расчетов спектра АИМ-сигнала сведены в таблицу
2.1.
Таблица 2.1 - Результаты расчета спектра модулированного
АИМ-сигнала.
|
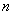 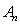 ,
В ,
В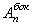 , В , В
|
|
|
|
|
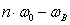 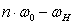 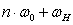 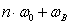
|
|
|
|
|
1
|
2,852
|
0
|
0,68936
|
0,60038
|
0
|
|
7
|
0,407
|
0
|
0,09244
|
0,09092
|
0
|
|
9
|
0,317
|
0
|
0,07174
|
0,07087
|
0
|
|
19
|
0,15
|
0
|
0,03384
|
0,03371
|
0
|
|
28
|
0,102
|
0
|
0,02294
|
0,0229
|
0
|
|
44
|
0,065
|
0
|
0,01458
|
0,01459
|
0
|
По полученным данным построим спектральную характеристику. На
графике видно, что каждая гармоника имеет несущую на частоте 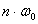 , на которую приходится большая часть энергии (большая
амплитуда) и две боковые полосы. Значения всех амплитуд постепенно уменьшаются
с ростом номера гармоники.
, на которую приходится большая часть энергии (большая
амплитуда) и две боковые полосы. Значения всех амплитуд постепенно уменьшаются
с ростом номера гармоники.

Рисунок 2.1 - Спектральная диаграмма АИМ сигнала
3.
Дискретизация сообщений по времени
Преобразование аналогового сигнала в дискретный называется
дискретизацией. В результате дискретизации получается амплитудно-импульсный
сигнал (АИМ). Различают амплитудно-импульсную модуляцию первого (АИМ-1) и
второго (АИМ-2) рода.
Задача восстановления непрерывного сигнала из последовательности
его дискретных отсчетов заключается в фильтрации модулирующего сигнала с
частотой 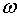 , находящегося в низкочастотной части спектра АИМ-сигнала,
с помощью ФНЧ.
, находящегося в низкочастотной части спектра АИМ-сигнала,
с помощью ФНЧ.
В тех случаях, когда модулирующий сигнал характеризуется спектром
с полосой частот от 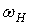 до
до 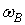 , спектральная диаграмма будет иметь более сложный вид.
Вместо отдельных пар боковых колебаний около частот
, спектральная диаграмма будет иметь более сложный вид.
Вместо отдельных пар боковых колебаний около частот 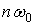 будут наблюдаться боковые полосы, а в низкочастотной части
спектра модулированного колебания - спектр модулирующего сигнала.
будут наблюдаться боковые полосы, а в низкочастотной части
спектра модулированного колебания - спектр модулирующего сигнала.
Многоканальные системы передачи в основном применяются для
передачи речевых сигналов, которые относятся к непрерывным. Для передачи
непрерывного сообщения с помощью ИКМ необходимо выполнить следующие операции:
дискретизация сообщения по времени (получение АИМ-сигнала);
квантование полученных импульсов (отсчетов, выборок) по амплитуде;
кодирование квантованных по амплитуде импульсов.
Дискретизация непрерывных сообщений производится АИМ-модуляторами
в соответствии с теоремой Котельникова. На выходе АИМ-модуляторов формируется
групповой АИМ-сигнал. Работой АИМ-модуляторов управляют последовательности
канальных импульсов. Групповой АИМ-сигнал поступает на кодер, который
одновременно с кодированием осуществляет операцию квантования по уровню.
Входные сигналы:
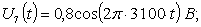
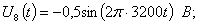
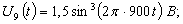
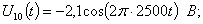
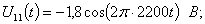
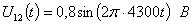 .
.
Значения времени 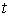 в
функциях выходных сигналов для соответствующих циклов передачи определяются по
формуле
в
функциях выходных сигналов для соответствующих циклов передачи определяются по
формуле

где 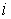 - номер канального интервала,
- номер канального интервала,
Ц - номер цикла. Ц = 1, 2, 3, 4.
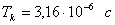 ;
;
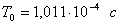 .
.
Входной сигнал имеет сложный вид, выполним его тригонометрические
преобразования:
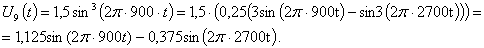
Расчет величины одного отсчета при  и
i=7, 8, 9, 10, 11, 12:
и
i=7, 8, 9, 10, 11, 12:
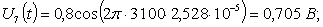
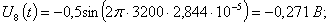
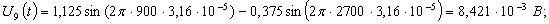
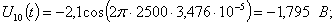
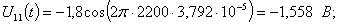
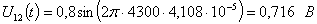 .
.
Результаты остальных расчетов приведем в таблице 3.1:
Таблица 3.1 - Результаты расчёта величин отсчётов входных
сигналов для 1-го цикла
|
i
|
t, с
|
U7 (t), В
|
U8 (t), В
|
U9 (t), В
|
U10 (t), В
|
U11 (t), В
|
U12 (t), В
|
|
0
|
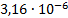
|
0.798
|
-0.032
|
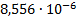
|
-2.097
|
-1,798
|
0.068
|
|
1
|
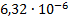
|
0.794
|
-0.063
|
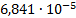
|
-2.09
|
-1,793
|
0.136
|
|
2
|
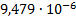
|
0.786
|
-0.095
|
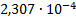
|
-2.077
|
-1,785
|
0.203
|
|
3
|
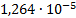
|
0.776
|
-0.126
|
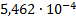
|
-2.059
|
-1,773
|
0.268
|
|
4
|
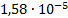
|
0.762
|
-0.156
|
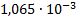
|
-2.036
|
-1,757
|
0.331
|
|
5
|
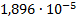
|
0.746
|
-0.186
|
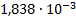
|
-2.008
|
-1,739
|
0.392
|
|
6
|
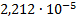
|
0.727
|
-0.215
|
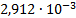
|
-1.975
|
-1,717
|
0.45
|
|
7
|
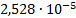
|
0.705
|
-0.243
|
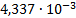
|
-1.937
|
-1,691
|
0.505
|
|
8
|
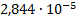
|
0.68
|
-0.271
|
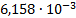
|
-1.894
|
-1,663
|
0.556
|
|
9
|
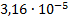
|
0.653
|
-0.297
|
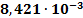
|
-1.847
|
-1,631
|
0.603
|
|
10
|
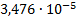
|
0.624
|
-0.322
|
0.011
|
-1.795
|
-1,596
|
0.646
|
|
11
|
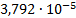
|
0.592
|
-0.345
|
0.014
|
-1.738
|
-1,558
|
0.684
|
|
12
|
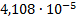
|
0.557
|
-0.368
|
0.018
|
-1.678
|
-1,518
|
0.716
|
|
13
|
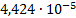
|
0.521
|
-0.388
|
0.023
|
-1.613
|
-1,474
|
0.744
|
|
14
|
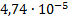
|
0.483
|
-0.408
|
0.028
|
-1.544
|
-1,427
|
0.767
|
|
15
|
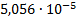
|
0.442
|
-0.425
|
0.034
|
-1.472
|
-1,378
|
0.783
|
|
16
|
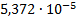
|
0.401
|
-0.441
|
0.04
|
-1.396
|
-1,326
|
0.794
|
|
17
|
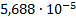
|
0.357
|
-0.455
|
0.047
|
-1.316
|
-1,272
|
0.8
|
|
18
|
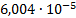
|
0.313
|
-0.467
|
0.055
|
-1.233
|
-7,215
|
0.799
|
|
19
|
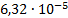
|
0.267
|
-0.478
|
0.064
|
-1.148
|
-1,156
|
0.793
|
|
20
|
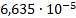
|
0.22
|
-0.486
|
0.074
|
-1.059
|
-1,094
|
0.78
|
|
21
|
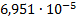
|
0.172
|
-0.493
|
0.084
|
-0.968
|
-1,031
|
0.763
|
|
22
|
0.124
|
-0.497
|
0.096
|
-0.874
|
-0,966
|
0.739
|
|
23
|
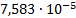
|
0.075
|
-0.499
|
0.108
|
-0.778
|
-0,898
|
0.71
|
|
24
|
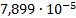
|
0.026
|
-0.5
|
0.121
|
-0.68
|
-0,829
|
0.676
|
|
25
|
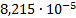
|
-0.024
|
-0.498
|
0.135
|
-0.581
|
-0,759
|
0.637
|
|
26
|
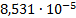
|
-0.073
|
-0.495
|
0.15
|
-0.48
|
-0,687
|
0.594
|
|
27
|
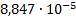
|
-0.122
|
-0.489
|
0.166
|
-0.378
|
-0,614
|
0.546
|
|
28
|
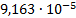
|
-0.17
|
-0.482
|
0.182
|
-0.275
|
-0,539
|
0.494
|
|
29
|
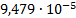
|
-0.218
|
-0.472
|
0.2
|
-0.172
|
-0,464
|
0.439
|
|
30
|
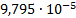
|
-0.265
|
-0.461
|
0.218
|
-0.068
|
-0,387
|
0.38
|
|
31
|
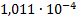
|
-0.311
|
-0.448
|
0.238
|
0.037
|
-0,31
|
0.319
|
Построим временные диаграммы входных сигналов для первого
цикла.
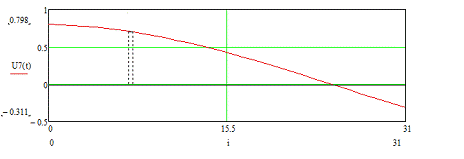
Рисунок 3.1 - Временная диаграмма входного сигнала U7 (t)
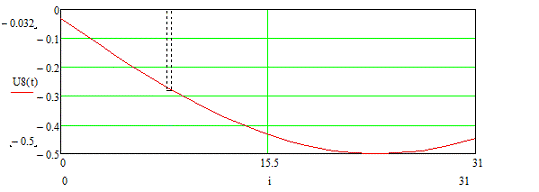
Рисунок 3.2 - Временная диаграмма входного сигнала U8 (t)
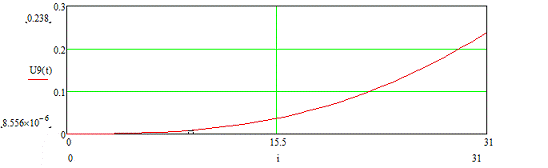
Рисунок 3.3 - Временная диаграмма входного сигнала U9 (t)
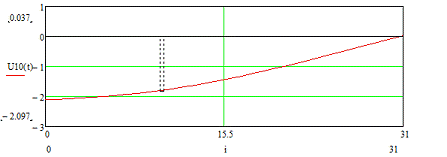
Рисунок 3.4 - Временная диаграмма входного сигнала U10 (t)
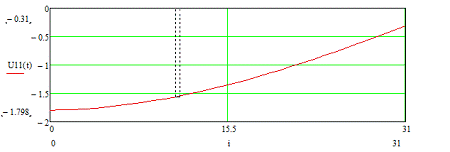
Рисунок 3.5 - Временная диаграмма входного сигнала U11 (t)
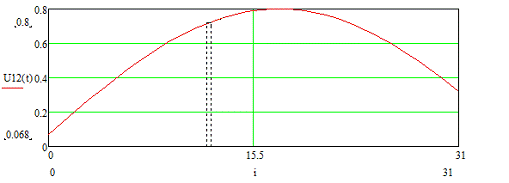
Рисунок 3.6 - Временная диаграмма входного сигнала U12 (t)
Расчет величины одного отсчета при 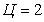 и
i=7, 8, 9, 10, 11, 12:
и
i=7, 8, 9, 10, 11, 12:
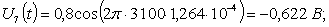
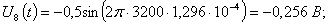
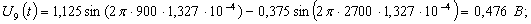
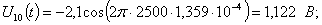
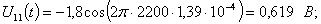
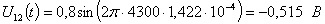 .
.
Результаты остальных расчетов приведем в таблице 3.2:
Таблица 3.2 - Результаты расчёта величин отсчётов входных
сигналов для 2-ого цикла
|
i
|
t, с
|
U7 (t), В
|
U8 (t), В
|
U9 (t), В
|
U10 (t), В
|
U11 (t), В
|
U12 (t), В
|
|
0
|
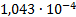
|
-0.355
|
-0.432
|
0.258
|
0.141
|
-0.232
|
0.255
|
|
1
|
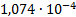
|
-0.399
|
-0.416
|
0.279
|
0.245
|
-0.154
|
0.189
|
|
2
|
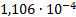
|
-0.441
|
-0.397
|
0.301
|
0.348
|
-0.076
|
0.122
|
|
3
|
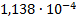
|
-0.481
|
-0.377
|
0.324
|
0.45
|
2.859e-3
|
0.055
|
|
4
|
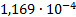
|
-0.519
|
-0.356
|
0.347
|
0.551
|
0.081
|
-0.014
|
|
5
|
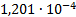
|
-0.556
|
-0.332
|
0.372
|
0.651
|
0.16
|
-0.082
|
|
6
|
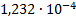
|
-0.59
|
-0.308
|
0.397
|
0.749
|
0.238
|
-0.149
|
|
7
|
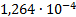
|
-0.622
|
-0.282
|
0.422
|
0.846
|
0.316
|
-0.216
|
|
8
|
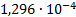
|
-0.652
|
-0.256
|
0.449
|
0.94
|
0.393
|
-0.281
|
|
9
|
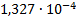
|
-0.679
|
-0.228
|
0.476
|
1.032
|
0.469
|
-0.344
|
|
10
|
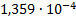
|
-0.704
|
-0.199
|
0.503
|
1.122
|
0.545
|
-0.404
|
|
11
|
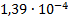
|
-0.726
|
-0.17
|
0.532
|
1.208
|
0.619
|
-0.461
|
|
12
|
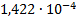
|
-0.745
|
-0.139
|
0.56
|
1.292
|
0.692
|
-0.515
|
|
13
|
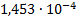
|
-0.762
|
-0.109
|
0.589
|
1.373
|
0.764
|
-0.566
|
|
14
|
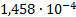
|
-0.775
|
-0.078
|
0.619
|
1.45
|
0.834
|
-0.612
|
|
15
|
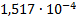
|
-0.786
|
-0.046
|
0.649
|
1.523
|
0.903
|
-0.654
|
|
16
|
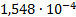
|
-0.794
|
-0.014
|
0.679
|
1.593
|
0.97
|
-0.691
|
|
17
|
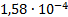
|
-0.798
|
0.017
|
0.71
|
1.659
|
1.036
|
-0.722
|
|
18
|
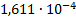
|
-0.8
|
0.049
|
0.74
|
1.721
|
1.099
|
-0.749
|
|
19
|
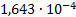
|
-0.799
|
0.081
|
0.771
|
1.779
|
1.16
|
-0.77
|
|
20
|
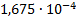
|
-0.794
|
0.112
|
0.802
|
1.832
|
1.219
|
-0.786
|
|
21
|
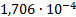
|
-0.787
|
0.143
|
0.833
|
1.88
|
1.276
|
-0.796
|
|
22
|
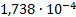
|
-0.776
|
0.173
|
0.864
|
1.924
|
1.33
|
-0.8
|
|
23
|
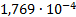
|
-0.763
|
0.202
|
0.895
|
1.964
|
1.382
|
-0.798
|
|
24
|
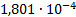
|
-0.747
|
0.231
|
0.925
|
1.998
|
1.431
|
-0.791
|
|
25
|
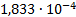
|
-0.728
|
0.258
|
0.956
|
2.028
|
1.477
|
-0.777
|
|
26
|
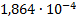
|
-0.706
|
0.285
|
0.986
|
2.052
|
1.521
|
-0.758
|
|
27
|
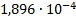
|
-0.682
|
0.311
|
1.016
|
2.072
|
1.561
|
-0.734
|
|
28
|
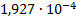
|
-0.654
|
0.335
|
1.045
|
2.086
|
1.599
|
-0.704
|
|
29
|
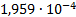
|
-0.625
|
0.358
|
1.074
|
2.096
|
1.633
|
-0.669
|
|
30
|
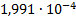
|
0.379
|
1.103
|
2.1
|
1.665
|
-0.629
|
|
31
|
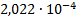
|
-0.559
|
0.399
|
1.131
|
2.099
|
1.693
|
-0.585
|
Построим временные диаграммы входных сигналов для второго
цикла.
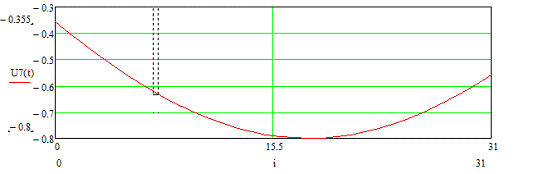
Рисунок 3.7 - Временная диаграмма входного сигнала U7 (t)
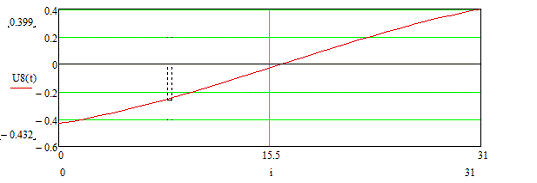
Рисунок 3.8 - Временная диаграмма входного сигнала U8 (t)
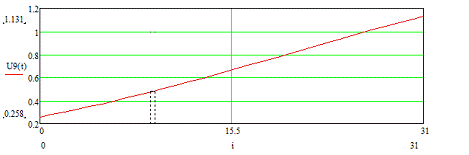
Рисунок 3.9 - Временная диаграмма входного сигнала U9 (t)
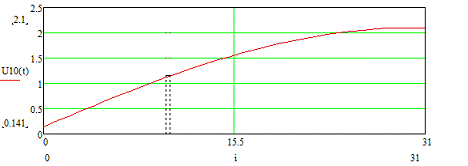
Рисунок 3.10 - Временная диаграмма входного сигнала U10 (t)
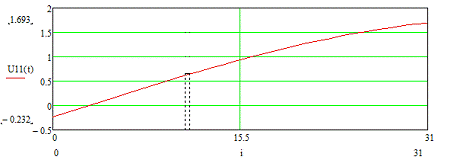
Рисунок 3.11 - Временная диаграмма входного сигнала U11 (t)
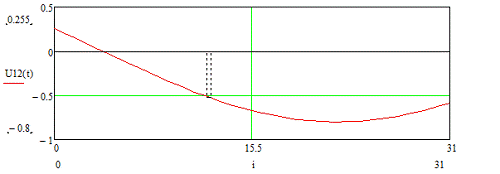
Рисунок 3.12 - Временная диаграмма входного сигнала U12 (t)
Расчет величины одного отсчета при 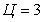 и
i=7, 8, 9, 10, 11, 12:
и
i=7, 8, 9, 10, 11, 12:
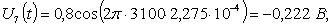
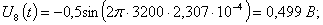
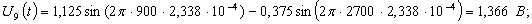
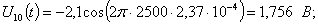
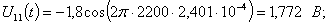
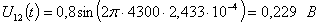 .
.
Результаты остальных расчетов приведем в таблице 3.3:
Таблица 3.3 - Результаты расчёта величин отсчётов входных
сигналов для 3-го цикла
|
i
|
t, с
|
U7 (t), В
|
U8 (t), В
|
U9 (t), В
|
U10 (t), В
|
U11 (t), В
|
U12 (t), В
|
|
0
|
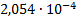
|
-0.523
|
0.417
|
1.158
|
2.092
|
1.718
|
-0.536
|
|
1
|
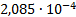
|
-0.484
|
0.434
|
1.185
|
2.081
|
1.74
|
-0.483
|
|
2
|
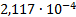
|
-0.444
|
0.449
|
1.21
|
2.065
|
1.758
|
-0.427
|
|
3
|
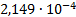
|
-0.403
|
0.462
|
1.235
|
2.043
|
1.774
|
-0.368
|
|
4
|
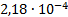
|
-0.359
|
0.473
|
1.26
|
2.016
|
1.785
|
-0.306
|
|
5
|
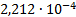
|
-0.315
|
0.483
|
1.283
|
1.985
|
1.794
|
-0.242
|
|
6
|
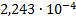
|
-0.269
|
0.49
|
1.305
|
1.948
|
1.799
|
-0.176
|
|
7
|
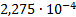
|
-0.222
|
0.495
|
1.327
|
1.907
|
1.8
|
-0.109
|
|
8
|
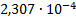
|
-0.174
|
0.499
|
1.347
|
1.861
|
1.798
|
-0.041
|
|
9
|
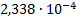
|
-0.126
|
0.5
|
1.366
|
1.811
|
1.793
|
0.027
|
|
10
|
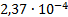
|
-0.077
|
0.499
|
1.384
|
1.756
|
1.784
|
0.095
|
|
11
|
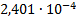
|
-0.028
|
0.497
|
1.401
|
1.696
|
1.772
|
0.163
|
|
12
|
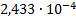
|
0.021
|
0.492
|
1.416
|
1.633
|
1.756
|
0.229
|
|
13
|
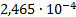
|
0.07
|
0.485
|
1.431
|
1.565
|
1.737
|
0.293
|
|
14
|
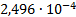
|
0.119
|
0.477
|
1.444
|
1.494
|
1.715
|
0.356
|
|
15
|
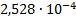
|
0.168
|
0.466
|
1.456
|
1.419
|
1.689
|
0.416
|
|
16
|
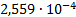
|
0.216
|
0.454
|
1.466
|
1.34
|
1.661
|
0.472
|
|
17
|
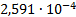
|
0.263
|
0.439
|
1.475
|
1.258
|
1.629
|
0.526
|
|
18
|
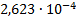
|
0.308
|
0.423
|
1.483
|
1.173
|
1.594
|
0.575
|
|
19
|
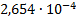
|
0.353
|
0.406
|
1.489
|
1.085
|
1.555
|
0.621
|
|
20
|
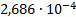
|
0.397
|
0.386
|
1.494
|
0.995
|
1.514
|
0.661
|
|
21
|
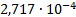
|
0.439
|
0.365
|
1.497
|
0.902
|
1.471
|
0.697
|
|
22
|
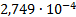
|
0.479
|
0.343
|
1.499
|
0.807
|
1.424
|
0.728
|
|
23
|
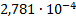
|
0.518
|
0.319
|
1.5
|
0.71
|
1.374
|
0.754
|
|
24
|
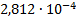
|
0.554
|
0.294
|
1.499
|
0.611
|
1.322
|
0.774
|
|
25
|
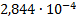
|
0.589
|
0.268
|
1.497
|
0.51
|
1.268
|
0.788
|
|
26
|
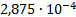
|
0.621
|
0.241
|
1.493
|
0.408
|
1.211
|
0.797
|
|
27
|
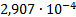
|
0.651
|
0.212
|
1.488
|
0.306
|
1.151
|
0.8
|
|
28
|
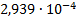
|
0.678
|
0.183
|
1.481
|
0.202
|
1.09
|
0.797
|
|
29
|
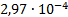
|
0.703
|
0.153
|
1.474
|
0.098
|
1.026
|
0.788
|
|
30
|
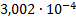
|
0.725
|
0.123
|
1.464
|
-5.837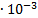 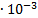 0.9610.774 0.9610.774
|
|
|
|
31
|
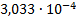
|
0.744
|
0.092
|
1.454
|
-0.11
|
0.893
|
0.754
|
Построим временные диаграммы входных сигналов для третьего
цикла.
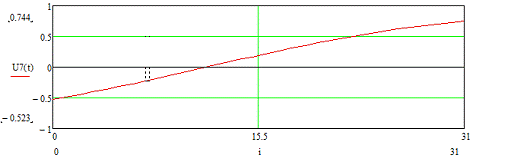
Рисунок 3.13 - Временная диаграмма входного сигнала U7 (t)
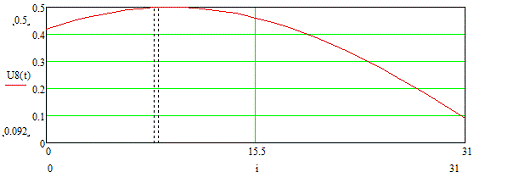
Рисунок 3.14 - Временная диаграмма входного сигнала U8 (t)
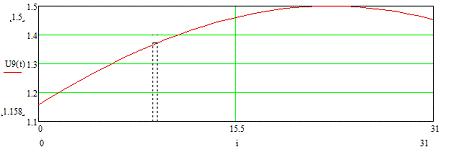
Рисунок 3.15 - Временная диаграмма входного сигнала U9 (t)
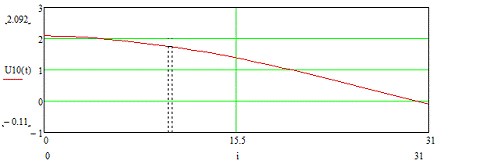
Рисунок 3.16 - Временная диаграмма входного сигнала U10 (t)
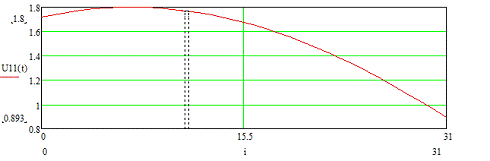
Рисунок 3.17 - Временная диаграмма входного сигнала U11 (t)
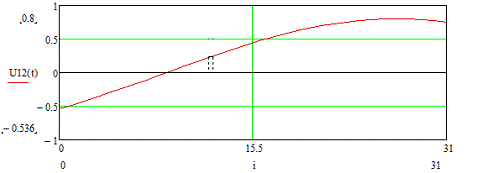
Рисунок 3.18 - Временная диаграмма входного сигнала U12 (t)
Расчет величины одного отсчета при 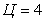 и
i=7, 8, 9, 10, 11, 12:
и
i=7, 8, 9, 10, 11, 12:
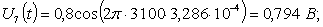
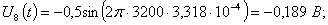
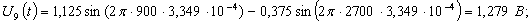
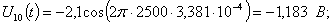
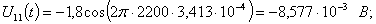
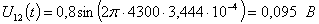 .
.
Результаты остальных расчетов приведем в таблице 3.4:
Таблица 3.4 - Результаты расчёта величин отсчётов входных
сигналов для 4-ого цикла
|
i
|
t, с
|
U7 (t), В
|
U8 (t), В
|
U9 (t), В
|
U10 (t), В
|
U11 (t), В
|
U12 (t), В
|
|
0
|
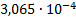
|
0.761
|
0.06
|
1.442
|
-0.214
|
0.824
|
0.728
|
|
1
|
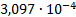
|
0.775
|
0.029
|
1.428
|
-0.317
|
0.754
|
0.697
|
|
2
|
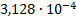
|
0.786
|
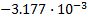
|
1.414
|
-0.42
|
0.682
|
|
3
|
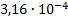
|
0.793
|
-0.035
|
1.398
|
-0.521
|
0.608
|
0.621
|
|
4
|
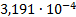
|
0.798
|
-0.067
|
1.381
|
-0.622
|
0.534
|
0.575
|
|
5
|
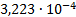
|
0.8
|
-0.098
|
1.363
|
-0.721
|
0.458
|
0.526
|
|
6
|
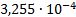
|
0.799
|
-0.129
|
1.343
|
-0.817
|
0.382
|
0.472
|
|
7
|
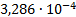
|
0.794
|
-0.159
|
1.323
|
-0.912
|
0.304
|
0.416
|
|
8
|
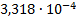
|
0.787
|
-0.189
|
1.301
|
-1.005
|
0.227
|
0.356
|
|
9
|
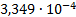
|
0.777
|
-0.218
|
1.279
|
-1.095
|
0.148
|
0.293
|
|
10
|
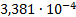
|
0.764
|
-0.246
|
1.255
|
-1.183
|
0.07
|
0.229
|
|
11
|
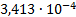
|
0.748
|
-0.273
|
1.231
|
-1.268
|
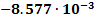
|
0.163
|
|
12
|
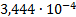
|
0.729
|
-0.299
|
1.206
|
-1.349
|
-0.087
|
0.095
|
|
13
|
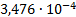
|
0.707
|
-0.324
|
1.18
|
-1.427
|
-0.166
|
0.027
|
|
14
|
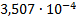
|
0.683
|
-0.348
|
1.153
|
-1.502
|
-0.244
|
-0.041
|
|
15
|
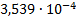
|
0.656
|
-0.37
|
1.126
|
-1.573
|
-0.321
|
-0.109
|
|
16
|
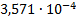
|
0.626
|
-0.39
|
1.098
|
-1.64
|
-0.398
|
-0.176
|
|
17
|
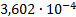
|
0.595
|
-0.409
|
1.069
|
-1.703
|
-0.475
|
-0.242
|
|
18
|
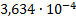
|
0.56
|
-0.427
|
1.04
|
-1.762
|
-0.55
|
-0.306
|
|
19
|
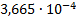
|
0.524
|
-0.442
|
1.011
|
-1.816
|
-0.624
|
-0.368
|
|
20
|
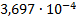
|
0.486
|
-0.456
|
0.981
|
-1.866
|
-0.697
|
-0.427
|
|
21
|
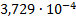
|
0.446
|
-0.468
|
0.951
|
-1.912
|
-0.769
|
-0.483
|
|
22
|
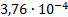
|
0.404
|
-0.479
|
0.92
|
-1.953
|
-0.84
|
-0.536
|
|
23
|
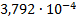
|
0.361
|
-0.487
|
0.889
|
-1.989
|
-0.908
|
-0.585
|
|
24
|
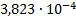
|
0.317
|
-0.493
|
0.858
|
-2.02
|
-0.975
|
-0.629
|
|
25
|
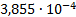
|
0.271
|
-0.497
|
0.828
|
-2.046
|
-1.04
|
-0.669
|
|
26
|
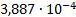
|
0.224
|
-0.5
|
0.797
|
-2.067
|
-1.104
|
-0.704
|
|
27
|
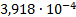
|
0.176
|
-0.5
|
0.766
|
-2.083
|
-1.165
|
-0.734
|
|
28
|
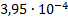
|
0.128
|
-0.498
|
0.735
|
-2.093
|
-1.223
|
-0.758
|
|
29
|
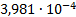
|
0.079
|
-0.494
|
0.704
|
-2.099
|
-1.28
|
-0.777
|
|
30
|
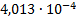
|
0.03
|
-0.489
|
0.674
|
-2.1
|
-1.334
|
-0.791
|
|
31
|
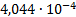
|
-0.019
|
-0.481
|
0.644
|
-2.095
|
-1.385
|
-0.798
|
Построим временные диаграммы входных сигналов для четвёртого
цикла.
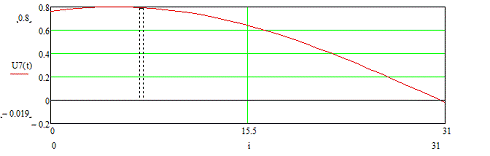
Рисунок 3.19 - Временная диаграмма входного сигнала U7 (t)
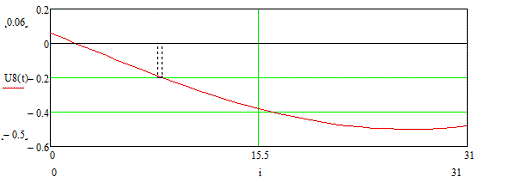
Рисунок 3.20 - Временная диаграмма входного сигнала U8 (t)
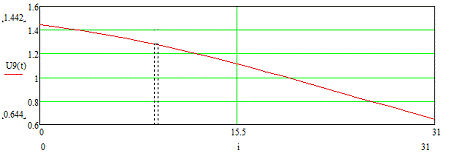
Рисунок 3.21 - Временная диаграмма входного сигнала U9 (t)
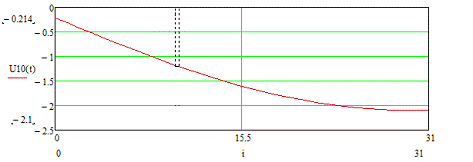
Рисунок 3.22 - Временная диаграмма входного сигнала U10 (t)
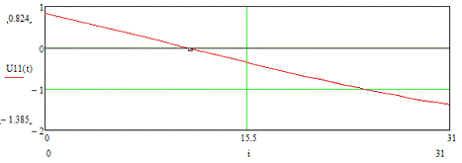
Рисунок 3.23 - Временная диаграмма входного сигнала U11 (t)
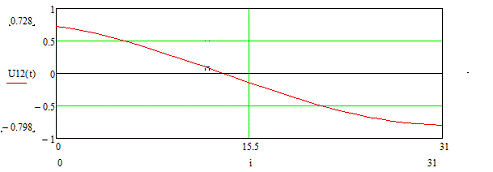
Рисунок 3.24 - Временная диаграмма входного сигнала U12 (t)
4.
Квантование отсчетов по уровню и их кодирование
Квантование по уровню применяется для получения конечного
числа амплитудных значений дискретных отсчетов сигнала взамен непрерывного
бесконечно большого количества их значений, т.е. процесс квантования аналогичен
процедуре округления числа до ближайшего разрешенного значения. Такое
округление всегда связано с погрешностью, называемой погрешностью квантования.
В результате квантования возникают специфические нелинейные
искажения, действие которых на передаваемый сигнал можно условно представить
как добавление к неискаженному сигналу некоторой аддитивной помехи - шума
квантования. Эти искажения неустранимы, но практически могут быть сделаны
неощутимыми для получателя сообщений при надлежащем выборе числа уровней
округляемой (квантуемой) величины сигнала.

Рисунок 4.1 - Амплитудная характеристика квантующего устройства
с равномерной шкалой
Как видно из рисунка 6, недостаток равномерной шкалы квантования
заключается в том, что относительная погрешность квантования, т.е. отношение
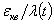
для сильных сигналов мала, в то время как для слабых сигналов она
велика.
В зависимости от разбивки динамического диапазона сообщения на
уровни квантования различают равномерное (линейное) и неравномерное
(нелинейное) квантования. В первом случае на всем динамическом диапазоне
сообщения шаг квантования выбирается одинаковым. При передаче речевых сигналов
наиболее вероятны сигналы с малыми мгновенными значениями, поэтому для передачи
их с меньшей погрешностью необходимо уменьшить шаг квантования. Обычно требуют,
чтобы защищенность речевого сигнала от шума квантования была не менее 20 дБ на
минимальном уровне средней мощности. Под защищенностью понимают
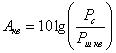
где 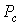 - мощность сигнала;
- мощность сигнала;
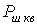 -
мощность шумов квантования.
-
мощность шумов квантования.
При равномерном квантовании для получения требуемой защищенности
от шумов квантования при передаче речевых сигналов кодирование должно
производиться достаточно большим числом разрядов кода, что нежелательно. При
увеличении числа разрядов кода уменьшается длительность импульсов и
соответственно расширяется спектр сигнала ИКМ, усложняются устройства
кодирования и декодирования, увеличиваются требования к их быстродействию.
Таким образом, недостатком равномерного квантования является то,
что защищенность от шумов квантования 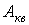 минимальна
для наиболее слабых сигналов и увеличивается пропорционально увеличению уровня
сигнала. Для выравнивания величины
минимальна
для наиболее слабых сигналов и увеличивается пропорционально увеличению уровня
сигнала. Для выравнивания величины 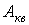 при
изменении уровня сигнала в широких пределах и соответственно для уменьшения
количества уровней квантования и уменьшения разрядности двоичного кода
применяют неравномерное квантование, при котором шаг квантования имеет
минимальное значение для слабых сигналов и увеличивается с увеличением уровня
входного сигнала.
при
изменении уровня сигнала в широких пределах и соответственно для уменьшения
количества уровней квантования и уменьшения разрядности двоичного кода
применяют неравномерное квантование, при котором шаг квантования имеет
минимальное значение для слабых сигналов и увеличивается с увеличением уровня
входного сигнала.
Нелинейная шкала квантования в системах передачи с ИКМ может быть
реализована несколькими способами: сжатием динамического диапазона сигнала
перед кодированием, для чего используются компрессоры, и последующим его
расширением после декодирования с помощью экспандеров; нелинейным кодированием
и декодированием; цифровым компандированием.
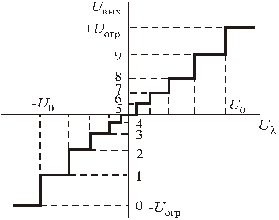
Рисунок 4.2 - Амплитудная характеристика квантующего устройства
с нелинейной (неравномерной) шкалой
При неравномерном квантовании непрерывных сигналов обычно ставится
задача: выбором закона изменения шага квантования обеспечить примерно равное
отношение сигнал-шум квантования в достаточно широком диапазоне уровней входных
сигналов. Если шаг квантования будет возрастать по мере увеличения входного
сигнала, то по сравнению с равномерным квантованием для слабых сигналов
отношение сигнал-шум возрастет, а для сильных снижается, оставаясь, однако,
достаточно высоким.
Рассмотрим один из возможных способов осуществления неравномерного
квантования - с использованием аналоговых компандеров.
Компрессор представляет собой устройство с нелинейной амплитудной
характеристикой, называемой характеристикой компрессии. Слабые сигналы
компрессор усиливает в большей степени, чем сильные, благодаря чему происходит
сжатие динамического диапазона (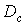 ).
).
Применение компрессора перед кодером с равномерным квантованием
позволяет получить неравномерное квантование. На приемном конце после декодера
сигнал поступает на экспандер, имеющий обратную компрессору амплитудную
характеристику, при этом суммарная амплитудная характеристика должна быть
линейной. Экспандер устраняет искажения, вносимые в сигнал компрессором, так
что результирующая амплитудная характеристика сигнала
"компрессор-экспандер" является линейной. Система, состоящая из
последовательно включенных компрессора и экспандера, называется компандером.
Применение неравномерного квантования позволяет обеспечить
требуемую защищенность от шумов квантования для наиболее слабых речевых
сигналов при восьмиразрядном кодировании вместо двенадцатиразрядного при равномерном
квантовании.
Недостатком аналогового компандирования является сложность
получения с большой точностью взаимообратных амплитудных характеристик
компрессора и экспандера, вследствие чего нелинейность суммарной амплитудной
характеристики приводит к нелинейным искажениям передаваемых сигналов.
Необходимое качество передачи сигналов в реальных условиях
достигается путем применения неравномерных кодирующих и декодирующих устройств
(методами нелинейного кодирования), когда формирование неравномерной квантующей
характеристики осуществляется непосредственно в кодере (декодере). Последний в
этом случае называется нелинейным.
Наиболее распространенными для кодеров с неравномерным шагом
квантования являются два приблизительно равноценных закона компрессии 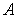 и
и 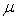 , с помощью которых получается квазилогарифмическая
характеристика компрессора.
, с помощью которых получается квазилогарифмическая
характеристика компрессора.
Дискретизация непрерывных сообщений производится АИМ -
модуляторами в соответствии с теоремой Котельникова. На выходе АИМ -
модуляторов формируется групповой АИМ - сигнал. Работой АИМ - модуляторов
управляют последовательности канальных импульсов. Групповой АИМ - сигнал
поступает на кодер, который одновременно с кодированием осуществляет операцию
квантования по уровню.
Многоканальные системы передачи в основном применяются для
передачи речевых сигналов, которые относятся к непрерывным. Для передачи
непрерывного сообщения с помощью ИКМ необходимо выполнить следующие операции:
· дискретизация сообщения по времени
(получение АИМ - сигнала);
· квантование полученных импульсов
(отсчетов, выборок) по амплитуде;
· кодирование квантованных по амплитуде
импульсов.
В результате квантования возникают специфические нелинейные
искажения, действие которых на передаваемый сигнал можно условно представить
как добавление к неискаженному сигналу некоторой аддитивной помехи - шума
квантования. Эти искажения неустранимы, но практически могут быть сделаны
неощутимыми для получателя сообщений при надлежащим выборе числа уровней округляемой
(квантуемой) величины сигнала.
В зависимости от разбивки динамического диапазона сообщения
на уровни квантования различают равномерное (линейное) и неравномерное
(нелинейное) квантования.
Наиболее распространенными для кодеров с неравномерным шагом квантования
являются два приблизительно равноценных закона компандирования μ и A, с помощью которых получается квазилогарифмическая характеристика
компрессора.
Характеристика компрессии закона A описывается следующим
уравнением:
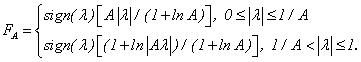
где sign (λ) - полярность сигнала;
λ - амплитуда входного сигнала;
А -
параметр, используемый для определения степени компрессирования.
В качестве
международного стандарта для нелинейных кодеров взвешивающего типа принята
сегментная характеристика компандирования типа А = 87,6/13.
Для законов квантования А = 87,6/13 рассчитаем для первых Ni отсчётов каждого входного сигналов в
первом цикле передачи:
· абсолютное значение отсчётов в условных
единицах;
· номер сегмента
(С) отсчётов;
· номер уровня квантования (К)
отсчётов в сегментах.
для 7-го канала для
8-го канала
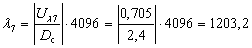
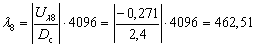
для 9-го канала для 10-го
канала
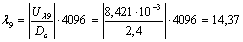
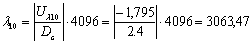
для 11-го канала для 12-го
канала
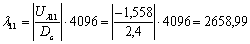
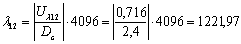
Номер сегмента С квантованного отсчёта определяется как
наименьшее целое из выражения:
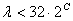 или
или
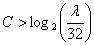
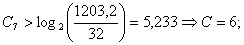
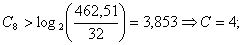
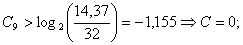
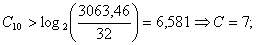
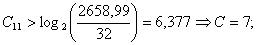
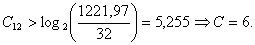
Найдем разность r между
амплитудой входного сигнала и величиной, соответствующей нижней конечности
точке данного сегмента:
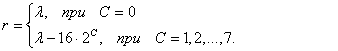
Подставляя значения в формулу, получим:
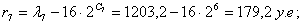
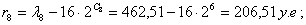
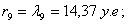
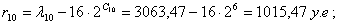
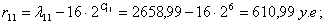
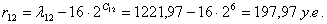
Номер уровня квантования К отсчёта в сегменте определяется
как наименьшее целое из выражения:
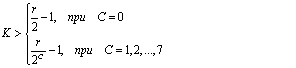
Подставляя значения в формулу, получим:
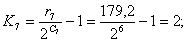
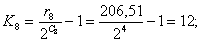
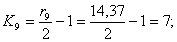
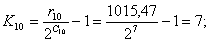
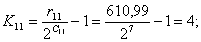
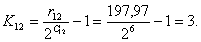
Аналогичные расчеты произведем для 2-го, 3-го и 4-го циклов
передачи. Результаты расчетов сведем в таблицу 4.1.
Таблица 4.1 - Результаты квантования отсчетов по уровню и
их кодирование
|
Номер цикла
|
Номер
исследуемого канала
|
Значение
отсчёта
|
Полярность
отсчёта
|
Код полярности
отсчёта
|
Номер сегмента
|
Код номера
сегмента
|
Уровень
квантования в сегменте
|
Код уровня
квантования в сегменте
|
Закодированное
значение отсчёта
|
|
|
В
|
у. е.
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
1
|
7
|
0,705
|
1203,2
|
+
|
1
|
6
|
110
|
2
|
0010
|
11100010
|
|
8
|
462,51
|
-
|
0
|
4
|
100
|
12
|
1100
|
01001100
|
|
9
|
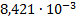
|
14,37
|
+
|
1
|
0
|
000
|
7
|
0111
|
10000111
|
|
10
|
-1,795
|
3063,47
|
-
|
0
|
7
|
111
|
7
|
0111
|
01110111
|
|
11
|
-1,558
|
2658,99
|
-
|
0
|
7
|
111
|
4
|
0100
|
01110100
|
|
12
|
0,716
|
1221,97
|
+
|
1
|
6
|
110
|
3
|
0011
|
11100011
|
|
2
|
7
|
-0,622
|
1061,55
|
-
|
0
|
6
|
110
|
0
|
0000
|
01100000
|
|
8
|
-0,256
|
436,91
|
-
|
0
|
4
|
100
|
11
|
1011
|
01001011
|
|
9
|
0,476
|
812,37
|
+
|
1
|
5
|
101
|
9
|
1001
|
11011001
|
|
10
|
1,122
|
1914,88
|
+
|
1
|
6
|
110
|
13
|
1101
|
11101101
|
|
11
|
0,619
|
1056,43
|
+
|
1
|
6
|
110
|
0
|
0000
|
11100000
|
|
12
|
-0,515
|
878,93
|
-
|
0
|
5
|
101
|
11
|
1011
|
01011011
|
|
3
|
7
|
-0,222
|
378,88
|
-
|
0
|
4
|
100
|
7
|
0111
|
01000111
|
|
8
|
0,499
|
851,63
|
+
|
1
|
5
|
101
|
10
|
1010
|
11011010
|
|
9
|
1,366
|
2331,31
|
+
|
1
|
7
|
111
|
2
|
0010
|
11110010
|
|
10
|
1,756
|
2996,91
|
+
|
1
|
7
|
111
|
7
|
0111
|
11110111
|
|
11
|
1,772
|
3024,21
|
+
|
1
|
7
|
111
|
7
|
0111
|
11110111
|
|
12
|
0,229
|
390,83
|
+
|
1
|
4
|
100
|
8
|
1000
|
11001000
|
|
4
|
7
|
0,794
|
1355,09
|
+
|
1
|
6
|
110
|
5
|
0101
|
11100101
|
|
8
|
-0,189
|
322,56
|
-
|
0
|
4
|
100
|
4
|
0100
|
01000100
|
|
9
|
1,279
|
2182,83
|
+
|
1
|
7
|
111
|
1
|
0001
|
11110001
|
|
10
|
-1,183
|
2018,99
|
-
|
0
|
6
|
110
|
15
|
1111
|
01101111
|
|
11
|
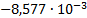
|
14,63
|
-
|
0
|
0
|
000
|
7
|
0111
|
00000111
|
|
12
|
0,095
|
162,13
|
+
|
1
|
3
|
011
|
4
|
0100
|
10110100
|
5. Расчёт погрешностей квантования
Абсолютное значение квантованного отсчета в условных единицах
на выходе кодера при законе компрессии А можно определить как
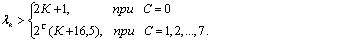
Абсолютное значение квантованного отсчета в единицах измерения
входного сигнала определяется по формуле:
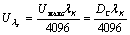
Погрешность (абсолютная) квантования равна
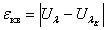
Относительная погрешность квантования определяется по формуле
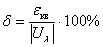
Для первого цикла передачи: 7-ой канал
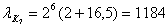
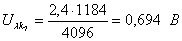
Абсолютная погрешность. Относительная
погрешность.
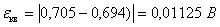
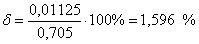
-ой канал
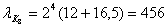
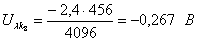
Абсолютная погрешность. Относительная погрешность.
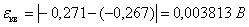
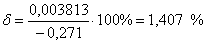
9-ой канал
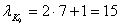
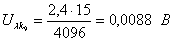
Абсолютная погрешность. Относительная
погрешность.
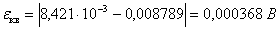
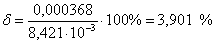
10-ой канал
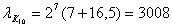
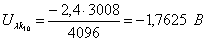
Абсолютная погрешность. Относительная
погрешность.
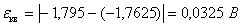
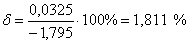
11-ой канал
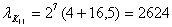
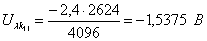
Абсолютная погрешность. Относительная
погрешность.
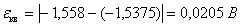
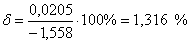
-ой канал
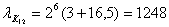
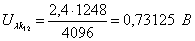
Абсолютная погрешность. Относительная погрешность.
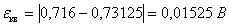
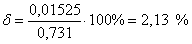
Аналогичные расчеты произведем для 2-го, 3-го и 4-го циклов
передачи. Результаты расчетов сведем в таблицу 5.1.
Таблица 5.1 - Результат расчета погрешностей квантования
|
Номер цикла
|
Номер
исследуемого канала
|
Значение
отсчёта
|
Значение
квантованного отсчёта входного сигнала
|
Абсолютная
погрешность квантования, В
|
Относительная
погрешность квантования, %
|
|
|
В
|
у. е.
|
В
|
у. е.
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
7
|
0,705
|
1203,2
|
0,69375
|
1184
|
0,01125
|
1,595745
|
|
8
|
-0,271
|
462,51
|
-0,26718
|
456
|
0,003813
|
1,406827
|
|
9
|
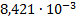
|
14,37
|
0,00879
|
15
|
0,000638
|
3,901044
|
|
10
|
-1,795
|
3063,47
|
-1,7625
|
3008
|
0,0325
|
1,810585
|
|
11
|
-1,558
|
2658,99
|
-1,5375
|
2624
|
0,0205
|
1,315789
|
|
12
|
0,716
|
1221,97
|
0,73125
|
1248
|
0,01525
|
2,129888
|
|
2
|
7
|
-0,622
|
1061,55
|
-0,61875
|
1056
|
0,00325
|
0,522508
|
|
8
|
-0,256
|
436,91
|
-0,25781
|
440
|
0,001812
|
0,708008
|
|
9
|
812,37
|
0,47815
|
816
|
0,002125
|
0,446429
|
|
10
|
1,122
|
1914,88
|
1,10625
|
1888
|
0,01575
|
1,403743
|
|
11
|
0,619
|
1056,43
|
0,61875
|
1056
|
0,00025
|
0,040388
|
|
12
|
-0,515
|
878,93
|
-0,51563
|
880
|
0,000625
|
0,121359
|
|
3
|
7
|
-0,222
|
378,88
|
-0,22031
|
376
|
0,001688
|
0,760135
|
|
8
|
0,499
|
851,63
|
0,49688
|
848
|
0,002125
|
0,425882
|
|
9
|
1,366
|
2331,31
|
1,3875
|
2368
|
0,0215
|
1,573939
|
|
10
|
1,756
|
2996,91
|
1,7625
|
3008
|
0,0065
|
0,370159
|
|
11
|
1,772
|
3024,21
|
1,7625
|
3008
|
0,0095
|
0,536117
|
|
12
|
0,229
|
390,83
|
0,22969
|
392
|
0,000687
|
0,300218
|
|
4
|
7
|
0,794
|
1355,09
|
0,80625
|
1376
|
0,01225
|
1,542821
|
|
8
|
-0,189
|
322,56
|
-0,
19219
|
328
|
0,003187
|
1,686508
|
|
9
|
1,279
|
2182,83
|
1,3125
|
2240
|
0,0335
|
2,619234
|
|
10
|
-1,183
|
2018,99
|
-1,18125
|
2016
|
0,00175
|
0,147929
|
|
11
|
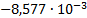
|
14,63
|
-0,00878
|
15
|
0,000212
|
2,472455
|
|
12
|
0,095
|
162,13
|
0,09609
|
164
|
0,001094
|
1,151316
|
6. Формирование линейного сигнала
Цифровые сигналы передаются по разным линиям связи -
кабельным, радиорелейным, волоконно-оптическим, спутниковым. В зависимости от
используемой среды распространения, сигналам в линии придают различный вид, при
котором параметры сигнала в наибольшей степени согласованы с параметрами линии.
Преобразование потока импульсов в код линии происходит в устройстве
согласования с линией.
Сигнал на выходе формирователя импульсов представляет собой
последовательность однополярных импульсов. Энергетический спектр этой
последовательности импульсов зависит от формы используемых импульсов и от
статистических характеристик импульсного потока, определяемых свойствами
кодируемого сигнала и типом кода.
Во избежание искажений этого сигнала из-за неравномерности
амплитудно-частотных характеристик линейного тракта и трудностей выделения
тактовой частоты применяют дополнительное преобразование двоичного цифрового
сигнала. Эта операция часто называется линейным кодированием. Она позволяет
заменить цифровой поток в виде сигнала, характеристики которого в большей
степени соответствуют параметрам линии. Полученный в результате преобразования
сигнал называют кодом линии.
К коду линии предъявляют следующие основные требования:
) Однозначность декодирования. Это означает, что из кода
линии должна однозначно формироваться исходная последовательность двоичных
импульсов;
) В энергетическом спектре сигнала должны быть ослаблены
низкочастотная и высокочастотная составляющие;
) В сигнале должна быть обеспечена высокая плотность
импульсов, т.е. число импульсов должно быть существенно больше числа пробелов.
Для большей концентрации энергии сигнала в области средних
частот, т.е. для ослабления роли его низкочастотных и высокочастотных
составляющих, успешно применяются квазитроичные (трехуровневые) коды. При
использовании квазитроичных кодов линейный сигнал в каждом тактовом интервале
может принимать одно из трех возможных значений: +1, 0, - 1, выраженных
соответственно положительным импульсом, пробелом или отрицательным импульсом,
которые с целью упрощения будем обозначать соответственно +, 0, - . Решающее
устройство регенератора должно распознавать три возможных уровня сигнала.
Однако это не значит, что для нумерации уровней квантования применяется
троичная система счисления - кодирование остается двоичным, лишь на входе линии
двоичный сигнал преобразуется в квазитроичный.
Во многих случаях исходный двоичный сигнал преобразуется в
код линии делением последовательности двоичных импульсов на группы и заменой
каждой из этих групп кодовой комбинацией кода линии с другим основанием. Такие
коды принято обозначать двумя буквами и двумя цифрами. Первая цифра определяет,
какое число импульсов исходного кода входит в перекодируемую группу. Затем
следует буква В (binary), указывающая на двоичное основание системы
счисления исходного кода. Вторая цифра соответствует числу импульсов в каждой
кодовой комбинации кода линии. Наконец, вторая буква обозначает основание
системы счисления: Т - троичное (ternary), Q - четверичное (quaternary) и т.д.
Примером кода 2В2Т является парно-избирательный
троичный (ПИТ) код. В процессе его формирования входной двоичный сигнал разбивается
на пары импульсов и каждой такой паре ставится в соответствие пара троичных
импульсов нового кода линии.
Правило формирования ПИТ-кода представлено в таблице 3, из
которой видно, что пары импульсов 00 и 11 преобразуются всегда однозначно, а
пары 01 и 10 преобразуются таким образом, чтобы положительные и отрицательные
импульсы кода 2В2Т встречались одинаково часто. Тогда код 2В2Т
оказывается полярно сбалансированным. Код 2В2Т является квазитроичным,
поскольку для передачи двоичных импульсов используются три уровня линейного
сигнала.
Таблица 6.1 - Формирование кода 2В2Т
|
Двоичный код
|
Код 2В2Т
|
Условие выбора
|
|
00
|
-+
|
|
|
11
|
+-
|
|
|
01
|
+0
|
Если предыдущая
пара 01 или 10 была представлена через "-0" или "0-"
|
|
-0
|
Если предыдущая
пара 01 или 10 была представлена через "+0" или "0+"
|
|
10
|
0-
|
Если предыдущая
пара 01 или 10 была представлена через "+0" или "0+"
|
|
0+
|
Если предыдущая
пара 01 или 10 была представлена через "-0" или "0-"
|
При использовании кода 2В2Т не может возникнуть
более двух пробелов подряд. Частота следования троичных импульсов у
рассмотренных кодов совпадает с тактовой частотой 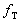 исходного двоичного кода.
исходного двоичного кода.
Хорошими данными обладает код 4В3Т, Он позволяет
снизить скорость передачи импульсов в линии по сравнению с передачей двоичных
импульсов на 33 %. Процедура перекодирования в троичный код 4В3Т
состоит в отображении четырех двоичных импульсов в три троичных. Из четырех
двоичных импульсов могут быть составлены 24 = 16 различных
комбинаций, а из трех троичных 33 = 27. При построении кодовой
таблицы из 27 троичных кодовых комбинаций надо выбрать 16 наиболее
благоприятных, т.е. существует значительная гибкость в их выборе. Например,
комбинацию, состоящую из трех нулей, целесообразно не использовать, чтобы
ограничить число нулей, идущих подряд в цифровом потоке.
В таблице 6.2 представлен один из возможных вариантов
преобразования двоичного кода в код передачи 4B3T.
Троичные комбинации в третьем столбце сбалансированы по величине
постоянной составляющей (Uпост = 0). Кодовые комбинации из второго и
четвертого столбцов для поддержания нулевого баланса постоянной составляющей
выбираются поочередно. Если было передано больше положительных импульсов, чем
отрицательных, выбирается второй столбец. Когда расхождение между числом положительных
и отрицательных импульсов меняется на обратное - выбирается четвертый столбец.
Таблица
6.2 - Формирование кода 4B3T
|
Двоичный код
|
Троичная
кодовая комбинация
|
|
─
|
0
|
+
|
|
1
|
2
|
3
|
4
|
|
0000
|
─ ─
─
|
|
+++
|
|
0001
|
─ ─
0 ─0
|
|
++0
|
|
0010
|
─0─
|
|
+0+
|
|
0011
|
0─ ─
|
|
0++
|
|
0100
|
─ ─+
|
|
++─
|
|
0101
|
─+─
|
|
+─+
|
|
0110
|
+─ ─
|
|
─++
|
|
0111
|
─00
|
|
+00
|
|
1000
|
0─0
|
|
0+0
|
|
1001
|
00─
|
|
00+
|
|
1010
|
|
0+─
|
|
|
1011
|
|
0─+
|
|
|
1100
|
|
+0─
|
|
|
1101
|
|
─0+
|
|
|
1110
|
|
+─0
|
|
|
1111
|
|
─+0
|
|




За четыре цикла передачи для заданных кодов с высокой плотностью
следования единиц рассчитать вероятности появления единиц в линейном сигнале по
формуле
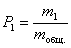 ,
,
где 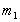 ─ количество единиц (+1, - 1) в линейном сигнале за
четыре цикла;
─ количество единиц (+1, - 1) в линейном сигнале за
четыре цикла;
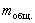 ─
общее количество импульсов (+1, 0, - 1) в линейном сигнале за четыре цикла.
─
общее количество импульсов (+1, 0, - 1) в линейном сигнале за четыре цикла.
В сигнале 2B2T: 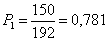
В сигнале 4В3Т: 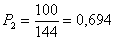
.
Расчет спектра линейного сигнала
Цифровые сигналы передаются по разным линиям связи -
кабельным, радиорелейным, волоконно-оптическим, спутниковым. В зависимости от
используемой среды распространения, сигналам в линии придают различный вид, при
котором параметры сигнала в наибольшей степени согласованы с параметрами линии.
Преобразование потока импульсов в код линии происходит в устройстве
согласования с линией (УСЛ). Для большей концентрации энергии сигнала в области
средних частот, т.е. для ослабления роли его низкочастотных и высокочастотных
составляющих, успешно применяются квазитроичные (трехуровневые) коды. При
использовании квазитроичных кодов линейный сигнал в каждом тактовом интервале
может принимать одно из трех возможных значений: +1, 0, - 1, выраженных
соответственно положительным импульсом, пробелом или отрицательным импульсом,
которые с целью упрощения будем обозначать соответственно +, 0, - . Решающее
устройство регенератора должно распознавать три возможных уровня сигнала. При
этом кодирование остается двоичным, лишь на входе линии двоичный сигнал
преобразуется в квазитроичный.
В данной системе передачи в качестве линейных сигналов
используются коды 2B2T
и 4B3T.
При передаче цифровых сигналов в качестве выходного сигнала
не используют сигнал на выходе кодера, так как он представляет собой
неравномерную последовательность однополярных импульсов.
Чтобы избежать искажения сигнала из-за АЧХ линии и трудностей
выделения тактовой частоты применяют дополнительное преобразование двоичного
сигнала. Эта операция называется линейным кодированием. Она позволяет заменить
цифровой поток в виде сигнала, характеристики которого в большей степени
соответствуют параметрам линии. Полученный в результате код называют кодом
линии.
В качестве линейных импульсов используются треугольные
импульсы. Рассчитаем спектр одиночного треугольного импульса. Одиночный
треугольный импульс описывается выражением:
0,t <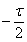
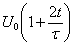 ,
,
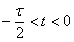 (7.1)
(7.1)
U (t) = 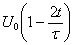
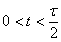
, 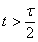
Энергетический спектр линейного сигнала описывается выражением:
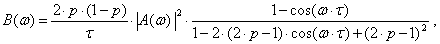 (7.2)
(7.2)
где G (w) - спектр одиночного треугольного
импульса;
p - вероятность появления единиц;
t - длительность кодового символа.
Спектр одиночного треугольного импульса:
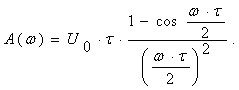
Вероятность появления единиц для кода 2B2T:
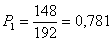
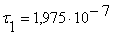
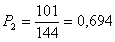
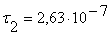
Произведём расчёт спектров и сведём полученные данные в таблицу
7.1 и 7.2 Также приведём по одному расчёту для
каждого из спектров при
i=2.
Для кода 2B2T:

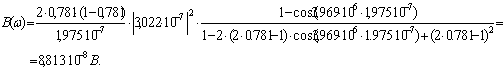
Для кода 4B3T:

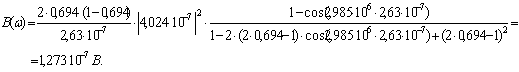
Таблица 7.1 - Результаты расчета энергетического спектра квазитроич - ного
кода 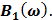
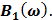
|
i
|
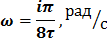
|
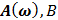
|
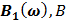
|
|
0
|
0
|
0
|
0
|
|
1
|
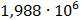
|
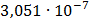
|
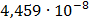
|
|
2
|
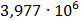
|
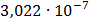
|
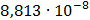
|
|
3
|
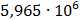
|
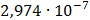
|
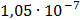
|
|
4
|
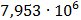
|
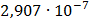
|
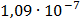
|
|
5
|
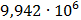
|
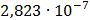
|
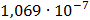
|
|
6
|
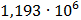
|
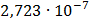
|
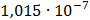
|
|
7
|
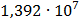
|
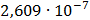
|
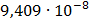
|
|
8
|
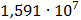
|
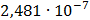
|
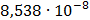
|
|
9
|
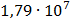
|
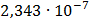
|
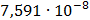
|
|
10
|
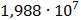
|
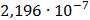
|
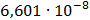
|
|
11
|
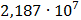
|
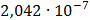
|
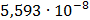
|
|
12
|
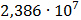
|
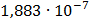
|
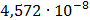
|
|
13
|
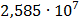
|
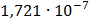
|
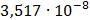
|
|
14
|
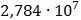
|
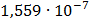
|
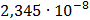
|
|
15
|
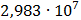
|
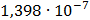
|
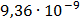
|
|
16
|
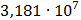
|
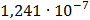
|
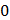
|
|
17
|
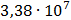
|
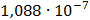
|
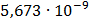
|
|
18
|
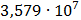
|
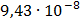
|
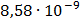
|
|
19
|
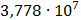
|
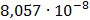
|
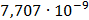
|
|
20
|
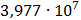
|
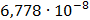
|
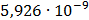
|
|
21
|
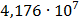
|
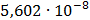
|
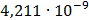
|
|
22
|
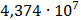
|
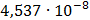
|
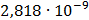
|
|
23
|
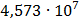
|
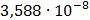
|
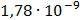
|
|
24
|
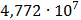
|
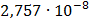
|
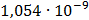
|
|
25
|
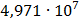
|
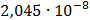
|
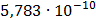
|
|
26
|
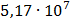
|
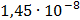
|
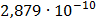
|
|
27
|
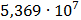
|
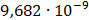
|
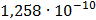
|
|
28
|
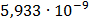
|
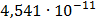
|
|
29
|
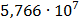
|
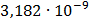
|
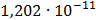
|
|
30
|
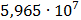
|
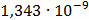
|
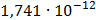
|
|
31
|
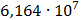
|
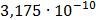
|
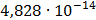
|
|
32
|
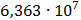
|
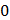
|
0
|
|
33
|
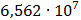
|
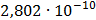
|
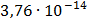
|
|
34
|
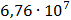
|
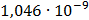
|
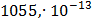
|
|
35
|
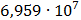
|
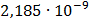
|
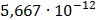
|
|
36
|
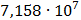
|
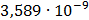
|
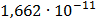
|
|
37
|
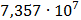
|

|
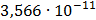
|
|
38
|
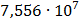
|
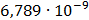
|
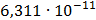
|
|
39
|
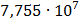
|
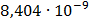
|
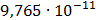
|
|
40
|
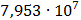
|
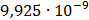
|
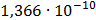
|
|
41
|
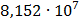
|
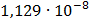
|
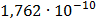
|
|
42
|
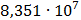
|
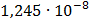
|
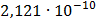
|
|
43
|
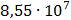
|
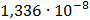
|
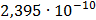
|
|
44
|
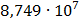
|
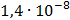
|
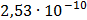
|
|
45
|
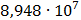
|
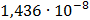
|
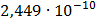
|
|
46
|
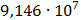
|
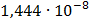
|
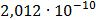
|
|
47
|
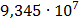
|
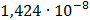
|
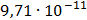
|
|
48
|
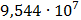
|
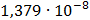
|
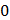
|
|
49
|
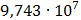
|
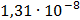
|
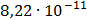
|
|
50
|
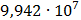
|
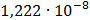
|
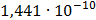
|
Таблица 7.2 - Результаты расчета энергетического спектра квазитроич - ного
кода 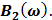
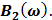
|
i
|
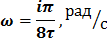
|
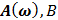
|
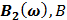
|
|
0
|
0
|
0
|
0
|
|
1
|
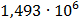
|
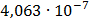
|
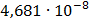
|
|
2
|
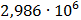
|
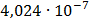
|
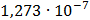
|
|
3
|
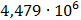
|

|
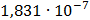
|
|
4
|
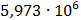
|
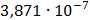
|
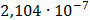
|
|
5
|
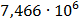
|
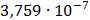
|
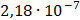
|
|
6
|
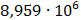
|
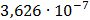
|
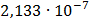
|
|
7
|
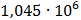
|
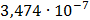
|
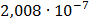
|
|
8
|
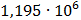
|
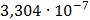
|
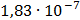
|
|
9
|
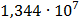
|
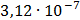
|
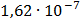
|
|
10
|
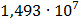
|
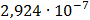
|
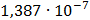
|
|
11
|
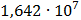
|
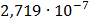
|
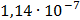
|
|
12
|
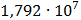
|
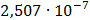
|
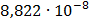
|
|
13
|
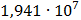
|
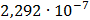
|
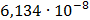
|
|
14
|
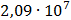
|
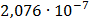
|
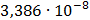
|
|
15
|

|
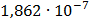
|
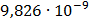
|
|
16
|
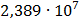
|
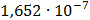
|
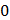
|
|
17
|
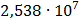
|
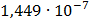
|
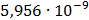
|
|
18
|
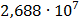
|
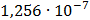
|
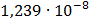
|
|
19
|
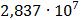
|
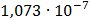
|
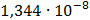
|
|
20
|
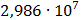
|
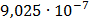
|
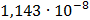
|
|
21
|
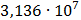
|
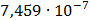
|
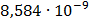
|
|
22
|
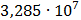
|
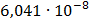
|
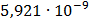
|
|
23
|
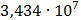
|
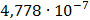
|
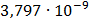
|
|
24
|
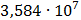
|
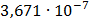
|
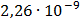
|
|
25
|
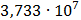
|
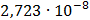
|
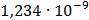
|
|
26
|
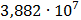
|
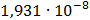
|
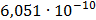
|
|
27
|
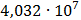
|
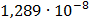
|
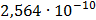
|
|
28
|
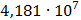
|
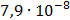
|
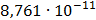
|
|
29
|
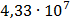
|
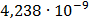
|
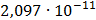
|
|
30
|
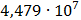
|
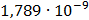
|
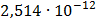
|
|
31
|
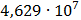
|
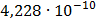
|
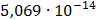
|
|
32
|
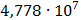
|
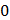
|
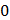
|
|
33
|
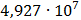
|
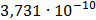
|
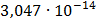
|
|
34
|
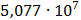
|
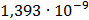
|
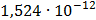
|
|
35
|
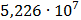
|
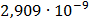
|
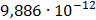
|
|
36
|
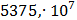
|
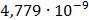
|
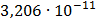
|
|
37
|
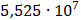
|
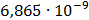
|
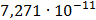
|
|
38
|
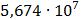
|
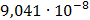
|
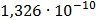
|
|
39
|
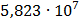
|
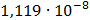
|
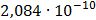
|
|
40
|
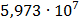
|
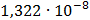
|
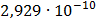
|
|
41
|
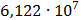
|
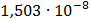
|
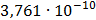
|
|
42
|
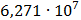
|
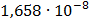
|
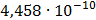
|
|
43
|
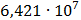
|
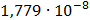
|
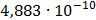
|
|
44
|
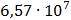
|
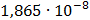
|
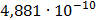
|
|
45
|
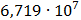
|
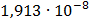
|
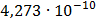
|
|
46
|
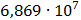
|
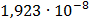
|
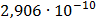
|
|
47
|
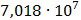
|
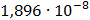
|
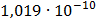
|
|
48
|
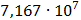
|
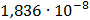
|
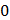
|
|
49
|
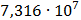
|
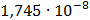
|
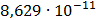
|
|
50
|
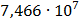
|
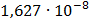
|
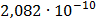
|
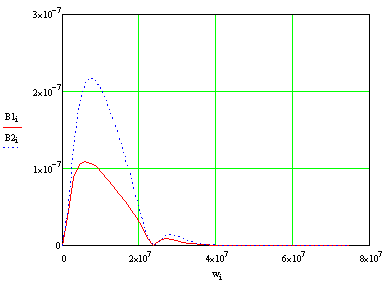
Рисунок 7.1 - Энергетический спектр для заданных
квазитроичных кодов
При построении группового энергетический спектра по
горизонтальной оси отложена циклическая частота. По вертикальной оси отложен
модуль спектральной плотности квазитроичного линейного кода и однополярной
последовательности импульсов.
На графике представлены энергетические спектры квазитроичных
кодов 2В2Т и 4В3Т. По графику можно сделать вывод, что код 4В3Т является более
эффективным, потому что большая часть мощности спектра этого кода размещается в
меньшей полосе частот.
8.
Разработка структурной схемы многоканальной системы передачи с ИКМ
Принцип работы передающего устройства поясняет структурная
схема системы передачи. Сообщения l1 (t), l2 (t),., l34 (t) от 1, 2,., 34 источников информации (абонентов) через
фильтры нижних частот (ФНЧ) и усилители низких частот (УНЧ) поступают на
канальные амплитудно-импульсные модуляторы АИМ (ключи). С помощью
АИМ-модуляторов осуществляется дискретизация передаваемых сигналов времени и
формирование группового АИМ-сигнала (гр. АИМпер). Управляют работой
АИМ-модуляторов последовательности управляющих канальных импульсов УКИ1-УКИ31,
поступающие от генераторного оборудования ГОпер. На АИМ-модуляторы
каналов канальные импульсы подаются поочередно, при этом длительность каждого
канального интервала составляет примерно T0/ (3.4) N0. Групповой АИМ-сигнал
поступает на кодирующее устройство (кодер), которое одновременно с кодированием
осуществляет операцию квантования по уровню.
Сигналы управления и взаимодействия (СУВ), передаваемые по
телефонным каналам для управления приборами автоматических телефонных станций
(АТС), поступают в передатчик СУВ (Пер. СУВ), где они дискретизуются
импульсными последовательностями СУВ, следующими от ГОпер. В
результате формируется групповой сигнал передачи СУВ (Гр. СУВ).
В устройстве объединения (УО) групповые сигналы, следующие от
кодера передатчика СУВ, а также передатчика синхросигналов (Пер. СС),
объединяются, образуя так называемый ИКМ - сигнал. Здесь формируется диаграмма
временных циклов системы, определяющая порядок следования циклов в сверхцикле и
кодовых групп в цикле передачи.
Сформированный ИКМ-сигнал представляет собой набор
однополярных двоичных символов, импульсы которых всегда имеют только одну
полярность, и не согласован с параметрами линии. При передачи по линии связи
такой сигнал подвержен значительным искажениям и быстро затухает. Поэтому перед
передачей в линию однополярный ИКМ-сигнал преобразуется в биполярный линейный
ИКМ-сигнал. Это происходит в преобразователе кода передачи ПКпер.
В процессе передачи по линии связи ИКМ-сигнал периодически
восстанавливается линейным регенератором (РЛ). На приеме сигнал
восстанавливается станционным регенератором (РС).
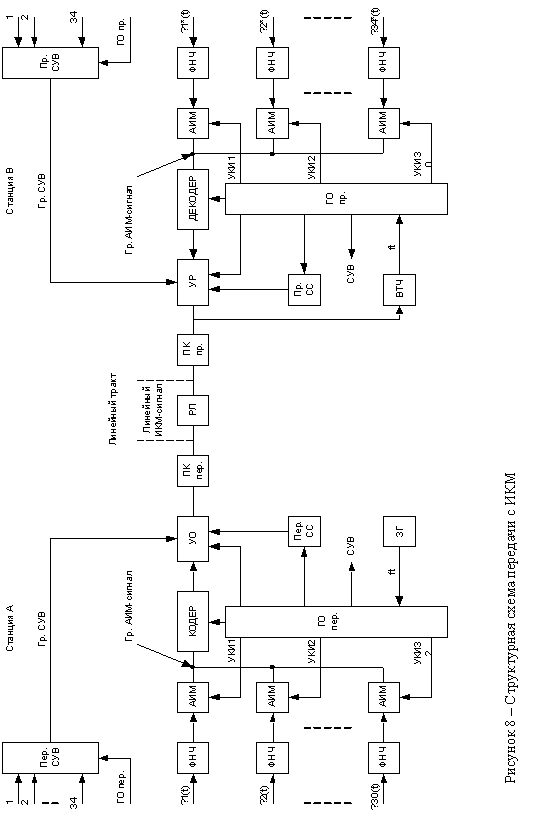
Рисунок 8.1 - Структурная схема передающего устройства
Заключение
В данной курсовой работе разработана цифровая многоканальная
система передачи аналоговых сообщений. Был произведён расчёт основных
параметров проектируемой цифровой системы информации: количество всех каналов,
организуемых по ИКМ-ВД, длительность канального интервала, временной интервал
между кодовыми символами в канальном интервале, длительность кодового символа,
тактовая частота линейного сигнала, длительность АИМ-импульсов с выхода
дискретизатора, требуемая полоса пропускания линейного тракта для системы
передачи с ИКМ-ВД.
Рассчитан спектр АИМ-сигнала: постоянная составляющей
спектра, нулевая, верхняя и нижняя частоты, значения гармонических составляющих
для гармоник 1, 7, 9, 19, 28, 44 и построена спектральная диаграмма АИМ
сигнала.
Основные преимущества систем передачи с ИКМ заключаются в
следующем:
1.
Высокая
помехоустойчивость за счет передачи сообщений двоичными сигналами.
2.
Меньшая чувствительность к искажениям.
3.
Удобство
настройки и эксплуатации цифровых систем.
4.
Возможность
использования сравнительно простых методов запоминания и хранения сообщений.
Недостатком данной системы связи является расширение полосы
частот, требуемой для передачи сообщений.
Построены временные диаграммы входных сигналов для 4 циклов
дискретизации сообщения по времени.
Произведено квантование отсчётов по закону компандирования типа 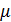
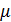 и
их кодирование кодами 2В2Т и 4В3Т. Рассчитаны погрешности квантования.
и
их кодирование кодами 2В2Т и 4В3Т. Рассчитаны погрешности квантования.
Построены временные диаграммы линейных сигналов для 4-х циклов.
Выполнен расчёт энергетического спектра линейного сигнала.
Разработанная система может использоваться для передачи речевых
каналов с повышенным качеством и для других целей.
Литература
1.
В.С.
Кострома, М.В. Нафтольский, В.Н. Фомичев. Цифровые системы передачи. Гомель:
БелИИЖТ, 1991.
2.
В.С.
Кострома, В.Н. Фомичев, В.Г. Шевчук Спектры видеоимпульсов. Пособие для
самостоятельной работы студентов по специальности "Автоматика,
телемеханика и связь на транспорте" по дисциплине "Теоретические
основы транспортной связи".
3.
М.Я.
Каллер, А.Ф. Фомин "Теоретические основы транспортной связи". М.: Транспорт,
1989.
4.
С.И.
Баскаков "Радиотехнические цепи и сигналы". М.: Радио и связь, 1988.
5.
Фомичев
В.Н. Цифровая система передачи информации: Пособие по курсовому проектированию.
- Гомель: БелГУТ, 2003. - 71 с.