Имитационное моделирование системы управления запасами с неудовлетворенным спросом
ФГОУ СПО «Волгоградский технологический
коледж»
Курсовой
проект
Имитационное
моделирование системы управления запасами с неудовлетворенным спросом
Содержание
1. Введение
. Понятие моделирования
. Системы и
модели управления запасами
4. Описание системы
4.1 Модельное время
.2 Классы и объекты
4.3 События и методы
5. Реализация программы
6. Анализ результатов
7. Заключение
8. Список использованной
литературы
1. Введение
Неизбежная рассогласованность ритма производства поставщиков
и потребителей, дискретность процесса поставок, возможность случайных колебаний
в интенсивности потребления или длительности интервалов между поставками
относительно среднего (расчетного) уровня вынуждают создавать в системах
снабжения запасы. Проблема совершенствования управления во всех звеньях
народного хозяйства очень важна. Хозяйственные организации представляют собой
сложные системы. Эффективность систем зависит от качества организационного
управления ими. Возросшая интенсивность производства и взаимозависимость
большого числа предприятий увеличивают экономический ущерб от просчетов в
планировании и предъявляют повышенные требования к качеству управления.
При решении широкого круга задач оптимизации управляющих решений по-лезны
методы теории управления запасами. Управление запасами в общем случае состоит
во взаимодействии на соотношение между двумя основными факторами - пополнением
и расходом запасов. Ясно, что чрезмерно большой запас приводит к избытку
материальных ценностей и требует больших затрат на хранение, недостаточный
запас может привести к перебоям в работе. Цель управления - оптимизация
некоторого критерия, зависящего от расходов на хранение запасов, стоимости
поставок, затрат, связанных с пополнением, штрафов и т. д.
Под запасами можно понимать выпускаемую некоторым
предприятием продукцию (пополнение), которая поставляется потребителем
определенными партиями (расход). При этом спрос на продукцию может быть
детерминированным или случайным. Управление запасами здесь состоит в
определении размеров необходимого выпуска продукции для удовлетворения данного
спроса при условии минимизации суммарных затрат на хранение и пополнение
запасов.
Под запасами можно понимать также запасы сырья или других
материалов, поставляемые дискретными партиями (пополнение) и обеспечивающие
непрерывное потребление в процессе производства (расход). Критерием
оптимальности могут служить суммарные затраты на поставки и хранение запасов. Запасами могут быть товары,
поставляемые в торговую сеть определенными партиями и предназначенные для
удовлетворения непрерывного случайного спроса. Критерий оптимизации - суммарные
затраты на поставки, хранение запасов и изменение производственного ритма в
связи с вариациями спроса.
Запасы - это и
сезонные товары, сохраняющиеся на складе ограниченной емкости. Их можно
покупать и продавать в различных количествах по ценам, меняющимся во времени.
Задача состоит в определении политики покупок и продаж, обеспечивающих максимум
суммарной прибыли. Капитал тоже может рассматриваться как запас, причем цена его
хранения определяется темпом инфляции.
Существует несколько причин относительно необходимости
создания запасов. Согласно одной из них наличие запасов позволяет быстро
удовлетворять запросы потребителей. Согласно другой
наличие запасов позволяет поставщику нейтрализовать колебания спроса в условиях
неравномерного потребления.
Весьма важной причиной, особенно для нашей страны, является
сезонность производства многих важнейших видов продовольствия зерна, овощей,
фруктов, и связанная с этим необходимость создания весьма больших запасов этих
видов продовольствия. Весомой причиной является также удаленность многих мест
потребления той или иной продукции от мест ее производства. Сравнительно
большие транспортные издержки на доставку этой продукции вынуждает доставлять
ее большими партиями, тем самым создавать запасы. К созданию запасов вынуждает
иногда необходимость отправлять произведенную продукцию (или сырье,
полуфабрикаты и т. п., т. е. запасы) сравнительно большими партиями (по
требованию транспортных организаций или по другим причинам).
Создание запасов требует больших затрат:
· запасы нужно где-то хранить, для этого нужно
строить соответствующие складские помещения, а они довольно дороги и окупаются
не очень быстро;
· значительные запасы ведут к омертвлению
вложенных в них средств;
· как правило, хранение запасов ведет к
ухудшению их характеристик, к их моральному старе нию.
Нельзя не согласиться с Ю.А. Беляевым в том, что «без запасов
никто и ничто существовать не может: ни
машина, ни человек, ни государство, ни вселенная. Без запаса прочности мост
разрушиться, а парашют прорвется при малейшей перегрузке. Надежность
технической системы создается запасом прочности конструкций, дублированием
элементов, приданием запчастей. Портфель заказов редакции обеспечивает
равномерную загрузку сотрудников и работу типографии. Запас мудрости
руководителей позволяет им предвидеть будущие заботы и разглядеть пророков в
своем отечестве; оценить неординарные идеи и справедливую критику; понять
пользу плюрализма мнений и гражданских свобод. Запасы скудоумия, инерции,
профессиональной неграмотности могут привести к не менее поразительным
результатам».
Избыточные запасы были причиной многих неудач в бизнесе,
оказывали дестабилизирующее влияние при кризисах. Излишние запасы являются
тормозом на пути научно-технического прогресса. Переход на новый вид продукции
обычно сдерживается требованием выработки всех именных запасов или
дорогостоящим списанием их. Все эти проблемы обострились в связи с ускорением
научно-технического прогресса, диверсификацией спроса и индивидуализацией
производства, сокращением сроков морального старения техники. Возросли
сложность решаемых задач и цена ошибочных решений. Сложившаяся ситуация вызвала
необходимость разработки разнообразных систем управлений запасами.
Целью данной курсовой работы является разработка модели системы управления запасами. Основой для разработки
модели в данной курсовой работе является метод имитационного моделирования. Так
же курсовая работа предполагает создание программы на языке C++, обеспечивающей ввод исходной
информации, ее обработку, реализацию алгоритма имитации процесса и выдачу
необходимой информации.
2. Понятие моделирования
моделирование программа
управление запас
Модель - это любой образ, аналог, мысленный или установленный,
изображение, описание, схема, чертеж, и т.п. какого-либо объекта, процесса или
явления, который в процессе познания (изучения) замещает оригинал, сохраняя
некоторые важные для данного исследования типичные свойства.
Моделирование - это исследование какого-либо объекта или
системы объектов путем построения и изучения их моделей. А также - это
использование моделей для определения или уточнения характеристик и
рационализации способов построения вновь конструируемых объектов.
Модель является средством для изучения сложных систем.
В общем случае сложная система представляется как
многоуровневая конструкция из взаимодействующих элементов, объединяемых в
подсистемы различных уровней. К сложным системам, в т.ч., относятся
информационные системы. Проектирование таких сложных систем осуществляется в
два этапа.
). Внешнее проектирование.
На этом этапе проводят выбор структуры системы, основных ее
элементов, организации взаимодействия между элементами, учет воздействия
внешней среды, оценка показателей эффективности системы.
). Внутреннее проектирование - проектирование отдельных
элементов системы.
Типичным методом исследования сложных систем на первом этапе
является моделирование их на ЭВМ. В результате моделирования получаются зависимости, характеризующие
влияние структуры и параметров системы на ее эффективность, надежность и другие
свойства. Эти зависимости используются для получения оптимальной структуры и
параметров системы.
Модель, сформулированная на языке математики с использованием
математических методов называется математической моделью.
Имитационное моделирование - воспроизведение на компьютере
(имитация) процесса функционирования исследуемой системы. Для него не требуется
приведение математической модели к виду, разрешимому относительно искомых
величин.
Для имитационного моделирования характерно воспроизведение
явлений, описываемых математической моделью, с сохранением их логической
структуры, последовательности чередования во времени. Для оценки искомых
величин может быть использована любая подходящая информация, циркулирующая в
модели, если только она доступна для регистрации и последующей обработке.
Искомые величины при исследовании процессов методом
имитационного моделирования обычно определяют как средние значения по данным
большого числа реализаций процесса. Если число реализаций N, используемых для
оценки искомых величин, достаточно велико, то в силу закона больших чисел
получаемые оценки приобретают статистическую устойчивость и с достаточной для
практики точностью могут быть приняты в качестве приближенных значений искомых
величин.
3. Системы и модели управления запасами
Возникновение теории управления запасами можно связать с работами Ф.
Эджуорта и Ф. Харриса, появившимися в конце XIX - начале XX вв., в которых
исследовалась простая оптимизационная модель определении экономичного размера
партии поставки для складской системы с постоянным равномерным расходом и
периодическим поступлением хранимого продукта. Запасами называется любой ресурс
на складе, который используется для удовлетворения будущих нужд. Примерами
запасов могут служить полуфабрикаты, готовые изделия, материалы, различные
товары, а также такие специфические товары, как денежная наличность,
находящаяся в хранилище. Большинство организаций имеют примерно один тип
системы планирования и контроля запасов. В банке используются методы контроля
за количеством наличности, в больнице применяются методы контроля поставки
различных медицинских препаратов. Простейшая схема системы управления запасами
выглядит следующим образом (рис 1):
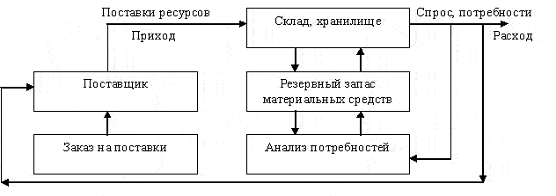
Рис.
1. Система управления запасами
Существуют
причины, побуждающие организации создавать запасы:
1. дискретность поставок при непрерывном потреблении;
2. упущенная прибыль;
. случайные колебания:
· в спросе за период между поставками;
· в объеме поставок;
· в длительности интервала между поставками;
4. предполагаемые изменения конъюнктуры:
· сезонность спроса;
· сезонность производства;
· ожидаемое повышение цен.
Имеются также причины, побуждающие предприятия стремиться к минимизации
запасов на складе:
· плата за физическое хранение запаса;
· потери в количестве запаса;
· моральный износ продукта.
Рассмотрим определяющие понятия теории управления запасами.
Издержки выполнения заказа (издержки заказа) - накладные расходы, связанные
с реализацией заказа. В промышленности такими издержками являются затраты на
подготовительно-заготовочные операции.
Издержки хранения - расходы, связанные с физическим содержанием товаров
на складе, плюс возможные проценты на капитал, вложенный в запасы. Обычно они
выражаются или в абсолютных единицах, или в процентах от закупочной цены и
связываются с определенным промежутком времени.
Упущенная прибыль - издержки, связанные с неудовлетворительным спросом,
возникающим в результате отсутствия продукта на складе.
Совокупные издержки за период представляют собой сумму издержек заказа,
издержек хранения и упущенного дохода. Иногда к ним прибавляются издержки на
покупку товаров.
Срок выполнения заказов - срок между заказом и его выполнением.
Точка восстановления - уровень запаса, при котором делается новый заказ.
Основные модели управления запасами:
.Модель оптимального размера заказа.
Предпосылки:
1. темп спроса на товар известен и постоянен;
2. получение заказа мгновенно;
. единственные меняющиеся параметры - издержки заказа и хранения;
. исключается дефицит в случае своевременного заказа.
Исходные данные: темп спроса; издержки заказа и хранения. Результат:
оптимальный размер заказа; время между заказами и их количество за период.
. Модель оптимального размера заказа в предположении, что получение
заказа не мгновенно. Следовательно, нужно найти объем запасов, при котором
необходимо делать новый заказ.
Исходные данные: темп спроса; издержки заказа и хранения; время
выполнения заказа.
Результат: оптимальный размер заказа; время между заказами; точка
восстановления запаса.
. Модель оптимального размера заказа в предположении, что допускается
дефицит продукта и связанная с ним упущенная прибыль. Необходимо найти точку
восстановления.
Исходные данные: темп спроса; издержки заказа и хранения; упущенная
прибыль.
Результат: оптимальный размер заказа; время между заказами; точка
восстановления запаса.
. Модель с учетом производства (в сочетании с условиями 1 - 3).
Необходимо рассматривать уровень ежедневного производства и уровень ежедневного
спроса.
Исходные данные: темп спроса; издержки заказа и хранения; упущенная
прибыль; темп производства.
Результат: оптимальный уровень запасов (точка восстановления)
. Модель с количественными скидками. Появляется возможность
количественных скидок в зависимости от размера заказа. Рассматривается
зависимость издержек хранения от цены товара. Оптимальный уровень заказа
определяется исходя из условия минимизации общих издержек дл каждого вида
скидок.
4.
Описание системы
В большом универмаге планируется ввести систему управления
запасами рдиоприемников. Время между поступлениями запросов покупателей на
покупку ра-диоприемника распределено экспоненциально с математическим
ожиданием0,2 недели. Если покупателю потребовался радиоприемник, а его нет в
запасе,покупатель в 80% случаев отправляется в ближайший магазин, представляя
со-бой тем самым несостоявшуюся для данного универмага продажу. В 20% такихслучаев
делается повторный заказ, и покупатели ждут поступления следующейпартии товара.
Магазин использует периодическую систему просмотра состоя-ния запасов, в
которой запас просматривается каждые 4 недели и принимаетсярешение о
необходимости осуществления (размещения) заказа на новую партиютовара.
Стратегия принятия решения состоит в размещении заказа, доводящегозапас до
контрольного уровня - 72 радиоприемников. Текущее состояние запасаопределяется
как наличный запас плюс заказанные ранее универмагом радио-приемники минус
неудовлетворенный спрос, под которым понимаются упомя-нутые ранее 20%
покупателей. Если текущее состояние запаса меньше или равно18 радиоприемникам
(точка заказа), заказ размещается. Время доставки заказа(между его размещением
и получением) постоянно и составляет 3 недели.
Необходимо смоделировать систему управления запасами за 6 лет
(312 недель)для получения статистических данных о следующих величинах:
· числе радиоприемников в запасе;
· неудовлетворенном спросе;
· количестве несостоявшихся продаж и
времени между ними.
Начальные условия для имитации: состояние запаса - 72
радиоприемника, неудовлетворенного спроса нет. Чтобы уменьшить смещение
статистических данных из-за начальных условий, все статистические данные,
накопленные к концупервого года шестилетнего периода имитации, должны очищаться
(обнуляться).
4.1 Модельное время
В качестве единицы модельного времени принимаем 1 ч. В самом
деле, если пе-ресчитать 0,2 недели в днях, получим среднее время между
поступлениями за-просов на покупку радиоприемника, равное 1,4. Следовательно,
день - слишкомгрубая единица времени, потому что при округлении
экспоненциальной случай-ной величины со средним 1,4 до ближайшего целого нам
придется отбрасыватьдробные части, сравнимые с самой случайной величиной. 1,4
дня составляет 33,6 ч, поэтому интенсивность
входного потока равна 1/33,6 ≈ 0,03 - ее мы иподставим в качестве
параметра экспоненциального распределения.
Тогда общая продолжительность
моделирования составит
312 • 7 • 24 = 52 416 ч - тактов модельного времени.
Значения же постоянных промежутком времени (4 недели и3
недели) представим в программе в днях (соответственно, 28 и 21).
При
инициализации объекта Супермаркет (Supermarket)
разыгрываем время, оставшееся до очередного просмотра состояния запасов, как
целочисленную случайную величину, равномерно распределенную на временном
отрезке 4 недели.
Если этот
отрезок выразить в часах, то выражение, вычисляющее случайную величину, должно
быть таким: rand()%672+l; если в днях - (rand)%28+l)*24. Второевыражение реализует равномерное распределение точнее.
Дело в том, что функция rand возвращает целочисленную случайную величину, равномерно распре-деленную
на отрезке от 0 до 32 767. Если необходимо снизить верхнюю границуинтервала до
некоторого числа К, то конструкция rand %K обеспечит равномерное распределение
только в том случае, если 32 768 делится на К без остатка. В противном случае некоторые значения
будут более вероятны, другие - менее. Нетрудно заметить, что нарушение равномерности распределения
будет тембольше, чем больше К. Например, для К = 3 различиями можно пренебречь,а для К = 32 767 значение 0 будет в два раза
вероятнее всех остальных. Поэтому при генерации равномерной случайной величины мы снижаем значение
делите-ля, а затем результат умножаем на 24. Этим мы нисколько не нарушаем
логику моделирования. Да и с точки
зрения здравого смысла, любой человек в описанной в задаче ситуации на вопрос:
«Сколько времени осталось до проверки?» -даст ответ в днях, а не в часах.
4.2 Классы и объекты
Данная задача по сути представляет собой усложненный вариант
процесса случайного блуждания, где в качестве случайной величины выступает
текущий запас товара. Система является открытой, а количество заявок в ней -
переменной величиной без фиксированной верхней границы. Определяющую рольв
системе играет объект Супермаркет, для которого нужно, разумеется,
создатькласс. Чтобы накапливать статистику о среднем времени ожидания товара
темиклиентами, которые при первом обращении не получили его и дали
повторныйзапрос, необходимо создать класс Клиент (Client)
и хранить
информацию о них вобъектах этого класса. В самом
деле, клиенты, сразу получившие товар, в системе не задерживаются, и объекты
для них создавать не нужно. То же самое относится и к клиентам, которые, не
получив товар, не пожелали ждать. Те же клиенты, которые согласились ждать
прибытия очередной партии товара, остаются всистеме, и вплоть до момента
получения ими товара информацию о них нужноотслеживать, а именно: вести учет
времени ожидания. Для объекта Радиоприемник, тоже участвующего в работе системы,
класс создавать нет необходимости, по-скольку на всем протяжении моделирования
мы работаем только с количества-ми радиоприемников и никакая статистика по
отдельно взятым единицам этоготовара не требуется.
Итак, с классом Клиент все ясно - его полями данных являются
уникальныйидентификатор и время, которое он к данному моменту провел в системе,
ожи-дая исполнения заказа. Опишем, какие поля данных должен иметь класс
Супер-маркет (SuperMarket).
Неизменяемые поля:
· интенсивность поступления клиентских
запросов (0,03 заявок в час);
· периодичность проверок состояния
запаса (28 дней);
· время исполнения заказа (21 день);
· нижний предел количества товара, при
выходе за который делается заказ (18);
· уровень наличия товара, исходя из
которого рассчитывается объем заказа (72);
· процент заявок, покинувших систему,
из числа тех, которые не застали товар в наличии (80).
Изменяемые поля:
· время, оставшееся до прибытия
следующего покупательского запроса на радиоприемник;
· время, оставшееся до получения
заказа; в случае, если в данный момент мыне ждем заказа, значение равно -1;
· время, оставшееся до начала следующей
проверки;
· объем заказа, получение которого
ожидается; в случае отсутствия заказа равен 0;
· текущее количество товара;
· список указателей на объекты класса Client, ожидающие получения товара. В данном случае именно список, а не
массив, так как»длина очереди не имеет верхней границы;
· текущая длина очереди, может быть
вычислена но списку указателей.
4.3 События и методы
Событий, меняющих состояние объекта Супермаркет, всего три:
поступление клиентского запроса, проверка состояния запаса и прибытие заказа.
Оформление заказа не является отдельным событием, а входит в алгоритм проверки
состояния запаса. Каждому из этих трех
событий соответствуют методы, алгоритмическая реализация которых совершенно
очевидна, не содержит никаких программных ухищрений и очевидным образом кодирует словесное описание
задачи. Объекты класса Client не являются активными участниками процесса
моделирования, так как все действия по их
созданию, обработке и удалению происходят внутри методов класса SuperMarket. Поэтому метода гип у класса Client нет.
С какой целью задано условие сброса накопленной статистики по
истечениипервого года? Дело в том, что если существует стационарный режим,
случайныйпроцесс достигает его вне зависимости от начальных условий. Но за
какое времяэто произойдет, заранее ответить невозможно. Поэтому, если целью
моделирования является получение стационарных характеристик, влияние начальных
условий на результаты надо каким-то образом нивелировать. Сделать это можно
двумяспособами: моделировать в течение длительного времени, так что
соотношениевремен, проведенных в стационарном и переходном режимах, будет таким
большим, что влиянием переходного режима можно пренебречь; в течение некоторого времени моделировать «вхолостую» и
только затем, считая, что стационарный режим уже достигнут, включать режим сбора статистики. Ни один
из способов,разумеется, не дает стопроцентной гарантии, поскольку заранее
ничего нельзясказать о длительности схождения процесса к стационарному режиму.
Условие «чернового» прогона в течение одного года с
промежуточным сбросомстатистики реализовано в функции main. Здесь важно учестьследующее
принципиальное обстоятельство. После сброса статистики возобновление
моделирования происходит уже не с того состояния объекта, с которогооно
начиналось. Поэтому очень важно, чтобы корректность работы методов независела
от начального состояния объекта. Чтобы проиллюстрировать этумысль, мы
специально не стали вводить в число глобальных стачистических переменных
счетчик числа заявок, покидающих очередь, который необходим дляподсчета
среднего времени ожидания. Опасность подстерегает нас в случае, еслизначение
этого счетчика подсчитывать косвенно:
entered-rejected-satisfied-q_length+l.
где entered - счетчик всех запросов;
rejected - счетчик потерянных запросов; satisfied - счетчик немедленно обслуженных
запросов;
q_length - текущая длина очереди.
Казалось бы, все
логично: после всех вычитаний остаются только тезаявки, которые побывали в
очереди и уже покинули ее. Здесь необходимо, од-нако, соблюдение одного
условия: в момент начала сбора статистики очередь должна быть пуста. Иначе мы получим
абсурдный результат в виде отрицатель-ного значения счетчика (например, в
начальный момент времени -q_length), чтоприведет к некорректному подсчету среднего времени
ожидания. Это затрудне-ние преодолено следующим образом. Для класса SuperMarket вводится дополни-тельное поле данных q_extra, которое инициализируется текущей длиной очередив момент
завершения «чернового» прогона. Тогда в методе Supertterket: :complete(),имитирующем поступление
заказа и удовлетворение за счет этого заявок, ожи-дающих в очереди, порядковый
номер удовлетворенной заявки в выходном по-токе можно рассчитать по формуле:
c=entered-rejected-satisfied-q_length*q_extra+l
Величина 1/с затем используется в качестве усредняющего
множителя для рас-чета среднего времени пребывания заявки в системе.
5. Реализация программы
Для моделирования системы управления запасами (с
неудолетворенным запросом) был выбран язык программирования C++ и написана программа на этом
языке, позволяющая в полной мере отразить функционирование системы.
Листинг программы файл 1.h. Описание протоколов классов
#include<cstdio>
#include<cstdlib>
#include<ctime>
#include<cmath>namespace std;
#include "random.h"
#include "List.h" *sojourn; //файл для сбора статистики о
времени ожидания
//товара*que; //файл для сбора статистики о длине очереди;
//пополняется один раз в неделюint entered=0L; //счетчик общего числа
заявок на товарint rejected=0L; //счетчик числа заявок, сразу покинувших
системуint satisfied=0L; //счетчик числа заявок, немедленно
удовлетворенныхnum_orders=0; //счетчик числа сделанных заказовsoj_ave=0;
//переменная для подсчета среднего времени ожиданияque_ave=0; //переменная для
подсчета средней длины очередиint total; //счетчик тактов модельного времени
(количество
//часов)
//Протокол класса Client Client
{int id; //уникальный идентификатор клиентаhours; //время, проведенное
клиентом в системе:class SuperMarket;() //метод-конструктор
{
//Вычисляем, какая это по счету заявка, поставленная в очередь,
//от момента начала моделирования, и назначаем ей
идентификатор=entered-rejected-satisfied+1; =0;
}Print();int getId();getTime();
};
{
//168 - количество часов в неделе ("id=%ld\n ждет исполнения заказа
%d недель\n", id, hours/168);
}
//Чтение идентификатора заявкиint Client::getId()
{(id);
}
//Чтение проведенного в системе времениClient::getTime()
{(hours);
}
//Протокол класса СупермаркетSuperMarket
{to_arrival; //время до прибытия следующей заявкиto_order; //время до
исполнения заказаorder; //объем ожидаемого заказаto_check; //время до следующей
проверкиq_length; //текущая длина очередиexist; //текущее количество
товара<Client> *queue; //очередь ожидающих заявок
//Описание неизменяемых полей данныхstatic int mu=3; static int
checking=28; static int ordering=21; static int level1=18; static int level2=72;
static int percentage=80;:(int i);run();arrival(); complete();
check();Print();getLength();q_extra; //переменная для хранения начальной длины
очереди
};
//Метод-конструктор. Параметр - исходное количество
товара::SuperMarket(int i)
{_length=0;_extra=0;=NULL;_arrival=(int)(get_exp((float)mu/100));
//"Насильственно" устанавливаем экспоненциальную случайную
величину
//в единицу, если после округления до целого она обратилась в ноль.
//Вероятность такой ситуации тем меньше, чем с большим коэффициентом
//промасштабировано время. В данном случае она равна
//1-exp(-0.03 * 0.5) = 0,015.(to_arrival==0)
to_arrival=1;_order=-1;=0;=i;
//Время до ближайшей проверки устанавливается случайным
образом_check=(rand()%checking+1)*24;
}
SuperMarket::getLength()
{(q_length);
}SuperMarket::Print()
{("Следующая заявка поступит через %d часов\n", to_arrival);
(to_order>0) {("Заказ прибудет через %d дней, он составляет %d единиц
товара\n", to_order/24, order);
}("Заказа нет\n"); ("Следующая проверка запасов состоится через
%d дней\n", to_check/24);("Ждут удовлетворения запроса %d
клиентов\n", q_length);("Имеется %d единиц товара\n", exist);
}
//Моделирование прибытия нового запросаSuperMarket::arrival()
{
//int i; *p=NULL;
//Разыгрываем новый интервал между прибытиями_arrival=(int)(get_exp((float)mu/100));(to_arrival==0)
to_arrival=1; ++; //инкремент общего счетчика запросов(exist>0) //товар есть
{-; //декремент количества товара++; //инкремент счетчика сразу
удовлетворенных
//запросов
}//товара нет
{(rand()%100<percentage) //клиент не стал ждать и ушел
{ ++; //инкремент счетчика потерянных клиентов;
}
//Создаем новый объект класса Client и новый элемент списка=new
Client();<Client> *ptr=new ListNode<Client>(p,NULL);
//Очереди нет. Новый элемент становится головой списка(q_length==0)
queue=ptr;
//Добавляем новый элемент в хвост
спискаListAdd<Client>(queue,ptr);_length++; //инкремент длины очереди
};
}
//Имитация прибытия заказаSuperMarket::complete()
{mi, i, b, c;_order=-1;+=order;=0;(q_length==0) return;
//Определяем, сколько единиц товара будет продано немедленно
(exist<q_length) mi=exist; else mi=q_length;(i=0;i<mi;i++)
{
//Отпускаем товар клиенту, находящемуся в голове
списка=queue->Data()->getTime();
//Время ожидания записываем в файл (в днях)(sojourn,"%.2f\n",
((float)b)/24);
//Определяем, каким по счету из покинувших очередь с момента начала
//моделирования является этот клиент. Учитывается начальная длина
очереди.=entered-rejected-satisfied-q_length+q_extra+1;_ave=soj_ave*(1-1.0/c)+(float)b/c;
//пересчет среднего времени
//ожидания
//Удаляем элемент из головы списка<Client> *ptr=queue;
=queue->Next();ptr;_length--; //декремент длины очереди-; //декремент
количества товара
}
}
//Имитация проверки состояния запасаSuperMarket::check()
{a;_check=checking*24;
//Вычисление текущего состояния
запаса=exist+order-q_length;(a>=level1) return; //заказ делать не нужно
//Заказ делать нужно_order=ordering*24;
//вычисление объема заказа=level2-a;_orders++; //инкремент количества
заказов
}
//Метод-диспетчерSuperMarket::run()
{
//int i;
//float a; <Client> *ptr;_arrival--; (to_arrival==0)
arrival();(to_order>0) to_order--;(to_order==0)
complete();_check--;(to_check==0) check();
//Инкремент текущего времени пребывания для всех клиентов, ожидающих
//исполнения заказа(queue!=NULL)
{=queue;(ptr!=NULL)
{
((ptr->Data())->hours)++;=ptr->Next();
}
//Еженедельная запись в файл текущей длины очереди(total%7==0)
fprintf(que,"%d\n", q_length);
//Пересчет средней длины
очереди_ave=que_ave*(1-1.0/(total+1))+((float)q_length)/(total+1);;
}
Листинг программы файл random.h
#include<cstdio>
#include<cmath>
#include<cstdlib>get_exp(float mu) //генератор
случайных чисел, распределенных
//экспоненциально
{r_num; float root, right;_num=rand(); /*получение случайного
целого
/числа*/=((float)r_num)/(RAND_MAX+1); /*проекция на интервал
(0;1)*/=-log(1-right)/mu; /*вычисление значения обратной
/функции*/(root);
}get_uniform(int a, int b)
{ //Генерация равномерно распределенной величины a+bx,
y;=rand()%(b+1);=rand()%2;(y==0) return(a-x);(a+x);
}
get_triangle(float A, float B, float C)
{r_num; float root, right;_num=rand(); //получение случайного
целого
//числа=((float)r_num)/(RAND_MAX+1); //проекция на интервал
(0;1).
//Константа RAND_MAX=32767 (215-1) определена в
cstdlib(right<(C-A)/(B-A))
root=A+sqrt(right*(B-A)*(C-A));root=B-sqrt((1-right)*(B-A)*(B-C));(root);
}get_pareto(float A, float B)
{r_num; float root, right;_num=rand(); /*получение случайного
целого числа*/=(float)r_num/RAND_MAX+1; /*проекция на интервал
(0;1)*/=A/(pow(1-right, (float)1.0/B)); /*вычисление значения обратной
функции*/(root);
}
Листинг программы файл List.h
template <class Type> //это постоянная «заставка»
//к класам и функциям
//c парметризированным типомListNode { :<Type>
*next; //указатель на следующий элемент списка*data; //указатель на данные
хранящиеся в элементе списка:(Type *d, ListNode<Type> *n); //конструктор
~ListNode(); //деструктор*Data(); //метод для чтения данных<Type>
*Next(); //метод для чтения указателя
//на следующий элементPutNext(ListNode<Type> *n); //метод для
записи указателя
//на следующий элементPrint(); //печать содержимого элемента списка
};<class Type><Type>::ListNode(Type *d, ListNode<Type>
*n) : next(n), data(d)
{
}<class Type><Type>::~ListNode()
{data;
}<class Type>*ListNode<Type>::Data()
{data;
}<class Type><Type> *ListNode<Type>::Next()
{next;
}<class Type>ListNode<Type>::PutNext(ListNode<Type> *n)
{=n;
}<class Type>ListNode<Type>::Print()
{>Print(); //предпологается наличие метода Print() для класса
//имя которого будет подставленно в пользовательском коде
}
//Описание класса-шаблона завершено, далее идут функции-шаблона,
работающие
//не с отдельным элементом, а со всеми списком
<class Type>ListAdd(ListNode<Type> *head,
ListNode<Type> *li)
//добавление нового элемента li в хвост списка с головой head
{<Type> *old, *v;
//ищем внешний хвост списка(v=head; v!=NULL;
v=v->Next())=v;>PutNext(li); //добавляем в след за найденым хвостом новый
элемент списка
}<class Type><Type> *ListDelete(ListNode<Type> *head,
ListNode<Type> *li)
//удаление элемента li из списка с голоыой head
//функция возвращает указатель на голову нового списка
{
//int j;<Type> *old, *o1;(li==head) //удаляемый элемент может быть
головой списка
//в этом случае голова у списка меняется
{=head->Next();li;o1;
}
//Удаляемый элемент не являеться головой списка. Голова остаеться
прежняя(ListNode<Type>* v=head; v!=li; v=v->Next())
//поиск элемента предшедствующего
удаляемому=v;=li->Next();>PutNext(o1);
//предшествующий элеиент теперь «видит» элемент стоящий в списке вслед
//за удаленнымli;head;
}
//печать всех элементов списка с головой head<class
Type>ListPrint(ListNode<Type> *head)
{(ListNode<Type>* v=head; v!=NULL; v=v->Next())>Print();
//подсчет количества элементов в списке с головой head
} <class Type>ListCount(ListNode<Type> *head)
{i; i=0;(ListNode<Type>* v=head; v!=NULL; v=v->Next())
{>Print();++;
}i;
}
Листинг программы функция main()
#include "stdafx.h"
#include "4.h"
#define N 52416 // общее время моделированияnamespace
std;main(){
//Открытие файлов для сбора
статистики=fopen("que1", "wt");=fopen("sojourn",
"wt");
//Инициализация генератора случайных
чисел((unsigned)time(0));s(72);
//"Черновой" прогон в течение года. 8760 -
количество часов в году(total=0L;total<8760;total++) {.run();
}(que); (sojourn);
//сброс статистики=fopen("que1",
"wt");=fopen("sojourn", "wt");=0L; =0L; =0L;
_orders=0;_ave=0;_ave=0;
//Запись текущей длины очереди в поле данных q_extra перед
началом сбора //статистики.q_extra=s.getLength();
//Основной моделирующий цикл(total=0L;total<N;total++){.run();
}(sojourn);(que);(LC_ALL, "Russian");
//Вывод на печать результатов имитационного
эксперимента<< "Всего поступило заявок " << entered
<< endl;<< "Доля потерянных заявок " <<
((float)rejected)/entered << endl;<< "Доля немедленно
обслуженных заявок " << ((float)satisfied)/entered <<
endl;<< "Количество заказов " << num_orders <<
endl;<< "Среднее время ожидания " << soj_ave/24 <<
" дней" << endl;<< "Средняя длина очереди "
<< que_ave << endl;
_gettch();
6. Анализ
результатов
Многократный прогон модели в течение 6 лет дал следующие
результаты:
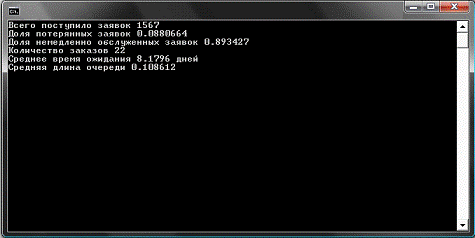
Рис.
2. Снимок работы программы
· количество заявок - 1567;
· доля потерянных заявок - 0,088;
· доля немедленно удовлетворенных
заявок - 0,89;
· количество заказов - 22;
· среднее время ожидания - 8,2 дней;
· средняя длина очереди - 0,109.
Более интересны другие зависимости. Предположим, что мы не
можем ни увеличить скорость выполнения заказа, ни снизить требовательность
клиентов, ни расширить складские площади
для хранения более 72 единиц товара. Тогда получается, что мы можем управлять
только периодичностью проверки запасов(она не может быть менее трех недель -
срока исполнения заказа) и нижним порогом заказа (он не может превышать 72). В
числе показателей эффективности функционирования оставим три: долю потерянных заявок, количество
заказов,среднее время ожидания.
На рис.
3-5 приведены зависимости этих
показателей от периодичности проверки, все времена измерены в днях. Мы видим, что зависимости эти
отнюдь не монотонны, хотя общие
тенденции к росту или уменьшению все же сохраняются.
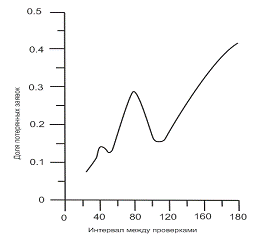
Рис.
3. Зависимость
доли потерянных заявок от периодичности проверки запасов
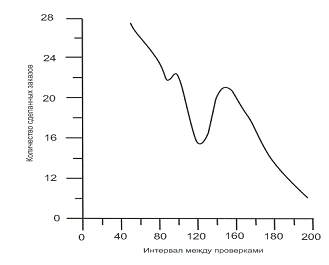
Рис. 4. Зависимость количества
заказов от периодичности проверки запасов
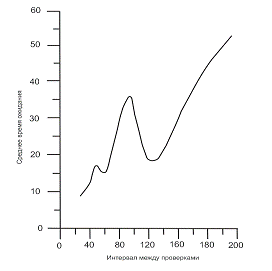
Рис. 5. Зависимость среднего
времени ожидания от периодичности проверки запасов
Суть его в том, что для данной задачи небольшое увеличение
периодичности проверки запасов совсем не обязательно, как это ни странно,
приводит к ухудшению показателей, а может, наоборот, значительно их улучшить.
Все зависит оттого, в какой момент мы «поймаем» проверкой запасов ситуацию,
когда текущий запас уменьшился до 18.
Предположим, что в момент времени T дней он стал равен 17.
Если периодичность проверки такова, что проверка произошла на (Т - 1)-й день, то эта ситуация очень
нехороша, так как то, что запас меньше критического значения, будет обнаружено очень нескоро,
соответственно, нескоро произойдет и пополнение. Если же увеличить периодичность
таким образом, что проверка произойдет на
несколько дней позже, чем Т, ситуация значительно улучшится, так как время от
уменьшения запаса до его пополнения сократится.
Таким образом, если мы, к примеру, хотим обеспечить долю потерянных заявок не более 0,2, периодичность проверки
либо должна быть менее 62 дней, либо лежать в интервале приблизительно от 92 до
122 дней (условие задачи этому ограничению как раз удовлетворяет - проверка
запасов выполняется раз в 28 дней).Этой же цели, как следует из графика,
изображенного на рис. 5, можно достичь, установив
нижний уровень заказа не более 5.
Монотонный характер зависимостей, изображенных на рис. 6-8, легко объясним. В процессе работы
супермаркета запас товара неуклонно уменьшается, и чем раньше мы начнем «бить тревогу»
(то есть сделаем заказ на его пополнение), тем качественнее обслужим своих
клиентов.
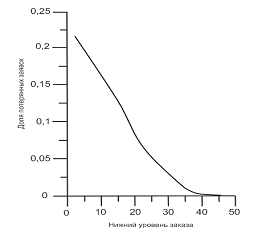
Рис. 6. Зависимость доли потерянных
заявок от нижнего уровня заказа
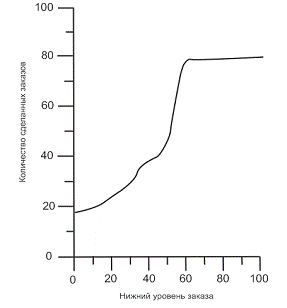
Рис. 7. Зависимость количества
заказов от нижнего уровня заказа
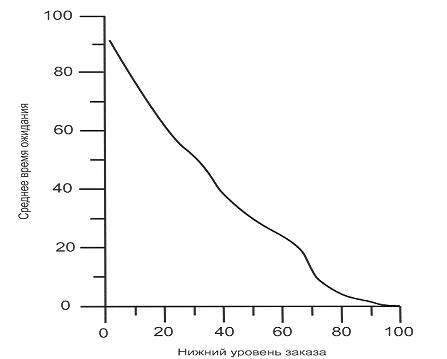
Рис. 8. Зависимость среднего
времени ожидания от нижнего уровня заказа
Можно поставить еще одну интересную задачу. Как видно из
приведенных нарисунках графиков, уменьшение доли потерянных заявок и среднего
времениожидания сопровождается увеличением количества сделанных заказов,
каждыйиз которых может сопровождаться определенными накладными расходами
внезависимости от объема заказанного товара. Если степень «дискомфорта»,
кото-рый доставляет нам единица каждой из этих величин, количественно
выразитьвесовыми коэффициентами с1, с2, с3, то возникает задача
минимизации целевойфункции:
F(P) = с1 • Lost + с2 • Orders + с3 • Tср
или
F(L) = с1 • Lose + с2 • Orders + с3 • Tср,
где Р - периодичность проверки;
Lost - доля потерянных заявок;
Orders - количество заказов;ср - среднее время ожидания;
L - нижний
уровень заказа.
Весовым коэффициентам можно придать вполне реальный смысл,
если предположить, что за каждую потерянную заявку, за каждый день ожидания
клиента и за каждый заказ мы платим
определенную сумму и нужно минимизировать общиерасходы. Чтобы приблизительно
выровнять значения слагаемых, примем с1 = 15,с2 = 1, Сз = 0,35.
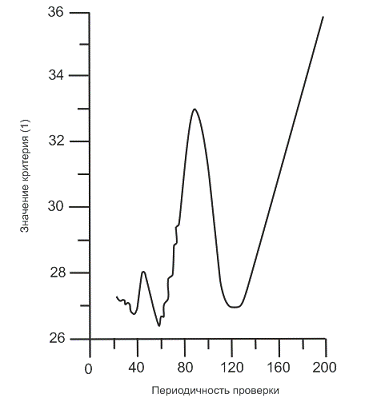
Рис. 9.
Зависимость
значения критерия от периодичности проверки
Все это реально, так как уход клиента без покупки, да еще с
намерением большев этот супермаркет не возвращаться - тяжелая потеря для
торговой организа-ции.
Согласно графику, приведенному на рис. 9, минимум критерия достигаетсяпри Р =
59, на значение минимума в этой точке - 26,3 - ненамного отличаетсяот значения
в другой точке локального минимума (Р = 36), равного 26,6. Видимо, лучше все-таки принять периодичность
проверки, равную 36 дням.
Проверим, можно ли улучшить решение за счет варьирования
нижнего уровнязаказа (сохраняя Р = 28 дней). График на рис. 10 показывает, что минимум кри-терия достигается при L = 8 и равен приблизительно 25,8, то
есть он немногоменьше минимума по параметру Р. Следовательно, формулируем
вывод: уменьшение запаса до значения 18 - еще не повод бить тревогу. Следует
сохранятьтерпение и выдержку и оформлять заказ на пополнение запаса только
тогда, когда запас уменьшится до 8.
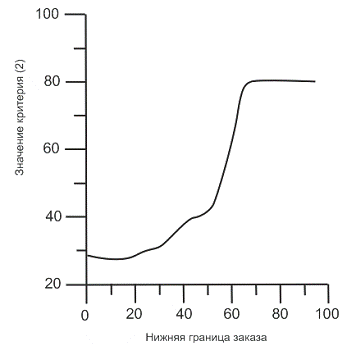
Рис. 9. Зависимость значения
критерия от нижнего уровня заказа
Разумеется, при иных значениях весовых коэффициентов
оптимальное решение тоже
будет иным. Задание этих коэффициентов близкими к реальным зависит исключительно от опыта и квалификации
эксперта, например главного бухгалтера или коммерческого директора
супермаркета.
7. Заключение
В результате выполнения курсовой работы были достигнуты следующие
результаты:
· изучены метод имитационного моделирования экономических
объектов;
· получены навыки проведения численных экспериментов на
имитационных моделях экономических систем;
· приобретен опыт проведения анализа по результатам данных
экспериментов на имитационной модели;
8. Список
использованной литературы
1. Труб И.И.
«Объектно-ориентированное моделирование на С++»: Учебный курс.-СПб.:Питер,
2006.-411с.:ил.
2. Речкалов
Системы и модели управления запасами. Режим доступа:
http://www.masters.donntu.edu.ua/2007/fvti/toichkina/library/invest7.htm
3. Системы
управления запасами: Режим доступа:
<http://www.znaytovar.ru/s/Sistemy_upravleniya_zapasami.html>
. Кельтон В., Лоу А. Имитационное моделирование. - СПб:
Питер, 2004. - 848 с
5. Вентцель Е.С. «Теория
вероятностей», М.: Высшая школа, 1999г., 576 стр.
1. 6. Федосеева В.В. «Экономико-математические методы и
прикладные модели»,
под
ред., Москва «Юнити» 2001 г.
. Грабовый
П.Г. Риски в современном бизнесе. -М.: Финансы и статистика, 2000. -200 с.
9. Дубров
А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рискованных ситуаций в
экономике и бизнесе. -М.: Финансы и статистика, 2004. -224 с.
10. Князевская
Н.В., Князевский В.С. Принятие рискованных решений в экономике и бизнесе. -М.: Контур,
1998. -160 с.
. Кремер
Н.Ш. Исследование операций в экономике. -М.: Банки и биржи, 2003. -407 с.
12. Шикин
Е.В. Математические методы и модели в управлении. -М.: Финансы и статистика,
2002. -430 с.
13. Эддоус
М., Стэнсфилд Р. Методы принятия решений. - М.: ЮНИТИ, 1997. -425 с.