Классификация поверхностей второго порядка
Содержание
Введение
. Поверхности
второго порядка
2.
Все канонические уравнение квадрик
3.
Приведение квадрики к каноническому виду
4.
Основные виды поверхностей второго порядка и их свойства
Приложение
Список литературы
Введение
В этой работе содержится материал по
поверхностям второго порядка. Что такое квадрика (или поверхность второго
порядка), даны все возможные семнадцать видов квадрик, их канонические формулы,
изображения и основные свойства.
Уделено внимание возможным видам любого
многочлена второй степени в пространстве, возможным видам квадрики
(доказывается что их всего семнадцать).
Затронуты свойства эллипсоида, однополостного и
двуполостного гиперболоидов, конуса второго порядка, гиперболического
параболоида. Рассматриваются прямолинейные образующие у отдельных видов
поверхностей второго порядка. Приведено решение типичных задач.
1. Поверхности
второго порядка
Поверхности второго порядка задаются в некоторой
аффинной системе координат уравнением:

При этом требуется, чтобы квадратичная часть
была отлична от нуля. Если ввести обозначения:

то уравнение примет вид:
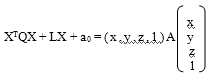
Определение. Алгебраической поверхностью второго
порядка (квадрикой) называется поверхность S,
уравнение которой в декартовой прямоугольной системе координат имеет вид:
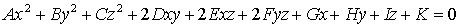 ,
,
где по крайней мере одна из шести
величин A, B, C, D, E, F не равна
нулю. Если это уравнение не удовлетворяется ни одной действительной точкой x=(x1, x2, x3), то
говорят, что оно определяет мнимую поверхность.
Теорема Пусть в некоторой прямоугольной
системе координат задана квадратичная часть q(x, y, z). Тогда найдется другая
прямоугольная система с тем же началом, в которой квадратичная часть примет
диагональный вид:
(x′, y′,
z′) + λ1(x′)2+
λ 2(y′)2+ λ 3(z′)2
где λ1,λ2,λ3-
собственные значения Q, то есть корни характеристического многочлена :
(λ)=det(Q- λE)=0,
а новые базисные вектора e'1 e'2 e'3
являются соответствующими собственными векторами. В частности, все собственные
значения вещественны, а собственные вектора, отвечающие различным собственным
значениям, ортогональны.
Лемма. Для любого многочлена второй
степени в пространстве существует прямоугольная система координат, в которой он
принимает один из следующих пяти видов:
(I) F= λ1x2 + λ2y2 + λ3z2 + τ (λ1 λ2 λ3 ≠0);
(II) F=λ1x2 + λ2y2 + 2b3z (λ1 λ2 b3≠0);
(III) F= λ1 x2 + λ2 y2+ τ (λ1 λ2 ≠0);
(IV) F= λ1 x2 + 2c2y (λ1 c2 ≠0);
(V) F= λ1 x2 + τ (λ1 ≠0);
Доказательство. В силу предыдущей
теоремы можем найти такую прямоугольную систему, в которой квадратичная часть
диагональна, то есть:
= λ1x2 + λ2y2 + λ3z2 + 2b1x + 2b2y + 2b3z + b0=0
Рассмотрим все возможные случаи.
(I). При λ1
λ2 λ3
≠0 имеем:
F=λ1(x
+ b1/ λ1)2
+λ1
(y + b2 / λ2)2
+ λ3(x
+ b3 / λ3)2
+ (b0 - (b1)2/
λ1 -
(b2)2/ λ2
- (b3)2/
λ3)
= λ1(x')2
+ λ2(y')2
+ λ3(z')2
+ τ.
(II) При
λ3
=0 и λ1
λ2
b3 ≠
0 имеем:
F = λ1(x+b1/
λ1)
2 + λ1(y+
b2/
λ2)
2 + 2b3z
+ (b0
- (b1)2/
λ1 -
(b2)2/
λ2)=λ1(x')2
+ λ2(y')2
+ 2b3z
+ τ = λ1x2
+ λ2y2
+ 2b3(z+
τ /2b3)=
λ1x2
+ λ2y2
+ 2b3z'.
(III) При
λ3=
b3 =0
и λ1 λ2
≠
0 имеем:
= λ1(x+b1/
λ1)
2 + λ1
(y+ b2/
λ2)
2 + (b0
- (b1)2/
λ1 -
(b2)2/
λ2)
=
λ1(x')2
+ λ2(y')2
+ τ.
(IV)
При λ3=
λ 2=0,
λ1≠0
и хотя бы один из b2
и b3 не
равен нулю. Тогда имеем:
= λ1(x
+ b1/
λ1)
2+ 2b2y
+ 2b3z
+ (b0 - (b1)2/
λ1)
= λ1(x')2
+ 2c2y'.
Где:
x' = x
+ b1/
λ1,
c2
= ((b2)2+(b3)2)1
/ 2
y' = ((b2)2
+(b3)2)-1/2 (b2y + b3z +
1/2(b0 - (b1)2/
λ1))'=((b2)2
+(b3)2)-1/22
(- b3y
+ b2z).
Такая "нормировка" функций перехода
гарантирует ортогональность соответствующей матрицы и, тем самым
ортогональность замены.
Если же b2
= b3 =
0, то мы сразу имеем выражение конечного вида.
(I). Пусть λ3
=
λ2 =
b2
= b3 =
0 и λ1
≠0.
Тогда имеем:
= λ1(x
+ b1/
λ1)
2 + (b0
- (b1)2/
λ1)
= λ1(x')2
+ τ.
Лемма доказана.
. Все
канонические уравнение квадрик
Для любой квадрики существует прямоугольная
система координат, в которой она имеет один из следующих семнадцати видов:
1) 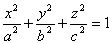
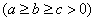 эллипсоид
эллипсоид
) 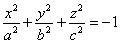
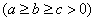 мнимый
эллипсоид
мнимый
эллипсоид
) 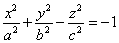
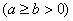 однополостный
гиперболоид
однополостный
гиперболоид
4) 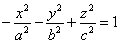
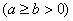 двуполостный
гиперболоид
двуполостный
гиперболоид
) 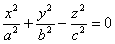
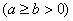 конус
второго порядка
конус
второго порядка
) 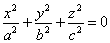
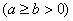 мнимый
конус второго порядка
мнимый
конус второго порядка
) 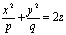
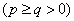 эллиптический
параболоид
эллиптический
параболоид
) 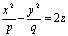
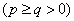 гиперболический
параболоид
гиперболический
параболоид
) 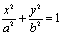
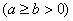 эллиптический
цилиндр
эллиптический
цилиндр
) 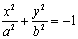
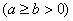 мнимый
эллиптический цилиндр
мнимый
эллиптический цилиндр
) 
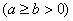 гиперболический
цилиндр
гиперболический
цилиндр
) 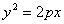 (p>0)
параболический цилиндр
(p>0)
параболический цилиндр
) 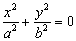
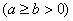 две мнимые
пересекающиеся плоскости
две мнимые
пересекающиеся плоскости
) 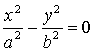
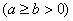 две
пресекающиеся плоскости
две
пресекающиеся плоскости
) 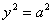 (a>0)
две
параллельные плоскости
(a>0)
две
параллельные плоскости
16) 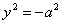 (a>0) две
мнимые параллельные плоскости
(a>0) две
мнимые параллельные плоскости
) 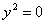 две
совпадающие плоскости
две
совпадающие плоскости
поверхность
квадрика аффинный эллипсоид
3.
Приведение к каноническому виду уравнения поверхности второго порядка
Пусть дана поверхность второго
порядка своим уравнением
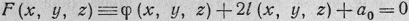 (1)
(1)
относительно некоторой
прямоугольной системы координат Oxyz.
Всегда существует по крайней мере одна прямоугольная система координат Ox'y'z',
оси которой имеют главные направления. В этой системе координат уравнение
поверхности (1) имеет вид
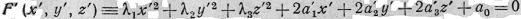
Начнем с центрального случая: δ≠0,
r = 3. В этом случае
λ1≠0,
λ 2≠0, λ
3
≠0. Если перенести начало координат О системы Ox'y'z'
в единственный центр поверхности (1), то уравнение (1') примет вид
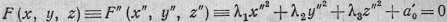 (I)
(I)
Помня, что большой и малый
детерминанты Δ и δ
суть
ортогональные инварианты, можем для их вычисления воспользоваться правой частью
уравнения (I), что дает δ
= λ1λ
2λ
3,
Δ
= λ1λ
2λ
3а'о,
т. е. а'о= Δ/
δ.
Итак, окончательный вид
уравнения (1) в выбранной нами прямоугольной системе координат есть (Пишем
снова х, у, z вместо х",
у", z".)
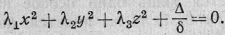 (I*)
(I*)
Здесь все коэффициенты
однозначно (с точностью до общего числового множителя k)
определены уравнением (1) поверхности, в какой бы исходной прямоугольной
системе координат Охуz
мы его ни задавали. Если та же поверхность задана в той же исходной системе
координат другим уравнением: G(x,
у, z) = 0,
то
в силу теоремы единственности все коэффициенты многочлена G
(х, у, z) получаются из
соответствующих коэффициентов многочлена F
(х, у, г) умножением на некоторое число k
≠
0. Так как при переходе к новой системе координат О'х'у'г' многочлены F
и G тождественно
преобразуются соответственно в многочлены F'(х',
у', z') и G'(x',
у', z'), то и для
соответствующих приведенных многочленов F'
и G' сохраняется
соотношение G' = kF',
так что, в частности, характеристические числа многочлена G
(т. е. квадратичной формы его старших членов) получаются из характеристических
чисел многочлена F умножением
на то же k; то же справедливо
и для отношения Δ/
δ
(при δ≠0).
Последнее ясно и непосредственно: так как детерминант Δ
- четвертого порядка, а δ -третьего, то
при умножении всех коэффициентов многочлена F
(х, у, z) на k
детерминант Δ умножается на k4,
а детерминант δ - на k3,
значит, Δ/
δ
умножается на k. Отсюда следует, в
частности, что, умножая, если нужно, обе части уравнения F
(х,у,г)=0 на k =-1, можно всегда
достигнуть того, чтобы (при δ≠0)
число Δ/
δ было
отрицательным (или равным нулю).
Теперь имеется две возможности:
Δ
= 0 и
Δ
≠
0. Начнем с первой.
1°. Δ=0.
Получаем конус второго порядка вещественный, если среди характеристических
чисел λ1,λ
2,λ
3 имеются
числа разных знаков (Здесь целесообразно привести так называемое правило
Декарта для определения знаков корней алгебраического уравнения, все корни
которого- действительные числа. Это правило в применении к уравнению третьей
степени с действительными корнями можно сформулировать так. Пусть дано
уравнение ax3+bx2+cx+d
= 0. Назовем "переменой знака" пару соседних коэффициентов в этом
уравнении (т. е. (а, b),
(b, с) или (с, d),
состоящую из двух чисел различных знаков. Оказывается, что число положительных
корней уравнения третьей степени (все корни которого действительны) равно числу
перемен знака в этом уравнении. При этом корни считаются вместе с их
кратностями. Умножая, если понадобится, обе части уравнения (1) на -1, можем
предположить, что среди его коэффициентов λ1,λ
2,λ
3 имеется
два положительных и один отрицательный. Изменив, если потребуется, наименования
осей координат и обозначая положительные коэффициенты через 1/a2,1/b2,
а отрицательный через -1/c2,
можем представить при Δ = 0 уравнение
(I*) в виде
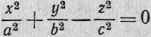
(причем здесь и всюду дальше
берем а, Ь, с положительными). Это каноническое уравнение вещественного конуса.
Заметим, что равенство λ1=λ
2 означает
а = b; тогда мы имеем
круговой конус или конус вращения, его сечения плоскостями z
= h суть окружности;
если λ1=λ
2=-λ
3,
то уравнение конуса превращается в
2+y2-z2=0
-имеем круговой конус,
образующие которого наклонены к его оси под углом π/4.
Если все характеристические
числа -одного знака, мы можем переписать уравнение (I*)
при Δ
= 0 в
виде
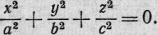
Это каноническое уравнение
мнимого конуса.
°. Пусть теперь Δ≠0;
это значит, что мы имеем невырожденную центральную поверхность.
Переписываем тогда уравнение (I*)
в виде
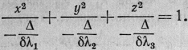 (I**)
(I**)
Возможны четыре случая (Пишем
снова х, у, z вместо х",
у", z".)
а) Все три характеристических
числа имеют один и тот же знак, и Δ > 0, тогда
можем положить
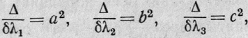
причем а, b,
с всегда считаем положительными. Переписываем уравнение (I**)
в виде
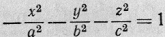
- получили каноническое
уравнение мнимого эллипсоида.
б) Все три характеристических
числа имеют один и тот же знак, и Δ < 0. Тогда
полагаем
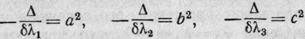
-получаем каноническое
уравнение вещественного эллипсоида
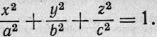
в) Характеристические числа
имеют разные знаки, и Δ < 0. Предположим,
что числа λ1
и λ2
имеют одинаковые знаки, а λ3
имеет
знак, им противоположный. Полагаем
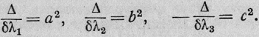
Получаем уравнение
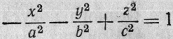
- каноническое уравнение
двуполостного гиперболоида. И наконец,
г) Характеристические числа
имеют разные знаки, и Δ > 0. Предположим
снова, что числа λ1
и λ2
имеют одинаковые знаки, а число λ3
- знак, им противоположный. Тогда, полагая
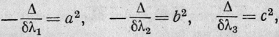
придаем уравнению (I**)
вид
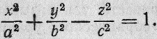
Это каноническое уравнение
однополостного гиперболоида.
Итак, каждая центральная
поверхность второго порядка есть либо конус (действительный или мнимый), либо
эллипсоид (действительный или мнимый), либо гиперболоид (двуполостный или
однополостный). Положительные числа а, b,
с в каноническом уравнении центральной поверхности, являющиеся ее полуосями,
выражаются через характеристические числа λ1,λ2,λ3
и детерминанты Δ, δ, т.
е. через ортогональные инварианты многочлена F(x,
у, z), и, значит, не
меняются при переходе от прямоугольной координатной системы Oxyz,
в которой задано уравнение F(x,
у, z) = 0
рассматриваемой поверхности, к любой другой прямоугольной координатной системе.
Но они не зависят также и от того, каким из уравнений, определяющих в
первоначальной системе Oxyz
данную поверхность, мы воспользовались. В самом деле, уравнения эти отличаются
друг от друга только числовым множителем k.
Но при умножении всех коэффициентов многочлена F(x,
у, z) на данное число k
на это же k умножаются и Δ/
δ, и
все характеристические числа λ1,λ2,λ3;
поэтому a2,
b2,
с2, значит, и а, b,
с остаются неизменными. Итак, полуоси центральной поверхности не зависят ни от
выбора прямоугольной системы координат, ни от того уравнения (из числа
определяющих данную поверхность), которым в этой системе координат мы нашу
поверхность задали; они зависят только от самой поверхности как геометрической
фигуры, т. е. как множества точек в пространстве.
Обратно, если дано наименование
центральной поверхности и ее полуоси а, b,
с, то поверхность вполне определена с точностью до ее положения в пространстве.
В самом деле, две одноименные поверхности с одними и теми же полуосями имеют
одно и то же каноническое уравнение; значит, отличаться они могут лишь тем, что
первая из них этим уравнением определена в одной прямоугольной координатной
системе, а вторая - в другой; но, совмещая первую координатную систему со второй
посредством (собственного или несобственного) движения, мы совместим одну из
наших поверхностей с другой. Итак, две центральные поверхности тогда и только
тогда изометричны между собою, когда они имеют одно и то же наименование и
когда их полуоси (соответствующие членам канонического уравнения данных знаков)
соответственно равны между собою.
Заметим, что (как
непосредственно следует из определений чисел а, b,
с) во всех рассмотренных случаях два характеристических числа равны между собою
тогда и только тогда, когда соответствующие две полуоси центральной поверхности
равны и входят в каноническое уравнение поверхности с одним и тем же знаком.
Мы видели, что равенство двух
каких-либо полуосей, например а=b,
эллипсоида означает, что мы имеем эллипсоид вращения (сферу, если а=b=с).
Поэтому признаком эллипсоида вращения является равенство двух
характеристических чисел, а признаком сферы - равенство λ1
= λ2 = λ3.
Точно так же однополостный гиперболоид является гиперболоидом вращения, если а2
= b2,
т. е. λ1=
= λ,2; то же верно и для
двуполостного гиперболоида, и для конуса. Итак, равенство двух
характеристических чисел необходимо и достаточно для того, чтобы центральная
поверхность была поверхностью вращения, а равенство λ1
= λ2 =
λ3 верно для сферы
(действительной или мнимой), и только для нее.
Переходим к случаю поверхности
(1) ранга r=2. Покажем, что в
этом случае уравнение (1) определяет: при Δ≠0
(т. е. R = 4) параболоид,
эллиптический,
если Δ
< 0,
гиперболический, если Δ > 0,
а при Δ
= 0, R =
3-"центральный" (т.е. эллиптический или гиперболический) цилиндр,
вырождающийся при R = r=2
в пару пересекающихся плоскостей.
Итак, пусть r
= 2. Тогда среди характеристических чисел многочлена F(x,y,z)
два, положим λ1
и λ2,
отличны от нуля и λ3=0.
В некоторой прямоугольной
системе координат Ox'y'z'
(с тем же началом, что и исходная система Oxyz)
уравнение (1) принимает вид
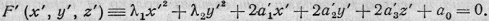
Имеем
 (2)
(2)
откуда заключаем, что Δ≠0
тогда и только тогда, когда а'3≠0. Рассмотрим сначала случай,
когда Δ≠0
и, следовательно, а'3≠0. Перенос начала координат О в
произвольную точку О' = (х'0, у'0, z'0)
т. е. преобразование
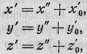
переводит многочлен F'
{х', у', z') в
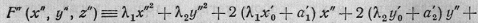
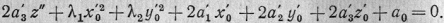
Определяя х'0, у'0
и z'0 из
уравнений
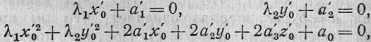
Получаем
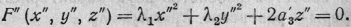
Итак, в надлежаще выбранной
прямоугольной системе координат уравнение всякой поверхности ранга r=2,
R = 4 принимает вид
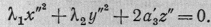 (II)
(II)
Из (2) получаем
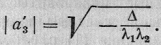
Так как а'3, -
вещественное число, то Δ имеет всегда
знак, противоположный знаку λ1λ2.
Другими словами, Δ положителен,
если характеристические числа λ1
и λ2
разных знаков (гиперболический случай), и отрицательно, если λ1
и λ2
одного и того же знака (эллиптический случай). Изменив, если нужно,
положительное направление оси z
на противоположное, всегда можем предположить, что знак а'3 противоположен
знаку λ1
так что уравнение (II)
можно переписать в виде (мы отбрасываем штрихи при координатах)
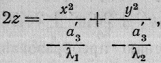 (II*)
(II*)
где- а'3/
λ1 есть положительное
число, которое мы обозначим через р:
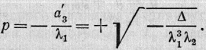
Число- а'3/
λ2 положительно, если
знак λ2
совпадает со знаком λ1
(т. е. в эллиптическом случае, Δ<0), и
отрицательно, если λ1
и
λ2
разных
знаков (т. е. в гиперболическом случае, Δ >
0). Поэтому, полагая в обоих случаях
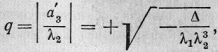
имеем:
q
= - а'3/ λ1
в эллиптическом случае, q
= а'3/ λ1
в гиперболическом случае.
Соответственно получаем: в
эллиптическом случае уравнение
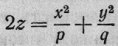
эллиптического, а в
гиперболическом случае уравнение
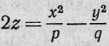
гиперболического параболоида.
Параметры р и q параболоида
выражаются через ортогональные инварианты Δ, λ1,λ2
и поэтому не зависят от той прямоугольной системы координат, в которой было
задано первоначальное уравнение (1) параболоида. Они не меняются при умножении
многочлена F(x,
y,z)
на числовой множитель k
(так как при этом Δ умножается
на k4,
а λ1
и λ
2
- на k), поэтому они зависят
лишь от самой поверхности (рассматриваемой как множество ее точек) и в свою
очередь определяют её однозначно (с точностью до ее положения в пространстве).
Равенство λ1=
λ 2 означает, что мы
имеем эллиптический параболоид с равными параметрами р=q,
т. е. параболоид вращения.
Пусть теперь Δ
= 0, значит,
и a3
= 0. Тогда большой ранг R≤3.
Уравнение (I') в этом случае
приобретает вид
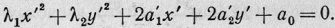 (3)
(3)
Применим к этому уравнению
преобразование параллельного переноса
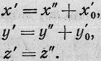
Тогда будем иметь
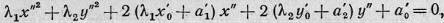 (4)
(4)
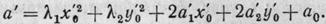
Определяя х'0 и у'0
из уравнений
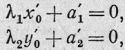
приведем уравнение (4) к виду
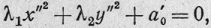 (III)
(III)
причем R=3,
если а'0≠0, и R
= 2, если а'0 = 0. Уравнение (1) задает (в системе координат O'x"y"z")
цилиндр над лежащей в плоскости z"
= 0 центральной кривой второго порядка, имеющей (в прямоугольной системе координат
О'х"у") тоже уравнение (III).
При R=3 (т. е. а'0≠0)
эта кривая нераспадающаяся, при R=2
она распадается на пару прямых, а цилиндр (III)
вырождается в пару пересекающихся плоскостей. Любая плоскость z"=h
пересекает цилиндрическую поверхность (III)
по кривой, имеющей то же уравнение (III),
в плоскости z"=h
(в системе координат с началом О" = (0, 0, h)
и теми же направлениями осей х" и у", что и в координатной системе O'x"y"z").
Все эти кривые конгруэнтны между собою; достаточно знать одну из них, чтобы цилиндрическая
поверхность (III) была
определена. Пусть R = 3. Тогда
полуоси a, b
кривой (III)
(называемые также полуосями цилиндрической поверхности (III)),
вместе с ее наименованием, полностью определяют поверхность (III)
с точностью до ее положения в пространстве и в свою очередь всецело
определяются ею. Чтобы определить полуоси а, b
по первоначальному уравнению (I),
надо только определить а'0. Для определения числа а' надо найти
какую-нибудь точку прямой центров (из системы определяющих ее уравнений в исходной
системе координат) и подставить координаты этой точки в левую часть
первоначального уравнения поверхности. Полученный результат не зависит от
выбора точки на прямой центров.
Переписывая уравнение кривой (III)
в каноническом виде, мы получаем и каноническое уравнение
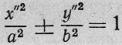
эллиптического, соответственно
гиперболического, цилиндра, а также (если
кривая (III) есть
мнимый эллипс) уравнение  мнимого
эллиптического цилиндра в прямоугольной системе координат O'x"y"z".
Снова равенство λ1
= λ2
является признаком того, что наша цилиндрическая поверхность есть поверхность
вращения, т. е. так называемый круглый цилиндр; его сечения плоскостями,
перпендикулярными к образующим, суть окружности.
мнимого
эллиптического цилиндра в прямоугольной системе координат O'x"y"z".
Снова равенство λ1
= λ2
является признаком того, что наша цилиндрическая поверхность есть поверхность
вращения, т. е. так называемый круглый цилиндр; его сечения плоскостями,
перпендикулярными к образующим, суть окружности.
Пусть теперь R
= r = 2; тогда а'0
= 0 и уравнение (III)
превращается в уравнение 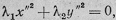 задающее
(в прямоугольной системе координат O'x"y"z")
пару пересекающихся плоскостей (вещественных, если λ1
и λ2
разных
знаков; мнимых, если λ1
и λ2 одного знака). При этом
отношение λ1/λ2,
характеризующее двугранный угол между плоскостями, полностью определяется этой
парой плоскостей и в свою очередь полностью ее определяет.
задающее
(в прямоугольной системе координат O'x"y"z")
пару пересекающихся плоскостей (вещественных, если λ1
и λ2
разных
знаков; мнимых, если λ1
и λ2 одного знака). При этом
отношение λ1/λ2,
характеризующее двугранный угол между плоскостями, полностью определяется этой
парой плоскостей и в свою очередь полностью ее определяет.
Переходим к поверхностям ранга r=1.
Для этих поверхностей лишь одно характеристическое число, пусть λ2,
отлично от нуля и λ1=λ3=0.
Если ось Оу' прямоугольной системы координат направить по единственному
главному направлению, соответствующему отличному от нуля корню
характеристического уравнения, а оси Ох' и Oz'
взять под прямым углом в плоскости, перпендикулярной к уже выбранной оси Оу' (а
в остальном-произвольно), то во всякой такой системе координат уравнение нашей
поверхности будет иметь вид
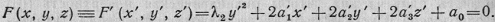 (5)
(5)
Для поверхности ранга r
=1 всегда R
≤3.
Пусть R
= 3; тогда по крайней мере один из коэффициентов а'1, а'3 отличен
от нуля (иначе в матрице коэффициентов многочлена F'
(х', у', z') все детерминанты
третьего порядка будут равны нулю).
Пусть, например, а'3≠0.
Покажем, что в рассматриваемом случае поверхность (5) будет параболическим
цилиндром. Наша задача сейчас-найти такую прямоугольную систему координат, в
которой уравнение (5) примет канонический вид
у2 = 2рх. (IV)
Для этого произведем поворот
координатной системы Ox'y'z'
вокруг оси у' на некоторый, пока произвольный, угол α,
т.
е. сделаем ортогональное преобразование координат
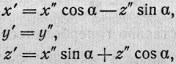
что тождественно преобразует
левую часть уравнения (5) в
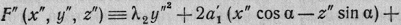
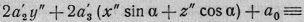
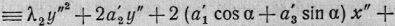
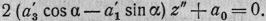
Приравниваем коэффициент при z"
нулю, что дает тригонометрическое уравнение
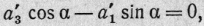
из которого и определяем α:
В полученной прямоугольной
системе координат уравнение 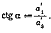 (5) приобретает
вид
(5) приобретает
вид
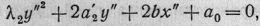
где положено
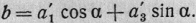
При этом b≠0
(иначе матрица коэффициентов уравнения (6) имела бы ранг ≤2 вопреки
предположению, что R = 3).
Уравнение (6) есть уравнение
цилиндра над параболой, лежащей в плоскости z"
= 0 и имеющей (в системе координат Ох"у") то же уравнение (6).
Остается только произвести сдвиг начала координат (в той же плоскости
Ох"у"). Мы получим после этого сдвига прямоугольную систему
координат, в которой уравнение (6) параболы, а следовательно, и построенного
над нею цилиндра примет канонический вид (IV).
Поставленная задача решена.
Число р, являющееся параметром
параболы, получающейся при сечении параболического цилиндра плоскостью,
перпендикулярной к его образующим, называется параметром параболического
цилиндра. Это число определено самим цилиндром и в свою очередь определяет его
с точностью до его положения в пространстве. Пусть
теперь R
≤2.
Тогда поверхность является парой параллельных (в широком смысле) плоскостей π1,
π2; канонической
системой координат будет произвольная прямоугольная система координат, одна из
осей которой (положим, ось у) перпендикулярна к плоскостям π1,
π2,
а две другие оси расположены в средней плоскости между этими плоскостями. Тогда
уравнение пары плоскостей π1,
π2 будет
=±b
(7)
К этому результату можно прийти
и из рассмотрения уравнения (5), в котором теперь непременно а1=а3
= 0 (если хотя бы один из коэффициентов аь а3 был ≠0,
то мы имели бы параболический цилиндр и, значит, R=3).
Итак, уравнение (5) имеет в
нашем случае вид
Посредством сдвига начала
координат по оси ординат преобразуем его в
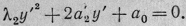 (V)
(V)
что эквивалентно каноническому
уравнению (7).
Общим итогом этого параграфа
является
Теорема 3. Каждая поверхность,
определяемая уравнением второй степени с вещественными коэффициентами,
принадлежит к одному из следующих семнадцати классов:
. Эллипсоиды вещественные.
. Эллипсоиды мнимые.
. Гиперболоиды однополостные.
. Гиперболоиды двуполостные,
. Конусы вещественные,
. Конусы мнимые,
. Параболоиды эллиптические,
. Параболоиды гиперболические.
. Цилиндры эллиптические
вещественные.
. Цилиндры эллиптические
мнимые.
. Цилиндры гиперболические.
. Цилиндры параболические.
. Поверхности, распадающиеся на
пару пересекающихся вещественных плоскостей.
. Поверхности, распадающиеся на
пару пересекающихся мнимых сопряженных плоскостей.
. Поверхности, распадающиеся на
пару (различных) параллельных вещественных плоскостей,
. Поверхности, распадающиеся на
пару (различных) параллельных мнимых сопряженных плоскостей.
. Поверхности, распадающиеся на
пару совпадающих вещественных плоскостей.
4.
Основные виды поверхностей второго порядка и их свойства
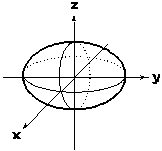
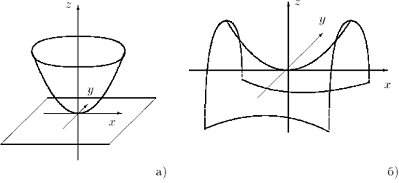
Рис. 1 Эллипсоид
Положительные числа а, b,
c называются
полуосями эллипса. Эллипсоид лежит внутри прямоугольного параллелепипеда -а ≤
x ≤
a, -b
≤
y ≤
a, -c
≤
z ≤
c.То есть эллипсоид
является ограниченной поверхностью.
Теорема 1. Плоское сечение поверхности второго
есть кривая порядка не выше двух.
Доказательство. Выберем систему координат, в
которой уравнение плоскости: Z=0.
Тогда уравнение сечения G(x,
y) := F(x,
y, 0) = 0.
Следствие 2. Непустое плоское сечение эллипсоида
- эллипс или точка.
Доказательство. Это единственные не пустые
ограниченные кривые 0, 1 или 2-ого порядка.
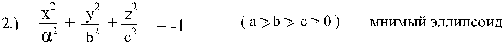
Мнимый эллипсоид не имеет ни одной вещественной
точки:
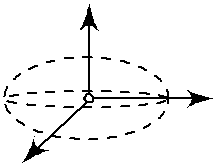
Рис. 2 мнимый эллипсоид
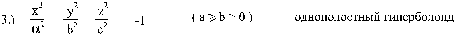
(Изображён на рисунке 3) В сечении плоскостью z
= 0 эллипс:
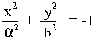
Называемый горловым. Однополостный гиперболоид
обладает следующим замечательным свойством.
Определение 3. Назовём прямолинейной образующей
поверхности прямую, целиком в ней содержащуюся. Как правило, это понятие не
применяется к распадающимся поверхностям.
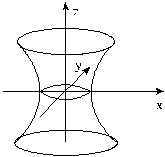
Рис. 3 однополостный гиперболоид
Доказательство. Указанные свойства аффинные,
поэтому достаточно доказать теорему для гиперболоида :
2
+ y2
-z2
= 1.
x2
- z2=1
- y2,
(x-z)(x+z)
= (1-y)(1+z)
Отсюда сразу видим два семейства прямолинейных
образующих:
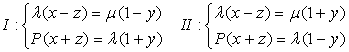
Где λ и μ - произвольные
вещественные числа, не обращающиеся в нуль одновременно.
Тогда:
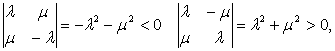
Так что пары плоскостей в
пересечении действительно дают прямую.
Пусть точка (x0,
y0,
z0)
принадлежит гиперболоиду. Тогда, взяв для I
λ = x0
+ y0
и μ
= 1 + y0,
а для II - λ = x0+z0
и μ=1-y0,
получим прямые, проходящие через данную точку.
Поскольку одно из чисел 1 - y0
или 1 + y0
отлично от 0, то пара (λ, μ) определенна
по точке (x0,
y0,
z0)
однозначно (с точностью до множителя) для каждого семейства.
Итак, через каждую точку проходит ровно одна
прямая каждого семейства.
Покажем, что других образующих нет. Допустим,
что образующая параллельна плоскости z
= 0, то есть содержится в плоскости z
= z0.
Тогда она должна содержатся в окружности x2
+ y2
= 1 + z²0
что невозможно. Итак, всякая образующая пересекает z=0,
а значит, и горловой эллипс (окружность). В силу вращательной симметрии
достаточно исследовать одну его точку, например, (1, 0, 0). Пусть через нее
проходит образующая с некоторым направляющим вектором (α,
β, γ):
=1+αt
y=βt
z=γt
так что уравнение (результат подстановки в
уравнение гиперболоида)
(α2+β2-γ2)t2+2αt=0
Должно иметь решением любое t,
откуда
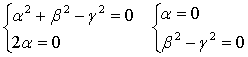
Значит, направляющий вектор (с точностью до
ненулевого множителя) равен (0,1,±1), то есть имеются две возможности, а мы их
уже нашли - это прямая первого семейства и
прямая второго. Итак, других образующих нет.
Из аналогичного соображения получаем, что прямые
одного семейства не могут пересекаться. Пусть они параллельны одному вектору (α,
β, γ). Значит, он параллелен каждой из четырёх
плоскостей, фигурирующих в записи двух прямых семейства. Тогда он является
ненулевым решением системы четырёх линейных уравнений с матрицей:
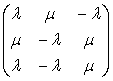
Аналогично в обратной ситуации. Значит, можно
считать, что μ=μ'=1, λ и
λ'
-
ненулевые. Тогда для условия rk
< 3 необходимо8
|
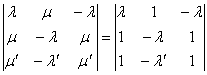 = =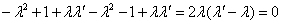
|
что в данной ситуации возможно только если λ
= λ' и прямые совпадают. Итак, две прямые одного
семейства скрещиваются.
Семейства не пересекаются, так как отображение (x,
y, z)
→ (-x, -y,
-z) переводит прямые
одного семейства в прямые другого, параллельные своим прообразам.
Действительно, если бы прямая принадлежала обоим семействам, то ее образ - так
же, и тем самым, мы имели две параллельные прямые из одного семейства.
Теперь рассмотрим две прямые l1 и l2 из разных
семейств. Пусть π
- плоскость,
проходящая через l1 и некоторую
точку Ρ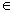 l2 P¢ l1 поэтому соответствующее
плоское сечение гиперболоида, являясь по теореме 1 кривой порядка не старше 2,
должно быть парой параллельных или пересекающихся прямых. Одна из них - l1 а другая -
некоторая прямолинейная образующая l
l2 P¢ l1 поэтому соответствующее
плоское сечение гиперболоида, являясь по теореме 1 кривой порядка не старше 2,
должно быть парой параллельных или пересекающихся прямых. Одна из них - l1 а другая -
некоторая прямолинейная образующая l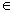 P. Она не
совпадает и не скрещивается с l1, поэтому,
по доказанному, не может принадлежать первому семейству, а значит, принадлежит
второму, и в силу единственности прямой второго семейства, проходящей через Р,
совпадает с l2.
P. Она не
совпадает и не скрещивается с l1, поэтому,
по доказанному, не может принадлежать первому семейству, а значит, принадлежит
второму, и в силу единственности прямой второго семейства, проходящей через Р,
совпадает с l2.
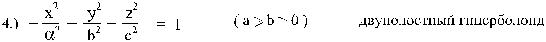
(изображён на рисунке 4)

Рис. 4 двуполостный гиперболоид
Плоскость z = 0 не
пересекает гиперболоид и разделяет его на две части, называемые полостями.
Теорема 4. Двуполостный гиперболоид не имеет
прямолинейных образующих, Доказательство.
Прямолинейная образующая не может пересекать плоскость z=0.
Значит, она лежит в плоскости z
= z0.Но
соответствующее плоское сечение
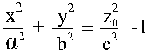
ограниченно (эллипс, точка или Ǿ) и не
может содержать прямую.
5.).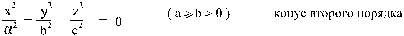
(изображён на рисунке 5а.).
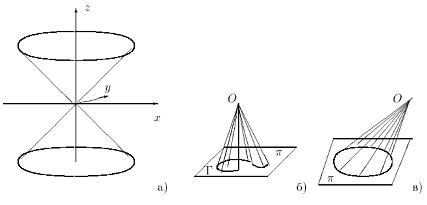
Рис. 5 Конус второго
порядка
Заметим, что уравнение однородно (второго
порядка); F(λx,
λy, λz)
= λ,2F(x,
y, z),
и
таким образом, любая прямая, содержащая О и некоторую другую точку конуса,
является прямолинейной образующей.
Определение 5.Пусть Г - произвольная
кривая, лежащая в плоскости π, а точка О не принадлежит π. Конической
поверхностью над Г с центром в О называется объединение всех прямых вида ОХ, Х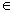 Г (рисунок 5
б).
Прямые
ОХ называются образующими, а кривая Г - направляющей конической поверхности
Г (рисунок 5
б).
Прямые
ОХ называются образующими, а кривая Г - направляющей конической поверхности
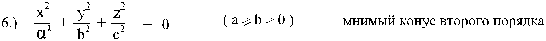
Мнимый конус не имеет ни одной вещественной
точки (рисунок 6)
Рис. 6 мнимый конус
Теорема 6. Коническая поверхность над эллипсом
является конусом второго порядка.
Доказательство. Выберем такую систему координат
с центром в О, что плоскость π задается
уравнением z = h
≠
0 (рисунок 5 в.). Если мы выберем направления осей Ох и Оу параллельно главным
осям эллипса Г, то уравнение эллипса в плоскости π примет
вид:
=(x,
y) =a11(x-x0)2+a22(y-y0)2-1=0
где 0<а11<а22. Тогда
уравнение конической поверхности над ним:
Ф(x, y, z) =
z2F(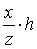 ,
, 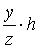 )=0
)=0
Действительно, точка (x, y, z), z ≠ 0,
принадлежит поверхности тогда и только тогда, когда точка ((x/z)*h, (y/z)h, h)
принадлежит кривой, то есть :
(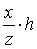 ,
,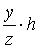 ) =0.
) =0.
Но при сделанном предположении z ≠ 0
данное уравнение равносильно выводимому. Осталось доказать, что при z = 0
выводимое уравнение определенно и его множество решений совпадает с О.
Определённость следует из того, что во втором сомножителе степень (1 / z) равна 2 и
при умножении пропадает.
После умножения уравнение
превращается (при z = 0) в h2q(x, y)=0.
Поскольку асимптотических направлений γ эллипса нет, то x = y = 0.
Итак,
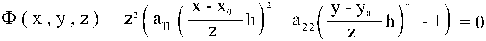
После замены x' = x - x0, y' = y - y0, z' = z получаем
Ф(x', y', z')
= a11h2(x')2+a22h2(y')2-(z')2=0
То есть конус.
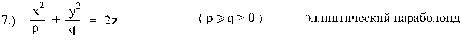
(изображён на рисунке 7 а.).
Теорема 7. Эллиптический параболоид
не имеет прямолинейных образующих.
Доказательство. Дословно как с
двуполостным гиперболоидом.
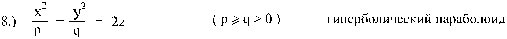
(изображён на рисунке 7 б.).
Определение 8. Ненулевой вектор (α, β,
γ)
задаёт асимптотические направление для поверхности F = 0, если
он обнуляет квадратичную форму уравнения:
q(α,
β, γ)=a11α2+a22β2+a33γ2+2a12αβ+2a13αγ+2α23βγ=0
Асимптотические направления не
зависят от выбора системы координат.
Теорема 9. прямолинейные образующие
любой поверхности имеют асимптотическое направление.
Доказательство. Пусть
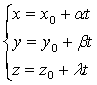
-прямолинейная образующая. Подставив
в уравнение F=0, получим
F2t2+2F1t+F0=0 для
любого t. Значит, F2 = q(α, β, γ) = 0
Теорема 10. Гиперболический параболоид имеет два
семейства образующих, проходящих через
каждую точку. Образующие одного семейства попарно скрещиваются и параллельны
одной плоскости, разных семейств пересекаются.
Доказательство. Асимптотические направления (α,β,
γ)
гиперболического
Параболоида находятся из уравнения 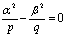 , т.е. лежат
в плоскостях:
, т.е. лежат
в плоскостях:
π1 : 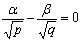 , π1 :
, π1 : 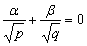 .
.
С учётом уравнения параболоида

Это означает, что имеются два
семейства прямолинейных образующих
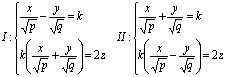
Действительно, если мы имеем
образующую, параллельную, скажем, 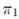 То расстояние (со знаком) от любой
её точки до
То расстояние (со знаком) от любой
её точки до 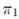 постоянно,
т.е.
постоянно,
т.е.
С некоторой константой k мы имеем
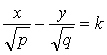
откуда из уравнения поверхности
получаем второе уравнение(1). Таким образом, других Образующих нет.
Через каждую точку параболоида
проходит ровно по одной образующей каждого семейства, так как 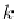 определяется
однозначно.
определяется
однозначно.
Заметим, что никакая вертикальная
прямая не может быть прямолинейной образующей. Действительно, в этом случае x =
const, откуда и z = const.
Два семейства не пересекаются.
Действительно, предположим, что общая прямая имеет направляющий вектор 
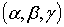
Тогда он должен удовлетворять
однородной части уравнений обеих систем:
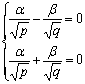
откуда α = β
= 0 и
прямая вертикальна, что невозможно.
Образующие одного семейства не могут
пересекаться, так как это противоречило бы единственности. Они не могут быть
параллельны, так как их направляющие вектора - (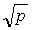 ,
,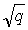 ,k) с
различными k. Значит,
они скрещиваются, причем (по определению) параллельны фиксированной плоскости.
,k) с
различными k. Значит,
они скрещиваются, причем (по определению) параллельны фиксированной плоскости.
Пусть теперь l1 и l2 - образующие
из разных семейств. Покажем, что они пересекаются. Рассмотрим плоское сечение
параболоида, проходящее через l1 и Р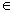 l2Р¢ l1. Это
кривая, порядка не выше двух, значит состоящая из двух прямых l2 и l.
Предположим l ≠ l2 причем они
пересекаются (в точке Р). Значит, l не
принадлежит второму семейству, то есть принадлежит первому. Но тогда она должна
скрещиваться с l1 и не может
лежать с ней в одной плоскости. Значит, l = l2. Допустим, l1║ l2. Тогда
координаты (α,
β, γ)
удовлетворяют уравнениям:
l2Р¢ l1. Это
кривая, порядка не выше двух, значит состоящая из двух прямых l2 и l.
Предположим l ≠ l2 причем они
пересекаются (в точке Р). Значит, l не
принадлежит второму семейству, то есть принадлежит первому. Но тогда она должна
скрещиваться с l1 и не может
лежать с ней в одной плоскости. Значит, l = l2. Допустим, l1║ l2. Тогда
координаты (α,
β, γ)
удовлетворяют уравнениям:
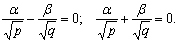
откуда α = β
= 0 и
образующая вертикальна, что невозможно.
Вернёмся к гиперболоидам. Их
асимптотический конус определяется уравнением:
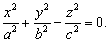
Из уравнения однополостного
гиперболоида имеем для положительных z:
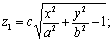
а из уравнения (21) -
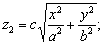
откуда:
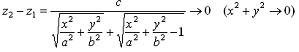
Аналогично для двуполостного.
Предложение 11. Асимптотические
направления (α,
β, γ)
однополостного гиперболоида совпадают с направлениями образующих его асимптотического
конуса и являются решениями (21).
Доказательство. По определению
асимптотических направлений.
Теорема 12. Никакие три различных
прямолинейных образующих однополостного гиперболоида из одного семейства не
параллельны одной плоскости. Любые три попарно скрещивающиеся прямые, не
параллельные одной плоскости, являются прямолинейными образующими некоторого
однополостного гиперболоида.
Доказательство. Рассмотрим три
прямолинейных образующих из одного семейства. Допустим, они параллельны одной
плоскости. Так как центральное плоское сечение (асимптотического) конуса
состоит из двух пересекающихся одной прямой, то две из трёх прямых должны быть
параллельны. Противоречие.
Рассмотрим три попарно
скрещивающиеся прямые и некоторую аффинную систему координат, в которой они
имеют вид:
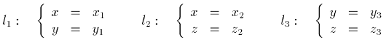
Следующая квадрика содержит все эти
прямые:
(x-x1)(y-y3)(z-z2)-(x-x2)(y-y1)(z-z3)=0
Это действительно квадрика, так как
коэффициент при х3 равен нулю, а, скажем, при ху равен -z2+z3≠0 так
как прямые скрещиваются. Из классификации квадрик и доказанных свойств следует,
что это - однополостный гиперболоид (у цилиндров таких образующих не может
быть, это мы докажем в следующем предложении 14)
Рассмотрим теперь не распадающиеся
цилиндры
Предложение 14. Все прямолинейные
образующие не распадающихся цилиндров являются их образующими (образующие
цилиндров определяются по аналогии с коническими поверхностями) и,
следовательно, параллельны между собой
Доказательство. Рассмотрим
произвольную прямолинейную образующую и спроектируем ее на плоскость z = 0. Тогда
результат проекции должен целиком принадлежать направляющей (конике), что
возможно только тогда, когда проекция - точка, то есть прямолинейная образующая
параллельна оси Oz, то есть образующим.
Рис. 8 эллиптический цилиндр
Рис. 9 мнимый эллиптический цилиндр
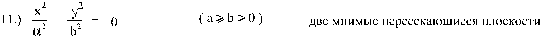
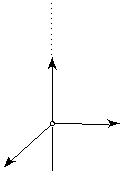
Рис. 10 две мнимые пересекающиеся
плоскости
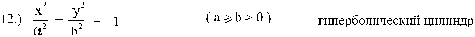
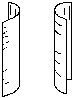
Рис. 11 гиперболический цилиндр
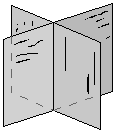
Рис. 12 две пересекающиеся плоскости
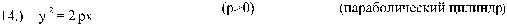
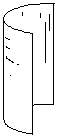
Рис. 13 параболический цилиндр
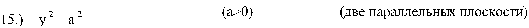
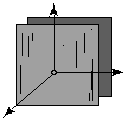
Рис. 14 две параллельные плоскости

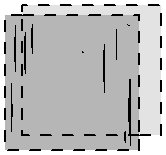
Рис. 15 две мнимые параллельные
плоскости

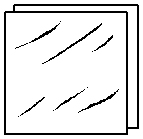
Рис. 16 две совпадающие плоскости
Список литературы
.Лекции по аналитической геометрии.
П. С. Александров 1968 г.
.Справочник по математике. Г.Корн. и
Т.Корн 1970 г.
.Аналитическая геометрия. П. С.
Моденов 1969 г.
.Линейная алгебра и многомерная
геометрия. Н.В. Ефимов. Э.Р. Розендорн 1970 г.
.Курс аналитической геометрии и
линейной алгебры. Д.В. Беклемишев 1987 г.
.Краткий курс по аналитической
геометрии. Н.В. Ефимов 1975 г.
7.Сборник задач по аналитической
геометрии. Д.В. Клетеник 1986 г.
Приложение 1
Задача 1.
Какую поверхность определяет уравнение:
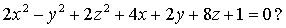
Решение. Чтобы привести данное
уравнение к каноническому виду выделяем полные квадраты по x, y, z :
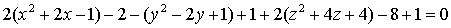
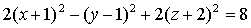
Отсюда:
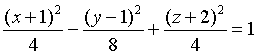
Сравнивая это уравнение с
каноническими выясним что это уравнение однополостного гиперболоида, центр
которого смещён в точку О`(-1 ; 1 ; -2) если ввести обозначения:
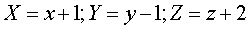
то уравнение примет вид:
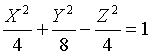
Новые оси O`X, O`Y и O`Z параллельны
старым. Так как a = c = 2 то это однополостный гиперболоид вращения вокруг оси
О`Y. Относительно новых осей гиперболоид имеет вид:
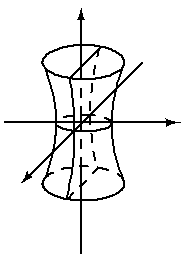
Рис. 17
Задача 2.
Исследовать форму и расположение
относительно системы координат поверхности:
4 - z = x2 + y2
Решение. Применим метод сечений.
Полагая в данном уравнение z = h получим
2+y2=4-h
отсюда следует что 4- h должна быть
величиной неотрицательной. Пусть 4 - h = R*R, получим в сечении плоскостью z =
h линию :
2+y2=R2 ; z = h
Эта линия, очевидно, является
окружностью радиуса R с центром на оси Oz. Следовательно данная поверхность
является поверхностью вращения вокруг оси Oz. Чтобы выяснить вращением какой
линии она получается, пересечём поверхность плоскостью x = 0. В сечении
получится парабола на плоскости yOz
2=4-z
; x=0 ;
Вершина её лежит в точке (0, 0, 4) а
направлена парабола в отрицательную сторону оси Oz. Таким образом исследуемая
поверхность параболоид вращения :
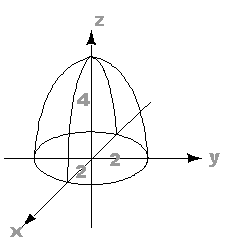
Рис. 18
Задача 3.
Показать, что уравнение :
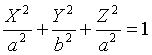
Определяет однополостный гиперболоид
вращения вокруг оси Oy.
Решение. Рассмотрим сечение данной
поверхности плоскостями y = h перпендикулярными оси Оу. В сечении получим
линию:
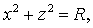
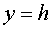 , где
, где 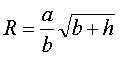
Таким образом, в любом сечении,
перпендикулярном оси Оу, получается окружность радиуса R, то есть данная
поверхность есть поверхность вращения вокруг оси Оу. Выясним, вращением какой
линии получена эта поверхность. Пересечём поверхность какой-либо плоскостью,
проходящей через ось вращения, например плоскостью хОу, в сечении получится
линия:
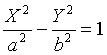
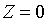
Эта есть гипербола с полуосями а, b.
Вращаясь вокруг оси Оу, она и образует данную поверхность, являющуюся поэтому
однополостным гиперболоидом вращения вокруг оси Оу.
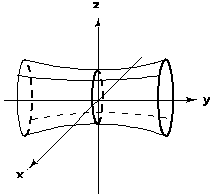
Рис. 19
Задача 4.
Найти точки пересечения эллипсоида
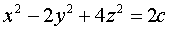
с прямой
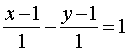 при
при 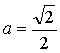
при каком значении а прямая касается
эллипсоида ?
Решение. Запишем параметрические
уравнения данной прямой :
x = 1 ; y = 1 + t ; z = a*t.
Подставляя значения x, y, z в
уравнение эллипсоида :
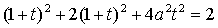
получим квадратное уравнение для t :
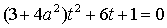
из которого находим значения
параметра t, отвечающие точкам пересечения прямой с эллипсоидом :
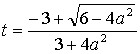
при 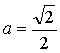 получатся два значения :
получатся два значения :
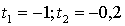
следовательно точки пересечения следующие:
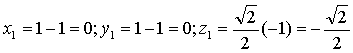
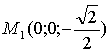
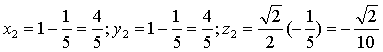
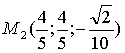
Если прямая касается эллипсоида, то
должно быть 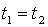 , а это
произойдёт
в
том случае, если подкоренное выражение
, а это
произойдёт
в
том случае, если подкоренное выражение 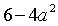 равно нулю.
равно нулю.
Значит при 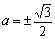 прямая
является касательной.
прямая
является касательной.
Задача 5.
Исследовать сечения эллипсоида
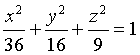
Плоскостями
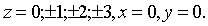
Решение. Рассмотрим сначала сечение
эллипсоида плоскостями z = h, где
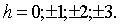
Подставляя в уравнение эллипсоида
получим :
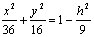
Отсюда
 .
.
Вводя обозначения
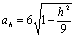 и
и 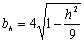
видим, что в сечении получится
эллипс
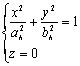
С полуосями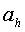
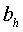 . При
. При 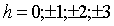 получаем
получаем
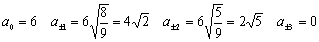
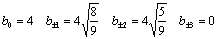
Таким образом, наибольший получается
в сечении плоскостью хОу. Если поднимать или опускать эту плоскость вдоль оси
Oz параллельно плоскости xOy, то размеры сечений уменьшаются до тех пор, пока
при z=3 z=-3 не превратятся в точку (0,0,3) или (0, 0, -3). При дальнейшем
увеличении h плоскость эллипсоида пересекать уже не будет, так как корень,
входящий в выражения для 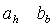 станет
мнимым.
станет
мнимым.
В сечении плоскостями, параллельными xOz и yOz,
будут также получаться эллипсы. В частности, в сечении координатными плоскостями
y
= 0 и x = 0 получатся наибольшие по размерам эллипсы:
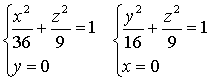
Проведённое исследование позволяет сделать
вывод, что эллипсоид является овальной
поверхностью:
Рис. 20
Задача 6.
Какую поверхность определяет уравнение
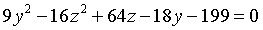

Решение. Эта поверхность есть гиперболический
цилиндр с образующими, параллельными оси
оХ. В самом деле, данное уравнение не содержит х, а
направляющая цилиндра есть гипербола
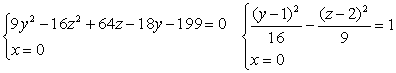
с центром в точке (0, 1, 2) и
действительной осью, параллельной оси Оу.
Приложение 2
Задача 1.8.
Составить уравнения сторон
треугольника, если А(-5 ; 5) и В(3 ; 1) две его вершины, а D(2, 5) -
точка пересечения высот.
Решение:
Уравнение АВ (как прямая проходящая
через две точки) :
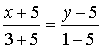 ; x + 5 = -2(y - 5) ; АВ:
-0.5x + 2.5 = y.
; x + 5 = -2(y - 5) ; АВ:
-0.5x + 2.5 = y.
Чтобы найти AC, найдём
сначала BD:
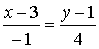 ;: -4x + 13 = y.
;: -4x + 13 = y.
Так как BD┴AC то κκ1 = -1, где κ = -4, и
значит κ1 = 0.25. (κ и κ1 угловые
коэффициенты BD и AC).
AC: y = 0.25x + b; b найдем
исходя из того что AC проходит через точку А(-5;5)
5 = 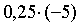 + b ; b = 6.25 ; AC: y=0.25x + 6.25
+ b ; b = 6.25 ; AC: y=0.25x + 6.25
Чтобы найти уравнение прямой ВС
вначале найдём уравнение DHab потом через
их пересечения найдём точку С и потом искомую прямую СВ.
κκ1 = -1, где κ = -0.5 для
АВ, и значит κ1 = 2. y = 2x + b. DHab пересекает D(2;5),
то
есть 5 = 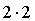 + b, b = 1, DHab : y = 2x + 1.
+ b, b = 1, DHab : y = 2x + 1.
y = 2x
+ 1
y = 0.25x
+ 6.25
2x - 0.25x + 1 - 6.25
= 0 ; x = 3 ; y = 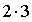 + 1 = 7 ;
значит С(3 ; 7)
+ 1 = 7 ;
значит С(3 ; 7)
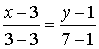 ; 6(x - 3) = 0(y - 1) ; x = 3.
; 6(x - 3) = 0(y - 1) ; x = 3.
Значит CB: x = 3.

Рис. 21
Ответ:
: y
= 0.25x + 6.25 ;
АВ: y
= -0.5x + 2.5 ;
CB : x
= 3.
Задача 2.8.
Даны вершины треугольника АВС. Найти длины
медианы, высоты, биссектрисы, проведённых из вершин А, найти угол при вершине
В. (назовём углом φ)
А(10 ; -1) В(-2 ; -6) С(-6 ; -3)
Решение:
АМ медиана, М(Хм ; Ум), Хм
= (-6 - 2)/2 = -4 ; Ум = (-3 - 6)/2 = -4,5
│АМ│= 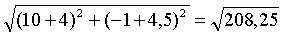
СВ: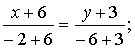 -0,75x - 7,5 = y ;
-0,75x - 7,5 = y ;
ρ(А, ВС) =│АН│=
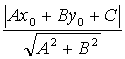 =
= 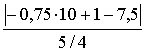 = 11,2
= 11,2
│AH│=11,2
- длина высоты.
AD -
биссектриса, значит λ
= AB/АC ;
=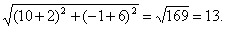 АС=
АС=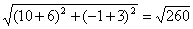
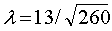
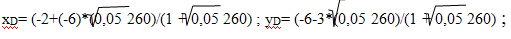
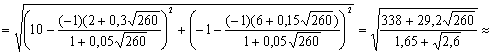
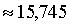 : -0,75x-7,5:
: -0,75x-7,5: 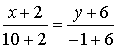 ; (5/12)*x -
(62/12) = y ;
; (5/12)*x -
(62/12) = y ;
κ = - 0,75
; κ1
= 5/12 ; φ =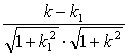 = (-14/12)
/ (65/48) ≈ -0,861538461…
= (-14/12)
/ (65/48) ≈ -0,861538461…
φ ≈ arccos(-0,86153846)
= 1200
Ответ : АМ медиана, равна 208,25 ≈
14,439…
АН высота, равна 11,2
AD биссектриса
равна ≈ 15,745
φ внутренний
угол равен ≈ 1200
(треугольник ABC изображён
на следующей странице на рисунке 22)

Рис. 22
Задача 4.8.
Найти точки пересечения кривой
второго порядка γ с прямой α :
γ: x2-2xy+y2-4x+4=0.
α: x+y-2=0.
Решение:
= -x+2; x2-2xy+y2-4x+4=
(x-y)2-4x+4= (2x+2) 2-4x+4=4x2-8x+4-4x+4=02-3x+2=0;
D=32-2*4=1;
x1,2=
(3±1)
/ 2 ; x1=
2/2=1 ; x2=
4/2=21=
-1+2=1 ; y2=
-2+2=2
Значит точки пересечения кривой второго порядка γ
с прямой α это точки А(1;1) и
В(2; 0)
Ответ: А(1;1) и В(2; 0)
Задача 7.8.
Для векторов: 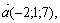
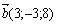 и
и 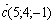 , заданных в
ортонормированном базисе R(O,
, заданных в
ортонормированном базисе R(O, 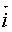 ,
, 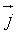 ,
, 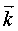 ) найти :
) найти :
. Направляющие косинусы вектора 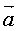 ;
;
. Площадь параллелограмма,
построенного на векторах 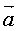 и
и 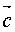 , имеющих
общее начало.
, имеющих
общее начало.
. Объём пирамиды, построенной на
векторах 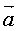 ,
, 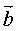 ,
, 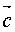 , имеющих
общее начало.
, имеющих
общее начало.
Решение:
. α β и γ есть углы
между ортами e1 e2 e3 вектора 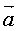 . Значит cos α, cos β, cos γ направляющие
косинусы этого вектора. (рисунок 23)
. Значит cos α, cos β, cos γ направляющие
косинусы этого вектора. (рисунок 23)
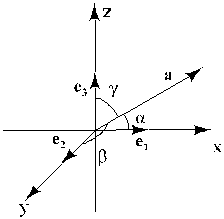
Рис. 23
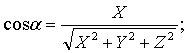
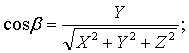
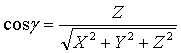 ;
;
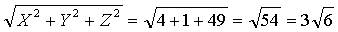
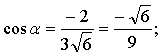
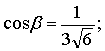
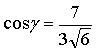
2. Площадь параллелограмма построенного на
векторах равна модулю их векторного произведения.

Рис. 24
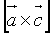 =
=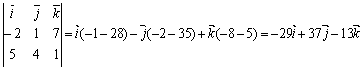
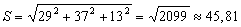
3. Объём пирамиды равен одной шестой
от объёма параллелепипеда, а объём параллелепипеда равен смешанному произведению
трёх векторов, на которых он основан.
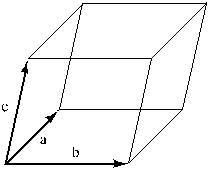
Vпар=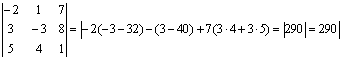
Vпирамиды
= (1/6) * Vпар
= (1/6) * 290 = 145/3.
Ответ:
. cos
α =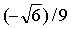 β
=
β
= 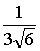 γ
=
γ
=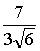
. S = 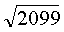 ≈ 45,81
≈ 45,81
. Vпирамиды
= 145/3.
Задача 12.8
Найти точки пересечения поверхности
и прямой
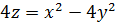
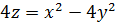 ,
, 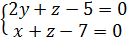
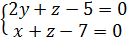
Решение:
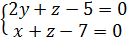
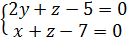 x,
x,
- базисные неизвестные; z - свободная
неизвестная
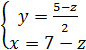
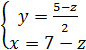
Пусть 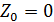
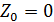 , тогда:
, тогда: 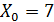
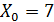 ,
, 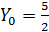
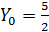
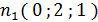
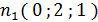
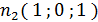
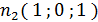
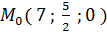
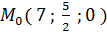
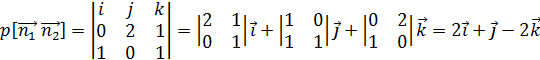
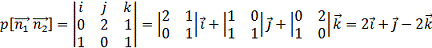
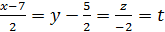
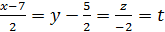
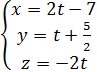
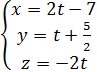
Подставим значения x, y, z в уравнение
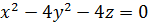
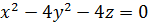 :
:
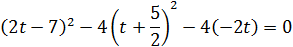
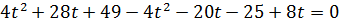
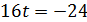
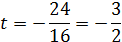
Найдём x, y, z:
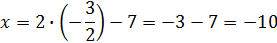
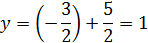
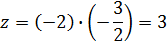
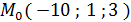
Ответ: 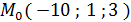
Ответы.
задача 1.8
AC: y
= 0.25x + 6.25 ;
АВ: y
= -0.5x + 2.5 ;
CB : x
= 3.
задача 2.8
АМ медиана, равна 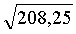 ≈
14,439…
≈
14,439…
АН высота, равна 11,2
AD биссектриса
равна ≈ 15,745
φ внутренний
угол равен ≈ 1200
задача 4.8
А(1;1) и В(2; 0)
задача 7.8
1. cos
α = (- 6) / 9
cos β =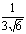
cos γ = 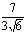
. S = 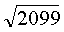 ≈
45,81
≈
45,81
. Vпирамиды = 145/3.
задача 12.8