Устойчивость микробов к антибиотикам

Министерство образования РФ

Томский политехнический университет

Факультет АВТ

Индивидуальное домашнее задание

«Теория вероятностей, математическая статистика и случайные процессы»

Вариант № 1

Выполнил

Студент группы 8В22

Аксенова НГ

Проверил

Преподаватель

Шалаев Ю.Н.

Томск 2004г.

Задание № 1

1. Привести пример пространства элементарных событий.

Записать совместные и несовместные события и найти их вероятности.

2 Доказать, что если независимы события А и U, то независимы события А и Ū.

3. По плотности распределения вероятностей системы двух случайных величин ξ и η найти:

-коэффициент А;

функцию распределения F(x,y) системы случайных величин;

функции распределения и плотности распределения отдельных составляющих системы случайных величин: F1(x), F2(y), f1(x), f2(y);

условные плотности распределения f(x/y), f(y/x);

числовые характеристики системы: математическое ожидание Mξ и Mη и дисперсию системы Dξ и Dη

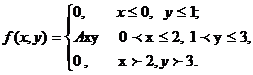
3. По выборке Х оценить закон генеральной совокупности и оценить его параметры:

X = {2.4, 2.2, 2.0, 1.6, 1.8, 2.2, 2.2, 2.0 , 2.0, 1.4, 1.6, 2.0, 1.8, 2.6, 2.4 }.

По выборке Х построить доверительный интервал для параметра “a” - математическое ожидание при уровне значимости α = 0.01.

По выборке Х построить эмпирическую функцию распределения.

5 Задана случайная функция

Y = X (t2 + 1)

где Х случайная величина с МХ = 3, DX = 1.2. Найти числовые характеристики MV, DV, K V (t 1, t 2 ) случайной функции

V = dY/dt

6. Задан случайный процесс

Z = X SIN(t) + Y e-2t

c MX = 1.2, DX = 3.4, MY = 4, DY = 3, r xy = 0.6.

Найти MZ, DZ, K Z (t1 , t2).

. Монету подбрасывают один раз.

Элементарными несовместными событиями в данном случае будут

ω1- выпадение цифры;

ω2- выпадение герба.

Ω={ ω1,ω2}

где Ω- пространство элементарных событий.

Вероятности того, что выпадет цифра или герб равны

P(ω1)= P(ω2)=0.5

1. Условие независимости двух событий: если А и В независимы, то

P(A/B)=P(A).

В данном случае P(A/Ǔ)=P(A)

Доказательство

P(A/Ǔ)=P(A∩ Ǔ)/P(Ǔ)=P(A(1-U))/P(Ǔ)=P(A-A*U)/ P(Ǔ)=P(A)P(1-U)/ P(Ǔ)=P(A)* P(Ǔ)/ P(Ǔ)=P(A)

2. Найдем коэффициент А

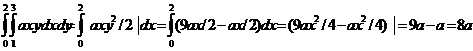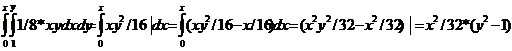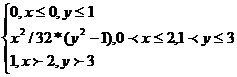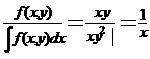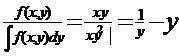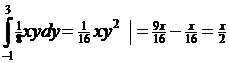=1=1/8(x,y)=(x,y)=(x/y)=(y/x)=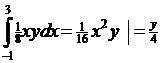 (x)=(x)=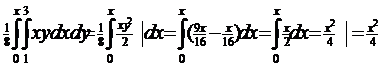(x)=(x)=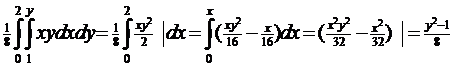

Mξ=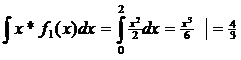

Mη=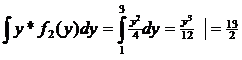

Dξ=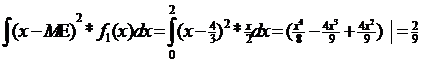

Dη=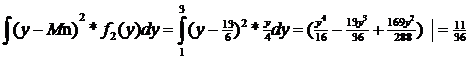

1. Вариационный ряд состоит из семи различных чисел.

Так как X- дискретная случайная величина, то составляем таблицу ряда

Строим эмпирическую функцию

-∞<x≤1.4             Fn(x)=1/15

.4<x≤1.6              Fn(x)=2/15

.6<x≤1.8              Fn(x)=2/15

.8<x≤2.0              Fn(x)=4/15

.0<x≤2.2              Fn(x)=3/15

.2<x≤2.4              Fn(x)=2/15

.4<x≤2.6              Fn(x)=1/15

.6<x<∞                Fn(x)=0

событие вероятность величина распределение

Fn(x)=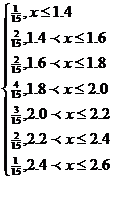

В качестве оценки для математического ожидания принимают эмпирическое среднее, т.е. среднее арифметическое всех полученных значений величины X.

xср=1/n*å xi

xср=1/15(1.4+2*1.6+2*1.8+4*2.0+3*2.2+2*2.4+2.6)=2.013

Выборочная дисперсия находится по формуле

ξ2 =1/n*å(xi-xср)2 -это смещенная оценка дисперсии генеральной совокупности.

ξ2 =1/15*((1.4-2.013)2+2*(1.6-2.013)2+2*(1.8-2.013)2+4*(2-2.013)2+

*(2.2-2.013)2+2*(2.4-2.013)2+(2.6-2.013)2)=0.10382=1/(n-1)*å(xi-xср)2 -это несмещенная оценка дисперсии

S2=0.1112

Среднеквадратичное отклонение

ξ =√1/n*å(xi-xср)2=0,3222 S=√1/(n-1)*å(xi-xср)2=0,3335

Для построения доверительного интервала определяем его границы по формулам

Aн=xср-ερ*S/√n

Aв=xср+ερ*S/√n

xср- выборочное среднее

S- выборочное среднеквадратичное отклонение несмещенной оценки

ερ- определяется по таблицам распределения Стьюдента, по уровню значимости α и числу степеней свободы

p=1- α

Из таблицы находим ερ=1,76

Тогда ερ*S/√n=1,76*0,335/3,74=0,158

Искомый доверительный интервал

m€(2,013-0,158;2,013+0,158)

m€(1.855;2.171)

3. Найдем V=dY/dt=2Xt

MV=M(2Xt)=2tMX=2t*3=6t=D(2Xt)=4t2DX=4t2*1.2=4.8t2(t1,t2)=M[(2X t1-6 t1)*(2X t2-6 t2)]=2 t1*2 t2*M[(X-3)*(X-3)]= 4 t1 t2*M(X-3)2=

t1 t2*M(X-MX)2=4 t1 t2*DX=4 t1 t2*1.2=4.8 t1 t2

т.к. M(X-MX)2= DX

Корреляционная функция Kv(t1,t2) характеризует степень тесноты линейной зависимости между двумя сечениями и разброс этих сечений относительно математического ожидания находится по формуле

Kv(t1,t2)=M[(V(t1)-Mv(t1))*( V(t2)-Mv(t2))]

. MX(t)=M[Xsint+Ye-2t]=sintMX+e-2tMY=1.2*sint+4e-2t=D[Xsint+Ye-2t]=sin2tDX+ e-4tDY=3.4*in2t+3e-4t(t1,t2)=MŻ(t1)*Ż(t2)

Ż(t1)=Xsin t1+Ye-2 t1-1.2 sin t1-4e-2 t1= sin t1 (X-1.2)+ e-2 t1 (Y-4)= sin t1X+ e-2 t1 Y

Аналогично

Ż(t2)= sin t2X+ e-2 t2 Y(t1,t2)=M[(sin t1X+ e-2 t1 Y)*( sin t2X+ e-2 t2 Y)]=M[sin t1 sin t2 X2+ e-2 t1 sin t2X Y+

+ e-2 t2 sin t1X Y+ e-2(t1+t2) Y2]= sin t1 sin t2 MX2+ e-2 t1 sin t2MX Y+ e-2 t2 sin t1MX Y+ +e-2(t1+t2) MY2= sin t1 sin t2 DX+ e-2 t1 sin t2KXY+ e-2 t2 sin t1KXY+ e-2(t1+t2) DY=

=3.4 sin t1 sin t2 +1.92 e-2 t1 sin t2+1.92 e-2 t2 sin t1+3 e-2(t1+t2)

с учетом того, что

rxy= KXY /√DX*DY → KXY = rxy*√DX*DY=1.92