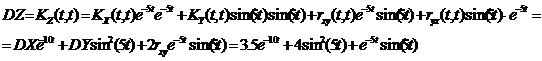Эволюция и генетика человека в контексте эпохи
Министерство
образования Российской Федерации
Томский
Политехнический Университет
Кафедра
ИПС
Индивидуальное
домашнее задание
По
дисциплине «Теория вероятностей МС и СФ»
Вариант
№9
Выполнил:
студент гр. 8В22 Осташкин М. В.
Проверил преподаватель:
Шалаев Ю.Н.
Томск
2004
Задание
1. Привести
пример пространства элементарных событий.
Записать совместные и несовместные события и
найти их вероятности.
2. Доказать,
что если независимы события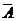 и
и 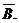 , то независимы
, то независимы
события A
и B.
3. По
плотности распределения вероятностей системы двух случайных величин ξ
и
η
найти:
-коэффициент А;
функцию распределения F(x,y)
системы случайных величин;
-функции распределения и плотности
распределения отдельных составляющих системы случайных величин: F1(x), F2(y), f1(x), f2(y);
условные плотности распределения f(x/y), f(y/x);
числовые характеристики системы:
математическое ожидание Mξ и Mη и дисперсию
системы Dξ и Dη:
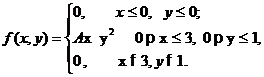
4. По
выборке Х оценить закон генеральной совокупности и оценить его параметры:
X = {4.3, 5.0, 4.8,
5.6, 5.0, 4.8, 5.0, 5.0, 5.0, 5.3, 4.8, 5.0, 5.3, 5.6, 4.3}.
По выборке Х построить доверительный интервал
для параметра “a” -
математическое ожидание при уровне значимости α
= 0.01.
По выборке Х построить эмпирическую функцию
распределения.
5. Задана
случайная функция
Y = X
е-5t,
где Х случайная величина с МХ = 5, DX
= 1.7. Найти числовые характеристики MV,
DV, K
V (t
1, t 2) случайной
функции
V = dY/dt.

. Задан случайный процесс
Z = X e-5t + Y SIN(5t)
c MX = 1.5,
DX = 3.5, MY = 3, DY = 4, r xy = 0.5.
Найти MZ, DZ, K Z
(t1 , t2).
1
Пример пространства элементарных
событий - вытягивание жребия: в шапке 6 бумажек - пять чистых и одна помеченная
крестиком, вытягивается 1 раз жребий.
Элементарные события:
w1 -
вытянутая бумажка чистая
w2 -
вытянутая бумажка помеченная
Ω = {w1,
w2}
= 22 = 4
A0 = {Æ};
A1 = {w1};
A2 = {w2};
A3 = {w1, w2};
Найдем вероятности этих событий:
(A0) = 0(A1)
= 5/6(A2) = 1/6(A3) = 1
Совместные события: A1 и A3, A2 и A3
Если A
и B независимые
события, то P(AÇB)
= P(A)×P(B)
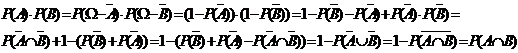
Равенство выполняется,
следовательно, события независимы.
Чтобы найти коэффициент A,
воспользуемся условием нормировки плотности системы случайных непрерывных
величин:
математический ожидание
распределение плотность
1)
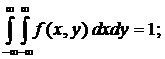
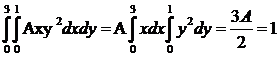
Из этого следует, что A = 2/3.
)
F(x,y) =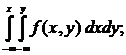
F(x,y) = 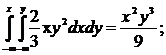 0<x£3,
0<y£1
0<x£3,
0<y£1
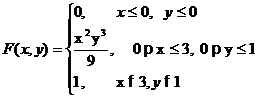
)
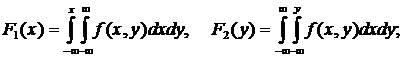
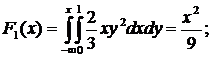 0<x£3
0<x£3
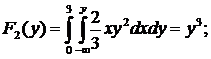 0<y£1
0<y£1
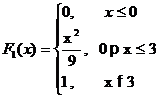
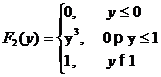
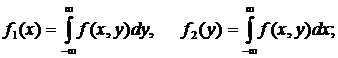
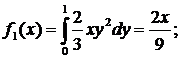 0<x£3
0<x£3
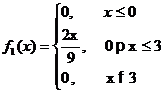
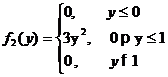
)
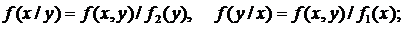
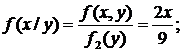 0<x£3
0<x£3
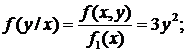 0<y£1
0<y£1
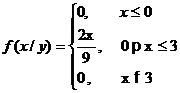
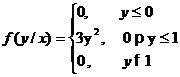
)
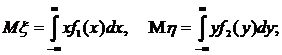
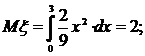
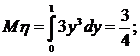
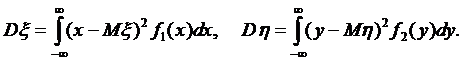
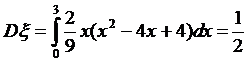 ;
;
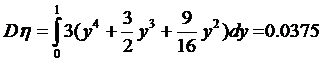
. = {4.3,
5.0, 4.8, 5.6, 5.0, 4.8, 5.0, 5.0, 5.0, 5.3, 4.8, 5.0, 5.3, 5.6, 4.3}
Строим вариационный ряд:
|
X
|
4.3
|
4.8
|
5.0
|
5.3
|
5.6
|
|
ni
|
2
|
3
|
6
|
2
|
2
|
Строим эмпирическую функцию распределения:
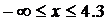 , Fn(x) =
, Fn(x) = 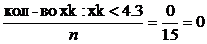 ;
;
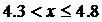 , Fn(x) =
, Fn(x) = 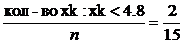 ;
;
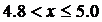 , Fn(x) =
, Fn(x) = 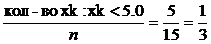 ;
;
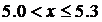 , Fn(x) =
, Fn(x) = 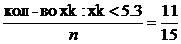 ;
;
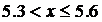 , Fn(x) =
, Fn(x) = 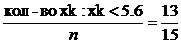 ;
;
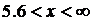 , Fn(x) = 1.
, Fn(x) = 1.
|
Fn(x) =
|
0, 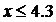
|
|
2/15, 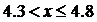
|
|
1/3, 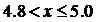
|
|
11/15, 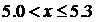
|
|
13/15, 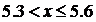
|
|
1, 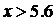
|
Построим полигон частот и эмпирическую функцию
распределения:
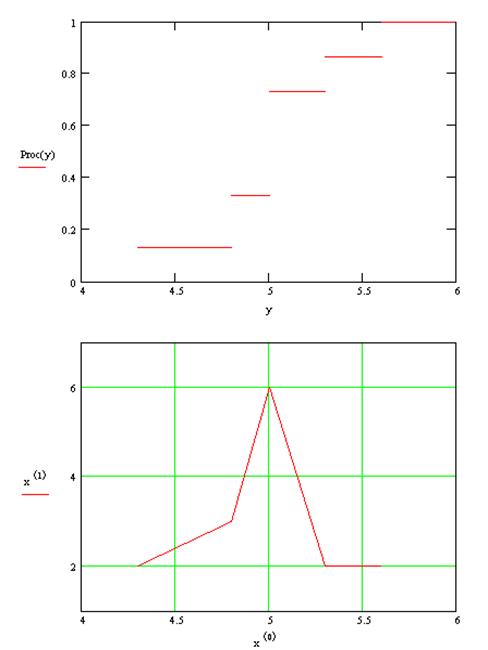
Выборочное среднее определяется по
соотношению:
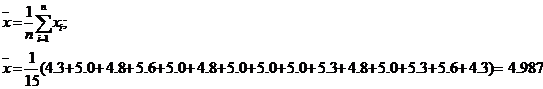
Выборочная дисперсия:
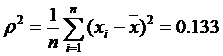 - смещенная оценка
- смещенная оценка
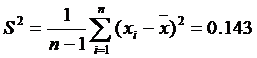 - несмещенная оценка
- несмещенная оценка
Доверительный интервал для параметра
“a”:
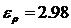 при
при 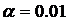 .
.
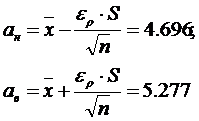
5.
(t) = X е-5t,
MX=5, DX =1.7.
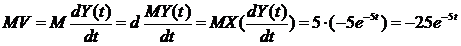 ;
;
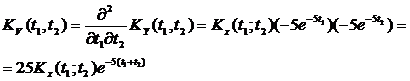
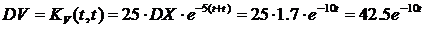 ;
;
.
= X e-5t + Y
SIN(5t), MX = 1.5, DX = 3.5, MY = 3, DY = 4, r xy = 0.5.
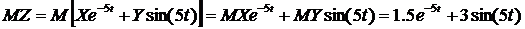 ;
;
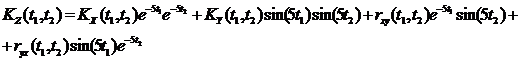
(т.к.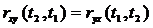 );
);