Синдром Кушинга
СИММЕТРИЧЕСКИЕ
МНОГОЧЛЕНЫ
ОТ ТРЕХ
ПЕРЕМЕННЫХ
КУРСОВАЯ
РАБОТА
ВВЕДЕНИЕ
Одним из самых сложных для школьников разделов алгебры является решение
систем уравнений высших степеней.
Для квадратного уравнения с одним неизвестным
x²+px+q=0
выводится формула
x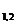 =-
=-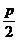 ±
±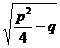 ,
,
указывающая
стандартный путь решения. Для систем уравнений первой степени тоже есть
стандартные приемы решения. Однако для систем уравнений высших степеней дело
обстоит сложнее.
Наиболее
общим способом решения таких систем является метод исключения неизвестных.
Теоретически из любой системы двух алгебраических уравнений с двумя
неизвестными можно, исключая одно неизвестное, получить уравнение второго
неизвестного. Однако не всегда процесс исключения является простым. Наибольшим
же неудобством метода исключения является то, что он часто приводит к уравнению
очень высокой степени. В высшей алгебре доказывается, что если одно уравнение
системы имеет степень n, а второе - m, то после исключения, как
правило, получается уравнение степени mn.
Возьмем,
например, систему
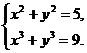
Из
первого уравнения находим: x²=5−y², и потому
x²=(5−y²)³=125−75y²+15y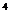 -y
-y .
.
Точно
так же из второго уравнения получаем: x³=9-y³, и потому
 =81-18y³+y
=81-18y³+y .
.
Приравнивая
найденные значения для x , получаем уравнение, содержащее только одно неизвестное y:
, получаем уравнение, содержащее только одно неизвестное y:
y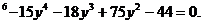
Из-за
этих недостатков метод исключения используют в школе довольно редко. Обычно
стараются решить систему с помощью какого-нибудь искусственного приема. Но
общих правил отыскания таких приемов нет. Каждая система решается своим
методом, и опыт, полученный при решении одной системы, мало помогает при
решении другой. В результате этот раздел школьной математики превращается в
набор головоломок и отдельных кустарных методов их решения.
Моя
цель - познакомить вас с одним довольно общим методом решения систем уравнений
высших степеней. Он не столь универсален, как метод исключения, так как может
быть применен не ко всякой системе. Однако этот метод применим к большинству
систем, с которыми сталкивается школьник. Существенно, что, в отличие от метода
исключения, он приводит не к повышению, а к понижению степени уравнений.
Метод,
о котором идет речь, основан на использовании теории так называемых
симметрических многочленов. Сама теория очень проста и она позволяет решать не
только многие системы алгебраических уравнений, но и различные другие
алгебраические задачи (решение иррациональных уравнений, доказательство
тождеств и неравенств, разложение на множители и так далее). С помощью теории
симметрических многочленов решение этих задач заметно упрощается и, что самое
главное, проводится стандартным приемом.
СИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ ОТ ТРЕХ ПЕРЕМЕННЫХ
Определение и примеры
В многочлене от трех переменных x, y, z перестановок можно сделать три: можно поменять местами x и y, или x и z, или, наконец, y и z. Назовем многочлен ƒ(x, y, z) от трех
переменных x, y, z симметрическим,
если при любой из этих трех перестановок он остается неизменным.
Условие симметричности многочлена ƒ(x, y, z) записывается
следующим образом:
ƒ(x, y, z)=ƒ(y, x, z)=ƒ(z, y, x)=ƒ(x, z, y).
Например, из коммутативности сложения вытекает, что симметричным является
многочлен x+y+z, а из
коммутативности умножения следует симметричность многочлена xyz.
Симметричны и степенные суммы, то есть многочлены
sk=xk+yk+zk.
Вот еще примеры симметрических многочленов от трех переменных:
xy+yz+xz, x3+y3+z3-3xyz,
(x+y)(x+z)(y+z), x(y4+z4)+y(x4+z4)+z(x4+y4).
Напротив, многочлен
x2z+y2z
не является симметрическим. Правда, при перестановке переменных x и y он не меняется:
x2z+y2z=y2z+x2z.
Но перестановка переменных x и z меняет вид этого многочлена - он
переходит в многочлен
z2x+y2x x2z+y2z.
x2z+y2z.
Наиболее
простыми являются симметрические многочлены
x+y+z, xy+xz+yz, xyz.
Их
называют элементарными симметрическими многочленами от трех переменных x, y, z и
обозначают через  ,
,  ,
,  :
:
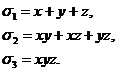
Заметим,
что  - многочлен первой степени,
- многочлен первой степени,  - второй степени и
- второй степени и  -
третьей.
-
третьей.
Основная теорема о симметрических многочленах от трех
переменных.
Возьмем
любой многочлен от переменных  ,
,  ,
,  и заменим
в нем
и заменим
в нем  на x+y+z,
на x+y+z,  - на xy+xz+yz и
- на xy+xz+yz и  - на xyz. В результате мы получим многочлен, симметрично
зависящий от x, y, z. Например, из многочлена
- на xyz. В результате мы получим многочлен, симметрично
зависящий от x, y, z. Например, из многочлена
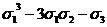
мы
получим таким путем многочлен
ƒ(x, y, z)=(x+y+z)3-3(x+y+z)(xy+xz+yz)-xyz.
Раскрывая
скобки и приводя подобные члены, получаем симметрический многочлен
ƒ(x, y, z)=x3+y3+z3-4xyz.
 Любой
симметрический многочлен от x, y, z можно представить в виде многочлена от
Любой
симметрический многочлен от x, y, z можно представить в виде многочлена от  ,
, 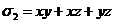 ,
, 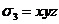 .
.
План
доказательства таков. Сначала мы покажем, что любая степенная сумма sk может быть выражено через элементарные симметрические многочлены  ,
,  ,
,  . Затем мы рассмотрим более сложные симметрические
многочлены, каждый из которых получается из некоторого одночлена всевозможными
перестановками переменных и суммированием получившихся результатов. Такие
симметрические многочлены будем называть орбитами соответствующих одночленов.
Мы покажем, что каждая орбита выражается через степенные суммы, а значит, в
конечном итоге, через
. Затем мы рассмотрим более сложные симметрические
многочлены, каждый из которых получается из некоторого одночлена всевозможными
перестановками переменных и суммированием получившихся результатов. Такие
симметрические многочлены будем называть орбитами соответствующих одночленов.
Мы покажем, что каждая орбита выражается через степенные суммы, а значит, в
конечном итоге, через  ,
,  ,
,  наконец, будет установлено, что всякий симметрический
многочлен представляется в виде суммы орбит.
наконец, будет установлено, что всякий симметрический
многочлен представляется в виде суммы орбит.
Выражение
степенных сумм через  ,
,  ,
,  .
.
Итак,
прежде всего мы покажем, что каждую степенную сумму Sk=xk+yk+zk можно представить в виде многочлена от  ,
,  ,
,  .
.
sk=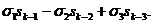 (1)
(1)
Эту
формулу мы не будем «выводить», а прямо проверим. Подставляя в правую часть
соотношения (1) вместо величин:
 ,
, 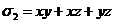 ,
, 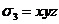 ,
,
sk-1=xk-1+yk-1+zk-1, sk-2=xk-2+yk-2+zk-2, sk-3=xk-3+yk-3+zk-3,
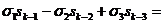 (x+y+z)(xk-1+yk-1+zk-1)-(xy+xz+yz)(xk-2+yk-2+zk-2)+
(x+y+z)(xk-1+yk-1+zk-1)-(xy+xz+yz)(xk-2+yk-2+zk-2)+
+xyz(xk-3+yk-3+zk-3)=(xk+yk+zk+xyk-1+xk-1y+xzk-1+xk-1z+yzk-1+yk-1z)-
(xk-1y+xyk-1+xk-1z+xzk-1+yk-1z+yzk-1+xyzk-2+xyk-2z+xk-2yz)+(xk-2yz+xyk-2z+xyzk-2)=xk+yk+zk=sk.
Таким
образом, правильность формулы (1) проверена.
Из
этой формулы и вытекает справедливость нашего утверждения. Легко видеть, что
степенные суммы s0, s1, s2
выражаются через  ,
,  ,
,  :
:
s0=x0+y0+z0=1+1+1=3;1=x+y+z= ;2=x2+y2+z2=(x+y+z)2-2(xy+xz+yz)=
;2=x2+y2+z2=(x+y+z)2-2(xy+xz+yz)=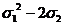 .
.
После
этого формула (1) позволяет последовательно находить выражения следующих
степенных сумм через  ,
,  ,
,  : сначала s3, затем s4, s5 и так далее Иными словами, имея выражение степенных
сумм s0, s1, s2 через
: сначала s3, затем s4, s5 и так далее Иными словами, имея выражение степенных
сумм s0, s1, s2 через  ,
,  ,
,  , мы с помощью метода математической индукции (на
основе формулы (1)) заключаем, что любая степенная сумма sk выражается через
, мы с помощью метода математической индукции (на
основе формулы (1)) заключаем, что любая степенная сумма sk выражается через  ,
,  ,
,  . Таким образом, наше утверждение доказано.
. Таким образом, наше утверждение доказано.
Формула
(3) не только доказывает возможность выразить степенные суммы через  ,
,  ,
,  , но и позволяет фактически находить эти выражения.
, но и позволяет фактически находить эти выражения.
Иными
словами, проведенное выше доказательство конструктивно, то есть оно указывает
вполне определенную последовательность действий, позволяющую за конечное число
шагов добраться до выражения произвольной степенной суммы sk через  ,
,  ,
,  . В таблице 1 сведены выражения степенных сумм (до s10) через
. В таблице 1 сведены выражения степенных сумм (до s10) через  ,
,  ,
, 
Таблица
1
Выражения
степенных сумм sn=xn+yn+zn через  ,
,  ,
, 
|
s0
|
3
|
|
s1
|

|
|
s2
|
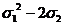
|
|
s3
|
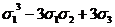
|
|
s4
|
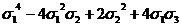
|
|
s5
|
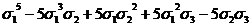
|
|
s6
|

|
|
s7
|

|
|
s8
|
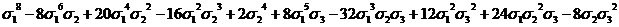
|
|
s9
|
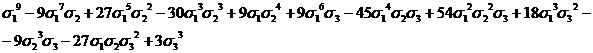
|
|
s10
|
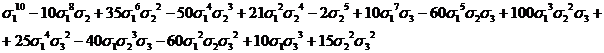
|
Орбиты одночленов
Существуют одночлены, не меняющиеся при перестановках переменных, то есть
симметрические. Легко видеть, что в такой одночлен все переменные должны
входить в одной и той же степени, то есть этот одночлен должен совпадать с
произведением xkykzk.
Если же среди показателей одночлена xkylzm имеются различные, то этот одночлен
уже не будет симметрическим. Чтобы получить симметрический многочлен, один из
слагаемых которого является одночлен xkylzm, надо добавить к нему другие
одночлены. Многочлен с наименьшим числом членов, одним из слагаемых которого
является одночлен xkylzm, назовем орбитой этого одночлена и обозначим через 0(xkylzm).
Ясно, что для получения орбиты одночлена xkylzm надо прибавить к нему одночлены,
получающиеся перестановкой переменных x, y, z. Если все три показателя k, l, m различны, то орбита 0(xkylzm) будет содержать шесть членов,
получающихся из одночлена xkylzm перестановками переменных. Например:
(x5y2z)=x5y2z+x5yz2+x2y5z+x2yz5+xy5z2+xy2z5;
(x3y)=0(x3yz0)=x3y+xy3+x3z+xz3+y3z+yz3.
Если
же в одночлене xkylzm два показателя совпадают, а третий одночлен от них,
скажем k=l (но k m), то
перестановка переменных x, y не меняет одночлена xkylzm. В этом случае орбита содержит только три члена:
m), то
перестановка переменных x, y не меняет одночлена xkylzm. В этом случае орбита содержит только три члена:
(xkylzm)=xkykzm+xkymzk+xmykzk
(m k). Например,
k). Например,
(xyz5)=xyz5+xy5z+x5yz,
(xy)=xy+xz+yz,
(x3y3)=x3y3+x3z3+y3z3.
Частными
случаями таких орбит являются степенные суммы:
(xk)=0(xky0z0)=xk+yk+zk=sk.
Наконец,
если k=l=m, то орбита является одночленом:
(xkykzk)=xkykzk.
Теперь
покажем, что орбита любого одночлена выражается через  и степенные суммы. А так как любая степенная сумма
выражается через
и степенные суммы. А так как любая степенная сумма
выражается через  ,
,  ,
,  , то отсюда будет следовать, что орбита любого
одночлена выражается через
, то отсюда будет следовать, что орбита любого
одночлена выражается через  ,
,  ,
,  . Это
будет вторым шагом в доказательстве основной теоремы.
. Это
будет вторым шагом в доказательстве основной теоремы.
Если
одночлен xkylzm зависит только от одного переменного x (то
есть l=m=0), наше утверждение очевидно: в этом случае орбита
0(xk)=sk сама является степенной суммой.
Перейдем
к случаю, когда одночлен зависит от двух переменных, то есть имеет вид xkyl. Если k l, то имеет
место формула
l, то имеет
место формула
0(xkyl)=0(xk)0(xl)-0(xk+l)
(k l). (2)
l). (2)
В
самом деле,
(xk)0(xl)-0(xk+l)=(xk+yk+zk)(xl+yl+zl)-(xk+l+yk+l+zk+l)=
=(xk+l+yk+l+zk+l+xkyl+xlyk+xkzl+xlzk+ykzl+ylzk)-(xk+l+yk+l+zk+l)=
=xkyl+xlyk+xkzl+xlzk+ykzl+ylzk=0(xkyl).
Если
же k=l, то формула (2) заменяется следующей:
(xkyk)=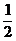 ((0(xk))2-0(x2k). (3)
((0(xk))2-0(x2k). (3)
Справедливость
формулы (3) также устанавливается непосредственной проверкой.
Наконец,
если одночлен xkylzm зависит от всех трех переменных x, y, z, то
одночлен xkylzm делится на некоторую степень одночлена xyz.
Поэтому в многочлене 0(xkylzm) можно вынести за скобки некоторую степень одночлена xyz,
после чего останется в скобках орбита некоторого одночлена, зависящего меньше
чем от трех переменных x, y, z. Например,
(x2y3z4)=x2y3z4+x2y4z3+x3y2z4+x3y4z2+x4y2z3+x4y3z2=
(xyz)2·(yz2+y2z+xz2+xy2+x2z+x2y)=(xyz)2 ·0(x2z),
(x3y5z5)= x3y5z5+x5y3z5+x5y5z3=(xyz)3·(y2z2+x2z2+x2y2)=(xyz)3·0(x2y2)
и
т. п. Вообще, если, например, k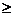 m, l
m, l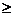 m, то
m, то
(xkylzm)=(xyz)m·0(xk-myl-m)=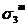 ·0(xk-myl-m). (4)
·0(xk-myl-m). (4)
Итак,
если одночлен xkylzm зависит только от одного переменного, то орбита 0(xkylzm) является степенной суммой; если он зависит от двух
переменных, то орбита 0(xkylzm) выражается через степенные суммы; наконец, случай,
когда этот одночлен зависит от всех трех переменных x, y, z,
сводится к предыдущим, если в многочлене 0(xkylzm) вынести за скобки общий множитель всех его членов.
Легко видеть, что орбита любого одночлена выражается через  и степенные суммы.
и степенные суммы.
Приведенное
выше доказательство также конструктивно: мы не только доказали возможность
выразить каждую орбиту одночлена через  ,
,  ,
,  , но и
получили вполне определенный алгоритм, позволяющий для любой конкретно заданной
орбиты найти ее выражение через
, но и
получили вполне определенный алгоритм, позволяющий для любой конкретно заданной
орбиты найти ее выражение через  ,
,  ,
,  . Основой
этого алгоритма служат формулы (2), (3), (4) и найденное ранее выражение
степенных сумм через
. Основой
этого алгоритма служат формулы (2), (3), (4) и найденное ранее выражение
степенных сумм через  ,
,  ,
,  .
.
Например,
(x2y2)=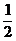 (0(x2)2-0(x4))=
(0(x2)2-0(x4))=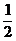 (s22-s4)=
(s22-s4)=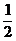 ((
((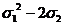 )2-(
)2-(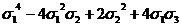 )=
)=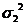 -2
-2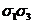 (здесь мы
применили формулу (3));
(здесь мы
применили формулу (3));
0(x4y2z)= ·0(x3y)=
·0(x3y)= (0(x3)0(x)-0(x4))=
(0(x3)0(x)-0(x4))= (s3s1-s4)=
(s3s1-s4)=
= (
( (
(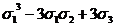 )-(
)-(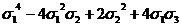 ))=
))= (
(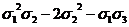 )
)
(применены
формулы (2) и (4)).
В
таблице 2 приведены выражения некоторых орбит 0(xkyl) через  ,
,  ,
,  .
.
Таблица
2
Выражения
орбит 0(xkyl) через  ,
,  ,
, 
|
0(xy)
|

|
|
0(x²y)
|
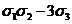
|
|
0(x³y)
|
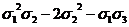
|
|
0(x²y²)
|
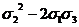
|
|
0(x4y)
|
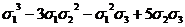
|
|
0(x³y²)
|
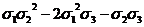
|
|
0(x5y)
|
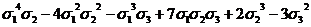
|
|
0(x4y2)
|
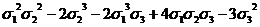
|
|
0(x³y³)
|
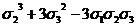
|
Доказательство основной теоремы
Теперь нетрудно завершить доказательство основной теоремы.
Пусть ƒ(x, y, z) - симметрический многочлен и аxkylzm - одно из его слагаемых. В силу
симметричности многочлена ƒ(x, y, z), он содержит вместе с этим
слагаемым и всю орбиту 0(xkylzm), взятую с коэффициентом а. Таким
образом,
ƒ(x, y, z)=а·0(xkylzm)+ƒ1(x, y, z),
где ƒ1(x, y, z)- некоторый
многочлен, который, симметричен и содержит меньше членов, чем ƒ(x, y, z). Из ƒ1(x, y, z) можно также выделить орбиту одного из его членов и так
далее После конечного числа шагов мы разложим многочлен ƒ(x, y, z) на сумму орбит
отдельных одночленов.
Итак,
Любой симметрический многочлен ƒ(x, y, z) есть сумма
конечного числа орбит одночленов.
А
так как каждая орбита выражается через  ,
,  ,
,  , то и
любой симметрический многочлен может быть выражен через
, то и
любой симметрический многочлен может быть выражен через  ,
,  ,
,  . Тем самым основная теорема полностью доказана.
. Тем самым основная теорема полностью доказана.
Все
доказательство является конструктивным: оно содержит сравнительно несложный
алгоритм, позволяющий любой симметрический многочлен выразить через  ,
,  ,
,  .
.
Найдем
выражение симметрического многочлена
ƒ(x, y, z)=x3+y3+z3-4xyz+2x2y+2xy2+2x2z+2xz2+2y2z+2yz2
через
 ,
,  ,
,  . Мы имеем:
. Мы имеем:
ƒ(x, y, z)=0(x3)-4·0(xyz)+2·0(x2y)=
=(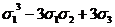 )-4
)-4 +2(
+2(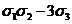 )=
)=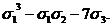
Обратные степенные суммы
Степенные суммы, соответствующие отрицательным показателем, то есть
выражения
s-k=x-k+y-k+z-k=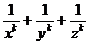
(где
k=1, 2, 3,…), иногда называют обратными степенными
суммами. Их легко выразить через  ,
,  ,
,  , если
заметить, что
, если
заметить, что
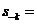
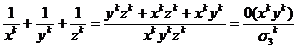 .(
.( )
)
Однако
можно поступить и по-другому. Достаточно заметить, что формула (1) справедлива
для любых значений k (в том числе и отрицательных), поскольку при выводе
этой формулы ни каких предположений относительно k не было
сделано. Заменяя в формуле (1) k на l+3, легко находим:
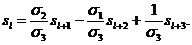 (
(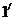 )
)
С
помощью полученной формулы (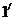 ) можно
последовательно находить значения обратных степенных сумм:
) можно
последовательно находить значения обратных степенных сумм:
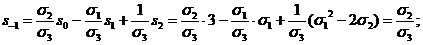
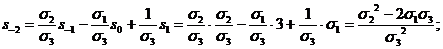
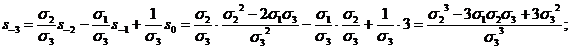
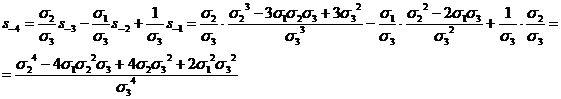
и
так далее Наоборот, имея вычисленные таким образом значения обратных степенных
сумм, можно легко находить орбиты 0(xkyk),
пользуясь формулой (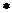 ):
):
(x2y2)=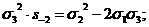
0(x3y3)=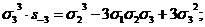
(x4y4)=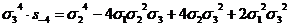
и
так далее.
Основные формулы необходимые для решения задач:
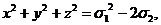
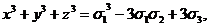
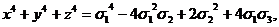
x2y+xy2+x2z+xz2+y2z+yz2=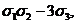
x2y2+x2z2+y2z2=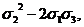
x3y+xy3+x3z+xz3+y3z+yz3=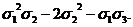
Справедливость
формул можно проверить, подставив значения  ,
,  ,
,  .
.
симметрический
многочлен уравнение переменное
ПРИМЕНЕНИЯ К ЭЛЕМЕНТАРНОЙ АЛГЕБРЕ
Решение систем уравнений с тремя неизвестными
Результаты
выше сказанного позволяют решать некоторые системы алгебраических уравнений с
тремя неизвестными. Если левые части уравнений симметрично зависят от
неизвестных x, y,z, то удобно принять  ,
,  ,
,  , за новые
неизвестные. Выгода такой замены неизвестных заключается в том, что степени
уравнений после замены уменьшаются (поскольку
, за новые
неизвестные. Выгода такой замены неизвестных заключается в том, что степени
уравнений после замены уменьшаются (поскольку 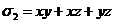 -
многочлен второй степени, а
-
многочлен второй степени, а 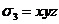 -
многочлен третьей степени). Иными словами, решение системы относительно новых
неизвестных
-
многочлен третьей степени). Иными словами, решение системы относительно новых
неизвестных  ,
,  ,
,  проще, чем решение первоначальной системы.
проще, чем решение первоначальной системы.
После
того как найдены значения величин  ,
,  ,
,  , нужно
найти значения первоначальных неизвестных x, y, z.
Это может быть сделано с помощью следующей теоремы.
, нужно
найти значения первоначальных неизвестных x, y, z.
Это может быть сделано с помощью следующей теоремы.
 Пусть
Пусть  ,
,  ,
,  - три произвольных числа. Кубическое уравнение
- три произвольных числа. Кубическое уравнение
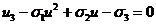 (
(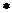 )
)
и
система уравнений
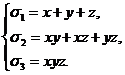 (
(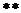 )
)
связаны
друг с другом следующим образом: если u1, u2, u3-корни кубического уравнения, (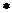 ), то система уравнений (
), то система уравнений ( ) имеет шесть решений
) имеет шесть решений
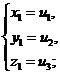
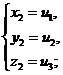
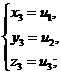
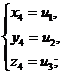
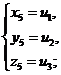
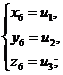
(получающихся
друг от друга перестановками) и других решений не имеет; обратно, если x=a, y=b, z=c -
решение системы ( ), то числа a, b, c
являются корнями кубического уравнения (
), то числа a, b, c
являются корнями кубического уравнения ( ).
).
Для доказательства этой теоремы нам понадобится следующая лемма.
 Если u1, u2, u3 - корни кубического уравнения u3+pu2+qu+r=0,
то имеют место соотношения:
Если u1, u2, u3 - корни кубического уравнения u3+pu2+qu+r=0,
то имеют место соотношения:
u1+u2+u3=-p,1u2+u1u3+u2u3=q,
u1u2u3=-r.
Эти
соотношения называются формулами Виета для кубического уравнения. Покажем,
откуда эти формулы вытекают. Итак, пусть u1, u2, u3 - корни кубического уравнения u3+pu2+qu+r=0;
числа u1, u2, u3 могут
быть действительными или комплексными. Тогда многочлен u3+pu2+qu+r
следующим образом разлагается на множители:
u3+pu2+qu+r=(u-u1)(u-u2)(u-u3).( )
)
Раскрывая
скобки в правой части, находим:
u3+pu2+qu+r=u3-(u1+u2+u3)u2+(u1u2+u1u3+u2u3)u-u1u2u3.
Написанное
равенство означает, что слева и справа стоит один и тот же многочлен, то есть
что соответствующие коэффициенты в левой и правой частях совпадают. Иными
словами,
-(u1+u2+u3)=p,1u2+u1u3+u2u3=q,
-u1u2u3=r,
что и доказывает лемму.
Доказательство
теоремы. Если u1, u2, u3 - корни
кубического уравнения ( ), то, согласно лемме, имеют место соотношения
), то, согласно лемме, имеют место соотношения
u1+u2+u3= ,1u2+u1u3+u2u3=
,1u2+u1u3+u2u3= ,1u2u3=
,1u2u3= .
.
Но
это и означает, что числа x=u1, y=u2, z=u3
составляют решение системы ( ). Еще
пять решений получаются из этого перестановками значений неизвестных. То, что
других решений система (
). Еще
пять решений получаются из этого перестановками значений неизвестных. То, что
других решений система ( ) не имеет, вытекает из последнего утверждения
теоремы, которое мы сейчас докажем.
) не имеет, вытекает из последнего утверждения
теоремы, которое мы сейчас докажем.
Итак,
пусть x=a, y=b, z=c - решение системы ( ), то есть
), то есть
a+b+c= ,+ac+bc=
,+ac+bc= ,=
,= .
.
Тогда мы имеем:
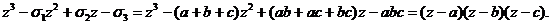
Это
означает, что числа a, b, c являются корнями кубического уравнения ( ). Теорема доказана.
). Теорема доказана.
Замечание.
Доказанная теорема показывает также, что если уже найденные значения величин  ,
,  ,
,  , то для нахождения значений первоначальных
неизвестных x, y, z (то есть для решения системы (
, то для нахождения значений первоначальных
неизвестных x, y, z (то есть для решения системы ( )) достаточно составить кубическое уравнение (
)) достаточно составить кубическое уравнение ( ) и найти его корни. В учебниках высшей алгебры можно
найти формулы для решения кубических уравнений. Однако формулы эти сложны и на
практике редко применяются. Чаще всего пытаются найти один корень кубического
уравнения, после чего пользуются теоремой Безу:
) и найти его корни. В учебниках высшей алгебры можно
найти формулы для решения кубических уравнений. Однако формулы эти сложны и на
практике редко применяются. Чаще всего пытаются найти один корень кубического
уравнения, после чего пользуются теоремой Безу:
 Остаток
от деления многочлена
Остаток
от деления многочлена
ƒ(x)=a0xn+a1xn-1+…+an
на
x-a равен значению этого многочлена при x=a, то
есть равен числу
ƒ(a)=a0an+a1an-1+…+an.
Чтобы
доказать эту теорему, разделим многочлен ƒ(x) на x-a. Мы
получим частное, которое обозначим через q(x), и
некоторый остаток r(x). Этот остаток является многочленом, степень которого
меньше степени делителя x-a, то есть равна нулю. Поэтому r(x)=r
является числом. Итак,
ƒ(x)=(x-a)q(x)+r.
Чтобы
найти число r, положим в этом равенстве x=a. Мы
получим ƒ(a)=r.
Теорема Безу доказана.
Подчеркнем
еще раз, что, решив кубическое уравнение ( ), мы
находим сразу шесть решений для первоначальных неизвестных x, y, z:
так как в систему (
), мы
находим сразу шесть решений для первоначальных неизвестных x, y, z:
так как в систему ( ) неизвестные x, y, z
входят симметрично, то можно переставлять их и в решении.
) неизвестные x, y, z
входят симметрично, то можно переставлять их и в решении.
Рассмотрим
пример.
1. Решить систему уравнений
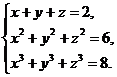
Введем
новые неизвестные  ,
,  ,
,  , положив
, положив
x+y+z= ,
,
xy+xz+yz= ,
,
xyz= .
.
В
силу формул, приведенных в таблице 1, мы имеем для новых неизвестных систему
уравнений:
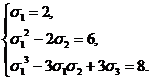
Из
этой системы находим: 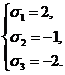
В
развернутом виде эта система записывается так:
x+y+z=2,
xy+xz+yz=-1,
xyz=-2.
Для
решения этой системы составляем (согласно теореме) кубическое уравнение
u3-(u1+u2+u3)u2+(u1u2+u1u3+u2u3)u-u1u2u3=0,3-2u2-u+2=0.
Левая
часть уравнения раскладывается на множители:
u3-2u2-u+2=(u-2)(u2-1).
Следовательно,
корнями этого уравнения являются числа
u1=2, u2=1, u3=-1.
Поэтому
наша исходная система имеет шесть решений, получающихся перестановками из
решения
x=2, y=1, z=-1.
Заметим,
что в некоторых случаях несложная предварительная замена переменных позволяет
свести несимметричную систему к симметричной.
Разложение на множители.
Переход
к элементарным симметрическим многочленам  ,
,  ,
,  удобен не
только для решения систем алгебраических уравнений, но и в других алгебраических
задачах. В этом пункте мы рассмотрим задачи о разложении на множители.
удобен не
только для решения систем алгебраических уравнений, но и в других алгебраических
задачах. В этом пункте мы рассмотрим задачи о разложении на множители.
Пусть
ƒ(x, y, z) -
симметрический многочлен от трех переменных. Чтобы разложить этот многочлен на
множители, можно выразить его через  ,
,  ,
,  и
попытаться разложить на множители получившийся многочлен от
и
попытаться разложить на множители получившийся многочлен от  ,
,  ,
,  .
.
Если
это удастся, то, подставляя значения  ,
, ,
,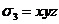 , мы получим разложение на множители исходного
многочлена ƒ(x, y, z).
, мы получим разложение на множители исходного
многочлена ƒ(x, y, z).
Рассмотрим
примеры.
1. Разложить на множители многочлен
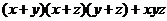
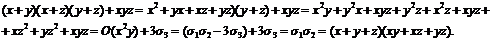
2. Разложить на множители многочлен
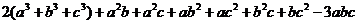
В
силу основных формул, необходимых для решения задач, наш многочлен можно
записать в виде
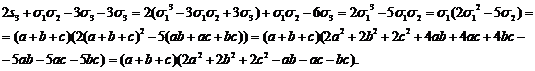
Указанные
приемы пригодны лишь в том случае, если симметрический многочлен удается
разложить на симметрические множители.
Доказательство тождеств
В целом ряде задач на доказательство тождеств с успехом могут быть
применены элементарные симметрические многочлены. Рассмотрим примеры.
1. Доказать тождество
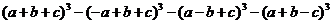 =
=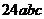
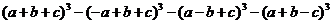 =
=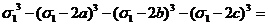
=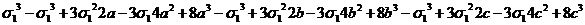 =
=
=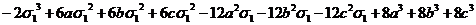 =
=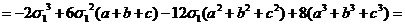

=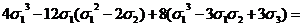
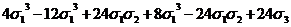 =
=
=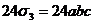 .
.
2. Доказать, что при a+b+c=0 справедливо тождество
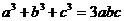 .
.
Согласно
таблице 3, мы имеем:
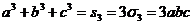 .
.
В
этом примере нам понадобилось вычислить значение степенной суммы 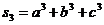 при условии, что
при условии, что 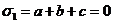 . Эти
значения приведены в следующей таблице:
. Эти
значения приведены в следующей таблице:
Таблица
3
Выражения
степенных сумм sn=xn+yn+zn через  ,
, 
при выполнении условия 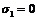
|
s1
|
0
|
s6
|
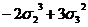
|
|
s2
|
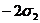 s7 s7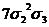
|
|
|
|
s3
|
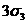 s8 s8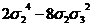
|
|
|
|
s4
|
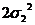 s9 s9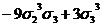
|
|
|
|
s5
|
 s10 s10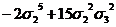
|
|
|
3. Разложить на множители многочлен
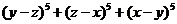 .
.
Полагая
a=y-z, b=z-x, c=x-y, находим:
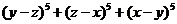 =
=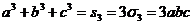 =
=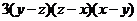
(мы
воспользовались формулой 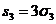 приведенной в таблице 3).
приведенной в таблице 3).
Неравенства
Ясно, что для любых действительных чисел x,y,z справедливо неравенство
(x-y) +(y-z)
+(y-z) +(z-x)
+(z-x) 0,
0,
причем
равенство достигается лишь в случае, когда x=y=z.
Левая часть написанного неравенства является симметрическим многочленом от x, y, z.
Раскрывая скобки, мы без труда перепишем это неравенство в виде 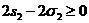 или, используя формулы, приведенные в таблице 1
или, используя формулы, приведенные в таблице 1
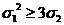 (5)
(5)
Итак,
для любых действительных чисел x,y,z справедливо неравенство (5); равенство достигается
лишь при x=y=z.
Из
соотношения (5) можно получить целый ряд других неравенств. Рассмотрим примеры.
1. Доказать, что для любых действительных чисел a, b, c, справедливо
неравенство
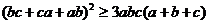
указанное
неравенство имеет вид 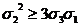 .
.
Неравенство
(5) имеет вид

Полагая
здесь x=ab, y=ac, z=bc, получаем:
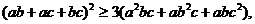
Или
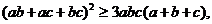
а
это и есть доказываемое неравенство. (Равенство 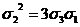 достигается
лишь в случае, если a=b=c или если среди чисел a, b, c
какие-либо два равны нулю.).
достигается
лишь в случае, если a=b=c или если среди чисел a, b, c
какие-либо два равны нулю.).
2. Доказать, что для любых положительных чисел a, b, c, справедливо
неравенство
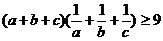 .
.
Указанное
неравенство можно переписать в виде 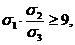 поскольку
поскольку
 можно записать
можно записать  .
.
Так
как числа a, b, c положительны, то 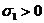 ,
,  ,
,  . Потому
неравенства
. Потому
неравенства 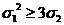 ,
, 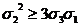 можно
перемножить. Мы получаем
можно
перемножить. Мы получаем 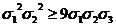 . Сокращая на положительную величину
. Сокращая на положительную величину 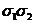 , мы получаем требуемое неравенство
, мы получаем требуемое неравенство  .
.
(Равенство
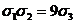 достигается лишь в случае, если a=b=c.).
достигается лишь в случае, если a=b=c.).
Освобождение от иррациональности в знаменателе
Симметрические многочлены позволяют решать многие трудные задачи на
освобождение от иррациональности в знаменателе.
В
случае, когда знаменатель имеет вид 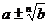 или
или 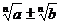 , эту задачу можно решить и без применения
симметрических многочленов. Для этого достаточно использовать формулы
, эту задачу можно решить и без применения
симметрических многочленов. Для этого достаточно использовать формулы
(x+y)(x-y)=x2-y2,
xn-yn=(x-y)(xn-1+xn-2y+xn=3y2+…+yn-1);
x2k+1+y2k+1=(x+y)(x2k-x2k-1y+x2k-2y2-…+y2k).
Например,
если надо освободиться от иррациональности в знаменателе выражения
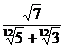 ,
,
то
сначала умножаем числитель и знаменатель на «сопряженное выражение» 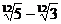 (что приводит знаменатель к виду
(что приводит знаменатель к виду 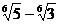 ), потом - на
), потом - на 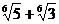 . Мы
получаем:
. Мы
получаем:
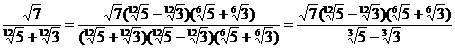 .
.
Теперь
уже можно использовать вторую из приведенных выше формул. Положим в ней x=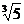 , y=
, y=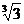 . Тогда ясно, что надо умножить числитель и
знаменатель на выражение
. Тогда ясно, что надо умножить числитель и
знаменатель на выражение
x2+xy+y2=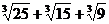 .
.
После
умножения получим:
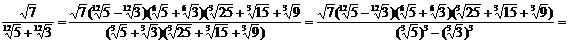
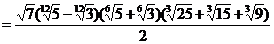 .
.
Сложнее
обстоит дело, если знаменатель состоит из трех или большего числа
иррациональных слагаемых. Здесь-то и могут помочь симметрические многочлены.
Запишем
формулы, которые позволяют избавиться от иррациональности в знаменателе с тремя
слагаемыми.
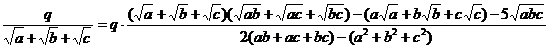
полагая
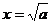 ,
, 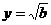 ,
, 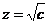 .
.
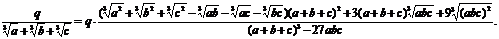
Рассмотрим
следующие примеры.
1. Освободиться от иррациональности в знаменателе выражения
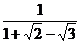
полагая
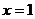 ,
, 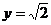 ,
, 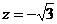 .
.
Воспользуемся
формулой:
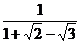 =
=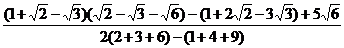 =
=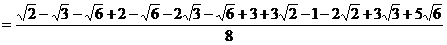 =
=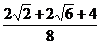 =
=
=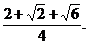
АНТИСИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ ОТ ТРЕХ ПЕРЕМЕННЫХ
Определение и примеры
До сих пор мы рассматривали симметрические многочлены, то есть
многочлены, не изменяющиеся при перестановке любых двух переменных. Теперь мы
рассмотрим другой, очень близкий класс многочленов - антисимметрические
многочлены. Так называют многочлены, меняющие знак при перестановке любых двух
переменных.
Рассмотрим антисимметрические многочлены от трех переменных. Примером
такого многочлена может служить многочлен
(x-y)(x-z)(y-z).
В самом деле, если поменять местами x и y, то
он превратится в многочлен
(y-x)(y-z)(x-z)=-(x-y)(x-z)(y-z).
Точно так же он меняет знак при перестановке любых других переменных.
Отметим следующее важное свойство антисимметрических многочленов: квадрат
антисимметрического многочлена является симметрическим многочленом.
В самом деле, после перестановки любых двух переменных антисимметрический
многочлен меняет знак. Но это оставляет неизменным квадрат многочлена. Значит,
квадрат антисимметрического многочлена не меняется при любой перестановке двух
переменных, то есть является симметрическим многочленом.
Но не только квадрат антисимметрического многочлена симметричен. Если мы
перемножим два произвольных антисимметрических многочлена, то получим в
произведении симметрический многочлен. Ведь при перестановке любых двух
переменных оба сомножителя меняют знаки, а потому произведение остается
неизменным.
Наконец,
при умножении симметрического многочлена на антисимметрический получается
антисимметрический многочлен.
В этом случае при перестановке двух переменных один множитель меняет знак,
а второй не меняет.
Основная теорема об антисимметрических многочленах
Выясним теперь, как устроен произвольный антисимметрический многочлен.
Последнее замечание предыдущего пункта указывает способ, с помощью которого
можно построить сколько угодно антисимметрических многочленов. Достаточно взять
какой-нибудь один такой многочлен и умножить его на всевозможные симметрические
многочлены; в произведении мы будем получать антисимметрические многочлены.
Покажем, что в этом случае искомым антисимметрическим многочленом
является многочлен (x-y)(x-z)(y-z). Иными словами верна следующая
 Любой
антисимметрический многочлен ƒ(x, y, z) от
трех переменных x, y, z имеет вид
Любой
антисимметрический многочлен ƒ(x, y, z) от
трех переменных x, y, z имеет вид
ƒ(x, y, z)=(x-y)(x-z)(y-z)g(x, y, z), (6)
где,
g(x, y, z) - симметрический многочлен от x, y, z.
Прежде
чем доказывать эту теорему, мы установим следующую лемму.
 Если ƒ(x, y, z) -
антисимметрический многочлен, то
Если ƒ(x, y, z) -
антисимметрический многочлен, то
ƒ(x, x, z)=ƒ(x, y, x)=ƒ(x, y, y)=0
то
есть если какие-нибудь два переменных совпадают, то антисимметрический
многочлен обращается в нуль.
Тогда,
в силу теоремы Безу, симметрический многочлен от трех переменных делится без
остатка на выражения x-y, x-z, y-z. Но тогда он должен делиться и на произведение этих
выражений, то есть на антисимметрический многочлен
Т=(x-y)(x-z)(y-z).
Таким
образом, каждый антисимметрический многочлен ƒ(x, x, z)
можно записать в виде ƒ(x, y, z)=(x-y)(x-z)(y-z)g(x, y, z),
где g(x, y, z) - некоторый многочлен.
Чтобы
закончить теперь доказательство теоремы, нам осталось показать, что многочлен g(x, y, z)
симметричен. Для этого поменяем в соотношении (6) местами x и y:
ƒ(y, x,
z)=(y-x)(x-z)(y-z)g(y, x, z).
Такая
замена допустима, поскольку соотношение (6) является тождеством, то есть
справедливо при любых значениях переменных x, y, z.
Так как по условию ƒ(x, y, z)=-ƒ(y, x, z) и
так как (x-y)(x-z)(y-z)=-(y-x)(y-z)(x-z), то отсюда вытекает, что
ƒ(x, y,
z)=(x-y)(x-z)(y-z)g(y, x, z).
Сравнивая
это соотношение с равенством (6), находим, что
(x-y)(x-z)(y-z)g(x, y, z)=(x-y)(x-z)(y-z)g(y, x, z),
и
потому при x y справедливо
равенство g(x, y, z)=g(y, x, z). При x=y последнее равенство принимает вид g(x, x, z)=g(x, x, z) и
также, очевидно, справедливо. Итак, при любых x,y,z имеет место равенство g(x, y, z)=g(y, x, z),
то есть g(x, y, z) - симметрический многочлен. Теорема доказана.
y справедливо
равенство g(x, y, z)=g(y, x, z). При x=y последнее равенство принимает вид g(x, x, z)=g(x, x, z) и
также, очевидно, справедливо. Итак, при любых x,y,z имеет место равенство g(x, y, z)=g(y, x, z),
то есть g(x, y, z) - симметрический многочлен. Теорема доказана.
Итак,
для антисимметрических многочленов от трех переменных имеет место следующее
утверждение.
 Любой
антисимметрический многочлен ƒ(x, y, z) от
трех переменных x, y, z является произведением многочлена
Любой
антисимметрический многочлен ƒ(x, y, z) от
трех переменных x, y, z является произведением многочлена
Т=(x-y)(x-z)(y-z)
на
некоторый симметрический многочлен g(x, y, z) от
трех переменных
x, y, z ƒ(x, y, z)=(x-y)(x-z)(y-z)g(x, y, z)=Т·g(x, y, z).
Дискриминант и его применение к исследованию корней
уравнения.
Мы видели, что в теории антисимметрических многочленов важную роль играют
простейшие антисимметрические многочлены, а именно, многочлен Т=(x-y)(x-z)(y-z) для трех переменных.
Квадрат простейшего антисимметрического многочлена называют дискриминантом.
Таким образом он равен
 =(x-y)2(x-z)2(y-z)2,
=(x-y)2(x-z)2(y-z)2,
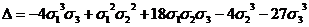 (7)
(7)
Для
сравнения приведем другой вывод формулы (7) с помощью метода частных значений.
Дискриминант  (x, y, z) является однородным многочленом шестой степени.
Поэтому в его выражение через
(x, y, z) является однородным многочленом шестой степени.
Поэтому в его выражение через  ,
,  ,
,  могут
входить (с некоторыми коэффициентами) лишь такие одночлены, для которых m+2n+3p=6
(так как
могут
входить (с некоторыми коэффициентами) лишь такие одночлены, для которых m+2n+3p=6
(так как  - многочлен первой степени,
- многочлен первой степени,  - второй и
- второй и  -
третьей). Уравнение m+2n+3p=6 имеет в целых неотрицательных числах семь решений,
указанных в таблице 4.
-
третьей). Уравнение m+2n+3p=6 имеет в целых неотрицательных числах семь решений,
указанных в таблице 4.
Таблица
4
|
m
|
n
|
p
|
m
|
n
|
p
|
m
|
n
|
p
|
|
6 4
|
0 1
|
0 0
|
3 2 1
|
0 2 1
|
1 0 1
|
0 0
|
3 0
|
0 2
|
Иными
словами, выражение дискриминанта  (x, y, z)
через
(x, y, z)
через  ,
,  ,
,  имеет вид
имеет вид
 (x, y, z)=
(x, y, z)=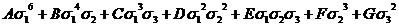 ,(
,( )
)
где
A, B, C, D, F, G - некоторые коэффициенты. Так как соотношение ( ) представляет собой тождество, то мы можем
подставлять в это соотношение любые значения x, y, z.
) представляет собой тождество, то мы можем
подставлять в это соотношение любые значения x, y, z.
Положим
x=1, y=z=0; в этом случае 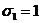 ,
, 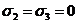 и
и  (1, 0, 0)=
=(1-0)2(0-0)2(0-1)2=0. Поэтому равенство (
(1, 0, 0)=
=(1-0)2(0-0)2(0-1)2=0. Поэтому равенство (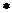 ) принимает вид 0=А. Итак, коэффициент А найден.
) принимает вид 0=А. Итак, коэффициент А найден.
Теперь
положим x=0, y=1, z=-1; в этом случае 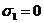 ,
, 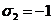 ,
, 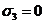 ,
,  =4, и соотношение (
=4, и соотношение (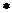 )
принимает вид 4=F·(-1)3, то есть F=-4.
)
принимает вид 4=F·(-1)3, то есть F=-4.
При
x=2, y=z=-1 (то есть 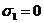 ,
, 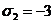 ,
, 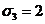 ) получаем
из соотношения (
) получаем
из соотношения ( ): (-4)·(-3)3+4G=0, откуда
находим G=-27.
): (-4)·(-3)3+4G=0, откуда
находим G=-27.
Затем
мы положим x=0, y=z=1 (то есть  ,
,  ,
,  ) и, кроме
того, x=0, y=1, z=2 (то есть
) и, кроме
того, x=0, y=1, z=2 (то есть 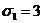 ,
, 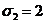 ,
, 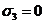 ). Это
даст нам (учитывая, что А=0, F=-4) следующие два соотношения:
). Это
даст нам (учитывая, что А=0, F=-4) следующие два соотношения:
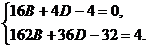
Рассматривая
эти соотношения как систему уравнений относительно неизвестных B и D,
легко находим: В=0, D=1.
Наконец,
придадим величинам x, y, z еще две системы значений: x=y=z=1 и
x=y=1, z=-1. Мы получим тогда (учитывая, что коэффициенты A, B, D, F, G нам уже известны) следующие
соотношения:
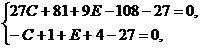
откуда
без труда находим C=-4, E=18.
Итак,
все коэффициенты A, B, C, D, F, G определены. Подставляя в соотношение (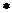 ) найденные значения этих коэффициентов, мы и получаем
формулу (7).
) найденные значения этих коэффициентов, мы и получаем
формулу (7).
Дискриминант
играет важную роль в теории алгебраических уравнений. С его помощью можно
узнать, совпадают ли их корни, исследовать число действительных корней и так
далее
Рассмотрим
квадратное уравнение. Пусть x1 и x2 - корни квадратного уравнения
x²+px+q=0
с действительными коэффициентами p и q. По
формулам Виета имеем:
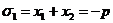 и
и 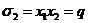 .
.
Поэтому
 =(x1-x2)2=
=(x1-x2)2=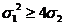 =p2-4q. (8)
=p2-4q. (8)
Мы
ограничимся рассмотрением уравнений с действительными коэффициентами. В этом
случае могут быть три возможности:
а) корни уравнения действительны и различны,
б) корни уравнения действительны и совпадают,
в) корни уравнения комплексно сопряжены.
Дискриминант
позволяет ответить на вопрос, какой же из этих случаев имеет место. Проще всего
выяснить, совпадают ли корни нашего уравнения. Ведь если они совпадают, то есть
если x1=x2, то  =(x1-x2)2=0,
и наоборот. Пользуясь формулой (8), получаем следующий ответ: корни квадратного
уравнения x²+px+q=0
совпадают тогда и только тогда, когда p2-4q=0. Ясно, что если корни совпадают, то они действительны
(поскольку x1+x2=-p). Пусть теперь x1 и x2
различны, то есть
=(x1-x2)2=0,
и наоборот. Пользуясь формулой (8), получаем следующий ответ: корни квадратного
уравнения x²+px+q=0
совпадают тогда и только тогда, когда p2-4q=0. Ясно, что если корни совпадают, то они действительны
(поскольку x1+x2=-p). Пусть теперь x1 и x2
различны, то есть 
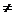 0.
Выясним, когда корни действительны, а когда они комплексно сопряжены. Если
корни x1 и x2 действительны, то число x1-x2 тоже
действительно, и потому
0.
Выясним, когда корни действительны, а когда они комплексно сопряжены. Если
корни x1 и x2 действительны, то число x1-x2 тоже
действительно, и потому  =(x1-x2)2 - положительное число. Если же корни x1 и x2
комплексно сопряжены, то есть x1=
=(x1-x2)2 - положительное число. Если же корни x1 и x2
комплексно сопряжены, то есть x1=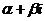 , x2=
, x2=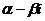 , то x1-x2=
, то x1-x2=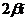 , и потому
, и потому  =(x1-x2)2=
=(x1-x2)2=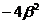 является отрицательным числом. Вспоминая, что
является отрицательным числом. Вспоминая, что  =p2-4q, мы
получаем следующий результат:
=p2-4q, мы
получаем следующий результат:
Пусть x²+px+q=0 - квадратное уравнение с действительными коэффициентами.
Тогда
а) если
 =p2-4q>0,
то корни уравнения действительны и различны;
=p2-4q>0,
то корни уравнения действительны и различны;
б) если
 =p2-4q=0,
то корни уравнения действительны и совпадают;
=p2-4q=0,
то корни уравнения действительны и совпадают;
в) если
 =p2-4q<0,
то корни уравнения комплексно сопряжены.
=p2-4q<0,
то корни уравнения комплексно сопряжены.
Таким образом, в случае квадратного уравнения дискриминант позволяет
полностью различить случаи, когда уравнение x²+px+q=0 с действительными коэффициентами имеет действительные
разные, действительные совпадающие комплексные корни. С этим связано и
происхождение термина «дискриминант»: по-латыни discriminatio означает различение.
Рассмотрим теперь кубическое уравнение
x3+nx2+px+q=0
с действительными коэффициентами n, p, q. Здесь могут встретиться такие
случаи:
а) все три корня уравнения действительны и различны между собой;
б) все три корня уравнения действительны, причем два из них
совпадают, а третий отличен от них;
в) все три корня уравнения совпадают (и действительны);
г) один корень уравнения действительный, а два других комплексно
сопряжены.
Иных случаев быть не может.
Чтобы отличить эти случаи друг от друга, снова образуем дискриминант трех
корней x1, x2, x3 нашего уравнения, то есть выражение
 =(x1-x2)2(x1-x3)2(x2-x3)2.(
=(x1-x2)2(x1-x3)2(x2-x3)2.( )
)
В
силу формул Виета для кубического уравнения (u1+u2+u3=-p, u1u2+u1u3+u2u3=q, u1u2u3=-r) имеем:
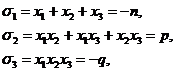
и
потому, согласно формуле (7),
 =-4n3q+n2p2+18npq-4p3-27q2.
=-4n3q+n2p2+18npq-4p3-27q2.
Ясно,
что если какие-нибудь два корня уравнения совпадают, то в выражении ( ) одна скобка обращается в нуль, а тогда и
дискриминант равен нулю. Если же все корни попарно различны (то есть среди них
нет ни одной пары совпадающих), то все скобки в выражении (
) одна скобка обращается в нуль, а тогда и
дискриминант равен нулю. Если же все корни попарно различны (то есть среди них
нет ни одной пары совпадающих), то все скобки в выражении ( ) отличны от нуля, а потому и дискриминант отличен от
нуля. Итак, для того чтобы среди корней уравнения
) отличны от нуля, а потому и дискриминант отличен от
нуля. Итак, для того чтобы среди корней уравнения
x3+nx2+px+q=0
было
хотя бы два совпадающих, необходимо и достаточно, чтобы выполнялось условие  =0.
=0.
Пусть
теперь все корни кубического уравнения действительны и различны. Тогда T=(x1-x2)(x1-x3)(x2-x3)
является отличным от нуля действительным числом, а значит,  =(x1-x2)2(x1-x3)2(x2-x3)2
- положительное число.
=(x1-x2)2(x1-x3)2(x2-x3)2
- положительное число.
Наконец,
пусть корень x1 -
действительный, а корни x2=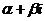 , и x3=
, и x3=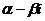 комплексно сопряжены. Тогда выражение T=(x1-x2)(x1-x3)(x2-x3)
принимает вид
комплексно сопряжены. Тогда выражение T=(x1-x2)(x1-x3)(x2-x3)
принимает вид
T=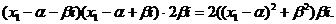
Поэтому
 =Т2=-4
=Т2=-4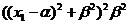 <0.
<0.
Итак,
мы доказали следующее утверждение.
Пусть
x3+nx2+px+q=0
кубическое
уравнение с действительными коэффициентами и
 =-4n3q+n2p2+18npq-4p3-27q2.
=-4n3q+n2p2+18npq-4p3-27q2.
дискриминант
этого уравнения. Тогда:
а) если
 >0, то все три корня x1, x2, x3 действительны и различны;
>0, то все три корня x1, x2, x3 действительны и различны;
б) если
 =0, то среди корней уравнения есть по крайней мере два
совпадающих;
=0, то среди корней уравнения есть по крайней мере два
совпадающих;
в) если
 <0, то один корень уравнения действительный, а два
другие комплексно сопряжены.
<0, то один корень уравнения действительный, а два
другие комплексно сопряжены.
Проведенное исследование не полно. Мы не научились еще отличать случай,
когда два корня уравнения совпадают, а третий отличен от них, от случая, когда
равны друг другу все три корня. Здесь уже дискриминант отказывается дать ответ
и надо искать другой симметрический многочлен. Проще всего взять в этом случае
в помощь дискриминанту симметрический многочлен
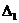 =(x1-x2)2+(x2-x3)2+(x3-x1)2=
=(x1-x2)2+(x2-x3)2+(x3-x1)2=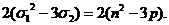
Ясно,
что если корни x1, x2, x3
действительны, то выражение 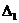 лишь
тогда обращается в нуль, когда все три корня x1, x2, x3 совпадают.
лишь
тогда обращается в нуль, когда все три корня x1, x2, x3 совпадают.
Таким
образом,
если
дискриминант  кубического уравнения x3+nx2+px+q=0
обращается в нуль, то при n2-3p
кубического уравнения x3+nx2+px+q=0
обращается в нуль, то при n2-3p 0 два
корня этого уравнения совпадают, а третий отличен от них, а при n2-3p=0 все три корня уравнения равны между собой.
0 два
корня этого уравнения совпадают, а третий отличен от них, а при n2-3p=0 все три корня уравнения равны между собой.
Заметим
в исключение, что если в произвольный кубический многочлен x3+nx2+px+q ввести
новое неизвестное y по формуле x=y-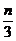 , то этот кубический многочлен примет вид y3+Py+Q, то есть в нем исчезнет член, содержащий квадрат
неизвестного. Таким образом, любое кубическое уравнение может быть указанной
заменой приведено к виду
, то этот кубический многочлен примет вид y3+Py+Q, то есть в нем исчезнет член, содержащий квадрат
неизвестного. Таким образом, любое кубическое уравнение может быть указанной
заменой приведено к виду
y3+Py+Q=0.
Если
уравнение уже приведено к такому виду, то выражения для  и
и 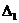 значительно
упрощаются:
значительно
упрощаются:
 =-4P3-27Q2,
=-4P3-27Q2, 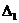 =-6P.
=-6P.
Четные и нечетные перестановки.
Определение симметрических многочленов от трех переменных x, y, z рассмотренное
ранее, можно сформулировать в несколько иной форме. Рассмотрим произвольную
перестановку переменных x, y, z. Таких перестановок существует шесть: x может перейти при перестановке в
любое из трех переменных x, y, z, затем в каждом из этих трех случаев y перейти в какое-либо из двух
оставшихся переменных. Это и дает шесть возможностей для получения перестановок
(при этом, если уже известно, во что переходят x и y, то
для z остается только одна возможность:
оно должно перейти в третье, оставшееся переменное). Все эти шесть возможных
перестановок переменных x, y, z показаны на следующей диаграмме:
x y z x y z x y z
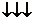
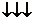
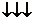
x z y z y x y x z
x y z x y z x y z
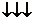
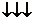
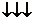 y z y z x z x y
y z y z x z x y
Первые
три перестановки (верхняя строка) заключаются в том, что некоторые два
переменных меняются местами, а третье переменное не меняется. Иными словами,
верхняя строка дает нам всевозможные перестановки двух переменных. Первая
перестановка в нижней строке является тождественной, то есть ни одно переменное
не меняется. Две другие перестановки, указанные в нижней строке, называются
циклическими. Название это объясняется тем, что переменные последовательно
заменяются одно другим (например, во второй перестановке нижней строки x
переходит в y, y переходит в z, а z - в x),
то есть эти перестановки можно схематически изобразить в виде кольца или, как
говорят математики, цикла:
x x
z y z y
Таким
образом, при циклической перестановки каждое переменное переходит по кругу в
следующее.
По
определению, многочлен
ƒ(x, y, z) называется симметрическим, если он не меняется при
перестановках, изображенных в верхней строке приведенной выше диаграммы.
Разумеется симметрический многочлен (да и вообще любой многочлен) не меняется
при тождественной перестановке, когда ни одно переменное x, y, z не
меняет своего значения.
Возникает
вопрос, остается ли симметрический многочлен неизменным и при циклических
перестановках? Оказывается, что остается. Дело в том, что каждая из циклических
перестановок может быть получена, если выполнить одну за другой две
перестановки, меняющие местами два переменных. Например, если сначала поменять
местами x и y, а после этого поменять местами x и z, то
в результате x перейдет в y,y в z, а z в x, то
есть получится циклическая перестановка. Но каждая перестановка двух переменных
оставляет симметрический многочлен неизменным. Поэтому он не меняется, если два
раза произвести перестановку двух переменных, а значит, не меняется и при
циклических перестановках:
ƒ(x, y, z)=ƒ(y, z, x)=ƒ(z, x, y,).
Итак,
определение симметрического многочлена от трех переменных можно сформулировать
следующим образом: многочлен от трех переменных называется симметрическим, если
он не изменяется ни при какой перестановке переменных.
Перестановки,
изображенные в верхней строке приведенной выше диаграммы, называются нечетными,
а перестановки указанные в нижней строке - четными. Объясняются эти названия
тем, что для получения перестановок нижней строки нужно произвести четное число
раз перестановку двух переменных (для циклических перестановок - 2 раз, а для
тождественной - 0 раз), а перестановки верхней строки получаются, если нечетное
число раз (а именно, 1 раз) переставить местами два переменных.
Как
же ведут себя при различных перестановках антисимметрические многочлены? По
определению, они меняют знак при нечетных перестановках (то есть при
перестановке двух каких-либо переменных - верхняя строка диаграммы). При четных
же перестановках антисимметрические многочлены не меняются: ведь если мы четное
число раз произведем перестановку двух переменных, то антисимметрический
многочлен четное число раз изменит знак, то есть в результате он совсем не
изменится.
Итак,
и симметрические и антисимметрические многочлены не изменяются при четных
перестановках переменных x, y, z. (При этом симметрические многочлены не меняются
также и при четных перестановках, а антисимметрические при таких перестановках
меняют знак.)
Четно-симметрические многочлены
Естественно рассмотреть класс многочленов, объединяющий симметрические и
антисимметрические многочлены. Именно, назовем многочлен четно-симметрическим,
если он не изменяется ни при какой четной перестановке переменных x1, x2, x3. Как мы видели, к числу четно-симметрических многочленов
относятся и симметрические и антисимметрические многочлены.
Возникает вопрос, насколько же широкий класс многочленов у нас получился?
Оказывается, расширение не слишком велико:
Любой четно-симметрический многочлен является суммой симметрического и
антисимметрического многочленов.
Для доказательства возьмем произвольный четно-симметрический многочлен Р(x, y, z) и переставим в
нем переменные x и y. При этом получится, вообще говоря,
другой многочлен Q(x, y, z). Но если
сделать перестановку любых двух переменных в многочлене Q(x, y, z), то по условию снова получится
многочлен Р(x, y, z) (ибо две
выполненные одна за другой перестановки двух переменных равносильны четной
перестановке переменных x, y, z, а при четной перестановке многочлен Р(x, y, z) не меняется). С
другой стороны, при перестановке в многочлене Р(x, y, z) любых других двух переменных
получится тот же самый многочлен Q(x, y, z), что и при
перестановке переменных x и y.
Итак, любая перестановка двух переменных превращает многочлен Р в Q, а многочлен Q - в Р. Но тогда многочлен
F(x, y, z)=Р(x, y,
z)+Q(x, y, z)
не меняется ни при какой перестановке двух переменных (лишь меняются
местами слагаемые). Поэтому он симметричен. Многочлен же
H(x, y, z)=Р(x, y,
z) - Q(x, y, z)
антисимметричен. Но ясно, что
P(x, y, z)=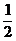 F(x,
y, z)+
F(x,
y, z)+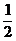 H(x, y, z).
H(x, y, z).
Тем
самым доказано, что любой четно-симметрический многочлен Р(x, y, z)
является суммой симметрического и антисимметрического многочленов.
Поскольку
мы знаем строение и симметрических и антисимметрических многочленов, получаем
следующий результат:
Любой
четно-симметрический многочлен от трех переменных x, y, z
может быть представлен в виде некоторого многочлена от многочленов  ,
,  ,
,  и T=(x-y)(x-z)(y-z). При этом многочлен Т входит в выражение не более
чем в первой степени, так как многочлен Т2=
и T=(x-y)(x-z)(y-z). При этом многочлен Т входит в выражение не более
чем в первой степени, так как многочлен Т2= является симметрическим и потому может быть выражен
через
является симметрическим и потому может быть выражен
через  ,
,  ,
,  .
.
ПРИМЕНЕНИЕ К ЭЛЕМЕНТАРНОЙ АЛГЕБРЕ
Разложение на множители
Доказанная ранее основная теорема об антисимметрических многочленах
позволяет значительно упростить решение целого ряда задач элементарной алгебры.
Так как любой антисимметрический многочлен от трех переменных x, y, z делится на
многочлен
T(x, y, z)=(x-y)(x-z)(y-z),
то мы сразу получаем возможность разложить любой антисимметрический
многочлен ƒ(x, y, z) на множители:
ƒ(x, y,
z)=T(x, y, z)·g(x, y, z),( )
)
где
g(x, y, z) - симметрический многочлен. В свою очередь,
симметрический многочлен g(x, y, z) также иногда может быть разложен на множители (его
можно выразить через  ,
,  ,
,  и попытаться разложить на множители получившийся
многочлен от
и попытаться разложить на множители получившийся
многочлен от  ,
,  ,
,  , если это удастся, то, подставляя значения
, если это удастся, то, подставляя значения  ,
, 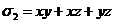 ,
, 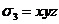 , мы получим разложение на множители исходного
многочлена g(x, y, z)). Заметим, что для отыскания частного
, мы получим разложение на множители исходного
многочлена g(x, y, z)). Заметим, что для отыскания частного
g(x, y, z)=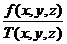
нецелесообразно
производить деление («в столбик») антисимметрического многочлена ƒ(x, y, z) на
кубический многочлен T(x, y, z). Более удобным (когда степень многочлена ƒ(x, y, z) не
слишком высока) является метод частных значений.
Именно,
если антисимметрический многочлен ƒ(x, y, z)
имеет третью степень, то частное
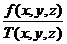 (
(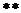 )
)
является
многочленом нулевой степени, то есть числом:
ƒ(x, y, z)=k·T(x, y, z).
Это
соотношение является тождеством, то есть справедливо при любых значениях x, y, z.
Поэтому для определения числа k достаточно
в последнем равенстве придать x, y, z какие-либо (попарно различные) числовые значения;
отсюда и определяется число k.
Если
антисимметрический многочлен ƒ(x, y, z)
является однородным многочленом четвертой степени, то частное ( ) является однородным симметрическим многочленом
первой степени, то есть имеет вид
) является однородным симметрическим многочленом
первой степени, то есть имеет вид 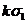 :
:
ƒ(x, y, z)=T(x, y, z)·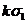
(k -
число). И здесь для определения неизвестного коэффициента k
достаточно придать x, y, z какие-либо числовые значения.
Аналогично,
если ƒ(x, y, z) -
однородный антисимметрический многочлен пятой степени, то частное ( ) является однородным симметрическим многочленом
второй степени, то есть имеет вид
) является однородным симметрическим многочленом
второй степени, то есть имеет вид 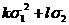 , где k и l -
неизвестные коэффициенты:
, где k и l -
неизвестные коэффициенты:
ƒ(x, y, z)=T(x, y, z)·(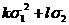 ).
).
Для
нахождения двух неизвестных коэффициентов k, l мы
должны дважды придать x, y, z некоторые числовые значения.
Если
ƒ(x, y, z) -
однородный антисимметрический многочлен шестой степени, то
ƒ(x, y, z)=T(x, y, z)·(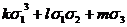 ),
),
и
так далее
Рассмотрим
примеры.
1. разложить на множители антисимметрический многочлен
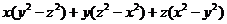
это
многочлен третьей степени, следовательно ƒ(x, y, z)=k·T(x, y, z).
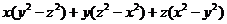 =
=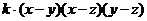 .
.
Чтобы
найти коэффициент k, положим x=-1, y=0, z=1
2=(-2)k, k=-1
Таким
образом,
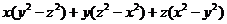 =
=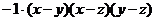 =
=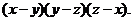
2. разложить на множители антисимметрический многочлен
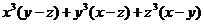
это
многочлен четвертой степени, следовательно ƒ(x, y, z)=T(x, y, z)·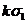 .
.
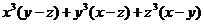 =
=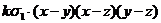 =
=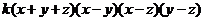 .
.
Полагая
x=0, y=1, z=2
=(-6)k, k=1
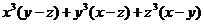 =
=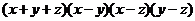 .
.
Упрощение алгебраических выражений
Приемы разложения на множители, рассмотренные в предыдущем пункте, удобно
применять также и при решении некоторых других алгебраических задач. Например,
эти приемы с успехом применяются для доказательства тождеств, в левой и правой
части которых стоят антисимметрические многочлены. Точно так же, если в
числителе и знаменателе дроби стоят антисимметрические многочлены от трех
переменных, то дробь заведомо может быть сокращена на T(x, y, z). Рассмотрим примеры.
1. упростить выражение
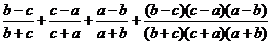
Приведем
к общему знаменателю, получим:
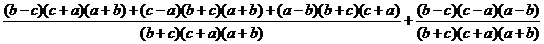 .
.
Числитель
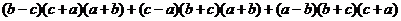 является антисимметрическим многочленом третьей
степени и потому пропорционален многочлену T(a, b, c)=(a-b)(a-c)(b-c),
то есть
является антисимметрическим многочленом третьей
степени и потому пропорционален многочлену T(a, b, c)=(a-b)(a-c)(b-c),
то есть
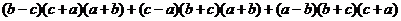 =
=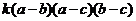
чтобы
найти k положим a=0, b=1, c=2.
Мы получим, что k=1, а потому
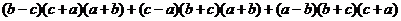 =
=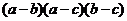
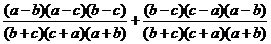 =
=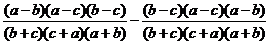 =0.
=0.
Разложение симметрических многочленов от трех переменных на
множители
В случае трех переменных симметрия многочлена значительно облегчает
отыскание его разложения на множители. В это разложение могут входить
симметрические и несимметрические множители. При этом, если в разложение входит
несимметричный множитель h(x, y, z), то, в силу
симметрии, разлагаемого многочлена, должны входить и все множители, получаемые
из h(x, y, z) перестановкой переменных x, y, z.
Как мы уже знаем переменные x, y, z можно переставлять шестью различными способами. Поэтому,
вообще говоря, вместе с несимметричным множителем h(x, y, z) должны входить еще пять множителей. Однако, если сам
множитель h(x, y, z) имеет частичную симметрию, то число
добавочных множителей уменьшается. Так, если множитель h(x, y, z) симметричен относительно x и y, то
есть удовлетворяет условию
h(x, y, z)=h(y, x, z),
то при перестановках переменных x, y, z получается еще два отличающихся от него множителя h(y, z, x) и h(z, x, y,). (Они получаются с помощью циклических перестановок.) Если
же многочлен h(x, y, z) четно-симметричен, то есть обладает
тем свойством, что
h(x, y, z)=h(y, z, x)=h(z, x, y,),
то в разложении с ним связан лишь один множитель h(y, x, z).
Итак, в разложении на множители симметрического многочлена ƒ(x, y, z) могут входить
следующие виды сомножителей:
1. симметричные множители h(x, y, z);
2. произведения вида h(x, y, z)·h(y, x, z),·где h(x, y, z) - многочлен, не меняющийся при четных перестановках;
. произведения вида h(x, y, z)·h(y, z, x)·h(z, x, y,), где h(x, y, z) - многочлен,
симметричный относительно x и y;
. произведения вида h(x, y, z)·h(y, z, x)·h(z, x, y,)·h(y, x, z)·h(x, z, y)·h(z, y, x,)
где h(x, y, z) - многочлен, не обладающий
симметрией.
Покажем теперь, как сделанные замечания позволяют разлагать
симметрические многочлены на множители. Разложение на симметричные множители мы
уже рассматривали. После того как многочлен разложен на симметричные множители,
надо разлагать далее (пользуясь сделанными замечаниями) сами эти множители.
Рассмотрим пример.
1. Разложить на множители многочлен
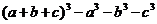 .
.
Указанный
многочлен имеет вид 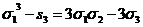 и потому на симметричные множители не разлагается.
Следовательно, остается возможность разложить его на три множителя первой
степени, причем эти множители должны быть симметричными относительно двух
переменных. Иначе говоря, разложение надо искать в виде
и потому на симметричные множители не разлагается.
Следовательно, остается возможность разложить его на три множителя первой
степени, причем эти множители должны быть симметричными относительно двух
переменных. Иначе говоря, разложение надо искать в виде
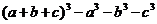 =
=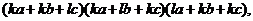 (
( )
)
где
k, l - искомые коэффициенты. Полагая в равенстве (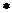 ) a=b=c=1, получаем
) a=b=c=1, получаем 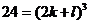 , откуда
, откуда 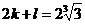 . Далее, при a=b=0, c=1
получаем
. Далее, при a=b=0, c=1
получаем 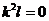 , то есть одно из чисел k, l
равно нулю. Наконец, при a=1, b=1, c=0 находим
, то есть одно из чисел k, l
равно нулю. Наконец, при a=1, b=1, c=0 находим 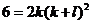 , откуда
видно, что k
, откуда
видно, что k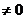 . Следовательно, l=0, k=
. Следовательно, l=0, k=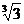 . Мы получаем, таким образом, разложение
. Мы получаем, таким образом, разложение
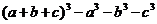 =
=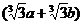
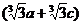
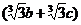 .
.
Если
теперь из каждой скобки вынести 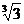 , то мы
получим:
, то мы
получим:
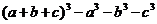 =
=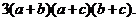
Симметрические многочлены от
нескольких переменных
Элементарные симметрические многочлены от нескольких
переменных
Перейдем теперь к изучению симметрических многочленов от любого числа
переменных. Основные их свойства видны уже на разобранном выше частном случае
симметрического многочлена от трех переменных. Но некоторые усложнения при
переходе к большему числу переменных все же возникают.
Определение симметрических многочленов в случае нескольких переменных
формулируется точно так же, как и в случае трех переменных: многочлен ƒ(x1, x2,…, xn) от n переменных x1, x2,…, xn называется симметрическим, если он не меняется ни при какой перестановке
переменных. Можно это определение сформулировать по-другому: многочлен ƒ(x1, x2,…, xn)называется симметрическим, если он
не меняется ни при какой перестановке переменных x1, x2,…, xn. Иными словами,
ƒ(x1, x2,…, xn)=ƒ(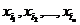 ),
),
где
i1, i2,…, in - это те же числа 1, 2,…,n, но
расположенные в любом другом порядке.
Большинство
понятий, введенных в случае симметрических переменных от трех переменных таким
же точно образом определяются и в общем случае. Например, степенной суммой
степени k от n переменных x1, x2,…, xn, называют выражение
sk=x1k+x2k+…+xnk.
Далее,
орбитой одночлена 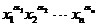 называют сумму всех одночленов, получаемых из
называют сумму всех одночленов, получаемых из 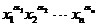 перестановками переменных. Например, в случае n=4,
то есть в случае четырех переменных x1, x2, x3, x4 имеем:
перестановками переменных. Например, в случае n=4,
то есть в случае четырех переменных x1, x2, x3, x4 имеем:
(x12x23)=x12x23+x12x33+x12x43+x22x13+x22x33+x22x43+x32x13+x32x23+
+x32x43+x42x13+x42x23+x42x33.
В
частности,
sk=0(x1k).
Для
дальнейшего полезно следующее замечание: чтобы получить орбиту одночлена 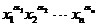 , можно переставлять не буквы x1, x2,…, xn, а показатели
, можно переставлять не буквы x1, x2,…, xn, а показатели 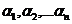 . Конечно, при этом в записи одночлена
. Конечно, при этом в записи одночлена 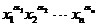 надо указать и не входящие в него буквы (с нулевыми
показателями). Например, одночлен x12x23, орбиту которого мы выше выписывали, следует записать
в виде x12x23x30x40 и затем
уже производить всевозможные перестановки показателей.
надо указать и не входящие в него буквы (с нулевыми
показателями). Например, одночлен x12x23, орбиту которого мы выше выписывали, следует записать
в виде x12x23x30x40 и затем
уже производить всевозможные перестановки показателей.
Кроме
того, отметим, что орбита одночлена порождается любым из входящих в нее
одночленов:
(x14x22x30)=0(x10x24x32)=0(x12x20x34) и так
далее
Несколько
сложнее определяются элементарные симметрические многочлены. Чтобы ввести соответствующее
определение, вспомним, как определялись эти многочлены в случае трех
переменных. Мы имели в этом случае три многочлена:

Первый
из них является суммой всех переменных x1, x2, x3, то есть орбитой одночлена x1:
 =0(x1).
=0(x1).
Второй
многочлен получается из одночлена x1x2 путем всевозможных перестановок переменных и
суммирования полученных результатов. Иными словами, он является орбитой
одночлена x1x2:
 =0(x1x2).
=0(x1x2).
Наконец,
 является орбитой одночлена x1x2x3 (в данном случае эта орбита состоит из одного
слагаемого).
является орбитой одночлена x1x2x3 (в данном случае эта орбита состоит из одного
слагаемого).
По
аналогии положим для случая нескольких переменных:
 =0(x1),
=0(x1),
 =0(x1x2),
=0(x1x2),
………………
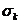 =0(x1x2…xk),
=0(x1x2…xk),
………………
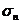 =0(x1x2…xn).
=0(x1x2…xn).
Из
этой записи видно, что число элементарных симметрических многочленов равно
числу переменных.
В
развернутом виде многочлены  ,
,  ,…,
,…, 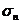 выглядят
следующим образом. Первый из них есть просто сумма всех n
переменных:
выглядят
следующим образом. Первый из них есть просто сумма всех n
переменных:
 =x1+x2+…+xn.
=x1+x2+…+xn.
Второй
многочлен  есть сумма всех произведений переменных, взятых по
два (при этом в произведениях сомножители располагаются в порядке возрастания
значков). Таким образом,
есть сумма всех произведений переменных, взятых по
два (при этом в произведениях сомножители располагаются в порядке возрастания
значков). Таким образом,
 =x1x2+x1x3+…+x1xn+x2x3+…+x2xn+…+xn-1xn,
=x1x2+x1x3+…+x1xn+x2x3+…+x2xn+…+xn-1xn,
или,
короче
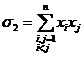
(знак
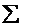 обозначает сумму; внизу указано, что i и j
меняются от 1 до n, причем в каждом произведении).
обозначает сумму; внизу указано, что i и j
меняются от 1 до n, причем в каждом произведении).
Точно
так же третий многочлен  получается, если перемножить переменные по три (так,
чтобы в каждом произведении значки увеличились) и сложить получившиеся
произведения. Таким образом,
получается, если перемножить переменные по три (так,
чтобы в каждом произведении значки увеличились) и сложить получившиеся
произведения. Таким образом,
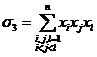 .
.
Вообще
k - й многочлен имеет вид
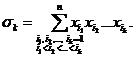
Наконец,
последний многочлен равен произведению всех переменных:
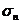 =x1x2…xn.
=x1x2…xn.
Ясно,
что k - й многочлен 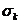 является
однородным и имеет степень k относительно переменных x1, x2,…, xn.
является
однородным и имеет степень k относительно переменных x1, x2,…, xn.
Пример.
Если n=4, то простейшие симметрические многочлены имеют вид
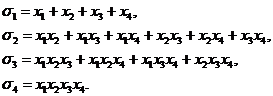
Число
слагаемых в элементарном симметрическом многочлене степени k от n
переменных равно числу сочетаний из n по k, то есть равно
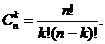
Основная теорема о симметрических многочленах от нескольких
переменных
Точно
так же как и в случае трех переменных, любой симметрический многочлен от n
переменных можно представить в виде многочлена от элементарных симметрических
многочленов  ,
,  ,…,
,…, 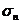 . Точнее говоря, имеем следующее утверждение.
. Точнее говоря, имеем следующее утверждение.
 Пусть ƒ(x1, x2,…, xn) - симметрический многочлен от n переменных.
Тогда существует такой многочлен
Пусть ƒ(x1, x2,…, xn) - симметрический многочлен от n переменных.
Тогда существует такой многочлен 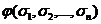 , что если
подставить в него вместо
, что если
подставить в него вместо  ,
,  ,…,
,…, 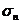 их выражения через x1, x2,…, xn, то есть
их выражения через x1, x2,…, xn, то есть
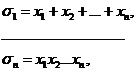
то
получится многочлен, тождественно равный ƒ(x1, x2,…, xn). Многочлен 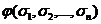 , обладающий указанным свойством, существует только
один.
, обладающий указанным свойством, существует только
один.
Эта
теорема доказывается примерно так же, как и в случае многочленов от трех
переменных, но с некоторыми усложнениями, вызванными увеличением числа
переменных.
Именно,
сначала доказывают, что любая степенная сумма может быть выражена через
элементарные симметрические многочлены. После этого доказывают, что орбита
любого одночлена, содержащего k переменных, выражается через орбиты одночленов от
меньшего числа переменных и, в конце концов, - через степенные суммы. Наконец,
любой симметрический многочлен от n переменных разлагают на орбиты
одночленов. Однако при проведении такого доказательства неудобно использовать
те орбиты, которые были определены выше, а следует применять полные орбиты.
Именно, если в одночлене 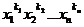 все показатели k1, k2,…, kn различны, то орбита 0(
все показатели k1, k2,…, kn различны, то орбита 0(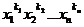 ) содержит
n! членов, получающихся из рассмотренного одночлена
всевозможными перестановками переменных x1,x2,…,xn. Выпишем это выражение орбиты 0(
) содержит
n! членов, получающихся из рассмотренного одночлена
всевозможными перестановками переменных x1,x2,…,xn. Выпишем это выражение орбиты 0(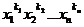 ) и
назовем его полной орбитой одночлена
) и
назовем его полной орбитой одночлена 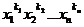 . Полную
орбиту 0П(
. Полную
орбиту 0П(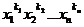 ) мы будем рассматривать не только в случае различных
показателей k1, k2,…, kn (когда она совпадает с обычной орбитой), но и в
случае любых показателей. В любом случае полная орбита 0П(
) мы будем рассматривать не только в случае различных
показателей k1, k2,…, kn (когда она совпадает с обычной орбитой), но и в
случае любых показателей. В любом случае полная орбита 0П(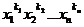 ) отличается от обычной орбиты 0(
) отличается от обычной орбиты 0(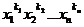 ) лишь числовым множителем, который легко найти, зная,
что при любых показателях k1, k2,…, kn сумма коэффициентов в полной орбите равна n!.
Именно, если среди показателей k1, k2,…, kn имеется n1 совпадающих между собой, затем n2 совпадающих показателей, отличных от первых, и так
далее, вплоть до последней группы nl равных между собой
показателей, то
) лишь числовым множителем, который легко найти, зная,
что при любых показателях k1, k2,…, kn сумма коэффициентов в полной орбите равна n!.
Именно, если среди показателей k1, k2,…, kn имеется n1 совпадающих между собой, затем n2 совпадающих показателей, отличных от первых, и так
далее, вплоть до последней группы nl равных между собой
показателей, то
П(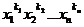 )=n1!n2!...nl!0(
)=n1!n2!...nl!0(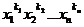 ).
).
Мы
не будем давать детального доказательства теоремы. Укажем те основные формулы,
которые используются в этом доказательстве:
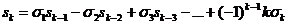 (9)
(9)
(в
этой формуле слагаемые 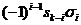 , у которых i>n, считаются
равными нулю),
, у которых i>n, считаются
равными нулю),
П(x1kx2l)=(n-2)!(sksl-sk+l),
(n-2)0П(x1kx2lx3m)=0П(x1kx2l)sm-0П(x1k+mx2l)-0П(x1kx2l+m)
и
так далее
Вообще,
для любых показателей k1,…, kr+1
справедливо соотношение
(n-r)0П(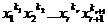 )=0П(
)=0П(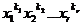 )
)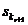 -=0П(
-=0П(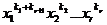 )-
)-
П(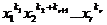 )-…-0П(
)-…-0П(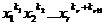 ).
).
Выражение степенных сумм через элементарные симметрические
многочлены
Формула
(9) дает возможность последовательно, одну за другой, вычислять степенные суммы
sk точно так же, как и в случае многочленов от двух или
трех переменных. Формула эта справедлива для любого числа переменных; надо
только помнить, что если рассматриваются многочлены от n переменных, то
в формуле (9) должны быть вычеркнуты все члены, содержащие выражения 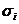 с индексами i, большими чем n.
Благодаря такому соглашению мы можем последовательно вычислять степенные суммы sk, и получающиеся формулы годятся для многочленов от любого числа
переменных. Именно, выпишем соотношение (9) для значений k=1,
2,…:
с индексами i, большими чем n.
Благодаря такому соглашению мы можем последовательно вычислять степенные суммы sk, и получающиеся формулы годятся для многочленов от любого числа
переменных. Именно, выпишем соотношение (9) для значений k=1,
2,…:
s1=1· ;
;
s2=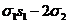
s3=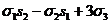 ;
;
s4=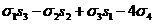
s5=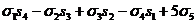 ;
;
s6=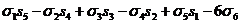 ;
;
Из
этих формул мы последовательно находим значения степенных сумм:
s1= ;
;
s2=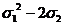 ;
;
s3=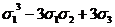 ;
;
s4=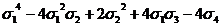 ;
;
s5=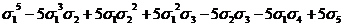 ;
;
s6=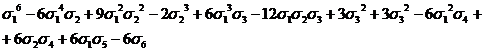 ;
;
Как
и формула (9), эти выражения степенных сумм справедливы для любого числа
переменных; надо только помнить, что если рассматриваются многочлены от n
переменных, то в этих соотношениях должны быть вычеркнуты все члены, содержащие
обозначения  с индексами i, большими чем n.
Например, если в этих формулах вычеркнуть все члены, содержащие
с индексами i, большими чем n.
Например, если в этих формулах вычеркнуть все члены, содержащие  ,
,  ,
, 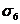 ,…, то мы получим выражения степенных сумм от трех
переменных, то есть получим формулы, приведенные в таблице 1. Если же мы
вычеркнем еще и члены, содержащие
,…, то мы получим выражения степенных сумм от трех
переменных, то есть получим формулы, приведенные в таблице 1. Если же мы
вычеркнем еще и члены, содержащие  , то
получим выражения степенных сумм от двух переменных и так далее
, то
получим выражения степенных сумм от двух переменных и так далее
Формула
Варинга также может быть написана для выражения степенных сумм от любого числа
переменных.
Она
имеет вид
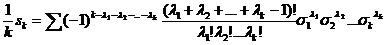 ;
;
суммирование
здесь распространено на все наборы неотрицательных целых чисел, удовлетворяющие
условию
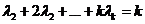 ,
,
а
символу 0!, если он встречается, приписывается значение 1. доказательство
формулы Варинга проводится методом математической индукции на основании
соотношения (9).
СПИСОК ЛИТЕРАТУРЫ
1. Болтянский
В.Г., Виленкин Н.Я.
Б79 Симметрия
в алгебре. - 2-е изд. - М.: МЦНМО, 2002. - 240с. - ISBN 5-94057-041-0.
2. Курош
А.Г.
К93 Курс
высшей алгебры. - 11-е изд. - М.: Наука, 1975. - 431с.