Значение иксодовых клещей в возникновении заболеваний у домашних животных
РЕГРЕССИОННЫЙ
АНАЛИЗ В ЗАДАЧАХ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЙ
ОГЛАВЛЕНИЕ
успеваемость нелинейная множественная регрессия уравнение
Введение
I. Теоретические
основы корреляционно-регрессионного анализа
.1
Метод регрессионного анализа
.2
Нелинейное уравнение регрессии
.3
Множественный корреляционно-регрессионный анализ. Исследовательская часть
2.1
Линейная регрессия при обработке результатов исследования
.2
Нелинейная регрессия в задачах исследования
.3
Множественная линейная регрессия в экспериментальных исследованиях
Заключение
Список
использованной литературы
ВВЕДЕНИЕ
Актуальность темы исследования. Психолого-педагогические
процессы представляют собой очень сложные взаимозависимости, которые довольно
тяжело обрабатывать с помощью математического аппарата. Это обусловлено тем,
что необходимо рассматривать функции, зависящие более чем от двух переменных.
Для того, чтобы хотя бы несколько упростить, поставленные перед педагогом -
психологом задачи обработки полученных наблюдений, приходится прибегать к
математическим моделям, в которых рассматриваются только наиболее влиятельные,
с точки зрения экспериментатора, факторы. В настоящее время, в период глубоких
образовательных реформ, насущной необходимостью является умение анализировать и
прогнозировать те процессы, которые связаны с обучением школьников.
Одной из основных задач школы является
подготовка учащегося с высоким уровнем знаний. К этому стремятся все педагоги
нашей отечественной школы, но, к сожалению, не всегда удается достичь намеченных
результатов. «В чем причина тех или иных показателей успеваемости?» - этот
вопрос неоднократно ставят перед собой многие педагоги, в том числе и педагоги
- психологи. Наряду со многими исследовательскими работами, связанными с
определенными психологическими факторами (Суходольский Г.В., Сидоренко Е.В.,
Кузьмина Е.В. и др.), так и с предлагаемыми новаторскими технологиями и
методиками (Эльконин Д.Б., Давыдов В.В., Занков Л.В., и др.), могут быть и
другие причины той или иной успеваемости учащихся. Педагогу - психологу
необходимо не только знание результатов исследовательских работ, но и умение
самому проводить определенную исследовательскую деятельность, основываясь не на
готовых результатах, а на построении собственной траектории исследования,
используя для этого научный аппарат и математические методы исследования.
В книге О.Ю.Ермолаева приводится пример
выявления взаимосвязи между успешностью обучения математике и показателем
невербального интеллекта, эстонский исследователь Я.Микк, изучая трудности понимания
текста, установил «формулу читаемости», которая представляет собой
множественную линейную регрессию, П.С. Ростовцев, В.С.Костин и др. на основе
автоматизации анализа социально - экономических данных составили и описали
уравнения регрессии для «курильщиков» и «некурильщиков», связанные с жилищными
условиями.
Целью нашей
исследовательской работы является выявление зависимости успеваемости учащихся
от таких факторов как: табакокурение, посещение дополнительных занятий, наличие
проблем в семье, количества времяпровождения в сети Интернет и количества
времени, уходящего на телефонные разговоры.
Объектом
исследования является уровень успеваемости учащихся старших классов.
Предметом
нашего исследования является регрессионный анализ в задачах психолого-педагогических
исследований.
Гипотеза исследования:
табакокурение, посещение дополнительных занятий, наличие проблем в семье,
количество времяпровождения в сети Интернет и количество времени, уходящих на
телефонные разговоры оказывают определенное влияние на успеваемость
старшеклассников.
Задачи исследовательской работы:
1. Изучение научной литературы по теме
«Регрессионный анализ. Его значение для психолого-педагогических исследований»;
2. выявление зависимостей от вышеназванных
факторов;
. составление уравнений регрессий.
Для реализации поставленной цели были
использованы научно - исследовательские методы такие как: анализ научной
литературы, проведение эксперимента, регрессионный анализ.
I. Теоретические
основы корреляционно-регрессионного анализа
.1 Метод регрессионного анализа
Взаимосвязь между переменными
величинами может быть описана разными способами. Например, эту связь можно
описать с помощью различных коэффициентов корреляции (линейных, частных,
корреляционного отношения и.т.п.). В то же время эту связь можно выразить
по-другому: как зависимость между аргументом (величиной) Х и функцией У. В этом
случае задача будет состоять в нахождении зависимости вида 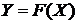 или,
напротив, в нахождении зависимости вида
или,
напротив, в нахождении зависимости вида 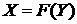 . При этом изменение функции в зависимости от
изменений одного или нескольких аргументов называется регрессией.
. При этом изменение функции в зависимости от
изменений одного или нескольких аргументов называется регрессией.
Графическое выражение регрессионного
уравнения называют линией регрессии. Линия регрессии выражает наилучшее
предсказание зависимой переменной (У) по независимым переменным (Х). Эти
независимые переменные, а их может быть много, носят название предикторов.
Регрессию выражают с помощью двух
уравнений регрессии , которые в самом простом случае выглядят , как уравнения
прямой , а именно так:
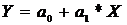 (1)
(1)
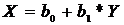 (2)
(2)
В уравнении (1) У - зависимая переменная,
а Х - независимая переменная, а0 свободный член, а1 -
коэффициент регрессии, или угловой коэффициент, определяющий наклон линии
регрессии по отношению к осям координат.
В уравнении (2) Х - зависимая
переменная, а У - независимая переменная, b0 свободный
член, а b1-
коэффициент регрессии, или угловой коэффициент, определяющий наклон линии
регрессии по отношению к осям.
Линии регрессии пересекаются в точке
О 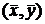 , с
координатами, соответствующими средним арифметическим значениям корреляционно
связанных между собой переменных Х и У. Линия АВ, проходящая через точку О,
соответствует линейной функциональной зависимости между переменными величинами
Х и У, когда коэффициент корреляции между Х и У равен
, с
координатами, соответствующими средним арифметическим значениям корреляционно
связанных между собой переменных Х и У. Линия АВ, проходящая через точку О,
соответствует линейной функциональной зависимости между переменными величинами
Х и У, когда коэффициент корреляции между Х и У равен 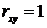 .При этом
наблюдается такая закономерность чем сильнее связь между Х и У, тем ближе обе
линии регрессии к прямой АВ, и, наоборот, чем слабее связь между этими
величинами, тем больше линии регрессии отклоняются от прямой АВ. При отсутствии
связи между Х и У регрессии оказываются под прямым углом по отношению друг к
другу и в этом случае
.При этом
наблюдается такая закономерность чем сильнее связь между Х и У, тем ближе обе
линии регрессии к прямой АВ, и, наоборот, чем слабее связь между этими
величинами, тем больше линии регрессии отклоняются от прямой АВ. При отсутствии
связи между Х и У регрессии оказываются под прямым углом по отношению друг к
другу и в этом случае  .
.
Количественное представление связи (зависимости)
между Х и У (между У и Х) называется регрессионным анализом. Главная задача
регрессионного анализа заключается, собственно говоря, в нахождении
коэффициентов а0, b0, a1 и b1 и
определений уровня значимости полученных аналитических выражений (1) и (2),
связывающих между собой переменные Х и У.
При этом коэффициенты регрессии а1 и
b1
показывают, насколько в среднем величина одной переменной изменяется при
изменении на единицу меры другой. Коэффициент регрессии а1 в уравнении (1)
можно подсчитать по формуле
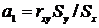 (3)
(3)
а коэффициент 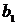 в уравнении
(2) по формуле (4)
в уравнении
(2) по формуле (4)
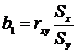 (4)
(4)
где 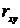 - коэффициент корреляции между переменными X и Y
- коэффициент корреляции между переменными X и Y
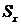 - среднеквадратическое отклонение, подсчитанное
для переменной X
- среднеквадратическое отклонение, подсчитанное
для переменной X
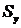 - среднеквадратическое отклонение, подсчитанное
для переменной
- среднеквадратическое отклонение, подсчитанное
для переменной 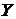 .
.
Коэффициенты регрессии можно
вычислить также без подсчета среднеквадратических отклонений по следующим
формулам
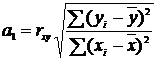 (5)
(5)
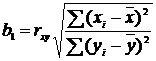 (6)
(6)
В том случае, если неизвестен
коэффициент корреляции, коэффициенты регрессии можно вычислить по следующим
формулам:
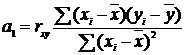 (7)
(7)
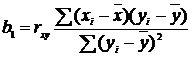 (8)
(8)
Сравнивая формулы (1) (вычисление 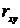 ) (7) и (8),
видим, что в числителе этих формул стоит одна и та же величина:
) (7) и (8),
видим, что в числителе этих формул стоит одна и та же величина: 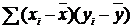 . Последнее
говорит о том, что величина
. Последнее
говорит о том, что величина 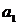 ,
, 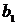 и
и 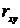 взаимосвязаны. Более того, зная две из них -
всегда можно получить третью. Например, зная величины
взаимосвязаны. Более того, зная две из них -
всегда можно получить третью. Например, зная величины 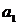 и
и 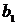 можно легко
получить
можно легко
получить 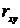 :
:
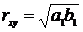 (9)
(9)
Формула (9) достаточно очевидна,
поскольку, умножив 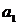 ,
вычисленный по формуле (3) на
,
вычисленный по формуле (3) на 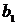 , вычисленный по формуле (4), получим:
, вычисленный по формуле (4), получим:
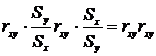
Формула (9) очень важна, поскольку
она позволяет по известным значениям коэффициентов регрессии 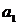 и
и 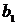 определить
коэффициент корреляции, и, кроме того, сравнивая вычисления по формулам (1) и
(9) , можно проверить правильность расчета коэффициента корреляции,
коэффициенты регрессии характеризуют только линейную связь и при положительной
связи имеют знак плюс, при отрицательной - знак минус.
определить
коэффициент корреляции, и, кроме того, сравнивая вычисления по формулам (1) и
(9) , можно проверить правильность расчета коэффициента корреляции,
коэффициенты регрессии характеризуют только линейную связь и при положительной
связи имеют знак плюс, при отрицательной - знак минус.
В свою очередь свободные члены 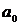 и
и 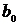 в
уравнениях регрессии придется вычислять по следующим формулам. Для подсчета
свободного члена
в
уравнениях регрессии придется вычислять по следующим формулам. Для подсчета
свободного члена 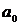 уравнения
регрессии (1) используется формула:
уравнения
регрессии (1) используется формула:
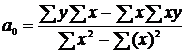 (10)
(10)
Для подсчета свободного члена 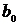 уравнения
регрессии (2) используется формула:
уравнения
регрессии (2) используется формула:
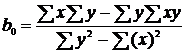 (11)
(11)
Вычисления по формулам (7), (8),
(10) и (11) достаточно сложны поэтому при расчетах коэффициентов регрессии
используют, как правило более простой метод. Он заключается в решении двух
систем уравнений. При решении одной системы находятся величины 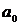 и
и 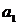 и при
решении другой -
и при
решении другой - 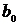 и
и 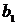 . Общий вид системы
уравнений для нахождения величин
. Общий вид системы
уравнений для нахождения величин 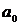 и
и 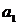 таков:
таков:
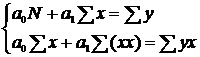 (12)
(12)
Общий вид системы уравнений для
нахождения величин - 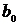 и
и 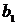 таков:
таков:
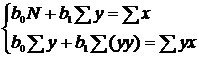 (13)
(13)
В системах уравнений (12) и (13)
используются следующие обозначения:
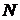 - число элементов в переменной X или в
переменнойY
- число элементов в переменной X или в
переменнойY
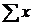 - сумма всех элементов переменной X
- сумма всех элементов переменной X
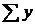 - сумма всех элементов переменной Y
- сумма всех элементов переменной Y
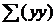 - произведение всех элементов переменной Y друг на
друга
- произведение всех элементов переменной Y друг на
друга
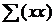 - произведение всех элементов переменной Y друг на
друга
- произведение всех элементов переменной Y друг на
друга
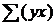 -попарное произведение всех элементов переменной
X на
соответствующие элементы переменной Y
-попарное произведение всех элементов переменной
X на
соответствующие элементы переменной Y
Для применения метода линейного
регрессионного анализа необходимо соблюдать следующие условия:
. Сравниваемые переменные X и Y должны быть
измерены в шкале интервалов или отношений.
. предполагается, что переменные X и Y имеют
нормальный закон распределения.
. Число варьирующих признаков в
сравниваемых переменных должно быть одинаковым.
.2 Нелинейное уравнение регрессии
Простейшие случаи парной нелинейной
корреляционной зависимости - это гиперболическая и параболическая. Их уравнения
имеют вид:
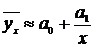 (14)
(14) 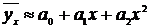 (15)
(15)
Как и в случае линейной зависимости,
параметры 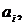
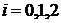 находятся
методом наименьших квадратов, который дает следующие системы нормальных
уравнений:
находятся
методом наименьших квадратов, который дает следующие системы нормальных
уравнений:
для
гиперболической зависимости 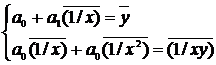 (16)
(16)
для
параболической зависимости 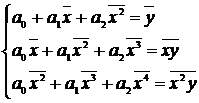 (17)
(17)
Параметры 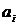 , находим
решая эти системы нормальных уравнений.
, находим
решая эти системы нормальных уравнений.
Теснота взаимосвязи между признаками
в нелинейной зависимости измеряется с помощью корреляционного отношения,
рассчитываемого по формуле
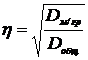 (18)
(18)
где 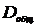 - общая дисперсия признака У;
- общая дисперсия признака У; 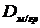 -
межгрупповая дисперсия признака У.
-
межгрупповая дисперсия признака У.
Общая дисперсия результативного
признака У складывается из двух дисперсий: межгрупповой и внутригрупповой, т.е.
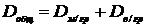 .
.
Межгрупповая дисперсия характеризует
вариацию признака У за счет учтенного фактора, а внутригрупповая дисперсия 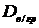 - за счет
неучтенных факторов
- за счет
неучтенных факторов
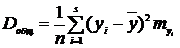 (19)
(19)
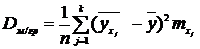 (20)
(20)
где 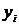 - значение признака
- значение признака 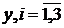
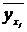 - условная средняя признака
- условная средняя признака 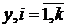 ;
;
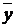 - общая средняя признака Y;
- общая средняя признака Y;
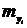 - частота значений признака Y;
- частота значений признака Y;
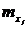 - частота значений признака X;
- частота значений признака X;
n - объем
выборки (сумма всех частот).
Корреляционное отношение изменяется
от 0 до 1, т.е. 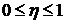 . Чем ближе
. Чем ближе 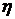 к 0, тем
слабее связь между результативным признаком У и учтенным фактором Х.
к 0, тем
слабее связь между результативным признаком У и учтенным фактором Х.
С помощью корреляционного отношения
можно оценить тесноту взаимосвязи между признаками и в случае линейной
зависимости , т.к. 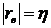 в случае
линейной зависимости.
в случае
линейной зависимости.
 - коэффициент детерминации, показывающий на
сколько процентов в среднем вариация результативного признака объясняется за
счет вариации учтенного факторного признака.
- коэффициент детерминации, показывающий на
сколько процентов в среднем вариация результативного признака объясняется за
счет вариации учтенного факторного признака.
§ 3. Множественный корреляционно -
регрессионный анализ
Корреляционная взаимосвязь между
тремя и более признаками (показателями) называется множественной корреляционной
зависимостью. Во множественной корреляционной зависимости решаются те же
задачи, что и в парной, а именно: оценивается теснота взаимосвязи между
признаками (корреляционный анализ), определяется аналитическое выражение этой
взаимосвязи приближенно в виде уравнения регрессии (регрессионный анализ). Но
во множественном регрессионном анализе предварительно решается еще одна задача
- отбор факторных признаков в уравнение регрессии (регрессионная модель). При
отборе факторных признаков в регрессионную модель необходимо учитывать
следующие условия:
1) в модель вводятся факторные признаки,
оказывающие сильное влияние на результативный признак;
2) факторные признаки, вводимые в модель,
должны быть линейно независимыми или иметь слабую связь между собой.
Если при анализе успешности обучения подростков
рассматривать различные независимые переменные, влияющие, с точки зрения
исследователя, на результативный признак, то в этом случае можно построить
линейное уравнение множественной регрессии, в которое будут входить все
рассматриваемые переменные. В общем случае, зависимость между несколькими
переменными величинами выражают уравнением множественной регрессии, которая
может быть как линейной, так и не линейной. В простейшем случае множественная
линейная регрессия выражается уравнением с двумя независимыми переменными
величинами X и Z
и имеет следующий вид:
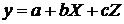 (21)
(21)
где a - свободный
член, b и c - параметры
уравнения (21).
Уравнение (21) может решаться
относительно зависимой переменной Z, тогда X и Y являются
независимыми переменными, и уравнение множественной регрессии имеет следующий
вид
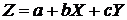 (22)
(22)
Можно решить уравнение (21) и
относительно X, тогда Z и Y будут
независимыми переменными, а уравнение будет иметь следующий вид
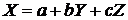 (23)
(23)
При проведении конкретных расчетов
выбор зависимых и независимых переменных определяется планом эксперимента.
Решение уравнений (21), (22), (23)
состоит в том, что находятся величины a, b, c на основе
решения системы из трех уравнений.
Для решения уравнения (21) система имеет
следующий вид
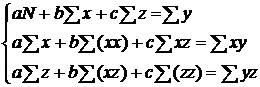 (24)
(24)
Для решения уравнения (22) система будет
выглядеть следующим образом
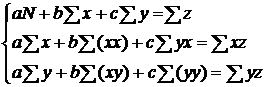 (25)
(25)
Для решения уравнения (23) система будет иметь
следующий вид
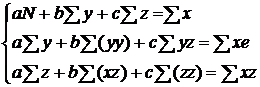 (26)
(26)
В общем случае уравнение регрессии
представляет собой сложный полином, описывающий зависимость сразу между
несколькими переменными. Такое уравнение множественной регрессии имеет вид
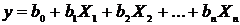 (27)
(27)
Где 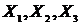 и т.д. независимые переменные, а Y - зависимая
переменная.
и т.д. независимые переменные, а Y - зависимая
переменная.
II.
ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ
§ 1 Линейная регрессия при обработке
результатов исследования
Использование метода мы проиллюстрируем на
эмпирических данных 2009г. мониторинга качества успеваемости учащихся.
Используются несколько классов из ряда городских школ и колледжей. В качестве
примера изучим, как связано с успеваемостью учащихся потребление табачных
изделий. Цель примера - исследование возможной зависимости между успеваемостью
и потреблением табачных изделий.
Может быть, табак употребляют, поскольку
материальное положение позволяет? Может быть, их употребление вызывает в целом
падение уровня достатка? Такие вопросы также возникли в ходе исследования, но
на настоящий момент они нами не изучены, а получены только анкетные данные.
В качестве тестируемых групп нами взяты ответы о
успеваемости по нескольким основным предметам, а также сведения о посещении
дополнительных занятий. Тестирование мы проводили по модели:
·
Модель
регрессии: отличаются ли группы различной зависимостью успеваемости от
потребления табачных изделий.
Тестирование мы проводили по следующей форме:
1. Пол _________ ________
жен
муж
2. Возраст __________________
3. Употребляете ли Вы табачные изделия?
_________ ________
да
нет
4. Успеваемость по предметам:
а) математика _________________________
б) русский язык и литература_____________
в) физика и химия ______________________
г) казахский язык и литература ___________
д) история ____________________________
е) физическая культура _________________
. Сколько детей в семье? ________________
. Какой возраст родителей:
мама__________
папа__________
. Употребляют ли родители табачные изделия?
________ _______
да
нет
8. Посещаете ли вы дополнительные занятия?
_______ ________
да
нет
9. Если посещаете, то какие? (перечислить)
____________________________________
____________________________________
. Являетесь ли Вы ответственным за какую-либо
работу в школе?
___ да___ нет
Если да, то какую? (можно не отвечать)
_________________________
. Считаете ли вы себя сильным человеком?
________ ________
да нет
. Считаете ли Вы себя общительным человеком?
________ _______
да нет
13. Возникают ли у Вас проблемы в семье или
школе? ______ ______
да нет
14. Часто ли Вы болеете простудными
заболеваниями?
______ ______
да нет
Если да, то примерно сколько раз в году?
_________________________
15. Сколько денег выделяют родители на Ваши
ежедневные карманные расходы? ____________
Тестирование было проведено в 8, 9, 10, 11
классах школ и колледжей города. Данные, которые были получены в ходе
исследования, мы отразили в таблицах, которые были обработаны в табличном
редакторе Excel и для
удобства их обработки мы использовали следующие условные обозначения:
Жен. пол - 1
Муж. пол - 0
«Да» - 1
«Нет» - 0
Для каждой отдельной таблицы найдены средние
арифметические значения по каждой отдельной графе, где это требовалось. Там где
необходимо было подсчитать общее количество - выведено общее значение. Таким
образом, мы получили всего семь таблиц по каждому классу (см. таблицы №1 - №7 в
Приложении №1). Затем составили сводную таблицу (см. таблицу №8), а также
таблицу, где были включены количество учащихся из данного класса, которые
употребляют табачные изделия, а также средняя успеваемость по отдельным
предметам для всего класса (см. таблицу №9).
Таблица 9
|
употр.ли
табач. Изделия
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
1
|
3,75
|
3,9
|
3,74
|
3,9
|
3,77
|
4,53
|
|
19
|
|
|
|
|
|
|
|
0
|
3,42
|
4,3
|
3,95
|
4,28
|
4,08
|
4,53
|
|
19
|
|
|
|
|
|
|
|
0
|
3,81
|
3,9
|
3,79
|
3,65
|
3,88
|
4
|
|
16
|
|
|
|
|
|
|
|
1
|
3,79
|
4
|
4,03
|
4
|
4,05
|
4,24
|
|
21
|
|
|
|
|
|
|
|
0
|
3,93
|
4,1
|
3,77
|
4,14
|
4,05
|
4,48
|
|
24
|
|
|
|
|
|
|
|
2
|
3,52
|
3,3
|
4,83
|
3,57
|
3,89
|
4,05
|
|
21
|
|
|
|
|
|
|
|
1
|
3,6
|
3,8
|
3,73
|
3,93
|
3,8
|
4,64
|
|
14
|
|
|
|
|
|
|
|
139
|
|
|
|
|
|
|
Теперь для решения поставленной задачи
используем метод регрессии. Расположим исходные данные в виде таблицы (см.
таблицу № 10), в которой произведем предварительные необходимые вычисления
Таблица 10
|
№
класса
|
x
|
y
|
xy
|
xx
|
yy
|
|
1
|
95
|
3,93
|
373,51
|
9025
|
15,46
|
|
2
|
100
|
4,09
|
409,00
|
10000
|
16,73
|
|
3
|
100
|
3,85
|
384,50
|
10000
|
14,78
|
|
4
|
95,5
|
4,02
|
383,75
|
9120,25
|
16,15
|
|
5
|
100
|
4,09
|
408,50
|
10000
|
16,69
|
|
6
|
91
|
3,86
|
351,26
|
8281
|
14,90
|
|
7
|
93,3
|
3,92
|
365,43
|
8704,89
|
15,34
|
|
суммы
|
674,8
|
27,75
|
2675,94
|
65131,14
|
110,04
|
С помощью решения системы уравнений
(12) необходимо найти уравнение регрессии Y на X, т.е.
определить коэффициенты 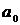 и
и 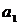 , и таким
образом ответить на вопрос - на сколько баллов повысится успеваемость, если
изменится процент учащихся употребляющих табачные изделия. В нашем случае, для
того, чтобы применить метод регрессии, необходимо было использовать процент
учащихся, не потребляющих табачные изделия. Исходя из этого, мы получаем
уравнение, в котором коэффициенты
, и таким
образом ответить на вопрос - на сколько баллов повысится успеваемость, если
изменится процент учащихся употребляющих табачные изделия. В нашем случае, для
того, чтобы применить метод регрессии, необходимо было использовать процент
учащихся, не потребляющих табачные изделия. Исходя из этого, мы получаем
уравнение, в котором коэффициенты 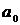 и
и 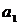 показывают зависимость баллов успеваемости от
увеличения или уменьшения процента учащихся, не потребляющих табачные изделия.
показывают зависимость баллов успеваемости от
увеличения или уменьшения процента учащихся, не потребляющих табачные изделия.
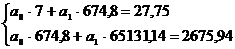 <=>
<=> 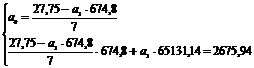
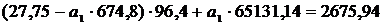
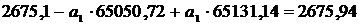
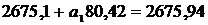

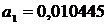
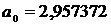
Следовательно искомое уравнение регрессии Y
на X будет иметь вид
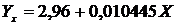 (28)
(28)
Теперь найдем уравнение регрессии X на Y. Для этого
необходимо решить систему уравнений на основании (13), чтобы определить
величины 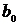 и
и 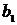 :
:
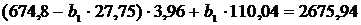
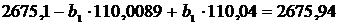
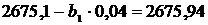
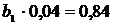
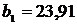
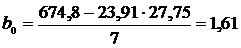
Тогда искомое уравнение регрессии X
на Y будет иметь вид
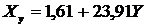 (29)
(29)
У нас получено два уравнения
регрессии (28) и (29), Коэффициенты 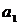 и
и 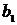 показывают, на сколько в среднем величина
одного признака, изменяется при изменении другого признака на единицу меры.
показывают, на сколько в среднем величина
одного признака, изменяется при изменении другого признака на единицу меры.
Иными словами, мы уже можем ответить
на вопрос нашей задачи. Так, согласно уравнению (28) при показателе 100% не
потребления табачных изделий или другими словами, процент потребления табачных
изделий в данном случае равен 0%, то показатель уровня успеваемости равен 3,96
балла. Если же показатель потребления табачных изделий равен 20%, а
следовательно показатель не потребления - 80%, то уровень успеваемости
становится равным 3,8 балла, т.е уменьшается на 4%. Согласно уравнению (29)
получаем, что повышения количества учащихся, потребляющих табачные изделия до
27% снижает успеваемость практически на 1 балл.
Выше было показано, что если известны
два коэффициента регрессии для обеих линий регрессий, то на их основе можно
получить коэффициент линейной корреляции между X и Y по формуле
(9). Проделаем эти вычисления
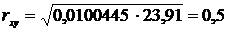 (30)
(30)
В завершении работы построим графики линий
регрессии
Для уравнения (29) имеем следующую таблицу:
|
Y
|
X
|
|
0
|
1,61
|
|
0,5
|
13,565
|
|
1
|
25,52
|
|
1,5
|
37,475
|
|
2
|
49,43
|
|
2,5
|
61,385
|
|
3
|
73,34
|
|
3,5
|
85,295
|
|
4
|
97,25
|
|
4,5
|
109,205
|
|
5
|
121,16
|
Для уравнения (14) имеем следующую таблицу:
|
X
|
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
|
Y
|
2,96
|
3,06445
|
3,1689
|
3,27335
|
3,3778
|
3,48225
|
3,5867
|
3,69115
|
3,7956
|
3,90005
|
4,0045
|
Проверим значимость коэффициента корреляции. Для
этого выдвигаем гипотезы:
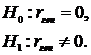 Примем уровень значимости
Примем уровень значимости 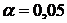 .
.
Для проверки нулевой гипотезы
используем случайную величину 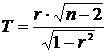 , имеющую распределение Стьюдента с
, имеющую распределение Стьюдента с 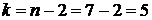 степенями
свободы. По экспериментальным данным находим наблюдаемое значение критерия
степенями
свободы. По экспериментальным данным находим наблюдаемое значение критерия 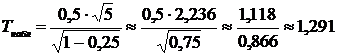 . По таблице
критических точек распределения Стьюдента находим
. По таблице
критических точек распределения Стьюдента находим 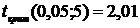 . Сравниваем
. Сравниваем
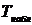 и
и 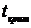 (0,05;5).
Т.к.
(0,05;5).
Т.к. 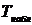 <
<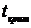 , т.е.
, т.е. 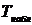 не попало в
критическую область, нулевая гипотеза не отвергается, следовательно,
коэффициент корреляции не значим. Признаки Х и У слабо коррелированны, т.е.
успеваемость и употребление табачных изделий не находятся в тесной зависимости.
не попало в
критическую область, нулевая гипотеза не отвергается, следовательно,
коэффициент корреляции не значим. Признаки Х и У слабо коррелированны, т.е.
успеваемость и употребление табачных изделий не находятся в тесной зависимости.
Найдем коэффициент детерминации. 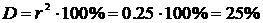 , т.е.
вариация изменения успеваемости на 1 балл в среднем на 25% объясняется
вариацией процента учащихся употребляющих табачные изделия.
, т.е.
вариация изменения успеваемости на 1 балл в среднем на 25% объясняется
вариацией процента учащихся употребляющих табачные изделия.
Для более полного исследования
вопроса об успеваемости мы продолжим изучение остальных факторов, которые
возможно оказывают влияние на успеваемость учащихся. Из проведенной анкеты
выберем несколько факторов: посещение дополнительных занятий, ответственность
за общественную работу, существование каких - либо семейных проблем.
Составим соответствующие таблицы.
Таблица 11
(посещение дополнительных занятий)
|
№
класса
|
x
|
y
|
xy
|
xx
|
yy
|
|
1
|
85
|
3,93
|
334,05
|
7225
|
15,46
|
|
2
|
73,7
|
4,09
|
301,433
|
5431,69
|
16,73
|
|
3
|
68,8
|
3,85
|
264,88
|
4733,44
|
14,78
|
|
4
|
13,6
|
4,02
|
54,672
|
184,96
|
16,15
|
|
5
|
95,8
|
4,09
|
391,822
|
9177,64
|
16,69
|
|
6
|
47,8
|
3,86
|
184,508
|
2284,84
|
14,90
|
|
7
|
40
|
3,92
|
156,8
|
1600
|
15,34
|
|
суммы
|
424,7
|
27,75
|
1688,165
|
30637,57
|
110,04
|
С помощью решения системы уравнений
(12) необходимо найти уравнение регрессии Y на X, т.е.
определить коэффициенты 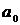 и
и 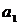 , и таким
образом ответить на вопрос - на сколько баллов повысится успеваемость, если
изменится процент учащихся посещающих дополнительные занятия.
, и таким
образом ответить на вопрос - на сколько баллов повысится успеваемость, если
изменится процент учащихся посещающих дополнительные занятия.
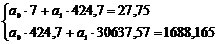 <=>
<=>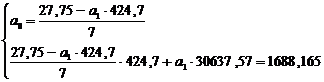
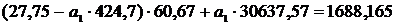

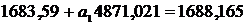

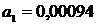
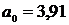
Следовательно
искомое уравнение регрессии Y на X будет иметь
вид
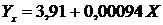 (31)
(31)
Теперь найдем уравнение регрессии X на Y. Для этого
необходимо решить систему уравнений на основании (13), чтобы определить
величины 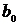 и
и 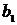 :
:
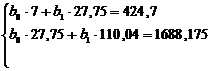 <=>
<=>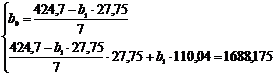
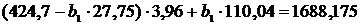
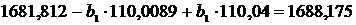
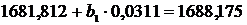
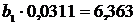
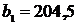
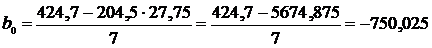
Тогда искомое уравнение регрессии X
на Y будет иметь вид
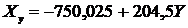 (32)
(32)
У нас получено два уравнения
регрессии (31) и (32), Коэффициенты 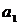 и
и 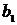 показывают, на сколько в среднем величина
одного признака, изменяется при изменении другого признака на единицу меры.
Т.е. согласно уравнению (28) при показателе 100% посещения учащимися
дополнительных занятий, то уровень успеваемости равен 4,004 балла. Если же
показатель посещения дополнительных занятий равен 20%, то уровень успеваемости
становится равным 3,9288 балла, т.е уменьшается на 2%. Согласно уравнению (18)
изменение на 1 балл успеваемости , например с 3 до 4 баллов дает изменение
процента посещения дополнительных занятий:
показывают, на сколько в среднем величина
одного признака, изменяется при изменении другого признака на единицу меры.
Т.е. согласно уравнению (28) при показателе 100% посещения учащимися
дополнительных занятий, то уровень успеваемости равен 4,004 балла. Если же
показатель посещения дополнительных занятий равен 20%, то уровень успеваемости
становится равным 3,9288 балла, т.е уменьшается на 2%. Согласно уравнению (18)
изменение на 1 балл успеваемости , например с 3 до 4 баллов дает изменение
процента посещения дополнительных занятий: 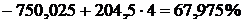 .
.
Выше было показано, что если
известны два коэффициента регрессии для обеих линий регрессий, то на их основе
можно получить коэффициент линейной корреляции между X и Y по формуле
(9). Проделаем эти вычисления
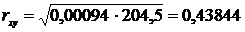 (33)
(33)
Полученный показатель коэффициента
корреляции низок, следовательно, опять делаем вывод, что посещение
дополнительных занятий в целом мало влияет на успеваемость учащихся.
Продолжим исследование на основании
вышеприведенных признаков, а именно, каким образом наличие проблем в семье
влияет на успеваемость учащихся (см. таблицу 12)
Таблица 12
|
№
класса
|
x
|
y
|
xy
|
xx
|
yy
|
|
1
|
60
|
3,93
|
235,8
|
3600
|
15,46
|
|
2
|
36,84
|
4,09
|
150,67
|
1357.18
|
16,73
|
|
3
|
31,25
|
3,85
|
120,31
|
976,56
|
14,78
|
|
4
|
22,72
|
4,02
|
91,33
|
516,19
|
16,15
|
|
5
|
41,66
|
4,09
|
170,38
|
1735,55
|
16,69
|
|
6
|
43,47
|
3,86
|
167,79
|
1889,64
|
14,90
|
|
7
|
26.66
|
3,92
|
104.5
|
710.75
|
15,34
|
|
суммы
|
262,6
|
27,75
|
1040.78
|
10785.87
|
110,04
|
С помощью решения системы уравнений
(12) найдем уравнение регрессии Y на X, т.е.
определим коэффициенты 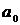 и
и 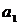 .
.
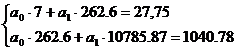 <=>
<=>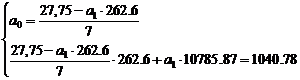
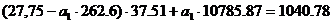
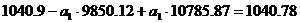
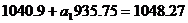
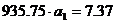
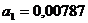
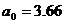
Следовательно искомое уравнение регрессии Y
на X будет иметь вид
 (34)
(34)
Теперь найдем уравнение регрессии X на Y. Для этого
необходимо решить систему уравнений на основании (13), чтобы определить
величины 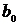 и
и 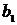 :
:
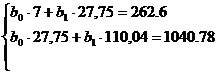 <=>
<=>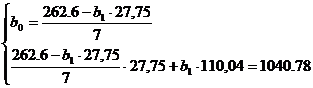
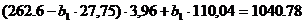
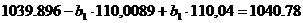
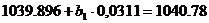
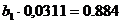

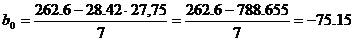
Тогда искомое уравнение регрессии X
на Y будет иметь вид
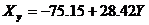 (35)
(35)
Выше было показано, что если
известны два коэффициента регрессии для обеих линий регрессий, то на их основе
можно получить коэффициент линейной корреляции между X и Y по формуле
(9). Проделаем эти вычисления
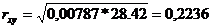 (36)
(36)
Коэффициент корреляции достаточно
низок, что дает основание считать, что проблемы в семье в целом не оказывают
влияния на среднюю успеваемость учащихся.
Для наглядности проделанной работы
построим графики линий регрессии (см. Приложение №2)
§ 2 Нелинейная регрессия в задачах
исследования
В последнее время все больше и
больше учащиеся проводят время в сетях Интернет. В нашем исследовании мы хотели
бы определить есть ли какая - либо взаимосвязь между количеством часов,
проводимых учащимися старших классов в Интернете и уровнем средней успеваемости
учащегося. Для этого нами было проведено анкетирование. Один из интересующих
нас вопросов - количество часов проводимых в сети Интернет (см. Приложение №3).
Пусть результативный признак - Y, а признак влияние которого мы
рассматриваем - X. Т.к. в системе координат XOY, согласно
полученным эмпирическим данным, прослеживается обратно пропорциональная
зависимость признака Y от признака X, то
используем соответствующую гиперболическую корреляционную зависимость. Для
составления уравнения регрессии, найдем из системы нормальных уравнений
параметры 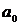 и
и 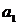 . С помощью
табличного редактора EXCEL вычислим вспомогательные
значения:
. С помощью
табличного редактора EXCEL вычислим вспомогательные
значения:
|
|
X
|
Y
|
XX
|
XY
|
1/X
|
1/XX
|
1/XY
|
|
1
|
1,5
|
4
|
2,25
|
6
|
0,666667
|
0,444444
|
0,166667
|
|
2
|
3
|
3,9
|
9
|
11,7
|
0,333333
|
0,111111
|
0,08547
|
|
3
|
2,5
|
3,9
|
6,25
|
9,75
|
0,4
|
0,16
|
0,102564
|
|
4
|
0,5
|
4,5
|
0,25
|
2,25
|
2
|
4
|
0,444444
|
|
5
|
3
|
4,1
|
9
|
12,3
|
0,333333
|
0,111111
|
0,081301
|
|
6
|
3,5
|
3,8
|
12,25
|
13,3
|
0,285714
|
0,081633
|
0,075188
|
|
7
|
3,5
|
4,2
|
12,25
|
14,7
|
0,285714
|
0,081633
|
0,068027
|
|
8
|
3
|
3,8
|
9
|
11,4
|
0,333333
|
0,111111
|
0,087719
|
|
9
|
2,5
|
4
|
6,25
|
10
|
0,4
|
0,16
|
0,1
|
|
10
|
6
|
3,7
|
36
|
22,2
|
0,166667
|
0,027778
|
0,045045
|
|
11
|
3
|
4
|
9
|
12
|
0,333333
|
0,111111
|
0,083333
|
|
12
|
0,1
|
4,6
|
0,01
|
0,46
|
10
|
100
|
2,173913
|
|
13
|
3,5
|
4,2
|
12,25
|
14,7
|
0,285714
|
0,081633
|
0,068027
|
|
14
|
0,1
|
3,9
|
0,01
|
0,39
|
10
|
100
|
2,564103
|
2,5
|
3,7
|
6,25
|
9,25
|
0,4
|
0,16
|
0,108108
|
|
16
|
8
|
3,2
|
64
|
25,6
|
0,125
|
0,015625
|
0,039063
|
|
17
|
12
|
3,3
|
144
|
39,6
|
0,083333
|
0,006944
|
0,025253
|
|
18
|
2,5
|
4,1
|
6,25
|
10,25
|
0,4
|
0,16
|
0,097561
|
|
19
|
5
|
3,9
|
25
|
19,5
|
0,2
|
0,04
|
0,051282
|
|
20
|
4
|
3,4
|
16
|
13,6
|
0,25
|
0,0625
|
0,073529
|
|
21
|
6,5
|
3,2
|
42,25
|
20,8
|
0,153846
|
0,023669
|
0,048077
|
|
22
|
4
|
3,6
|
16
|
14,4
|
0,25
|
0,0625
|
0,069444
|
|
23
|
1
|
4
|
1
|
4
|
1
|
1
|
0,25
|
|
24
|
3
|
4,1
|
9
|
12,3
|
0,333333
|
0,111111
|
0,081301
|
|
25
|
3
|
4
|
9
|
12
|
0,333333
|
0,111111
|
0,083333
|
|
26
|
1
|
3,6
|
1
|
3,6
|
1
|
1
|
0,277778
|
|
27
|
2,5
|
3,5
|
6,25
|
8,75
|
0,4
|
0,16
|
0,114286
|
|
28
|
6
|
3,2
|
36
|
19,2
|
0,166667
|
0,027778
|
0,052083
|
|
29
|
5,5
|
3,3
|
30,25
|
18,15
|
0,181818
|
0,033058
|
0,055096
|
|
30
|
0,5
|
3,7
|
0,25
|
1,85
|
2
|
4
|
0,540541
|
|
31
|
3
|
3,9
|
9
|
11,7
|
0,333333
|
0,111111
|
0,08547
|
|
32
|
6
|
3
|
36
|
18
|
0,166667
|
0,027778
|
0,055556
|
|
33
|
6
|
3,2
|
36
|
19,2
|
0,166667
|
0,027778
|
0,052083
|
|
34
|
2
|
4
|
4
|
8
|
0,5
|
0,25
|
0,125
|
|
35
|
2
|
4,1
|
4
|
8,2
|
0,5
|
0,25
|
0,121951
|
|
36
|
2,5
|
3,9
|
6,25
|
9,75
|
0,4
|
0,16
|
0,102564
|
|
37
|
5
|
3,5
|
25
|
17,5
|
0,2
|
0,04
|
0,057143
|
|
38
|
6
|
3,4
|
36
|
20,4
|
0,166667
|
0,027778
|
0,04902
|
|
39
|
6
|
3,7
|
36
|
22,2
|
0,166667
|
0,027778
|
0,045045
|
|
40
|
0,1
|
4,7
|
0,01
|
0,47
|
10
|
100
|
2,12766
|
|
41
|
3,5
|
4,5
|
12,25
|
15,75
|
0,285714
|
0,081633
|
0,063492
|
|
42
|
1
|
4
|
1
|
4
|
1
|
1
|
0,25
|
|
43
|
2
|
4,1
|
4
|
8,2
|
0,5
|
0,25
|
0,121951
|
|
44
|
2
|
4
|
4
|
8
|
0,5
|
0,25
|
0,125
|
|
45
|
1,5
|
4,3
|
2,25
|
6,45
|
0,666667
|
0,444444
|
0,155039
|
|
46
|
6
|
3,8
|
36
|
22,8
|
0,166667
|
0,027778
|
0,04386
|
|
47
|
6
|
3,7
|
36
|
22,2
|
0,166667
|
0,027778
|
0,045045
|
|
48
|
3
|
5
|
9
|
15
|
0,333333
|
0,111111
|
0,066667
|
|
49
|
5
|
4,5
|
25
|
22,5
|
0,2
|
0,04
|
0,044444
|
|
50
|
7
|
4,8
|
49
|
33,6
|
0,142857
|
0,020408
|
0,029762
|
|
51
|
3
|
4,2
|
9
|
12,6
|
0,333333
|
0,111111
|
0,079365
|
|
52
|
2
|
4,3
|
4
|
8,6
|
0,5
|
0,25
|
0,116279
|
|
53
|
6
|
3,9
|
36
|
23,4
|
0,166667
|
0,027778
|
0,042735
|
|
54
|
2
|
3,4
|
4
|
6,8
|
0,5
|
0,25
|
0,147059
|
|
55
|
2
|
4,6
|
4
|
9,2
|
0,5
|
0,25
|
0,108696
|
|
56
|
1
|
3,4
|
1
|
3,4
|
1
|
1
|
0,294118
|
|
57
|
3
|
3,8
|
9
|
11,4
|
0,333333
|
0,111111
|
0,087719
|
|
58
|
5,5
|
3,1
|
30,25
|
17,05
|
0,181818
|
0,033058
|
|
59
|
6
|
3,3
|
36
|
19,8
|
0,166667
|
0,027778
|
0,050505
|
|
Сумма
|
208,8
|
228,5
|
1040,28
|
780,17
|
53,34486
|
317,6921
|
12,86441
|
Составим систему уравнений на основании (16)
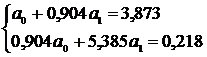
и решим ее, используя метод Крамера:
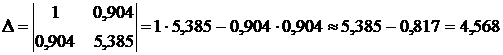
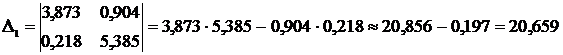
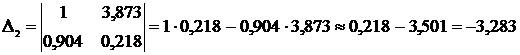

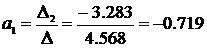
Тогда уравнение регрессии, согласно
(14), имеет вид 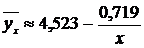 , т.е.
увеличение времени провождения в Интернете на 1 ч понижает уровень успеваемости
в среднем на 0,719 баллов.
, т.е.
увеличение времени провождения в Интернете на 1 ч понижает уровень успеваемости
в среднем на 0,719 баллов.
Определим тесноту полученной
взаимосвязи. Между признаками с помощью корреляционного отношения (18) 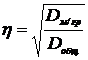 . Используем
вспомогательную таблицу
. Используем
вспомогательную таблицу
|
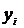 i i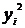 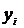 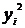
|
|
|
|
|
3,8
|
14.44
|
4,5
|
20,25
|
|
3,8
|
14.44
|
4
|
16
|
|
3,6
|
12,96
|
4,1
|
16,81
|
|
3,7
|
13,69
|
4,2
|
17,64
|
|
3,7
|
13,69
|
4
|
16
|
|
3,2
|
10,24
|
4
|
16
|
|
3,3
|
10,89
|
4,6
|
21,16
|
|
3,4
|
11,56
|
4,2
|
17,64
|
|
3,2
|
10,24
|
4,1
|
16,81
|
|
3,6
|
12,96
|
4
|
16
|
|
3,5
|
12,25
|
4,1
|
16,81
|
|
3,2
|
10,24
|
4
|
16
|
|
3,3
|
10,89
|
4
|
16
|
|
3,7
|
13,69
|
4,1
|
16,81
|
|
3
|
9
|
4,7
|
22,09
|
|
3,2
|
10,24
|
4,5
|
20,25
|
|
3,9
|
15,21
|
4
|
16
|
|
3,5
|
12,25
|
4,1
|
16,81
|
|
3,4
|
11,56
|
4
|
16
|
|
3,7
|
13,69
|
4,3
|
18,49
|
|
3,8
|
14,44
|
5
|
25
|
|
3,7
|
13,69
|
4,5
|
20,25
|
|
3,9
|
15,21
|
4,8
|
23,04
|
|
3,4
|
11,56
|
4,2
|
17,64
|
|
3,4
|
11,56
|
4,3
|
18,49
|
|
3,8
|
14,44
|
4,6
|
21,16
|
|
3,1
|
9,61
|
3,9
|
15,21
|
|
3,3
|
10,89
|
3,9
|
15,21
|
|
3,9
|
15,21
|
3,9
|
15,21
|
|
3,9
|
15,21
|
|
|
|
105.9
|
375,95
|
122.6
|
520,78
|
Для этого найдем
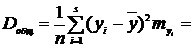
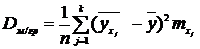
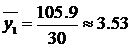
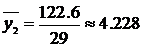
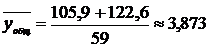
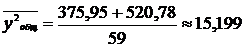
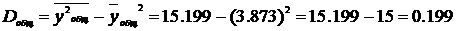
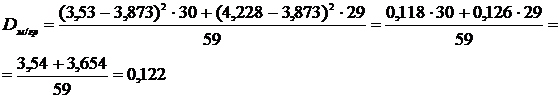
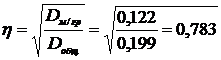 .
.
Теперь вычислим коэффициент
детерминации
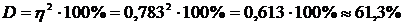 , т.е. колеблемость Y в среднем
на 61,3% объясняется за счет вариации X. Значит
связь между времяпровождением в Интернет и успеваемостью довольно тесная.
, т.е. колеблемость Y в среднем
на 61,3% объясняется за счет вариации X. Значит
связь между времяпровождением в Интернет и успеваемостью довольно тесная.
§ 3 Множественная линейная регрессия
в экспериментальных исследованиях
На основании полученных данных из
Приложения№3 попытаемся выяснить влияние одновременно двух признаков на
успеваемость учащихся, а именно времяпровождение в Интернете и время,
затраченное в среднем на телефонные разговоры. Составим вспомогательную
таблицу:
|
|
X
|
Y
|
XX
|
XY
|
Z
|
ZZ
|
ZY
|
ZX
|
|
1
|
1,5
|
4
|
2,25
|
6
|
0,2
|
0,04
|
0,8
|
0,3
|
|
2
|
3
|
3,9
|
9
|
11,7
|
1
|
1
|
3,9
|
3
|
|
3
|
2,5
|
3,9
|
6,25
|
9,75
|
1
|
1
|
3,9
|
2,5
|
|
4
|
0,5
|
4,5
|
0,25
|
2,25
|
0,01
|
0,0001
|
0,045
|
0,005
|
|
5
|
3
|
4,1
|
9
|
12,3
|
5
|
25
|
20,5
|
15
|
|
6
|
3,5
|
3,8
|
12,25
|
13,3
|
1
|
1
|
3,8
|
3,5
|
|
7
|
3,5
|
4,2
|
12,25
|
14,7
|
0,5
|
0,25
|
2,1
|
1,75
|
|
8
|
3
|
3,8
|
9
|
11,4
|
0,01
|
0,0001
|
0,038
|
0,03
|
|
9
|
2,5
|
4
|
6,25
|
10
|
0,01
|
0,0001
|
0,04
|
0,025
|
|
10
|
6
|
3,7
|
36
|
22,2
|
3
|
9
|
11,1
|
18
|
|
11
|
3
|
4
|
9
|
12
|
1
|
1
|
4
|
3
|
|
12
|
0,1
|
4,6
|
0,01
|
0,46
|
0,01
|
0,0001
|
0,046
|
0,001
|
|
13
|
3,5
|
4,2
|
12,25
|
14,7
|
1,5
|
2,25
|
6,3
|
5,25
|
|
14
|
0,1
|
3,9
|
0,01
|
0,39
|
1
|
1
|
3,9
|
0,1
|
|
15
|
2,5
|
3,7
|
6,25
|
9,25
|
2,5
|
6,25
|
9,25
|
6,25
|
|
16
|
8
|
3,2
|
64
|
25,6
|
0,5
|
0,25
|
1,6
|
4
|
|
17
|
12
|
3,3
|
144
|
39,6
|
1
|
1
|
3,3
|
12
|
|
18
|
2,5
|
4,1
|
6,25
|
10,25
|
1
|
1
|
4,1
|
2,5
|
|
19
|
5
|
3,9
|
25
|
19,5
|
0,5
|
0,25
|
1,95
|
2,5
|
|
20
|
4
|
3,4
|
16
|
13,6
|
0,3
|
0,09
|
1,02
|
1,2
|
|
21
|
6,5
|
42,25
|
20,8
|
2
|
4
|
6,4
|
13
|
|
22
|
4
|
3,6
|
16
|
14,4
|
3
|
9
|
10,8
|
12
|
|
23
|
1
|
4
|
1
|
4
|
0,25
|
0,0625
|
1
|
0,25
|
|
24
|
3
|
4,1
|
9
|
12,3
|
3
|
9
|
12,3
|
9
|
|
25
|
3
|
4
|
9
|
12
|
3
|
9
|
12
|
9
|
|
26
|
1
|
3,6
|
1
|
3,6
|
0,1
|
0,01
|
0,36
|
0,1
|
|
27
|
2,5
|
3,5
|
6,25
|
8,75
|
2
|
4
|
7
|
5
|
|
28
|
6
|
3,2
|
36
|
19,2
|
0,1
|
0,01
|
0,32
|
0,6
|
|
29
|
5,5
|
3,3
|
30,25
|
18,15
|
0,01
|
0,0001
|
0,033
|
0,055
|
|
30
|
0,5
|
3,7
|
0,25
|
1,85
|
0,65
|
0,4225
|
2,405
|
0,325
|
|
31
|
3
|
3,9
|
9
|
11,7
|
1
|
1
|
3,9
|
3
|
|
32
|
6
|
3
|
36
|
18
|
2,5
|
6,25
|
7,5
|
15
|
|
33
|
6
|
3,2
|
36
|
19,2
|
0,01
|
0,0001
|
0,032
|
0,06
|
|
34
|
2
|
4
|
4
|
8
|
2
|
4
|
8
|
4
|
|
35
|
2
|
4,1
|
4
|
8,2
|
1
|
1
|
4,1
|
2
|
|
36
|
2,5
|
3,9
|
6,25
|
9,75
|
2,5
|
6,25
|
9,75
|
6,25
|
|
37
|
5
|
3,5
|
25
|
17,5
|
1,5
|
2,25
|
5,25
|
7,5
|
|
38
|
6
|
3,4
|
36
|
20,4
|
6
|
36
|
20,4
|
36
|
|
39
|
6
|
3,7
|
36
|
22,2
|
4
|
16
|
14,8
|
24
|
|
40
|
0,1
|
4,7
|
0,01
|
0,47
|
1
|
1
|
4,7
|
0,1
|
|
41
|
3,5
|
4,5
|
12,25
|
15,75
|
0,5
|
0,25
|
2,25
|
1,75
|
|
42
|
1
|
4
|
1
|
4
|
3
|
9
|
12
|
3
|
|
43
|
2
|
4,1
|
4
|
8,2
|
1
|
1
|
4,1
|
2
|
|
44
|
2
|
4
|
4
|
8
|
0,5
|
0,25
|
2
|
1
|
|
45
|
1,5
|
4,3
|
2,25
|
6,45
|
0,75
|
0,5625
|
3,225
|
1,125
|
|
46
|
6
|
3,8
|
36
|
22,8
|
2
|
4
|
7,6
|
12
|
|
47
|
6
|
3,7
|
36
|
22,2
|
2
|
4
|
7,4
|
12
|
|
48
|
3
|
5
|
9
|
15
|
0,01
|
0,0001
|
0,05
|
0,03
|
|
49
|
5
|
4,5
|
25
|
22,5
|
0,01
|
0,0001
|
0,045
|
0,05
|
|
50
|
7
|
4,8
|
49
|
33,6
|
0,3
|
0,09
|
1,44
|
2,1
|
|
51
|
3
|
4,2
|
9
|
12,6
|
0,01
|
0,0001
|
0,042
|
0,03
|
|
52
|
2
|
4,3
|
4
|
8,6
|
0,5
|
0,25
|
2,15
|
1
|
|
53
|
6
|
3,9
|
36
|
23,4
|
0,5
|
0,25
|
1,95
|
3
|
|
54
|
2
|
3,4
|
4
|
6,8
|
5
|
25
|
17
|
10
|
|
55
|
2
|
4,6
|
4
|
9,2
|
0,2
|
0,04
|
0,92
|
0,4
|
|
56
|
1
|
3,4
|
1
|
3,4
|
5
|
25
|
17
|
5
|
|
57
|
3
|
3,8
|
9
|
11,4
|
2
|
4
|
7,6
|
6
|
|
58
|
5,5
|
3,1
|
30,25
|
17,05
|
5,5
|
30,25
|
17,05
|
30,25
|
|
59
|
6
|
3,3
|
36
|
19,8
|
2
|
4
|
6,6
|
12
|
|
Сумма
|
208,8
|
1040,28
|
780,17
|
87,44
|
267,5784
|
323,161
|
330,886
|
Тогда на основании (24)
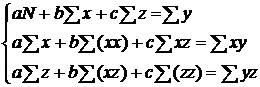
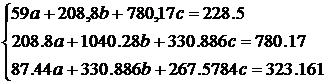
Решим систему методом Гаусса:
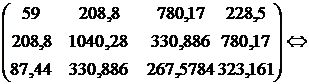
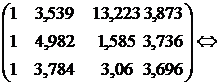
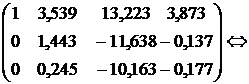

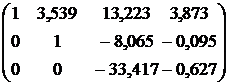 .
.
Значит искомые значения
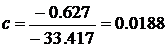
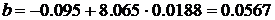
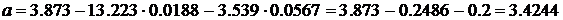
Следовательно искомое уравнение
регрессии будет выглядеть так 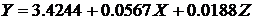 . Полученное уравнение множественной регрессии
позволяет определить ожидаемую величину переменной У, в зависимости от X и Z.
. Полученное уравнение множественной регрессии
позволяет определить ожидаемую величину переменной У, в зависимости от X и Z.
ЗАКЛЮЧЕНИЕ
Все представленные экспериментальные результаты
могут использоваться для научных сопоставлений, так как это реальные научные
данные, полученные нами в собственных исследованиях.
Применение реальных данных позволяет избежать
тех несообразностей, которые часто возникают при рассмотрении искусственно
придуманных задач. Принцип реальности позволяет по-настоящему почувствовать
«подводные камни» и тонкости в использовании статистических методов и
интерпретации полученных результатов. Кроме того, полученные результаты
позволят некоторым учащимся, которые не задумываются над тем, как потребление табачных
изделий влияет на их успеваемость, сделать определенные выводы и отказаться от
столь пагубной привычки.
Полученные нами данные позволяют продолжить
начатое исследование в различных аспектах и научно обосновать те или иные
выдвинутые нами гипотезы. Также мы намерены расширить круг нашего исследования
и протестировать гораздо больше учащихся, что позволит в некоторой мере также
повысить коэффициент, ранговой корреляции, т.е. уточнить полученное нами в ходе
исследования уравнение линейной регрессии.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Ермолаев
О.Ю. Математическая статистика для психологов. - М.: Московский
психолого-социальный институт, Флинта, 2003. - 335с.
2. Тимофеева
Л.К., Суханова Е.И. Математика для экономистов. Сборник задач по теории
вероятностей и математической статистике. - М.: 1998 - 184с.
. Методы
системного педагогического исследования. Под ред. Н.В.Кузьмина. - М.: Народное
образование, 2002 - 207 с.
. П.С.Ростовцев,
В.С.Костин, А.Л. Олех, A.C. Жданов. Автоматизация анализа социально-экономических
данных. Детерминация моделей - Исследование поддержано грантом РФФИ 00-06-80221
. Суходольский
Г.В.Основы математической статистики для психологов. - Издательство
Ленинградского университета:1972 - 430с.
. Солодовников
А.С. Теория вероятностей.- М.: Просвещение - 1983 - 208с.
Таблица 1
|
№п/п
|
пол
|
возраст
|
|
употр.ли
вы таб. изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
папа
|
Употр.ли
род. таб. изд.
|
посещаете
ли вы ДПУ
|
Какие
ДПУ
|
ответст.
ли вы за общ. Раб.
|
сильный
ли человек
|
.общит.
ли вы человек
|
сущ.
ли у вас пробл.в семье ,шк.
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
1
|
16
|
|
0
|
5
|
5
|
4
|
5
|
4
|
4
|
1
|
40
|
41
|
0
|
1
|
|
0
|
1
|
1
|
1
|
1
|
200
|
|
2
|
1
|
16
|
|
0
|
4
|
5
|
4
|
4,5
|
4
|
5
|
2
|
47
|
51
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
200
|
|
3
|
1
|
16
|
|
0
|
4
|
5
|
4
|
5
|
4
|
5
|
2
|
38
|
39
|
1
|
1
|
|
0
|
1
|
1
|
1
|
0
|
200
|
|
4
|
1
|
16
|
|
0
|
3,5
|
4
|
3,5
|
4
|
4
|
5
|
1
|
41
|
41
|
1
|
1
|
|
1
|
1
|
1
|
0
|
0
|
200
|
|
5
|
1
|
16
|
|
0
|
2,5
|
3
|
3
|
4
|
3
|
3
|
2
|
41
|
40
|
0
|
1
|
|
0
|
1
|
1
|
1
|
1
|
200
|
|
6
|
1
|
16
|
|
0
|
4
|
5
|
4
|
4
|
4
|
5
|
1
|
56
|
54
|
1
|
1
|
|
0
|
0
|
1
|
1
|
0
|
200
|
|
7
|
1
|
16
|
|
0
|
4
|
4
|
4
|
5
|
4
|
5
|
2
|
48
|
47
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
200
|
|
8
|
1
|
16
|
|
0
|
|
|
|
|
|
|
5
|
55
|
59
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
1000
|
|
9
|
0
|
16
|
|
0
|
4
|
3,5
|
4
|
3,5
|
3
|
4
|
1
|
39
|
41
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
150
|
|
10
|
0
|
16
|
|
0
|
4
|
4
|
4
|
3
|
4
|
4
|
1
|
|
39
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
150
|
|
11
|
0
|
16
|
|
0
|
4
|
4
|
3
|
3
|
4
|
4
|
1
|
58
|
58
|
1
|
0
|
|
0
|
1
|
1
|
1
|
1
|
125
|
|
12
|
1
|
16
|
|
0
|
4
|
4,5
|
4
|
4
|
4,5
|
5
|
2
|
37
|
36
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
200
|
|
13
|
1
|
16
|
|
0
|
5
|
5
|
5
|
5
|
5
|
осв.
|
2
|
47
|
54
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
250
|
|
14
|
1
|
16
|
|
0
|
|
|
|
|
|
|
2
|
42
|
46
|
0
|
1
|
|
1
|
1
|
0
|
0
|
350
|
|
15
|
1
|
16
|
|
0
|
4
|
4
|
4
|
4,5
|
4,5
|
5
|
2
|
40
|
42
|
0
|
1
|
|
1
|
1
|
1
|
0
|
0
|
350
|
|
16
|
1
|
16
|
|
0
|
4
|
4,5
|
5
|
5
|
5
|
4
|
2
|
42
|
43
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
100
|
|
17
|
1
|
16
|
|
0
|
4
|
4,5
|
4
|
5
|
4
|
4
|
2
|
58
|
45
|
0
|
1
|
|
1
|
1
|
1
|
0
|
0
|
0
|
|
18
|
1
|
17
|
|
0
|
4
|
4,5
|
4
|
5
|
4
|
4
|
1
|
47
|
62
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
0
|
|
19
|
0
|
16
|
|
0
|
4
|
3
|
3
|
3
|
4
|
5
|
2
|
34
|
40
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
500
|
|
20
|
0
|
16
|
|
0
|
4
|
3,5
|
3,5
|
4
|
4
|
5
|
2
|
46
|
42
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
200
|
|
21
|
0
|
16
|
|
0
|
3
|
4
|
3
|
4
|
4
|
5
|
3
|
35
|
37
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
200
|
|
22
|
0
|
16
|
|
0
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
41
|
43
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
0
|
|
23
|
0
|
16
|
|
0
|
3,5
|
3
|
3
|
3
|
3
|
4
|
1
|
46
|
50
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
100
|
|
24
|
0
|
17
|
|
0
|
4
|
4
|
3
|
3,5
|
3
|
5
|
3
|
44
|
46
|
1
|
1
|
|
0
|
1
|
1
|
1
|
0
|
1500
|
|
жен.
|
15
|
16,1
|
да
|
0
|
3,93
|
4,14
|
3,77
|
4,14
|
4,05
|
4,5
|
1,71
|
44,4
|
46
|
10
|
23
|
1,7
|
4
|
23
|
24
|
10
|
3
|
273,96
|
|
муж.
|
9
|
|
нет
|
24
|
|
|
|
|
|
|
|
|
|
14
|
1
|
|
20
|
1
|
0
|
14
|
21
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2
|
№п/п
|
пол
|
возраст
|
|
употр.ли
вы таб.изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
папа
|
употр.
ли род. Таб изд.
|
посещаете
ли вы ДПУ
|
какие
ДПУ
|
ответст.
Ли вы за общ. Работу
|
сильный
ли вы человек
|
Общ.ли
вы человек
|
сущ.ли
у вас пробл.в семье , шк.
|
простудн.
Заболев.
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
0
|
15
|
|
1
|
3
|
3
|
3
|
3
|
3
|
0
|
2
|
34
|
37
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
150
|
|
2
|
0
|
15
|
|
0
|
3
|
4
|
3,4
|
3
|
4,3
|
4
|
3
|
40
|
44
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
|
3
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
0
|
2
|
39
|
44
|
0
|
1
|
2
|
0
|
0
|
0
|
1
|
1
|
300
|
|
4
|
1
|
14
|
|
0
|
5
|
5
|
4,5
|
5
|
4
|
5
|
3
|
47
|
52
|
0
|
1
|
2
|
1
|
0
|
1
|
1
|
0
|
350
|
|
5
|
1
|
16
|
|
0
|
3
|
3
|
3,4
|
3
|
3
|
4
|
2
|
43
|
40
|
1
|
1
|
2
|
0
|
1
|
1
|
1
|
0
|
350
|
|
6
|
1
|
15
|
|
0
|
5
|
5
|
4,5
|
5
|
5
|
5
|
3
|
42
|
42
|
1
|
1
|
2
|
1
|
1
|
1
|
0
|
1
|
225
|
|
7
|
0
|
15
|
|
0
|
3
|
3
|
4
|
3
|
3
|
5
|
2
|
45
|
48
|
0
|
1
|
3
|
0
|
1
|
1
|
1
|
0
|
0
|
|
8
|
1
|
16
|
|
0
|
4
|
4
|
3
|
4
|
3
|
5
|
1
|
45
|
0
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
0
|
0
|
|
9
|
0
|
15
|
|
0
|
3
|
4
|
3,4
|
4
|
4
|
5
|
3
|
38
|
38
|
1
|
1
|
2
|
1
|
1
|
1
|
0
|
1
|
250
|
|
10
|
1
|
15
|
|
0
|
4
|
3
|
4
|
4
|
4
|
5
|
2
|
37
|
37
|
0
|
1
|
3
|
1
|
1
|
1
|
1
|
0
|
175
|
|
11
|
1
|
15
|
|
0
|
3
|
4
|
4
|
4
|
4
|
4
|
1
|
55
|
0
|
0
|
1
|
2
|
0
|
1
|
1
|
0
|
1
|
300
|
|
12
|
0
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
0
|
2
|
39
|
40
|
0
|
1
|
3
|
1
|
1
|
1
|
0
|
0
|
100
|
|
13
|
1
|
14
|
|
0
|
4
|
4
|
3
|
5
|
4
|
3
|
3
|
42
|
51
|
0
|
1
|
3
|
0
|
1
|
1
|
1
|
0
|
0
|
|
14
|
1
|
16
|
|
0
|
4
|
4
|
4
|
3
|
3
|
0
|
1
|
37
|
41
|
1
|
1
|
2
|
1
|
0
|
0
|
1
|
0
|
100
|
|
15
|
1
|
15
|
|
0
|
4
|
4
|
4
|
5
|
4
|
5
|
3
|
41
|
41
|
0
|
1
|
2
|
0
|
1
|
1
|
1
|
0
|
200
|
|
16
|
1
|
16
|
|
0
|
4
|
4
|
4,5
|
5
|
4
|
5
|
2
|
37
|
39
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
200
|
|
17
|
1
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
5
|
1
|
34
|
39
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
150
|
|
18
|
0
|
15
|
|
0
|
4
|
4
|
3
|
3
|
4
|
4
|
2
|
44
|
43
|
1
|
1
|
2
|
1
|
1
|
0
|
1
|
1
|
350
|
1
|
15
|
|
0
|
4
|
5
|
4
|
4
|
4
|
4
|
1
|
38
|
0
|
0
|
1
|
2
|
0
|
1
|
0
|
0
|
0
|
100
|
|
20
|
0
|
14
|
|
0
|
3
|
3
|
3
|
3
|
3
|
0
|
2
|
46
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
жен.
|
13
|
15,1
|
да
|
1
|
3,75
|
3,9
|
3,74
|
3,9
|
3,77
|
4,53
|
2,05
|
41,2
|
42,25
|
7
|
17
|
2,18
|
9
|
15,5
|
13
|
12
|
8
|
165
|
|
муж.
|
17
|
|
нет
|
19
|
|
|
|
|
|
|
|
|
|
13
|
3
|
|
11
|
1
|
7
|
8
|
12
|
|
Таблица 3
|
№п/п
|
пол
|
возраст
|
|
Употр.ли
вы таб.изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
папа
|
употр.
ли род. таб.. изд.
|
посещаете
ли вы ДПУ
|
Какие
ДПУ
|
ответст.
вы за общ. раб.
|
сильный
ли вы человек
|
Общ.ли
вы человек
|
сущ.
ли у вас пробл. в семье ,шк.
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
0
|
18
|
|
0
|
3
|
4
|
3
|
5
|
4
|
5
|
2
|
38
|
44
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
|
2
|
1
|
17
|
|
0
|
4
|
4,5
|
4
|
4
|
4
|
0
|
2
|
41
|
0
|
0
|
1
|
2
|
1
|
1
|
1
|
0
|
1
|
350
|
|
3
|
1
|
17
|
|
0
|
4
|
5
|
4,5
|
5
|
5
|
5
|
2
|
38
|
41
|
1
|
1
|
3
|
0
|
0
|
1
|
1
|
1
|
200
|
|
4
|
1
|
16
|
|
0
|
3
|
4
|
4
|
4
|
4
|
4
|
2
|
42
|
44
|
0
|
1
|
2
|
0
|
1
|
1
|
1
|
1
|
0
|
|
5
|
1
|
18
|
|
0
|
4
|
5
|
4
|
4
|
4
|
4
|
2
|
50
|
51
|
0
|
1
|
3
|
0
|
1
|
1
|
0
|
0
|
0
|
|
6
|
1
|
18
|
|
0
|
4
|
5
|
4,5
|
5
|
4
|
0
|
2
|
40
|
39
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
100
|
|
7
|
1
|
17
|
|
0
|
4
|
4
|
4
|
5
|
4
|
5
|
2
|
40
|
40
|
0
|
1
|
2
|
0
|
1
|
1
|
0
|
0
|
500
|
|
8
|
1
|
17
|
|
0
|
3
|
4,5
|
4
|
4
|
4
|
4
|
3
|
58
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
175
|
|
9
|
1
|
17
|
|
0
|
4
|
5,4
|
4
|
4
|
4
|
0
|
2
|
36
|
42
|
0
|
1
|
3
|
0
|
1
|
1
|
0
|
1
|
200
|
|
10
|
1
|
17
|
|
0
|
4
|
5
|
4
|
5
|
4
|
5
|
1
|
37
|
42
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
300
|
|
11
|
1
|
17
|
|
0
|
4
|
4
|
4
|
4
|
4
|
5
|
3
|
43
|
43
|
0
|
1
|
2
|
1
|
1
|
1
|
0
|
0
|
0
|
|
12
|
1
|
16
|
|
0
|
3
|
4
|
4
|
4
|
4
|
5
|
3
|
41
|
44
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
750
|
|
13
|
1
|
17
|
|
0
|
3
|
4
|
4
|
4
|
4
|
5
|
2
|
35
|
36
|
1
|
1
|
2
|
0
|
1
|
1
|
0
|
0
|
750
|
|
14
|
0
|
17
|
|
0
|
3
|
4
|
3
|
3
|
4
|
4
|
1
|
42
|
42
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
200
|
|
15
|
1
|
18
|
|
0
|
3
|
4
|
4
|
5
|
4,5
|
4,5
|
3
|
50
|
50
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
400
|
|
16
|
1
|
17
|
|
0
|
3
|
3
|
4
|
4,3
|
4
|
4
|
3
|
54
|
55
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
0
|
0
|
|
17
|
1
|
17
|
|
0
|
3
|
4
|
4
|
4
|
4
|
4
|
2
|
40
|
40
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
0
|
0
|
|
18
|
0
|
17
|
|
0
|
3
|
4
|
4
|
4
|
4
|
5
|
2
|
43
|
0
|
0
|
1
|
3
|
1
|
1
|
1
|
0
|
0
|
200
|
|
19
|
1
|
17,5
|
|
0
|
3
|
4
|
4
|
4
|
4
|
4
|
1
|
38
|
35
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
|
жен.
|
16
|
17,1
|
да
|
0
|
3,4
|
4,2
|
3,95
|
4,28
|
4,08
|
4,53
|
2,11
|
42,4
|
43
|
4
|
14
|
2,07
|
10
|
18
|
19
|
7
|
8
|
217,11
|
|
муж.
|
3
|
|
нет
|
19
|
|
|
|
|
|
|
|
|
|
15
|
5
|
|
9
|
1
|
0
|
12
|
11
|
|
Таблица 4
|
№п/п
|
пол
|
возраст
|
|
Употр.ли
вы таб.изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
папа
|
употребл.
ли род. таб. изд.
|
посещаете
ли вы ДПУ
|
какие
ДПУ
|
ответст.
ли вы за общ. Раб.
|
сильный
ли вы человек
|
Общ.ли
вы человек
|
сущ.
Ли у вас проблемы в семье,шк.
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
0
|
14
|
|
0
|
3
|
4
|
4
|
4
|
4
|
4
|
3
|
45
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
500
|
|
2
|
0
|
15
|
|
0
|
3
|
3
|
4
|
3
|
3
|
3
|
1
|
39
|
37
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
|
3
|
1
|
17
|
|
0
|
4
|
3
|
4
|
3
|
3
|
4
|
3
|
39
|
0
|
1
|
2
|
0
|
1
|
1
|
0
|
0
|
100
|
|
4
|
1
|
17
|
|
0
|
4
|
5
|
4
|
4
|
5
|
5
|
4
|
43
|
46
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
300
|
|
5
|
0
|
14
|
|
0
|
4
|
4
|
3
|
4
|
4
|
4
|
4
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
|
6
|
0
|
15
|
|
0
|
3
|
4
|
3
|
3
|
3
|
4
|
1
|
38
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
|
7
|
1
|
17
|
|
0
|
4
|
3
|
3
|
4
|
4
|
3
|
5
|
42
|
47
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
100
|
|
8
|
0
|
17
|
|
0
|
4
|
5
|
4
|
4
|
5
|
5
|
2
|
42
|
42
|
1
|
1
|
5
|
1
|
1
|
1
|
1
|
0
|
0
|
|
9
|
0
|
17
|
|
0
|
4
|
5
|
4
|
4
|
5
|
5
|
2
|
40
|
41
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
200
|
|
10
|
0
|
17
|
|
0
|
4
|
4,5
|
5,4
|
4
|
4
|
5
|
2
|
37
|
39
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
200
|
|
11
|
0
|
17
|
|
0
|
3
|
3
|
3
|
3
|
3
|
3
|
2
|
39
|
47
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
200
|
|
12
|
1
|
17
|
|
0
|
4
|
4,5
|
4,3
|
4
|
4
|
4
|
1
|
46
|
0
|
0
|
1
|
2
|
1
|
0
|
1
|
0
|
0
|
200
|
|
13
|
1
|
14
|
|
0
|
4
|
3
|
3
|
3
|
3
|
3
|
4
|
42
|
43
|
0
|
1
|
3
|
1
|
1
|
1
|
0
|
0
|
100
|
|
14
|
0
|
18
|
|
0
|
5
|
4
|
5
|
3,4
|
5
|
5
|
1
|
52
|
54
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
|
15
|
1
|
17
|
|
0
|
4
|
4
|
3
|
4
|
3
|
3
|
1
|
43
|
45
|
0
|
1
|
2
|
0
|
1
|
1
|
0
|
0
|
200
|
|
16
|
0
|
17
|
|
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
42
|
41
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
200
|
|
жен.
|
6
|
16,3
|
да
|
0
|
3,81
|
3,94
|
3,79
|
3,65
|
3,8
|
4
|
2,38
|
41,9
|
43,4
|
2
|
11
|
1,9
|
9
|
15
|
14
|
5
|
2
|
143,75
|
|
муж.
|
10
|
|
нет
|
16
|
|
|
|
|
|
|
|
|
|
14
|
5
|
|
7
|
1
|
2
|
11
|
14
|
|
Таблица 5
|
№п/п
|
пол
|
возраст
|
|
Употр.ли
вы таб.изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
кол-во
детей в семье
|
мама
|
папа
|
Употр.ли
род.таб.изд.
|
посещаете
ли вы ДПУ
|
какие
ДПУ
|
Ответст.ли
за общ.раб.
|
сильный
ли вы человек
|
Общ.ли
вы человек
|
сущ.
Ли у вас пробл. в семье шк.
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
1
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
34
|
44
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
175
|
|
2
|
0
|
15
|
|
0
|
3
|
3
|
3
|
3
|
3
|
3
|
2
|
36
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
100
|
|
3
|
1
|
15
|
|
1
|
5
|
4
|
4
|
5
|
4
|
0
|
2
|
40
|
42
|
0
|
1
|
3
|
1
|
1
|
1
|
1
|
0
|
750
|
|
4
|
1
|
15
|
|
0
|
4
|
3
|
4
|
3
|
3
|
5
|
1
|
32
|
32
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
75
|
|
5
|
0
|
14
|
|
0
|
3
|
3
|
3
|
5
|
4
|
4
|
2
|
33
|
0
|
0
|
1
|
3
|
0
|
0
|
1
|
0
|
0
|
0
|
|
6
|
0
|
14
|
|
0
|
3
|
3
|
3
|
4
|
3
|
5
|
1
|
33
|
34
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
100
|
|
7
|
1
|
14
|
|
0
|
4
|
3
|
4
|
4
|
3
|
0
|
1
|
38
|
41
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
200
|
|
8
|
0
|
14
|
|
0
|
3
|
3
|
3
|
3
|
3
|
4
|
3
|
38
|
42
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
50
|
|
9
|
0
|
15
|
|
0
|
3
|
3
|
3
|
4
|
3
|
5
|
2
|
44
|
43
|
0
|
0
|
1
|
2
|
1
|
0
|
0
|
0
|
100
|
|
10
|
1
|
14
|
|
0
|
5
|
4
|
5
|
4
|
4
|
3
|
2
|
32
|
33
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
100
|
|
11
|
1
|
14
|
|
0
|
4
|
4
|
3
|
4
|
4
|
5
|
4
|
49
|
0
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
0
|
100
|
|
12
|
0
|
14
|
|
0
|
3
|
3
|
4
|
3
|
4
|
4
|
3
|
39
|
39
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
100
|
|
13
|
1
|
14
|
|
0
|
4
|
3
|
3
|
4
|
4
|
4
|
2
|
34
|
38
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
175
|
|
14
|
0
|
15
|
|
0
|
3
|
4
|
3
|
2
|
3
|
4
|
1
|
36
|
39
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
|
15
|
1
|
14
|
|
0
|
3
|
3
|
3
|
3
|
3
|
2
|
36
|
39
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
500
|
|
16
|
0
|
14
|
|
0
|
3
|
3
|
3
|
3
|
3
|
3
|
2
|
33
|
33
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
150
|
|
17
|
1
|
15
|
|
0
|
4
|
3
|
4
|
4
|
3
|
4
|
3
|
33
|
36
|
0
|
1
|
2
|
1
|
1
|
1
|
0
|
0
|
200
|
|
18
|
0
|
14
|
|
0
|
4
|
3
|
4
|
3
|
3
|
5
|
2
|
40
|
43
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
100
|
|
19
|
1
|
14
|
|
1
|
3
|
4
|
3
|
4
|
3
|
4
|
3
|
40
|
38
|
0
|
1
|
2
|
0
|
1
|
1
|
1
|
1
|
200
|
|
20
|
1
|
13
|
|
0
|
3
|
3
|
4
|
3
|
4
|
4
|
2
|
42
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
200
|
|
21
|
0
|
14
|
|
0
|
3
|
3
|
3
|
3
|
3
|
3
|
2
|
36
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
100
|
|
22
|
1
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
33
|
37
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
200
|
|
23
|
1
|
14
|
|
0
|
3
|
3
|
4
|
3
|
3
|
5
|
1
|
41
|
37
|
1
|
1
|
2
|
0
|
0
|
0
|
1
|
1
|
100
|
|
жен.
|
13
|
14,3
|
да
|
2
|
3,52
|
3,3
|
4,83
|
3,57
|
3,89
|
4,05
|
2
|
37
|
38
|
8
|
11
|
1,82
|
10
|
20
|
19
|
10
|
4
|
164,13
|
|
муж.
|
10
|
|
нет
|
21
|
|
|
|
|
|
|
|
|
|
15
|
12
|
|
13
|
3
|
4
|
13
|
19
|
|
Таблица 6
|
№п/п
|
пол
|
возраст
|
|
Употр.ли
вы таб.изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
папа
|
Употр.ли
род.таб изд..
|
посещаете
ли вы ДПУ
|
какие
ДПУ
|
ответст.
Ли вы за общ. Раб.
|
сильный
ли вы человек
|
Общ.ли
вы человек
|
сущ.
ли у вас проблемы в семье ,шк.
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
0
|
16
|
|
0
|
3
|
4
|
4
|
4
|
3
|
5
|
2
|
38
|
40
|
0
|
1
|
2
|
1
|
1
|
1
|
1
|
0
|
30
|
|
2
|
0
|
16
|
|
0
|
3
|
4
|
4
|
4
|
4
|
4
|
2
|
45
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
100
|
|
3
|
0
|
16
|
|
0
|
0
|
4
|
4
|
4
|
4
|
4
|
2
|
0
|
46
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
100
|
|
4
|
0
|
|
0
|
0
|
0
|
0
|
0
|
4
|
0
|
3
|
45
|
45
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
70
|
|
5
|
0
|
16
|
|
0
|
3
|
4
|
4
|
3
|
4
|
4
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
100
|
|
6
|
0
|
16
|
|
1
|
0
|
0
|
0
|
0
|
0
|
4
|
3
|
36
|
37
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
150
|
|
7
|
0
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
50
|
51
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
100
|
|
8
|
0
|
16
|
|
0
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
200
|
|
9
|
0
|
16
|
|
0
|
5
|
4
|
5
|
5
|
5
|
5
|
1
|
40
|
0
|
1
|
1
|
2
|
0
|
1
|
1
|
1
|
0
|
200
|
|
10
|
1
|
16
|
|
0
|
4
|
4
|
3
|
4
|
4
|
4
|
2
|
37
|
37
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
500
|
|
11
|
0
|
16
|
|
0
|
3
|
3
|
3
|
4
|
3
|
3
|
3
|
46
|
45
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
50
|
|
12
|
1
|
15
|
|
0
|
4
|
3
|
3
|
3
|
3
|
4
|
3
|
35
|
38
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
100
|
|
13
|
0
|
17
|
|
0
|
4
|
4
|
4
|
4
|
5
|
4
|
3
|
48
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
14
|
1
|
16
|
|
0
|
4
|
4
|
4,5
|
4
|
4
|
5
|
3
|
47
|
47
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
250
|
|
15
|
1
|
16
|
|
0
|
3
|
4
|
3
|
3
|
3
|
3
|
1
|
38
|
38
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
300
|
|
16
|
1
|
16
|
|
0
|
4
|
4
|
3
|
4
|
4
|
4
|
3
|
42
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
250
|
|
17
|
1
|
16
|
|
0
|
4
|
5
|
5
|
5
|
5
|
5
|
3
|
50
|
50
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
200
|
|
18
|
1
|
16
|
|
0
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
44
|
45
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
200
|
|
19
|
1
|
17
|
|
0
|
5
|
5
|
5
|
4
|
5
|
4
|
2
|
38
|
41
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
200
|
|
20
|
16
|
|
0
|
4
|
4
|
5
|
4
|
5
|
5
|
3
|
40
|
42
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
350
|
|
21
|
0
|
16
|
|
0
|
4
|
4
|
5
|
5
|
5
|
5
|
1
|
47
|
47
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
150
|
|
22
|
0
|
17
|
|
0
|
3
|
4
|
4
|
4
|
3
|
5
|
1
|
42
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
50
|
|
жен.
|
9
|
16
|
да
|
1
|
3,79
|
4
|
4
|
4
|
4,05
|
4,24
|
2,32
|
42,53
|
43,2
|
5
|
3
|
|
10
|
20
|
20
|
5
|
6
|
165,91
|
|
муж.
|
13
|
|
нет
|
21
|
|
|
|
|
|
|
|
|
|
17
|
19
|
1,67
|
12
|
2
|
2
|
17
|
16
|
|
Таблица 7
|
№п/п
|
пол
|
возраст
|
|
Употр.ли
вы таб. изд.
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
папа
|
Употр.ли
род.таб.изд.
|
посещаете
ли вы ДПУ
|
какие
ДПУ
|
ответст.
Ли вы за общ. раб.
|
сильный
ли вы человек
|
Общ.ли
вы человек
|
Сущ.ли
у вас пробл.в семье,шк.
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
1
|
0
|
14
|
|
1
|
2
|
2
|
3
|
3
|
2
|
2
|
1
|
33
|
33
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
|
2
|
0
|
17
|
|
0
|
4
|
4
|
4
|
4
|
5
|
5
|
2
|
47
|
47
|
0
|
1
|
4
|
1
|
1
|
1
|
0
|
1
|
200
|
|
3
|
1
|
17
|
|
0
|
4
|
5
|
4
|
5
|
4
|
5
|
1
|
39
|
40
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
100
|
|
4
|
0
|
18
|
|
0
|
3
|
3
|
3
|
4
|
3
|
5
|
3
|
45
|
49
|
0
|
1
|
4
|
1
|
1
|
1
|
0
|
0
|
500
|
|
5
|
0
|
16
|
|
0
|
4
|
4
|
4
|
4
|
4
|
5
|
1
|
48
|
50
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
100
|
|
6
|
0
|
17
|
|
0
|
3
|
3
|
3
|
3
|
3
|
5
|
1
|
45
|
46
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
200
|
|
7
|
0
|
15
|
|
0
|
4
|
4
|
4
|
4
|
4
|
3
|
2
|
46
|
57
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
100
|
|
8
|
0
|
15
|
|
0
|
3
|
3
|
3
|
3
|
4
|
5
|
1
|
41
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
200
|
|
9
|
1
|
13
|
|
0
|
4
|
4
|
4
|
4
|
3
|
5
|
2
|
32
|
33
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
300
|
|
10
|
1
|
13
|
|
0
|
5
|
5
|
5
|
5
|
5
|
5
|
2
|
32
|
36
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
300
|
|
11
|
1
|
16
|
|
0
|
3
|
5
|
4
|
5
|
4
|
5
|
1
|
41
|
41
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
200
|
|
12
|
1
|
15
|
|
0
|
5
|
4
|
4
|
4
|
4
|
5
|
1
|
34
|
35
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
300
|
|
13
|
1
|
15
|
|
0
|
3
|
4
|
4
|
3
|
4
|
5
|
2
|
47
|
47
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
100
|
|
14
|
1
|
15
|
|
0
|
4
|
4
|
4
|
5
|
5
|
5
|
1
|
44
|
46
|
0
|
1
|
2
|
1
|
1
|
1
|
0
|
0
|
500
|
|
15
|
1
|
14
|
|
0
|
3
|
3
|
3
|
3
|
3
|
0
|
2
|
33
|
35
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
400
|
|
жен.
|
8
|
15,3
|
да
|
1
|
3,6
|
3,8
|
3,73
|
3,9
|
3,8
|
4,64
|
1,53
|
40,47
|
42,5
|
6
|
6
|
2,17
|
7
|
13
|
14
|
4
|
6
|
233,33
|
|
муж.
|
7
|
|
нет
|
14
|
|
|
|
|
|
|
|
|
|
9
|
9
|
|
8
|
2
|
1
|
11
|
9
|
|
Таблица 8
|
№п/п
|
пол
|
возраст
|
|
употр.ли
табач. Изделия
|
матем
|
рус.яз.
и литер.
|
физика
и химия
|
каз.яз
и литер.
|
история
|
физ-ра
|
кол-во
детей в семье
|
мама
|
ппапа
|
употребл.
Ли родители табач. Издел.
|
посещаете
ли вы ДПУ
|
какие
ДПУ
|
ответст.
Ли вы за общ. Работу
|
сильный
ли вы человек
|
Общит.ли
вы человек
|
сущ.
Ли у вас проблемы в семье или школе
|
простудн.
Заболевания
|
ежедневн.
Карман. Расходы
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
9
класс
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
13
|
15,1
|
да
|
1
|
3,75
|
3,9
|
3,74
|
3,9
|
3,77
|
4,53
|
2,05
|
41,2
|
42,25
|
7
|
17
|
2,18
|
9
|
16
|
13
|
12
|
8
|
165
|
|
муж.
|
17
|
|
нет
|
19
|
|
|
|
|
|
|
|
|
|
13
|
3
|
|
11
|
1
|
7
|
8
|
12
|
|
|
11
класс
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
16
|
17,1
|
да
|
0
|
3,42
|
4,3
|
3,95
|
4,28
|
4,08
|
4,53
|
2,11
|
42,4
|
43
|
4
|
14
|
2,07
|
10
|
18
|
19
|
7
|
8
|
217,11
|
|
муж.
|
3
|
|
нет
|
19
|
|
|
|
|
|
|
|
|
|
15
|
5
|
|
9
|
1
|
0
|
12
|
11
|
|
|
Колледж
9кл.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
6
|
16,3
|
да
|
0
|
3,81
|
3,9
|
3,79
|
3,65
|
3,88
|
4
|
2,38
|
41,9
|
43,42
|
2
|
11
|
1,91
|
9
|
15
|
14
|
5
|
2
|
143,75
|
|
муж.
|
10
|
|
нет
|
16
|
|
|
|
|
|
|
|
|
14
|
5
|
|
7
|
1
|
2
|
11
|
14
|
|
|
колледж.11кл.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
9
|
16
|
да
|
1
|
3,79
|
4
|
4,03
|
4
|
4,05
|
4,24
|
2,32
|
42,5
|
43,27
|
5
|
3
|
|
10
|
20
|
20
|
5
|
6
|
165,91
|
|
муж.
|
13
|
|
нет
|
21
|
|
|
|
|
|
|
|
|
|
17
|
19
|
1,67
|
12
|
2
|
2
|
17
|
16
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
15
|
16,1
|
да
|
0
|
3,93
|
4,1
|
3,77
|
4,14
|
4,05
|
4,48
|
1,71
|
44,4
|
45,67
|
10
|
23
|
1,74
|
4
|
23
|
24
|
10
|
3
|
273,96
|
|
муж.
|
9
|
|
нет
|
24
|
|
|
|
|
|
|
|
|
|
14
|
1
|
|
20
|
1
|
0
|
14
|
21
|
|
|
8
класс
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
13
|
14,3
|
да
|
2
|
3,52
|
3,3
|
4,83
|
3,57
|
3,89
|
4,05
|
2,04
|
37
|
38,33
|
8
|
11
|
1,82
|
10
|
20
|
19
|
10
|
4
|
164,13
|
|
муж.
|
10
|
|
нет
|
21
|
|
|
|
|
|
|
|
|
|
15
|
12
|
|
13
|
3
|
4
|
13
|
19
|
|
|
частн.шк.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жен.
|
8
|
15,3
|
да
|
1
|
3,6
|
3,8
|
3,73
|
3,93
|
3,8
|
4,64
|
1,53
|
40,5
|
42,5
|
6
|
6
|
2,17
|
7
|
13
|
14
|
4
|
6
|
233,33
|
|
муж.
|
7
|
|
нет
|
14
|
|
|
|
|
|
|
|
|
|
9
|
9
|
|
8
|
2
|
1
|
11
|
9
|
|
|
пол
|
возраст
|
|
|
хобби
|
сколько
времени уходит на интернет
|
кол-во
времени, которое уходит на развлечение
|
встречаетесь
ли вы с кем - нибудь
|
испытывали
ли вы чувство влюбленности
|
сколько
времени уходит на дом. Хлопоты
|
круг
общения
|
какие
места вы посещаете
|
время
разговоров по телефону
|
честно
ли отвечали на вопросы
|
средняя
успеваемость
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
1
|
17
|
|
11б
|
слушать
музыку
|
1-2ч
|
1ч
|
0
|
0
|
3ч
|
однокл.,
друзья
|
дома
|
10мин
|
1
|
4
|
|
1
|
17
|
|
11б
|
худож.,
спорт
|
3
ч
|
нет
|
0
|
1
|
2ч.
|
однокл.,
друзья
|
худож.
|
1ч
|
1
|
3,9
|
|
0
|
18
|
|
11б
|
много
|
2-3ч.
|
нет
|
0
|
1
|
2-3ч
|
однокл.,
друзья
|
школа,
секция
|
1
|
1
|
3,9
|
|
1
|
16
|
|
11б
|
танцы.
Спорт
|
1
раз в 3 нед
|
редко
|
0
|
0
|
2ч.
|
друзья.
Сверстники
|
везде
|
0
|
1
|
4,5
|
|
1
|
17
|
|
11б
|
петь.
Танцевать
|
3ч.
|
1ч.
|
0
|
0
|
8ч
|
однокл.,
друзья
|
кухня,
детская
|
5ч
|
1
|
4,1
|
|
0
|
16
|
|
11б
|
футбол,
компьют.
|
3-4ч
|
иногда
|
0
|
0
|
1ч
|
однокл.,
друзья
|
школа,
секция
|
1ч
|
1
|
3,8
|
|
0
|
17
|
|
11б
|
муз.книги.комп.англ.
|
35%
развл. 65% учеба
|
3ч
|
0
|
1
|
1,5
|
ранообразный
|
разные
|
0,5ч
|
0
|
4,2
|
|
0
|
17
|
|
11б
|
баскетбол.
Музыка
|
3ч.
|
2ч
|
0
|
1
|
-
|
однокл.,
друзья
|
-
|
1
|
3,8
|
|
0
|
17
|
|
11б
|
-
|
2-3ч.
|
-
|
1
|
1
|
-
|
однокл.,
друзья
|
-
|
-
|
0,5
|
4
|
|
1
|
17
|
|
11б
|
музыка
|
6ч
|
0,5
|
0
|
1
|
24ч
|
однокл.,
друзья
|
гуляю
|
много
|
1
|
3,7
|
|
1
|
17
|
|
11б
|
музыка,
бильярд
|
3ч.
|
1ч
|
0
|
1
|
3ч
|
однокл.,
друзья
|
кинотеатр
|
1ч
|
1
|
4
|
|
1
|
17
|
|
11б
|
читать,
музыка
|
-
|
-
|
0
|
0
|
4ч
|
однокл.,
друзья
|
кухня,
детская
|
-
|
1
|
4,6
|
|
1
|
17
|
|
11б
|
читать,
музыка
|
3-4ч
|
1ч
|
0
|
0
|
2-3ч
|
однокл.,
друзья
|
дома
|
1,5ч
|
1
|
4,2
|
|
1
|
17
|
|
11б
|
-
|
немного
|
2ч
|
0
|
1
|
8ч
|
однокл.,
друзья
|
кино,
кафе
|
1ч
|
1
|
3,9
|
|
1
|
17
|
|
11б
|
музыка
|
2-3ч.
|
1ч
|
0
|
1
|
2-3ч
|
однокл.,
друзья, соседи
|
кино,
кафе
|
2-3ч
|
1
|
3,7
|
|
0
|
17
|
|
11б
|
баскетбол,
гитара, комп.
|
8ч
|
3ч
|
0
|
1
|
2-3ч.
|
разн.
круг общения
|
разные
|
0,5ч
|
1
|
3,2
|
|
0
|
17
|
|
11б
|
гитара,
комп.музыка
|
12ч
|
0,25ч
|
1
|
1
|
1ч
|
однокл.
|
школа
|
1ч
|
1
|
3,3
|
|
1
|
17
|
|
11б
|
вышивание,рисование
|
2-3
дня
|
редко
|
0
|
1
|
2-3ч
|
однокл.
|
дома
|
1ч
|
1
|
4,1
|
|
0
|
17
|
|
11в
|
борьба,
плавание
|
5ч
|
0
|
0
|
0
|
0,5ч
|
друзья
по выпивке
|
бассейн,
подъзд
|
0,5ч
|
1
|
3,9
|
|
0
|
17
|
|
11в
|
нет
|
4ч
|
1ч
|
0
|
1
|
1,5
|
школа,
друзья, двор
|
двор
|
0,3
ч
|
1
|
3,4
|
|
1
|
17
|
|
11в
|
капоэйра,
интернет
|
6,5ч
|
3
|
1
|
1
|
2ч.
|
однокл.,друзья
|
тренировки,
улица
|
2ч
|
1
|
3,2
|
|
1
|
17
|
|
11в
|
большой
теннис, конный спорт
|
4ч
|
6ч
|
1
|
1
|
1ч
|
разнообразный
|
развлекательные
места
|
3ч
|
1
|
3,6
|
|
1
|
17
|
|
11в
|
рисование,
бассейн, курсы
|
1ч
|
0,5
|
1
|
1
|
2ч.
|
разнообразный
|
клубы,
кафе, кинотеатры, магазины
|
0,25ч
|
1
|
4
|
|
1
|
17
|
|
11в
|
гулять,
читать
|
3ч.
|
1-1,5ч
|
1
|
1
|
2ч.
|
друзья
в школе
|
аллейки,
гости
|
3ч
|
1
|
4,1
|
|
1
|
17
|
|
11в
|
музыка,
иностр.
|
3ч.
|
2ч
|
1
|
1
|
2ч.
|
друзья
|
кафе,
улица
|
3ч
|
1
|
4
|
|
0
|
17
|
|
11в
|
футбол,
компьют.
|
1ч
|
1ч
|
0
|
1
|
2ч.
|
с
однокл.
|
в
развл.центрах
|
мало
|
1
|
3,6
|
|
0
|
17
|
|
11в
|
футбол,
компьют.
|
2-3ч.
|
0,5ч
|
0
|
1
|
2-3ч.
|
со
всеми
|
разные
|
2ч
|
1
|
3,5
|
|
0
|
17
|
|
11в
|
конный
спорт
|
много
|
0
|
-
|
0
|
3ч
|
однокл.,
друзья
|
дома
|
мало
|
1
|
3,2
|
|
0
|
17
|
|
11в
|
футбол
|
5-6ч
|
0
|
1
|
6ч
|
0
|
большой
|
школа
|
-
|
1
|
3,3
|
|
1
|
18
|
|
11в
|
музыка
|
мало
|
1-3ч
|
0
|
1
|
1ч
|
друзья
|
как
придется
|
0,65ч
|
1
|
3,7
|
|
1
|
18
|
|
11в
|
муз.театр.искусство
|
2-4ч
|
-
|
0
|
1
|
0,25
|
родственники,
друзья
|
улицы
города
|
1ч
|
1
|
3,9
|
|
1
|
16
|
|
ходить
по магазинам
|
весь
день
|
3ч
|
0
|
1
|
6ч
|
однокл.
|
мега
и токсим
|
2,5ч
|
1
|
3
|
|
1
|
17
|
|
11в
|
все
понемногу
|
6ч
|
6ч
|
0
|
1
|
6ч
|
подруги
|
мега,
токсим
|
-
|
1
|
3,2
|
|
1
|
17
|
|
11в
|
танцы,
искусство, музыка
|
2ч
|
3ч
|
1
|
1
|
3ч
|
друзья,
родственники
|
дворец
школьн.,улица
|
2ч
|
1
|
4
|
|
1
|
17
|
|
11в
|
каратэ-до
|
2ч
|
2ч
|
0
|
1
|
2ч.
|
со
всеми
|
откр.помещения
|
1ч
|
1
|
4,1
|
|
1
|
16
|
|
11в
|
музыка
|
2-3ч.
|
3ч
|
0
|
1
|
2ч.
|
однокл.
|
по
разному
|
2-3ч
|
1
|
3,9
|
|
1
|
17
|
|
11в
|
коньки,
плавание
|
5ч
|
2-3ч
|
0
|
1
|
3-4ч
|
однокл,
друзья
|
мега,
парк,откр.пом.
|
1,5-2ч
|
1
|
3,5
|
|
1
|
17
|
|
11в
|
таэквон-до
|
6ч
|
3ч
|
0
|
1
|
2ч.
|
со
всеми
|
парк
|
6ч
|
1
|
3,4
|
|
1
|
17
|
|
11а
|
фотошоп
|
6ч
|
-
|
0
|
1
|
1ч
|
друзья
|
кафе,
улица
|
4ч
|
1
|
3,7
|
|
0
|
17
|
|
11а
|
вышивание,
книги
|
0ч
|
0ч
|
1
|
1
|
-
|
обширный
|
библиотека
|
1ч
|
1
|
4,7
|
|
0
|
18
|
|
11а
|
рэп,
футбол
|
3-4ч
|
-
|
0
|
1
|
1-2ч
|
друзья
|
спортзал
|
0,5ч
|
1
|
4,5
|
|
0
|
18
|
|
11а
|
баскетбол
|
1ч
|
-
|
0
|
1
|
-
|
-
|
-
|
3ч
|
0
|
4
|
|
1
|
17
|
|
11а
|
бассейн
|
2ч
|
-
|
0
|
1
|
2,5ч
|
одноклю,
друзья
|
парк
|
1ч
|
1
|
4,1
|
|
1
|
17
|
|
11а
|
танцы,рисов..футбол
|
2ч
|
-
|
1
|
1
|
3ч
|
друзья,
родители
|
дома
|
0,5
|
1
|
4
|
|
0
|
17
|
|
11а
|
технология,
худож.
|
1-2ч
|
-
|
0
|
1
|
3-4ч
|
однокл.,
друзья
|
казактелеком
|
0,75ч
|
1
|
4,3
|
|
1
|
17
|
|
11а
|
вышивание
крестиком
|
6ч
|
-
|
1
|
1
|
2ч.
|
широкий
|
нет
своб.врмени
|
2ч
|
1
|
3,8
|
|
1
|
17
|
|
11а
|
аппликация
|
6ч
|
-
|
0
|
1
|
3ч
|
широкий
|
нет
своб.времени
|
2ч
|
1
|
3,7
|
|
1
|
17
|
|
11а
|
музыка,
читать
|
3ч.
|
-
|
0
|
1
|
3ч
|
однокл.
|
нет
своб. времени
|
-
|
1
|
5
|
|
1
|
17
|
|
11а
|
музыка,
бассейн
|
5ч
|
-
|
0
|
1
|
2-3ч
|
однокл.
|
курсы
|
-
|
1
|
4,5
|
|
1
|
17
|
|
11а
|
-
|
7ч
|
-
|
1
|
1
|
2-3ч
|
однокл.друзья,семья
|
Дарын
|
0,3ч
|
1
|
4,8
|
|
1
|
17
|
|
11а
|
музыка
|
3ч.
|
-
|
0
|
0
|
3ч
|
друзья
детства
|
кафе,
улица
|
-
|
1
|
4,2
|
|
1
|
16
|
|
11а
|
рисование,музыка,кухня
|
2ч
|
-
|
0
|
0
|
1,5ч
|
одноклассники
|
торговые
дома
|
0,5
|
1
|
4,3
|
|
1
|
17
|
|
11а
|
музыка,
кино
|
6ч
|
-
|
0
|
1
|
3ч
|
однокл.друзья,семья
|
кинотеатр
|
0,5ч
|
1
|
3,9
|
|
1
|
17
|
|
11а
|
-
|
2ч
|
-
|
1
|
1
|
0
|
однокл.
|
курсы
|
5ч
|
0
|
3,4
|
|
1
|
17
|
|
11а
|
практ.,
бассейн
|
2ч
|
-
|
0
|
1
|
широкий
|
Дарын
|
0,2ч
|
1
|
4,6
|
|
0
|
17
|
|
11а
|
бассейн,
футбол
|
1ч
|
-
|
0
|
1
|
0,5ч
|
однокл.друзья,семья
|
школа
|
5ч
|
0
|
3,4
|
|
0
|
17
|
|
11а
|
футбол
|
3ч.
|
-
|
0
|
1
|
2ч.
|
друзья
|
спортзал
|
2ч
|
1
|
3,8
|
|
0
|
17
|
|
11а
|
музыка,
компьют.
|
5-6ч
|
-
|
0
|
1
|
2ч.
|
однокл.
|
школа
|
5-6ч
|
0
|
3,1
|
|
0
|
17
|
|
11а
|
-
|
6ч
|
-
|
0
|
0
|
0,6ч
|
-
|
-
|
2ч
|
1
|
3,3
|
|
|
|
да
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет
|
|
|
|
|
|
|
|
|
|
|
|
|
Отзыв
на научный проект ученицы 10 класса
многопрофильной средней школы №27 г. Актобе Сисембиной Карины «Математические
методы выявления зависимости успеваемости учащихся от табакокурения»
Тема научного проекта является актуальной, т.к.
касается вопросов успеваемости учащихся и направлена на выяснение причин,
связанных с изменением успеваемости учащихся в период школьного обучения в
старших классах.
Проект посвящен исследованию наличия зависимости
успеваемости учащихся старших классов от потребления табачных изделий. В работе
приводится описание метода линейной регрессии и применение этого метода для
обработки данных, полученных экспериментальным путем. На основании применения
этого метода автор выводит уравнение зависимости успеваемости от потребления
табачных изделий.
Кроме этого в работе представлены основные
теоретические сведения связанные с нелинейной и множественной регрессией, а
также применение их на практике в вопросах исследования взаимосвязи отдельных
факторов, которые, с точки зрения исследователя, могут оказывать влияние на успеваемость
учащихся. Проводится тщательный анализ и математическая обработка этих
вопросов.
Сисембина Карина самостоятельно разобралась в
таких вопросах как случайные события, случайные величины, распределение
случайной величины, регрессионный и корреляционный анализ и др. Провела
экспериментальную работу в нескольких классах. В решении поставленной задачи на
применение метода регрессионного анализа также самостоятельно нашла искомые
коэффициенты и сделала выводы.
Ее самостоятельным вкладом является вывод
уравнения зависимости успеваемости учащихся от потребления табачных изделий,
зависимости от посещения дополнительных занятий по предметам, зависимости от
наличия проблем в семье. С помощью нелинейного уравнения регрессии найдена
зависимость успеваемости учащихся от времяпровождения в сети Интернет, а также
уравнение зависимости множественной регрессии от двух факторов: времени
нахождения в сети Интернет и продолжительности телефонных разговоров в течение
дня.
Рассматриваемый проект удовлетворяет требованиям
к научным проектам, школьников, а Сисембина Карина заслуживает высокой оценки.
Ст. преподаватель Актюбинского
государственного педагогического
института А.З.Медведева
Абстракт
Научный проект ученицы 10 класса многопрофильной
средней школы №27 г. Актобе Сисембиной Карины «Математические методы
выявления зависимости успеваемости учащихся от табакокурения»
Цель исследования:
изучение математических методов, в частности регрессионного анализа, и
иллюстрация применения его на практике при решении поставленных задач.
Гипотеза:
если использовать математические методы при решении задач
социально-психологического плана, то это позволит найти определенные
закономерности и доказать наличие тех или иных причин в негативных явлениях.
Процедура исследования состояла из
следующих этапов:
а) разбор метода регрессионного анализа;
б) решение задачи на применение вышеназванного
математического метода.
Новизна исследования:
вывод уравнения зависимости успеваемости учащихся от потребления табачных
изделий, зависимости от посещения дополнительных занятий по предметам,
зависимости от наличия проблем в семье. С помощью нелинейного уравнения
регрессии найдена зависимость успеваемости учащихся от времяпровождения в сети
Интернет, а также уравнение зависимости множественной регрессии от двух
факторов: времени нахождения в сети Интернет и продолжительности телефонных
разговоров в течение дня.
Результаты работы и выводы:
Получено два уравнения регрессии
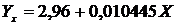 (1)
(1)
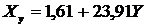 (2)
(2)
Коэффициенты 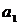 и
и 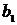 показывают,
на сколько в среднем величина одного признака, изменяется при изменении другого
признака на единицу меры.
показывают,
на сколько в среднем величина одного признака, изменяется при изменении другого
признака на единицу меры.
Иными словами, можно ответить на
вопрос задачи . Так, согласно уравнению (1) при показателе 100% не потребления
табачных изделий или другими словами, процент потребления табачных изделий в
данном случае равен 0%, то показатель уровня успеваемости равен 3,96 балла.
Если же показатель потребления табачных изделий равен 20%, а следовательно
показатель не потребления - 80%, то уровень успеваемости становится равным 3,8
балла, т.е уменьшается на 4%. Согласно уравнению (2) получаем, что повышения
количества учащихся, потребляющих табачные изделия до 27% снижает успеваемость
практически на 1 балл.
Выше было показано, что если
известны два коэффициента регрессии для обеих линий регрессий, то на их основе
можно получить коэффициент линейной корреляции между X и Y :
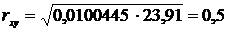 (3)
(3)
Кроме этого получены следующие
уравнения:
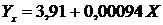 (4)
(4)
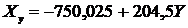 (5)
(5)
 (6)
(6)
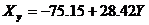 (7)
(7)
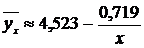 (8)
(8)
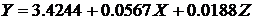 (9)
(9)
Области практического использования
результатов:
математические методы можно и нужно применять в различных исследованиях
различных спектров вопросов, что позволит учащимся более углубленно и вдумчиво
относится к самому предмету математики, как к прекрасному и совершенному
инструменту, позволяющему глубоко раскрыть корни тех или иных окружающих нас
явлений.