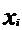
|
|
-5
|
-2
|
0
|
3
|
4
|
5
|
7
|
10
|
|
|
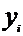
-31
|
-13
|
-2
|
12
|
16
|
20
|
30
|
40
|
Оценим математические ожидания, дисперсии, среднее квадратические
отклонения и коэффициент корреляции случайных величин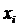 
и 
.
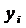Математические ожидания:
корреляционный регресионный математический
дисперсия
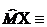
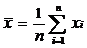и 
; 
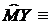
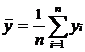
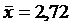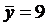
Несмещенные дисперси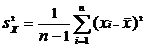и:
и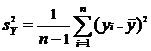 
; 
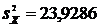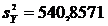
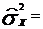
Смещенные дисперси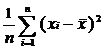и:
и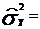 
; 
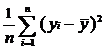
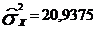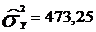
Несмещенные средние квадратические отклонения:
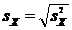и 
; 
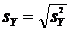
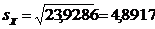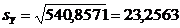
Смещенные средние квадратические отклонения:
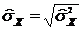и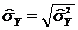 
; 
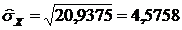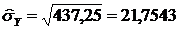
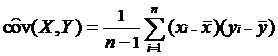
Подставив исходные данные, получаем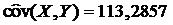 
. Оценка ковариации 
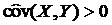, поэтому можно утверждать, что между
переменными существует прямая зависимость.
Теперь используем полученные данные оценки ковариации в нахождении
коэффициента корреляции: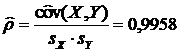 
. Оценка коэффициента корреляции характеризует силу связи
между параметрами. Так как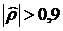 
устанавливаем, что сила связи между 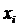и 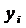весьма высокая. Определение оценки
коэффициента корреляции дает возможность проверки гипотезы о наличии линейной
статистической связи. Если гипотеза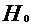 
о равенстве нулю коэффициента корреляции
будет отвергнута, то соответствующие величины связаны линейным соотношением,
если же она будет принята, тогда устанавливают, что величины линейно не связаны
друг с другом. В данной ситуации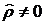 
, поэтому гипотеза 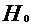отвергается.
Нанесем точки из таблицы на координатную плоскость (Рис. 1 Исходные
данные на координатной плоскости):
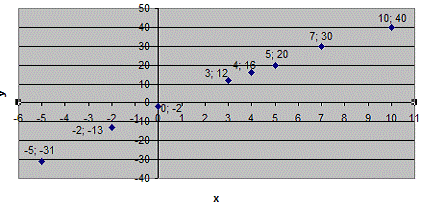
Рис. 1 Исходные данные на координатной плоскости
Построим регрессионную модель вида: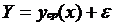 
.
Построение регрессионной модели заключается в оценивании параметров и
вида функции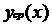 
, распределения и параметров случайной величины 
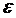, поэтому регрессионную модель
записывают в виде: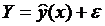 
, где конкретная зависимость 
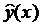называется эмпирическим уравнением
регрессии.
Для построения регрессионной модели в качестве эмпирического уравнения
регрессии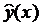 
выберем линейную функцию:
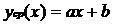. Если использовать прямой метод
построения линейных регрессионных моделей, тогда необходимо записать
эмпирическое уравнение регрессии следующим образом:
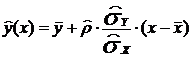- для уравнения Y на X;
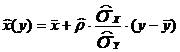- для уравнения X на Y, где 
, 
, 
, 
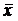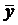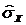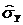и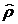 
были вычислены заранее.
Подставив все имеющиеся данные, вычисляем уравнение Y на X (Рис. 2 Графический метод построения линейных регрессионных
моделей):
;
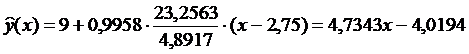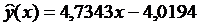
Уравнение X на Y (Рис. 2 Графический метод построения
линейных регрессионных моделей):
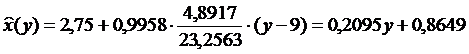
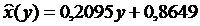
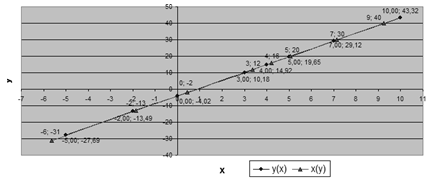
Рис. 2 Графический метод построения линейных регрессионных моделей
После построения линейных регрессионных моделей в качестве эмпирического
уравнения регрессии 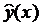выберем параболу 
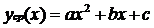и, используя метод наименьших
квадратов, находим коэффициенты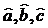 
, решая систему уравнений:
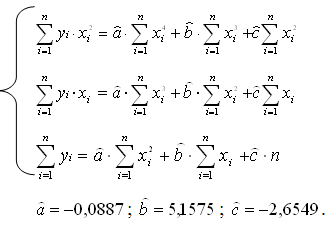
Уравнение параболической модели: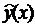 
=-0,0887
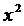+5,1575
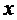-2,6549 (Рис. 3 Графический метод
построения параболической регрессионной модели)
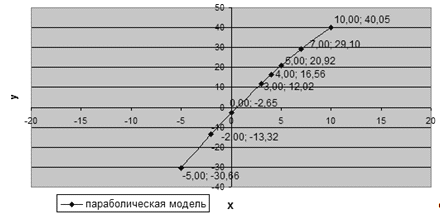
Рис. 3 Графический метод построения параболической регрессионной модели
Теперь оценим среднее квадратическое отклонение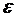 
для обеих моделей: и для линейной, и
для параболической.
Линейная модель (l=2, n=8):
1) 
,
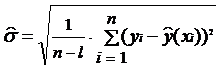где l - число неизвестных параметров
функции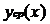 
;
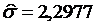2) 
,
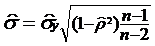где n - число исходных данных
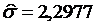
Параболическая модель (l=3, n=8):
,
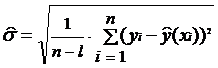подставив данные, получаем: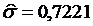 
Для параболической регрессии оценим корреляционное отношение. Прежде чем
это сделать, необходимо оценить величину, называемую коэффициентом детерминации
и характеризующую степень тесноты детерминированной связи:
,
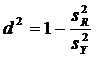причем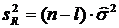 
и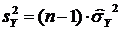 
. В корреляционном анализе вместо 
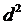пользуются оценкой корреляционного
отношения: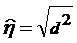 
, то есть
.
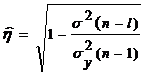Подставляем в формулу имеющиеся данные и получаем:
.
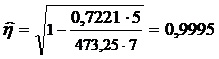Результат вычислений сравним с вычисленным ранее значением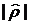 
. Так как 
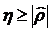, в качестве 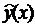можно брать нелинейную функцию.
На следующем этапе вычислений найдем доверительный интервал для условного
математического ожидания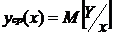 
с доверительной вероятностью 1-α=0,97 при предположении о нормальном
условном распределении случайной величины Y.
Сначала в качестве эмпирического уравнения регрессии 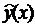выберем линейную модель с .
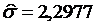Для вычисления доверительного интервала воспользуемся формулой:
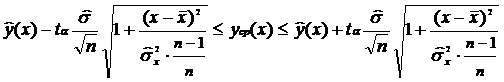
Итак, имеем следующие данные: 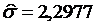; n=8; 
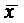=2,75; 
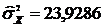. Так как в таблице квантилей распределения Стьюдента не дано
значения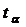 
соответствующего доверительной
вероятности 1-α, вычислим его самостоятельно, используя уравнение прямой,
проходящей через две точки: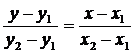 
.
Выберем в таблице значений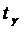 
два ближайших значения по отношению к
установленной доверительной вероятности γ=0,97: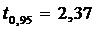 
и 
;
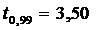γ=0,95 и γ=0,99
соответственно.
Подставим все имеющиеся данные в уравнение прямой, проходящей через две точки:
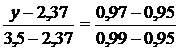, получаем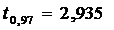 
После нахождения всех необходимых данных строим доверительный интервал
(Рис. 4 Доверительный интервал для условного математического ожидания на основе
линейной регрессионной модели)
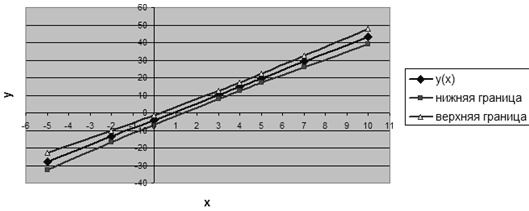
Рис. 4 Доверительный интервал для условного математического ожидания на
основе линейной регрессионной модели
Для построения доверительного интервала можно также использовать параболическую
модель с 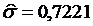(Рис. 5 Доверительный интервал для
условного математического ожидания на основе параболической модели)
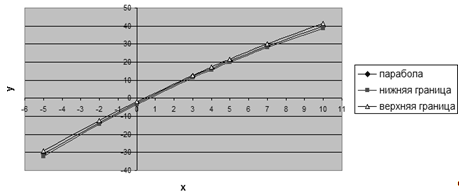
Рис. 5 Доверительный интервал для условного математического ожидания на
основе параболической модели
В исходных данных приведено значение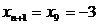 
, взятое из той же генеральной
совокупности. Рассчитаем доверительный интервал для условного математического
ожидания с доверительной вероятностью γ=0,97, употребляя указанное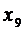 
:
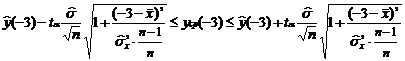
При использовании линейной модели 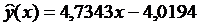, где ,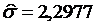 
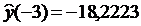, а также n=8, 
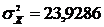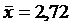, и 
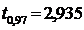, получаем следующий доверительный интервал:
-22, 0515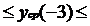
-14,3931
При использовании параболической модели 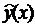=0,0887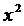+5,1575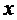-2,6549, где 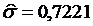и 
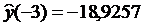, доверительный интервал: -20,129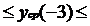-17,7224.
Таким образом, устанавливаем, что эти доверительные интервалы накрывают
истинное среднее значение изменения общего дохода филиала (в %) с вероятность
0,97. Можно сказать, что истинное среднее значение находится в этом интервале
(интервале, вычисленном по линейной модели или по параболической).
Регрессионные модели используются для косвенного оценивания значения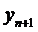 
по информации о значении 
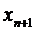, то есть при подстановке 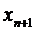в выражение 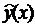мы оценили только среднее значение
величины y с некоторым доверительным интервалом:
-22, 0515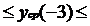-14,3931 (линейная регрессионная
модель), -20,129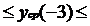-17,7224 (параболическая регрессионная модель).
Для того, чтобы получить оценку индивидуального значения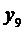 
необходимо определить толерантный
интервал, в который с заданной вероятностью р=0,95 и γ
=0,97 попадает значение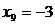 
:
,
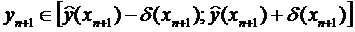где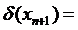 
, 
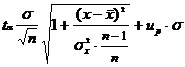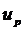- квантиль условного распределения 
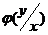, находящиеся по таблице.
Ф ()=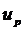
,
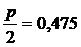то есть, используя таблицу, устанавливаем, что 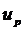=1,96.
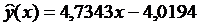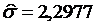Если в качестве регрессионной модели берется линейная модель , где и 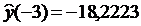, тогда толерантный интервал: -26,555
<
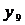< -9,8896.
Для нахождения толерантного интервала можно также использовать
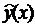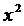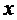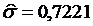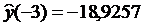параболическую регрессионную модель =0,0887+5,1575-2,6549 с и . В этом случае толерантный интервал
примет следующий вид: -21,5443 <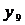< -16,3071.
Из проведенного выше анализа, можно сделать следующие выводы: изменение
объема продаж бытовой техники и изменение общего дохода филиала торговой сети
тесно взаимосвязаны. В ходе интервального оценивания было выяснено, что при
выполнении предсказания аналитиков, а именно спад объема продаж бытовой техники
в 2011 году на 3%, приведут к уменьшению общего дохода. Используя результаты
вычислений, с указанными ранее вероятностями, на основе линейной регрессионной
модели, можно установить, что уменьшение дохода будет находиться в диапазоне от
9,5% (точнее 9,8896%) до 26,5% (точнее 26,555%), по данным параболической
регрессионной модели - от 16,3% (точнее 16,3071%) до 21,5% (точнее 21,5443%).
Источники и
литература
. Маслов В.Н. Теория вероятностей и математическая
статистика: Учебное пособие. - ВВАГС, 1999.;
. Гмурман В.Е. Руководство к решению задач по теории
вероятностей и математической статистике: учеб. пособие. - 11-е изд., перераб.
- М.: Высшее образование, 2008.;
3. Колемаев В.А., Калинина В.Н. Теория вероятностей и
математическая статистика: Учебник / Под ред. В.А. Колемаева. - М.: ИНФРА-М,
1997.;
4. Статья "Применение корреляционно-регрессионного
метода в анализе финансового состояния организации"