Энергетические вещества тканей почки

Энергетические вещества тканей почки

Вопросы

1. Что изучает теория вероятностей

. Испытание. Событие. Классификация событий

.Понятие вероятности события. Классическое определение вероятности

. Относительная частота события. Статистическое определение вероятности

. Понятие комбинаторики. Основные правила комбинаторики

. Основные комбинаторные соединения

. Алгебра событий

. Условная вероятность. Теоремы умножения вероятностей

. Теоремы сложения вероятностей. Вероятность появления хотя бы одного события

. Формула полной вероятности

. Вероятность гипотез. Формула Байеса

. Формула Бернулли

. Формула Пуассона

. Наивероятнейшее число появления события

. Понятие и виды случайных величин

. Закон распределения вероятностей ДСВ. Способы задания

. Биноминальное распределение

. Пуассоновское распределение

. Геометрическое распределение

. Математическое ожидание ДСВ и его свойства

. Дисперсия ДСВ и её свойства. Формула для вычисления дисперсии. Среднее квадратическое отклонение

. Функция распределения вероятностей и её свойства

. Плотность распределения вероятностей и её свойства

. Числовые характеристики НСВ

. Равномерное распределение и его свойства

. Показательное распределение и его свойства

. Нормальное распределение и его свойства

. Правило трёх сигм. Центральная предельная теорема Ляпунова

. Закон больших чисел

. Задачи математической статистики

. Выборочный метод

. Типы выборок и способы отбора

. Вариационные ряды

. Эмпирическая функция распределения

. Полигон и гистограмма

. Точечные оценки параметров распределения

. Генеральная и выборочная средние

. Генеральная и выборочная дисперсии

. Оценка генеральной средней по выборочной средней

. Метод моментов для точечной оценки параметров распределения

. Метод наибольшего правдоподобия для точечной оценки параметров распределения

. Интервальные оценки параметров распределения

. Доверительные интервалы для параметров нормального распределения

. Виды зависимостей между случайными величинами

. Выборочные уравнения регрессии

. Коэффициент корреляции

. Линейная корреляция

. Статистическая гипотеза

. Виды ошибок

. Статистический критерий. Критическая область

. Сравнение выборочной средней с математическим ожиданием

. Сравнение двух дисперсий нормальных генеральных совокупностей

. Что изучает теория вероятностей

вероятность событие комбинаторика статистика

Теория вероятностей - это раздел математики, изучающий модели случайных явлений. Случайными явлениями называются явления с неопределенным исходом, происходящие при неоднократном воспроизведении определенного комплекса условий. Становление и развитие теории вероятностей связано с именами таких великих ученых, как: Кардано, Паскаль, Ферма, Бернулли, Гаусса, Чебышева, Калмогорова и многих других. Закономерности случайных явлений впервые были обнаружены в16 - 17 вв. на примере азартных игр, подобных игре в кости. Очень давно известны так же закономерности рождения и смерти. Например, известно, что вероятность новорожденному быть мальчиком ≈ 0,515. В 19-20 вв. было открыто большое число закономерностей в физике, химии, биологии и т. д. В настоящее время методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей. В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.

2. Испытание. Событие. Классификация событий

Испытание - это многократное воспроизведение одного и того же комплекса условий, при котором производится наблюдение. Качественный результат испытания - событие. Пример 1: В урне имеются цветные шары. Из урны на удачу берут один шар. Испытание - извлечение шара из урны; Событие - появление шара определенного цвета. О. 2: Множество взаимоисключающих исходов одного испытания называется множеством элементарных событий или элементарных исходов. Пример 2: Игральная кость подбрасывается один раз. Испытание - подбрасывание кости; Событие - выпадение определенного числа очков. Множество элементарных исходов - {1,2,3,4,5,6}. События обозначаются заглавными буквами латинского алфавита: А_1,А₂,…,А,В,С,… Наблюдаемые события (явления) можно подразделить на следующие три вида: достоверные, невозможные, случайные. О. 3: Событие называется достоверным, если в результате испытания оно обязательно произойдет. О. 4: Событие называется невозможным, если в результате испытания оно никогда не произойдет. О. 5: Событие называется случайным, если в результате испытания оно может либо произойти, либо не произойти. Пример 3: Испытание - мяч подбрасывается вверх. Событие A ={мяч упадет} - достоверное; Событие B={мяч зависнет в воздухе} - невозможное; Событие C={мяч упадет на голову бросавшему} - случайное. Случайные события (явления) можно подразделить на следующие виды: совместные, несовместные, противоположные, равновозможные. О. 6: Два события называются совместными, если при одном испытании, появление одного из них не исключает появление другого. О. 7: Два события называются несовместными, если при одном испытании, появление одного из них исключает появление другого. Пример 4: Монета подбрасывается два раза. Событие A - {Первый раз выпал герб}; Событие B - {Второй раз выпал герб}; Событие C - {Первый раз выпал орел}. События A и B - совместные, A и C - несовместные. О. 8: Несколько событий образуют полную группу в данном испытании, если они попарно несовместны и в результате испытания одно из этих событий обязательно появится. Пример 5: Мальчик бросает монетку в игральный автомат. Событие A ={мальчик выиграет}; Событие B={мальчик не выиграет}; A и B - образуют полную группу событий. О. 9: Два несовместных события, образующих полную группу называются противоположными. Событие противоположное событию A обозначается 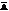. Пример 6. Делается один выстрел по мишени. Событие A - попадание; Событие 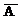 - промах.

О. 10: События называются равновозможными, если есть основания считать, что одно из них не является более возможным, чем другое. Пример 7: В урне содержится 10 шаров: 5 синих и 5 красных. Наудачу извлекается один шар. Событие A ={извлеченный шар красный}; Событие B={извлеченный шар синий}; A и B - равновозможные события.

3. Понятие вероятности события. Классическое определение вероятности

,

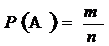где n - общее число элементарных событий, - число элементарных событий благоприятствующих событиюA. Пример 1. Даны числа от 1 до 30. Наудачу выбирается одно число. Найти вероятность того, что это число является делителем 30.Решение: n=30, А={1,2,3,5,6,10,15,30}, m=8, 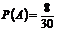. Свойства вероятности. Вероятность достоверного события A равна единице, т. к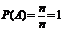; Вероятность невозможного событияA равна нулю, т. к. 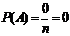; Вероятность случайного событияA есть положительное число, заключенное между нулем и единицей, т. к. 0<m<n, то 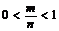. Недостатки классического определения. 1. Определение не применимо, если число элементарных исходов испытания бесконечно.

4. Относительная частота события. Статистическое определение вероятности

Часто не возможно представить результат испытания в виде совокупности элементарных событий. 3. Трудно указать основания, позволяющие считать события равновозможными. О равновозможности исходов опыта заключают из соображений симметрии. Для преодоления 3 недостатка вводятся статистические вероятности, а для преодоления 1 недостатка - геометрические (вероятности попадания точки в область). Рассмотрим более подробно понятие статистической вероятности. 3. Статистическое определение вероятности. Относительная частота события

Пусть произошло n испытаний, причем в этих испытаниях событие A появилось m раз. Число m называют абсолютной частотой события A. О. 3. Относительной частотой P*(A) события A называется отношение числа испытаний, в которых событие A появилось к общему числу проведенных испытаний

,

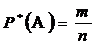где n - общее число испытаний, m - число появлений событияA. Пример 2. Среди 1000 новорожденных оказалось 515. Чему равна частота рождения мальчиков. Событие A - родился мальчик. Относительная частота события A: .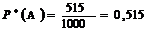

Вероятность события может быть посчитана без проведения испытания, а относительная частота считается только в том случае, если испытание проведено фактически. Если в одинаковых условиях проводят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает следующее свойство: в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. О. 4. (статистическое определение) Вероятностью события A в данном испытании называется число P(A), около которого группируется значения относительной частоты P*(A) при больших n Р(А)≈Р*(А) прип→∞. Недостатки статистического определения. Неоднозначность статистической вероятности.

5. Понятие комбинаторики. Основные правила комбинаторики

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества.

Использование формул комбинаторики значительно облегчает проведение расчетов в теории вероятностей. 2. Основные правила комбинаторики Пусть А₁,А₂,…,А_k - это элементы заданного конечного множества. Правило суммы: Если элемент A₁ можно выбрать n₁ способами, A₂ можно выбрать n₂ способами, A_n можно выбрать n_k способами отличными от всех предыдущих, то выбор 1-го из элементов А1,А2,…,Аk может быть осуществлен n₁+n₂+…+n_k способами. Пример 1. В коробке 20 шаров, причем 5 из них красные, 6 синие, а остальные зеленые. Сколько существует способов извлечь из ящика 1 шар или красного или синего цвета. Решение: n₁+n₂=5+6=11. Правило произведения: Пусть элемент A₁ можно выбрать n₁ способами, после каждого такого выбора элемент A₂ можно выбрать n₂ способами, после (k-1) - го выбора элемент A_nможно выбрать n_k способами, тогда выбор всех элементов в указанном порядке может быть осуществлен n₁∙n₂∙…∙n_k способами. Пример 2. В конкурсе участвуют 10 человек. Для определения порядка выступления конкурсантов проводят жеребьевку. Сколькими способами можно выбрать трех человек для выступления под номерами 1,2,3. Решение: n₁∙n₂∙n₃ = 10∙9∙8=720

6. Основные комбинаторные соединения

Пусть дано множество из n элементов. Из этого множества могут быть составлены подмножества (комбинации) по m элементов 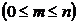 трех основных видов: 1. перестановки; 2. размещения; 3. сочетания. Перестановки (m=n) О. 1. Перестановками без повторений называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их следования. Число всевозможных перестановок без повторений P_n=n! Пример 3. Сколько пятизначных чисел можно составить из цифр: числа 12345. 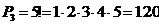Решение:  О. 2. Перестановками с повторениями называются перестановки, в которых из общего числа n элементов имеется только k различных элементов, причем 1-й элемент повторяется n₁ раз, 2-й элемент повторяется n₂ раз, k-й элемент повторяется n_k раз ().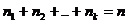

Число всевозможных перестановок с повторениями

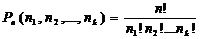
Пример 4. Сколько пятизначных чисел можно составить из цифр числа 12213. Решение: 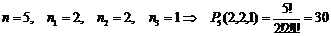.